<3年p.306>
動かして考えよう ◁P.212
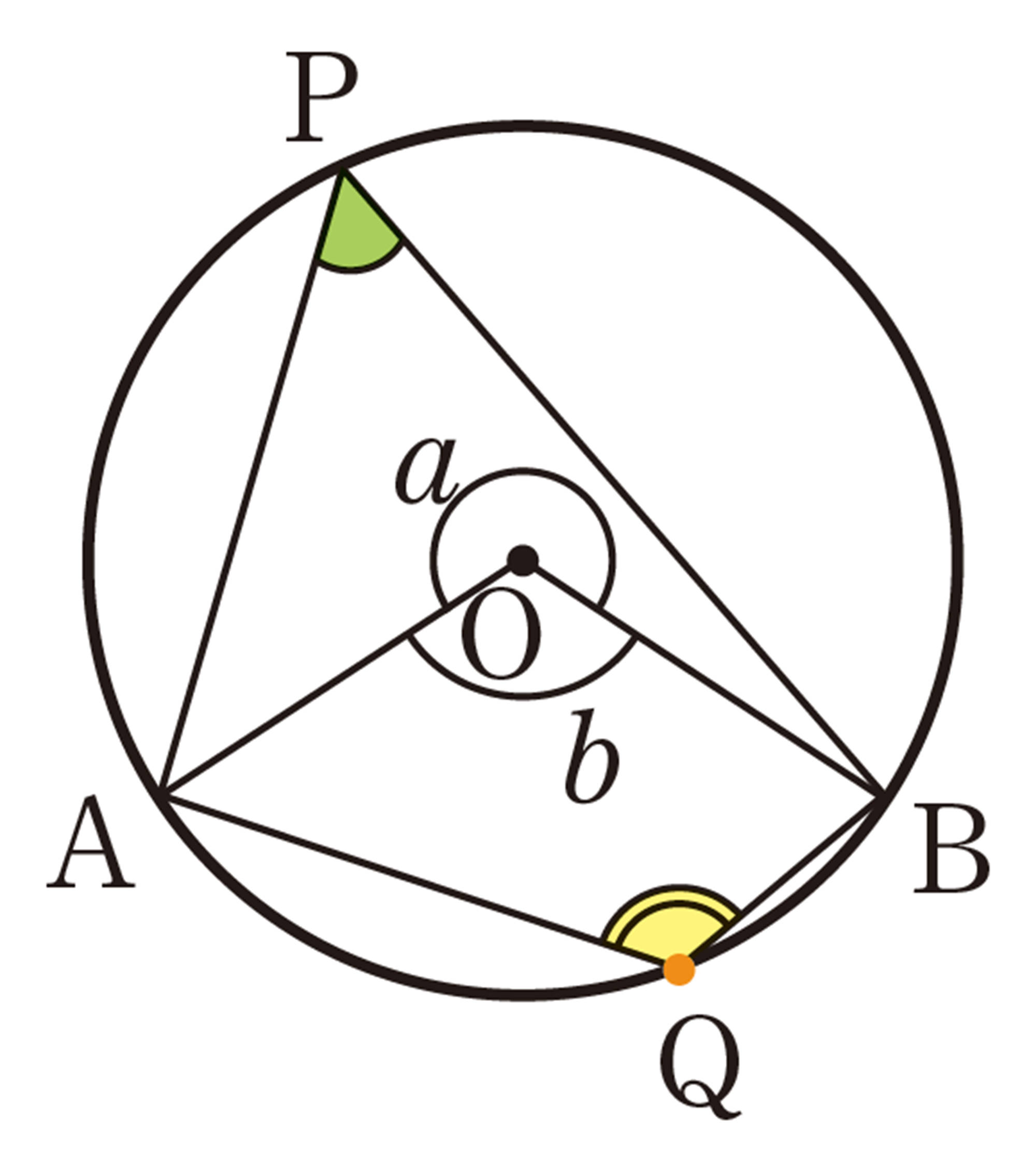
① [mathjax]\(\angle APB = \angle AQC\)
② [mathjax]\(\angle APB + \angle AQB = 180^{\circ}\)
③（例）AとO，BとOをそれぞれ結ぶ。
右の図のように，円周角が[mathjax]\(\angle Q\)のときの弧に対する中心角を[mathjax]\(\angle a\)，円周角が[mathjax]\(\angle P\)のときの弧に対する中心角を[mathjax]\(\angle b\)とすると，
[mathjax]\(\angle Q = \dfrac{1}{2} \angle a\)，[mathjax]\(\angle P = \dfrac{1}{2} \angle b\)
[mathjax]\(\angle a + \angle b = 360^{\circ}\)であるから，
7章 三平方の定理 [解答]
トライ ◁P.220
略
トライ ◁P.229
略
7章のまとめの問題 ◁P.236〜238
基本
１
⑴ [mathjax]\(c=\sqrt{17}\)
⑵ [mathjax]\(b=2 \sqrt{3}\)
２
⑴ いえる
⑵ いえない
⑶ いえない
⑷ いえる
３
[mathjax]\(AB=\sqrt{13}\)，[mathjax]\(BC=\sqrt{13}\)，[mathjax]\(CA=\sqrt{26}\)
([mathjax]\(\angle B = 90^{\circ}\)の)直角二等辺三角形
４
⑴ 高さ…[mathjax]\(\sqrt{7}\)cm，体積…[mathjax]\(12\sqrt{7}\)cm³
⑵ 84cm²
５
⑴ 点B…直角三角形[mathjax] \(OAA´\)をかき，斜辺[mathjax] \(OA´\)と等しい長さでOBをとる。
点C…直角三角形[mathjax] \(OBB´\)をかき，斜辺[mathjax] \(OB´\)と等しい長さでOCをとる。
⑵ 2
⑶
応用
１
[mathjax]\(12\sqrt{3}\)cm²
２
[mathjax]\(\dfrac{7}{8}\)cm
３
340 m
４
⑴ 12cm
⑵ [mathjax]\(\triangle ABH\)と[mathjax]\(\triangle ADC\)において，仮定から，[mathjax]\(\angle AHB = 90^{\circ}\)
半円の弧に対する円周角は[mathjax]\(90^{circ}\)だから，
[mathjax]\(\angle ACD = 90^{\circ}\)
したがって，[mathjax]\(\angle AHB = \angle ACD \quad \cdots \cdots\mathsf{①}\)
[mathjax]\(\stackrel{\huge\frown}{AC}\)に対する円周角は等しいから，
[mathjax]\(\angle ABH = \angle ADC \hspace{50pt} \cdots \cdots\mathsf{②}\)
①，②より，2組の角がそれぞれ等しいから，
[mathjax]\(\triangle ABH \backsim \triangle ADC\)
⑶ [mathjax]\(\dfrac{65}{8}\)cm
活用
１
① ㋐，㋑の長さを測定し，三平方の定理を使って，[mathjax]\(a=\sqrt{AC²-CB²}\)として求める。
② ㋐，㋑，㋒の長さを測定し，三平方の定理を使って， [mathjax]\(b=\sqrt{AE²-ED²}+\sqrt{EB²-ED²}\)として求める。
２
⑴ 約[mathjax]\(6.9\)m
⑵ 約[mathjax]\(6.9\)m
３
㋐，㋑，㋒の長さを測定し，三平方の定理を使って，[mathjax]\(c=\sqrt{AE²-ED²}-\sqrt{GE²-ED²}\)として求める。
約[mathjax]\(2.3\)m
釣瓶岳から富士山が撮影できた？ ◁P.239
① 約233km
② 約113m
8章 標本調査 [解答]
8章のまとめの問題 ◁P.254〜255
１
適切であるとはいえない。
(理由) インターネットのあるサイトを利用した調査であり，サイトにアクセスする人の男女比や年齢層などの分布が，日本国民の分布と同じであるとはいえないため。
２
推定した値は略。実際の母平均は，[mathjax]\(7.715\)秒より，約[mathjax]\(7.7\)秒
