<3年p.290>
3年の復習
1章 式の計算
1 次の計算をしなさい。
⑴ [mathjax]\(-4a(2a-7)\)
⑵ [mathjax]\((5x+3y) \times 2y\)
⑶ [mathjax]\((8a+4b) \times \dfrac{3}{2}a\)
⑷ [mathjax]\((-15x²+10x)\div 5x\)
⑸ [mathjax]\((9a²b-6ab²) \div 3ab\)
⑹ [mathjax]\((-12xy+3y²) \div \require{physics} \left(-\dfrac{3}{4}y\right)\)
2 次の式を展開しなさい。
⑴ [mathjax]\((2x-3y)(3x+5y)\)
⑵ [mathjax]\((a-3b)(2a+b-5)\)
⑶ [mathjax]\((x-8)(x+5)\)
⑷ [mathjax]\((a+5)²\)
⑸ [mathjax]\((x-2y)²\)
⑹ [mathjax]\(\require{physics} \left(y+\dfrac{1}{2}\right)\require{physics} \left(y-\dfrac{1}{2}\right)\)
⑺ [mathjax]\((2a-b-6)(2a-b+1)\)
⑻ [mathjax]\((x-y-4)²\)
3 次の計算をしなさい。
⑴ [mathjax]\((x-6)²-(x+8)(x-3)\)
⑵ [mathjax]\((x-7)(x-2)-(x-3)(3+x)\)
4 次の式を因数分解しなさい。
⑴ [mathjax]\(ax-2bx\)
⑵ [mathjax]\(4x²y+3xy²-xy\)
⑶ [mathjax]\(x²-5x-14\)
⑷ [mathjax]\(x²-6x+8\)
⑸ [mathjax]\(x²-8xy+16y²\)
⑹ [mathjax]\(4x²+20x+25\)
⑺ [mathjax]\(16a²-49b²\)
⑻ [mathjax]\(\dfrac{x²}{9}-\dfrac{y²}{16}\)
⑼ [mathjax]\(3x²+12x+9\)
⑽ [mathjax]\(-3xy²+12x\)
⑾ [mathjax]\((x+3)²-5(x+3)-6\)
⑿ [mathjax]\(a(x-2)+b(x-2)\)
⒀ [mathjax]\(ab-4a-4b+16\)
5 [mathjax]\(a=37\),[mathjax]\(b=12\)のとき,[mathjax]\(a²-9b²\)の値を求めなさい。
6 次の式をくふうして計算しなさい。
⑴ [mathjax]\(14²-112+4²\)
⑵ [mathjax]\(0.98 \times 1.02\)
7 3の倍数より1大きい数の2乗から,同じ3の倍数より1小さい数の2乗をひいた差は,12の倍数になることを証明しなさい。
<3年p.291>
2章 平方根
1 次の数の平方根を求めなさい。
⑴ [mathjax]\(49\)
⑵ [mathjax]\(13\)
⑶ [mathjax]\(\dfrac{9}{64}\)
⑷ [mathjax]\(0.36\)
2 次の数を,根号を使わずに表しなさい。
⑴ [mathjax]\(\sqrt{121}\)
⑵ [mathjax]\(-\sqrt{25}\)
⑶ [mathjax]\(\sqrt{(-0.16)²}\)
⑷ [mathjax]\((-\sqrt{7})²\)
3 次の問いに答えなさい。
⑴ 次の数を小さい順に並べなさい。
5,[mathjax]\(-\sqrt{15}\),[mathjax]\(-\sqrt{20}\),[mathjax]\(\sqrt{24}\),[mathjax]\(-4\)
⑵ 次の数を,有理数と無理数に分けなさい。
[mathjax]\(\sqrt{144}\),[mathjax]\(-\sqrt{13}\),[mathjax]\(\dfrac{\pi}{2}\),[mathjax]\(-\sqrt{\dfrac{1}{4}}\),[mathjax]\(\dfrac{5}{2}\)
4 次の計算をしなさい。
⑴ [mathjax]\(\sqrt{2} \times \sqrt{6}\)
⑵ [mathjax]\(2\sqrt{10} \times 4\sqrt{5}\)
⑶ [mathjax]\(\sqrt{270} \div \sqrt{6}\)
⑷ [mathjax]\(6\sqrt{14} \div 3\sqrt{21}\)
5 [mathjax]\(\sqrt{7}=2.646\),[mathjax]\(\sqrt{70}=8.367\)として,次の数の近似値を求めなさい。
⑴ [mathjax]\(\sqrt{700}\)
⑵ [mathjax]\(\sqrt{7000}\)
⑶ [mathjax]\(\sqrt{0.7}\)
⑷ [mathjax]\(\sqrt{252}\)
6 次の計算をしなさい。
⑴ [mathjax]\(10 \sqrt{13} + 3 \sqrt{13}\)
⑵ [mathjax]\(4 \sqrt{6} – 6 \sqrt{2} + 3 \sqrt{6}\)
⑶ [mathjax]\(\sqrt{27} – 5 \sqrt{3}\)
⑷ [mathjax]\(\sqrt{24} – 4 \sqrt{6} + \sqrt{54}\)
⑸ [mathjax]\(4 \sqrt{5} – \dfrac{10}{\sqrt{5}}\)
⑹ [mathjax]\(\sqrt{50} – \dfrac{8}{\sqrt{2}} + \sqrt{72}\)
7 次の計算をしなさい。
⑴ [mathjax]\(\sqrt{6} \times \sqrt{10} – \dfrac{3 \sqrt{5}}{\sqrt{3}}\)
⑵ [mathjax]\(\sqrt{3}(4\sqrt{6} +2 \sqrt{3})\)
⑶ [mathjax]\((\sqrt{6} – \sqrt{3})²\)
⑷ [mathjax]\((\sqrt{7} – 2)(\sqrt{7} + 5) – \dfrac{7} {\sqrt{7}}\)
8 半径4cmの円と半径8cmの円があります。この2つの円の面積の和に等しい面積の円をつくるには,半径を何cmにすればよいですか。
<3年p.292>
3章 2次方程式
1 次の方程式を解きなさい。
⑴ [mathjax]\((x-1)(x+8)=0\)
⑵ [mathjax]\(x(x+4)=0\)
⑶ [mathjax]\(x²+6x-27=0\)
⑷ [mathjax]\(x²-9x+18=0\)
⑸ [mathjax]\(x²-3x-40=0\)
⑹ [mathjax]\(x²-18x+81=0\)
⑺ [mathjax]\(9x²-25=0\)
⑻ [mathjax]\(x²-3x+5=-8x-1\)
⑼ [mathjax]\((x+4)(x-4)=-6x\)
⑽ [mathjax]\((x-6)(x+8)=-13\)
2 次の方程式を解きなさい。
⑴ [mathjax]\(x²-18=0\)
⑵ [mathjax]\(6x²=150\)
⑶ [mathjax]\(x²-\dfrac{1}{3}=0\)
⑷ [mathjax]\(9x²-8=0\)
⑸ [mathjax]\((x+3)²=28\)
⑹ [mathjax]\((x-6)²-24=0\)
3 次の方程式を,解の公式を使って解きなさい。
⑴ [mathjax]\(x²+3x+1=0\)
⑵ [mathjax]\(x²-6x+3=0\)
⑶ [mathjax]\(4x²-3x-2=0\)
⑷ [mathjax]\(2x²+x-1=0\)
⑸ [mathjax]\(3x²+4x-2=0\)
⑹ [mathjax]\(-2x²=3x-9\)
<3年p.293>
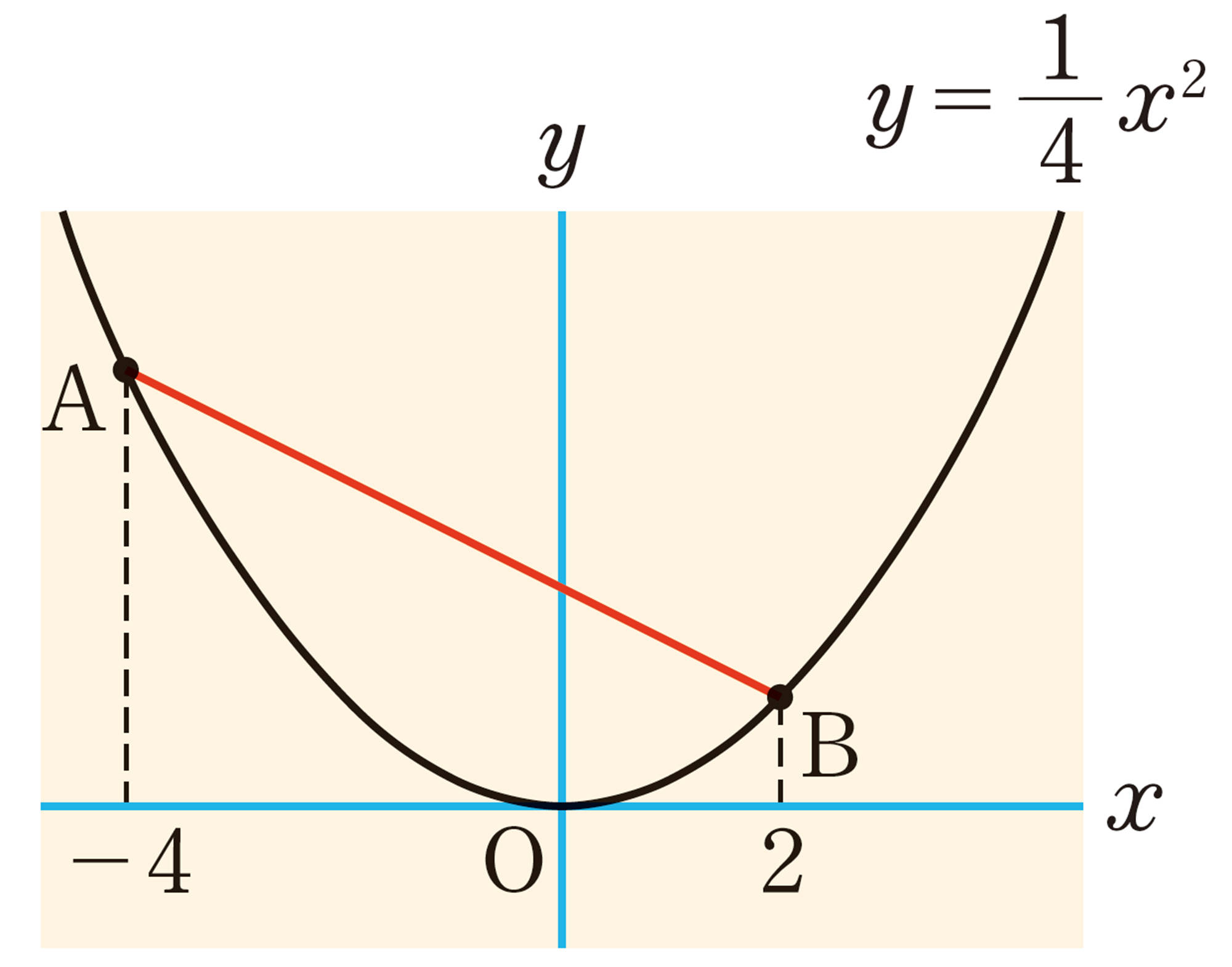
4章 関数 [mathjax]\(y=ax²\)
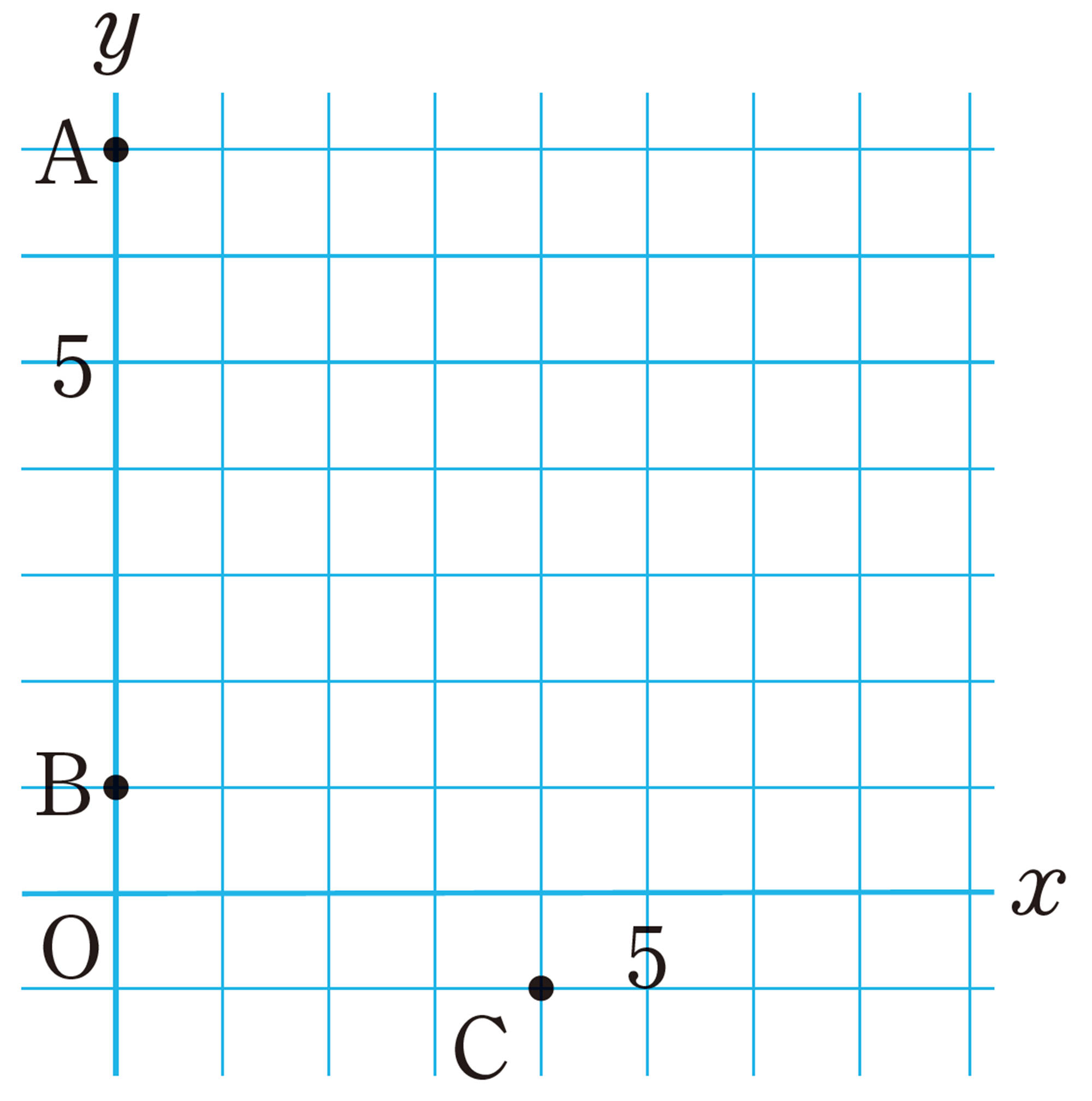
1 次の問いに答えなさい。
⑴ yはxの2乗に比例し,[mathjax]\(x=-4\)のとき,[mathjax]\(y=4\)です。yをxの式で表しなさい。また,[mathjax]\(x=6\)のときのyの値を求めなさい。
⑵ 関数[mathjax]\(y=ax²\)のグラフが点[mathjax]\((3,-6)\)を通るとき,aの値を求めなさい。
⑶ 放物線[mathjax]\(y=-4x²\)と,x軸について対称な放物線の式を答えなさい。
⑷ 関数[mathjax]\(y= \dfrac{1}{2}x²\)で,xの変域が[mathjax]\(-6 \leqq x \leqq 4\)のときのyの変域を求めなさい。
2 次の問いに答えなさい。
⑴ 関数[mathjax]\(y= \dfrac{2}{3}x²\)で,xの値が[mathjax]\(-6\)から[mathjax]\(-3\)まで変化するときの変化の割合を求めなさい。
⑵ 関数[mathjax]\(y=ax²\)で,xの値が1から5まで変化するとき,変化の割合は18です。aの値を求めなさい。
4 周期[mathjax]\((\)1往復するのにかかる時間[mathjax]\()\)がx秒の振り子のひもの長さをymとすると,xとyの間には,およそ[mathjax]\(y=\dfrac{1}{4}x²\)の関係があります。次の問いに答えなさい。
⑴ 周期が2秒の振り子のひもの長さは約何mですか。
⑵ 振り子のひもの長さが4mのとき,周期は約何秒ですか。
⑶ ⑴の振り子の周期を6秒にするには,振り子のひもの長さを約何m長くすればよいか求めなさい。
<3年p.294>
5章 相似な図形
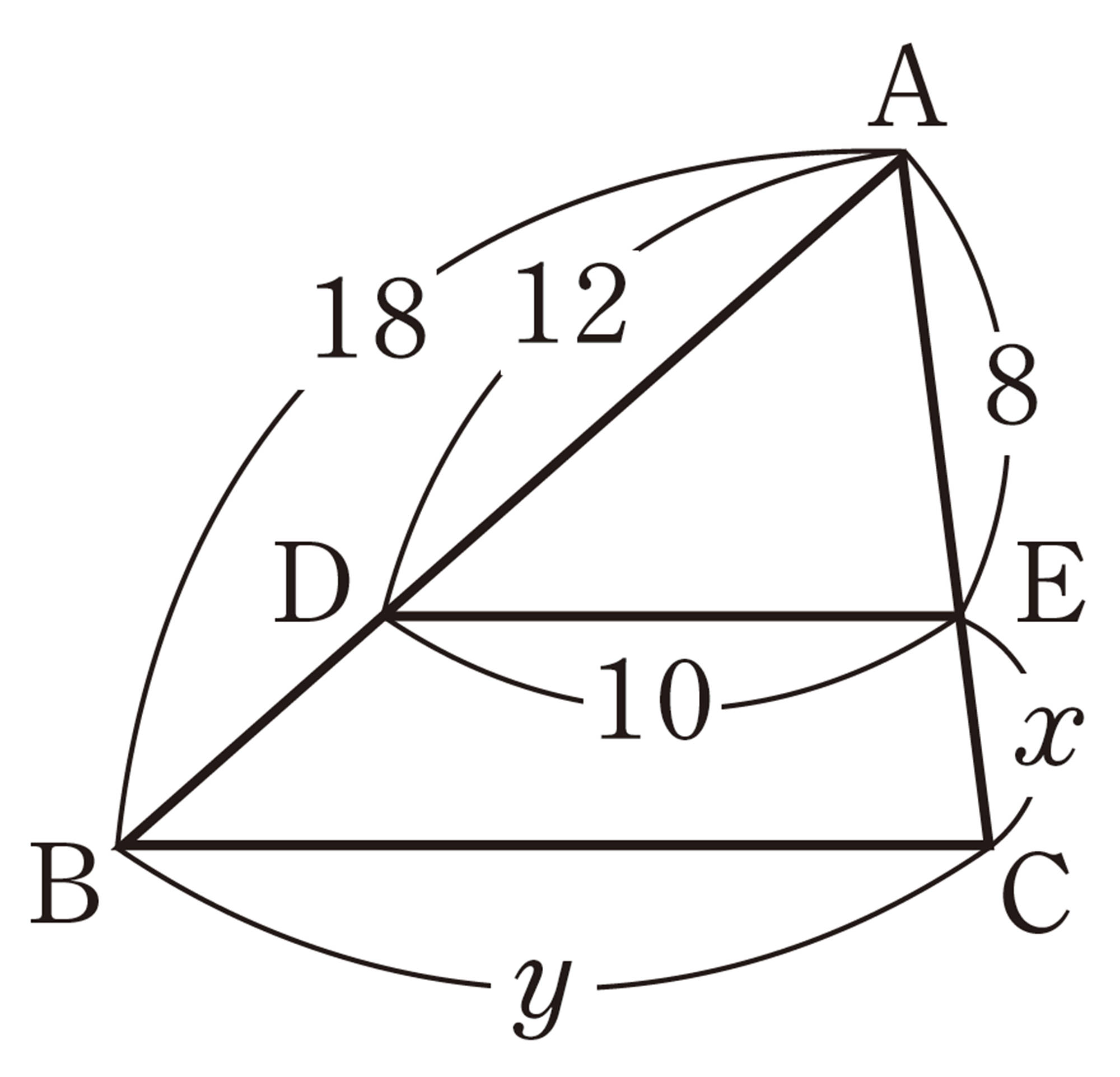
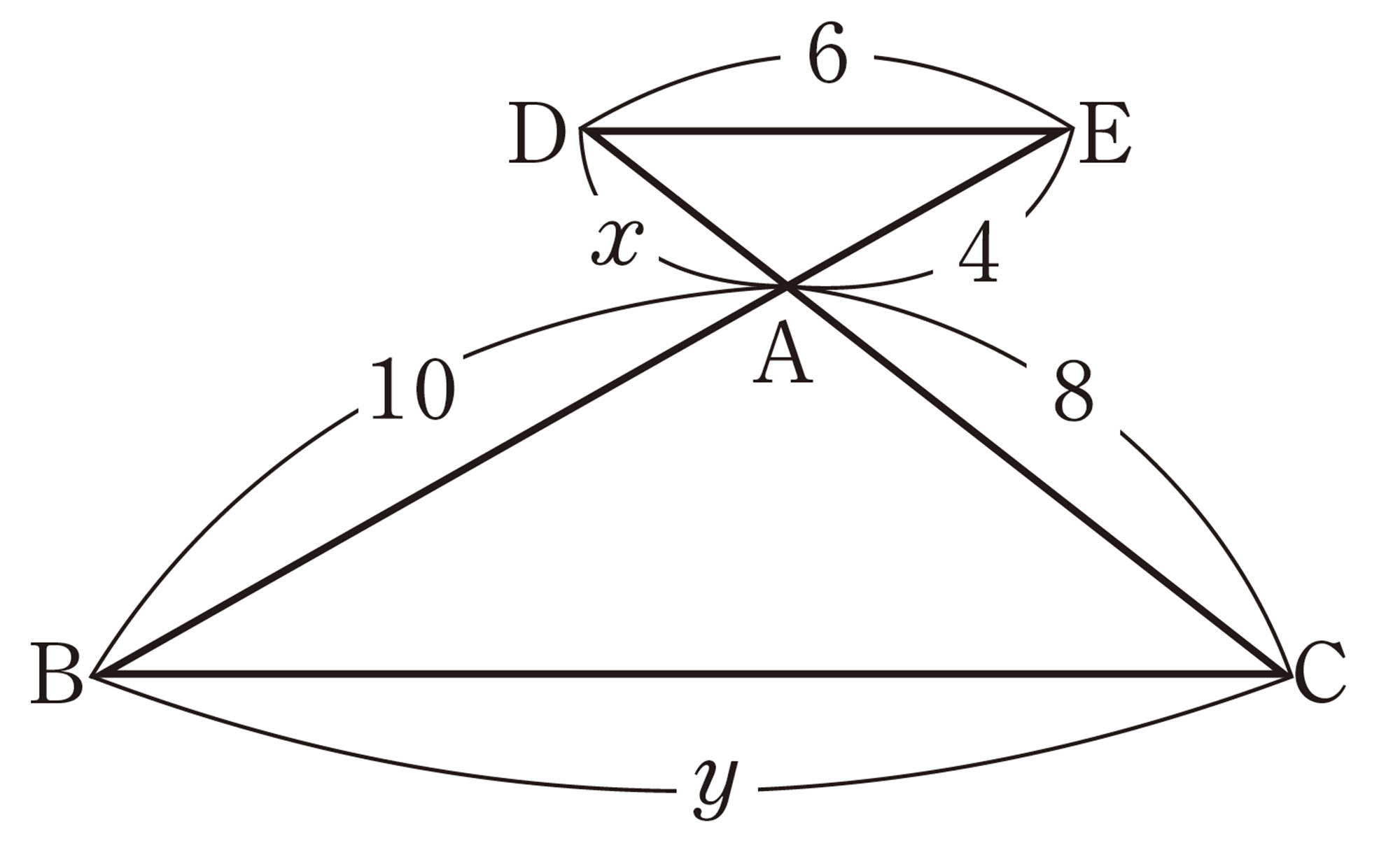
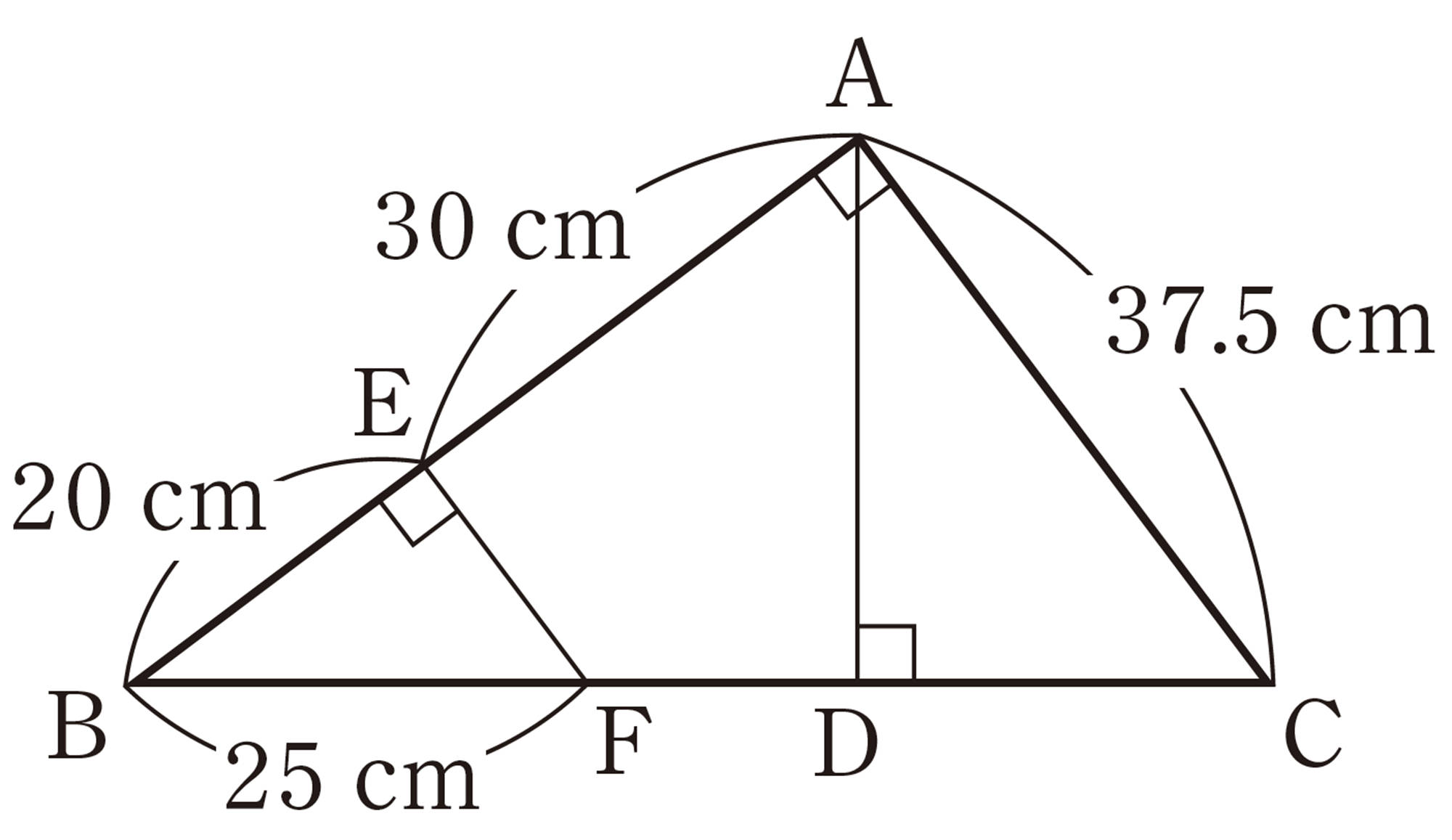
1 次の図で,[mathjax]\(BC /\!/ DE\)であるとき,x,yの値を求めなさい。
3 芽衣さんが身長を測ったところ,小数第二位を四捨五入して得られた測定値は,[mathjax]\(157.4\)cmでした。このとき,真の値をacmとして,aの範囲を不等号を使って表しなさい。また,誤差の絶対値は何cm以下となりますか。
<3年p.295>
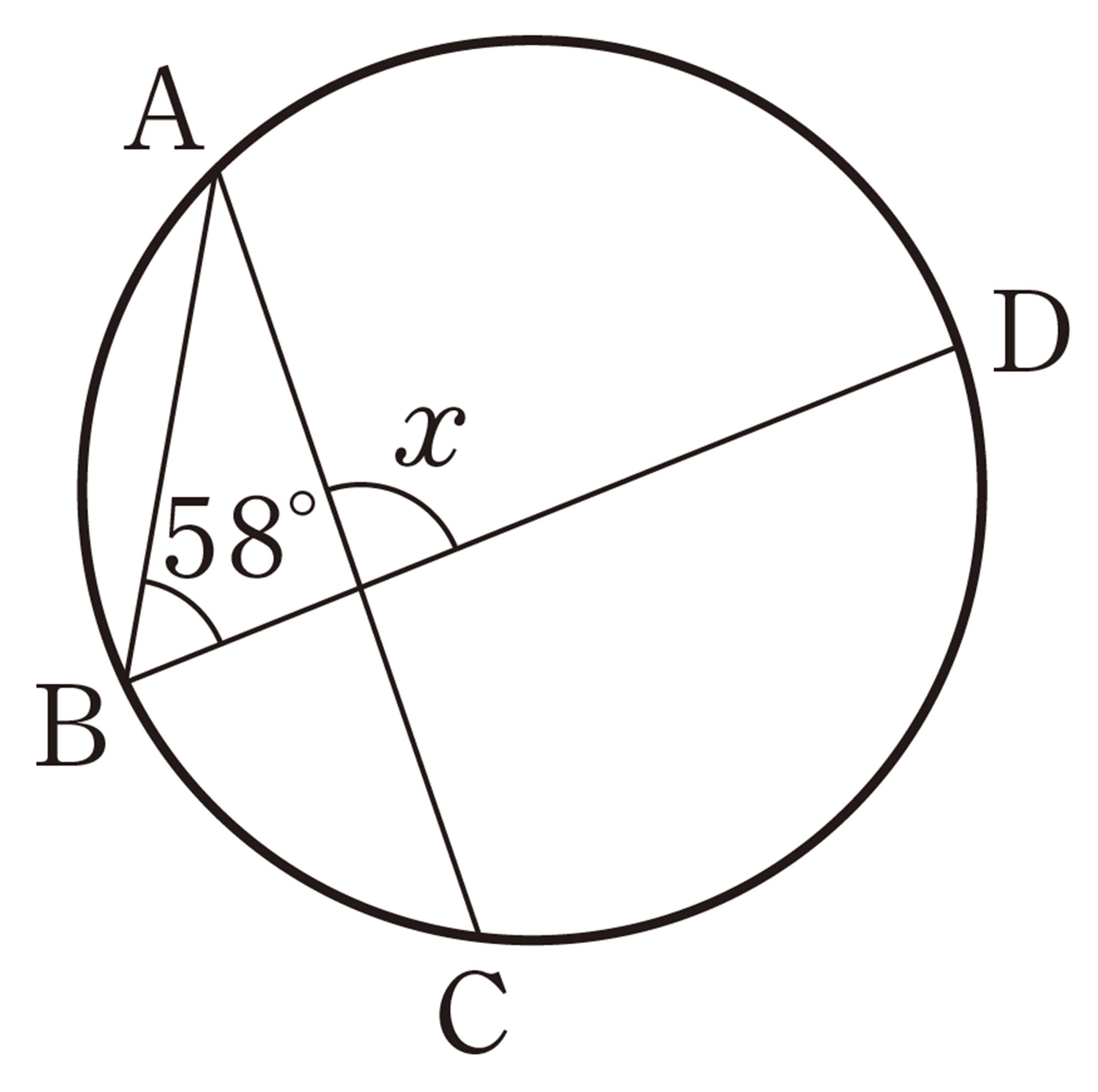
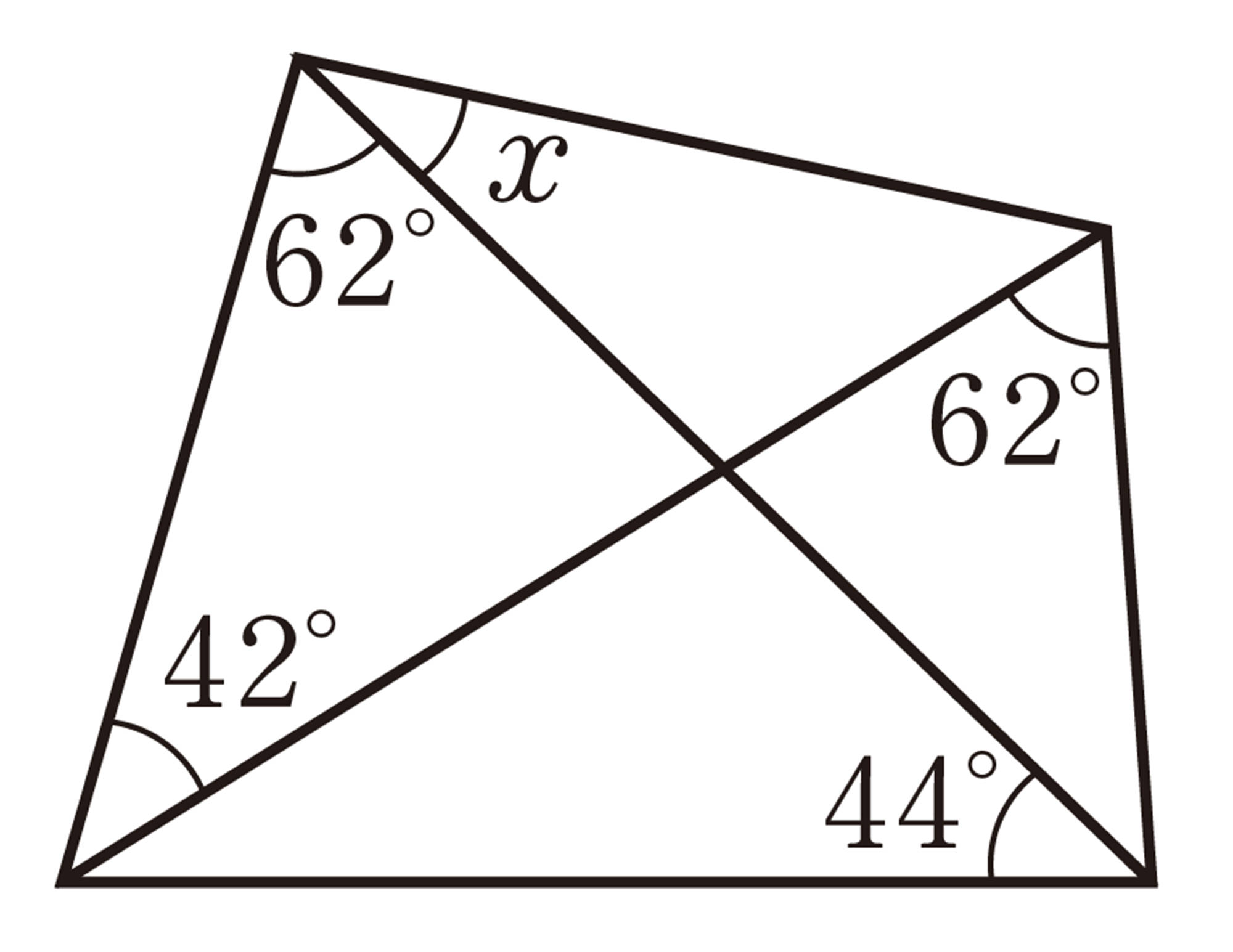
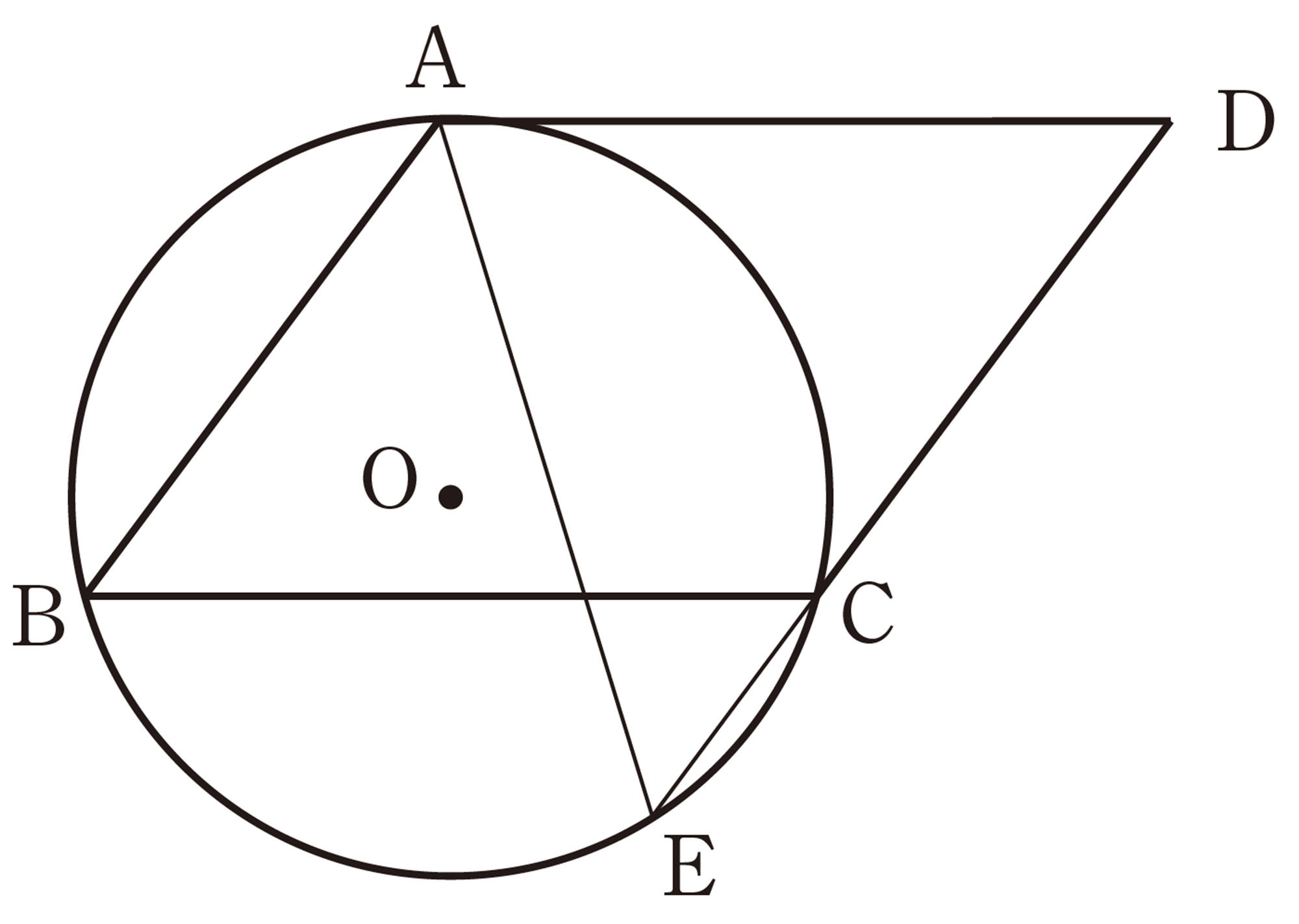
6章 円
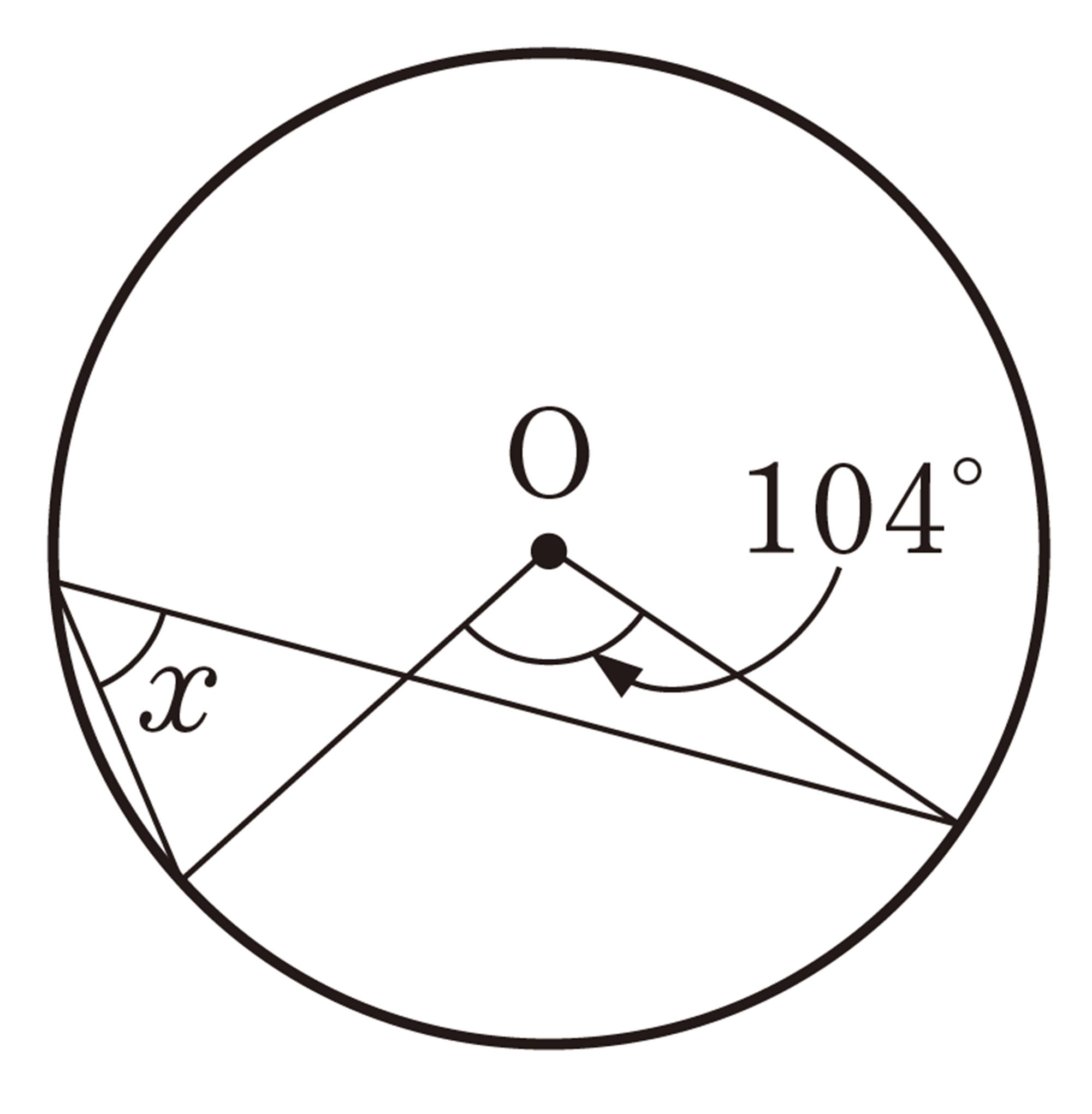
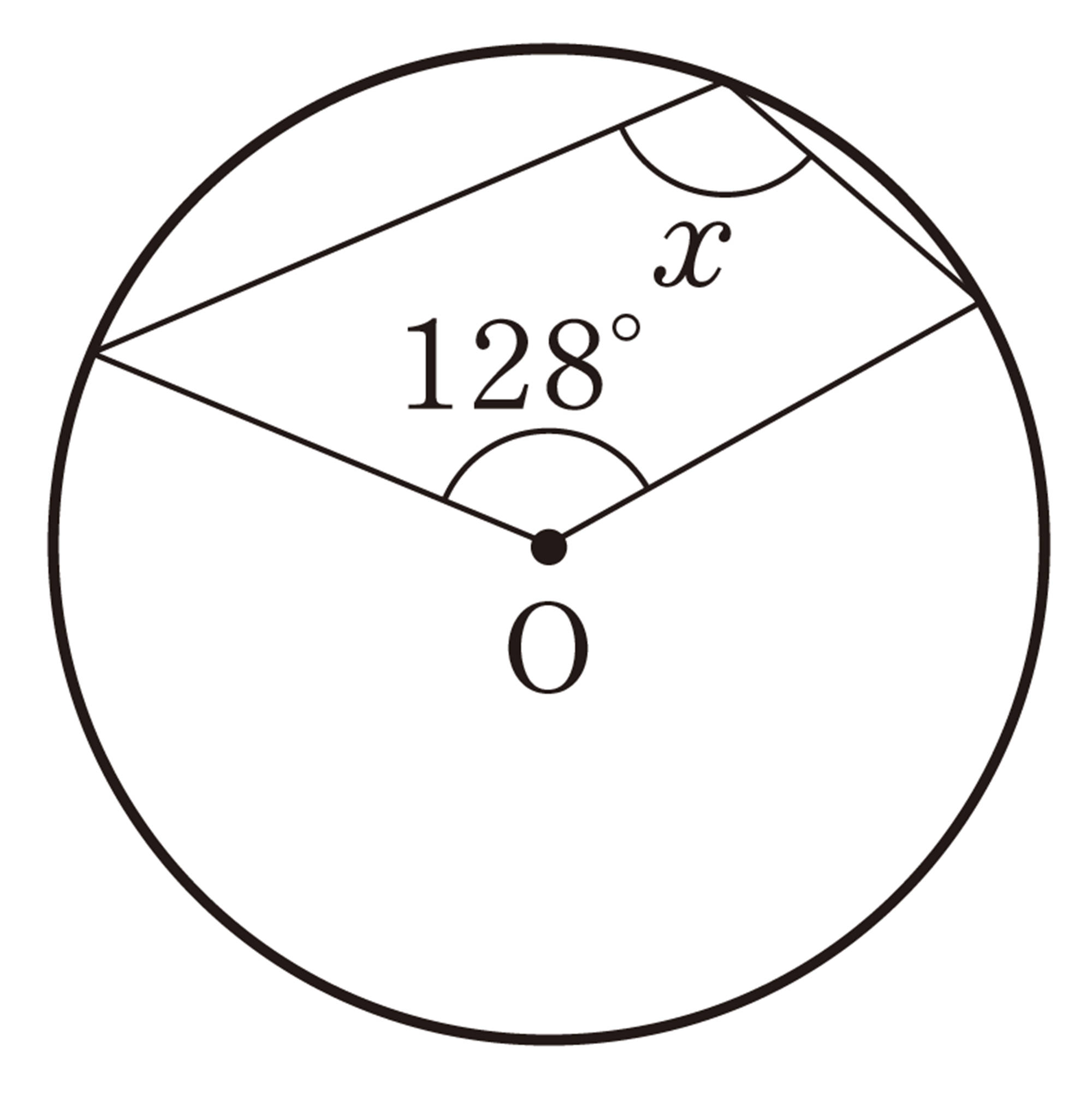
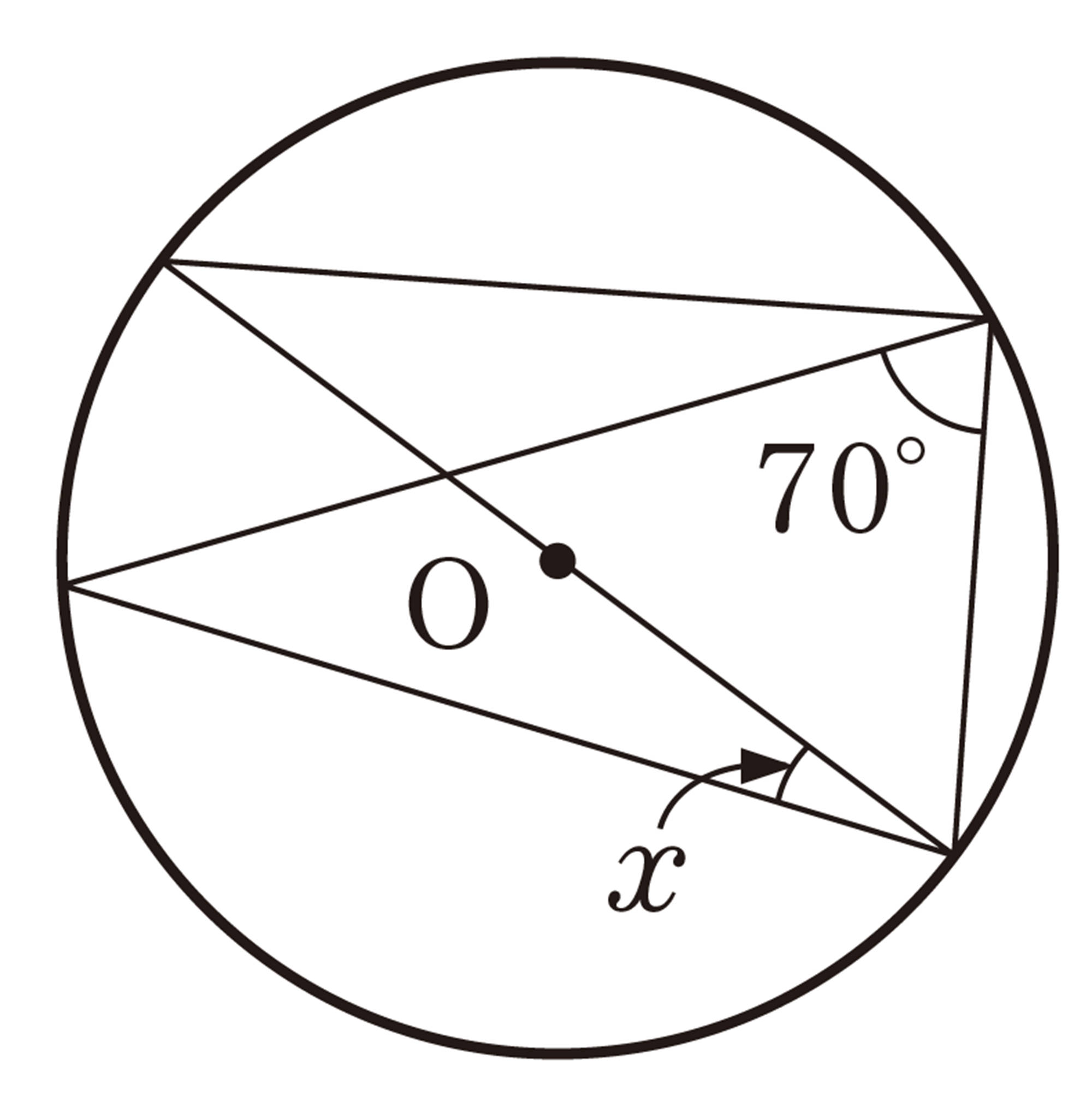
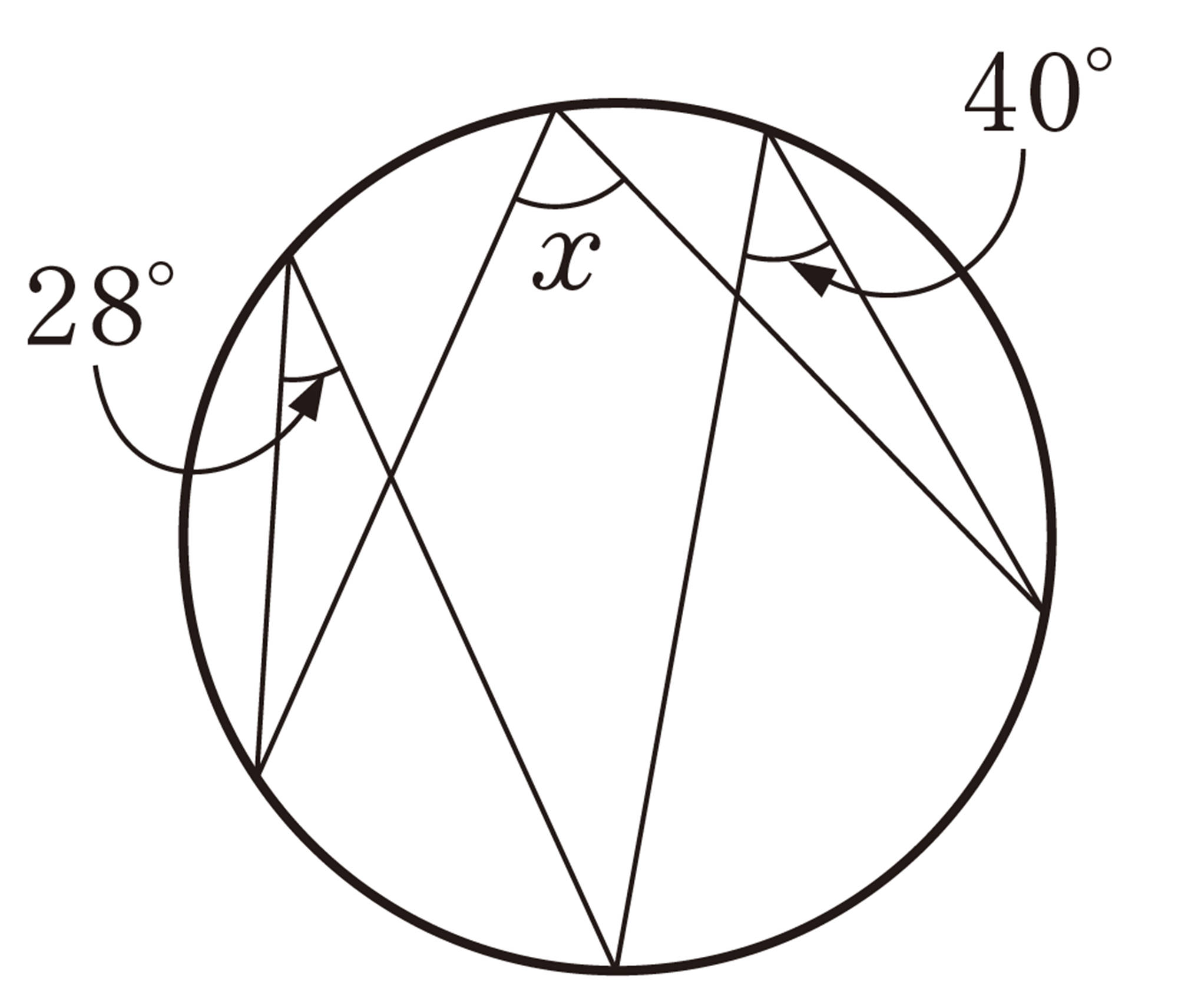
1 次の図で,[mathjax]\(\angle x\)の大きさを求めなさい。
<3年p.296>
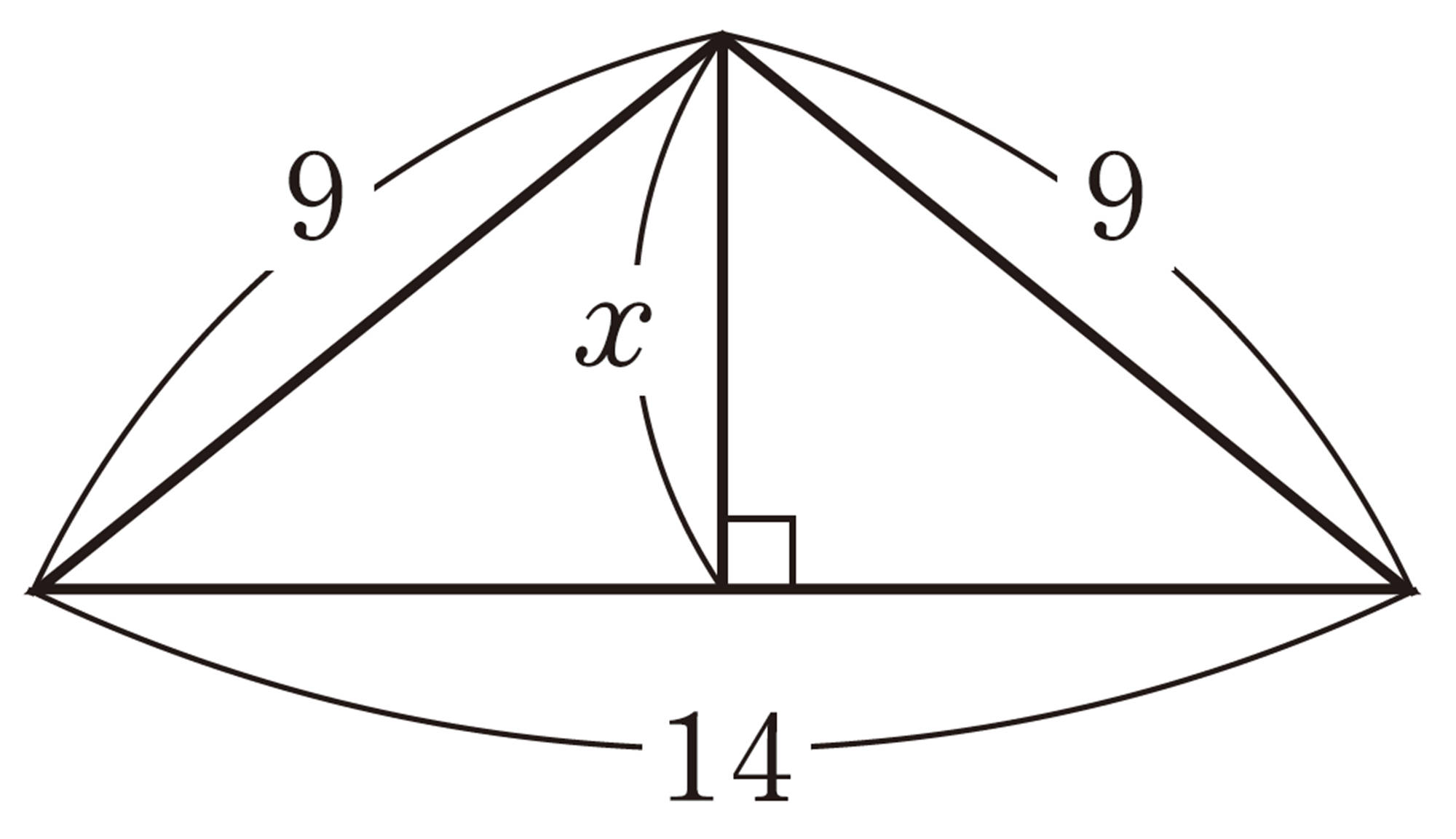
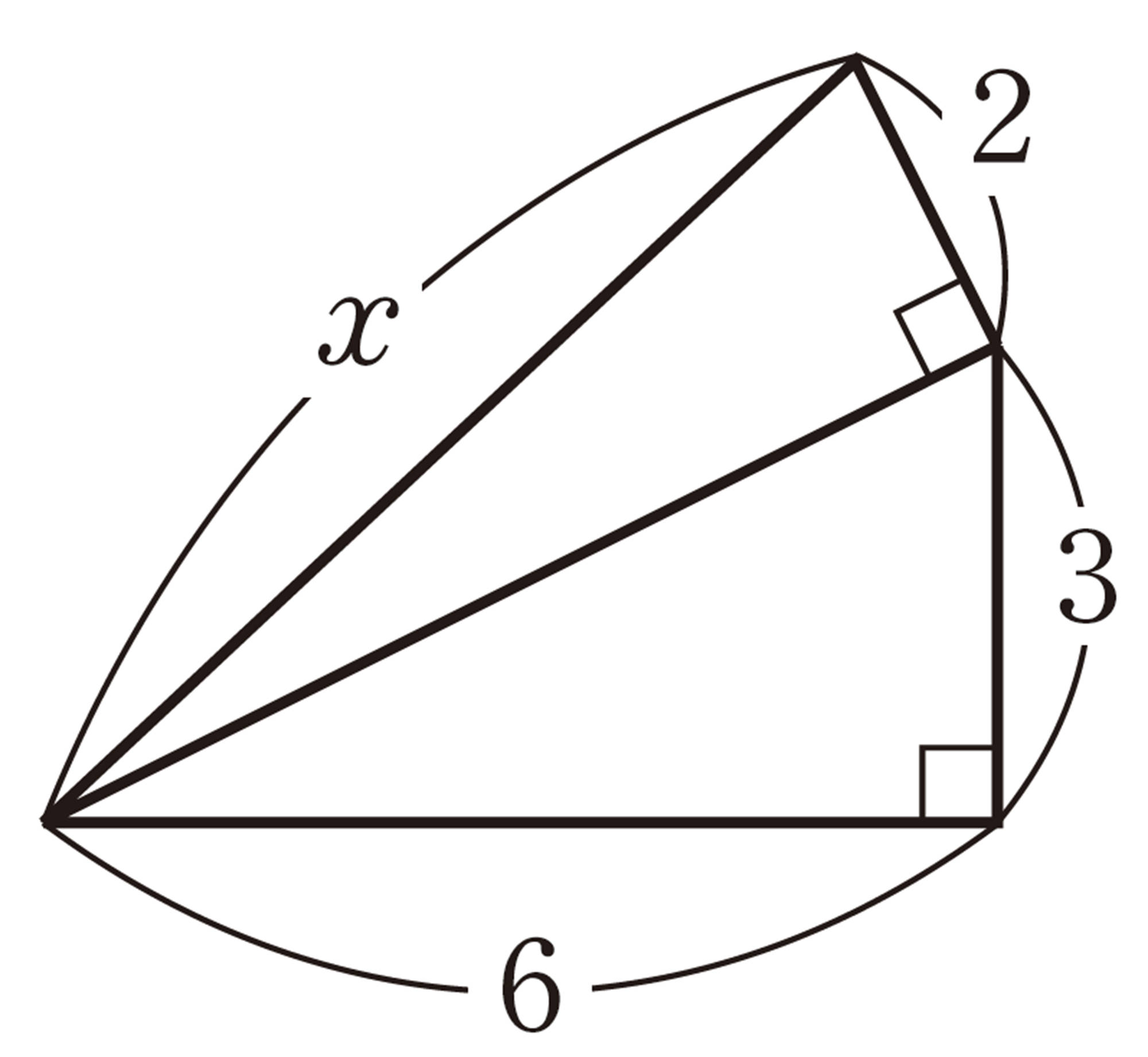
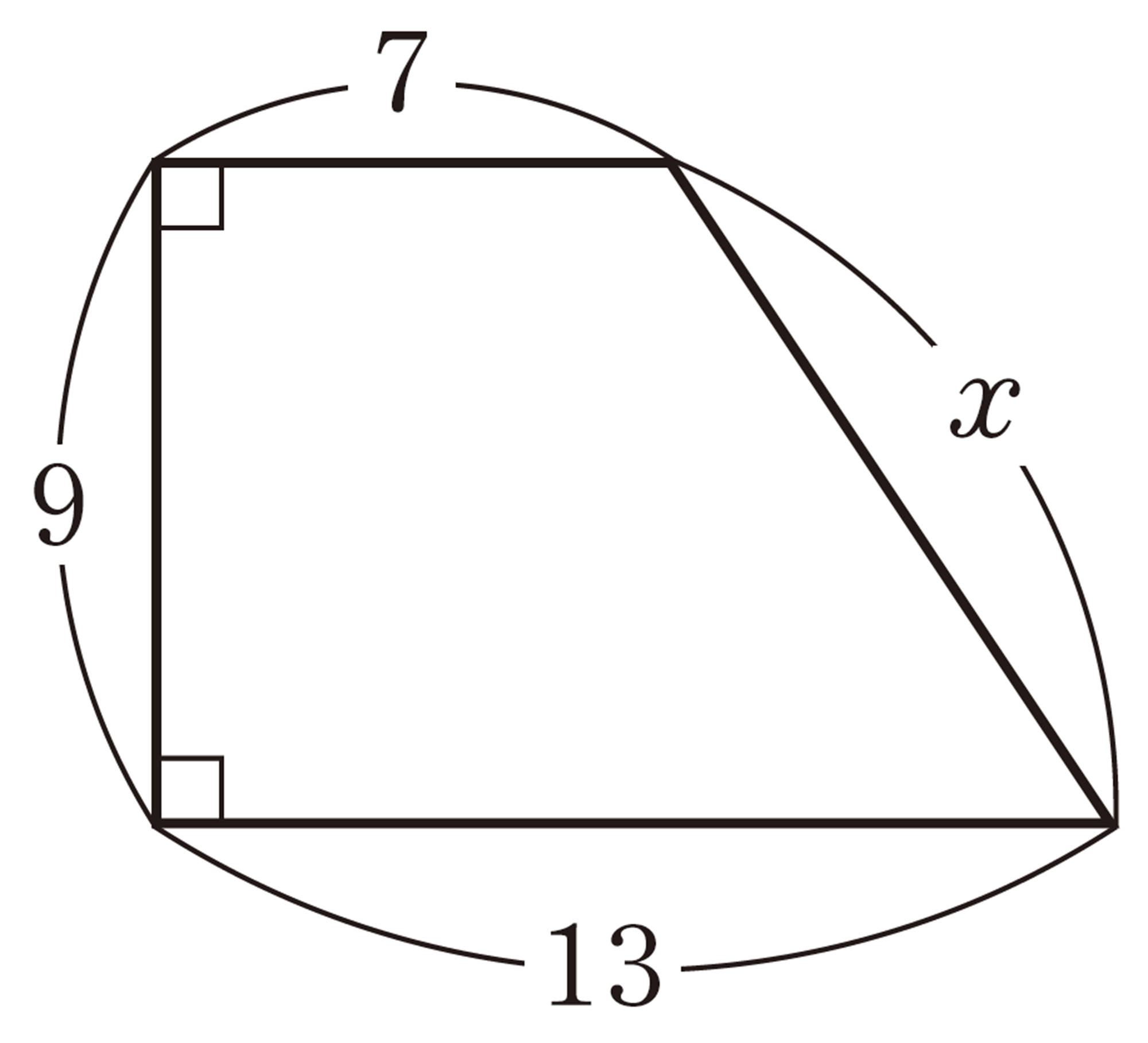
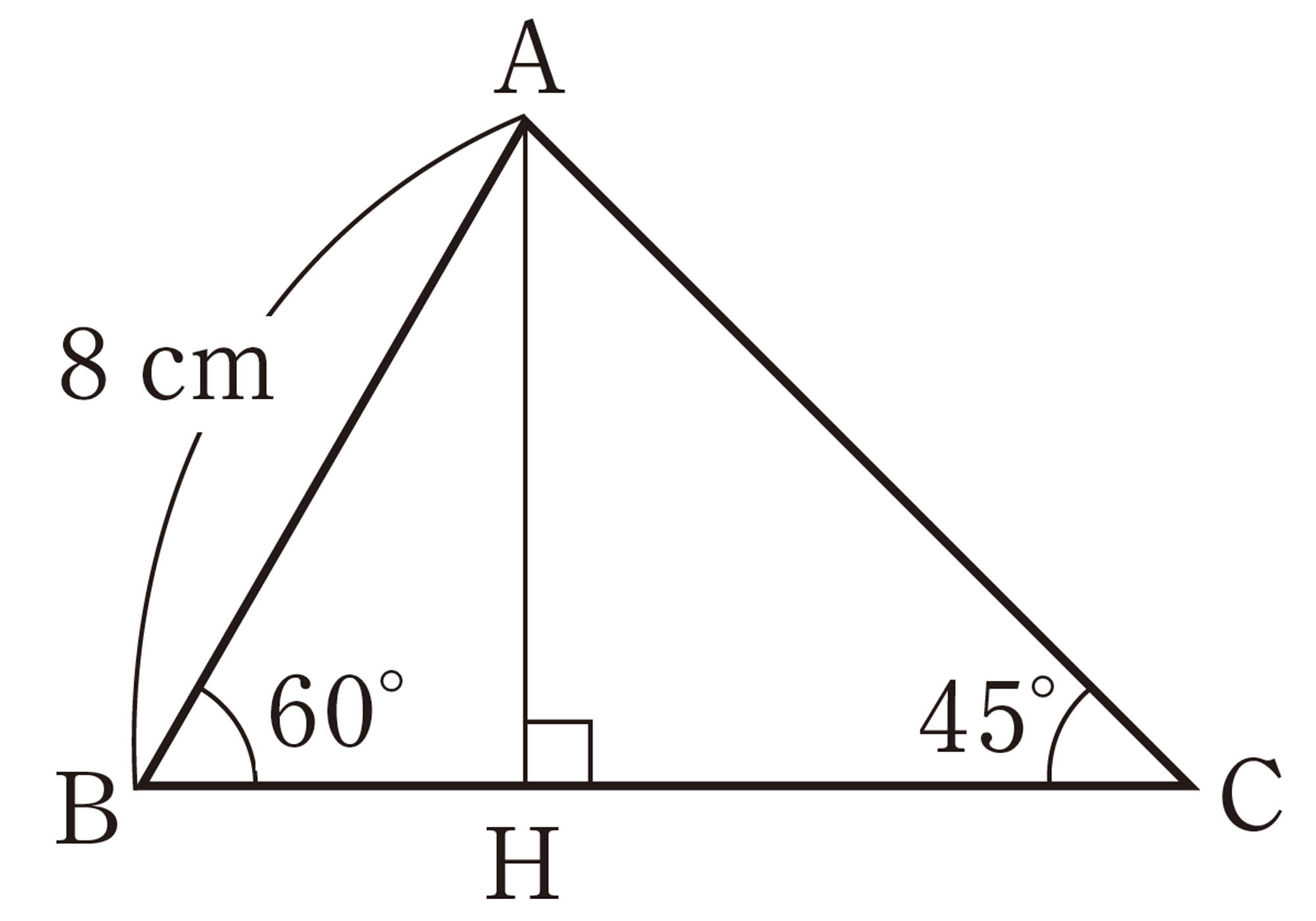
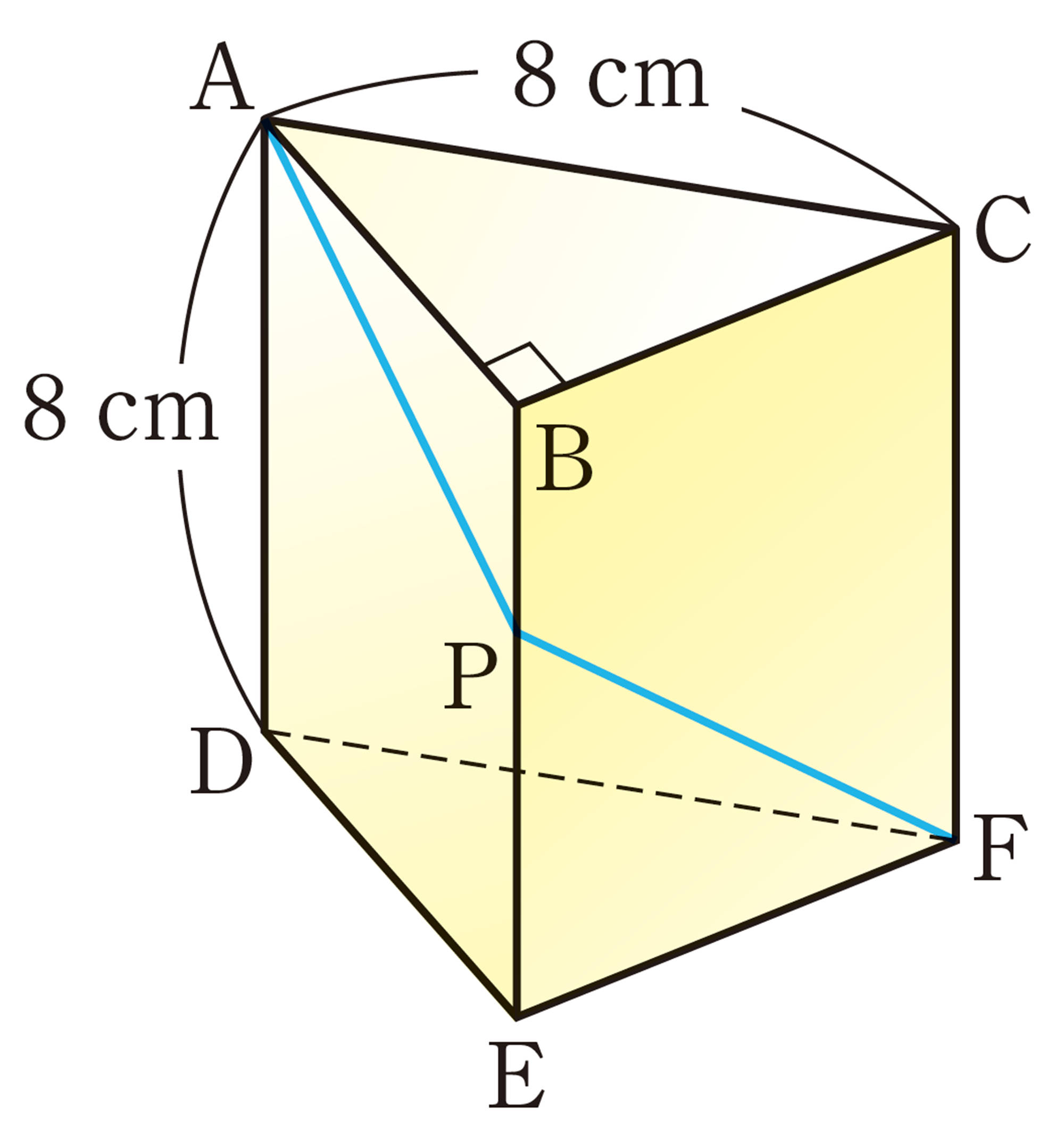
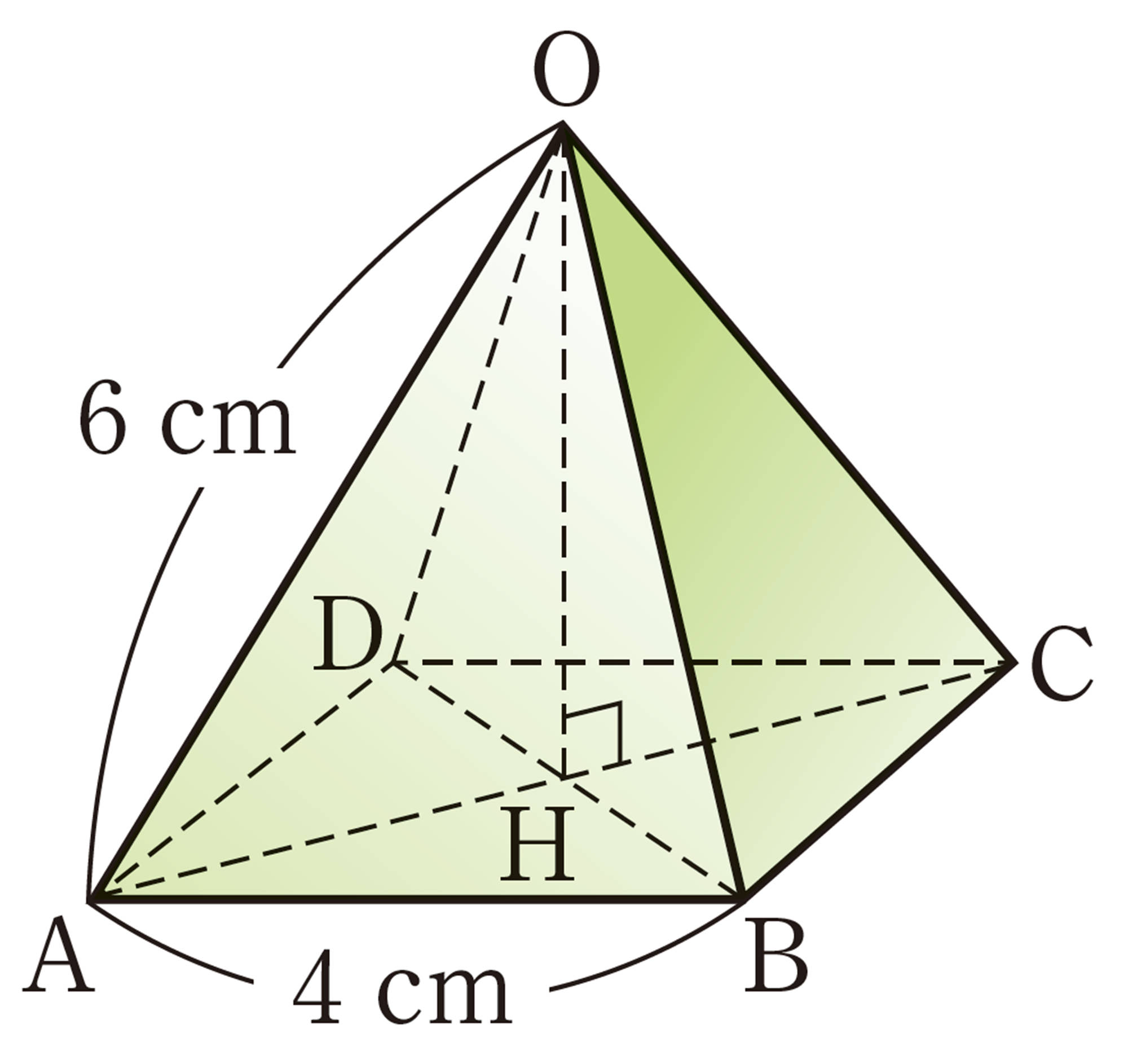
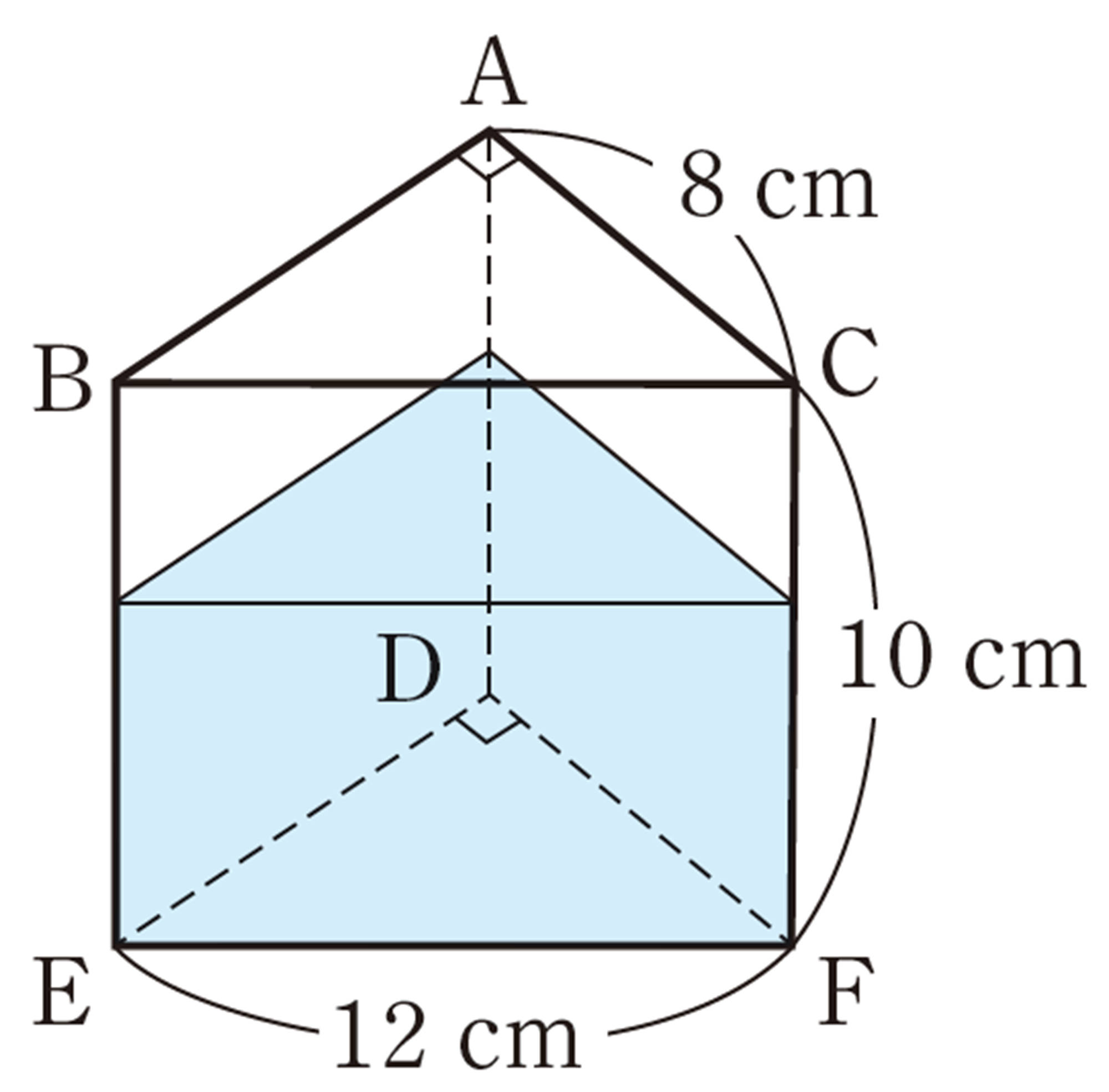
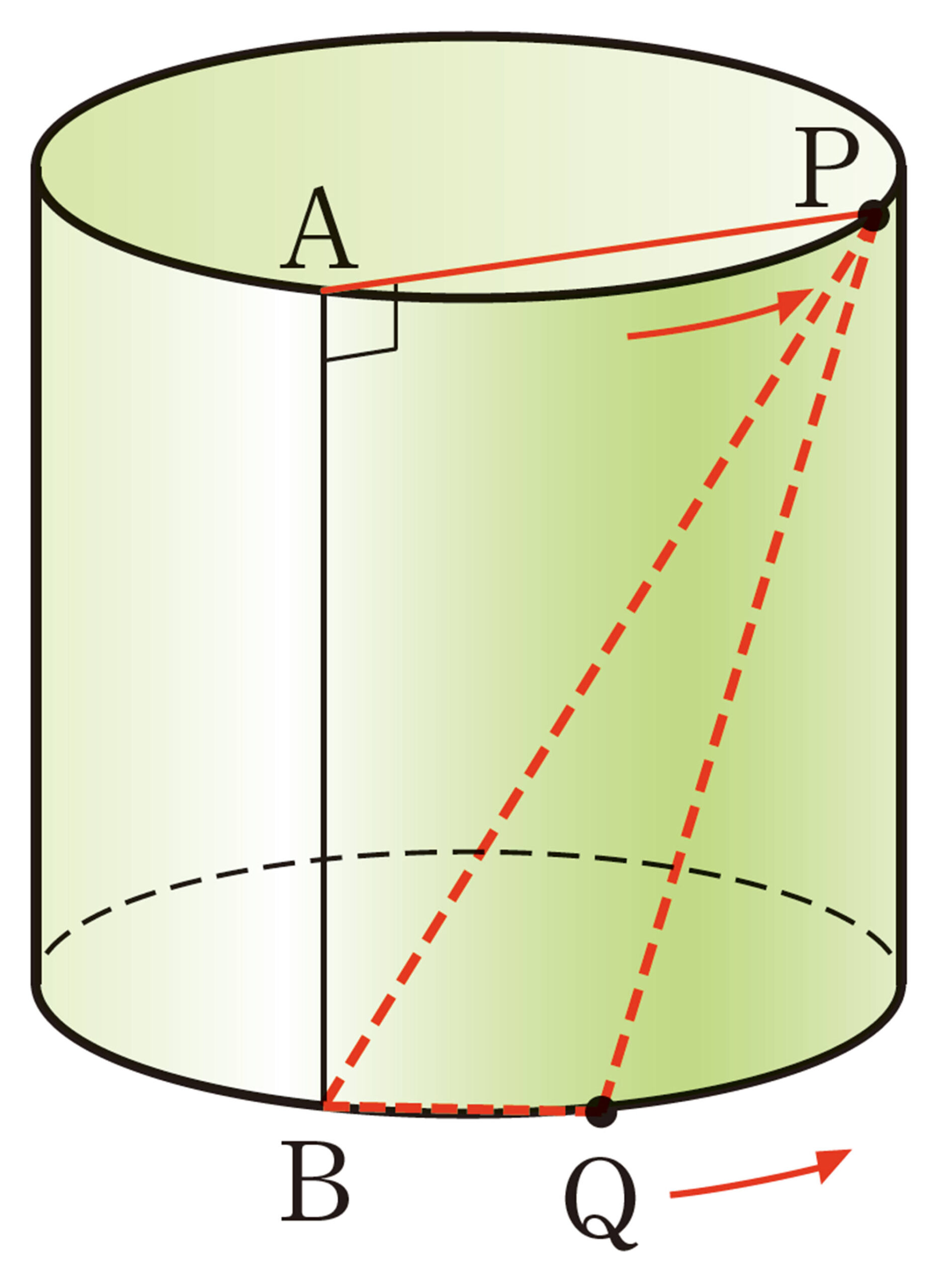
7章 三平方の定理
1 次の図で,xの値を求めなさい。
<3年p.297>
8章 標本調査
1 次の調査では,全数調査と標本調査のどちらが適していると考えられますか。
⑴ 国内の人口などを調べるために行われる国勢調査
⑵ 土壌汚染調査
⑶ 製薬会社で製造する薬の品質検査
⑷ 学校で行う出欠席の調査
⑸ 新聞社が行う内閣支持率などの世論調査
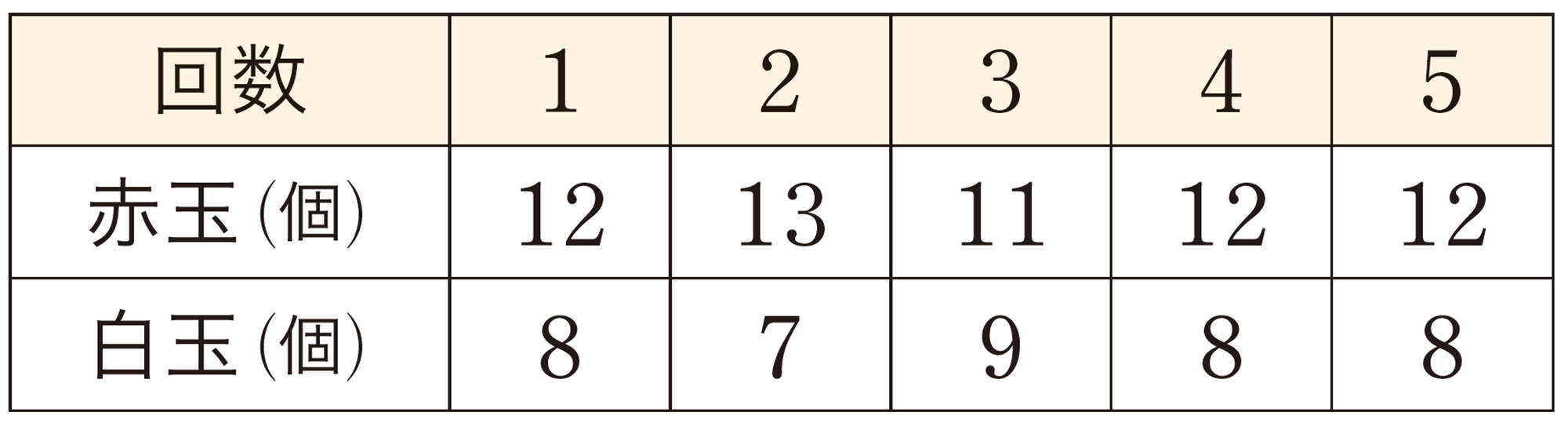
2 次のデータは,ある中学校の3年男子の身長の平均値を推定するために,3年男子全員の中から10人を無作為抽出して身長を調べたものです。このデータをもとにして,3年男子全員の身長の平均値を推定しなさい。
(単位:cm)
[mathjax]\(\boxed{\quad 155,176,161,165,157,163,170,168,171,164\quad}\)
<3年p.298>
総合問題
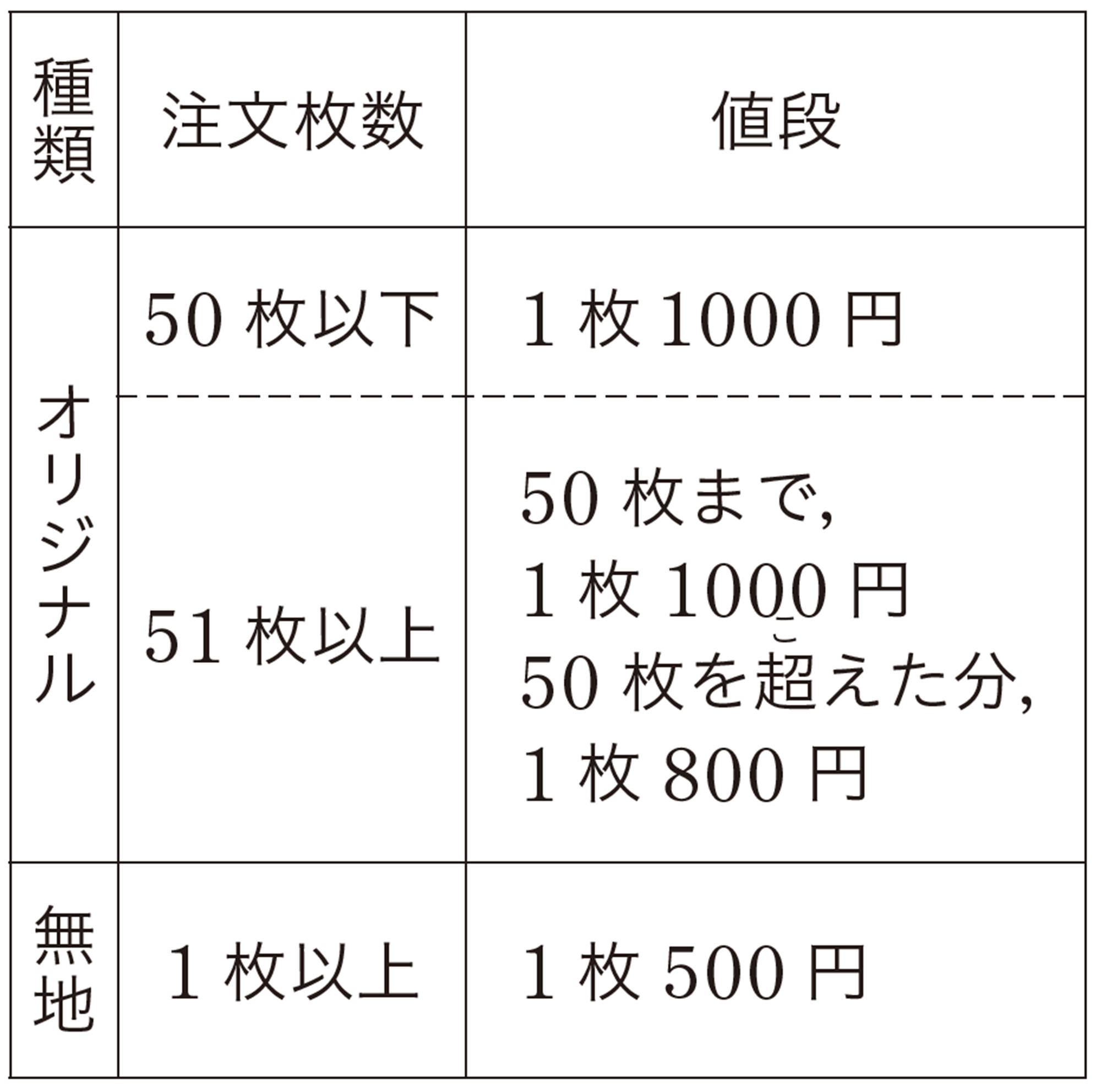
2 ある町の1か月当たりの家庭用の水道料金は,次の表のように,基本料金と使用水量に応じた料金の和になっています。下の問いに答えなさい。
⑴ 水の使用水量がxm³のときの水道料金をy円として,次の①,②についてyをxの式で表しなさい。
① 使用水量が10m³以下のとき
② 使用水量が10m³を超えたとき
⑵ 使用水量が7m³,18m³のときの水道料金を,それぞれ求めなさい。
<3年p.299>
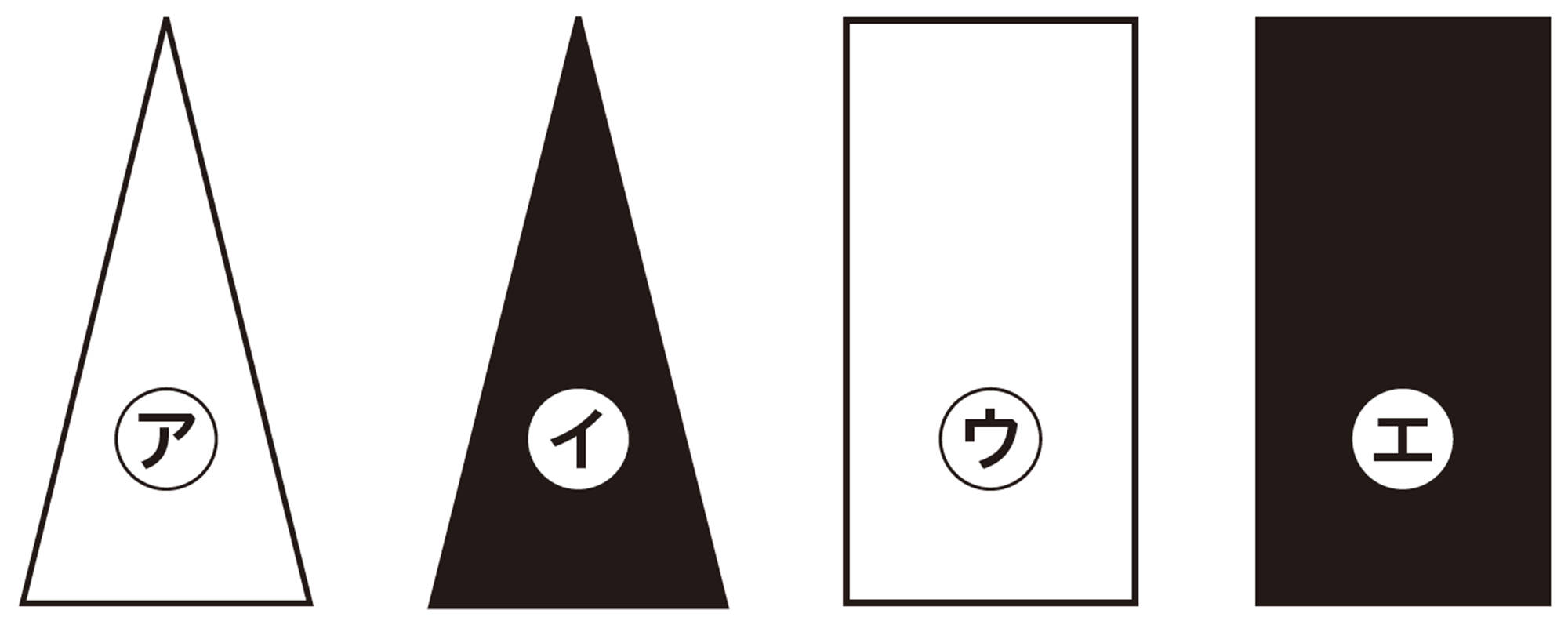
⑴ ㋐〜㋓のタイルのうち,20番目のタイルと同じ種類のタイルはどれか答えなさい。
⑵ 100番目のタイルより左側にある,すべての㋑,㋓のタイルの面積の和を求めなさい。