<1年p.286>
Theme 疑問を考えよう
米は何粒？
累乗の数に関連して，次のような話が伝えられています。
豊臣秀吉
曽呂利新左衛門
なんでも好きなほうびをやろう。
それでは…。
この広間の1枚目の畳に米1粒，2枚目にその2倍の2粒，3枚目にその2倍の4粒，…と置いていって，百畳分全部いただきたい。
その程度の米でいいのか。
よーし，わかった！それをほうびにやろう。
大変です！城にある米を全部集めても，まったくたりません！
えっ
まいった…。
秀吉は，どうして失敗したのかな。
そんなに驚くような量になるのかな。
① 1枚目の畳から順に，それぞれの畳の米粒の数を調べてみましょう。
米粒の数は，1粒の2倍，その2倍，そのまた2倍，…と増えていくので，2の累乗で表されます。このとき，畳の順番と累乗の指数との関係を考えてみましょう。
<1年p.287>
② 米粒の数を1枚目から順に加えた合計を求め，その結果がどんな式で表されるかを調べてみましょう。
③ 畳100枚の米粒の合計を，[mathjax](\(2\mathsf{の累乗}-1)\)の形で表してみましょう。
③で式に表した畳100枚の米粒の合計を計算すると，次のようになります。
1267650600228229401496703205375粒
すごい数だけど，どのくらいの量か想像できないよ。
売っている米の量は，重さで表しているから，重さがわかれば想像しやすいね。
④ 米1kgで，米粒が約50000粒になります。畳100枚の米粒の合計を1268000000000000000000000000000粒と考えて，およその重さを求めてみましょう。
何 kgぐらいになるのかな。
全国の米の収穫量と比べると，どちらが多いのかな。
⑤ 2022年の日本全国の米の収穫量は，約727万tでした。畳100枚の米粒と，2022年の日本全国の米の収穫量を比べてみましょう。また，そのことから，秀吉がどうして失敗したのか，その理由を説明してみましょう。
<1年p.288>
複雑な形の面積は？
右の図のような，複雑な形の面積を求める方法を考えてみましょう。
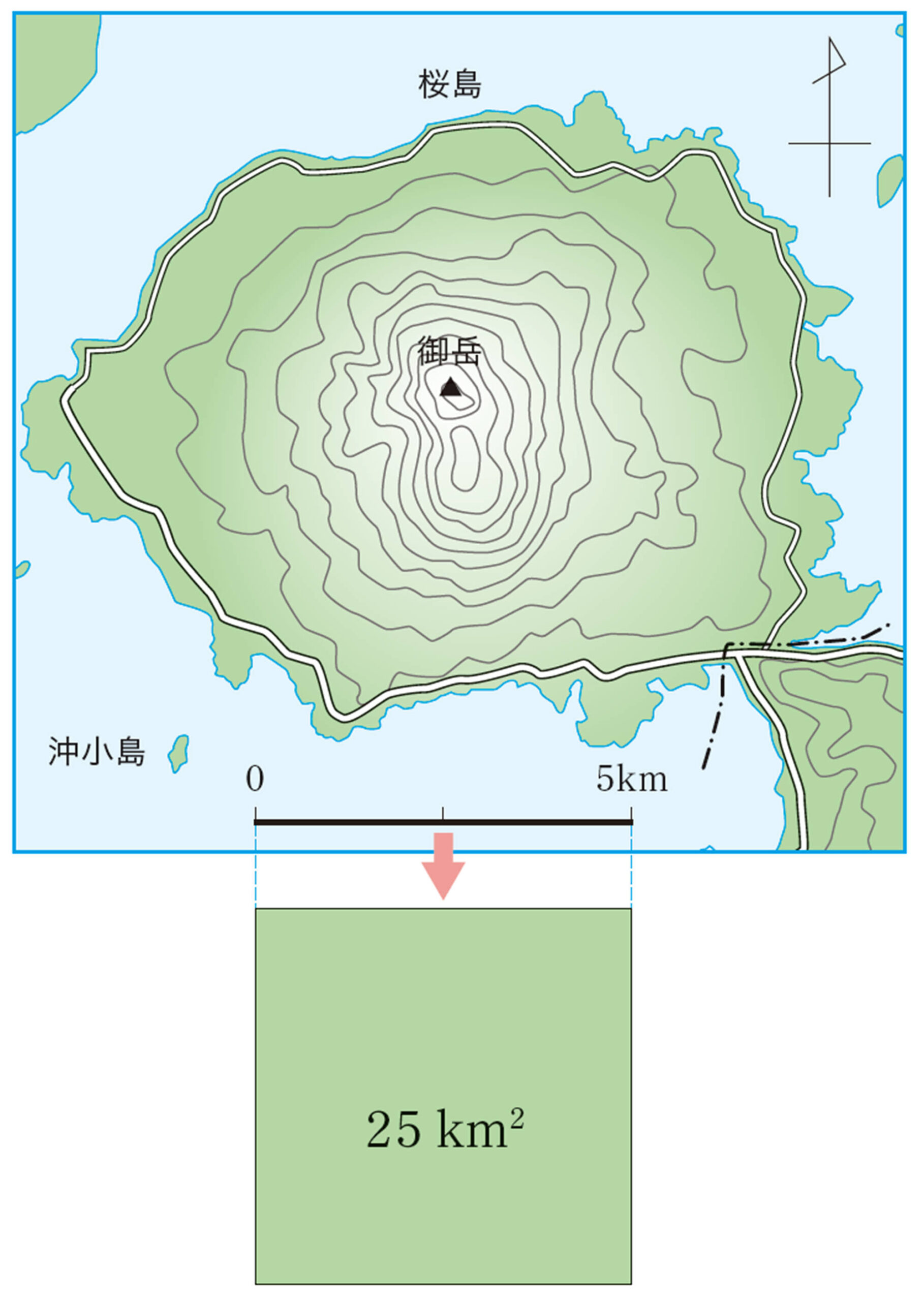
小学校では，複雑な形の面積は，方眼を使って考えたね。
似ている図形におきかえて考えたよ。
① 桜島の面積を， 次のようにして求めてみましょう。
① 桜島の地図をカーボン紙を使って厚紙にうつし取る。
② ①でうつし取った部分を切りぬき，その重さを量る。
③ 同じ厚紙で， 1辺が地図の縮尺で5 kmに等しい正方形を切りぬき，その重さを量る。
④ ②，③の結果をもとに， 桜島の面積を求める。
どんな考え方を利用しているかな。
針金の重さから長さを求めたときと，同じような考え方が使えるかな。
② 桜島の実際の面積は約80 km²です。①で求めた値と比べてみましょう。
この方法で，自分の住む市区町村や都道府県の面積を求めてみよう。
<1年p.289>
道路のカーブの半径は？
カーブした道路では，右の写真のような表示を見かけることがあります。「[mathjax]\(R=600\)」は，カーブが半径600 mの円の弧をえがいていることを示しています。
地図を使って，道路のカーブの半径を求められるかな。
弧の一部から円の中心を求めた方法が使えるかな。
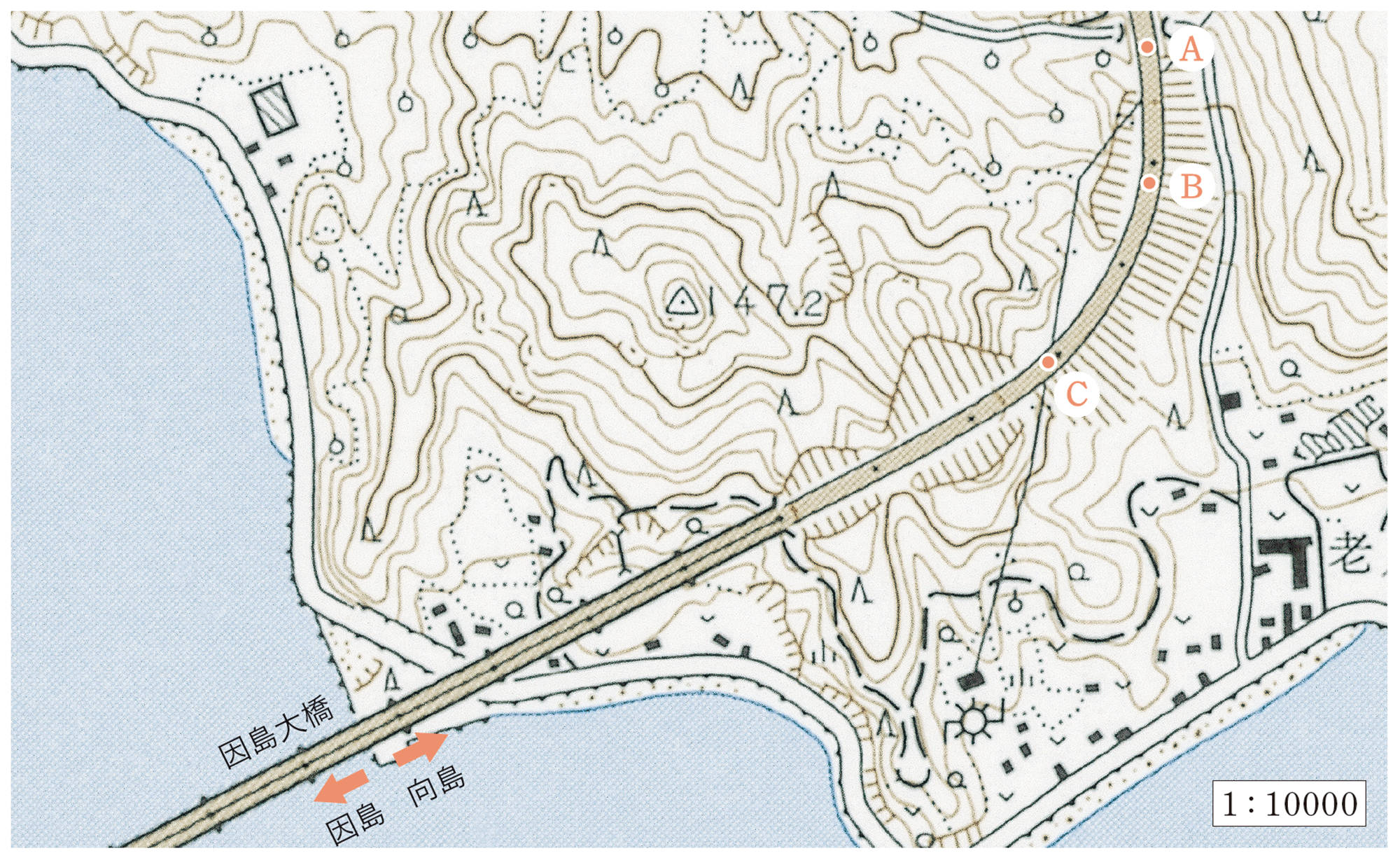
① 下の図は，広島県と愛媛県を結ぶ「瀬戸内しまなみ海道」の，因島大橋を渡って向島に入った付近の地図です。この地図に大きくカーブした道路がありますが，その半径を，次の手順で求めてみましょう。
① カーブを円の弧と考え，3点 A，B，C を通る円の中心Oを，作図によって求める。
② 半径 OAの長さを測る。
③ 縮尺が[mathjax]\(\dfrac{1}{10000}\)であることから，実際のカーブの半径を求める。
② 自分の身のまわりの地域の地図を使って，道路のカーブの半径を求めてみましょう。また，実際の表示と比べてみましょう。
<1年p.290>
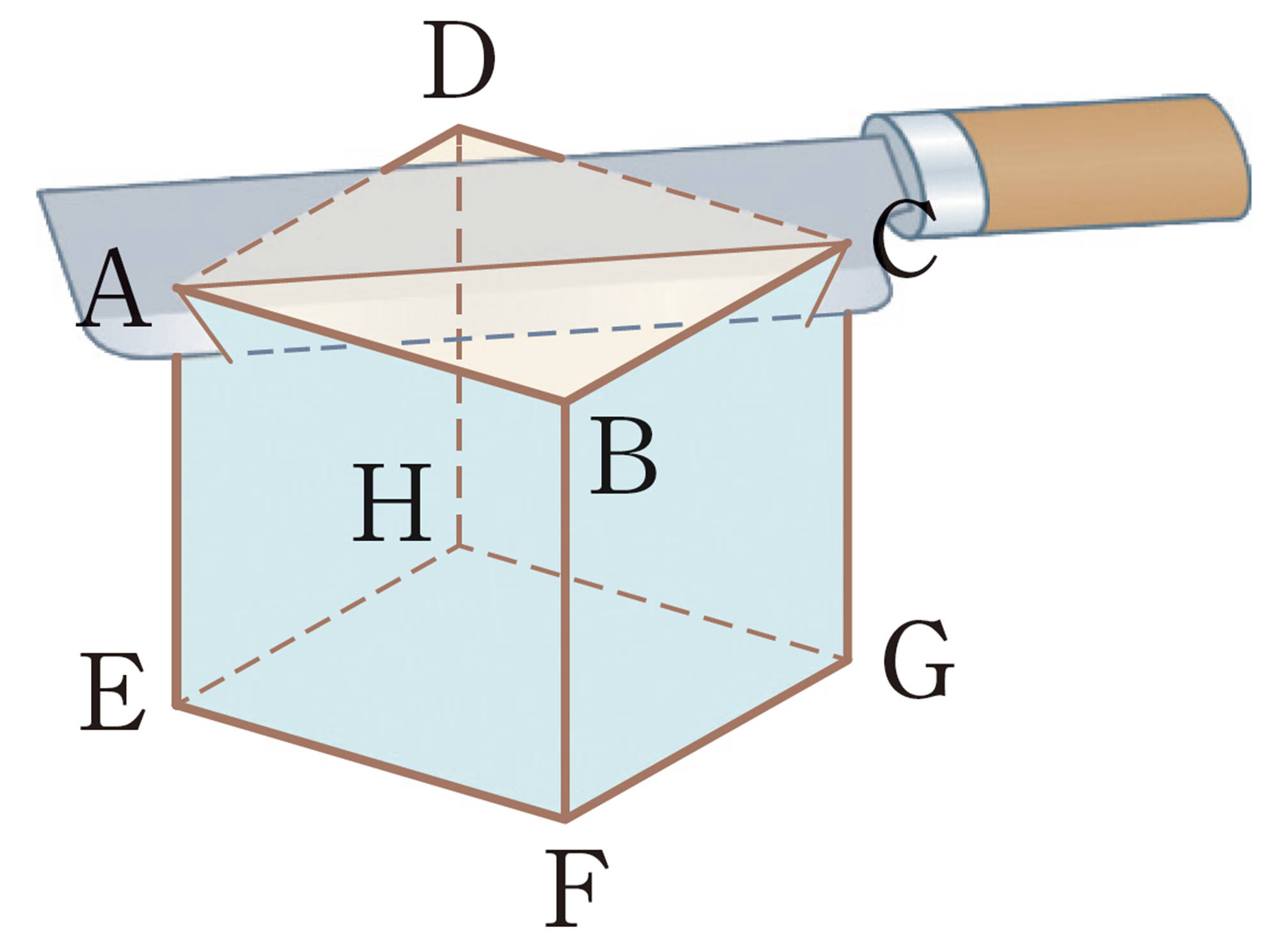
立方体の切り口の形は？ 発展
3点を通る平面はただ1つに決まります。このことを手がかりにして，立方体を平面で切ったときの切り口の形を考えてみましょう。
立方体だから，四角形になるんじゃないかな。
どこを切っても同じ形になるのかな。
まず，立方体を，2点 A，C を通る平面で切る場合を考えてみましょう。
右の図の㋐のように，2点 A，C と点 E を通る平面で切ると，切り口の形は長方形になります。
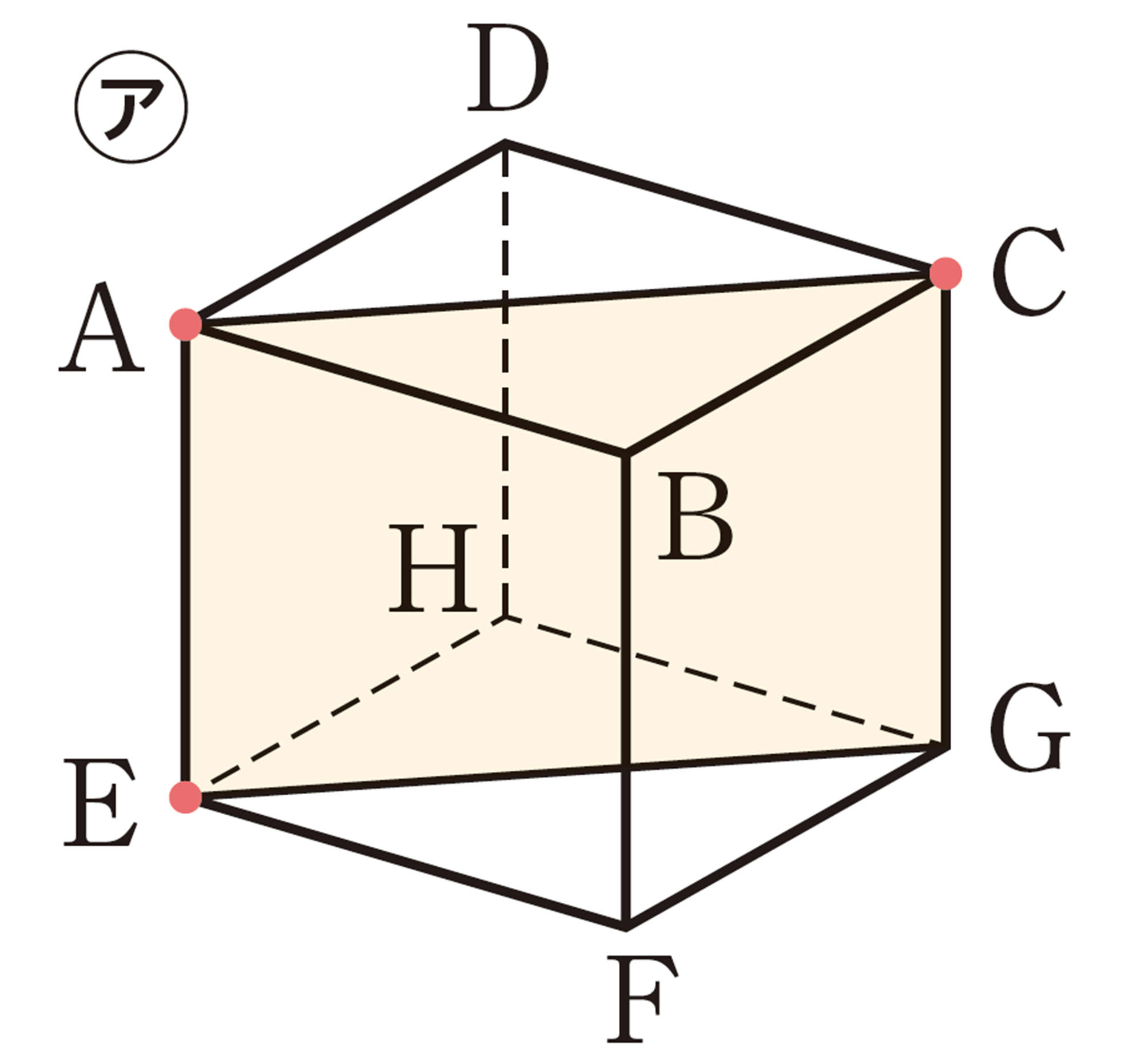
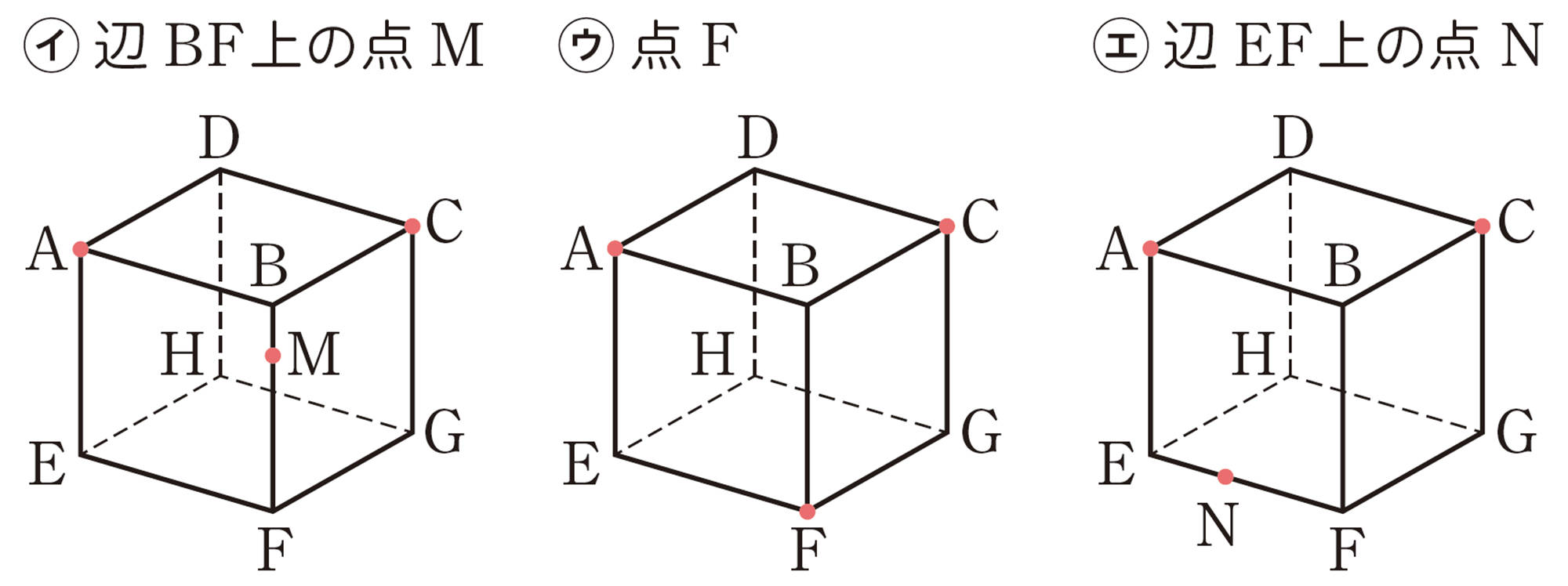
① 2点 A，C と，次の㋑，㋒，㋓で示した点 ● を通る平面で切ると，切り口の形はそれぞれどんな図形になるでしょうか。次の図にかき入れてみましょう。
次に，いろいろな平面で切る場合を考えてみましょう。
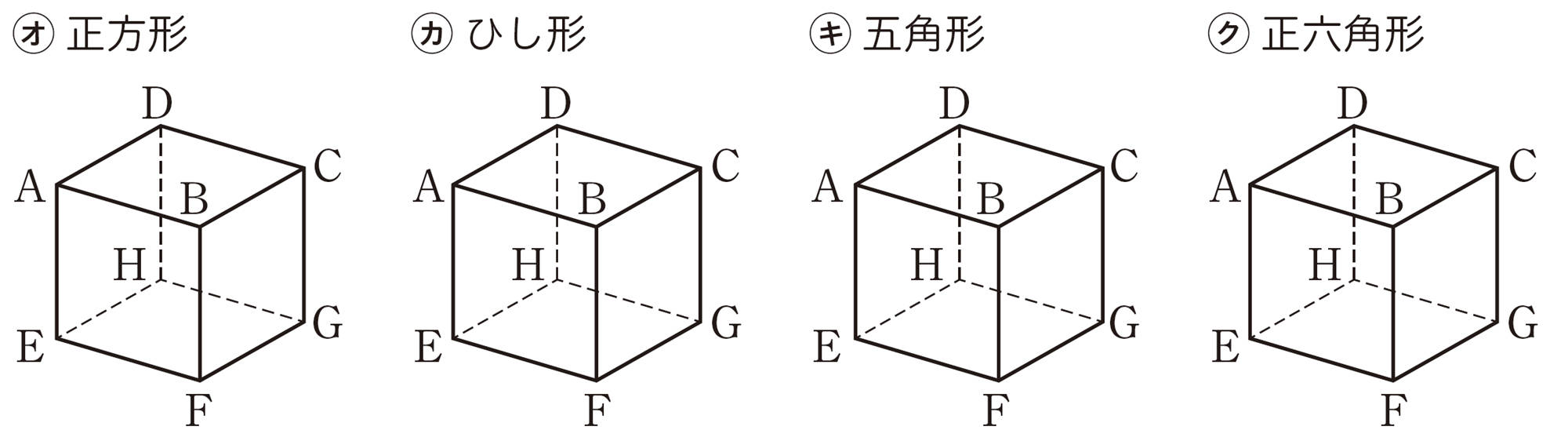
② 切り口の形を，次の㋔，㋕，㋖，㋗で示した図形にするには，それぞれどんな平面で切ればよいでしょうか。切り口を次の図にかき入れてみましょう。
<1年p.291>
Theme 数学の歴史の話
ディオファントスと方程式
方程式の基礎を築いたのは，3世紀頃の古代ギリシャの数学者ディオファントスといわれています。「代数学の父」と呼ばれることもあります。彼は，13巻におよぶ『算術』という本を著したことで有名です。
彼の生涯については，いつ生まれて，いつ亡くなったか，よく知られていません。
しかし，彼の墓石に刻まれていたといわれている『ディオファントスの墓碑銘』と呼ばれる，次のような文章があります。この文章から，彼が何歳まで生きたかを知ることができます。
ディオファントスは，
一生の[mathjax]\(\dfrac{1}{6}\)を少年，[mathjax]\(\dfrac{1}{12}\)を青年として過ごしました。
さらに，一生の[mathjax]\(\dfrac{1}{7}\) を過ごしてから結婚し，その5年後に子どもが生まれました。
その子どもは，父より4年前に，父の一生の半分でこの世を去りました。
① ディオファントスは，何歳まで生きたのでしょうか。次の図をもとに，彼が[mathjax]\(x\)歳まで生きたとして，方程式をつくって解いてみましょう。
② ディオファントスが結婚したのは，何歳のときでしょうか。
<1年p.292>
円周率[mathjax]\(\pi\)の話
人間は，4000年以上前の大昔から，円周率を追い求めてきました。
紀元前2000年頃古代バビロニアでは，円周率として3や[mathjax]\(\dfrac{25}{8}\)を使っていました。また，同じ頃古代エジプトでは，円周率として[mathjax]\(\dfrac{256}{81}=3.16049\cdots\)を使っていました。
現在の円周率に近い値を求めたのは，古代ギリシャのアルキメデス(紀元前287頃～紀元前212)です。アルキメデスは，円周の長さが円の内側に接する正多角形のまわりの長さより大きく，円の外側に接する正多角形のまわりの長さより小さいことを利用して，円周率を求めました。
その正多角形を正六角形から正96角形まで増やすことで円周率を求め，[mathjax]\(3\dfrac{10}{71} \lt \pi \lt 3\dfrac{1}{7}\)であることを示しました。小数に直すと，[mathjax]\(3.1408 \cdots \lt \pi \lt 3.1428\cdots\)となります。
なお，円周率を表す「[mathjax]\(\pi\)」は，「円周」や「周囲」を意味するギリシャ語「 περιμετρος （ペリメトロス）」の頭文字からとられたといわれています。
オランダのルドルフ(1540～1610)は，同じ方法で，正262角形まで増やし，小数点以下35桁まで計算しましたが，そのためにほとんど一生を費やしたといわれています。
日本でも，江戸時代，日本独自の数学である「和算」が発達し，円周率の計算をする人々が現れました。関孝和(1640頃～1708)は，正13万1072角形から，円周率を小数点以下10桁まで正確に求めました。また，関の弟子である建部賢弘(1664～1739)は，円周率を小数点以下41桁まで求めました。
<1年p.293>
17世紀以降，限りなく続く数の和や積を使って，[mathjax]\(\pi\)の値を計算する公式が発見されました。たとえば，次のような公式があります。
[mathjax]\(\dfrac{\pi}{4}=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{13}-\dfrac{1}{15}+\cdots\)
この式は，計算をし続けてもなかなかπの正確な値に近づかないため，あまり実用的とはいえませんでした。しかし，さらに効率的な多くの公式が発見されるきっかけになりました。たとえば，この後発見された公式には，次のようなものがあります。
[mathjax]\(\dfrac{\pi²}{6}=\dfrac{1}{1²}+\dfrac{1}{2²}+\dfrac{1}{3²}+\dfrac{1}{4²}+\dfrac{1}{5²}+\dfrac{1}{6²}+\cdots\)
そして，1946年には，[mathjax]\(\pi\)の値は小数点以下620桁まで計算されました。
20世紀中頃からはコンピュータが利用できるようになり，[mathjax]\(\pi\)の計算は飛躍的に前進しました。1987年には1億桁，2011年には10兆桁，2022年には100兆桁まで計算されました。
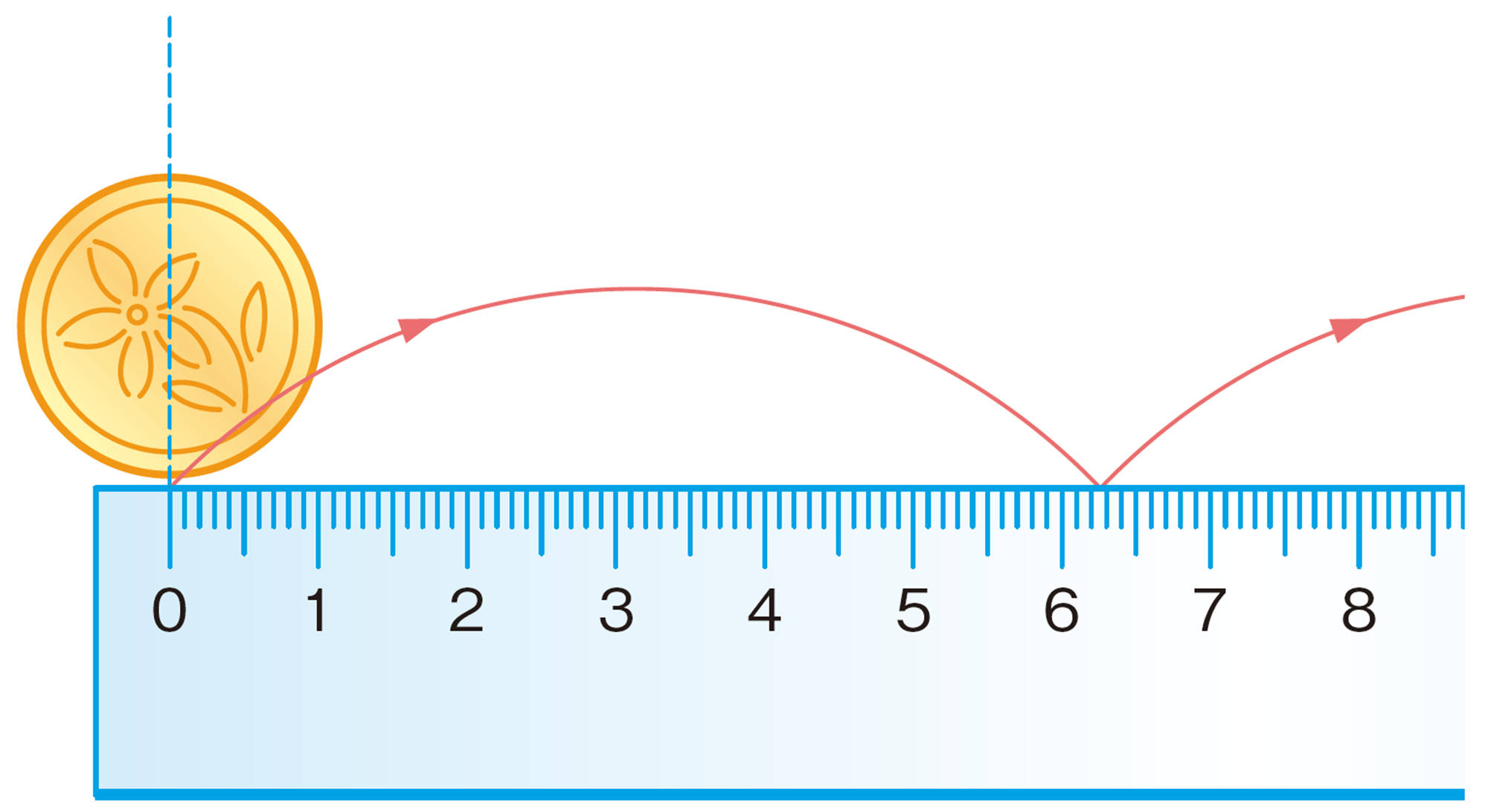
① 円形のコインを使って直径とまわりの長さを測り，[mathjax]\(\pi\)の値を求めてみましょう。どのくらい正確な値が得られるでしょうか。
①コインの直径を測る
コイン10個を並べて測り，その値を10でわるとよい
②コインの周囲を測る
コインを3〜5回転させ， 1回転分の平均を求めるとよい
② 本やインターネットを利用して，πの計算の歴史や，計算方法を調べてみましょう。
