<3年p.259>
さらなる数学へ
協働学習のページ
260 「見方・考え方」をまとめよう
262 今の自分を知ろう
266 表現する力を身につけよう
266 レポートの作成
267 発表のしかた
268 レポート例
270 疑問を考えよう
270 黄金比って何?
【関連】2次方程式,相似な図形
271 「三平方の定理の逆」の証明はほかにもある?
【関連】 三平方の定理
272 放物線はみな相似? 発展
【関連】 関数[mathjax]\(y=ax²\),相似な図形
274 ドローンを使った撮影範囲は?
【関連】 相似な図形
276 震源の位置を特定できる?
【関連】 円,三平方の定理
278 数学の歴史の話
278 地球の測り方
280 精密な日本地図を最初につくった人物
281 三平方の定理の証明
282 高校へのかけ橋 発展
<3年p.260>
Theme 「見方・考え方」をまとめよう
中学校3年の数学の学習では,新しいことを学び,いろいろなことができるようになりました。数学の学習を進めていくにあたって,どんな「見方・考え方」をしてきたかまとめてみましょう。
「見方・考え方」はここにあるだけでなく,いろいろな場面でいろいろな「見方・考え方」を使います。

1 身のまわりや数学の中から問題を発見しよう
2 数学の問題として考えよう
<3年p.261>
3 解決しよう
ほかにも,いろいろなところで,「見方・考え方」を見つけてみよう!

4 新たな問題を見つけよう
<3年p.262>
Theme 今の自分を知ろう
SDGs(Sustainable Development Goals)とは,2015年9月の国連サミットで採択された2016年から2030年までの国際目標です。持続可能な世界を実現するための17のゴール・169のターゲットから構成され,地球上の誰一人として取り残さない(leave no one behind)ことを誓っています。SDGsは発展途上国のみならず,先進国自身が取り組むユニバーサル(普遍的)なものであり,日本としても積極的に取り組んでいます。
SDGsの17の目標のうち,これまで身につけた数学の力を使って,自分たちにできることがないか調べて,取り組んでみましょう。
洋服屋さんに,古着の回収ボックスがあったよ。


環境のために服もリサイクルしているのかな。
エシカル消費ということばを聞いたことがあるよ。


エシカルってどういうことかな。
<3年p.263>
Mission
たとえば,衣料品を買うときに,値段や見た目などを考えながら買い物をするとします。そこに,「環境に配慮して作られている」,「買うことで寄付につながる」などの社会的な貢献を考えること,それがエシカル消費です。
エシカル消費について調べ,自分たちでまとめていきましょう。
エシカルとは,「倫理的な・道徳的な」という意味を表し,多くの人が正しい・公平であると思うことを指しています。
すなわち,エシカル消費は,「地域の活性化や雇用などもふくむ,人や社会・環境に配慮した消費行動」とされ,社会や環境に配慮した商品・サービスを積極的に選択することで,消費者それぞれが社会的課題や環境問題の解決を考慮した消費活動を行うことといえます。
たとえば,
・環境への配慮…エコマーク商品,リサイクル製品,持続可能な森林経営や漁業の認証商品の選択
・社会への配慮…フェアトレード商品,寄付つきの商品の選択
・人への配慮…障害者支援につながる商品の選択や地産地消や被災地産品の応援消費等
が,エシカル消費にふくまれると考えられています。
Data_1
<3年p.264>
Data_2
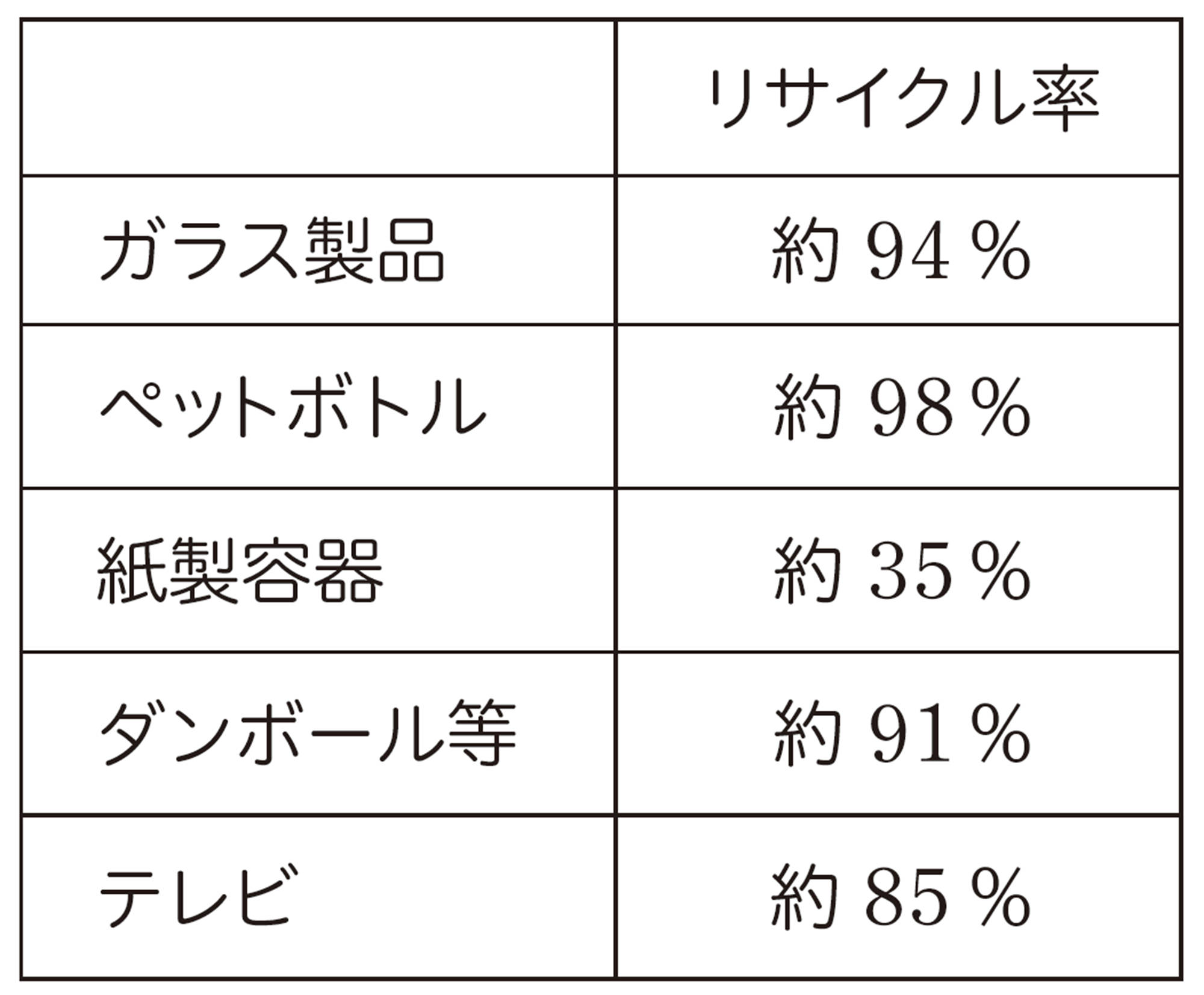
右の表1はいろいろなものの2019年のおよそのリサイクル率を表したものです。この表から気づいたことを話し合ってみましょう。
Data_3
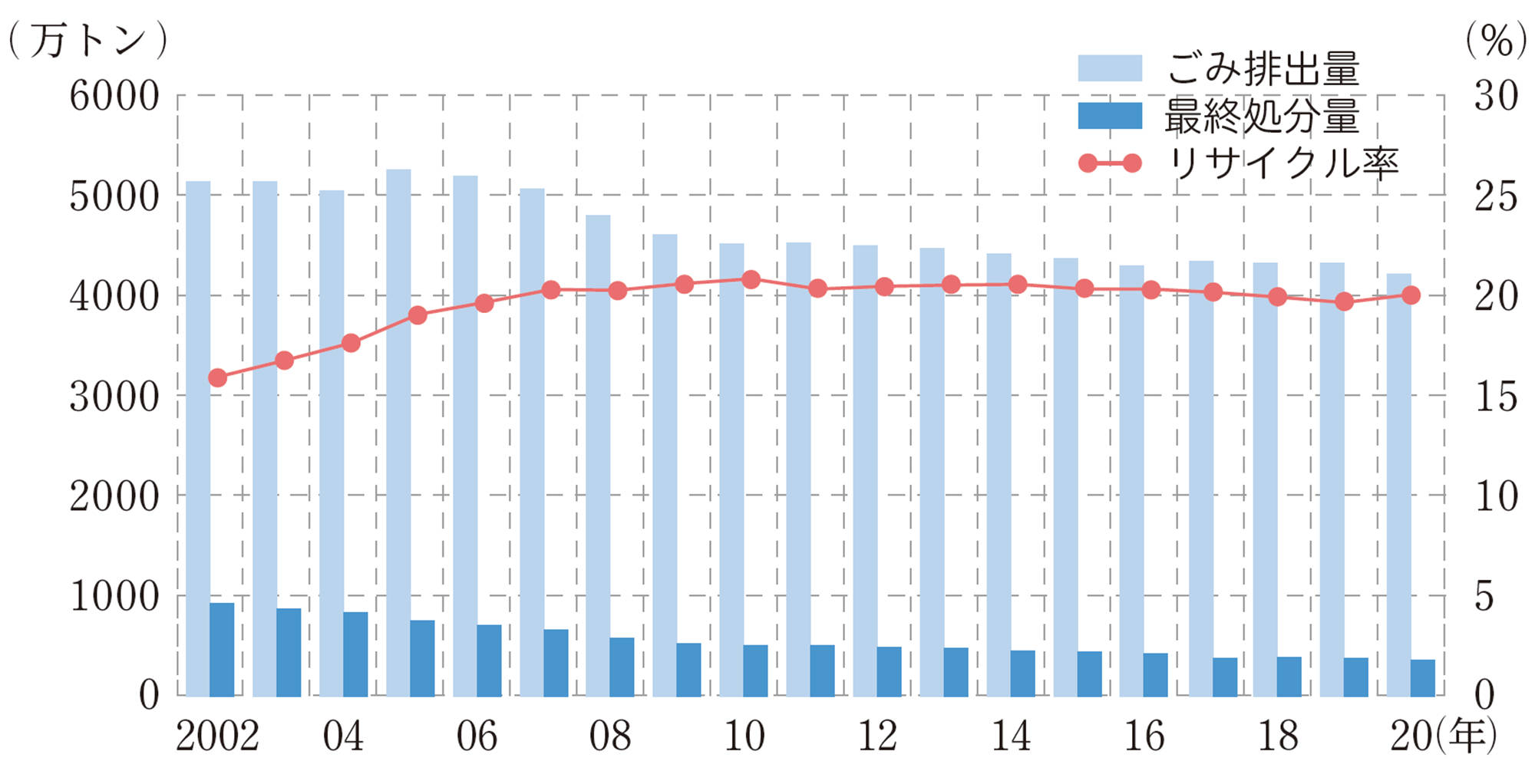
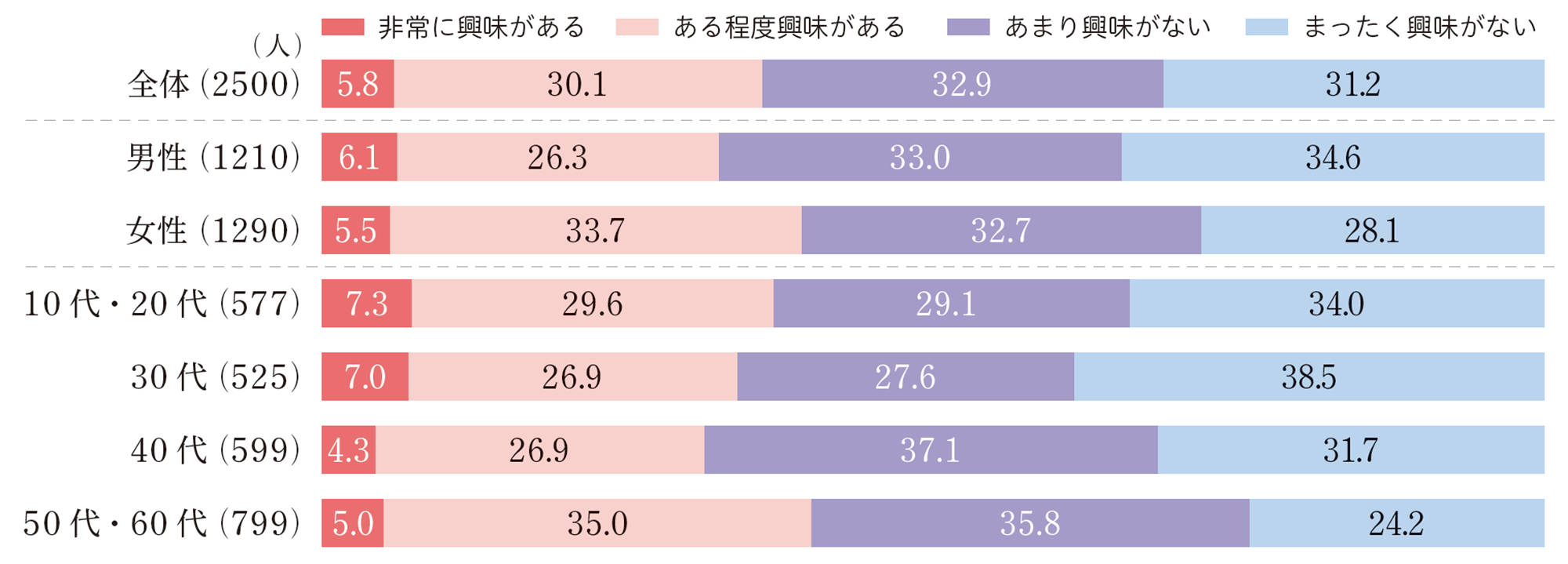
次の図2は,日本の2016年のエシカル消費への関心度を調べたデータです。このグラフから,日本のエシカル消費に対する意識についてどんなことがいえるでしょうか。
Report
自分たちの身のまわりには,次のようなマークが表示された商品がいろいろあります。
これらのマークが表示された商品について,学校内でどのくらいの人が知っているか,積極的にこれらのマークが表示された商品を買っているかなどを調べてみましょう。
また,エシカル消費について,これまで調べたことから,これから自分たちにどんなことができるか調べて,まとめてみましょう。
エシカル消費についてくわしく説明しているサイトにリンクしています。
<3年p.266>
Theme 表現する力を身につけよう
〜自分の考えを見直そう〜
自分の考えをまとめたり伝えたりするために,レポートをつくってみましょう。レポートにまとめることで,学習したこと以外に新たな発見をしたり,疑問が生まれたりします。それこそが,本当の数学のおもしろさです。

レポートの作成
1 興味や関心をもったことをテーマにしよう
数学の学習のときやふだんの生活の中で, 「なぜだろう」,「別の条件ならどうだろう」,「もっと知りたい」と感じたことをレポートのテーマにしましょう。ふだんから気になったことをノートなどに記録しておくと,テーマを決めるときに役立ちます。
2 資料の収集方法の計画を立てよう
自分で考えるだけでなく,
・実験や観察,調査などをする
・アンケート調査をする
・図書館の本や新聞記事,インターネット等で調べる
など,目的に合わせた資料の収集方法を計画することが大切です。
3 資料を集め,整理して分析しよう
調べた情報やデータを分析して,資料の特徴を見つけましょう。収集した情報やデータは,何を参考にしたのかわかるように記録しておきましょう。インターネットで検索するとたくさんの情報が得られますが,信頼できる情報かどうかに注意する必要があります。
4 自分の考えを整理してまとめよう
レポートの作成を通して, 調べた内容や調査過程,そのおもしろさや価値などが友だちにわかりやすく伝わるように, 整理してまとめましょう。レポートという形にこだわらず,新聞やポスターなど,発表のしかたに合わせて形式を選ぶと,さらによいものをつくることができます。
5 レポートを発表し,コメントをもらおう
作成したレポートを発表し,発表内容について,友だちから質問やコメントをもらいましょう。また,聞いている人は,疑問点や感じたこと,よりよいレポートにするために自分だったらどうするかなどについてコメントをしましょう。
6 よりよいレポートに仕上げよう
友だちの意見を参考にして,自分の研究をふりかえりましょう。必要があればデータの整理の方法や分析のしかたを改善し,レポートを書き直しましょう。
<3年p.267>
発表のしかた
発表する人は…
自分の考えや思いがどうやったらうまく伝わるかを考えて発表しよう
- 何について調べて,何を伝えたいのかをはっきりさせておこう。
- グループの中でリハーサルを行い,相手にわかりやすい話し方を見つけよう。
- 話す順序や資料を示すタイミングをくふうして,説得力のある展開を考えておこう。
- 学習した内容と自分で考えた内容を区別して話そう。
- わからなかったことを伝えて,みんなから意見をもらおう。
- どんな「見方・考え方」を使ったか伝えよう。
発表を聞く人は…
発表している人の考えや思いをくみ取りながら聞こう
聞きながら,気づいたことをメモにとろう。
発表のしかたや内容について,印象に残った点をメモにとろう。
数学の「見方・考え方」がどんなところで使われているかに注目しよう。
自分のレポートに取り入れられる考え方があるかどうかに注意して聞こう。
自分の考えと比較してちがう点を伝えよう。
もっとわかりやすい見せ方や説明,調べ方があれば,アドバイスをしてあげよう。
発表している人がわからなかったところについて,いっしょに考えよう。
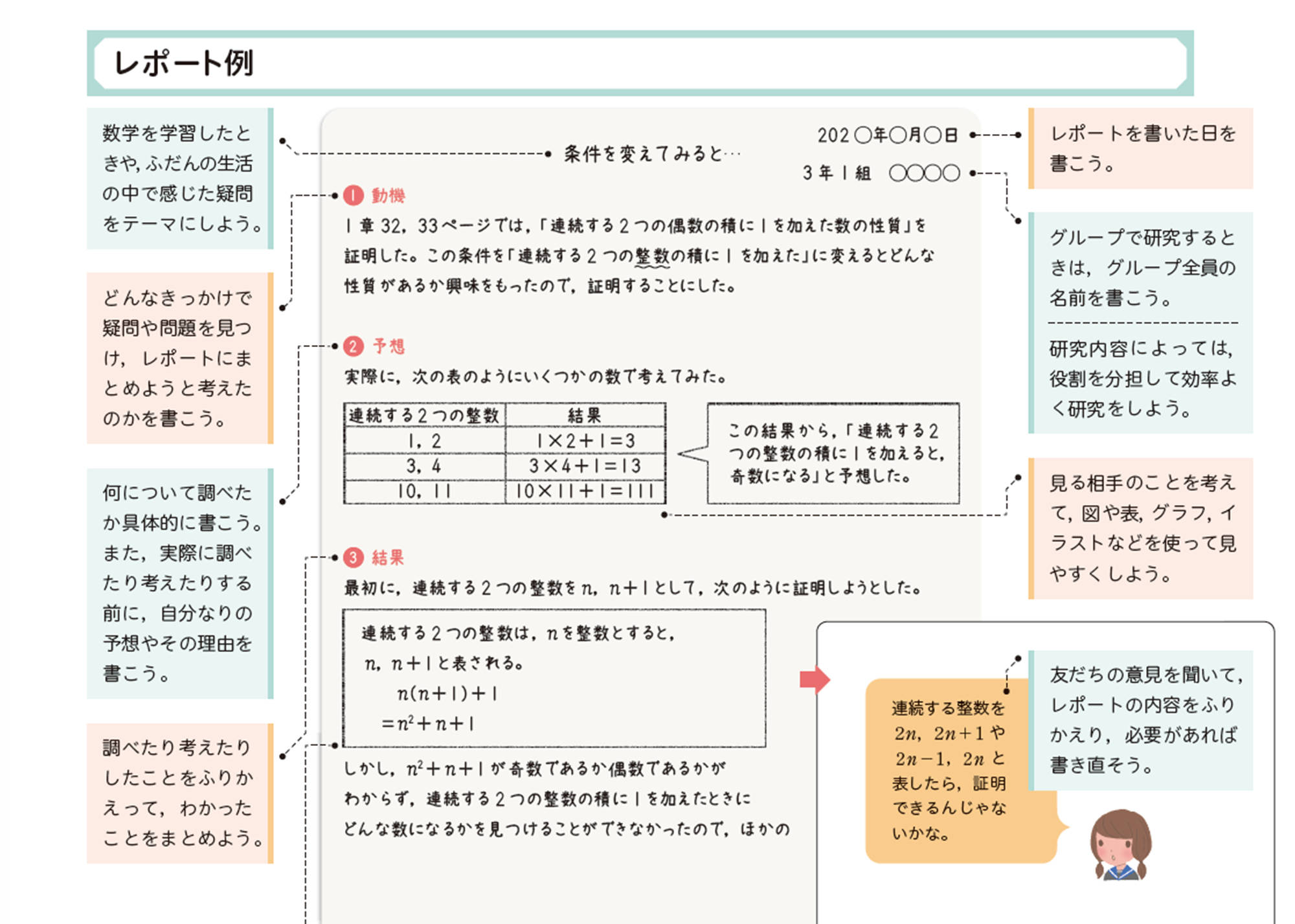
レポート例
レポートを書いた日を書こう。
数学を学習したときや,ふだんの生活の中で感じた疑問をテーマにしよう。
グループで研究するときは,グループ全員の名前を書こう。
研究内容によっては,役割を分担して効率よく研究をしよう。
どんなきっかけで疑問や問題を見つけ,レポートにまとめようと考えたのかを書こう。
何について調べたか具体的に書こう。また,実際に調べたり考えたりする前に,自分なりの予想やその理由を書こう。
見る相手のことを考えて, 図や表,グラフ,イラストなどを使って見やすくしよう。
調べたり考えたりしたことをふりかえって,わかったことをまとめよう。
連続する整数を[mathjax]\(2n\),[mathjax]\(2n+1\)や[mathjax]\(2n-1\),[mathjax]\(2n\)と表したら,証明できるんじゃないかな。
友だちの意見を聞いて,レポートの内容をふりかえり,必要があれば書き直そう。
条件を変えてみると…
202◯年◯月◯日
3年1組 ◯◯◯◯
❶動機
1章32,33ページでは,「連続する2つの偶数の積に1を加えた数の性質」を証明した。この条件を「連続する2 つの整数の積に1 を加えた」に変えるとどんな性質があるか興味をもったので,証明することにした。
❷予想
実際に,次の表のようにいくつかの数で考えてみた。
この結果から,「連続する2つの整数の積に1を加えると,奇数になる」と予想した。
❸結果
最初に,連続する2つの整数をn,[mathjax]\(n+1\)として,次のように証明しようとした。
連続する2つの整数は,nを整数とすると,n,[mathjax]\(n+1\)と表される。
しかし,[mathjax]\(n²+n+1\)が奇数であるか偶数であるかがわからず,連続する2つの整数の積に1を加えたときにどんな数になるかを見つけることができなかったので,ほかの
[mathjax]\(2n²+n\) は整数だから,[mathjax]\(2(2n²+n)+1\) は奇数である。
したがって,連続する2つの整数の積に1を加えると,奇数になる。
必要に応じて,レポートを書きかえたり,書き加えたりしよう。
はじめはわからなかったことでも,先生や友だちに教えてもらって解決したことがあれば書こう。
学習した内容で,どんな考え方を使ったか書こう。
わからなかったことがあれば,どんな点がわからなかったのかを書こう。
くふうしたことや難しかったことなどを書こう。
新たに知ったことや今後調べてみたいことなどを書こう。
引用した資料や参考にした文献があるときは,最後に示しておこう。
例│参考文献 著者名(発行年)『書名』出版社名
総務省統計局
レポートができたら,グループ内で発表しよう!
練習の成果を生かして,みんなの前で発表しよう!