<1年p.294>
小学校の計算
次の計算をしなさい。
1 整数のたし算，ひき算
⑴ [mathjax]\(42+21\)
⑵ [mathjax]\(36+58\)
⑶ [mathjax]\(76+49\)
⑷ [mathjax]\(57-34\)
⑸ [mathjax]\(73-46\)
⑹ [mathjax]\(41-34\)
2 整数のかけ算，わり算
⑴ [mathjax]\(12 \times 7\)
⑵ [mathjax]\(58 \times 5\)
⑶ [mathjax]\(6 \times 98\)
⑷ [mathjax]\(24 \times 36\)
⑸ [mathjax]\(700 \times 40\)
⑹ [mathjax]\(54 \div 9\)
⑺ [mathjax]\(91 \div 13\)
⑻ [mathjax]\(252 \div 63\)
⑼ [mathjax]\(4800 \div 600\)
3 小数のたし算，ひき算
⑴ [mathjax]\(4.7+3.2\)
⑵ [mathjax]\(3.6+2.7\)
⑶ [mathjax]\(2.6+9.4\)
⑷ [mathjax]\(8.7-5.4\)
⑸ [mathjax]\(7.4-2.6\)
⑹ [mathjax]\(5-0.4\)
4 小数のかけ算，わり算
⑴ [mathjax]\(3.4 \times 8\)
⑵ [mathjax]\(4 \times 2.7\)
⑶ [mathjax]\(3.2 \times 1.9\)
⑷ [mathjax]\(4.2 \div 7\)
⑸ [mathjax]\(5.4 \div 0.9\)
⑹ [mathjax]\(7.8 \div 2.6\)
5 分数のたし算，ひき算
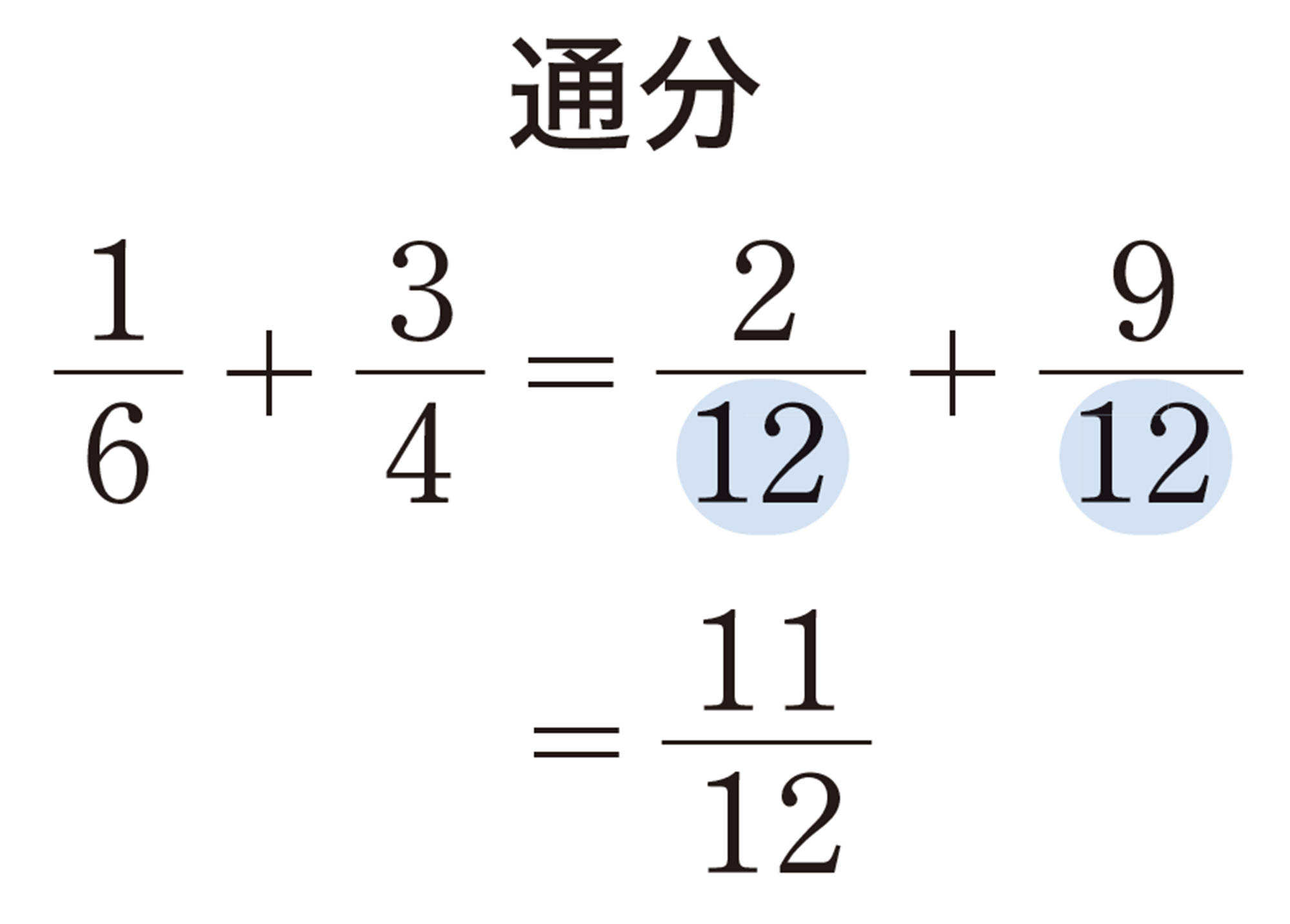
通分
⑴ [mathjax]\(\dfrac{3}{5}+\dfrac{2}{5}\)
⑵ [mathjax]\(\dfrac{1}{3}+\dfrac{1}{5}\)
⑶ [mathjax]\(\dfrac{5}{14}+\dfrac{1}{7}\)
⑷ [mathjax]\(\dfrac{3}{4}+\dfrac{2}{3}+\dfrac{1}{2}\)
⑸ [mathjax]\(\dfrac{7}{8}-\dfrac{3}{8}\)
⑹ [mathjax]\(3-\dfrac{5}{6}\)
⑺ [mathjax]\(\dfrac{11}{6}-\dfrac{11}{9}\)
⑻ [mathjax]\(\dfrac{4}{5}-\dfrac{1}{3}+\dfrac{1}{2}\)
6 分数のかけ算，わり算
約分
⑴ [mathjax]\(\dfrac{7}{8} \times 2\)
⑵ [mathjax]\(\dfrac{2}{7} \times \dfrac{1}{4}\)
⑶ [mathjax]\(\dfrac{5}{12} \times \dfrac{4}{5}\)
⑷ [mathjax]\(\dfrac{3}{4} \times \dfrac{8}{9}\)
⑸ [mathjax]\(\dfrac{4}{5} \div 8\)
⑹ [mathjax]\(\dfrac{2}{3} \div \dfrac{1}{15}\)
⑺ [mathjax]\(\dfrac{2}{5} \div \dfrac{2}{7}\)
⑻ [mathjax]\(\dfrac{7}{8} \div \dfrac{21}{16}\)
<1年p.295 >
1年の復習
1 次の問いに答えなさい。
⑴ 次の数の大小を，不等号を使って表しなさい。
[mathjax]\(-3\)，[mathjax]\(-7\)，[mathjax]\(+2\)
⑵ 絶対値が2以下の整数をすべて答えなさい。
2 次の計算をしなさい。
⑴ [mathjax]\((+5)+(-12)\)
⑵ [mathjax]\((-7)+(-11)\)
⑶ [mathjax]\((-4)-(+13)\)
⑷ [mathjax]\((-5)-(-9)\)
⑸ [mathjax]\(\require{physics} \left(+\dfrac{2}{3}\right)-\require{physics} \left(-\dfrac{1}{4}\right)\)
⑹ [mathjax]\(3.5-7.2\)
⑺ [mathjax]\(-6+(-3)-(-2)\)
⑻ [mathjax]\(3-12+6-2\)
⑼ [mathjax]\(-\dfrac{3}{4}+\require{physics} \left(-\dfrac{5}{6}\right)+\dfrac{5}{12}\)
3 次の計算をしなさい。
⑴ [mathjax]\((+7) \times (-5)\)
⑵ [mathjax]\((-1.5) \times 8\)
⑶ [mathjax]\(\require{physics} \left(-\dfrac{2}{3}\right) \times \require{physics} \left(-\dfrac{6}{5}\right)\)
⑷ [mathjax]\(-2.5 \times 7 \times (-4)\)
⑸ [mathjax]\(-2⁴\)
⑹ [mathjax]\((-54) \div (-6)\)
⑺ [mathjax]\(\dfrac{9}{4} \div \require{physics} \left(-\dfrac{3}{8}\right)\)
⑻ [mathjax]\(45 \div (-9) \times 6\)
⑼ [mathjax]\(8 \div \require{physics} \left(-\dfrac{4}{3}\right) \times \require{physics} \left(-\dfrac{3}{5}\right)\)
4 次の計算をしなさい。
⑴ [mathjax]\(4+(-3) \times 9\)
⑵ [mathjax]\(-\dfrac{1}{4}-(-2) \div 4\)
⑶ [mathjax]\(27 \div \{ -3-(-6) \}\)
⑷ [mathjax]\(-3² \times 4\)
⑸ [mathjax]\(9 \div (-6)²\)
⑹ [mathjax]\(3 \times\require{physics} \left(-\dfrac{1}{2}\right)^{2} \div (-6)\)
⑺ [mathjax]\((-5) \times 2-(-12) \div 4\)
⑻ [mathjax]\(\dfrac{5}{8} – \require{physics} \left(-\dfrac{3}{4}\right)^{2}\)
⑼ [mathjax]\(\dfrac{5}{6} \times (-3)-2 \div \dfrac{4}{7}\)
⑽ [mathjax]\(-6² \div \{ (-8)-4 \} \times \dfrac{1}{9}\)
⑾ [mathjax]\(\require{physics} \left(\dfrac{8}{7}-\dfrac{4}{3}\right) \times 21\)
⑿ [mathjax]\(2.3 \times (-8)+2 \times (-2.3)\)
5 右の表で，上の段は，ある図書館の月曜日から金曜日までの利用者数を，下の段は，水曜日を基準にして，それぞれの利用者数を表したものです。
⑴ ア，イの値を求めなさい。
⑵ 5日間の利用者数の平均を求めなさい。
6 [mathjax]\(432\) にできるだけ小さい自然数をかけて，その積がある自然数の2乗になるようにします。どんな数をかければよいですか。
<1年p.296 >
1 次の式を，文字式の表し方にしたがって表しなさい。
⑴ [mathjax]\(b \times (-2) \times a\)
⑵ [mathjax]\(x \times x \times 3 \times y\)
⑶ [mathjax]\((a+b) \div 7\)
⑷ [mathjax]\(4 \times x-y \div 5\)
2 次の数量を，文字式で表しなさい。
⑴ 1個x円のケーキ2個を買って，[mathjax]\(1000\) 円出したときのおつり
⑵ 片道 [mathjax]\(a\) mの道のりを，行きは分速 [mathjax]\(70\) m，帰りは分速 [mathjax]\(60\) mの速さで歩いたとき，往復にかかる時間
3 次の問いに答えなさい。
⑴ [mathjax]\(x=-4\) のとき，[mathjax]\(x²+3\) の値を求めなさい。
⑵ [mathjax]\(x=2\) ，[mathjax]\(y=-3\) のとき，[mathjax]\(4x-2y\) の値を求めなさい。
4 次の計算をしなさい。
⑴ [mathjax]\(4a-7a\)
⑵ [mathjax]\(-1.2x-4.9x\)
⑶ [mathjax]\(\dfrac{1}{3}x-\dfrac{3}{4}x\)
⑷ [mathjax]\(3x-5-8x+6\)
⑸ [mathjax]\(-0.7a+0.3-0.3a-1.2\)
⑹ [mathjax]\((7x-11)+(5x-1)\)
⑺ [mathjax]\(\require{physics} \left(\dfrac{1}{4}x-\dfrac{3}{7}\right)+\require{physics} \left(-\dfrac{3}{4}x-\dfrac{5}{7}\right)\)
⑻ [mathjax]\((-6a+1)-(5-2a)\)
⑼ [mathjax]\(\require{physics} \left(-\dfrac{1}{2}x+9\right)-\require{physics} \left(\dfrac{2}{3}x-2\right)\)
⑽ [mathjax]\((2y-5) \times (-4)\)
⑾ [mathjax]\(9x \div \require{physics} \left(-\dfrac{5}{3}\right)\)
⑿ [mathjax]\((12x-18) \div 6\)
⒀ [mathjax]\(5(a-3)+3(-2a+7)\)
⒁ [mathjax]\(-(2x+3)-3(5x-6)\)
⒂ [mathjax]\(\dfrac{1}{3}(6x-9)-\dfrac{3}{4}(12x+4)\)
⒃ [mathjax]\(2(6a-3)-(10-5a) \div 5\)
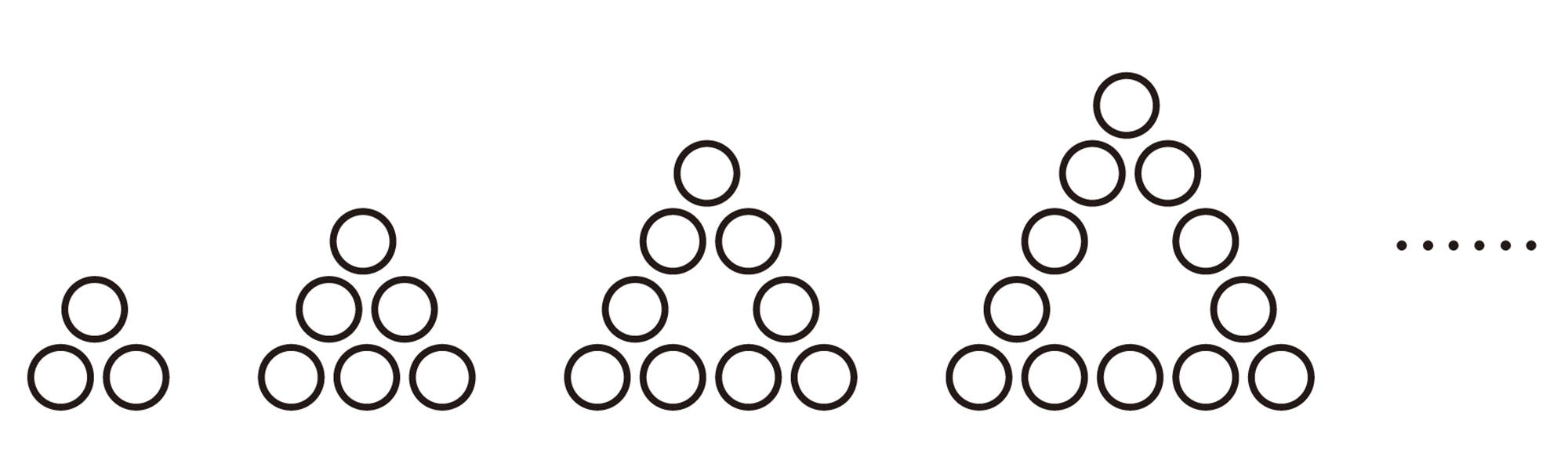
5 次の図のように，碁石を並べて正三角形をつくるとき，下の問いに答えなさい。
⑴ 1辺に並べる碁石の個数が8個の正三角形をつくるとき，碁石は何個必要ですか。
⑵ 1辺に並べる碁石の個数がa個の正三角形をつくるとき，碁石は何個必要ですか。
<1年p.297 >
3章 1次方程式
1 次の数量の関係を，等式や不等式で表しなさい。
⑴ [mathjax]\(38\) 枚の折り紙をx枚ずつ5人に配ると3枚あまった。
⑵ x円の商品を2割引きで買い，[mathjax]\(5000\) 円札を出したらおつりがあった。
2 次の方程式や，比例式を解きなさい。
⑴ [mathjax]\(4x+7=15\)
⑵ [mathjax]\(5x-9=6\)
⑶ [mathjax]\(8x-2=9x\)
⑷ [mathjax]\(2x-7=5x+11\)
⑸ [mathjax]\(-x+22=2x+7\)
⑹ [mathjax]\(-2x-3=5x+18\)
⑺ [mathjax]\(17-5x=-9x-13\)
⑻ [mathjax]\(12:x=8:6\)
⑼ [mathjax]\(5:4=x:18\)
3 次の方程式や，比例式を解きなさい。
⑴ [mathjax]\(6x-4(x-7)=18\)
⑵ [mathjax]\(3x+9=5(2x-3)-4\)
⑶ [mathjax]\(2.7x+0.8=1.5x-1.6\)
⑷ [mathjax]\(0.32x-1.4=0.4x-0.68\)
⑸ [mathjax]\(\dfrac{2}{5}x-2=\dfrac{x}{3}\)
⑹ [mathjax]\(\dfrac{1}{2}(x-2)=\dfrac{5}{6}(x-4)\)
⑺ [mathjax]\(\dfrac{2}{3}x-\dfrac{3}{4}=\dfrac{5}{6}x+\dfrac{1}{4}\)
⑻ [mathjax]\(\dfrac{5x-4}{3}=\dfrac{x+2}{2}\)
⑼ [mathjax]\(\dfrac{2x-14}{3}=\dfrac{x+2}{2}+3x\)
⑽ [mathjax]\(4:6=(x-5):9\)
⑾ [mathjax]\(2:5=(x-2):(x+7)\)
⑿ [mathjax]\(\require{physics} \left(\dfrac{1}{2}x-3\right):\require{physics} \left(\dfrac{1}{3}x+1\right)=3:5\)
4 xについての方程式 [mathjax]\(3(x-1)-2a=4\) の解が [mathjax]\(-3\) のとき，[mathjax]\(a\) の値を求めなさい。
5 りんご5個ともも4個を買ったところ，代金の合計が [mathjax]\(1500\) 円でした。もも1個の値段がりんご1個の値段より [mathjax]\(60\) 円高いとき，りんご1個の値段ともも1個の値段を求めなさい。
6 ボールが何個かと，それを入れるための箱が何箱かあります。1箱に [mathjax]\(90\) 個ずつボールを入れていくと，[mathjax]\(17\) 個あまりました。また，1箱に [mathjax]\(100\) 個ずつボールを入れていくと，最後の箱には7個しか入りませんでした。ボールは全部で何個ありますか。
7 ある液体肥料は，肥料 [mathjax]\(150\) mLに対して水 [mathjax]\(250\) mLで薄めて使います。肥料が [mathjax]\(78\) mL しかないとき，何mLの水で薄めればよいでしょうか。
<1年p.298 >
4章 比例と反比例
1 次の⑴〜⑶について， [mathjax]\(y\) を [mathjax]\(x\) の式で表しなさい。このうち， [mathjax]\(y\) が [mathjax]\(x\) に比例するものはどれですか。また， [mathjax]\(y\) が [mathjax]\(x\) に反比例するものはどれですか。
⑴ 1本 [mathjax]\(80\) 円の鉛筆 [mathjax]\(x\) 本を買ったときの代金は [mathjax]\(y\) 円である。
⑵ [mathjax]\(10\) Lの燃料を1時間に [mathjax]\(x\) Lずつ使うと， [mathjax]\(y\) 時間使うことができる。
⑶ 1辺 [mathjax]\(x\) cmの正三角形のまわりの長さは [mathjax]\(y\) cmである。
2 次の問いに答えなさい。
⑴ [mathjax]\(y\) は [mathjax]\(x\) に比例し，[mathjax]\(x=-2\) のとき [mathjax]\(y=-6\) です。 [mathjax]\(y\) を [mathjax]\(x\) の式で表しなさい。また，[mathjax]\(x=3\) のときの [mathjax]\(y\) の値を求めなさい。
⑵ [mathjax]\(y\) は [mathjax]\(x\) に反比例し，[mathjax]\(x=6\) のとき [mathjax]\(y=-2\) です。 [mathjax]\(y\) を [mathjax]\(x\) の式で表しなさい。また，[mathjax]\(x=-4\) のときの [mathjax]\(y\) の値を求めなさい。
3 A 市からB 市まで自動車で行くのに，時速 [mathjax]\(40\) kmで走ると3時間かかります。この道のりを時速 [mathjax]\(x\) kmで走ると [mathjax]\(y\) 時間かかるとして，次の問いに答えなさい。
⑴ [mathjax]\(y\) を [mathjax]\(x\) の式で表しなさい。
⑵ 時速 [mathjax]\(50\) kmで走ると何時間何分かかりますか。
⑶ 2時間で行くためには，時速何kmで走ればよいですか。
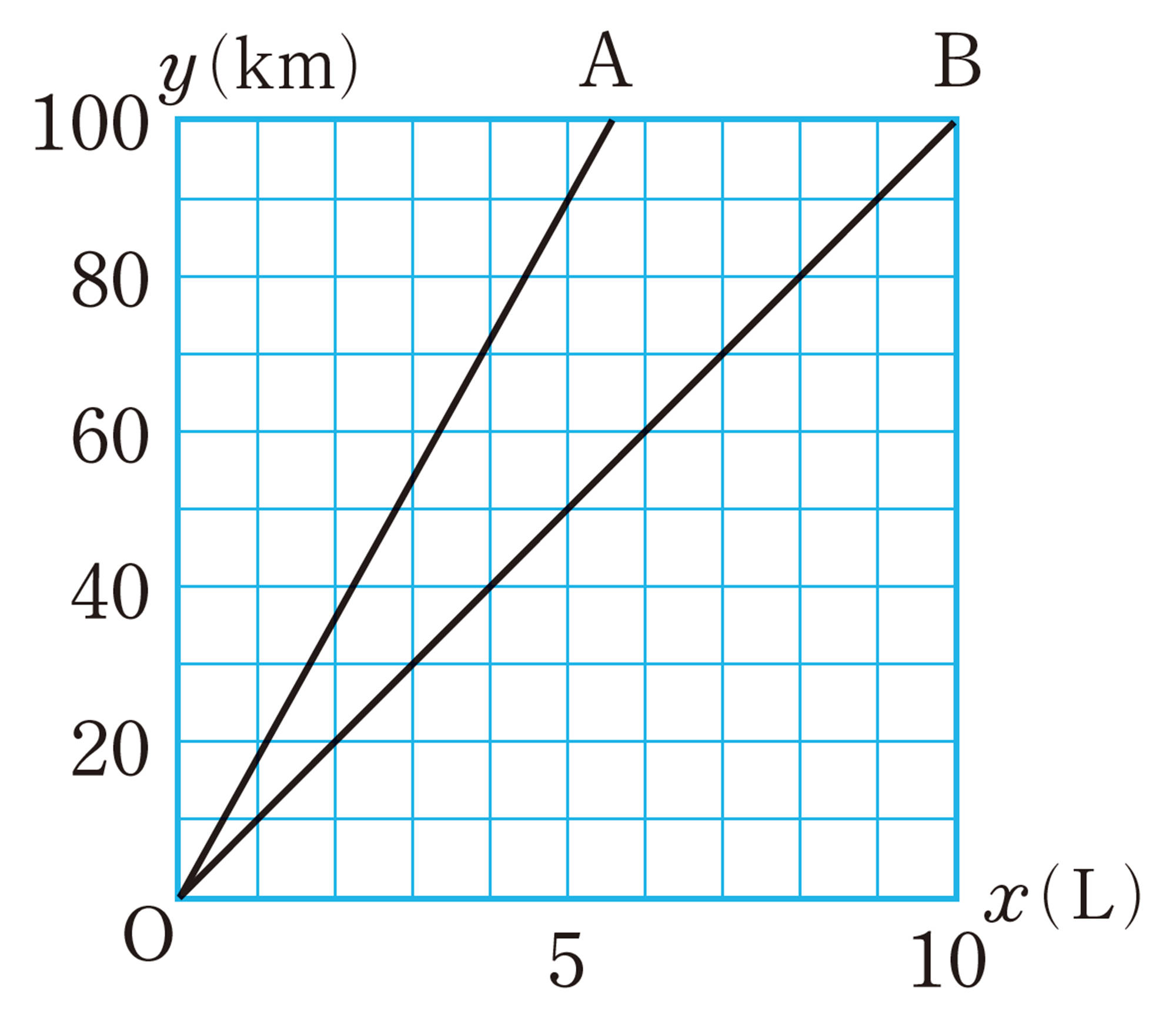
4 右のグラフは，自動車 A ，B がある一定の速さで走ったときの，消費したガソリンの量と走った距離との関係を表したものです。次の問いに答えなさい。
⑴ 自動車 A はガソリン1Lで何km走ることができますか。
⑵ ガソリン [mathjax]\(x\) Lで [mathjax]\(y\) km走ることができるとして，自動車A ，B それぞれについて， [mathjax]\(y\) を [mathjax]\(x\) の式で表しなさい。
⑶ 自動車 A ，B が，それぞれこの速さで [mathjax]\(270\) kmの距離を走ったとするとき，消費するガソリンの量は，どちらがどれだけ多いかを求めなさい。
<1年p.299 >
5章 平面図形
1 右の図の [mathjax]\(\triangle ABC\) で，次の点を作図によって求めなさい。
⑴ [mathjax]\(\angle B\)の二等分線と辺 AC との交点 P
⑵ 2点 B，C から等しい距離にある辺 AB 上の点 Q
2 右の図の線分 AB を直径とする円 O を作図しなさい。また，点 A を接点とする円 O の接線を作図しなさい。
3 右の図のように，地点 A，B と壁があります。地点 A からスタートし，壁にタッチして地点 B まで走るとき，走る距離を最短にするには，壁のどの点にタッチすればよいですか。タッチする点 P を作図によって求めなさい。
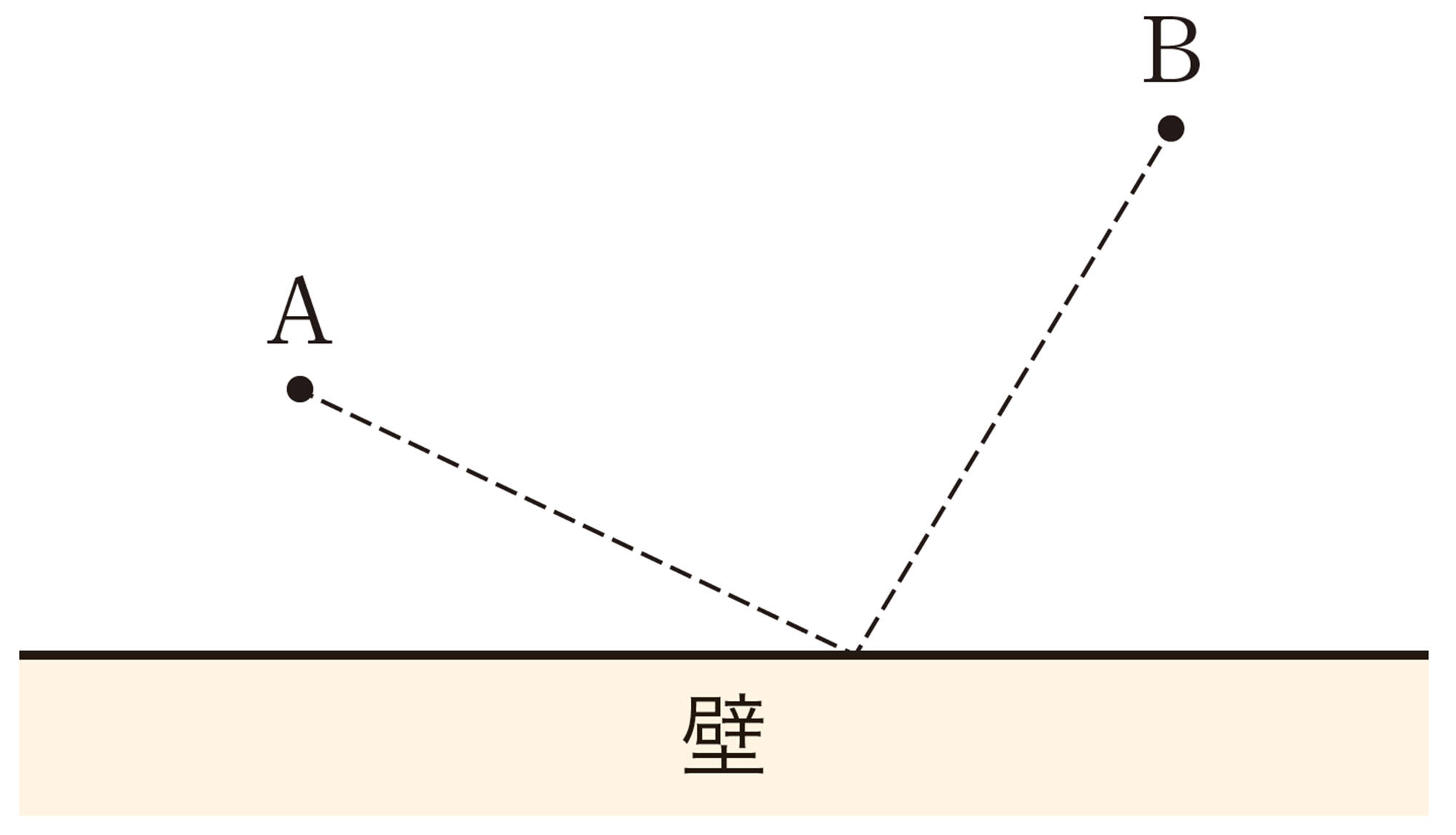
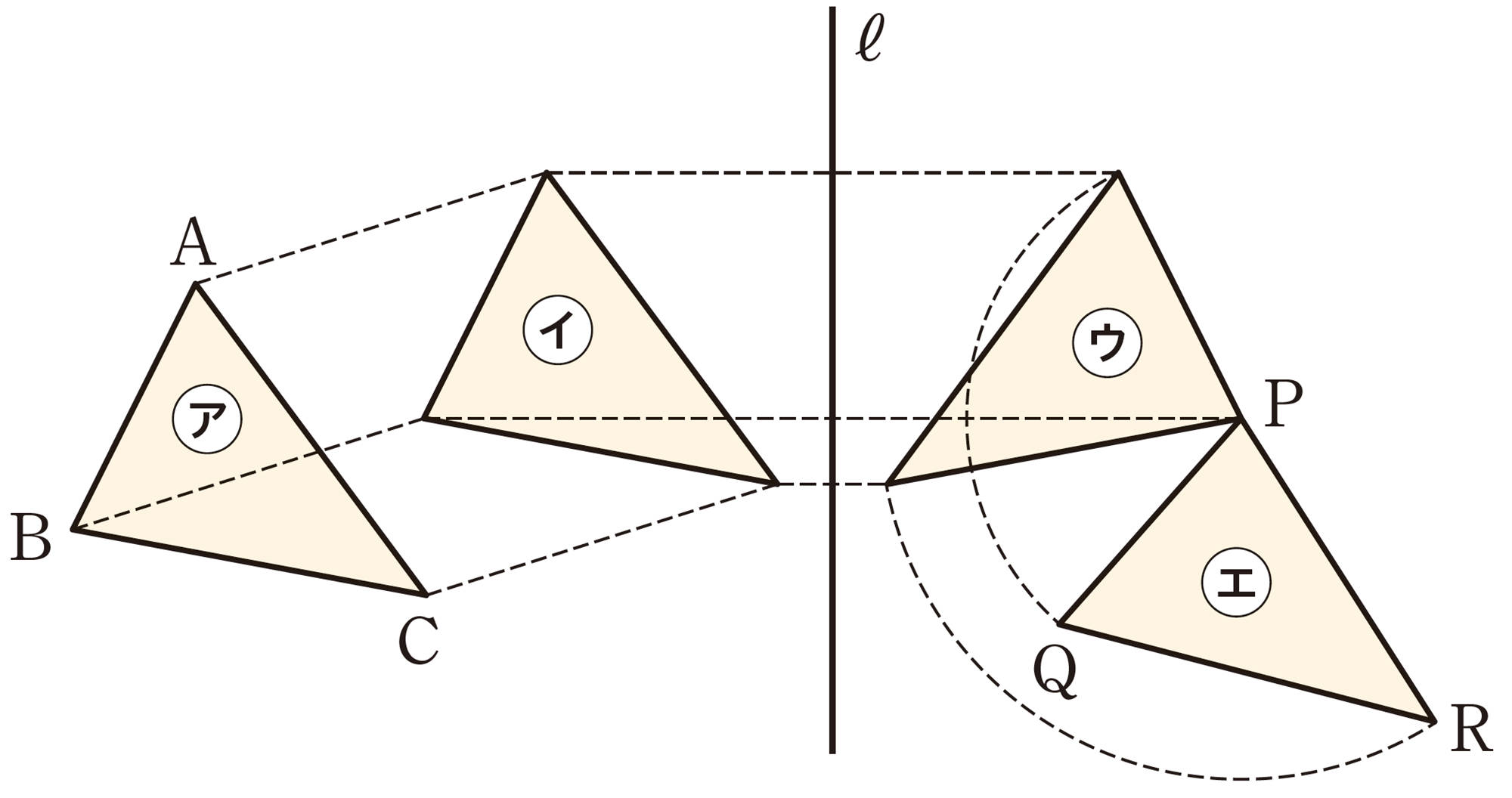
4 下の図は，三角形㋐を三角形㋓の位置まで移動したことを示しています。次の問いに答えなさい。
⑴ ㋐を㋑，㋑を㋒，㋒を㋓に移動するとき，それぞれどんな移動をしていますか。移動の種類を答えなさい。
⑵ ㋐の辺 AC に対応するのは，㋓のどの辺ですか。
<1年p.300 >
6章 空間図形
1 右の図の正五角柱について，次の辺や面をいいなさい。
⑴ 面 ABCDE と平行な辺
⑵ 辺 CH と平行な辺
⑶ 辺 EJ と垂直な面
⑷ 辺 AE とねじれの位置にある辺
2 右の図は，底面の半径が [mathjax]\(6\) cm，母線の長さが [mathjax]\(15\) cmの円錐の展開図です。次の問いに答えなさい。
⑴ おうぎ形の中心角を求めなさい。
⑵ この円錐の側面積を求めなさい。
⑶ この円錐の表面積を求めなさい。
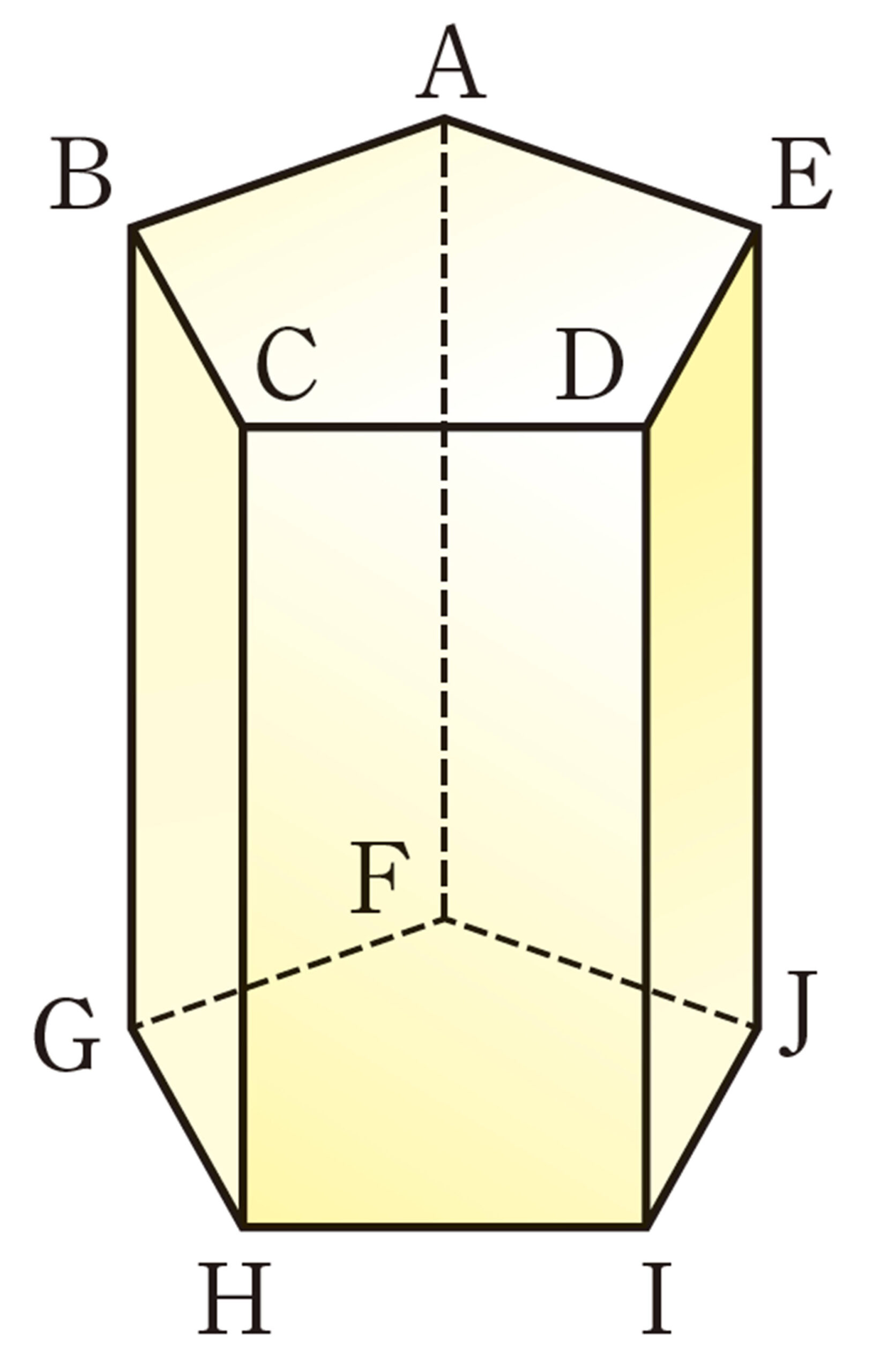
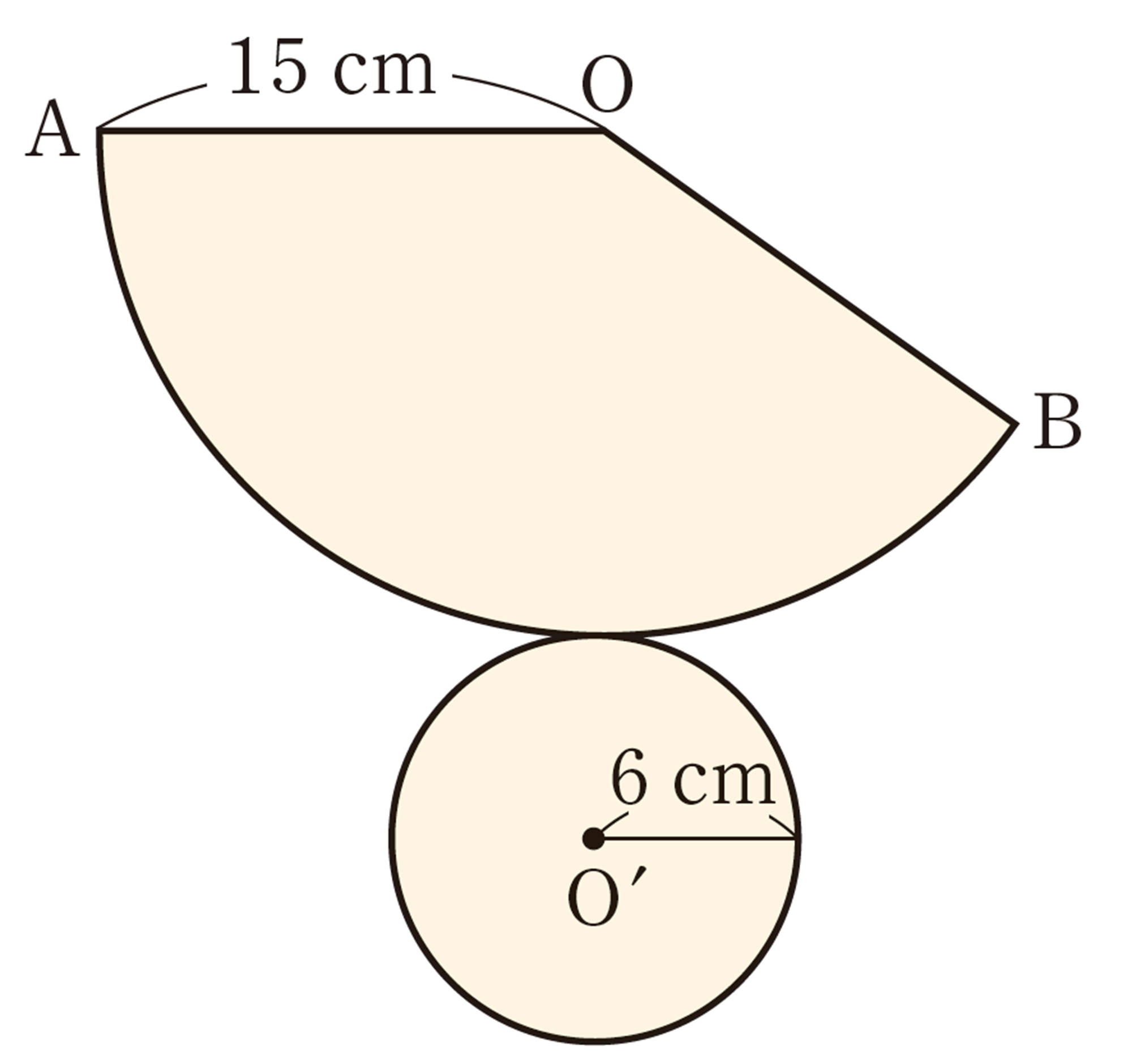
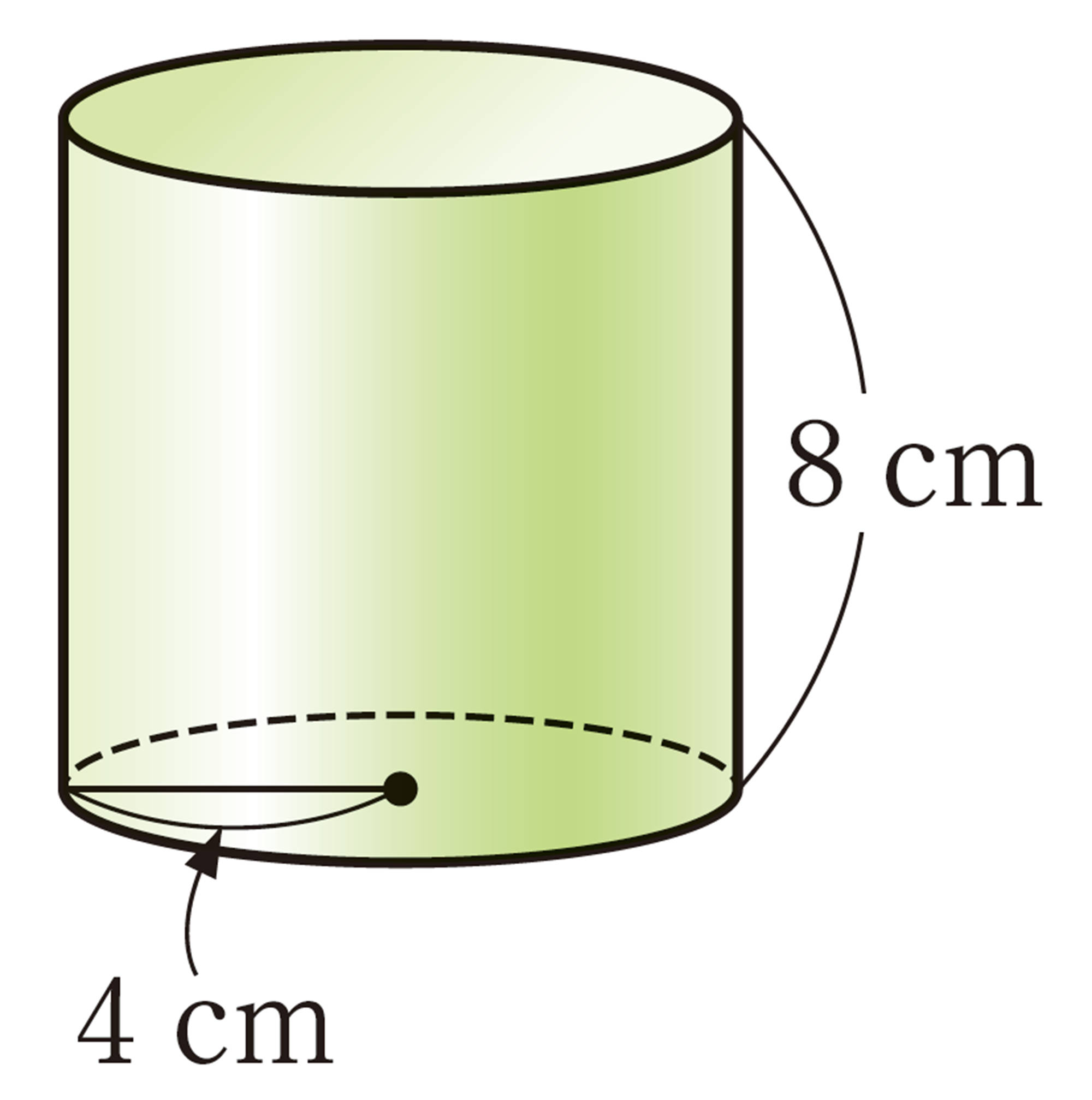
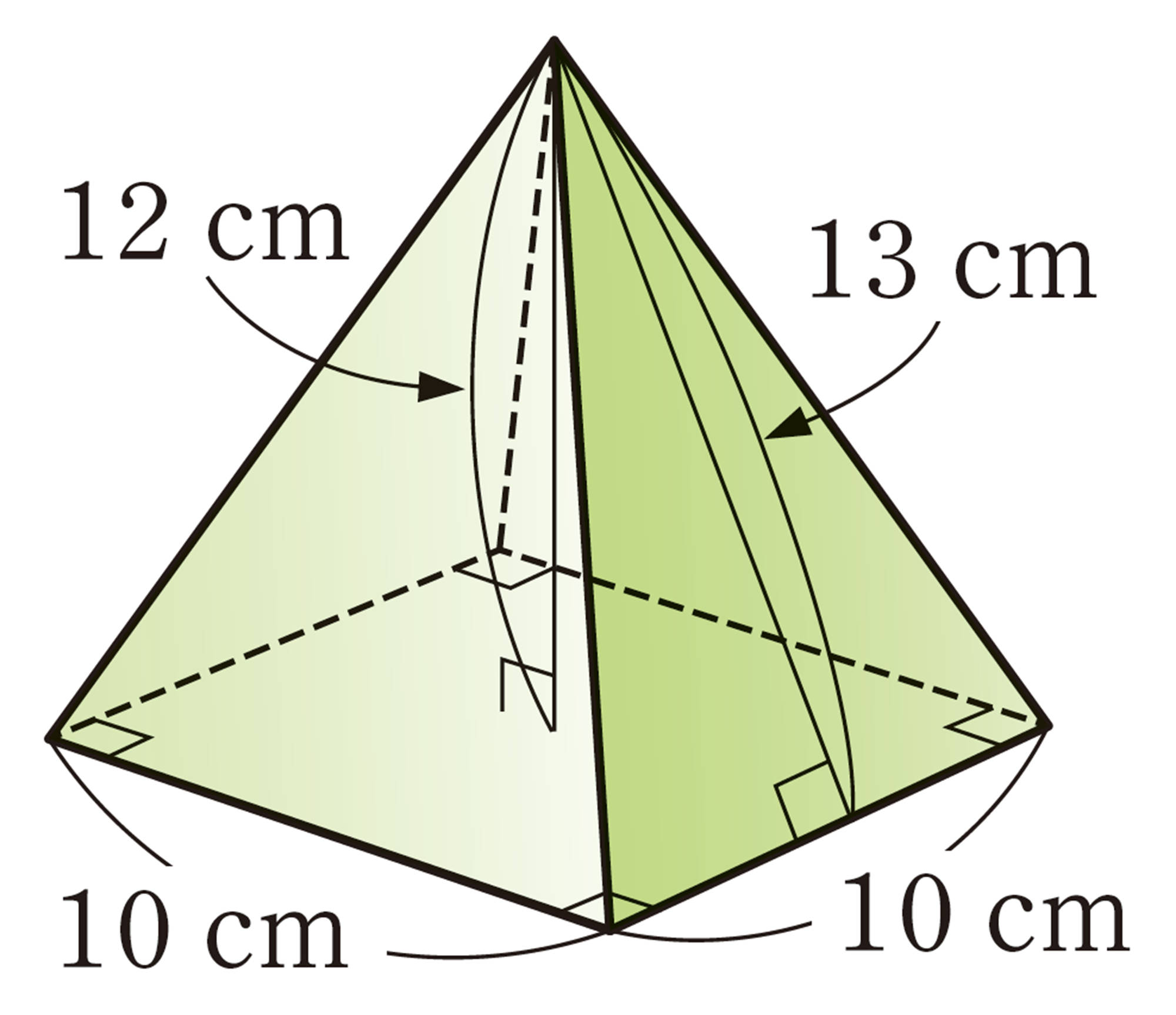
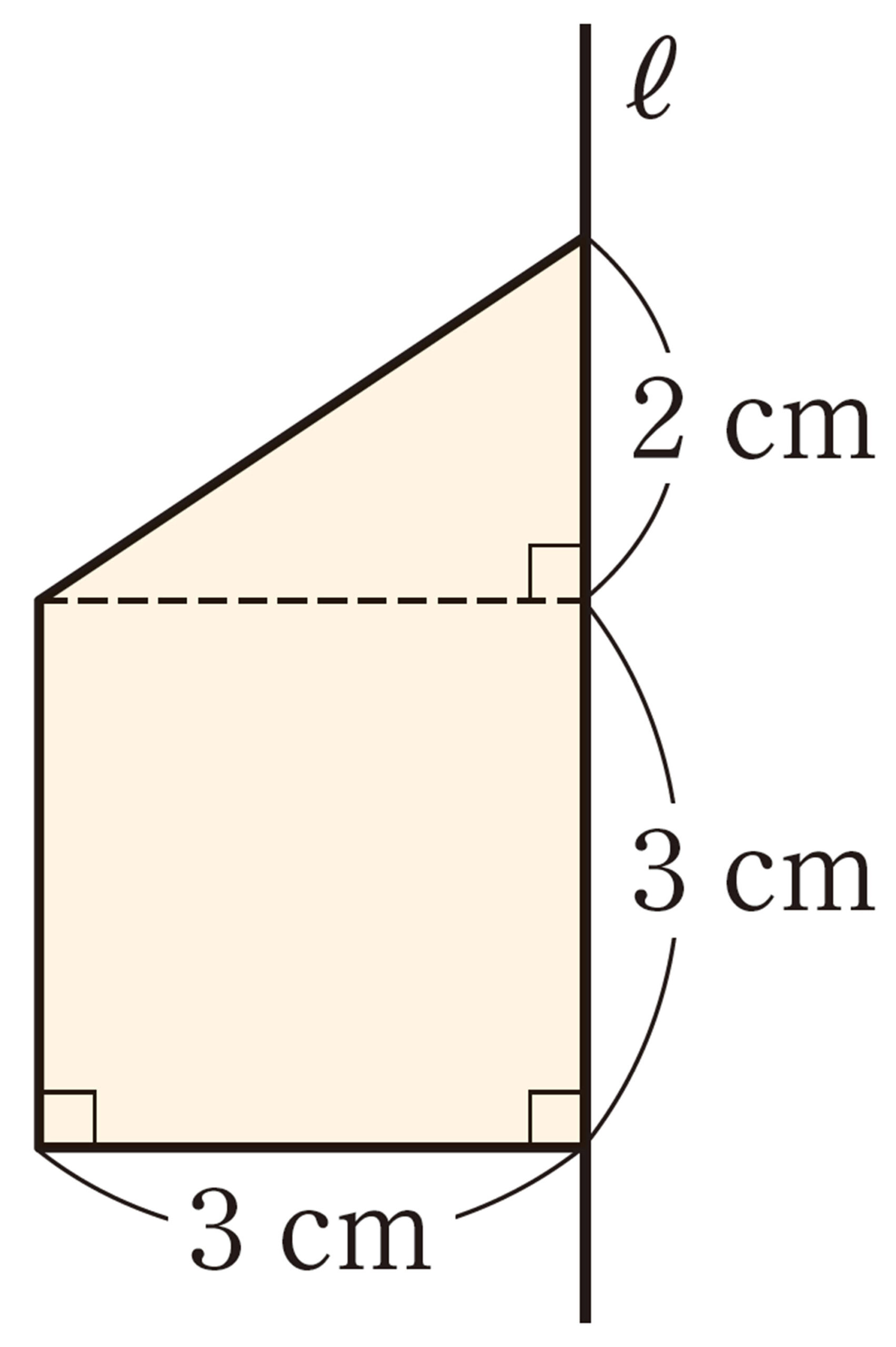
3 次の立体の表面積と体積を求めなさい。
⑴ 円柱
⑵ 正四角錐
⑶ 球
4 右の図のような四角形を，直線 [mathjax]\(ℓ\) を軸として1回転してできる立体について，次の問いに答えなさい。
⑴ 見取図をかきなさい。
⑵ 投影図をかきなさい。
⑶ 体積を求めなさい。
<1年p.301 >
7章 データの活用
1 右の図は，あるクラスで行われた [mathjax]\(10\) 点満点のテストの結果をヒストグラムに表したものです。次の問いに答えなさい。
⑴ テストを受けた生徒の人数を求めなさい。
⑵ 中央値を求めなさい。
⑶ 平均値を小数第一位まで求めなさい。
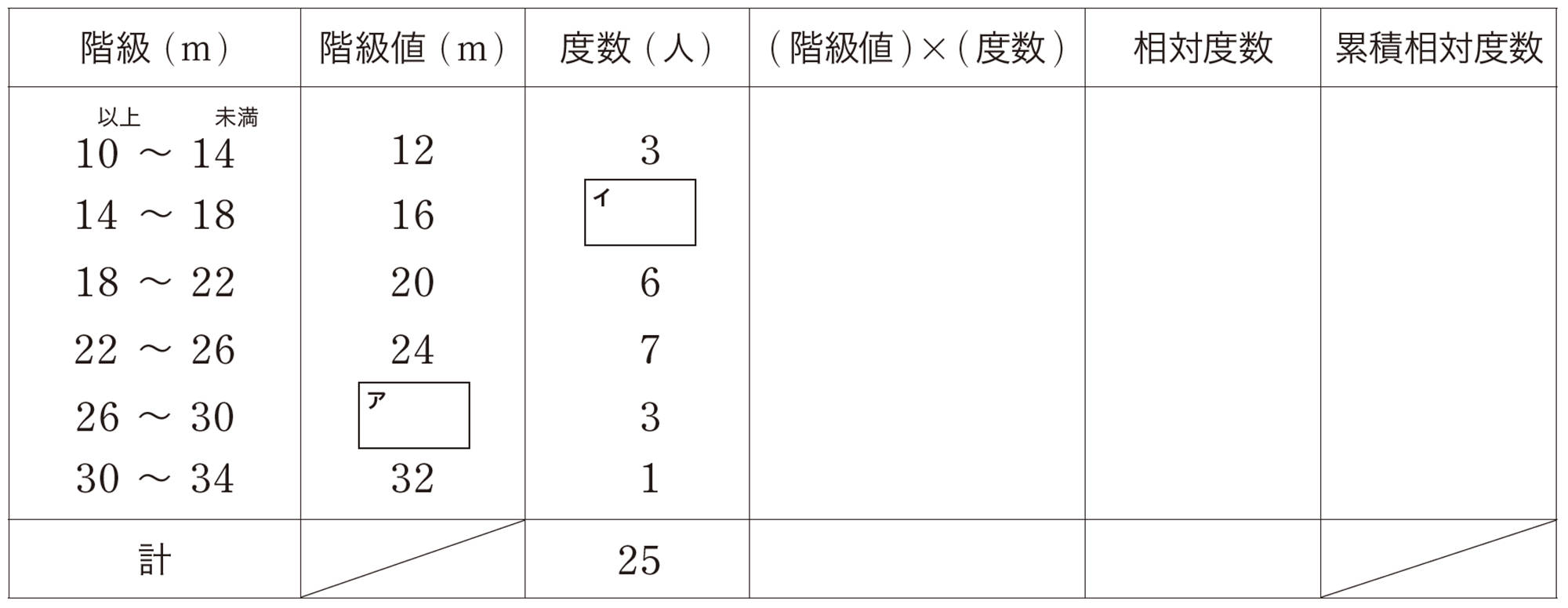
2 次の度数分布表は，1年生の男子 [mathjax]\(25\) 人のハンドボール投げの記録をまとめたものです。下の問いに答えなさい。
⑴ ア，イにあてはまる値を書き入れなさい。
⑵ 中央値がふくまれる階級をいいなさい。
⑶ 最頻値をいいなさい。
⑷ [mathjax]\((\mathsf{階級値}) \times (\mathsf{度数})\) の欄を記入し，平均値を小数第一位まで求めなさい。
⑸ 相対度数を小数第二位まで求め，相対度数，累積相対度数の欄を記入しなさい。
⑹ 全体の [mathjax]\(56\) ％の生徒は，何m未満であるといえますか。
3 右のような将棋の駒を投げて，立った状態になる回数を調べたところ，次の表のようになりました。表を完成させ，将棋の駒が立つ確率を小数第二位まで求めなさい。
