教科書アドバイザー「マスマス！」

１年１章３節－５（親ページ）061-064

gkt-horizontal-line

<1年p.61>

１章のまとめの問題　解答　P.302〜303　基本

１　次のにあてはまる数やことばをいいなさい。

⑴　2より3小さい数はであり， $- 4$ より6大きい数はである。
⑵　「いまから5年前」を $- 5$ 年と表すとき，「いまから5年後」はと表すことができる。
⑶　絶対値が7である数は，とである。
⑷　ある数に負の数を加えると，もとの数よりなる。また，ある数から負の数をひくと，もとの数よりなる。

２　次の各組の数の大小を，不等号を使って表しなさい。

⑴　 $- 3$ ， $1$

⑵　 $- 6$ ， $- 7$

⑶　 $4$ ， $- 5$ ， $- 2$

３　次の計算をしなさい。

⑴　 $6 + (- 4)$

⑵　 $(- 1) + (- 9)$

⑶　 $(- 7) - (+ 8)$

⑷　 $(- \frac{2}{3}) - (- \frac{1}{3})$

⑸　 $- 2 + 6 - 5 + 7$

⑹　 $3 - (+ 4) - (- 9)$

⑺　 $(- 8) \times (+ 2)$

⑻　 ${(- \frac{3}{4})}^{2}$

⑼　 $0.4 \times (- 0.2)$

⑽　 $(- 28) \div (- 4)$

⑾　 $9 \div (- 12)$

⑿　 $(- \frac{9}{14}) \div \frac{6}{7}$

４　次の計算をしなさい。

⑴　 $- 2 \times 9 \times (- 5)$

⑵　 $3 \div (- 6) \times 8$

⑶　 $9 + 2 \times (- 3)$

⑷　 $- 2 \times (5 - 9)$

⑸　 $(- 6) \times 2 - 21 \div (- 7)$

⑹　 $36 \div (- 3 ²)$

⑺　 $(\frac{1}{4} - \frac{2}{3}) \times 12$

⑻　 $\frac{5}{6} - \frac{1}{2} \div (- 3)$

５　次の各組の数の最大公約数と最小公倍数を求めなさい。

⑴　 $32$ ， $40$

⑵　 $36$ ， $54$

gkt-horizontal-line

<1年p.62>

６　次の表は，弘前市の2022年1月1日から10日までの最高気温と最低気温を表したものです。下の問いに答えなさい。

2022年1月の弘前市の最高気温と最低気温

\begin{array}{ccc} 日 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ 最高気温(℃) & - 1.4 & 4.8 & - 0.2 & - 1.3 & - 0.6 & 3.1 & 0.6 & 2.9 & 4.1 & 3.4 \\ 最低気温(℃) & - 8.4 & - 3.9 & - 5.0 & - 6.4 & - 6.1 & - 7.5 & - 3.0 & - 3.1 & - 3.3 & - 6.0 \end{array}

⑴　最高気温と最低気温の差がもっとも大きかったのは1月何日ですか。
⑵　最高気温と最低気温の差がもっとも小さかったのは1月何日ですか。

gkt-horizontal-line

１章のまとめの問題　応用

１　次の計算をしなさい。

⑴　 $- 6 ² - (5 - 8) ²$

⑵　 $(- 4) ² + 16 \div (- 4 ²)$

⑶　 $- \frac{5}{14} + \frac{6}{7} \times \frac{1}{3}$

⑷　 $\frac{1}{3} - (- \frac{7}{8}) \div \frac{7}{2}$

⑸　 $\frac{1}{8} - {(- \frac{3}{4})}^{2} \div 3$

⑹　 $6 \div (- \frac{3}{2}) + \frac{5}{2} \times (- 4)$

２　右の表で，上の段は，A，B，C，D，E の5人の新体力テストの得点を，下の段は，C の得点を基準として，それぞれの得点を表したものです。次の問いに答えなさい。

\begin{array}{ccc} A & B & C & D & E \\ 得点(点) & 52 & 56 & 55 & 60 & 47 \\ C を基準と \\ した得点(点) & + 1 & 0 \end{array}

⑴　表を完成させなさい。
⑵　Cの得点を基準として，5人の得点の平均を求めなさい。ただし，答えを求めるための式も書きなさい。

３　次のそれぞれの数をすべて求めなさい。

⑴　71と103のどちらをわっても，7あまる自然数
⑵　9でわっても，15でわっても4あまる2桁の自然数

gkt-horizontal-line

<1年p.63>

　活用

１　悠さんの家では，屋根に太陽電池を設置して，太陽光による自家発電をすることにしました。悠さんは，「発電した電力と消費した電力のどちらが大きいかを調べたい」と考えました。ある1日の 2時間ごとの時間帯と太陽電池によって発電した電力，消費した電力，余剰電力（発電した電力 $-$ 消費した電力 $=$ 余剰電力）を調べたところ，それぞれ次の表のようになりました。下の問いに答えなさい。

\begin{array}{ccc} 時間帯(時) & 0 〜 2 & 2 〜 4 & 4 〜 6 & 6 〜 8 & 8 〜 10 & 10 〜 12 \\ 発電した電力 (k W h) & 0 & 0 & 0.02 & 1.12 & 2.53 \\ 消費した電力 (k W h) & 0.9 & 0.8 & 2.4 & 1.6 & 0.8 \\ 余剰電力 (k W h) & - 0.9 & - 0.6 & - 1.28 & 0.93 & 2.3 \end{array}

\begin{array}{ccc} 12 〜 14 & 14 〜 16 & 16 〜 18 & 18 〜 20 & 20 〜 22 & 22 〜 24 \\ 2.98 & 2.05 & 1.41 & 0 \\ 0.6 & 1.2 & 3.46 & 2.74 & 2.2 \\ 2.38 & 0.85 & - 1 & - 2.63 & - 2.74 & - 2.2 \end{array}

＊1 kWh(キロワットアワー)は，1 kWを1時間で発電または消費した電力量のことをいう。

⑴　上の表では，発電した電力が0 kWhになる時間帯があります。その理由を説明しなさい。
⑵　上の表を完成させなさい。
⑶　余剰電力がもっとも小さい時間帯と，もっとも大きい時間帯を答えなさい。
⑷　この日1日で考えると，「発電した電力と消費した電力ではどちらが大きかったか」を調べる方法を説明しなさい。

＞＞　　関連する職業・仕事　　［エンジニア］

gkt-horizontal-line

<1年p.64>

　深めよう　時刻がもどる？

3 月2 日に成田を出発する国際線の飛行機の時刻表を見ていたら，出発する時刻よりも到着する時刻の方が早い時刻になっているものがありました。

\begin{array}{ccc} 発地 & 出発 & 到着 & 所要時間 & 着地 \\ 成田 & 3 / 2 17 : 55 & 3 / 2 10 : 55 & 10 時間 & ロサンゼルス \end{array}

avatar

出発した時刻より到着した時刻の方が早いね。どうしてかな。

時差があると聞いたことがあるよ。

avatar

私たちがふだん用いている時刻は，地球上の位置によってちがいがあります。国や地域によって生じる時刻の差を時差といいます。

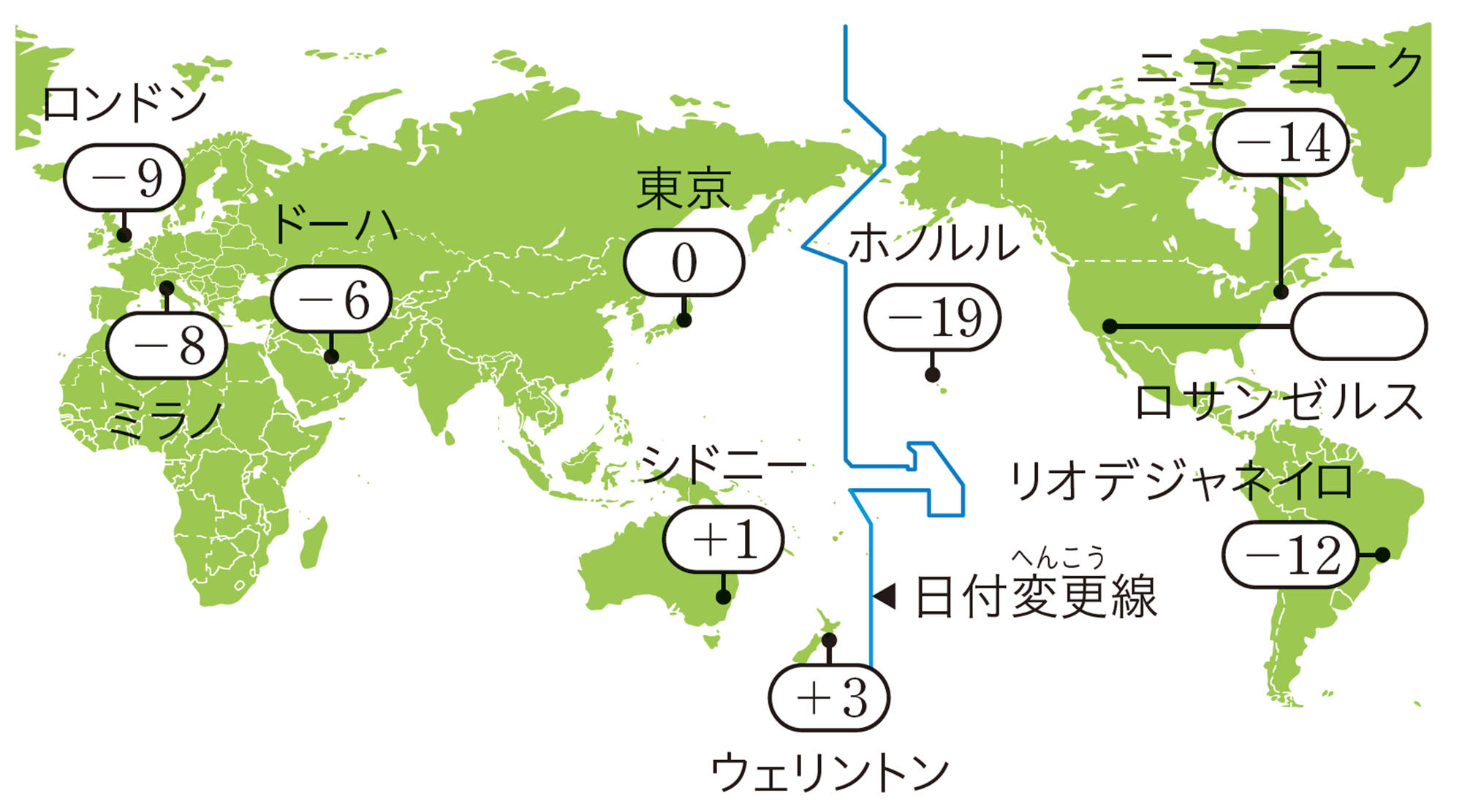
次の図は，東京の時刻を基準としたときの各都市の時差を示したものです。

右の図から，東京の時刻が20 時のとき，

シドニーの時刻は， $20 + 1$ より21 時

ロンドンの時刻は， $20 - 9$ より11 時

になります。

①　ロンドンの時刻を基準としたとき，ドーハの時差とホノルルの時差を求め，正の数，負の数で表しましょう。

②　成田発ロサンゼルス行きの飛行機が，ロサンゼルスに到着するときの東京の時刻を求めましょう。また，東京を基準としたとき，東京とロサンゼルスの時差を正の数，負の数で表しましょう。

③　次の表は，3 月2 日のロサンゼルス発成田行きの飛行機の時刻表です。飛行機の所要時間を求めましょう。

\begin{array}{ccc} 発地 & 出発 & 到着 & 所要時間 & 着地 \\ ロサンゼルス & 3 / 2 10 : 35 & 3 / 3 15 : 30 & 成田 \end{array}

１章のまとめの問題　解答　P.302〜303　基本

１章のまとめの問題　応用

活用

深めよう　時刻がもどる？

＜ミライ教科書３学年分もくじ＞

＜スグラパ＞

＜ドリルまとめ＞

１章のまとめの問題 解答 P.302〜303 基本

１章のまとめの問題 応用

活用

深めよう 時刻がもどる？

＜ミライ教科書３学年分もくじ＞

＜スグラパ＞

＜ドリルまとめ＞

１章のまとめの問題　解答　P.302〜303　基本

１章のまとめの問題　応用

　活用

　深めよう　時刻がもどる？