<1年p.268>
7章 「データの活用」を学んで
できるようになったこと 身のまわりの課題へ P.271,272
データを,度数分布表やヒストグラムに表すと,データの傾向がわかりやすくなります。
相対度数を利用すると,全体の数がちがうデータを比較することができます。また,相対度数を確率とみなすことにより,未来の予測をすることができます。
さらに学んでみたいこと
これからもっと学んでみたいことや,疑問に思ったことを書いておこう。
数学へのいざない 資料集めに利用しやすいホームページ
総務省 統計局のページ
国勢調査,家計調査などさまざまな調査結果を掲載
「なるほど統計学園」には,統計データの探し方などを掲載
気象庁 各種データ・資料のページ
地域別の天気や気温などに関するデータを掲載
文部科学省 統計情報のページ
学校に関するデータや新体力テストの記録などを掲載
農林水産省 統計情報のページ
農作物の収穫高など農業,林業,漁業に関するデータを掲載
経済産業省 統計のページ
資源やエネルギーに関するデータを掲載
環境省 環境統計のページ
地球環境やリサイクルなどに関するデータを掲載
<1年p.269>
7章のまとめの問題 解答P.306〜307 基本
1 次の⑴ ~ ⑶の場合, それぞれ代表値として何を用いるとよいでしょうか。また,そのように判断した理由をいいなさい。
⑴ 洋服メーカーが,今年1 年間に売れた洋服のサイズごとのデータをもとにして,来年,どのサイズの洋服をもっとも多く製造するかを決める。
⑵ リレーで走る2チームのメンバー全員の50m 走の記録をもとにして,この2チームの勝敗を予想する。
⑶ クラスの女子15人のハンドボール投げの記録をもとにして,自分の記録がクラスの女子の中で上位7人以内に入っているかどうかを調べる。
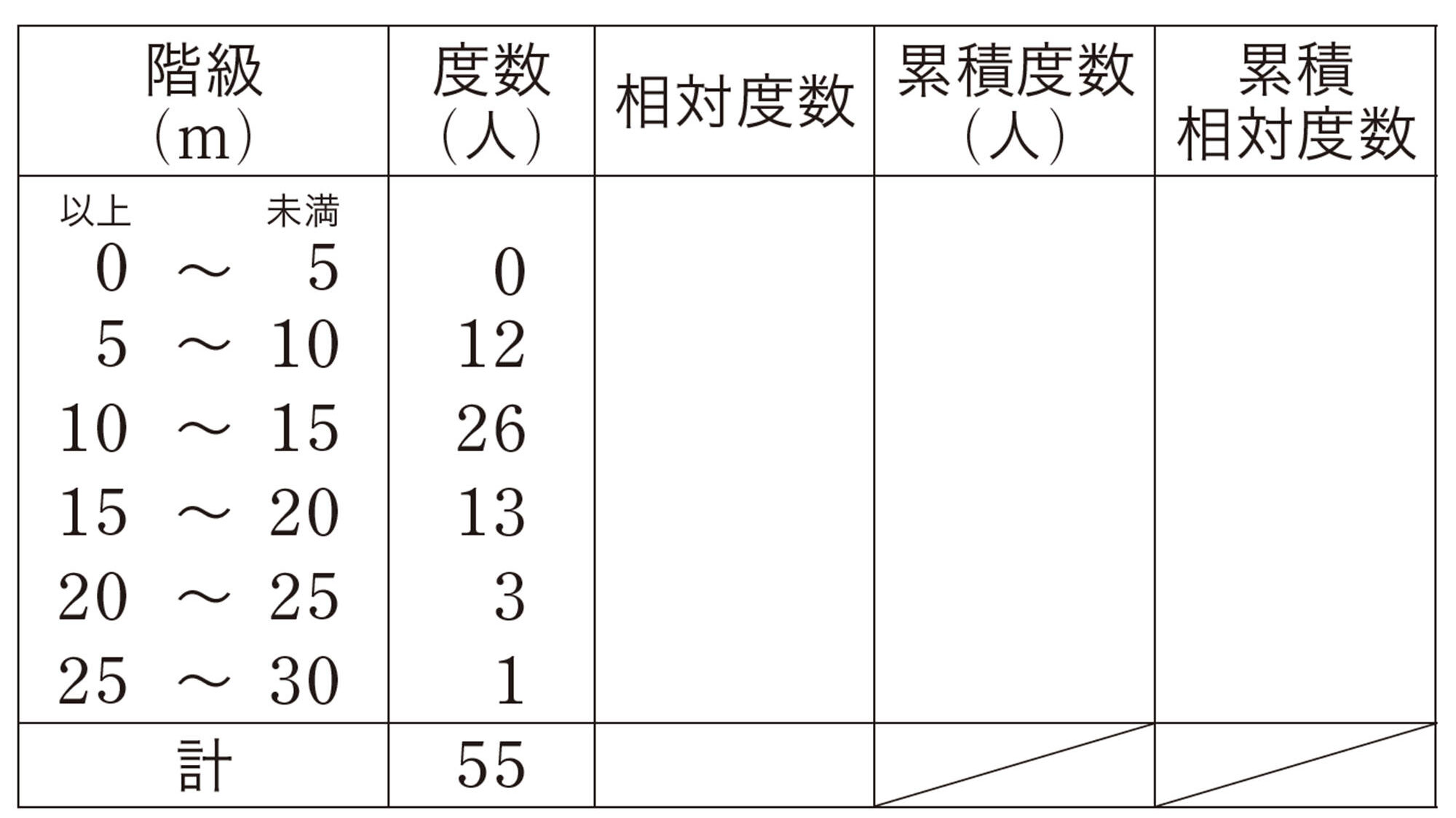
3 次の表は,A中学校男子の握力の記録です。表を完成させなさい。相対度数は,小数第二位まで求めなさい。
<1年p.270>
7章のまとめの問題 応用
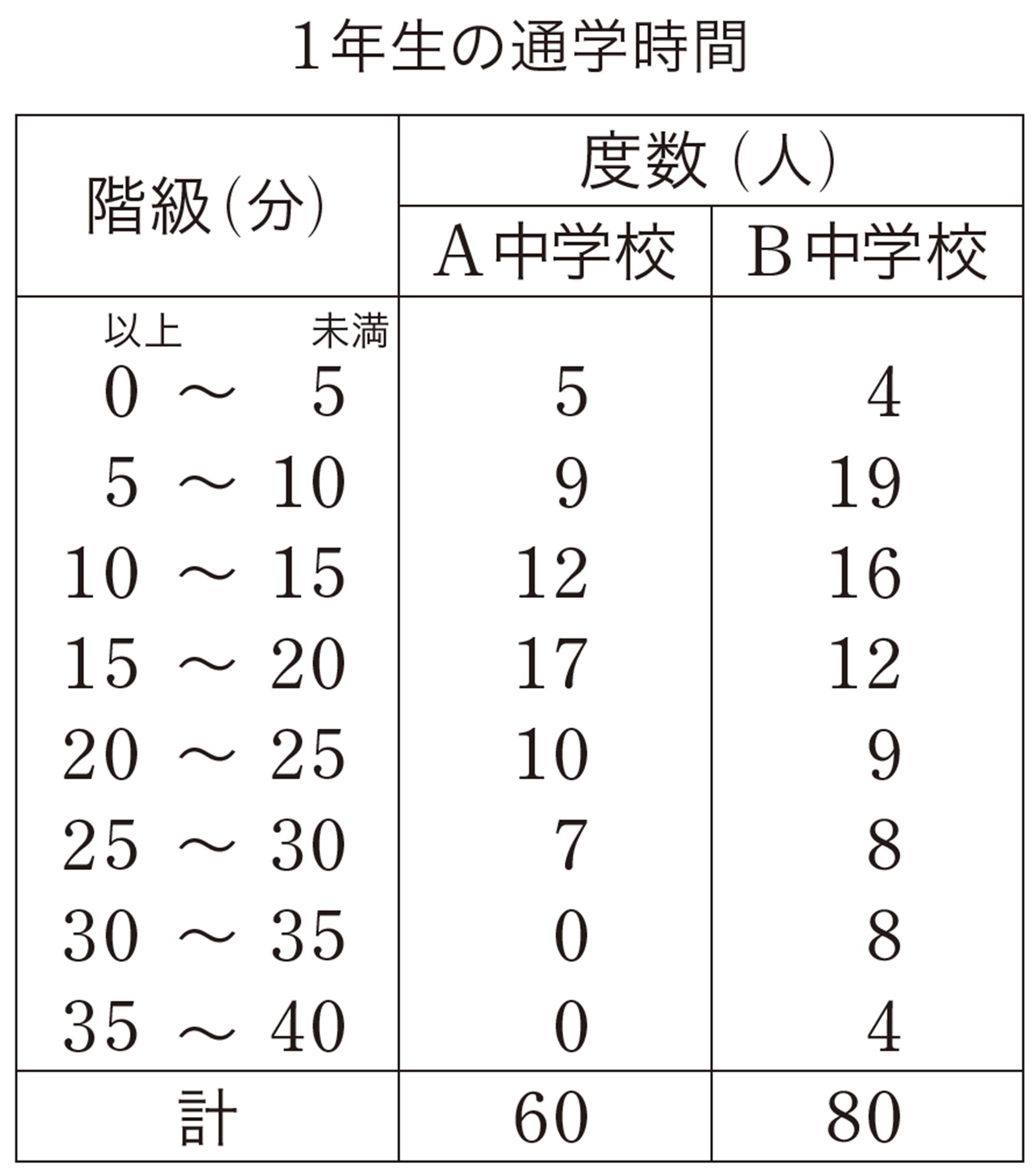
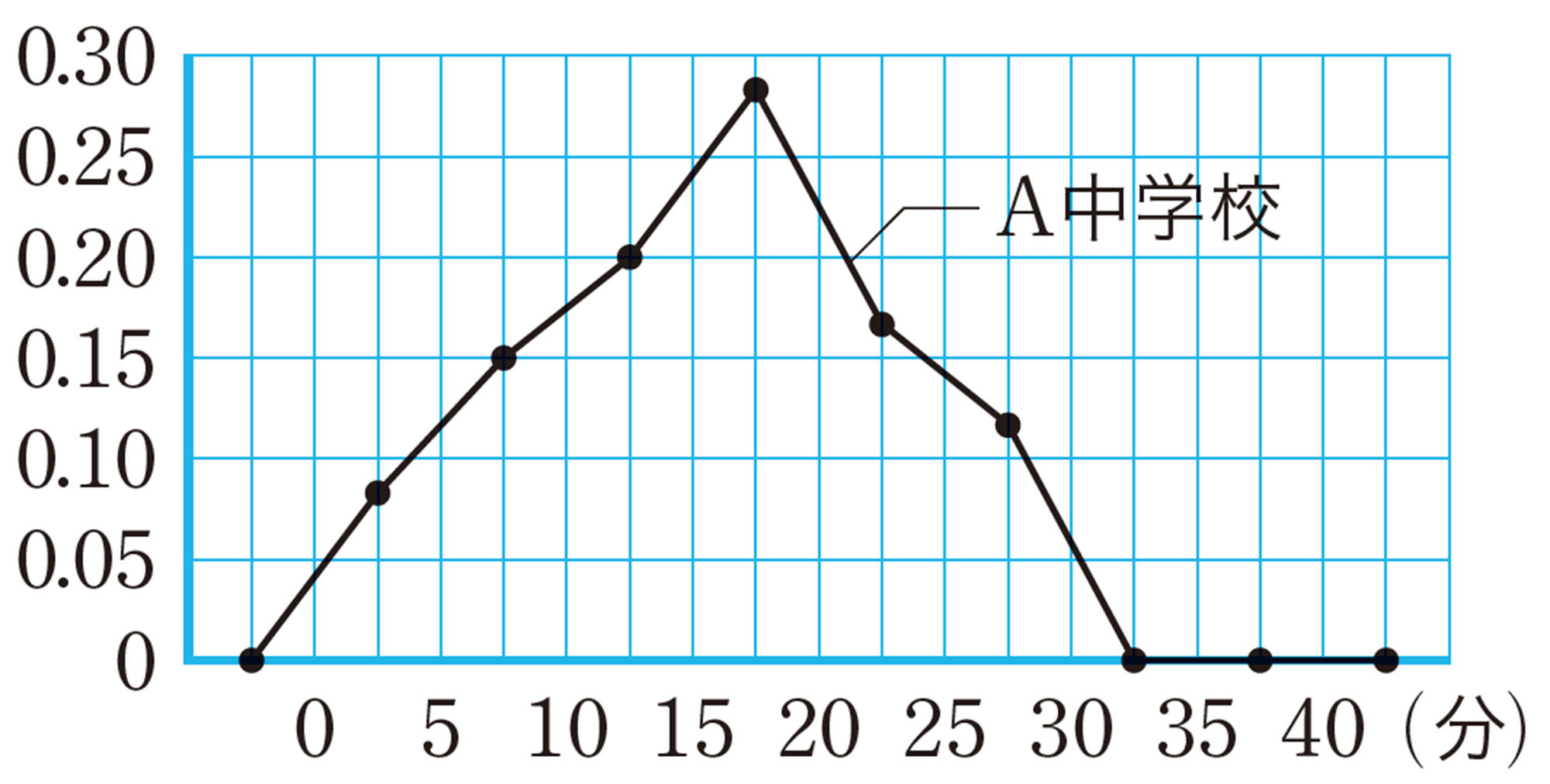
2 次の表は,A中学校1年女子のハンドボール投げの記録です。次の問いに答えなさい。
<1年p.271>
活用
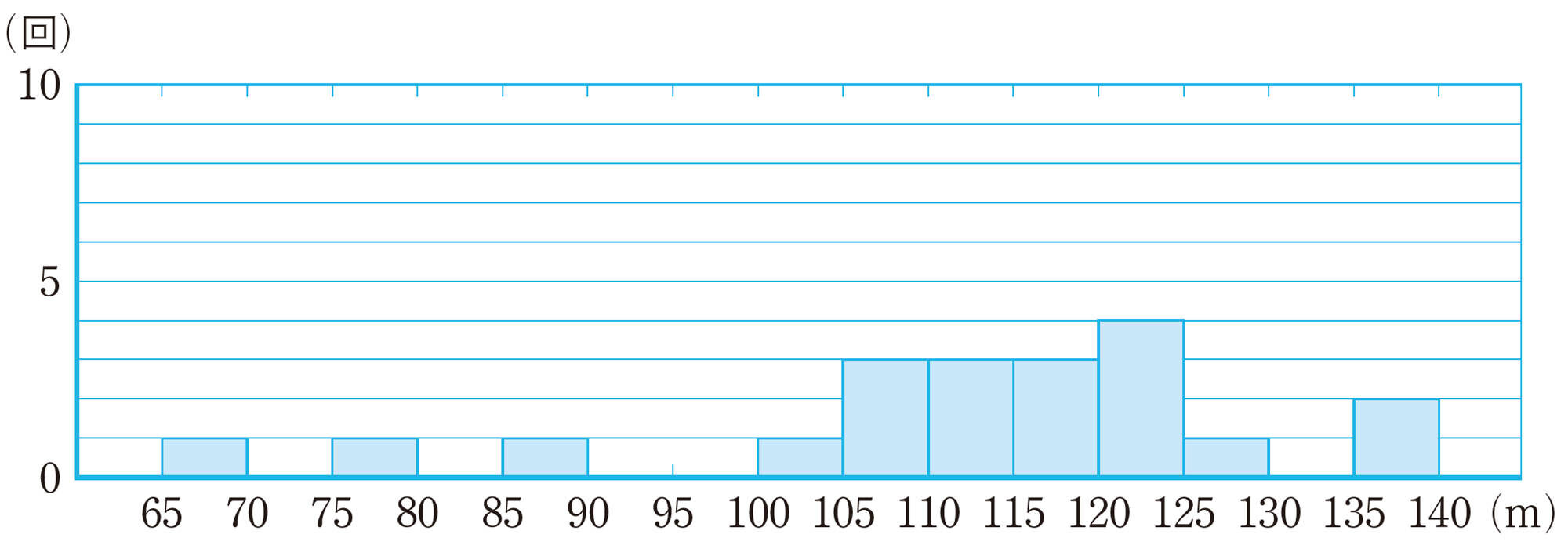
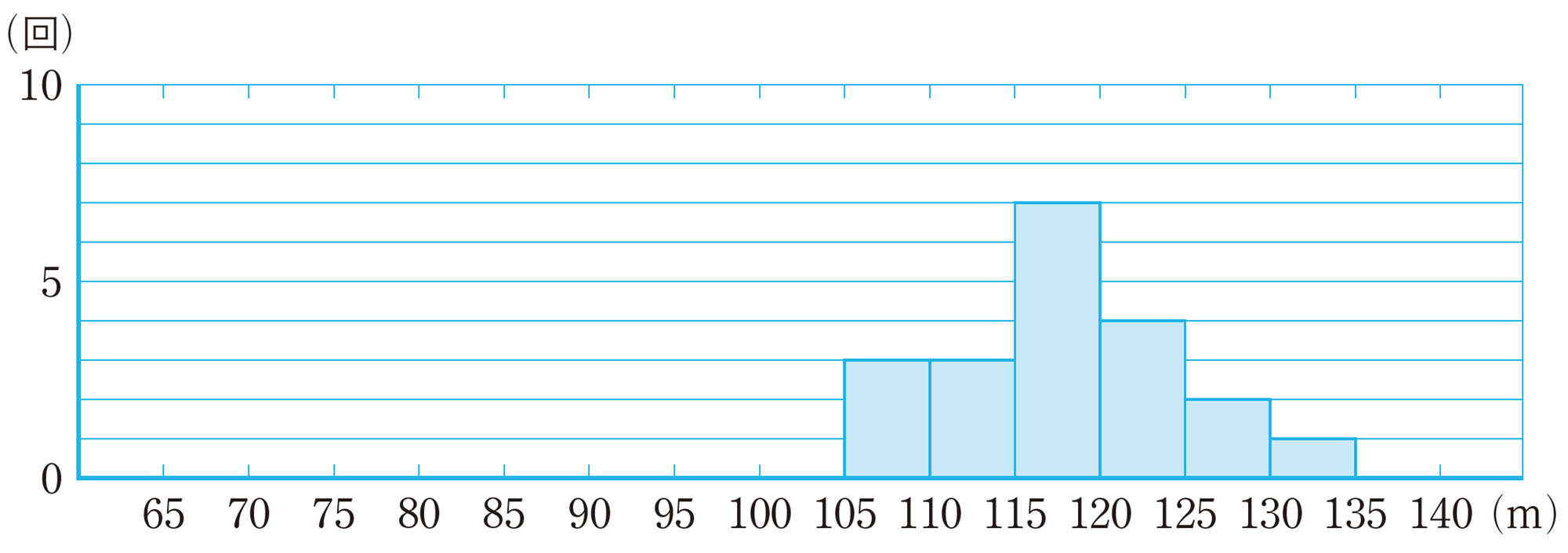
⑴ 2人のヒストグラムから,2人の飛んだ回数が同じであることがわかります。その回数を求めなさい。
⑵ 2人のヒストグラムから,それぞれの飛んだ距離の平均値を求めなさい。
⑶ 2人のヒストグラムを比較して,そこからわかる特徴をもとに,次の大会でより遠くへ飛びそうな選手を1人選ぶとするとき,あなたならどちらの選手を選びますか。また,その選手を選んだ理由を,2人のヒストグラムの特徴を比較して説明しなさい。
<1年p.272>
深めよう POSデータとABC 分析
POSデータのPOSとは,「Point-of-Sales」の略です。POSデータとは,「販売情報」のことであり,「何が,いつ,いくつ,いくらで売れたのか」を示します。この「販売情報」を活用するためのしくみとして構築されるのが,「POSシステム」です。
この「POSシステム」は,売上高を把握したり,在庫を補充したり,新たな商品を仕入れたりするために,重要な役割を担っています。そして,この「POSシステム」で大切なことは,「データの活用」にあります。POSデータにはいろいろな分析の方法がありますが,ここではABC分析について紹介します。
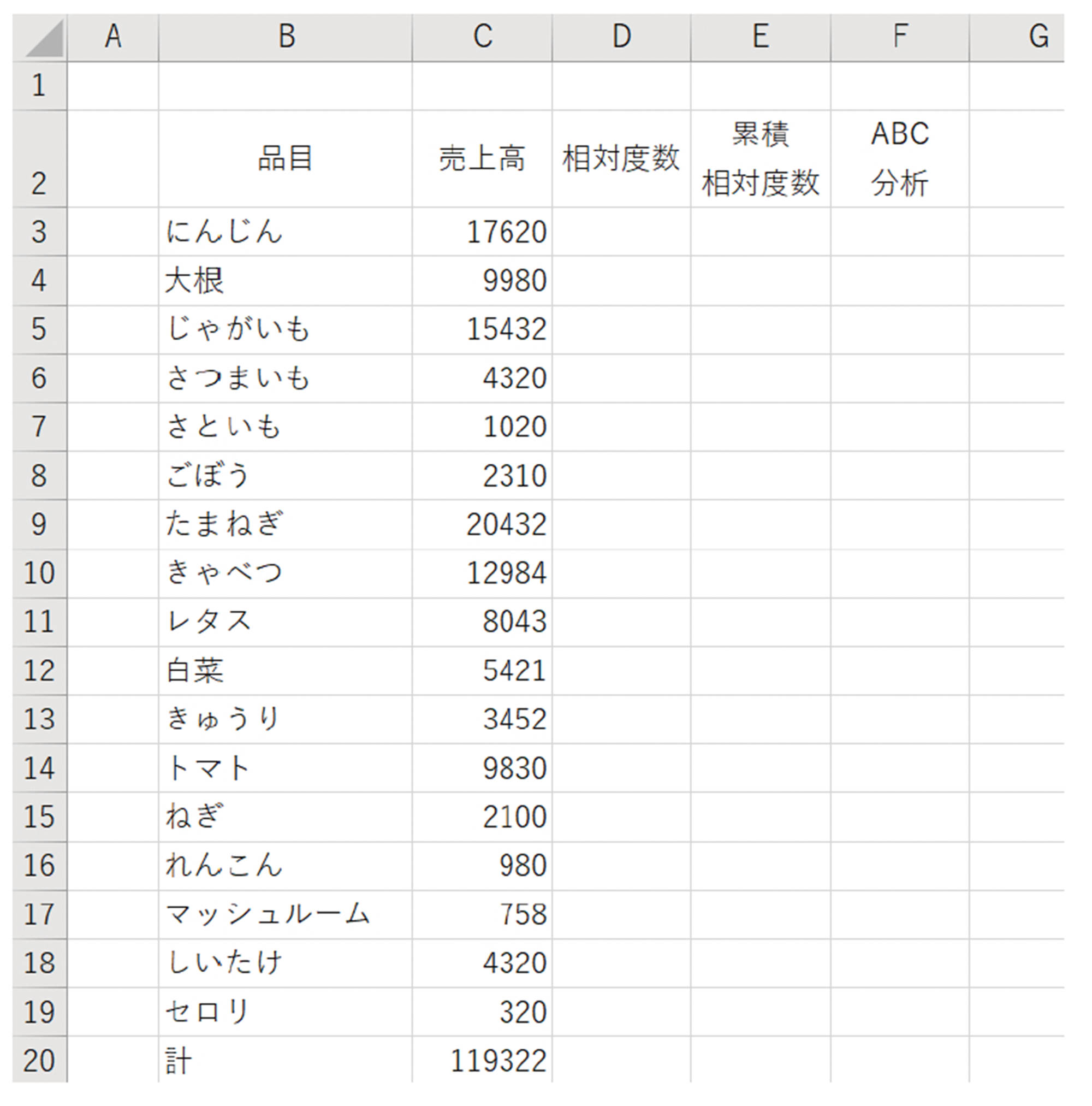
ABC分析とは,データをもとに商品をA,B,Cの3 項目に分けて重要度をはっきりさせます。たとえば,重要度を売上高とした場合,売上高の順に取り扱い商品を並べ,売上高の高い順に商品をA,B,Cに分けます。その重要度にそって,商品の発注などを効率的に行います。
以上で完成です。これより,どの品目が売上高に貢献しているのかを判断することができます。優先的に発注するものや,商品の取り扱いを中止するかどうかを検討する判断に使うことができます。
取り扱い商品の重要度は売上高だけではなく,売上総利益や販売個数なども重要度となり得るので,事業の実態に合わせて複数の重要度にそって分析することが大切です。
<1年p.273>
表計算ソフトを使ってみよう
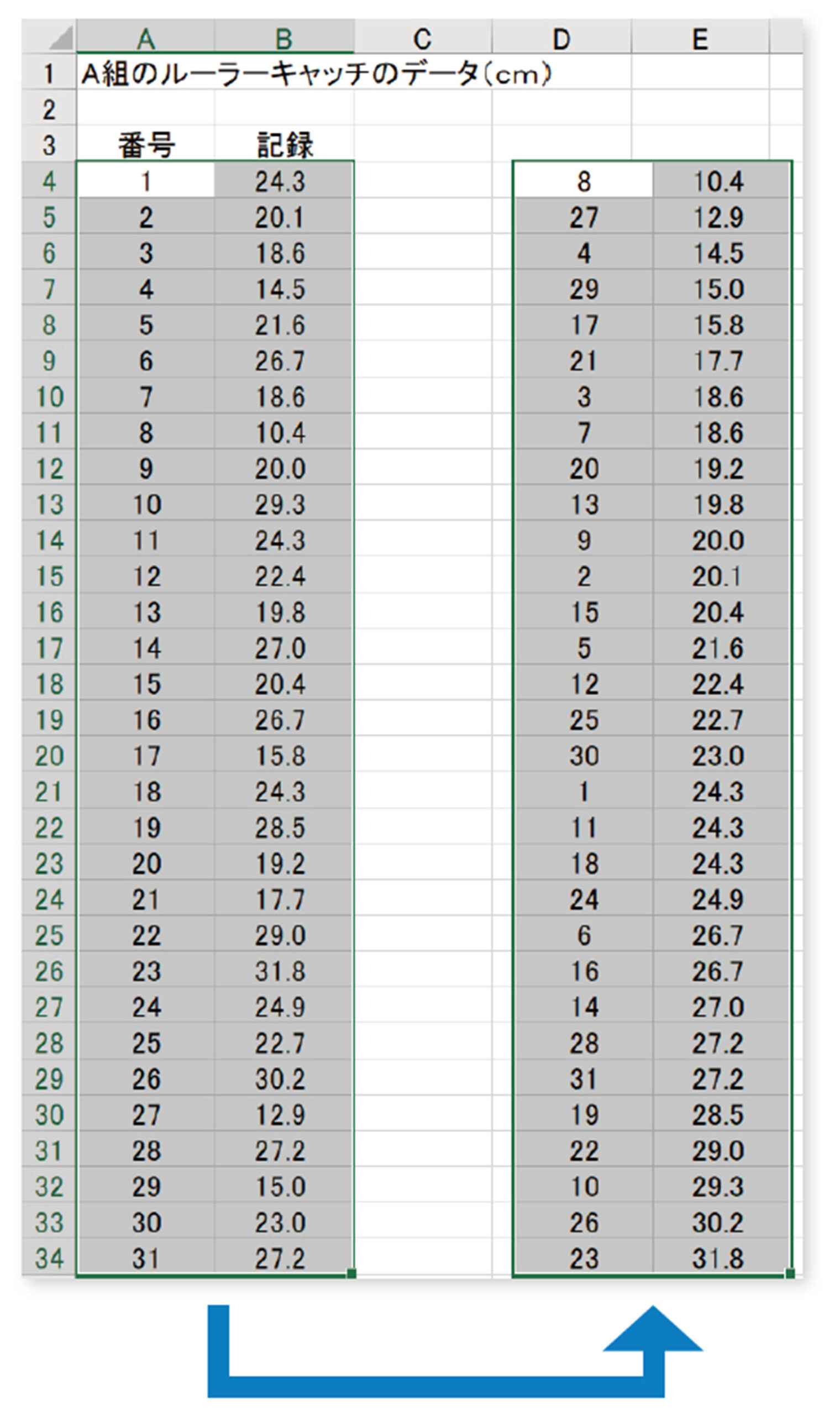
① データの並べかえ
注意 小さい方から順に並べかえるときは「昇順」,大きい方から順に並べかえるときは「降順」を選択します。
【1】 A組のルーラーキャッチのデータを表計算ソフトに入力し,昇順,降順に並べかえてみましょう。また,245ページのB組のルーラーキャッチのデータも入力し,同様に並べかえてみましょう。
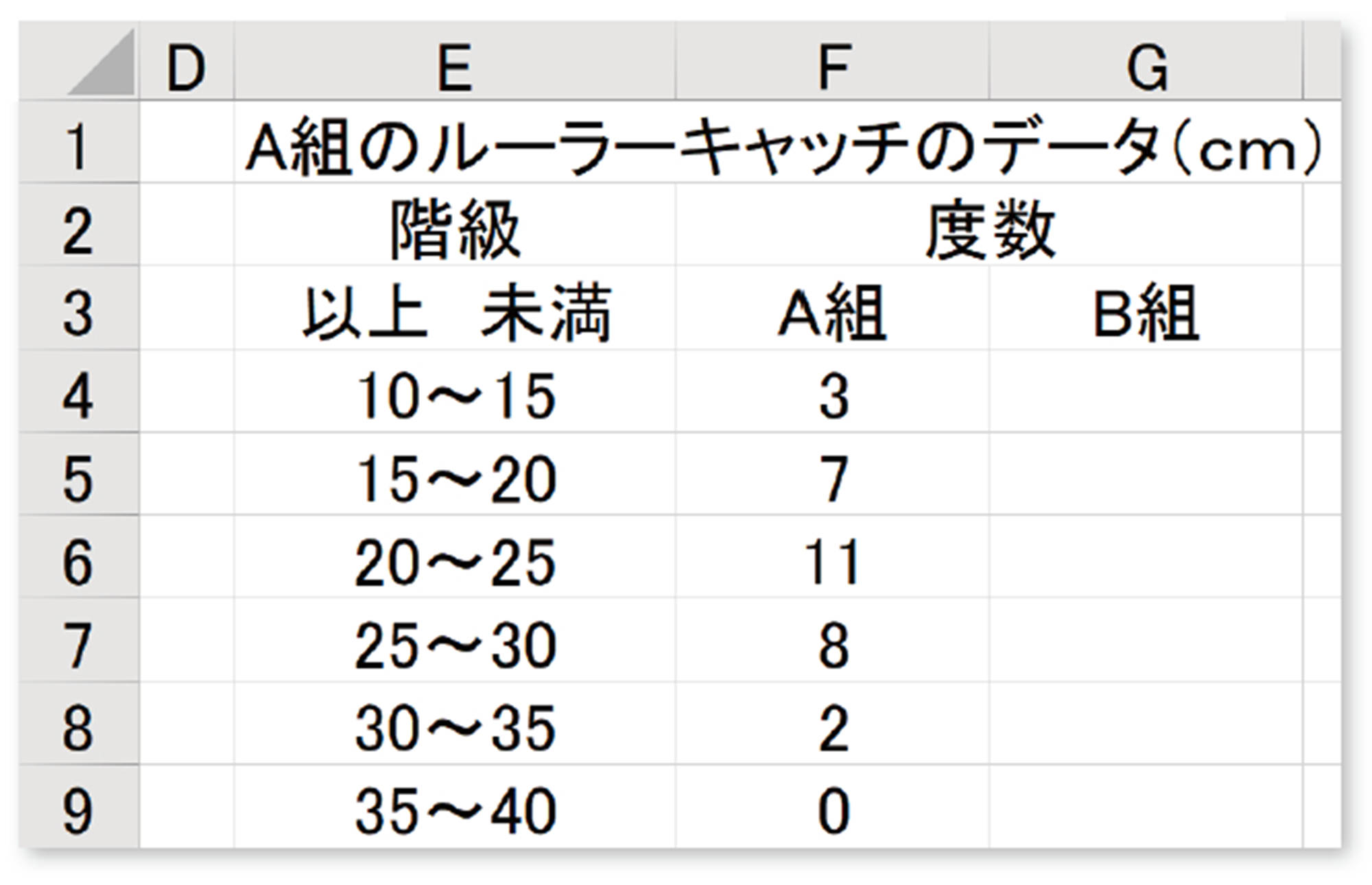
② 度数分布表とグラフの作成
【2】 上の表を作成してみましょう。また,【1】 で作成した表を利用して,B組の度数も入力しましょう。
<1年p.274>
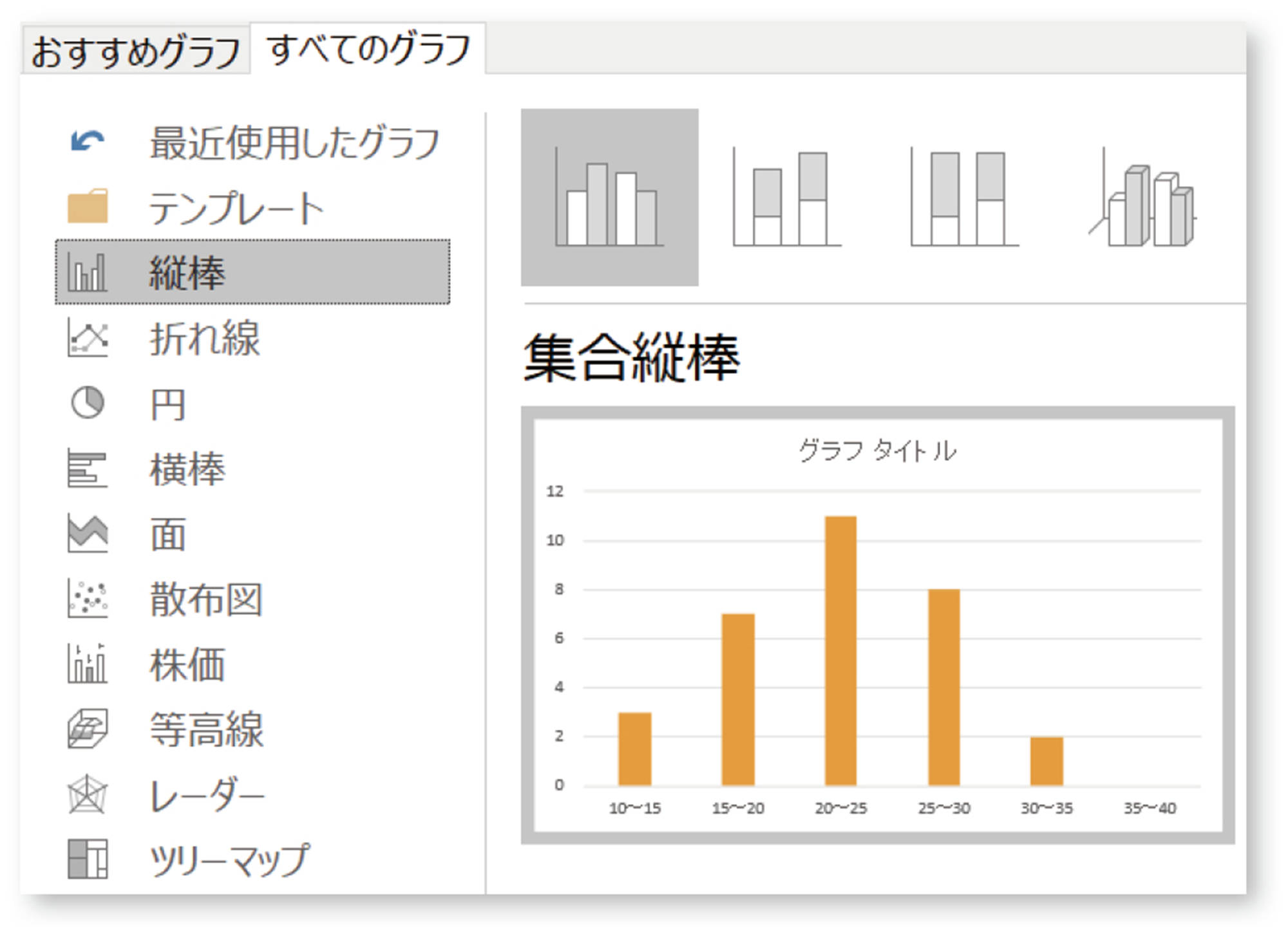
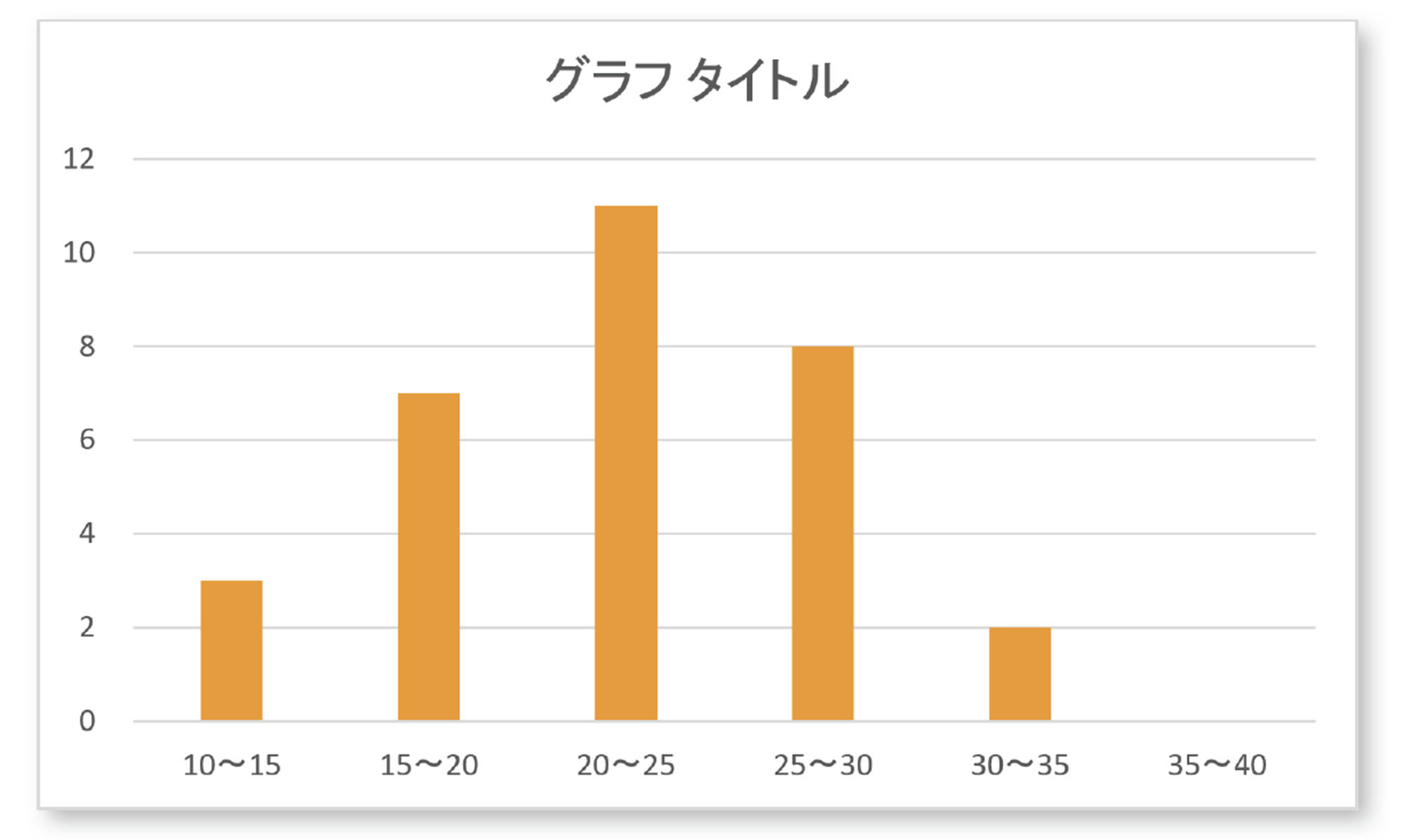
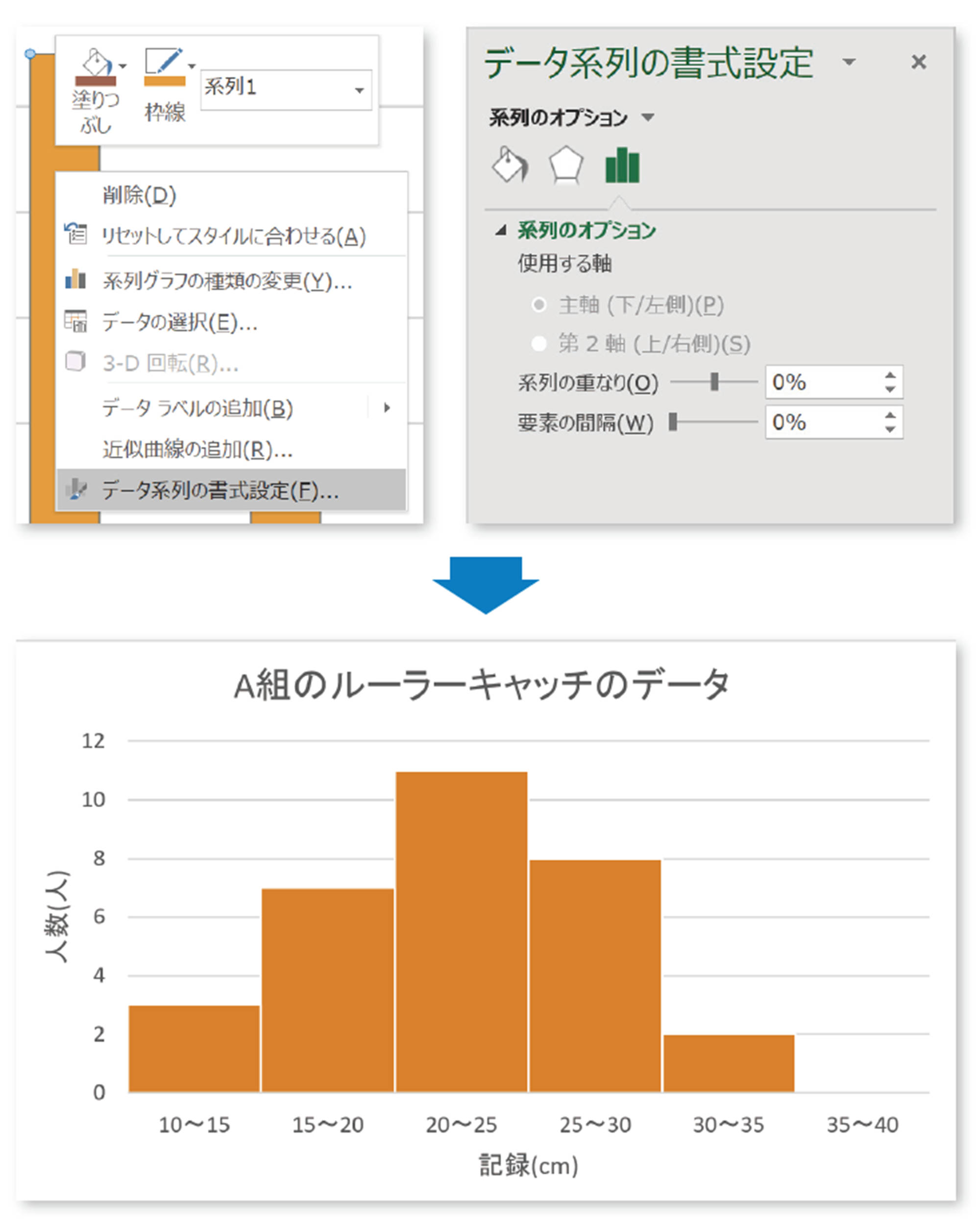
②で作成した度数分布表をもとに,ヒストグラムを作成することができます。
③ 代表値などの求め方
表計算ソフトには「関数」と呼ばれる機能があり,最大値や最小値,平均値,最頻値,中央値,合計などを簡単に求めることができます。それらの「関数」を表示させるセルを指定し,
[mathjax]\(= 関数名 (範囲の始点:範囲の終点)\)
を入力します。
[mathjax]\(\mathsf{最大値}= MAX(B 4:B34)\)
[mathjax]\(\mathsf{最小値}= MIN(B 4:B34)\)
[mathjax]\(\mathsf{平均値}= AVERAGE(B 4:B34)\)
[mathjax]\(\mathsf{最頻値}= MODE(B 4:B34)\)
[mathjax]\(\mathsf{中央値}= MEDIAN(B 4:B34)\)
[mathjax]\(\mathsf{合計}= SUM(B 4:B34)\)
【3】 A組とB組のルーラーキャッチのデータについて,最大値,最小値,平均値,中央値を求め,それぞれ比べてみましょう。