<1年p.72>
問 3 次の数量を,文字式の表し方にしたがって表しなさい。
⑴ 長さ2m の紙テープx本の長さの合計
⑵ 1個akgの荷物1個と1個bkgの荷物5個の重さの合計
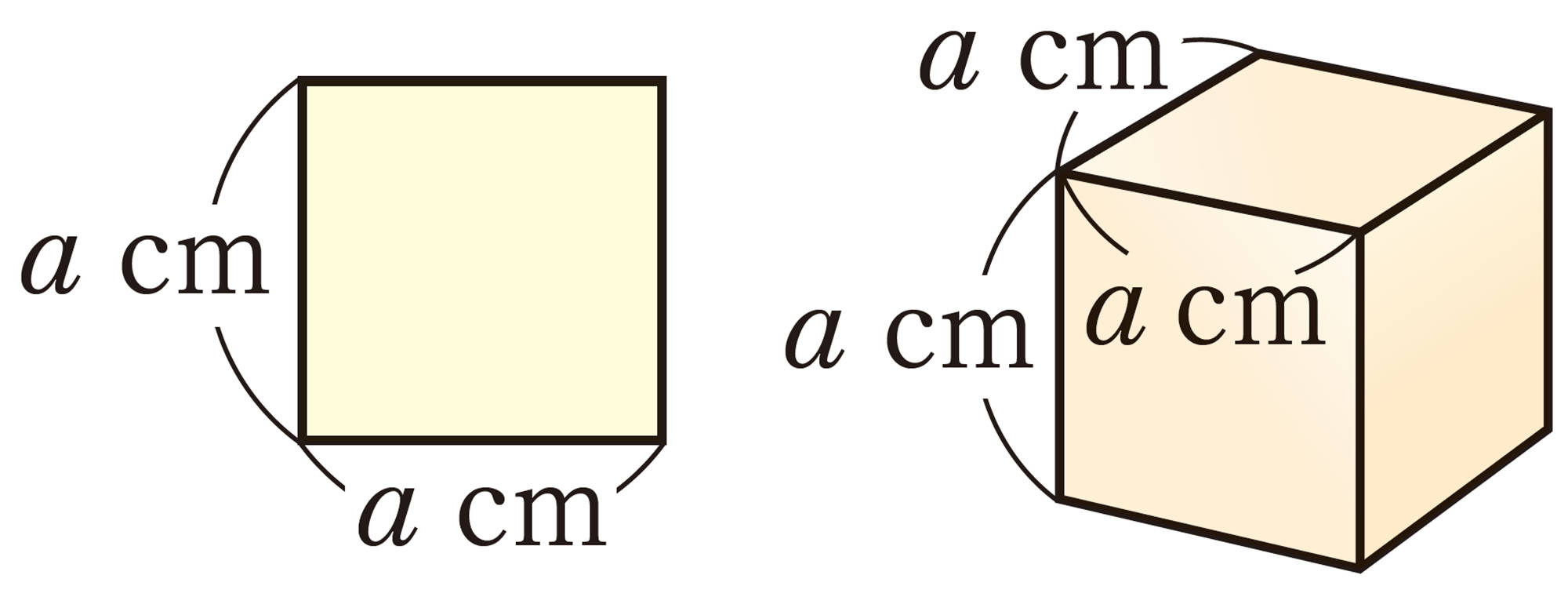
累乗の表し方
Q Question

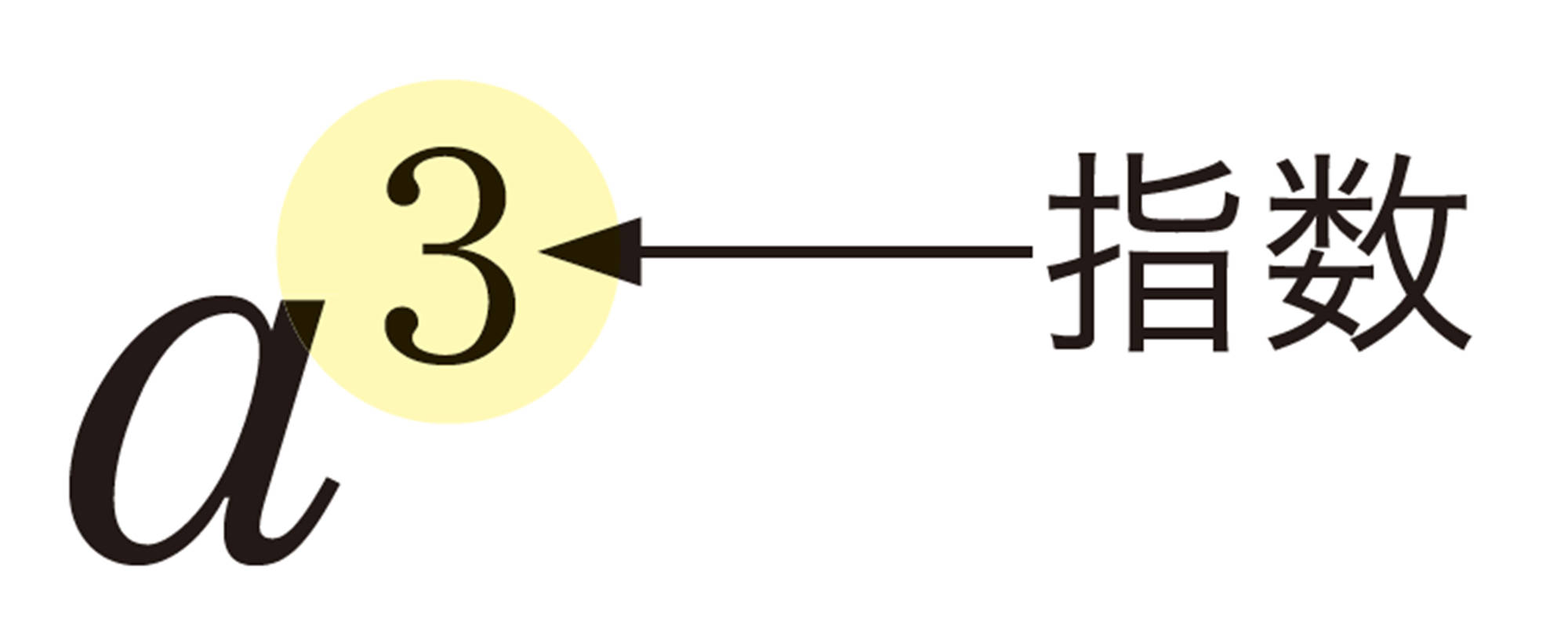
数では,累乗を指数を使って表したね。
文字も指数を使って表していいのかな。

見方・考え方
数と同じように考えられるかな。
累乗の表し方
同じ文字の積は,累乗の指数を使って表す。
おしえて!
P.77
累乗で,[mathjax] \(a¹\)や[mathjax] \(a⁰\)と表すことはあるのかな?
例 2
⑴ [mathjax]\(x \times x \times 3=3x²\)
⑵ [mathjax]\(a \times (-1) \times a \times a=-a³\)
⑶ [mathjax]\(a \times a \times a \times b \times b=a³b²\)
問 4 次の式を,累乗の指数を使って表しなさい。
⑴ [mathjax]\(a \times 7 \times a\)
⑵ [mathjax]\(x\times x \times (-2)\times x\)
⑶ [mathjax]\(x \times y \times y \times x \times y\)
問 5 次の式を,乗法の記号[mathjax]\(\times\)を使って表しなさい。また,[mathjax]\(a=\dfrac{1}{3}\) のときの式の値を求めなさい。
⑴ [mathjax] \(-12a\)
⑵ [mathjax]\(9a²-2\)
問 6 次の式を,乗法の記号[mathjax]\(\times \)を使って表しなさい。また,[mathjax]\(a=-4\),[mathjax]\(b=2\)のときの式の値を求めなさい。
⑴ [mathjax] \(-a\)
⑵ [mathjax] \(a²\)
⑶ [mathjax]\(3a+5b\)
⑷ [mathjax]\(2a-4b²\)