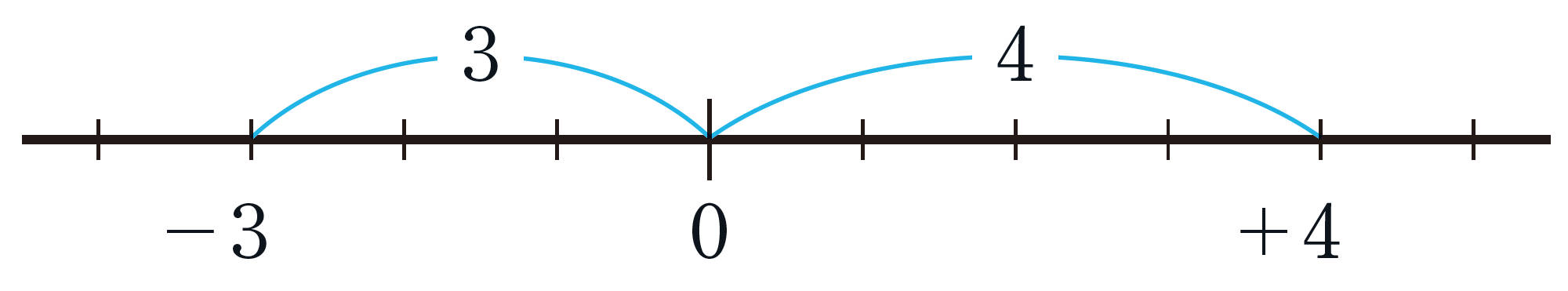gkt-horizontal-line
<1年p.17>
数直線上で，ある数に対応する点と原点との距離を，その数の絶対値 という。たとえば，[mathjax] \(+4\)の絶対値は4，[mathjax] \(-3\)の絶対値は3である。
0の絶対値は0である。
2つの正の数[mathjax] \(+4\)と[mathjax] \(+6\)を比べると，絶対値は[mathjax] \(+6\)の方が大きく，数直線上では[mathjax] \(+6\)の方が右にある。
このように，2つの正の数では，絶対値の大きい数の方が大きい。
問 ４ 2つの負の数の大小について，絶対値で比べるとどんなことがいえますか。例をあげて，「数直線」，「絶対値」ということばを使って説明しなさい。
問 ５ [mathjax] \(-7\)，[mathjax] \(+5.2\)の絶対値を，それぞれいいなさい。
問 ６ 絶対値が10である数，[mathjax] \(\dfrac{2}{3}\) である数を，それぞれいいなさい。
gkt-horizontal-line
2数の大小について，次のようにまとめることができる。
2数の大小
① 正の数は0より大きく，負の数は0より小さい。 また，正の数は負の数より大きい。
② 2つの正の数では，絶対値の大きい数の方が大きい。
③ 2つの負の数では，絶対値の大きい数の方が小さい。
どんなことがわかったかな
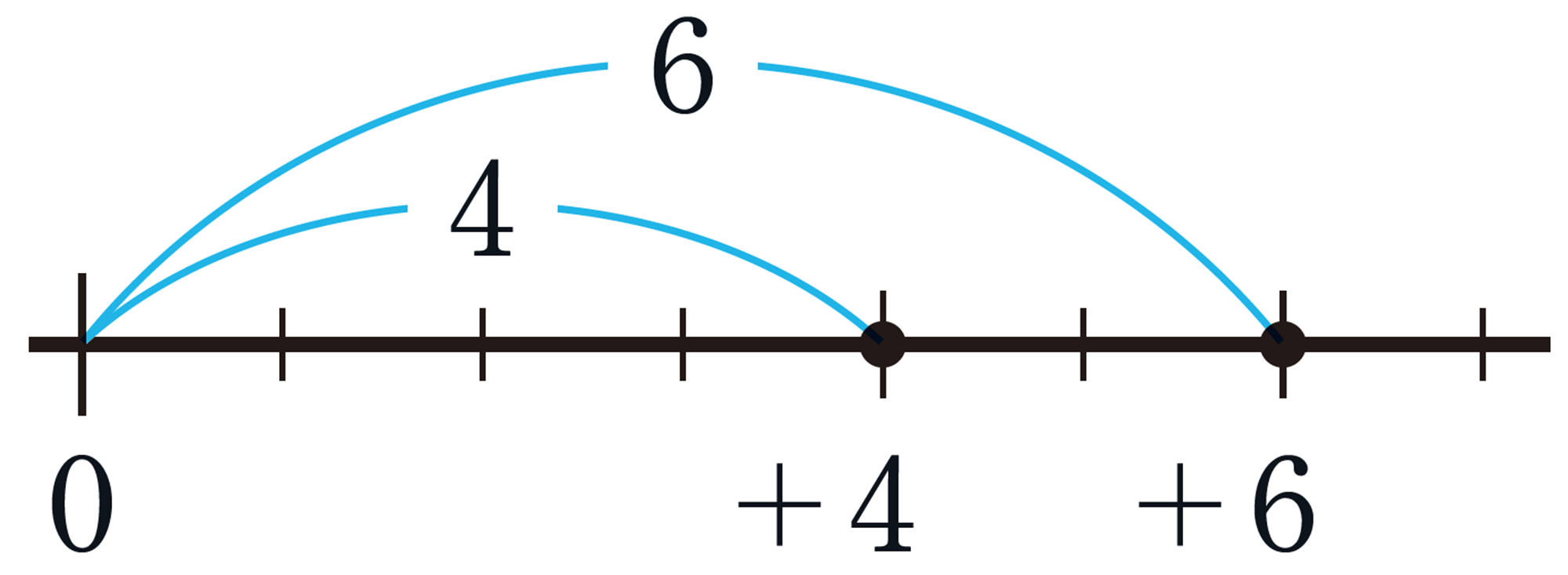
負の数も，正の数と同じように，数直線上に表して大小を比べることができます。
次の課題へ！
正の数，負の数の計算は，小学校のときの計算と同じようにできるのかな？
P.19
