<3年p.236>
7章のまとめの問題 解答 P.306 基本
2 次の長さを3辺とする三角形は,直角三角形といえますか。
⑴ 3cm,3cm,[mathjax]\(3\sqrt{2}\)cm
⑵ [mathjax]\(\sqrt{3}\)cm,2cm,[mathjax]\(\sqrt{6}\)cm
⑶ [mathjax]\(\sqrt{3}\)cm,[mathjax]\(\sqrt{3}\)cm,3cm
⑷ 2cm,[mathjax]\(\sqrt{5}\)cm,3cm
3 3点 [mathjax]\(A(2,3)\),[mathjax]\(B(-1,1)\),[mathjax]\(C(1,-2)\)があります。線分 AB,BC,CAの長さを求めなさい。また,[mathjax]\(\triangle ABC\)はどんな三角形ですか。
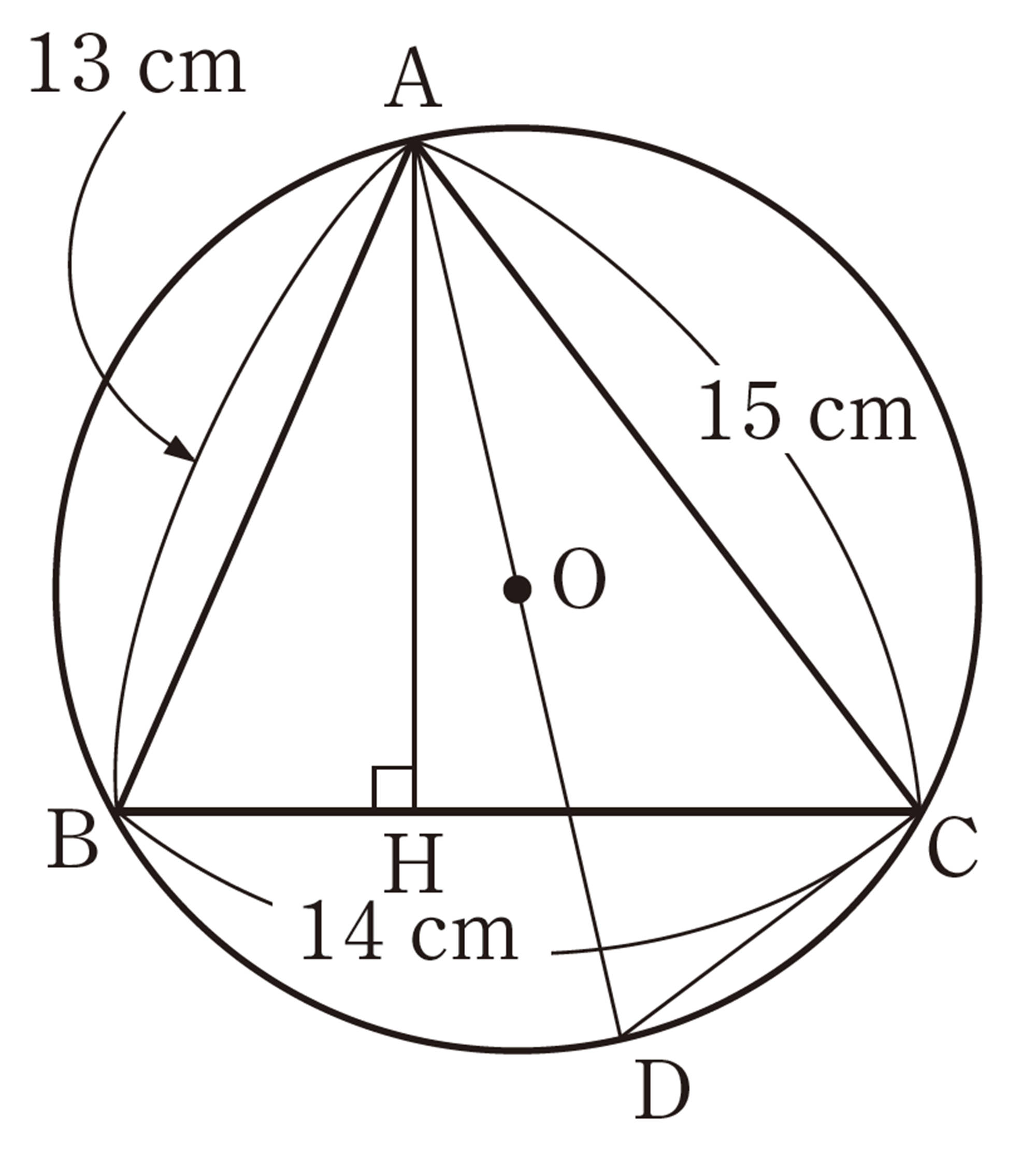
4 底面の1辺が6cm,他の辺が5cm の正四角錐があります。次の問いに答えなさい。
⑴ 高さと体積を求めなさい。
⑵ 表面積を求めなさい。
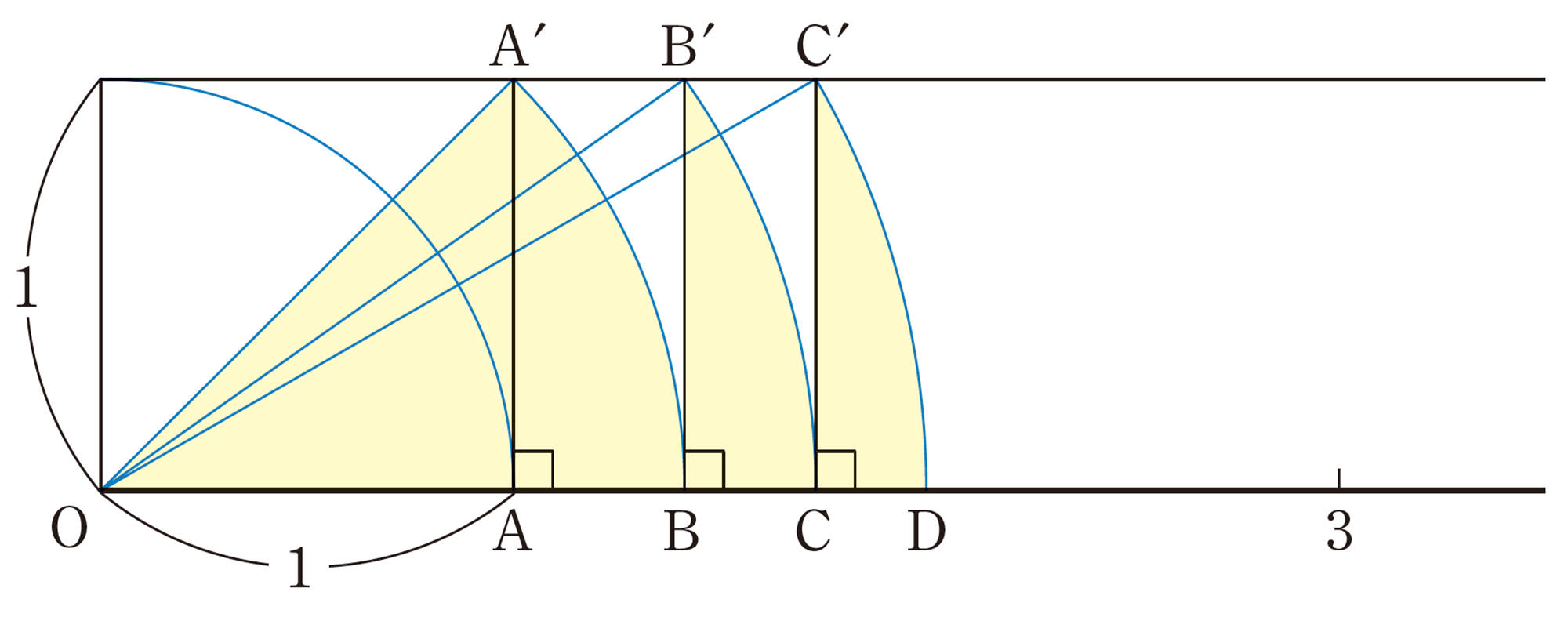
5 下の図は,[mathjax]\(OA=1\)として,数直線上に,[mathjax]\(OB=\sqrt{2}\),[mathjax]\(OC=\sqrt{3}\),…の長さをとる方法を示しています。次の問いに答えなさい。
⑴ 点 B,Cの求め方を説明しなさい。
⑵ 線分ODの長さを求めなさい。
⑶ この方法で,次の数直線上に[mathjax]\(\sqrt{5}\),[mathjax]\(\sqrt{6}\),[mathjax]\(\sqrt{7}\)の長さをとりなさい。
<3年p.237>
応用
<3年p.238>
7章のまとめの問題 活用
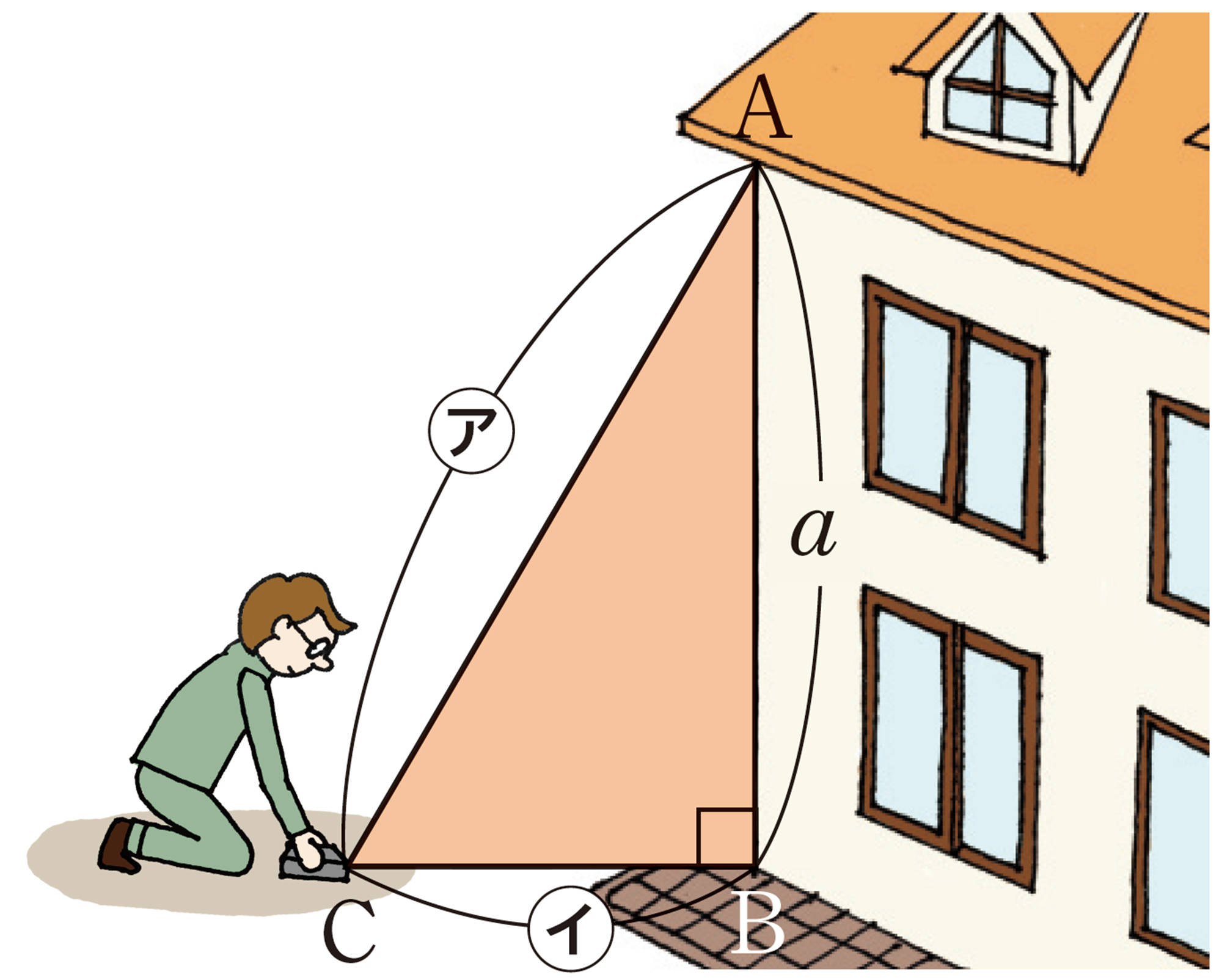
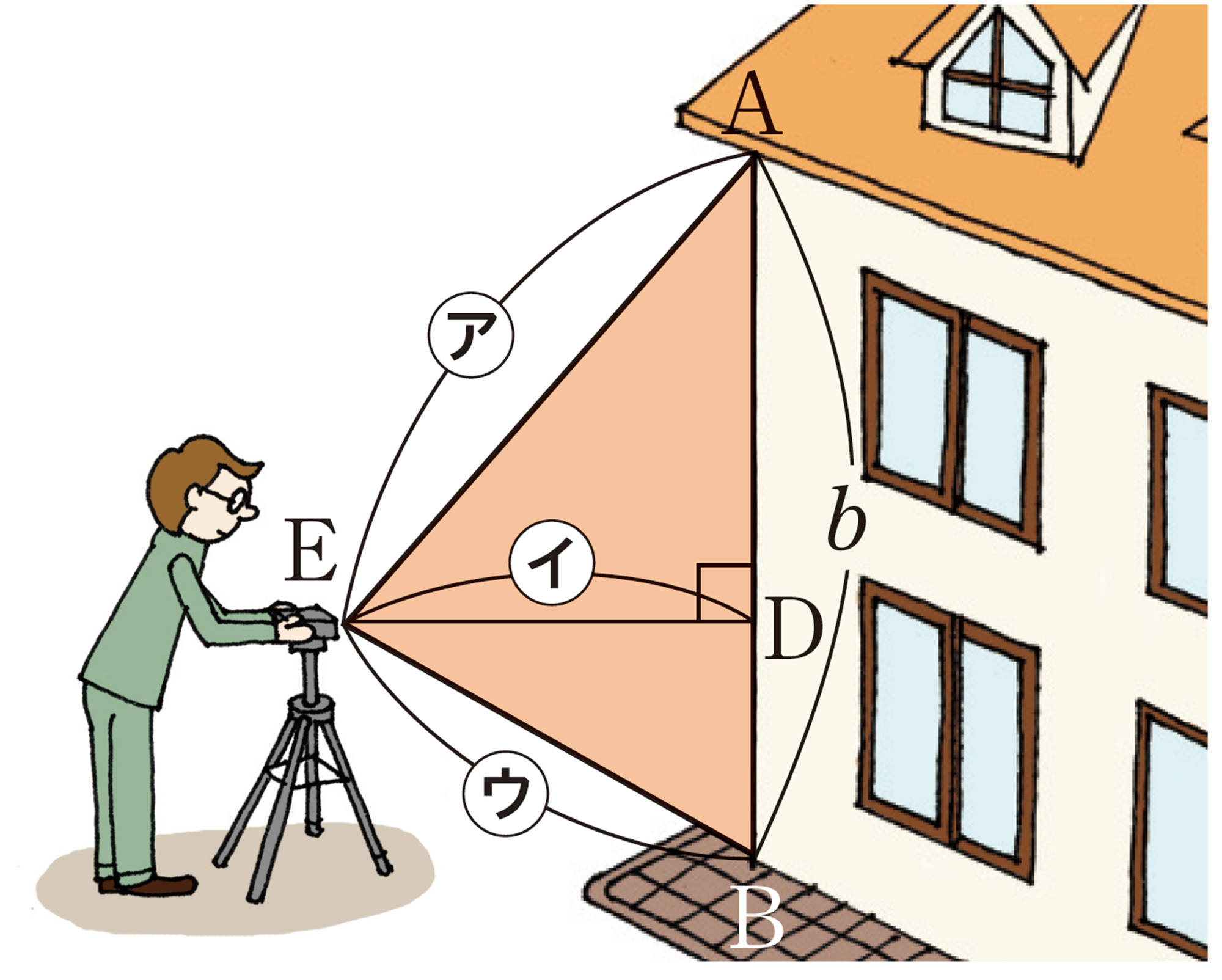
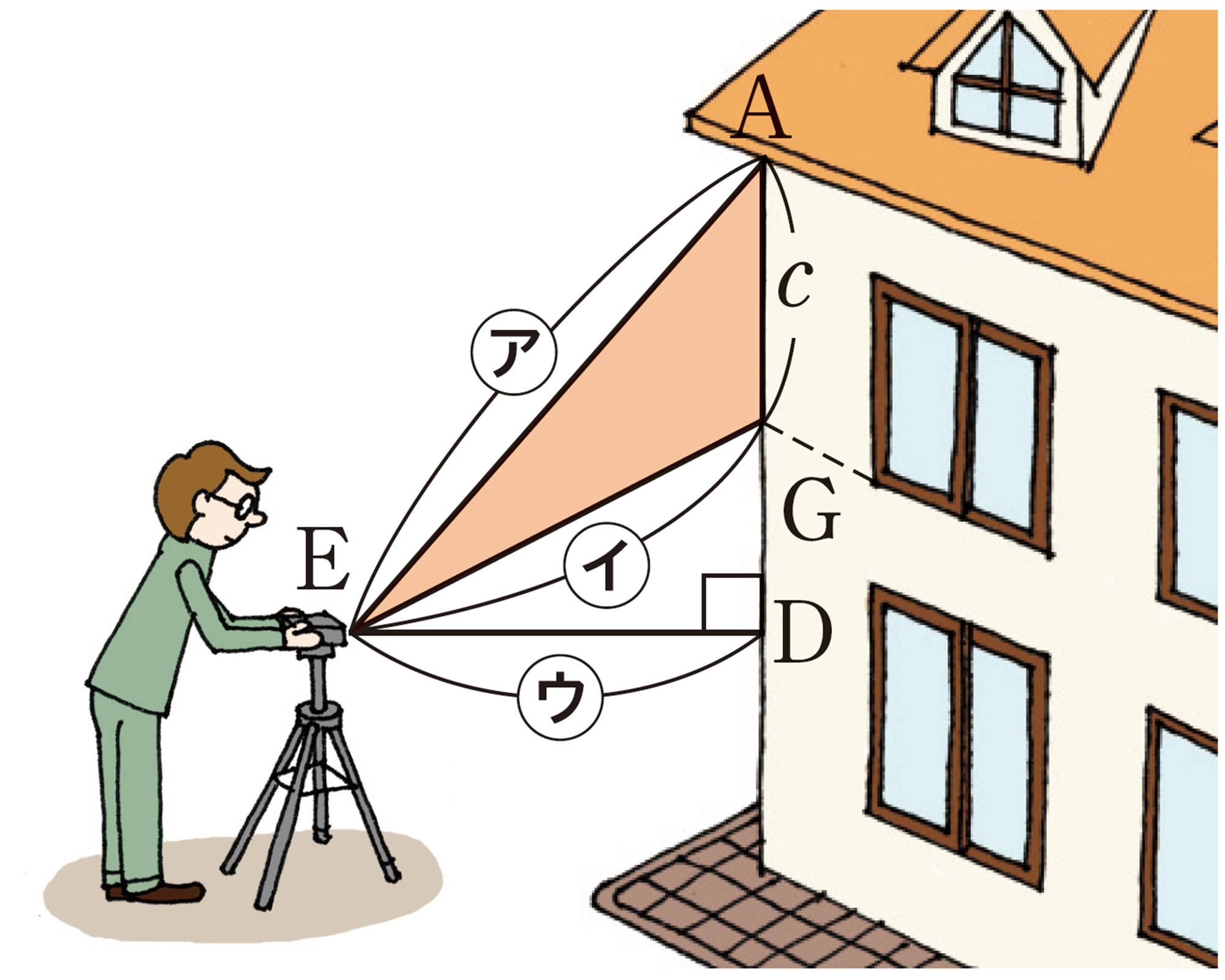
1 地面から軒下までの長さa,bを求めるのに,次の①,②のように,㋐,㋑,㋒の長さを測定して求める2つの方法があります。それぞれどのように長さを求めればよいか説明しなさい。
2 「1」について,次の長さを小数第一位まで求めなさい。
⑴ ①の方法で,㋐が8m,㋑が4mのときの長さa
⑵ ②の方法で,㋐が[mathjax]\(6.9\)m,㋑が4m,㋒が[mathjax]\(4.2\)mのときの長さb
>> 関連する職業・仕事 [測量士]
<3年p.239>
深めよう
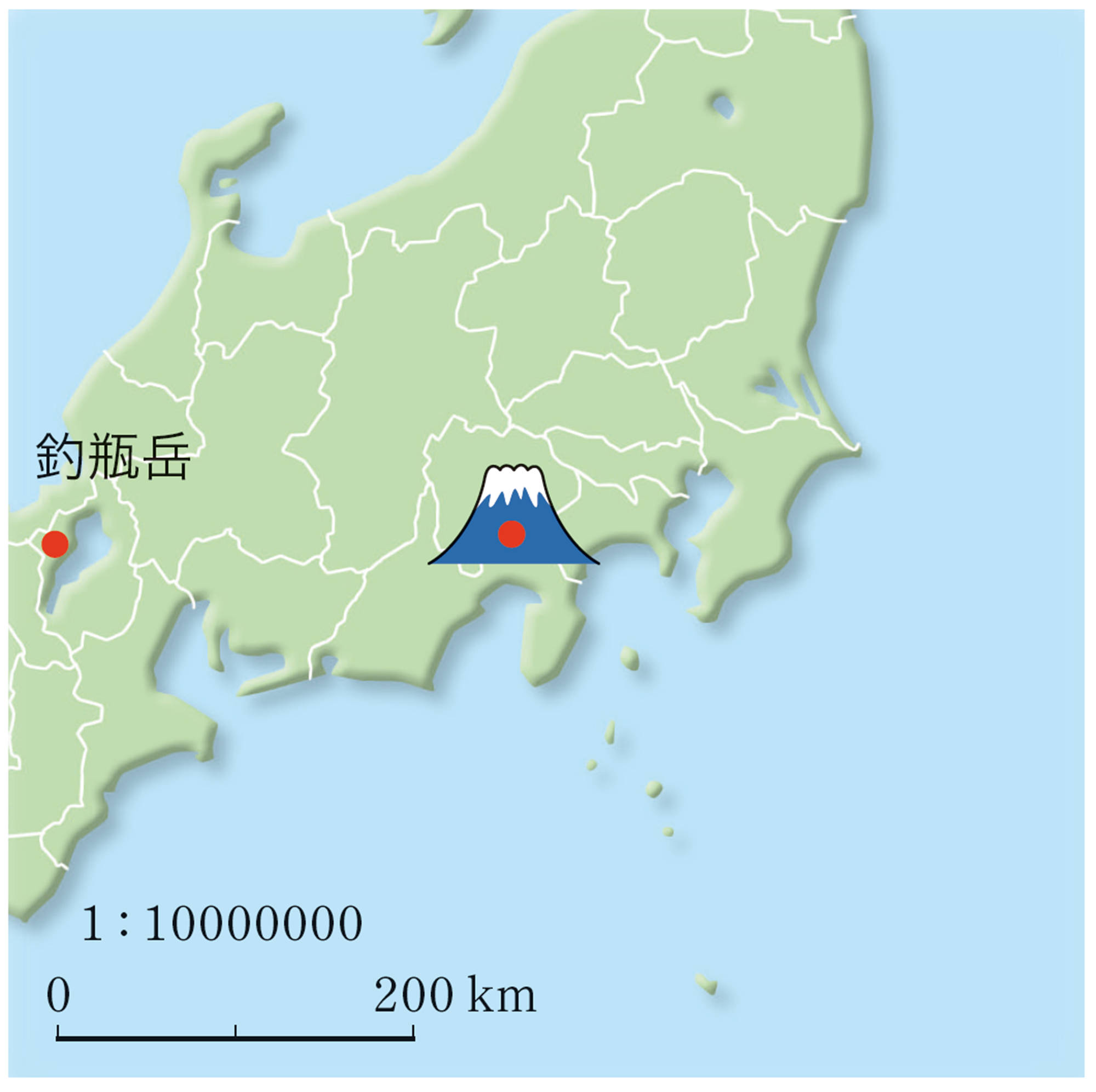
釣瓶岳から富士山が撮影できた?
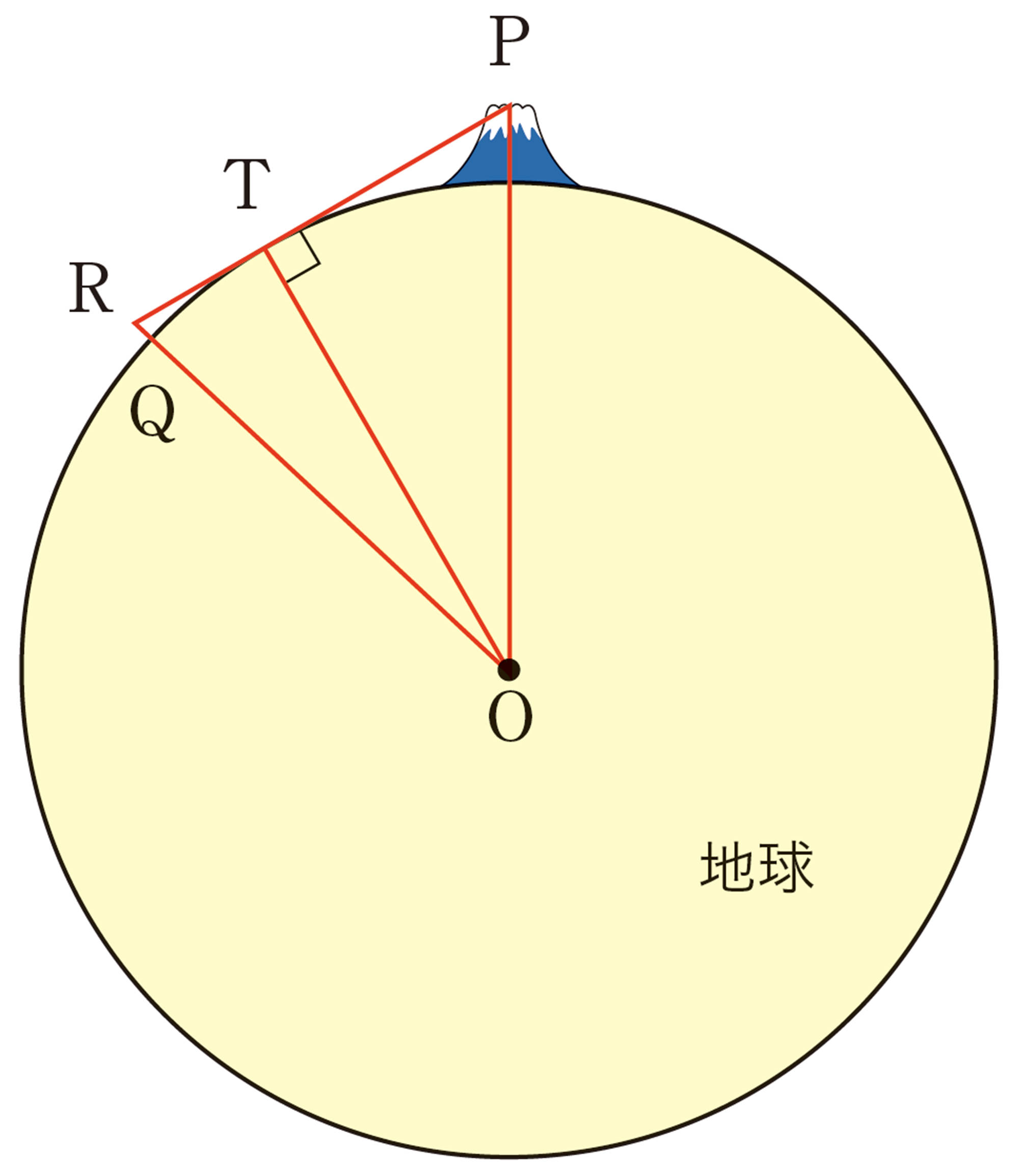
① 遠くを見るとき光の屈折によって実際には約6%遠くまで見渡すことができます。光の屈折を考えて233ページで求めた富士山が見える範囲を求めてみましょう。
まだ257kmには届かないね。


釣瓶岳は標高1098mだから,標高も関係していそうだね。