<3年p.222>
２節 三平方の定理の利用
丸太から切り取れる角材の大きさは？
【1】直径20 cm の丸太から，切り口が正方形の角材を切り取ります。もっとも太い角材を切り取るには，切り口の正方形の1 辺の長さをどのように求めればよいでしょうか。
丸太の直径を正方形の対角線にすればいいね。
対角線の長さから，正方形の1辺の長さが求められないかな。
次の課題へ!
身のまわりの事象について，三平方の定理を使って，考えられるかな？
P.222，228
1 平面図形での利用
目標 ▷ 三平方の定理を使って，平面図形のいろいろな長さを求めよう。
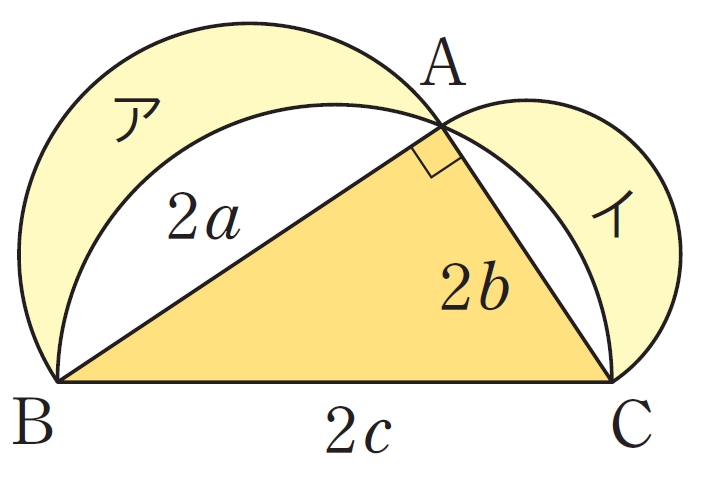
対角線の長さや三角形の高さ
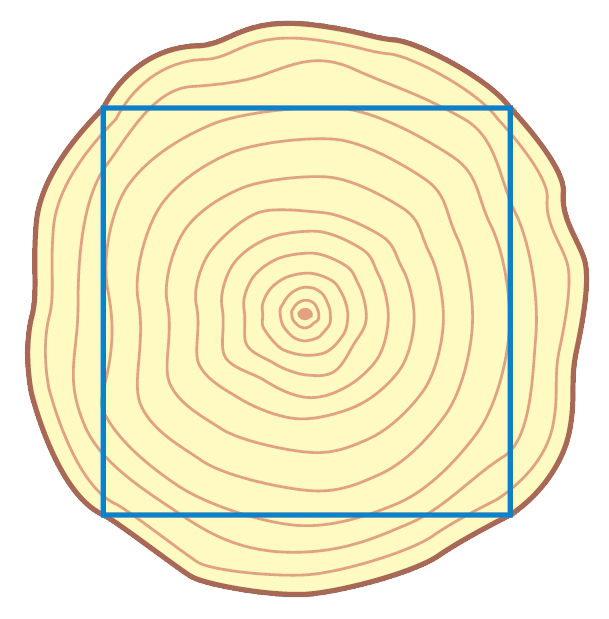
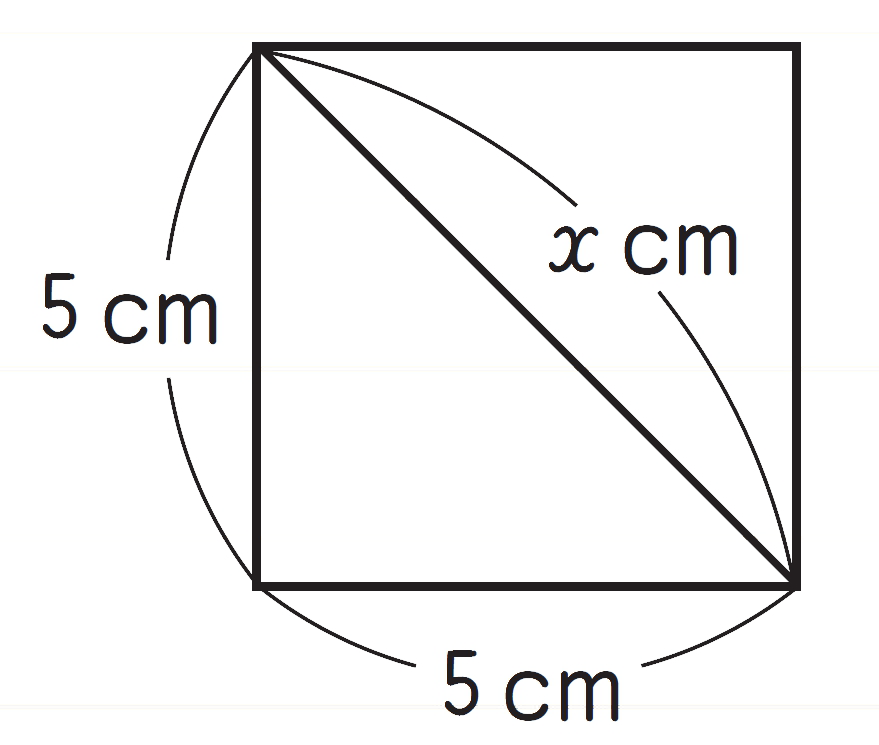
もっとも太い角材を切り取るには，切り口の正方形の対角線の長さを丸太の直径と同じにすればよい。正方形の1 辺の長さを[mathjax] \( x \) cm として，三平方の定理をもとに方程式をつくると，次のようになる。
[mathjax] \( x²+x²=20² \)
関連 ▷ P.72
例 １
1 辺5 cm の正方形の対角線の長さを求めなさい。
解答
対角線の長さを[mathjax] \( x \) cm とすると，
三平方の定理により，[mathjax] \( x²=5²+5²=50 \)
[mathjax] \( x \gt 0 \) であるから，[mathjax] \( \quad x=\sqrt{50}=5\sqrt{2} \)
答 [mathjax] \( 5\sqrt{2} \)cm
<3年p.223>
問 ２ 1辺6 cm の正方形の対角線の長さを求めなさい。
問 ３ 1 辺 [mathjax] \( a \) cm の正方形の対角線の長さを求めなさい。また，このことから，正方形の1 辺の長さと対角線の長さには，どんな関係があるといえますか。
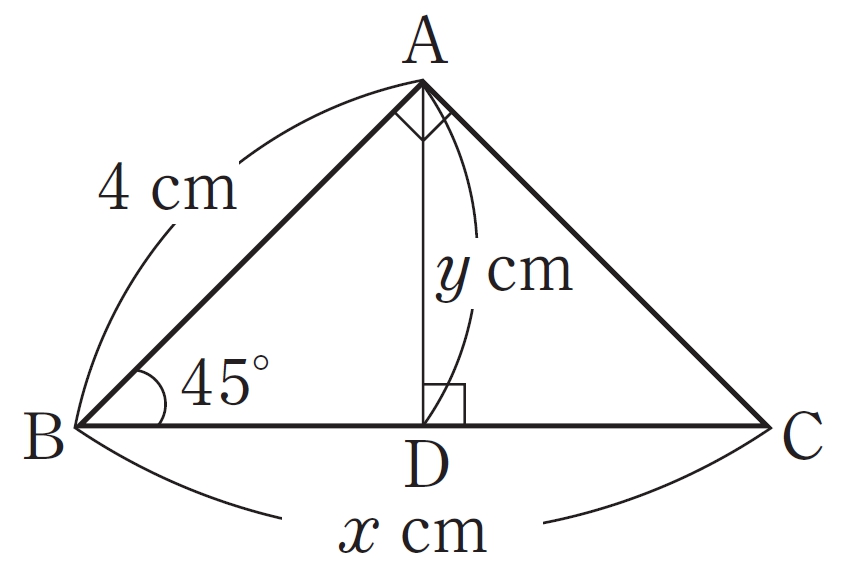
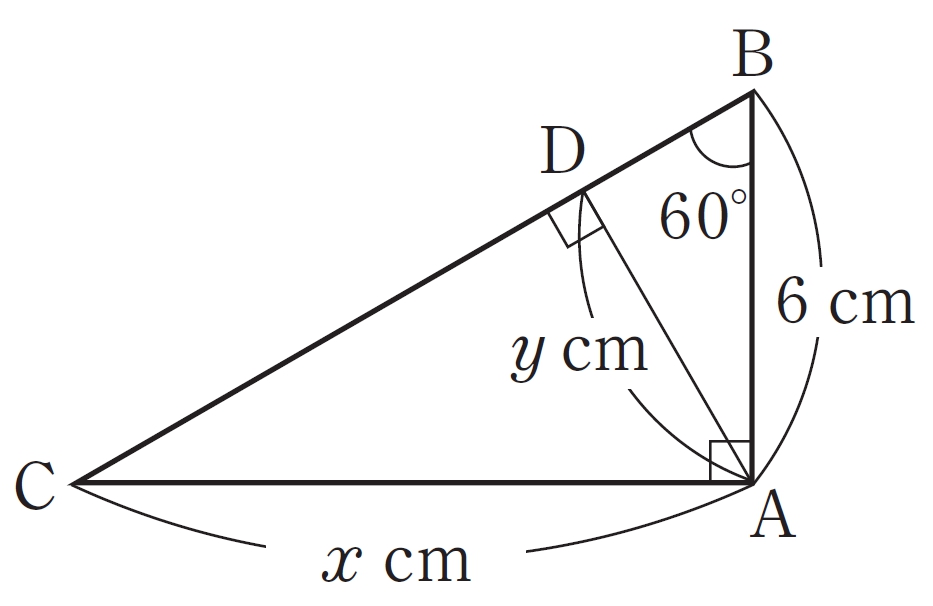
例 ２
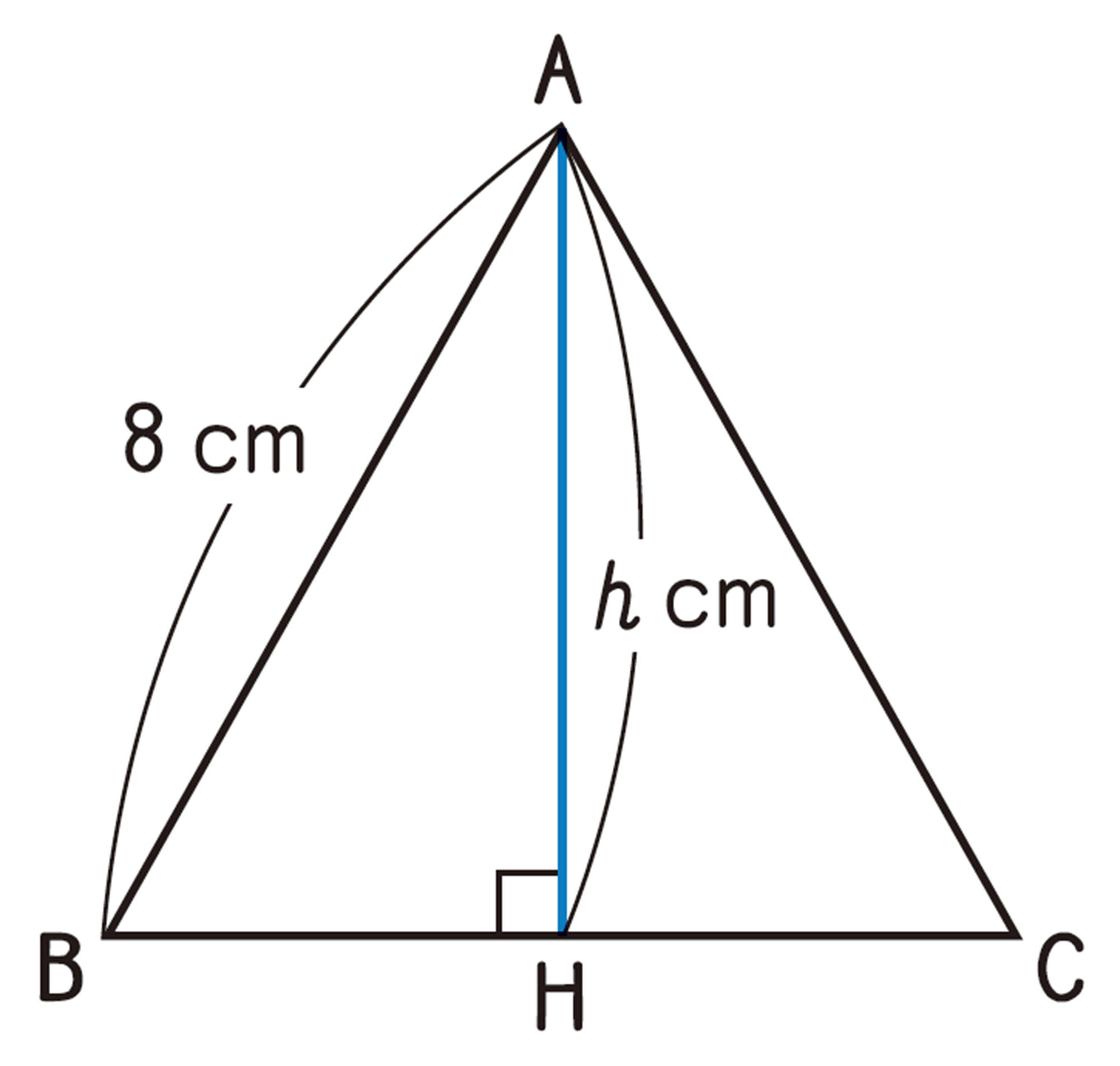
1 辺8 cm の正三角形 ABC の高さを求めなさい。
考え方
点 A から辺 BC に垂線を引き， 直角三角形をつくって三平方の定理を使う。
解答
点Aから辺BCに垂線AHを引くと，Hは辺BCの中点となるので，[mathjax] \(BH=4\)
高さAHを[mathjax] \( h \) cmとすると，
三平方の定理により，
答 [mathjax] \( 4\sqrt{3} \)cm
問 ４ 例 2の[mathjax] \(\triangle ABC\) の面積を求めなさい。
問 ５ 1 辺 [mathjax] \( 2a \) cmの正三角形の高さを求めなさい。また，このことから，正三角形の1 辺の長さと高さには，どんな関係があるといえますか。
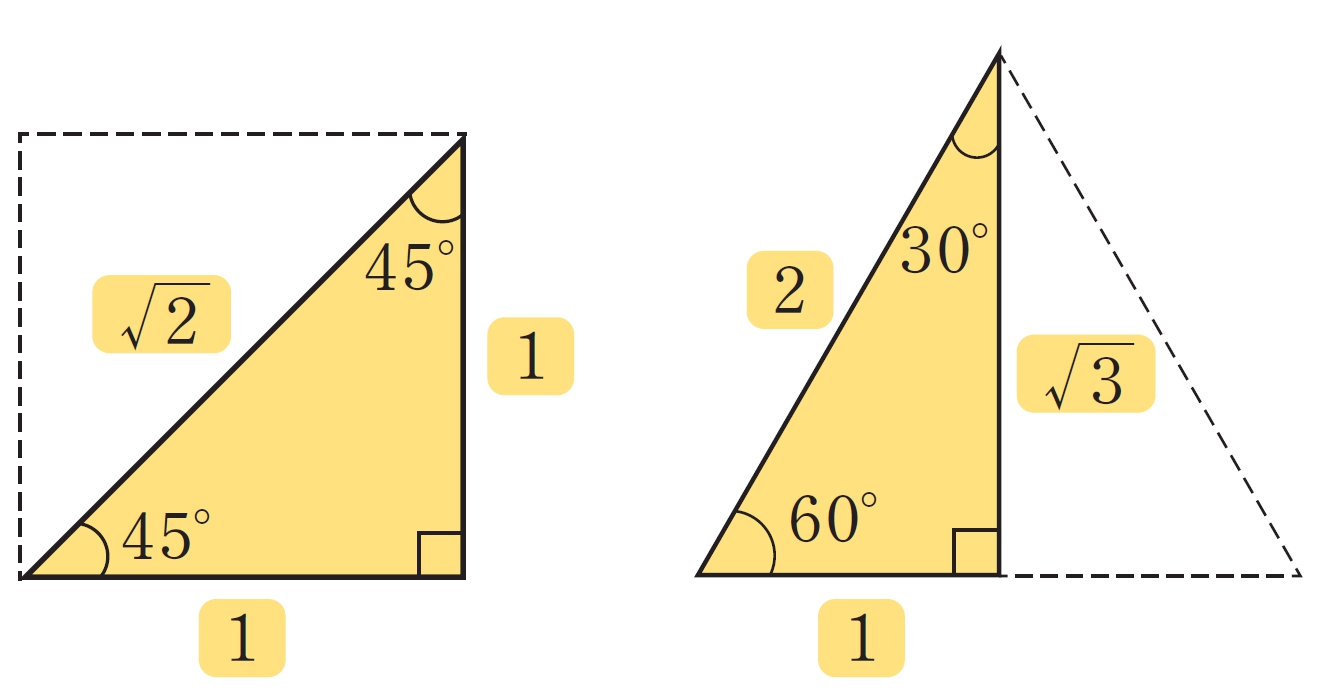
これまで調べたことから，直角二等辺三角形の3 辺の長さの比と，[mathjax] \(60^{\circ}\) の角をもつ直角三角形の3 辺の長さの比は，それぞれ次の図に示した比であることがわかる。
三角定規はこの3 辺の長さの比になっているね。
注意 3辺の長さの比をそれぞれ [mathjax] \(1:1:\sqrt{2}\) ， [mathjax] \(1:\sqrt{3}:2\) などと表すことがある。
<3年p.224>
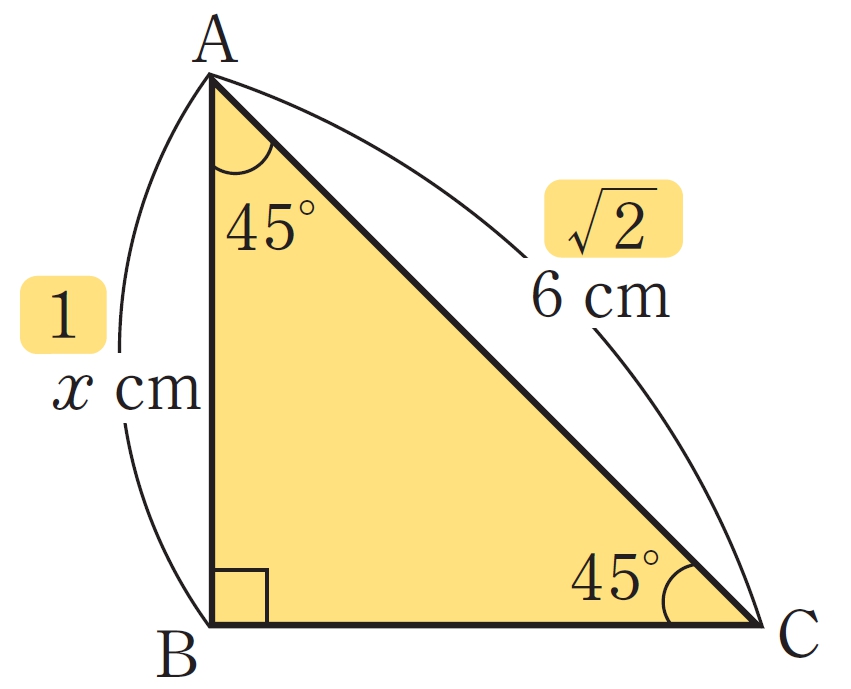
例 ３ 右の図の直角二等辺三角形ABC で，辺ABの長さを求めなさい。
解答
[mathjax] \( AB:AC＝1:\sqrt{2} \) であるから，[mathjax] \( AB＝x \) cmとすると，
したがって，[mathjax] \( AB=3\sqrt{2} \)cm
答 [mathjax] \(3 \sqrt{2} \)cm
問 6 次の図で，[mathjax]\( x \)，[mathjax]\( y \) の値を求めなさい。
⑴
⑵
ヒポクラテスの月 Tea Break
紀元前5 世紀，古代ギリシャにヒポクラテスという数学者がいました。このヒポクラテスがおもしろい発見をしています。
右の図のように，直角三角形 ABC の3 辺をそれぞれ直径とする3 つの半円をかきます。
ヒポクラテスは，この図から，
[mathjax]\((\mathsf{アの面積})+(\mathsf{イの面積})=(\mathsf{直角三角形} ABC \mathsf{の面積})\)
という関係が成り立つことに気づきました。この図は「ヒポクラテスの月」と呼ばれています。
ヒポクラテスの月で，上の式が成り立つことを証明してみましょう。
<3年p.225>
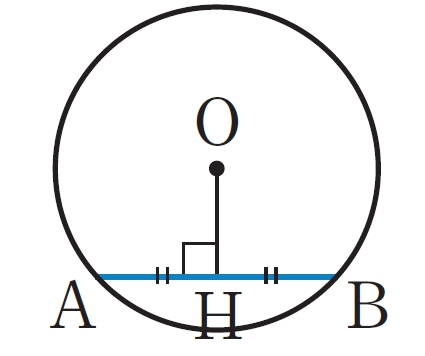
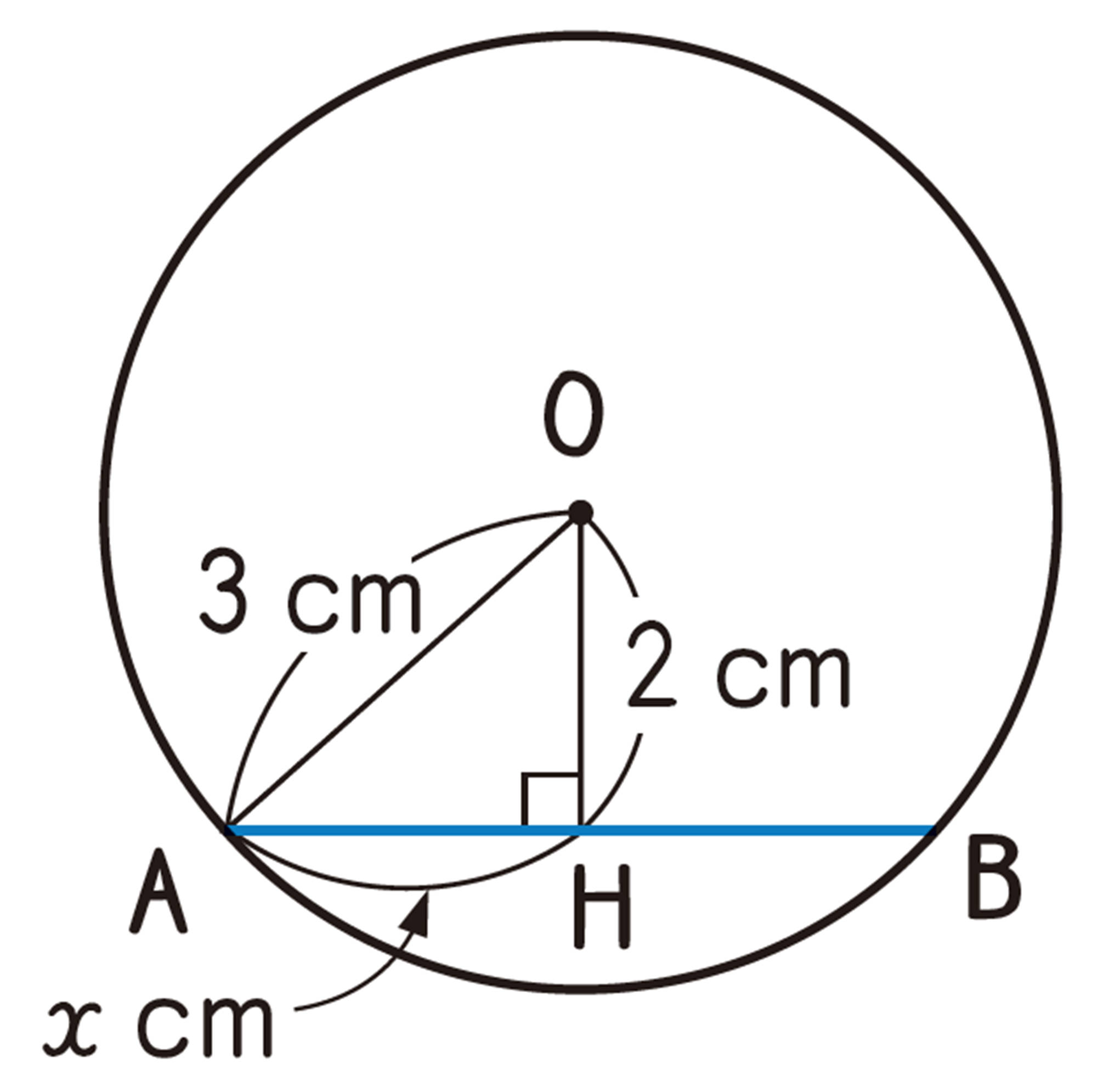
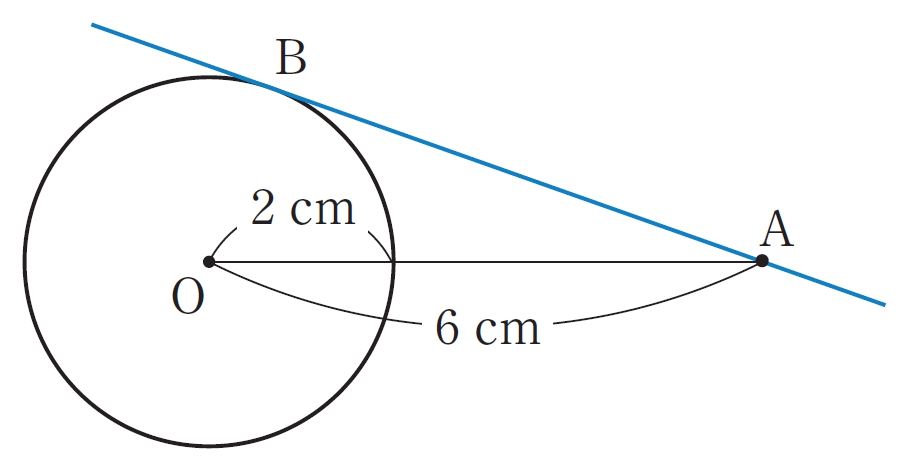
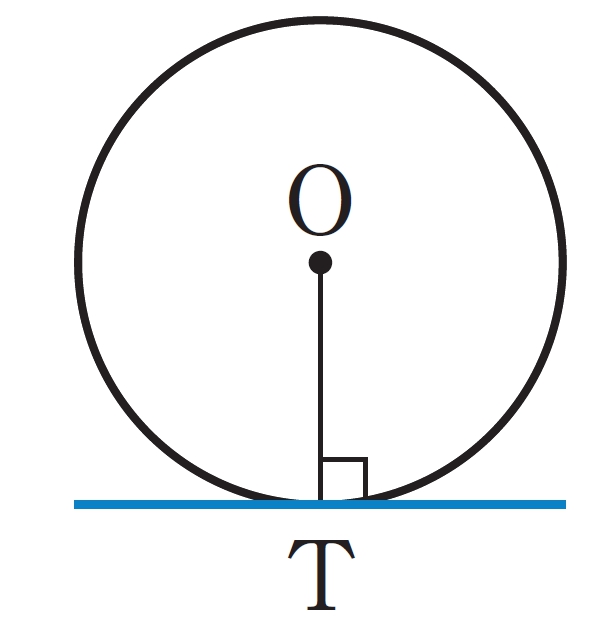
弦や接線の長さ
例 ４ 半径3 cm の円O で，中心からの距離が 2 cm である弦AB の長さを求めなさい。
考え方 円の中心O から弦AB に垂線OH を引くと，OH はAB の垂直二等分線になるので，[mathjax]\(\triangle OAH\) は直角三角形になる。
ふりかえり ▷ 1年
弦AB の垂直二等分線は，円の中心Oを通る。
解答
右の図で， 点H は弦AB の中点である。[mathjax] \( AH=x \) cm とすると，
[mathjax] \( \triangle OAH\) は [mathjax] \( \angle AHO=90^{\circ}\) の直角三角形であるから，
答 [mathjax] \( 2\sqrt{5} \)cm
問 ７ 半径5 cm の円 O について，次の問いに答えなさい。
⑴ 中心Oとの距離が3 cm である弦 AB の長さを求めなさい。
⑵ 弦 CD の長さが2 cm のとき，中心Oと弦CDとの距離を求めなさい。
問 ８ 次の図で，直線AB は点B を接点とする円 O の接線です。円Oの半径を2cm ，線分OAの長さを6 cm とするとき，線分AB の長さを求めなさい。
ふりかえり ▷ 1年
円の接線は，接点を通る半径に垂直である。
<3年p.226>
2点間の距離
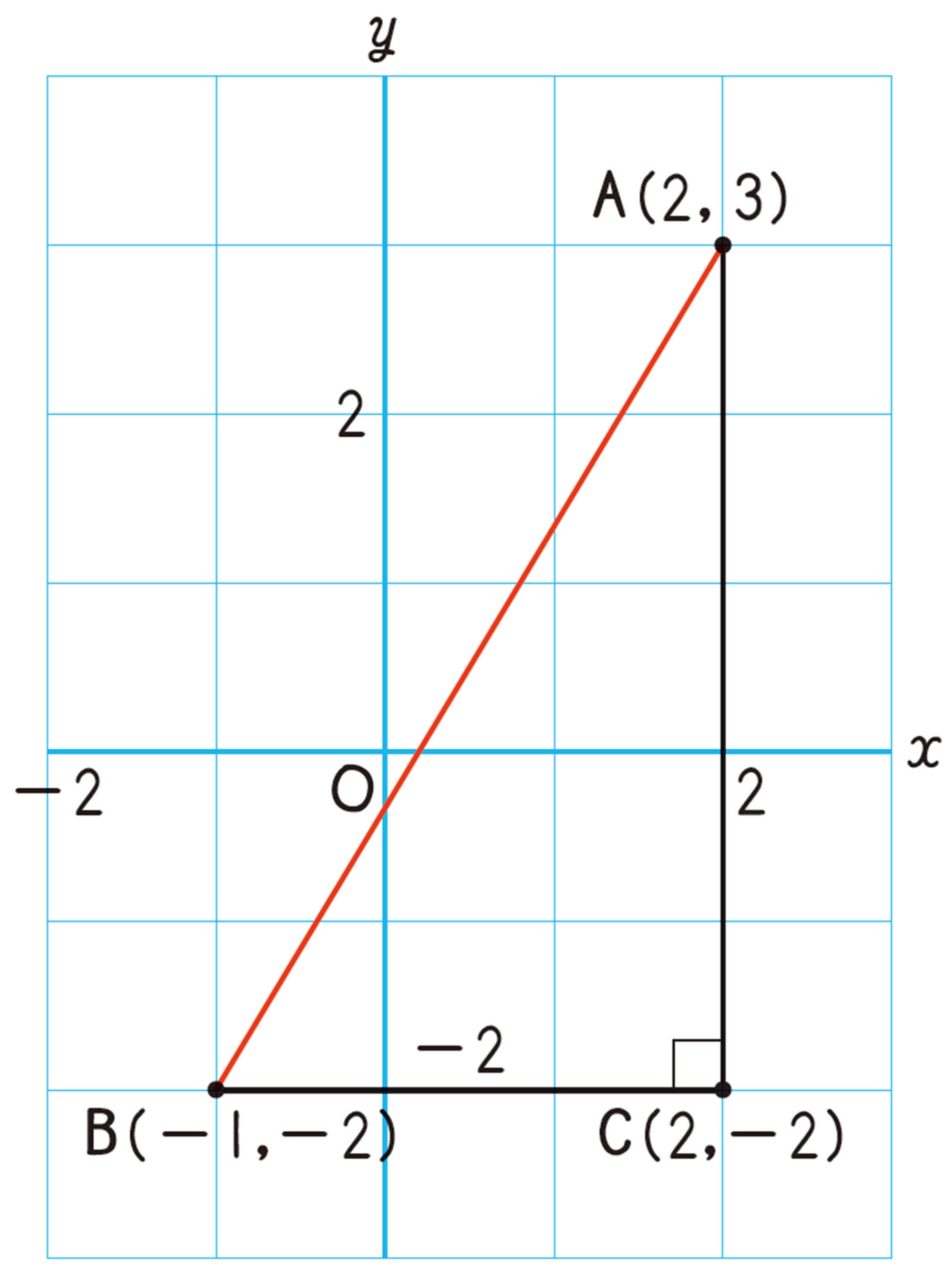
例 ５ 2点[mathjax]\(Ａ(2，3)\)，[mathjax]\(Ｂ(-1，-2)\)間の距離を求めなさい。
考え方 2点を結ぶ線分を斜辺とし，x軸，y軸にそれぞれ平行な2つの辺をもつ直角三角形をつくる。
解答
点Aからy軸に平行に引いた直線と，点Bからx軸に平行に引いた直線との交点[mathjax]\((2，-2)\)をCとする。
[mathjax]\(\triangle ABC\)は[mathjax]\(\angle C=90^{\circ}\)の直角三角形であるから，
[mathjax]\(AB \gt 0\)であるから，[mathjax]\(AB=\sqrt{34}\)
答 [mathjax]\(\sqrt{34}\)
注意 AB²は，ABの長さの2乗を表す。
問 ９ 次の2点間の距離を，それぞれ求めなさい。
⑴ [mathjax]\(A(2，5)\)，[mathjax]\(B(-1，1)\)
⑵ [mathjax]\(C(1，-2)\)，[mathjax]\(D(-3，-4)\)
⑶ [mathjax]\(E(0，0)\)，[mathjax]\(F(-1，5)\)
問 10 次の3点を頂点とする[mathjax]\(\triangle ABC\)の3辺の長さを求めなさい。また，[mathjax]\(\triangle ABC\)が直角三角形であることを示しなさい。
[mathjax]\(Ａ(2，0)\)，[mathjax]\(Ｂ(-2，3)\)，[mathjax]\(Ｃ(0，-1)\)
<3年p.227>
相似な図形への利用
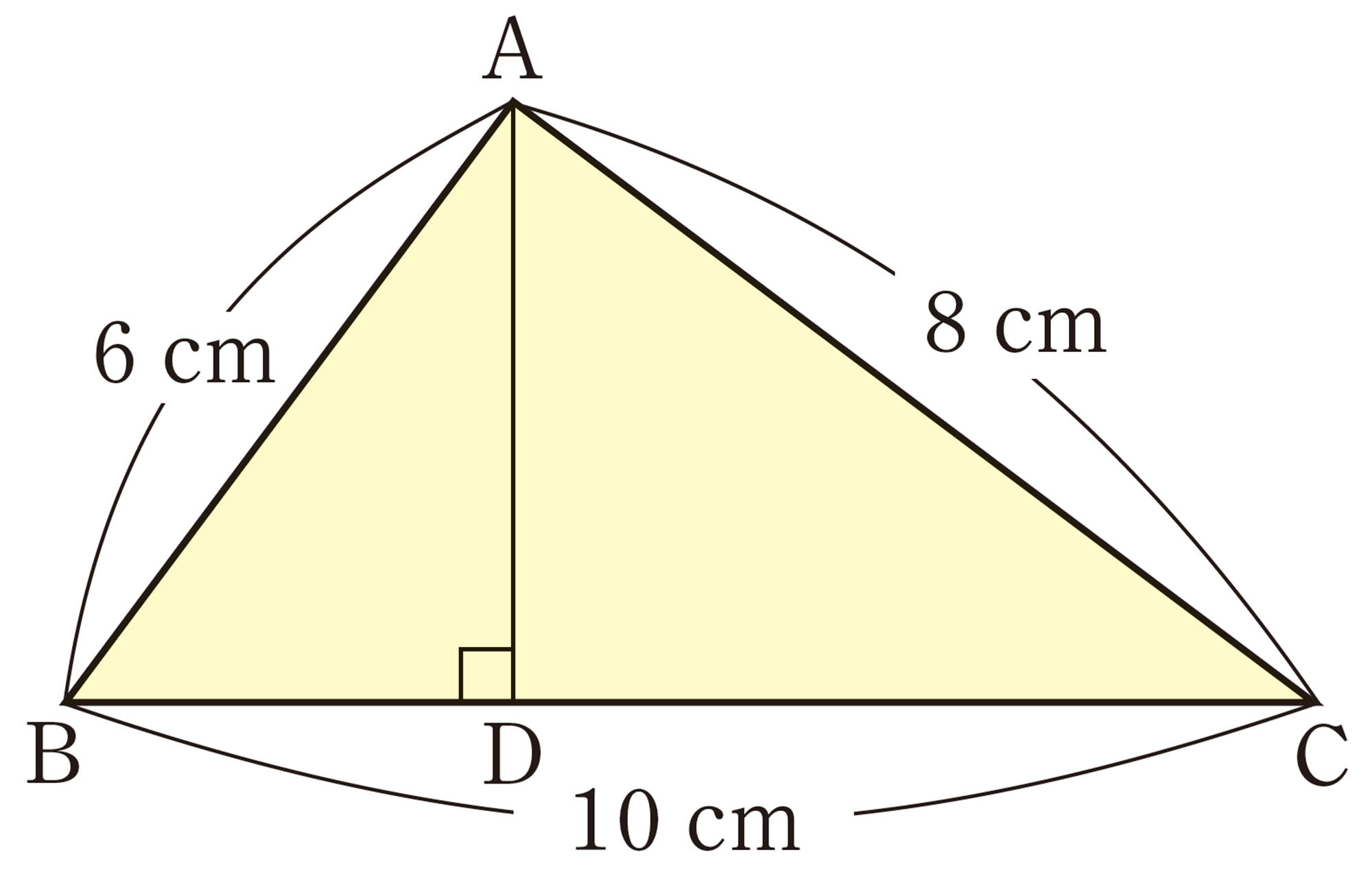
問 11 右の図で，[mathjax]\(\triangle ABC\)は，[mathjax]\(AB=6\)cm，[mathjax]\(BC=10\)cm，[mathjax]\(CA=8\)cm で，ADは頂点Aから辺BCに引いた垂線です。このとき，次の問いに答えなさい。
⑴ [mathjax]\(\triangle ABC\)が直角三角形であることを示しなさい。
⑵ [mathjax]\(\triangle ABC \backsim \triangle DAC\)であることを証明しなさい。
⑶ [mathjax]\(\triangle ABC \backsim \triangle DAC\) であることを利用して，垂線ADの長さを求めなさい。
⑷ [mathjax]\(\triangle ABC\)の面積を利用して，垂線ADの長さを求め，⑶の答えと比べなさい。
問 12 右の図のように，縦4cm，横6cmの長方形ABCDの紙を，頂点Cと頂点Aが重なるように折りました。辺AD上で折った点をE，頂点Dが移った点を[mathjax] \(D´\)とするとき，次の問いに答えなさい。
⑴ [mathjax]\(\triangle AOE \backsim \triangle ADC\)であることを証明しなさい。
⑵ [mathjax]\(\triangle ADC\)の斜辺ACの長さを求めなさい。
⑶ ⑴，⑵を利用して，AEの長さを求めなさい。
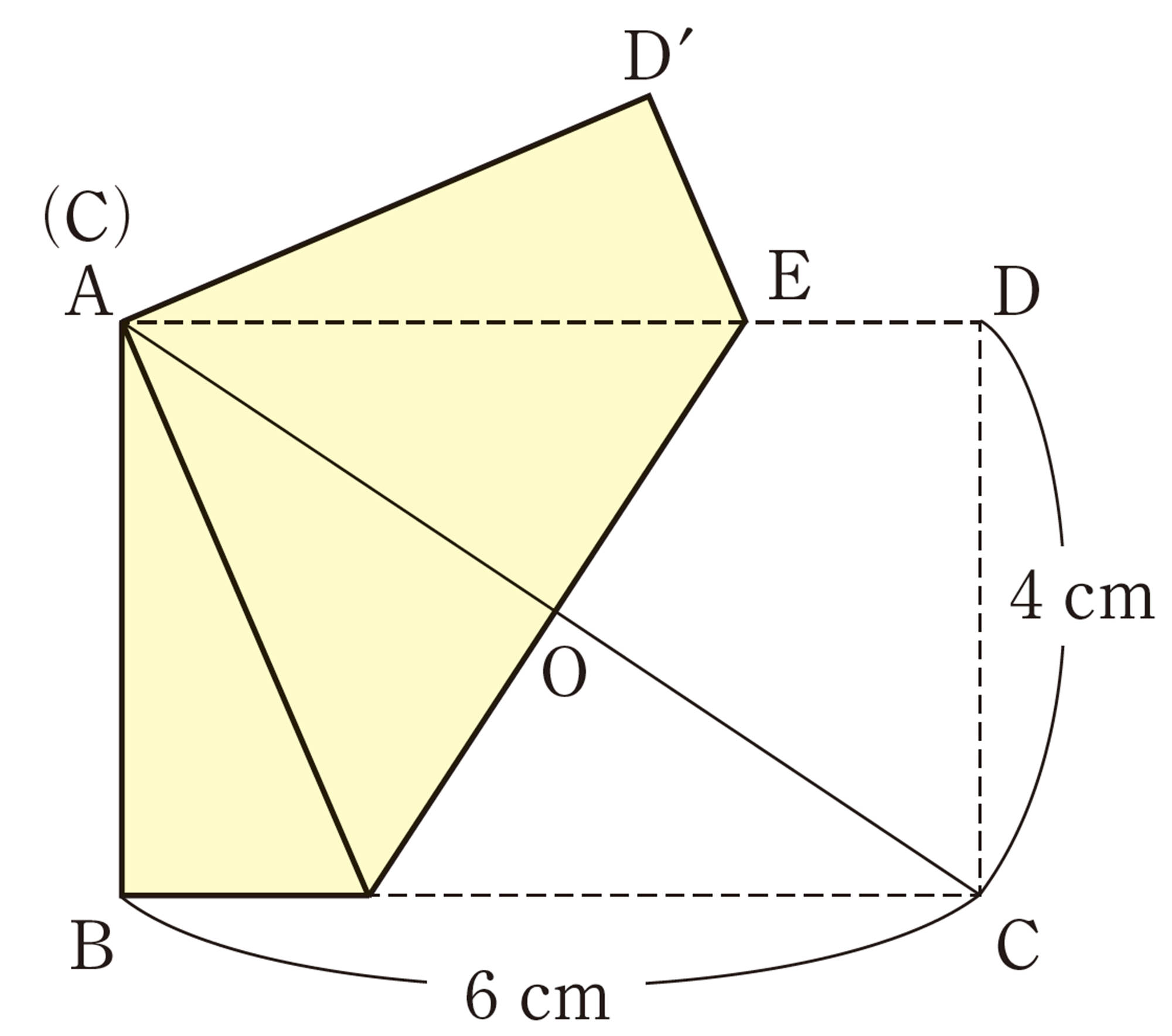
問 13 問12で，美月さんは[mathjax]\(\triangle AED´\)に着目してAEの長さを求めました。次の問いに答えなさい。
⑴ [mathjax]\(AE=x\)とするとき，[mathjax] \(ED´\)の長さをxを使って表しなさい。
⑵ [mathjax]\(\triangle AED´\)において，三平方の定理を利用して，AEの長さを求めなさい。
どんなことがわかったかな
三平方の定理を利用すると，正方形の対角線の長さや正三角形の高さなど，2点間の距離を求めることができます。
