<3年p.219>
２ 三平方の定理の逆
Q Question
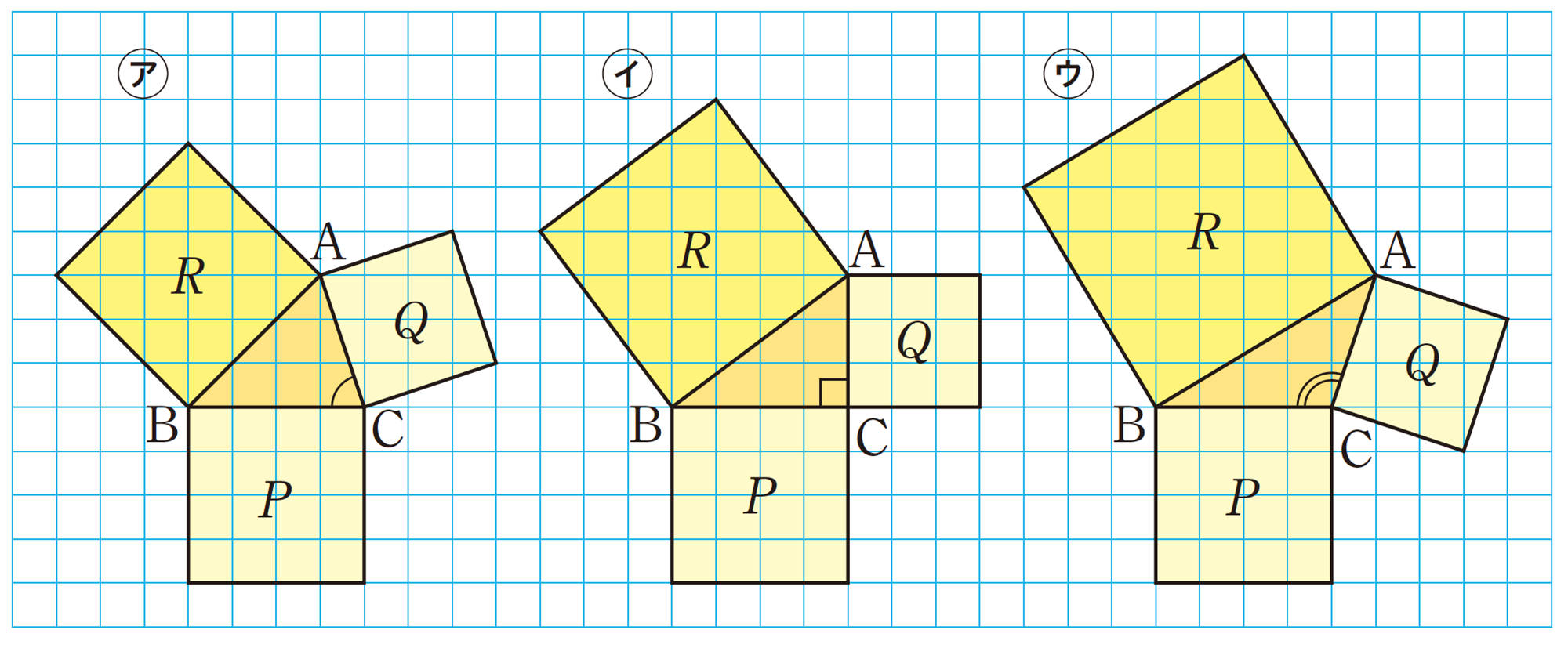
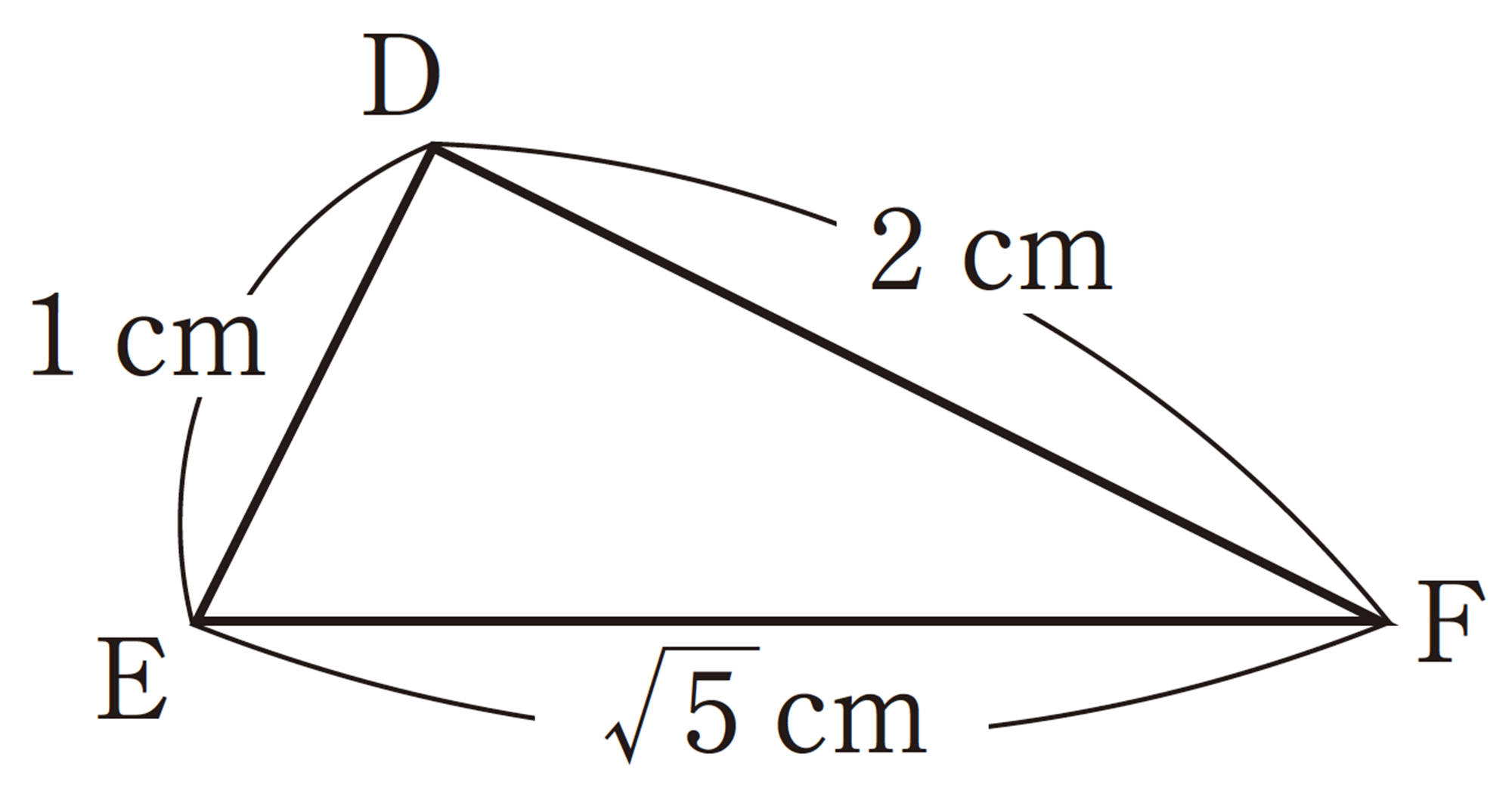
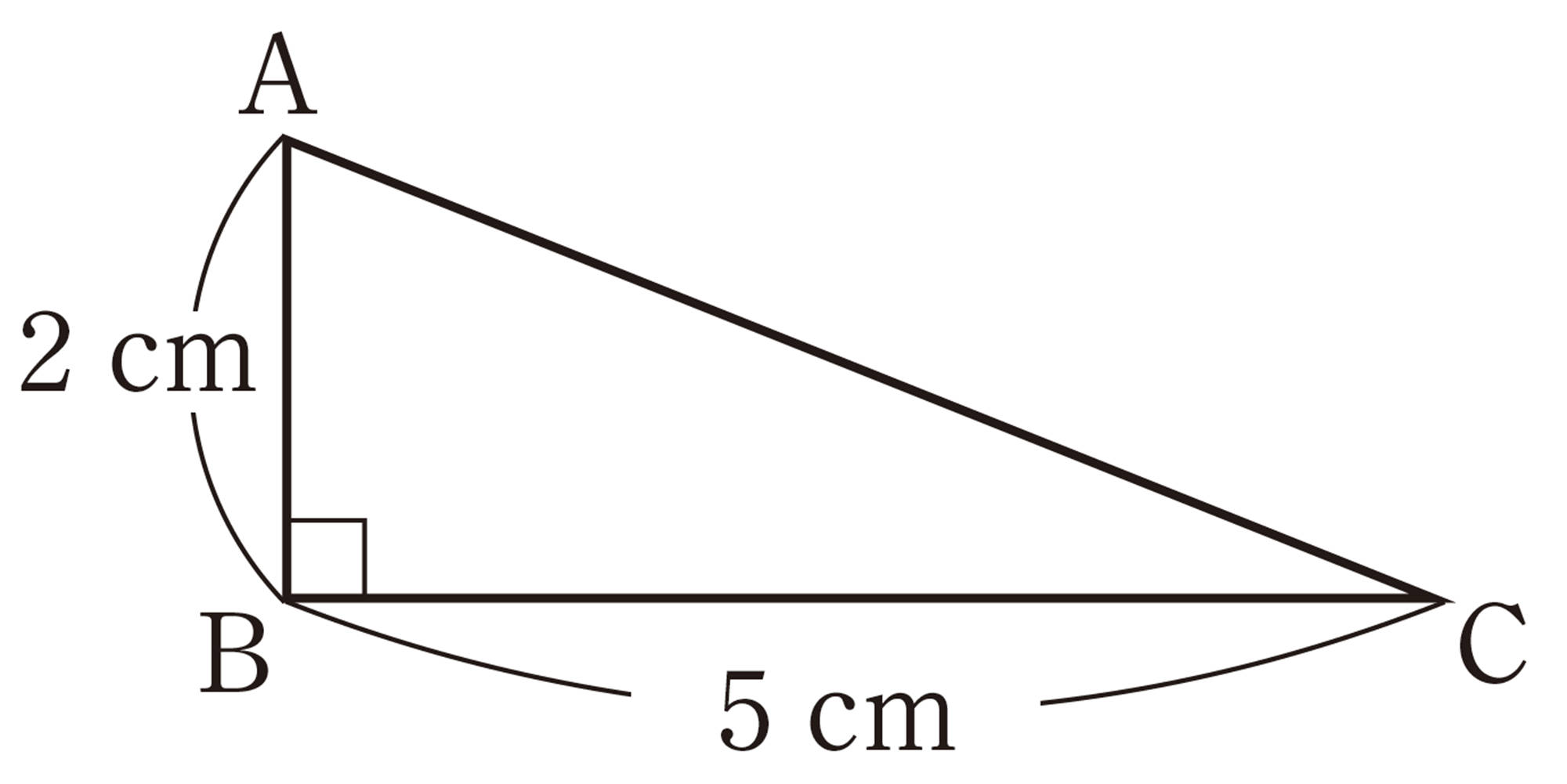
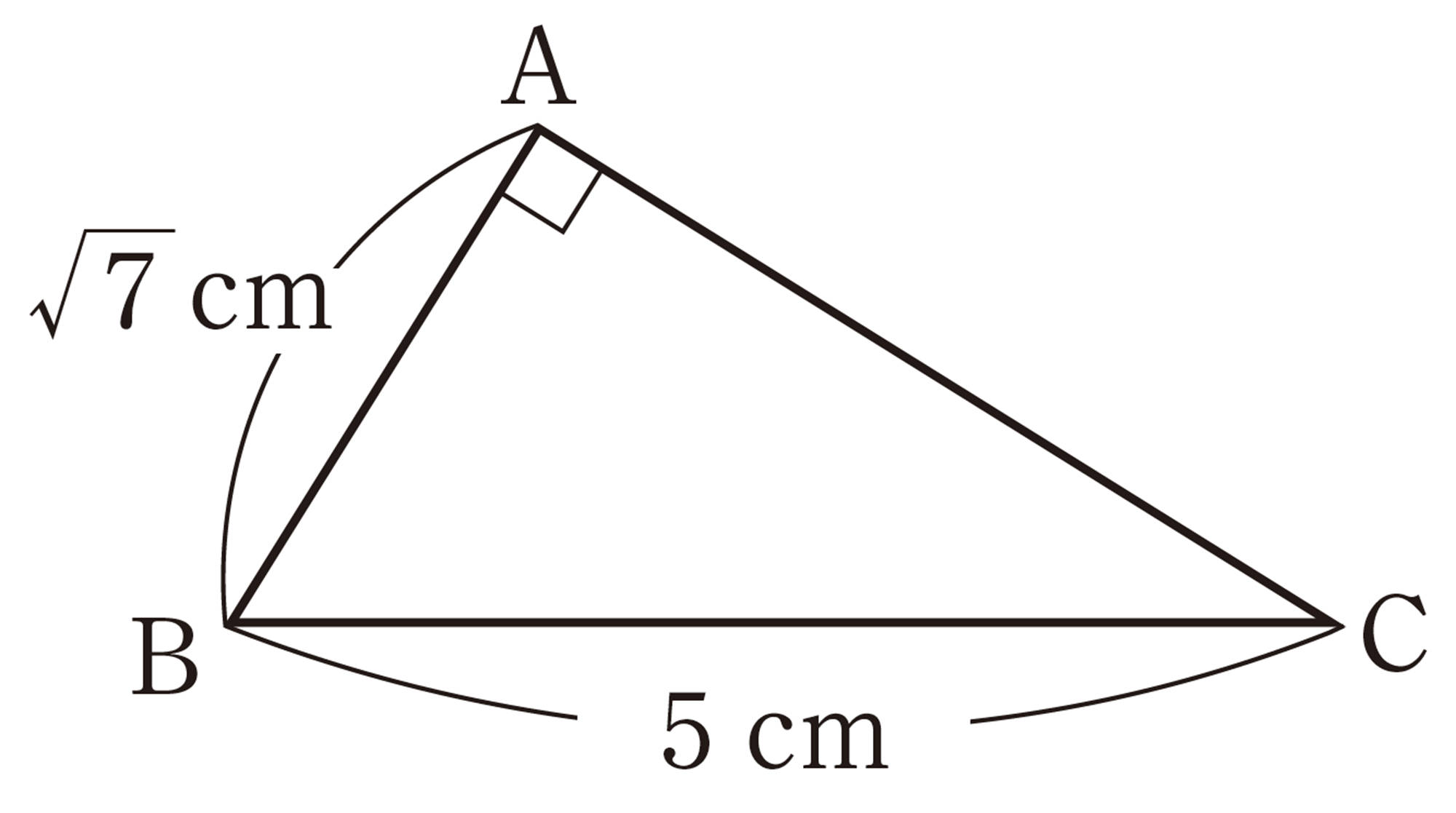
次の㋐，㋑，㋒の図について，[mathjax]\(\triangle ABC\)の各辺を1辺とする正方形の面積P，Q，Rの関係を，それぞれ調べてみましょう。
[mathjax]\(P+Q=R\)の関係が成り立つのは，[mathjax]\(\angle C = 90^{\circ}\)のときだけといえるのかな。
見方・考え方
いくつかの三角形を調べて，どんな性質があるか見つけられるかな。
目標 ▷ 三平方の定理が成り立つのは，直角三角形のときだけかどうか調べよう。
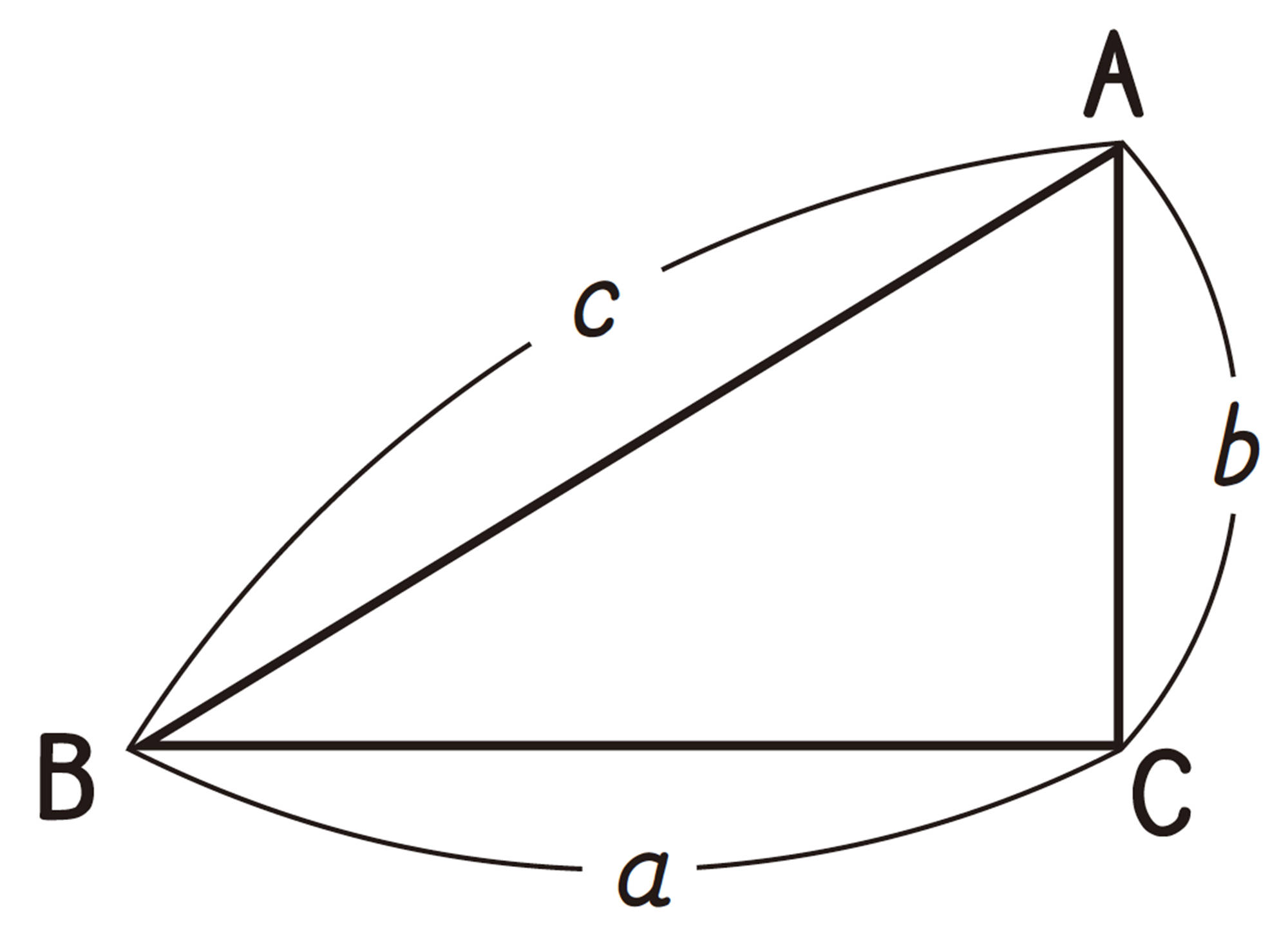
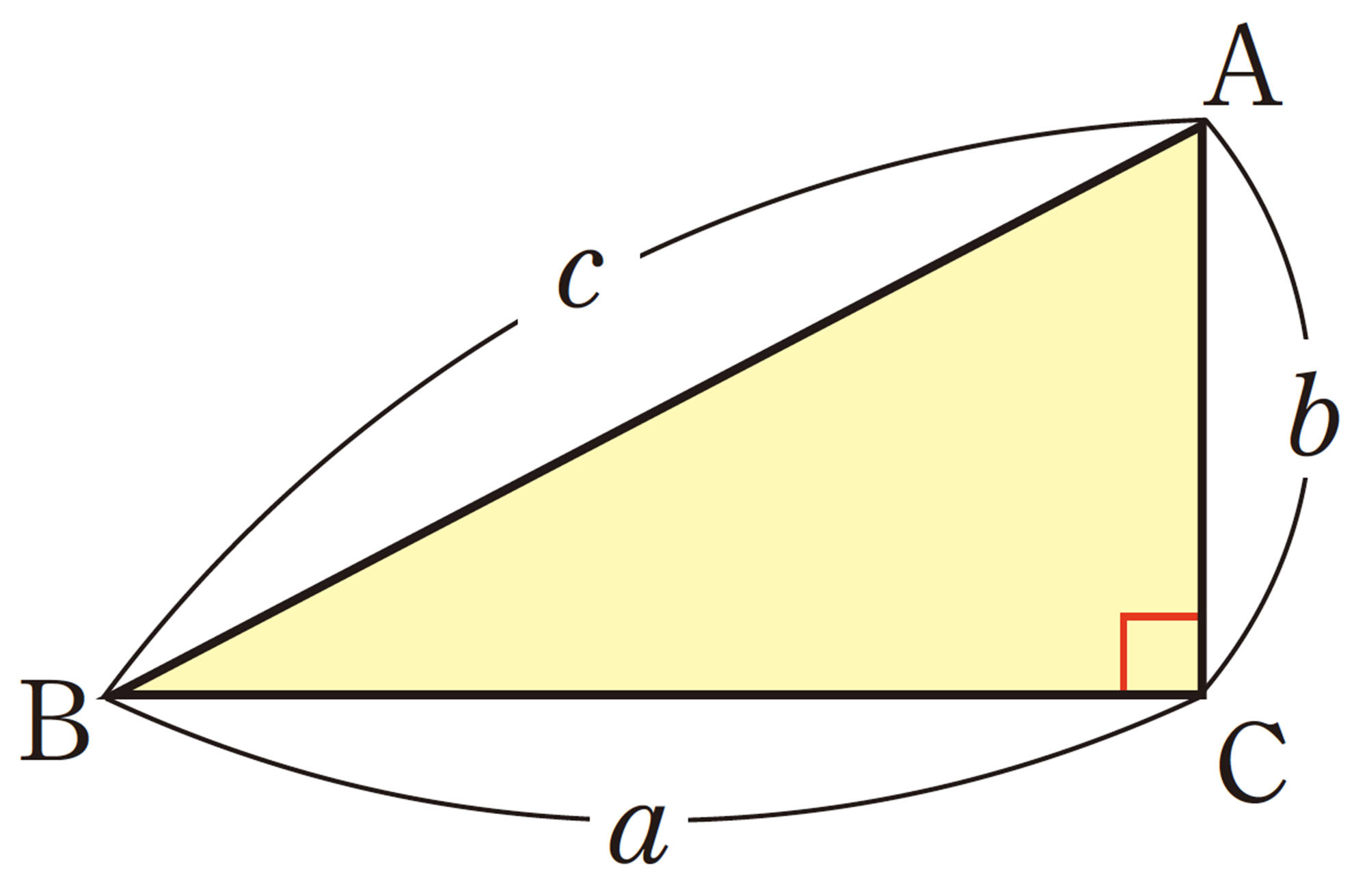
右下の図で，[mathjax]\(\triangle ABC\) の3辺の長さa，b，cの間に [mathjax]\(a²+b²=c²\) の関係が成り立つとき，[mathjax]\(\angle C=90^{\circ}\) である。このことは，
次のようにして証明することができる。
証明
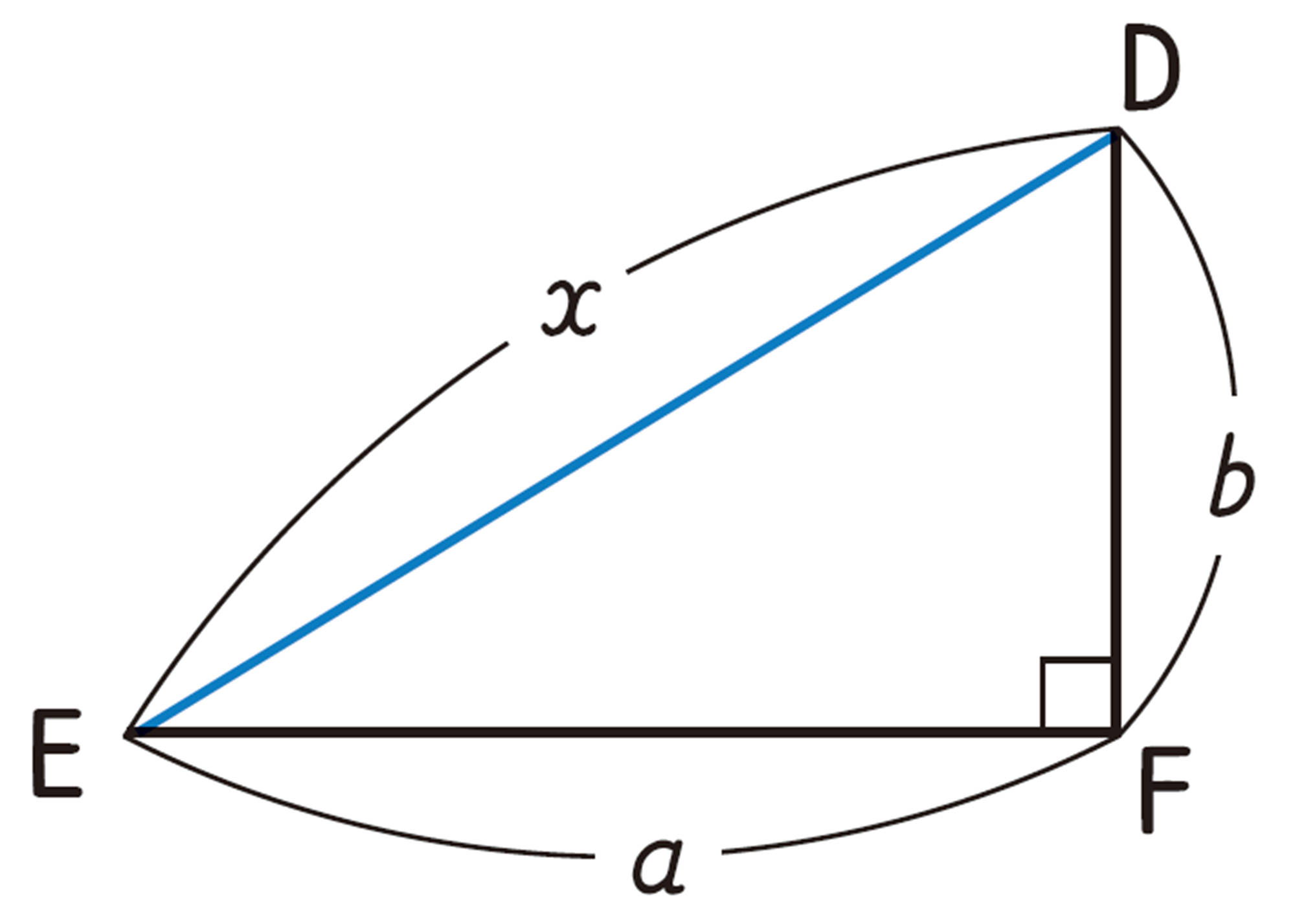
[mathjax]\(EF=a\)，[mathjax]\(FD=b\)，[mathjax]\(\angle F=90^{\circ}\) である [mathjax]\(\triangle DEF\) をかき，[mathjax]\(DE=x\) とする。[mathjax]\(\triangle DEF\) は直角三角形であるから，
三平方の定理により， [mathjax]\(a²+b²=x² \quad \cdots \cdots\mathsf{①}\)
また，仮定から， [mathjax]\(\hspace{18pt}a²+b²=c² \quad \cdots \cdots\mathsf{②}\)
①，②から， [mathjax]\(\hspace{54pt}x²=c²\)
[mathjax]\(x \gt 0\)，[mathjax]\(c \gt 0\) であるから， [mathjax]\(x=c\)
すなわち，[mathjax]\(\triangle ABC\) と [mathjax]\(\triangle DEF\) において，[mathjax]\(AB=DE\) ，[mathjax]\(BC=EF\) ，[mathjax]\(CA=FD\) となり，3組の辺がそれぞれ等しいから，[mathjax]\(\triangle ABC \equiv \triangle DEF\)
したがって，[mathjax]\(\angle C=\angle F=90^{\circ}\)
<3年p.220>
定理
三平方の定理の逆
[mathjax]\(\triangle ABC\)の3辺の長さa，b，cの間に，
[mathjax]\(a²+b²=c²\)
の関係が成り立てば，[mathjax]\(\angle C=90^{\circ}\)である。
この定理により，三角形の3辺の長さがわかっていれば，それが直角三角形であるかどうかを調べることができる。
例 １ 右の図の[mathjax]\(\triangle DEF\)は，直角三角形といえますか。
考え方 [mathjax]\(\triangle DEF\)の3辺のうち，もっとも長いEFの長さをc，他の2辺の長さをa，bとして，[mathjax]\(a²+b²=c²\) の関係が成り立つかどうかを調べる。
解答
[mathjax]\(a=1\)，[mathjax]\(b=2\)，[mathjax]\(c=\sqrt{5}\) とすると，
したがって，[mathjax]\(a²+b²=c²\) が成り立つ。
答 直角三角形といえる
EFが斜辺で，それに向かい合う[mathjax]\(\angle D\)が直角だね。
問 １ 次の長さを3辺とする三角形㋐〜㋓のうち，直角三角形はどれですか。
㋐ 4cm，5cm，6cm
㋑ 8cm，15cm，17cm
㋒ 1cm，[mathjax]\(\sqrt{3}\)cm，2cm
㋓ [mathjax]\(\sqrt{6}\)cm，3cm，4cm
▲トライ 三平方の定理の逆を利用して，教室やグラウンドで1つの辺の長さが3mの直角三角形をつくるにはどうしたらよいか考えてみよう。
どんなことがわかったかな
三平方の定理の逆が成り立つことから，三角形の3つの辺の長さがわかれば，その三角形が直角三角形かどうか判断できます。
次の課題へ！
三平方の定理やその逆は，どんなところで使えるのかな？
P.222
<3年p.221>
確かめよう 1節 三平方の定理
１ 次の直角三角形ABCで，辺ACの長さを求めなさい。
⑴
⑵
２ 次の長さを3辺とする三角形は，直角三角形といえますか。
⑴ [mathjax]\(\sqrt{11}\)cm，5cm，6cm
⑵ 6cm，7cm，9cm
ピタゴラス数 Tea Break
([mathjax] \(3\)，[mathjax] \(4\)，[mathjax] \(5\))，([mathjax] \(5\)，[mathjax] \(12\)，[mathjax] \(13\))，([mathjax] \(8\)，[mathjax] \(15\)，[mathjax] \(17\))のように，[mathjax]\(a²+b²=c²\)を成り立たせる自然数の組は，「ピタゴラス数」と呼ばれています。
ピタゴラス数(a，b，c)は，次の式で得られることが知られています。
2つの異なる自然数m，nで，[mathjax]\(m \gt n\)とすると，
[mathjax]\(a=m²-n²\)，[mathjax]\(b=2mn\)，[mathjax]\(c=m²+n²\)
これらの式で [mathjax]\(a²+b²=c²\) が成り立つことを確かめてみよう。
たとえば，[mathjax]\(m=2\)，[mathjax]\(n=1\)をこれらの式に代入すると，
[mathjax]\(a=2²-1²=3\)，[mathjax]\(b=2 \times 2 \times 1 =4\)，[mathjax]\(c=2²+1²=5\)
となり，ピタゴラス数([mathjax]\(3\)，[mathjax]\(4\)，[mathjax]\(5\))が得られます。
m，nの値を自分で決めて，いろいろなピタゴラス数を求めてみましょう。
おしえて！
▷P.229
[mathjax]\(a³+b³=c³\)
[mathjax]\(a⁴+b⁴=c⁴\)
…
を成り立たせる自然数の組はあるのかな？
