<3年p.213>
７章 Chapter ７ 三平方の定理
1節 三平方の定理
2節 三平方の定理の利用
直角三角形のまわりに，正方形を並べています。正方形㋑と正方形㋒の各部分を並べかえて正方形㋐の上にぴったりとしきつめてみましょう。
巻末④の図を切り取って使いましょう。
並べてみると，ぴったりおさまるね。
なぜかな。何か秘密があるのかな。
？ 直角三角形にはどんな秘密があるのかな？
<3年p.214>
1節 三平方の定理
３つの正方形の面積の関係は？
紀元前500年頃，古代ギリシャのピタゴラスは，次のような石畳の模様を見て，「直角二等辺三角形の斜辺を1辺とする正方形の面積は，他の2辺をそれぞれ1辺とする正方形の面積の和と等しい」……㋐
ということを発見したといわれています。
ピタゴラスが発見したことは，いつでも正しいといえるのかな。
上の図で，確かめてみよう。
この関係は，ほかの直角三角形でも成り立つのでしょうか。直角三角形の各辺を1辺とする3つの正方形の面積の関係を調べてみましょう。
<3年p.215>
【１】 次の図①〜③で，直角三角形の各辺を1辺とする正方形の面積を，それぞれ求めてみましょう。
【２】 上の方眼にいろいろな直角三角形をかき，1と同じことを調べてみましょう。また，3つの正方形の面積の間にはどんな関係があるかを予想し，前ページの㋐のように，ことばに表してみましょう。
次の課題へ！
上で調べたことは，どんな直角三角形でもいえるのかな？
P.216
次の課題へ！
直角三角形以外の三角形でも，同じことがいえるのかな？
P.219
<3年p.216>
１ 三平方の定理
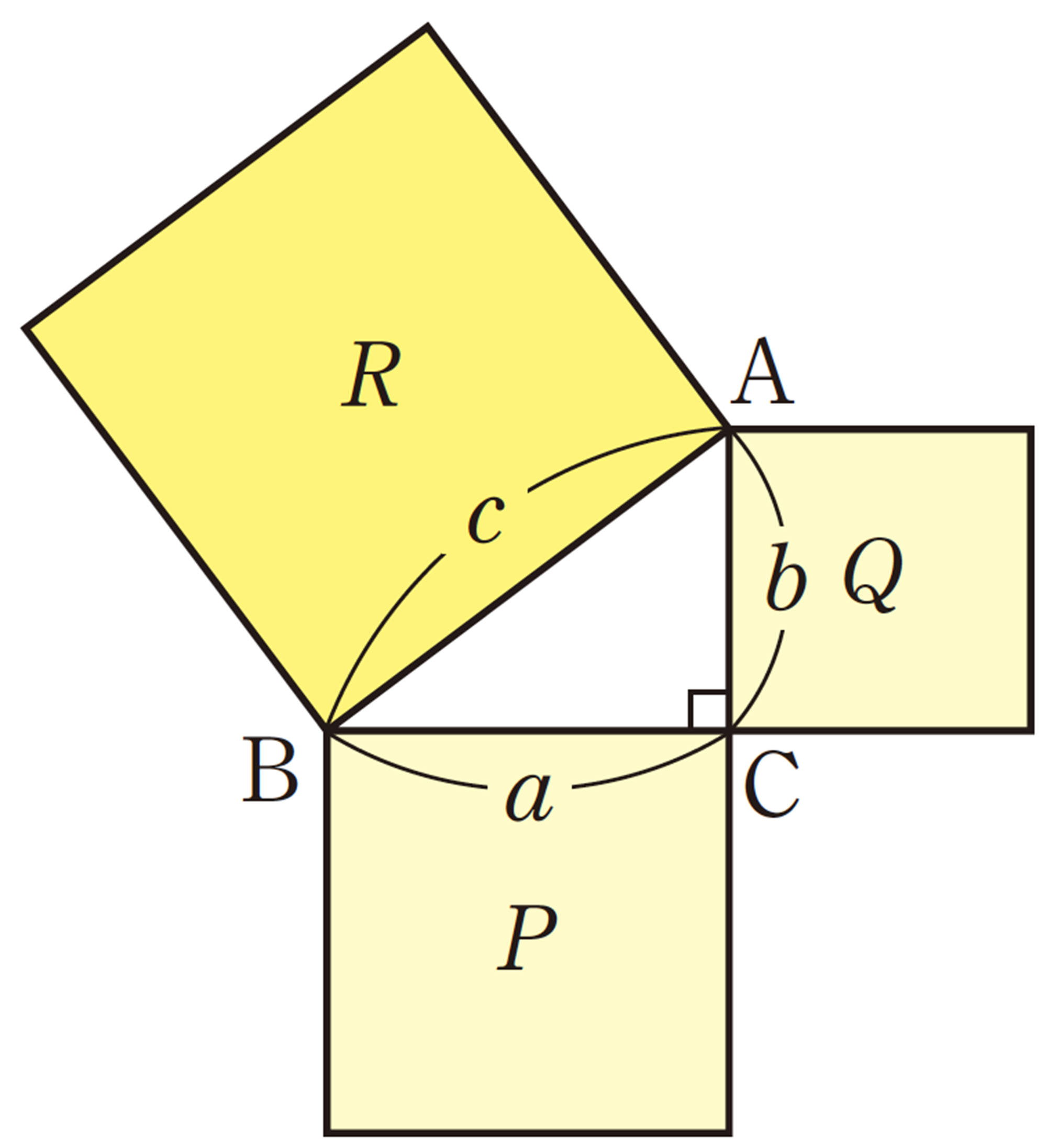
目標 ▷ 直角三角形の3辺をそれぞれ1辺とする正方形の面積について調べよう。
直角三角形の各辺を1辺とする正方形の面積を，右の図のように，それぞれP，Q，Rとすると，前ページで調べたことから，
[mathjax]\(P+Q=R\)
という関係が成り立つことが予想できる。
直角三角形の直角をはさむ2辺の長さをa，b，斜辺の長さをcとすると，上の式は，次のように表すことができる。
[mathjax]\(a²+b²=c²\)
頂点Aの対辺の長さをaとおくよ。
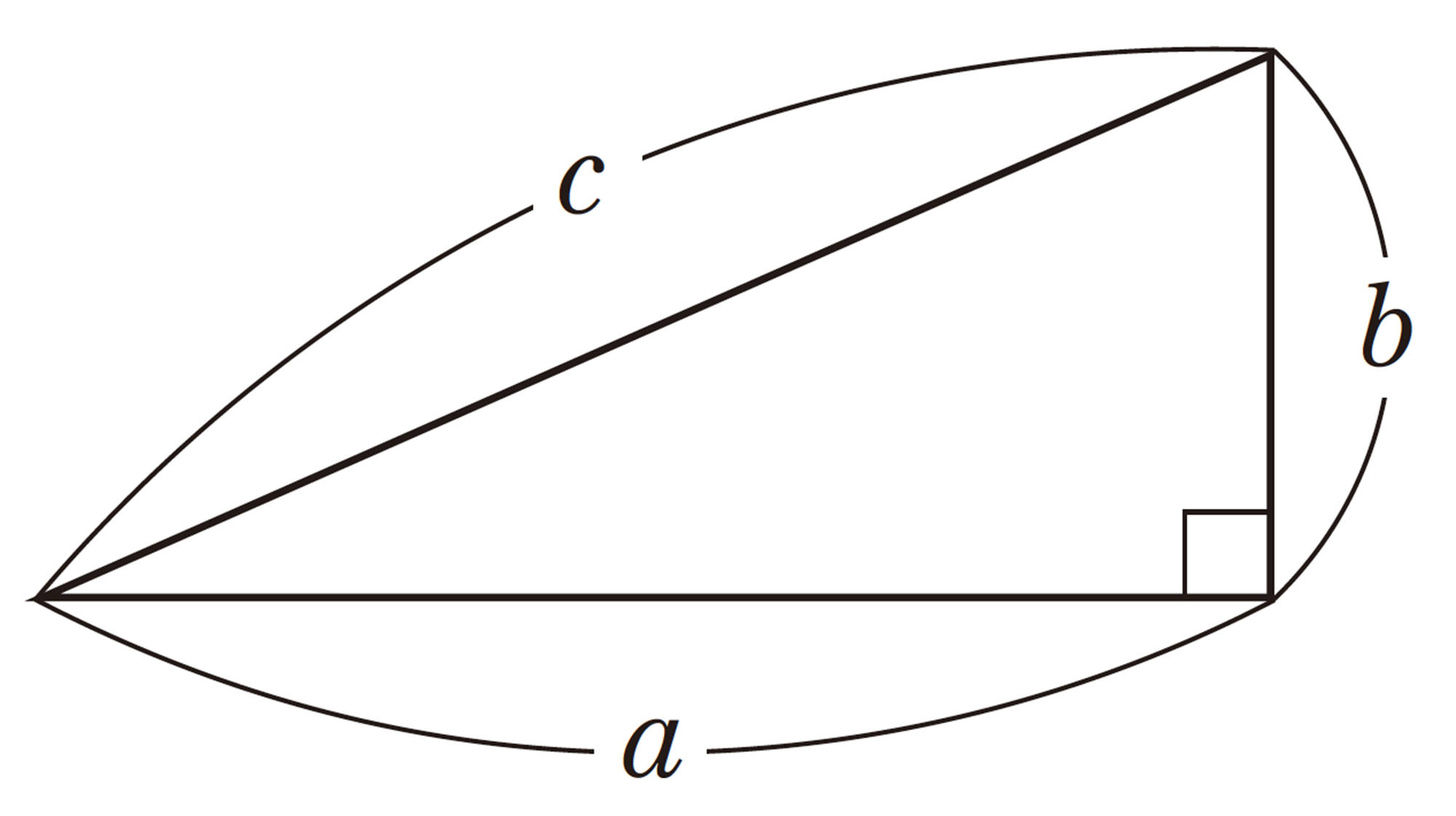
直角三角形で，[mathjax]\(a²+b²=c²\)の関係が成り立つことを証明してみよう。
証明をするためには，「仮定」と「結論」をはっきりさせておく必要があるね。ことばにすると，どうなるかな。
仮定は，「直角三角形で，直角をはさむ2辺の長さをa，b，斜辺の長さをcとするならば」になるのかな。
結論は，「[mathjax]\(a²+b²=c²\)」だね。
<3年p.217>
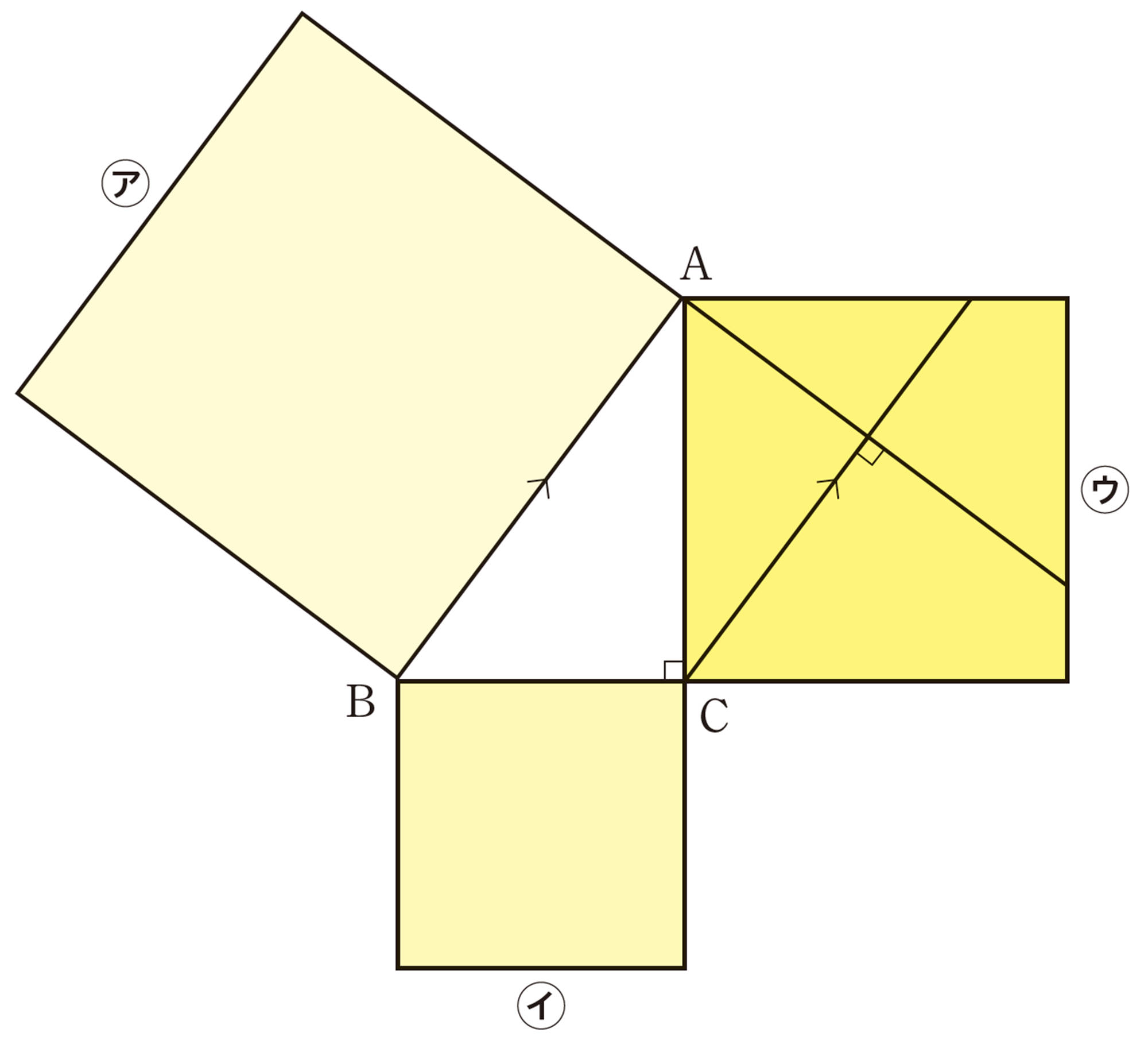
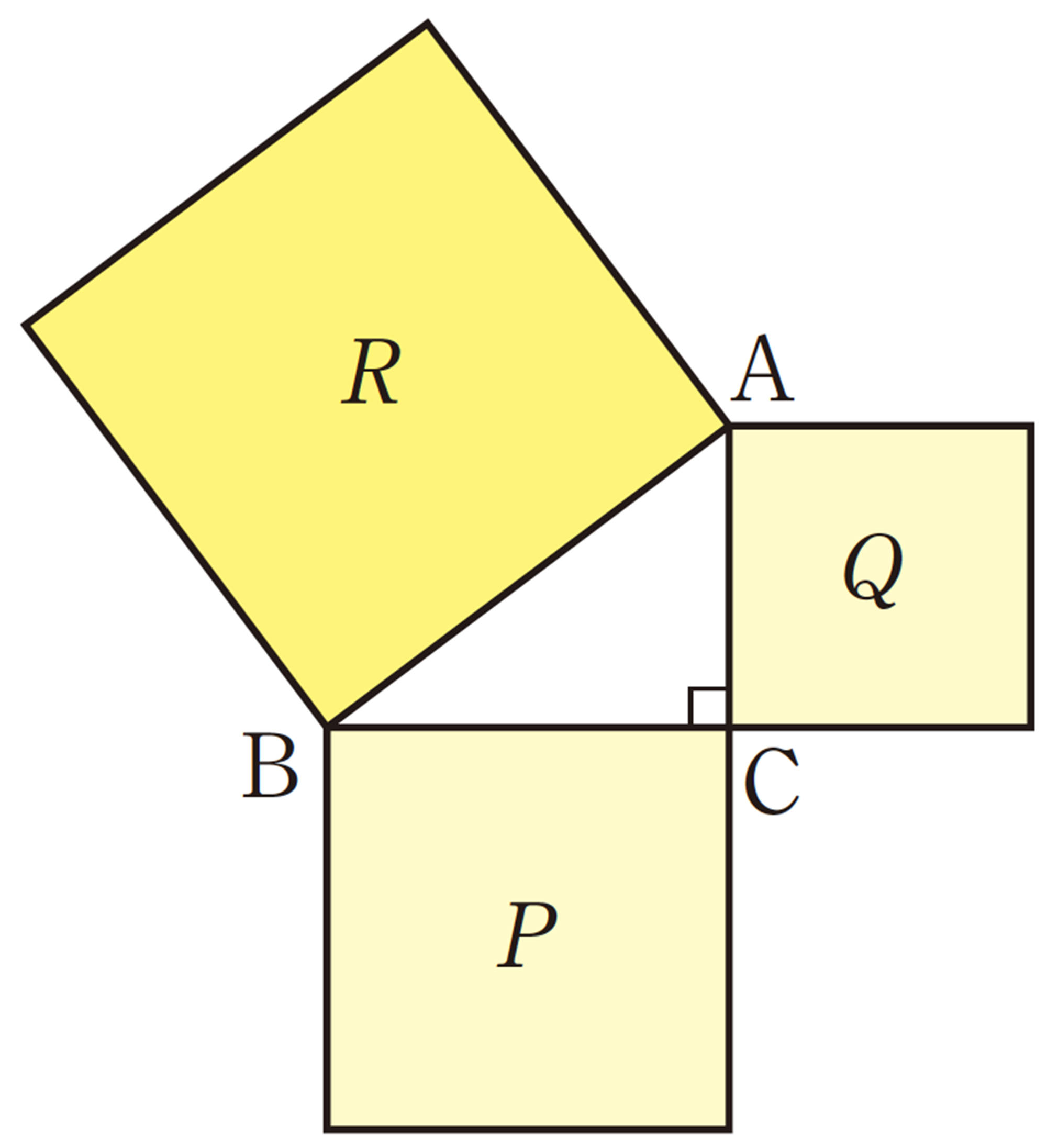
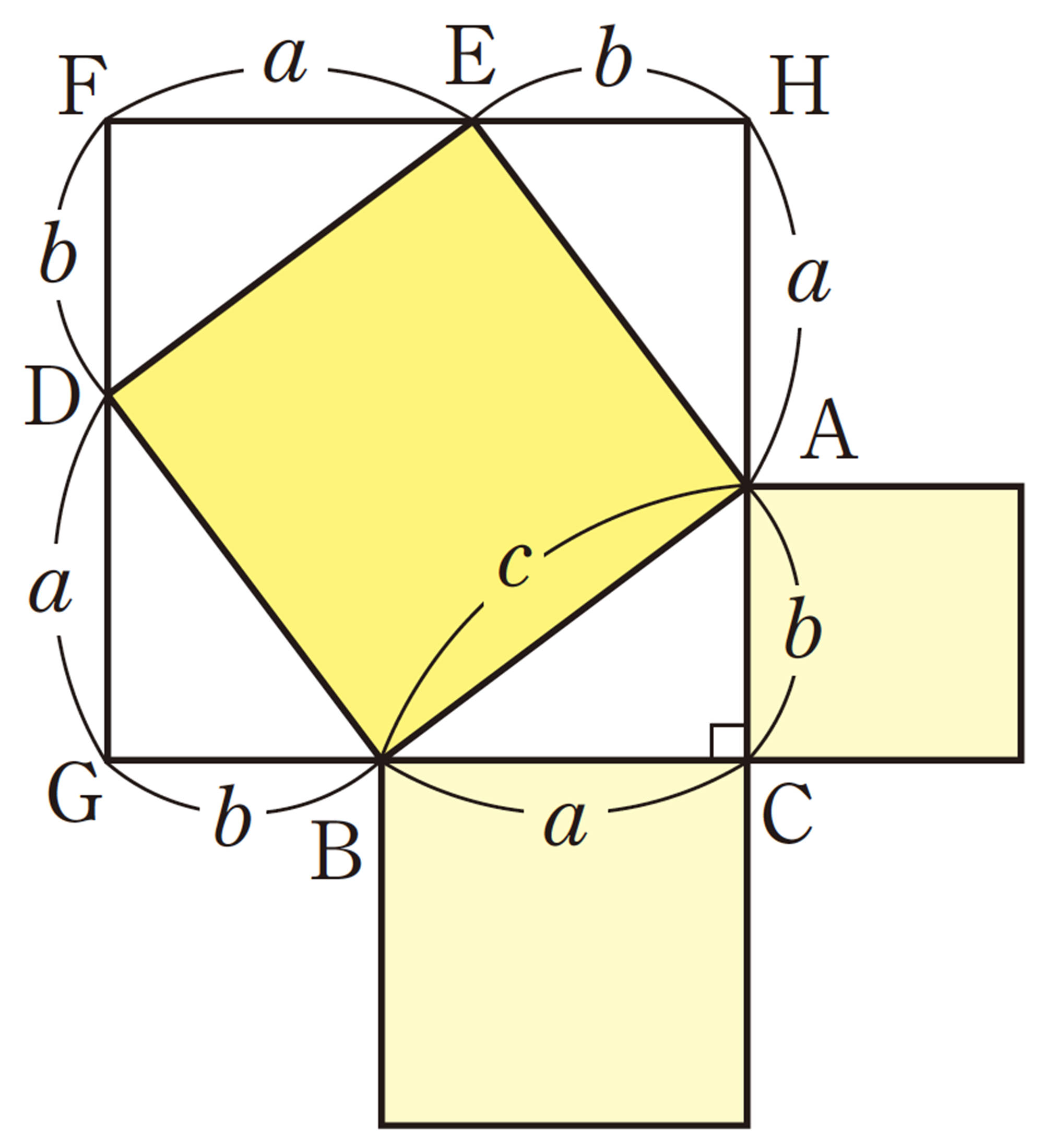
右の図のように，正方形DBAEの外側に[mathjax]\(\triangle ABC\)と合同な三角形を3つかき加えると，1辺の長さが[mathjax]\(a+b\)の正方形FGCHができる。
正方形DBAEの面積は，正方形FGCHの面積から4つの直角三角形を除いた面積と等しい。したがって，
すなわち，[mathjax]\(a²+b²=c²\)
ほかにも，いろいろな証明の方法があるよ。
関連 ▷ P.281
直角三角形の3辺の長さに関するこの関係を，三平方の定理という。この定理を最初に証明したのは，古代ギリシャのピタゴラスであるといわれている。そのため，三平方の定理は，ピタゴラスの定理とも呼ばれている。
「平方」とは，同じ数を2つかけ合わせることだったね。
定理
三平方の定理
直角三角形の直角をはさむ2辺の長さをa，b，斜辺の長さをcとすると，次の関係が成り立つ。
[mathjax]\(a²+b²=c²\)
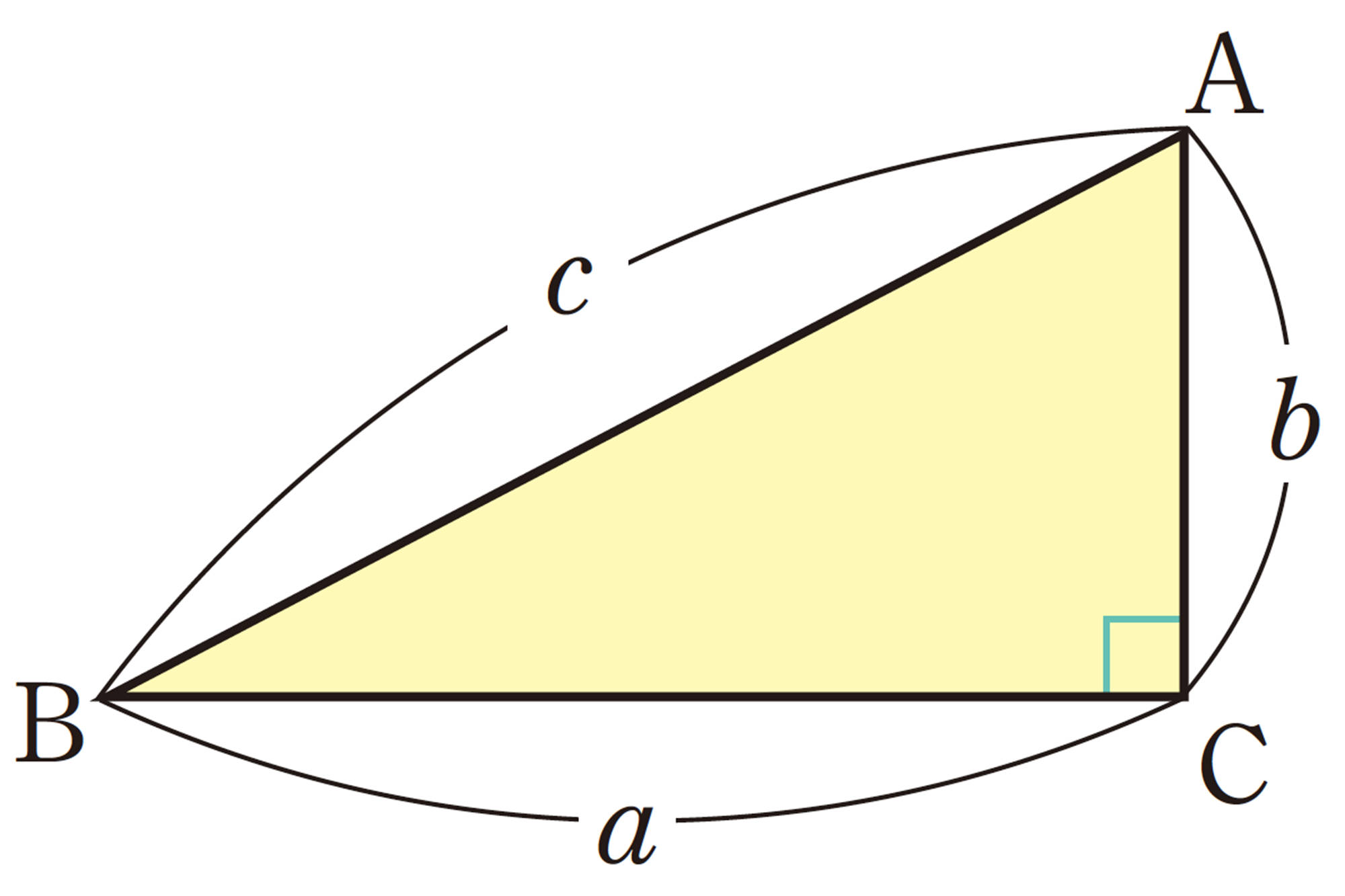
注意 上の定理で，[mathjax]\(a²+b²=c²\)を，[mathjax]\(BC²+CA²=AB²\)と書くこともある。
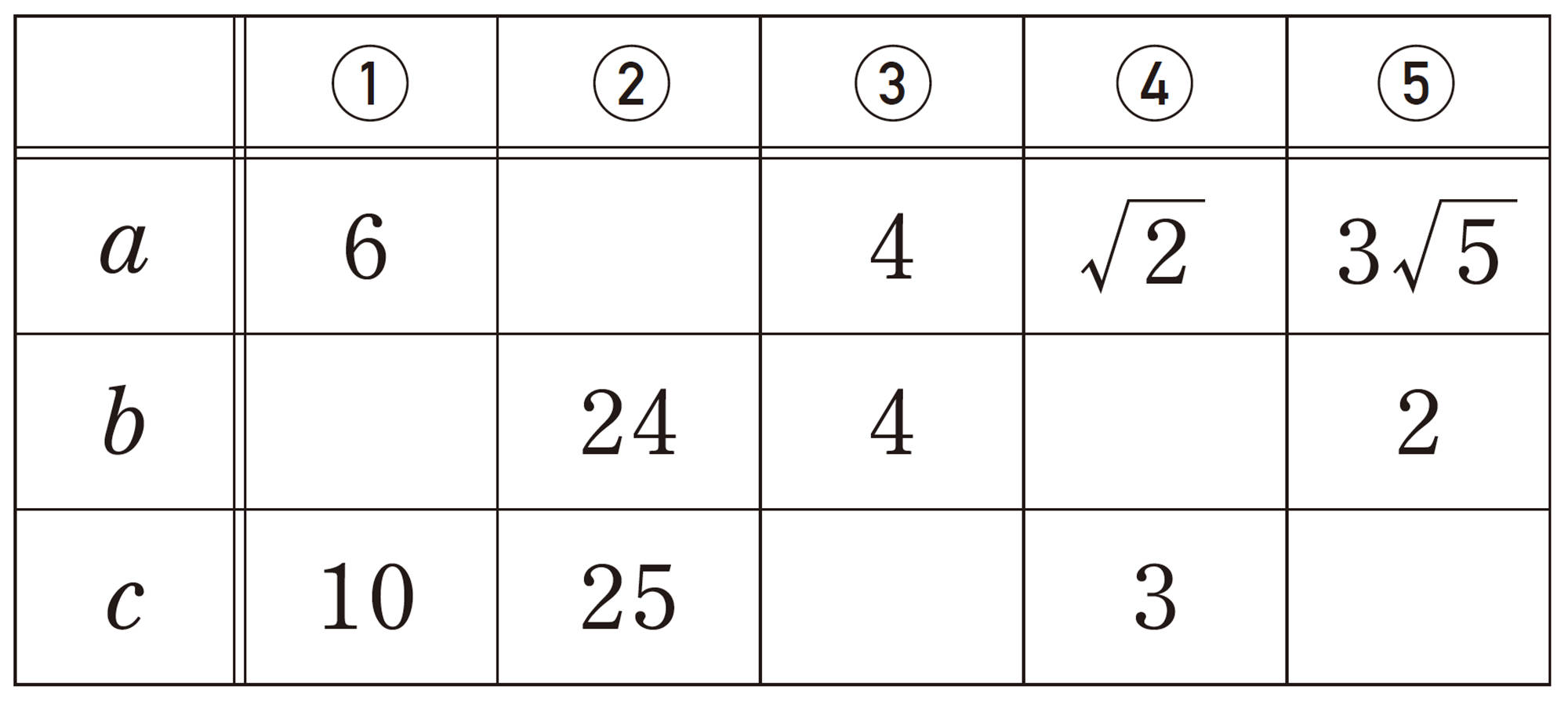
三平方の定理を使って，直角三角形の辺の長さを求めてみよう。
<3年p.218>
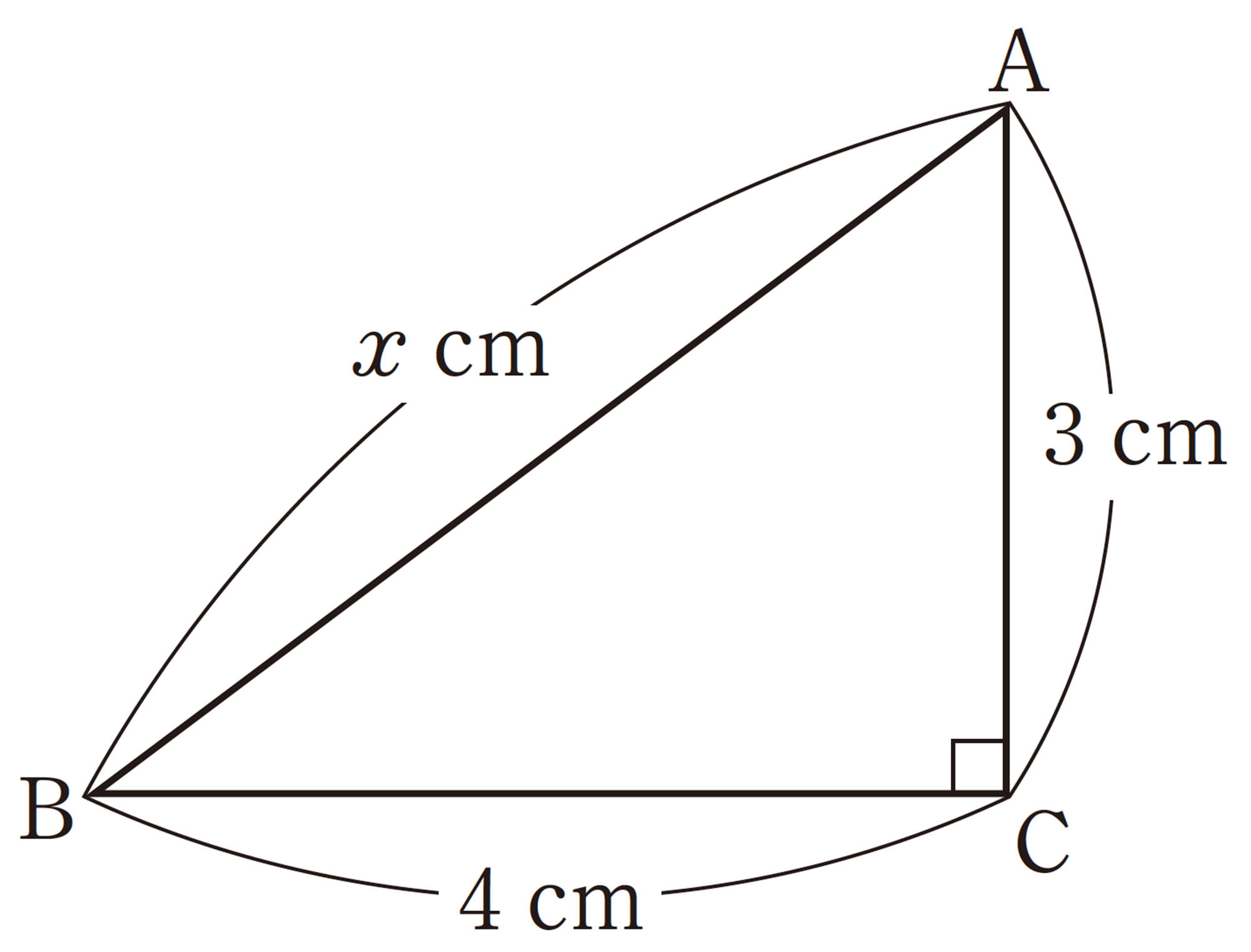
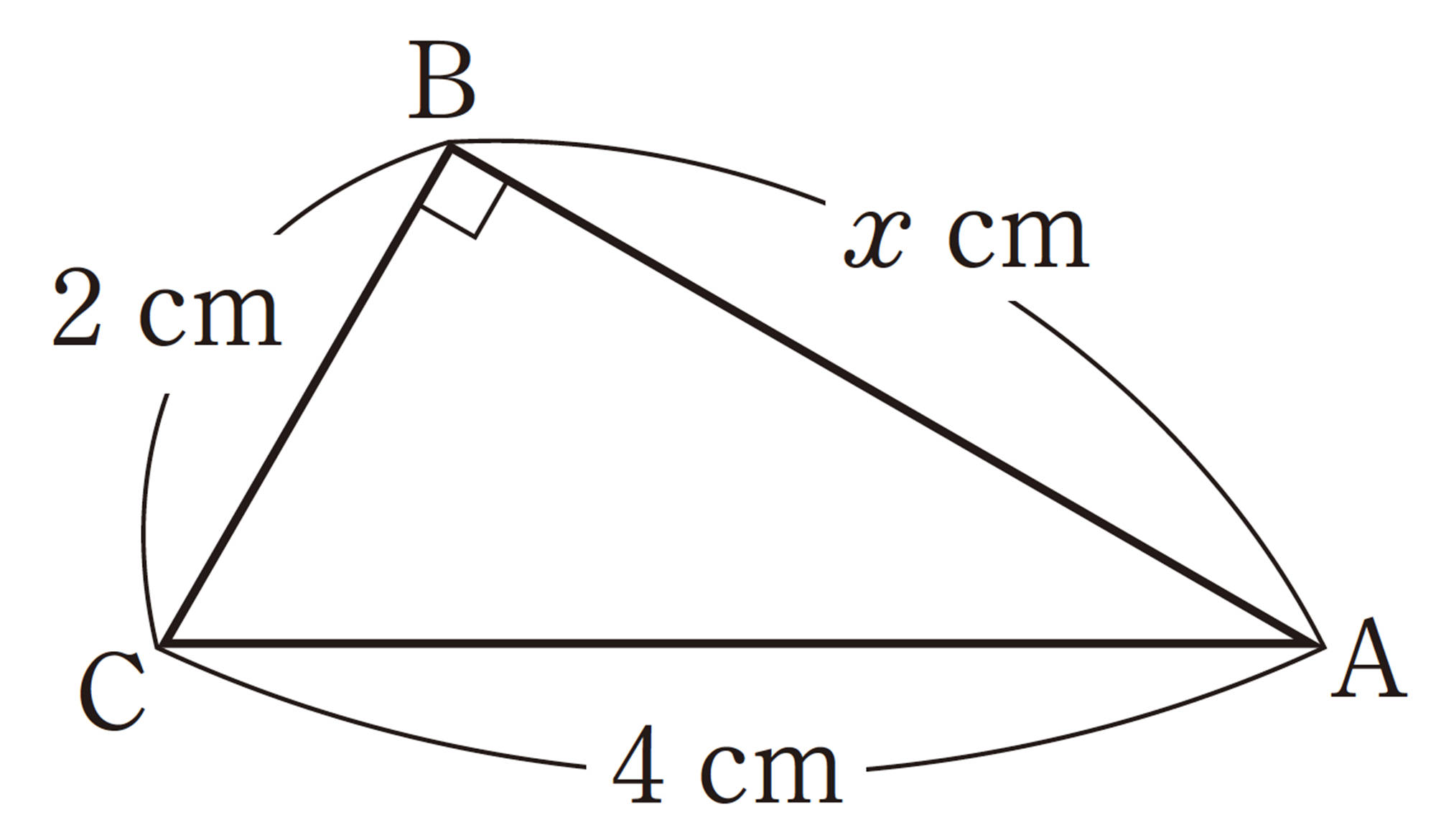
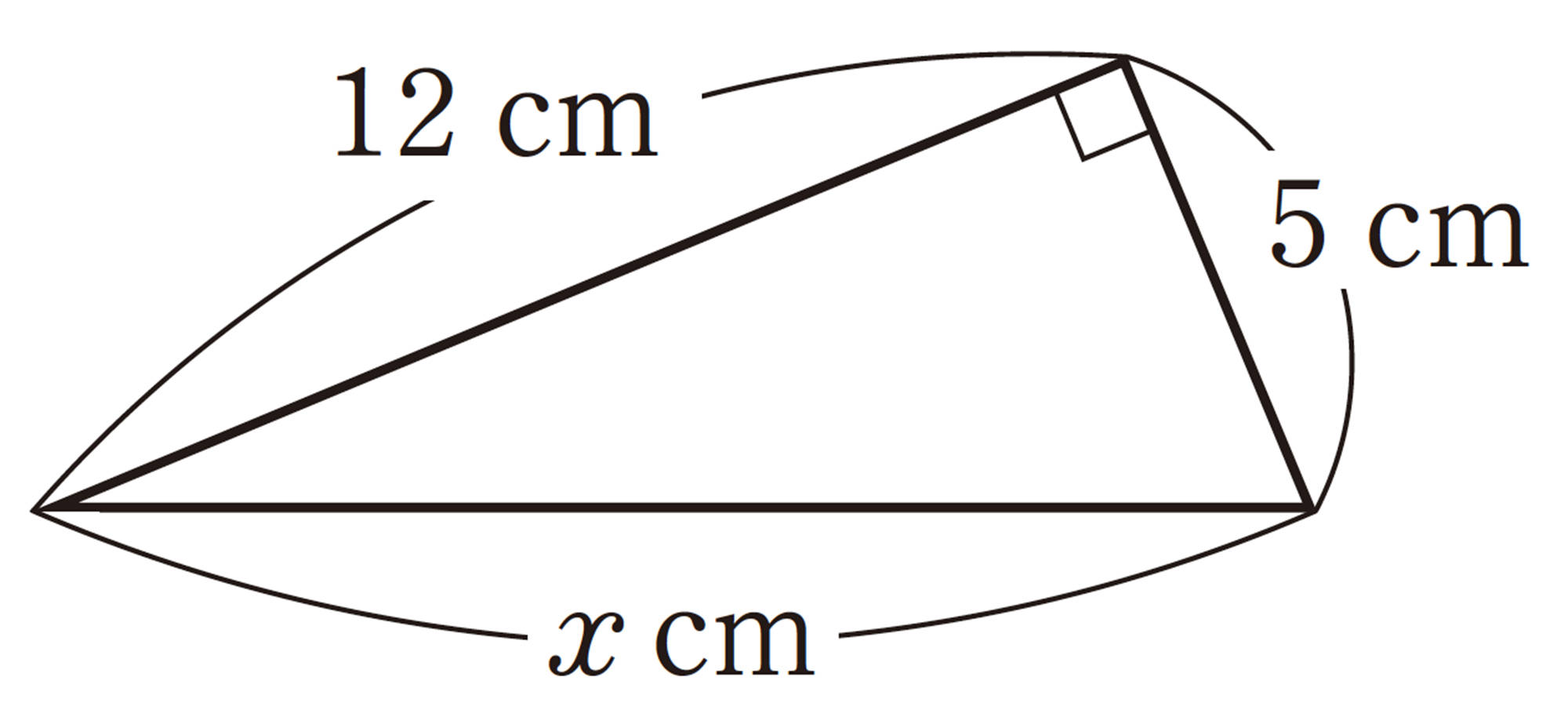
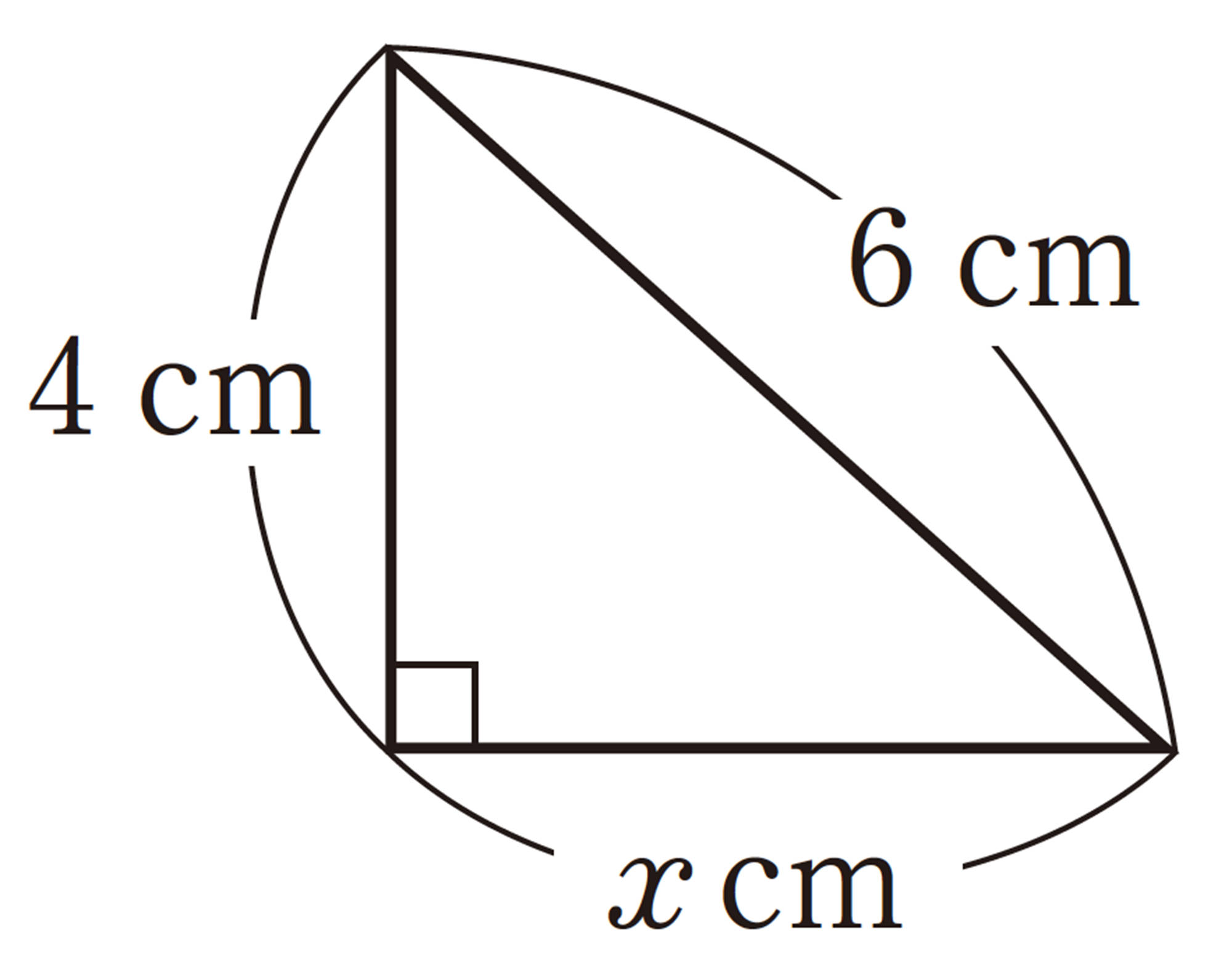
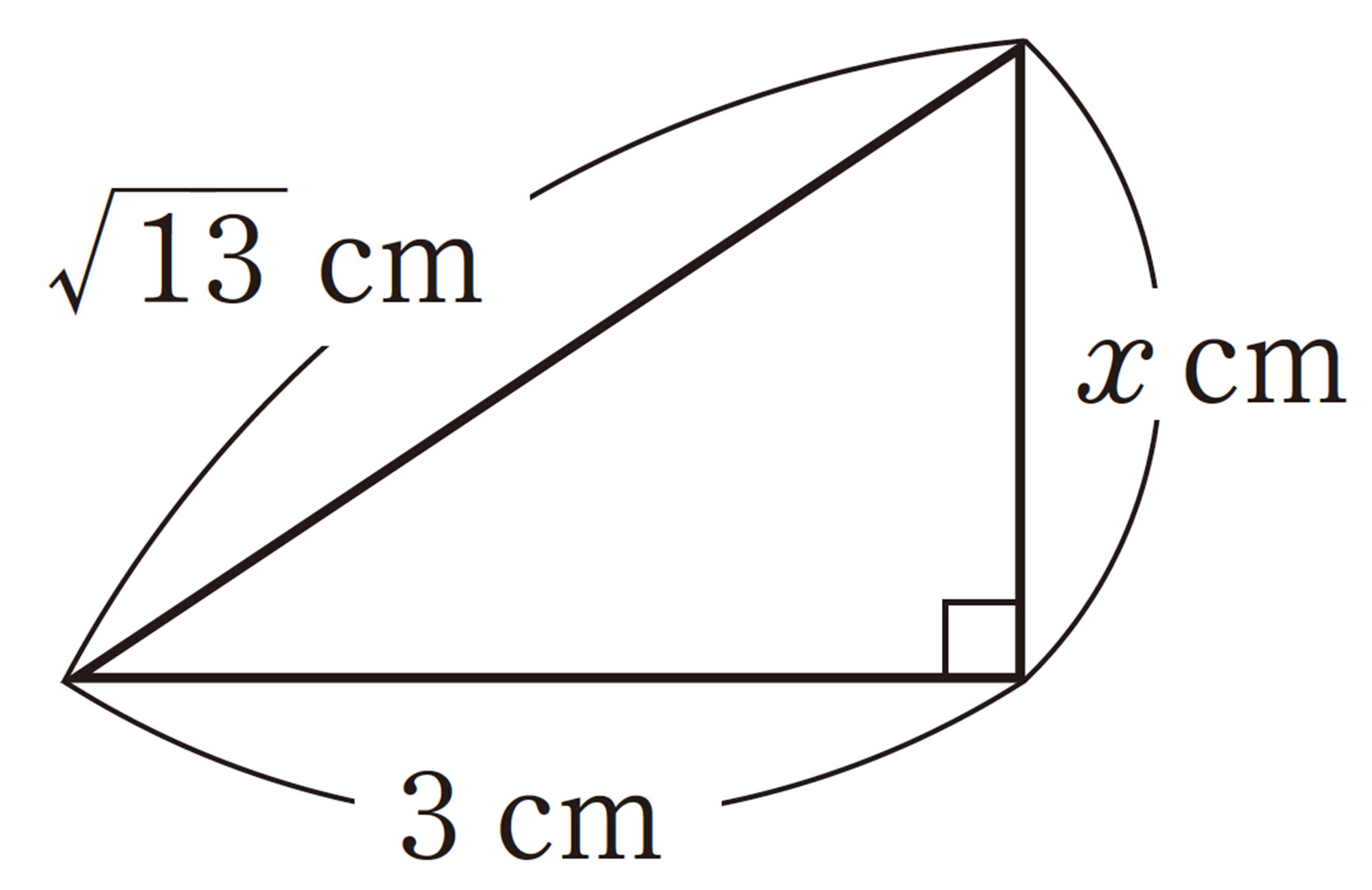
例 １ 次の直角三角形で辺ABの長さを求めなさい。
⑴
⑵
図の長さを測って，計算で求めた答えと比べてみよう。
解答
⑴ 斜辺がxcmであるから，
[mathjax]\(\hspace{18pt}x \gt 0\)であるから，
[mathjax]\(\hspace{50pt}x=5\)
したがって，[mathjax]\(AB=5\)cm
答 5cm
⑵ 斜辺が4cmであるから，
[mathjax]\(\hspace{18pt}x \gt 0\)であるから，
[mathjax]\(\hspace{50pt}x=2 \sqrt{3}\)
したがって，[mathjax]\(AB=2 \sqrt{3}\)cm
答 [mathjax]\(2 \sqrt{3}\)cm
問 １ 次の直角三角形で，xの値を求めなさい。
⑴
⑵
⑶
問 ２ 直角三角形の斜辺の長さをc，他の2辺の長さをa，bとして，次の表を完成させなさい。
どんなことがわかったかな
どんな直角三角形でも三平方の定理が成り立つので，直角三角形の 2つの辺の長さがわかっているとき，もう1つの辺の長さを求めることができます。
