gkt-horizontal-line
<3年p.209>
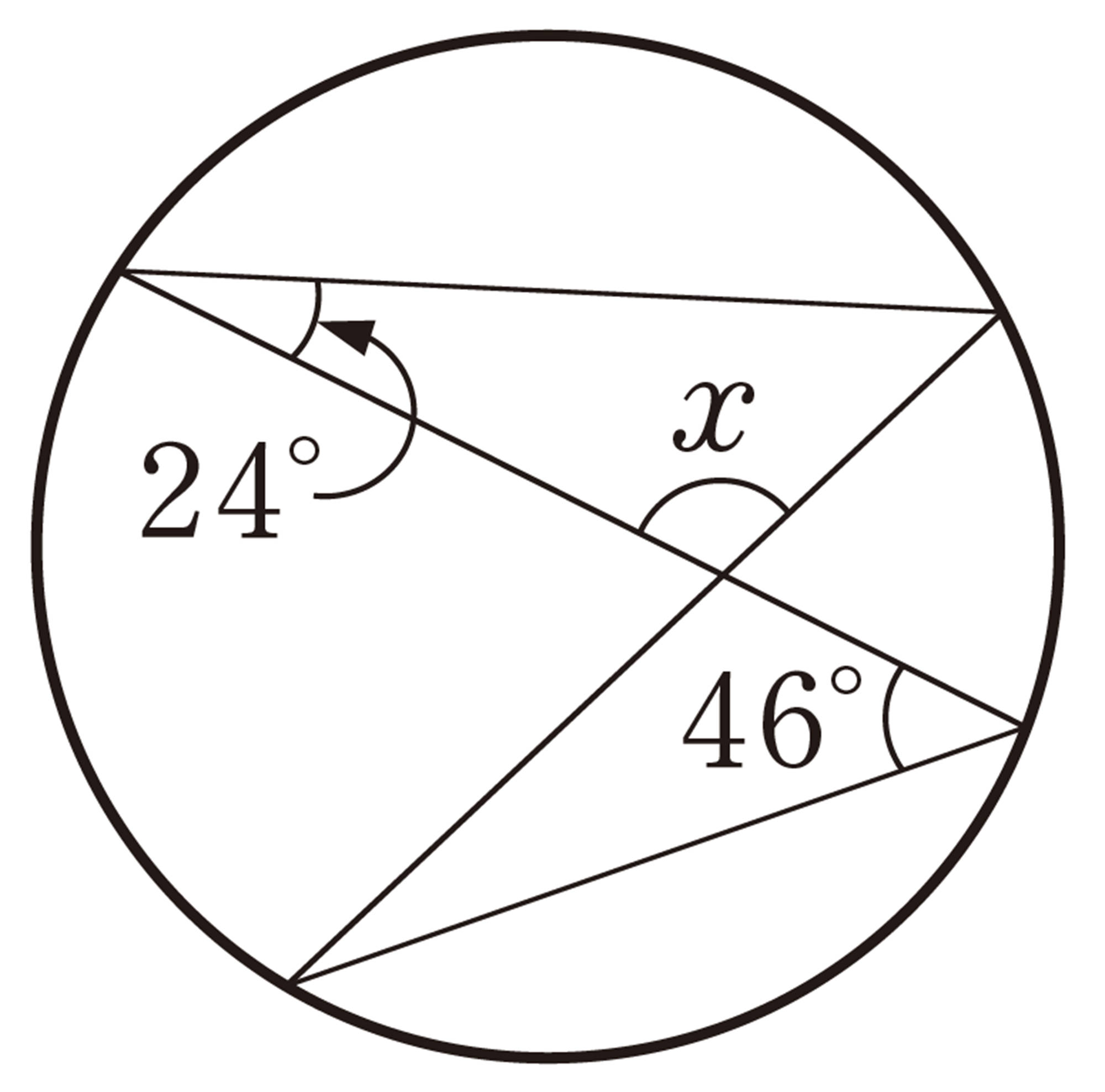
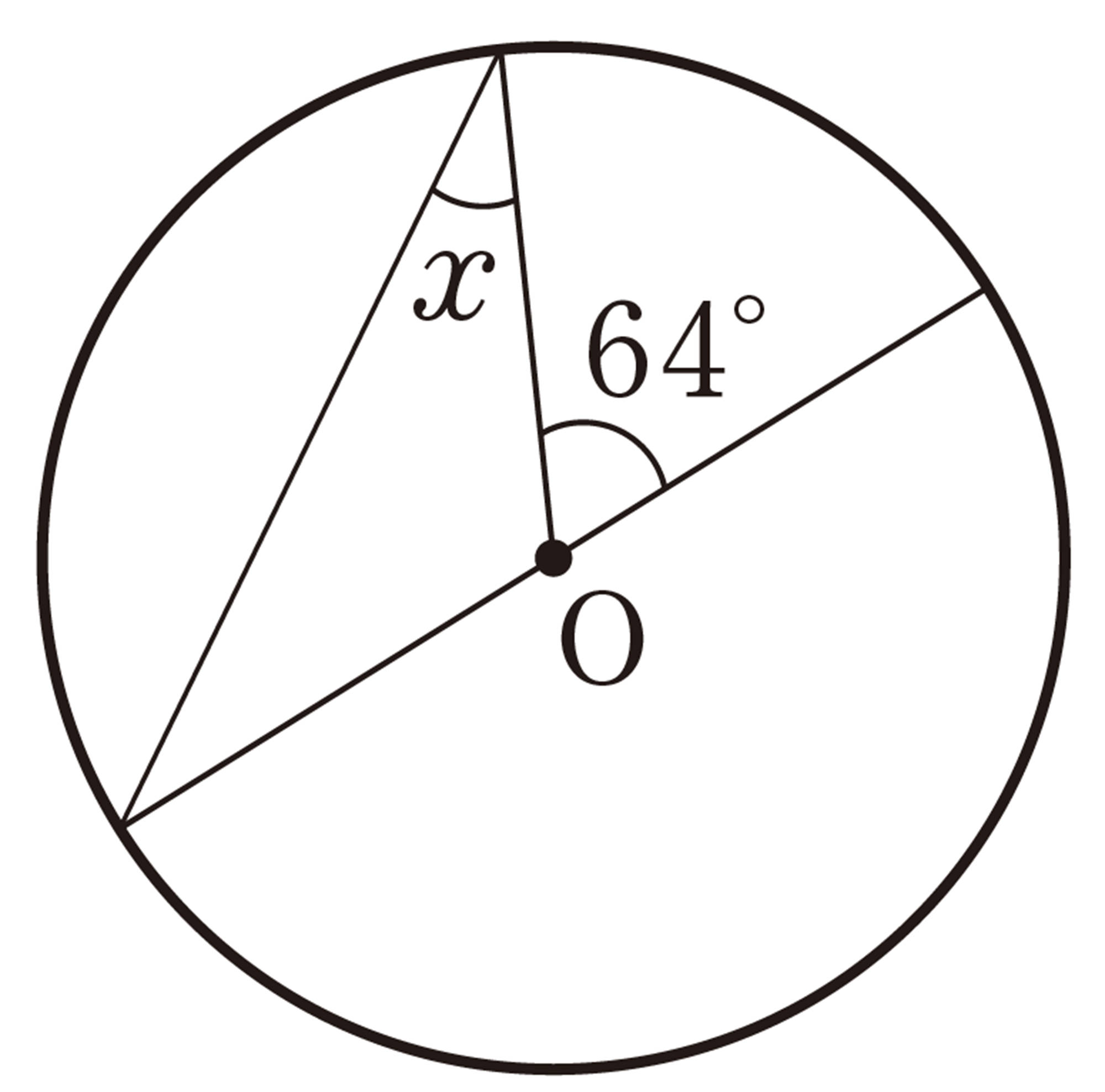
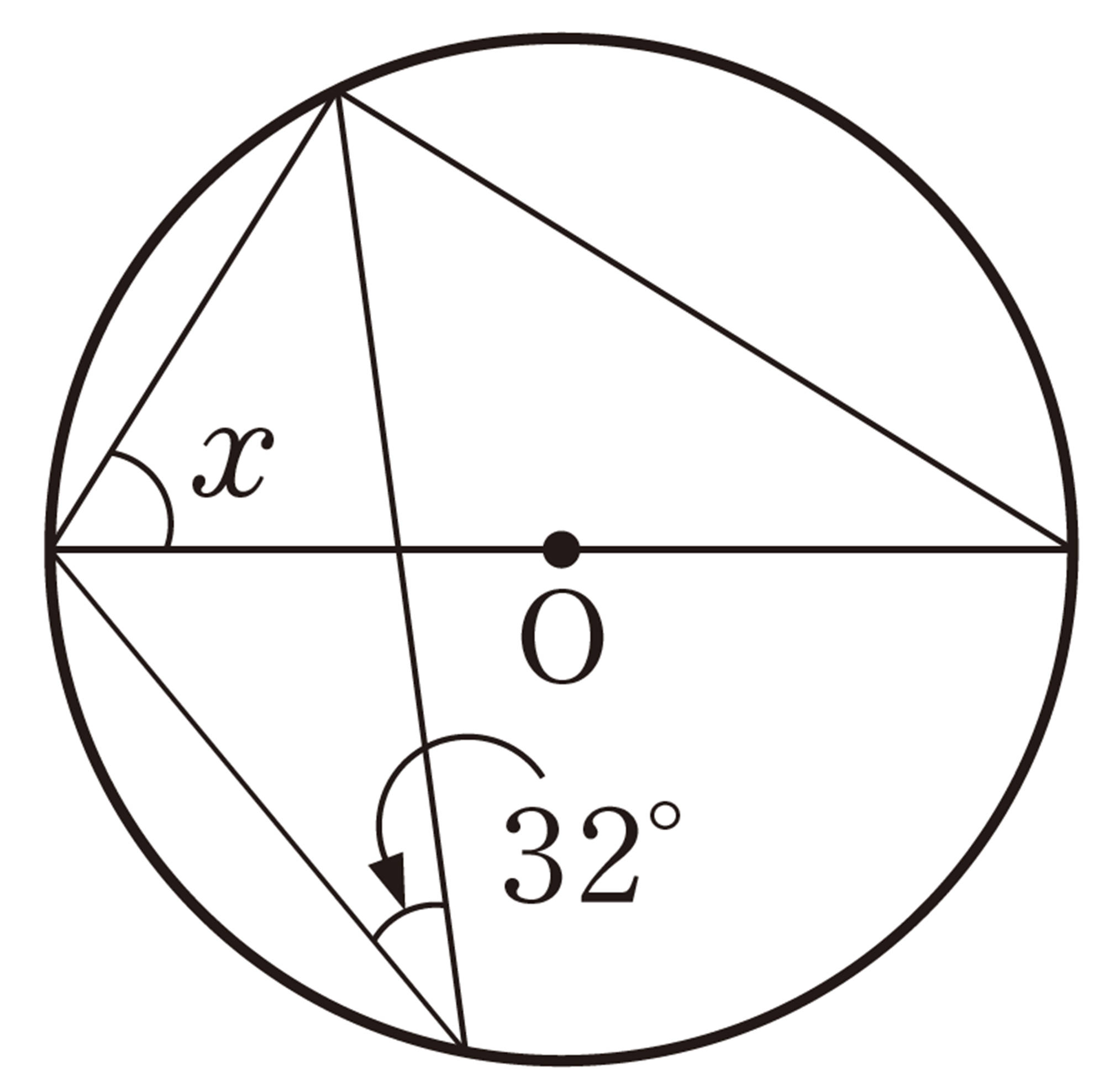
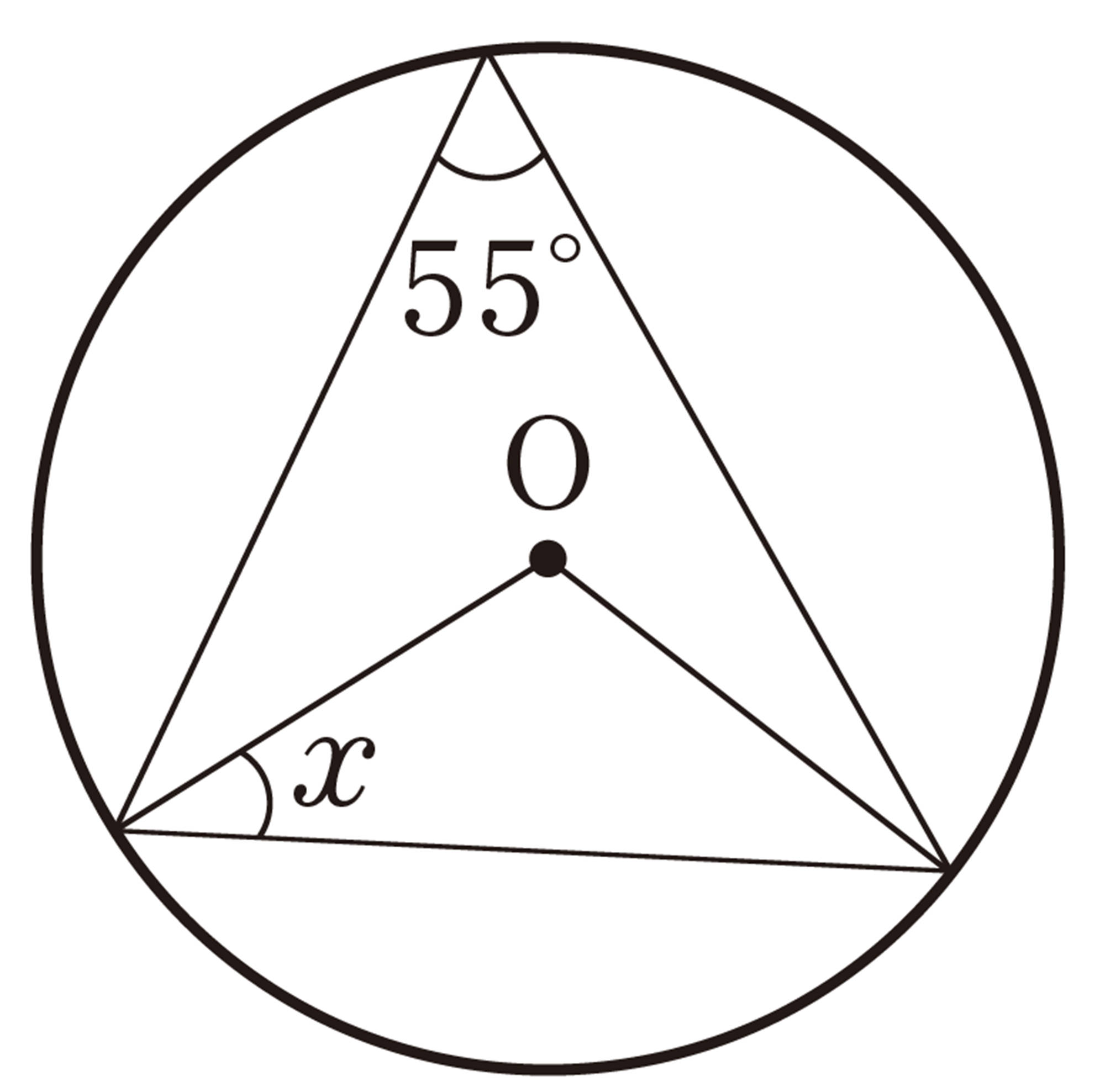
6章のまとめの問題 解答 P.305 基本
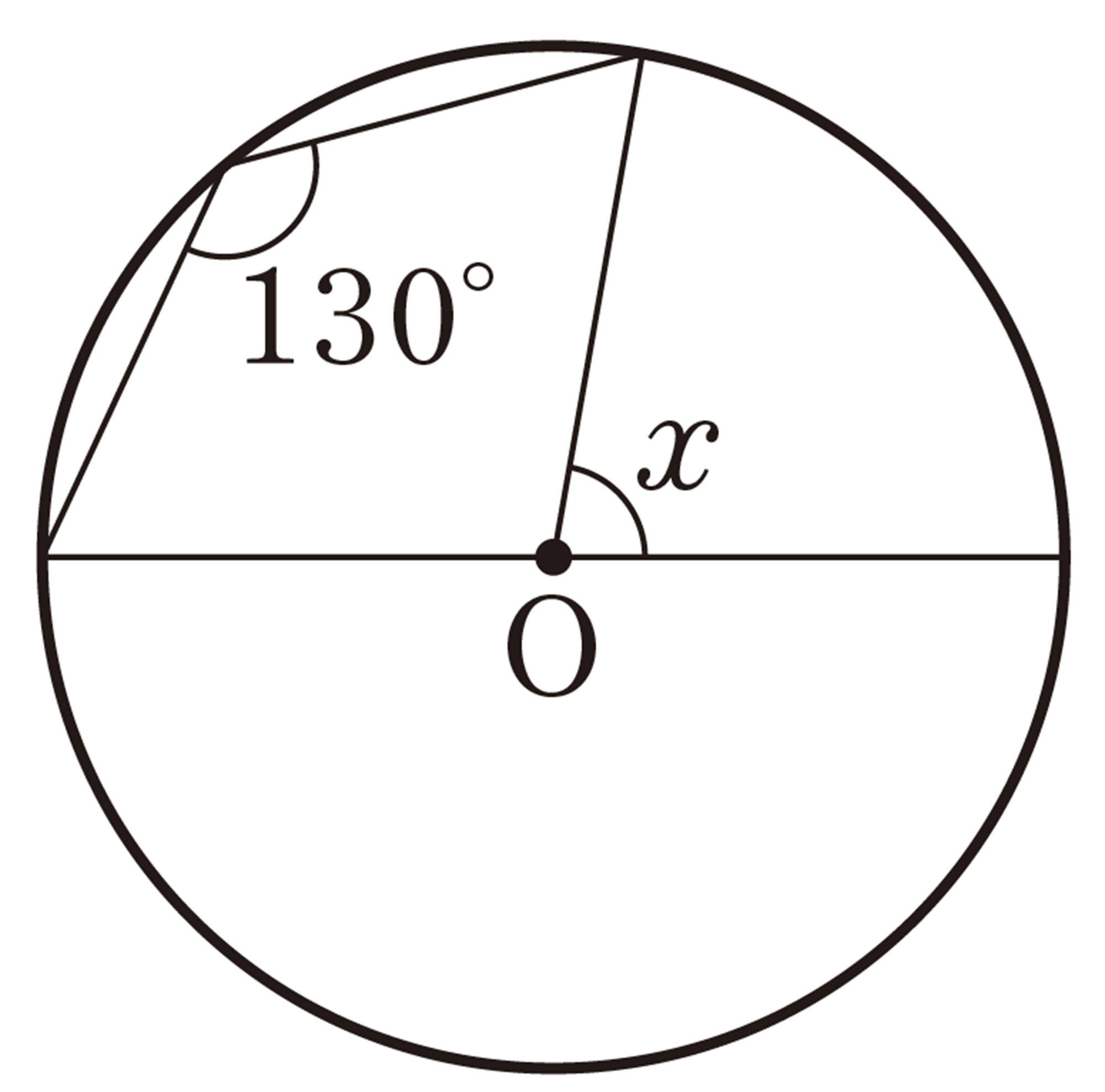
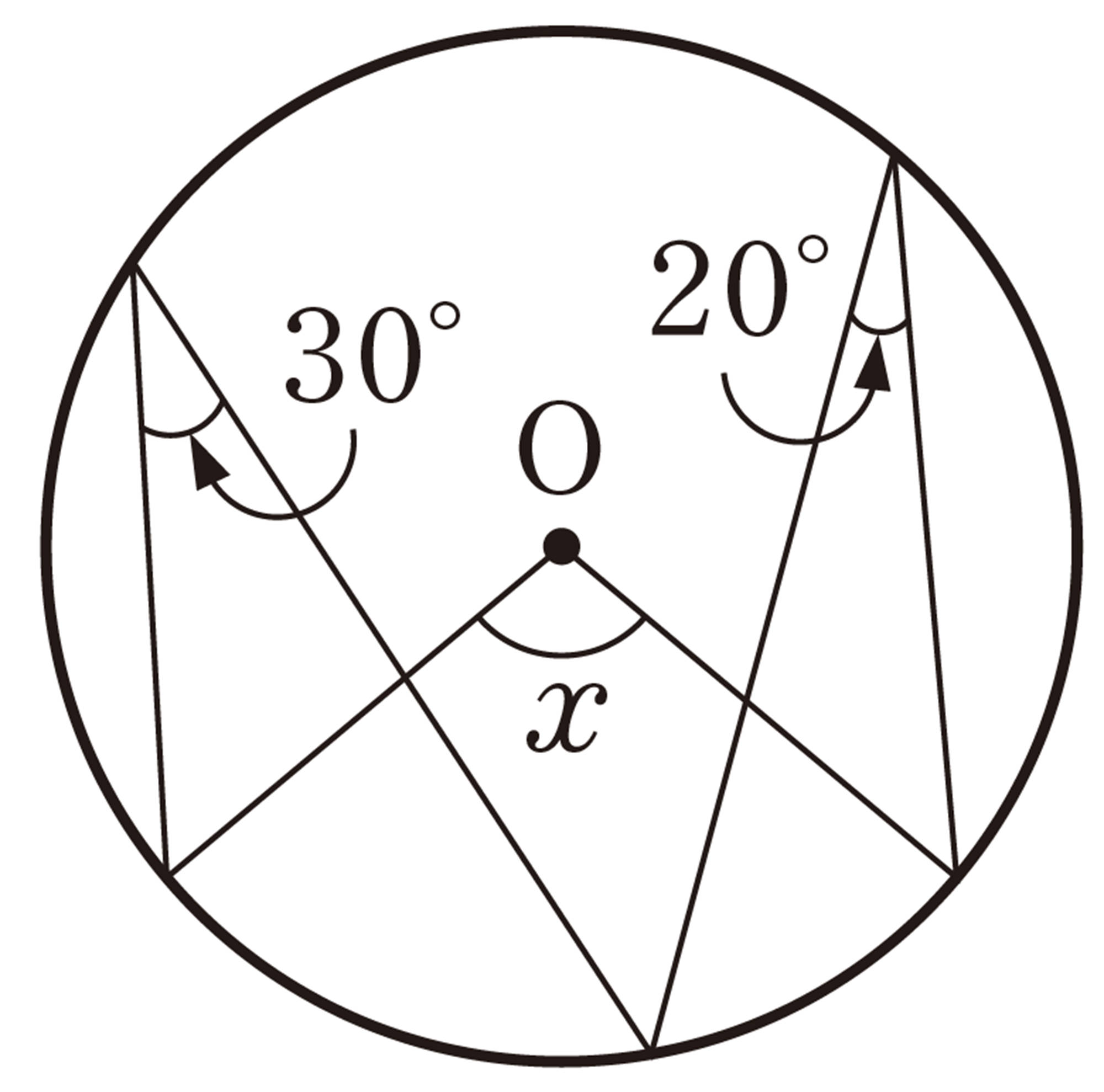
1 次の図で,[mathjax]\(\angle x\)の大きさを求めなさい。
gkt-horizontal-line
<3年p.210>
6章のまとめの問題 応用
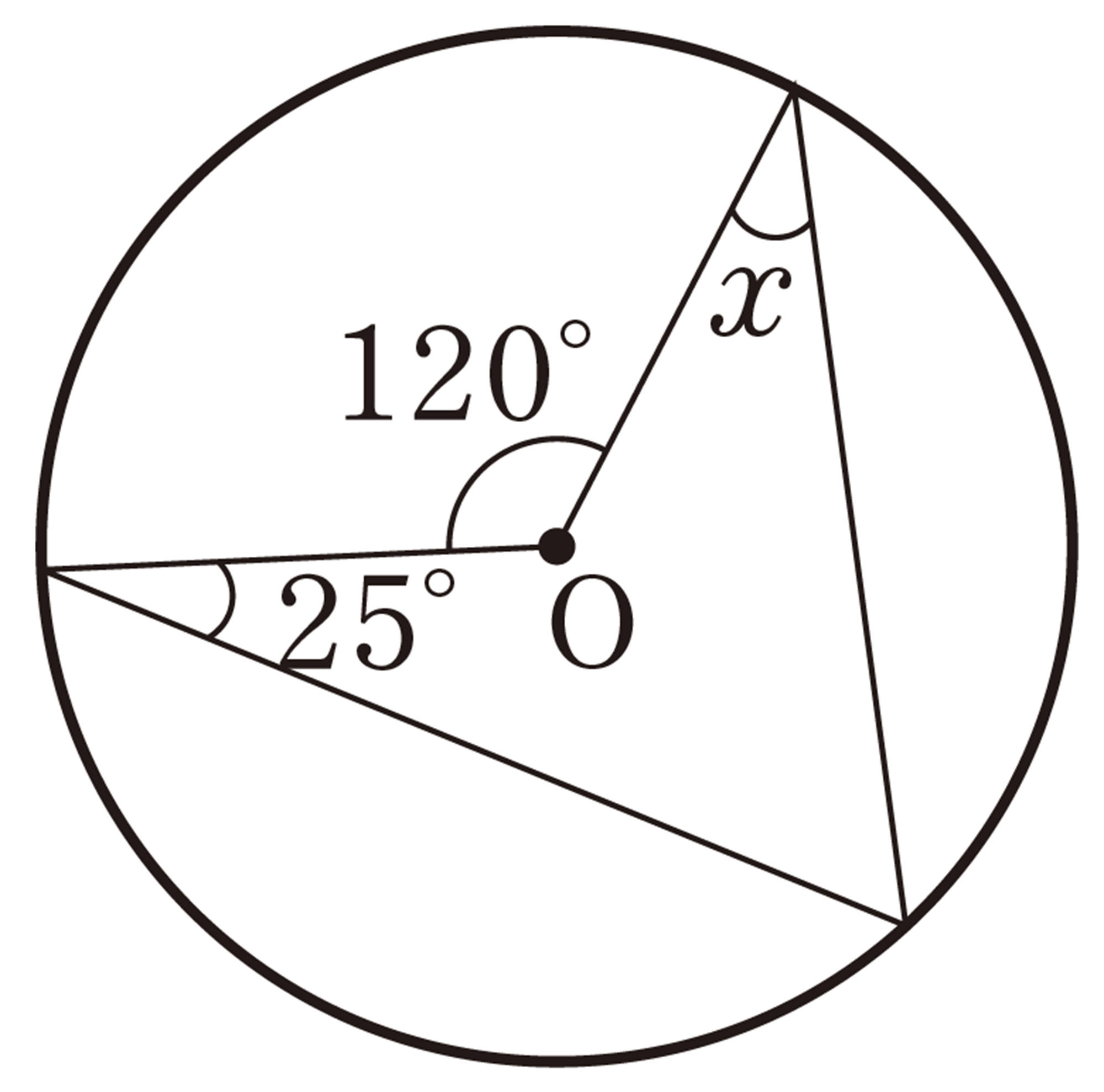
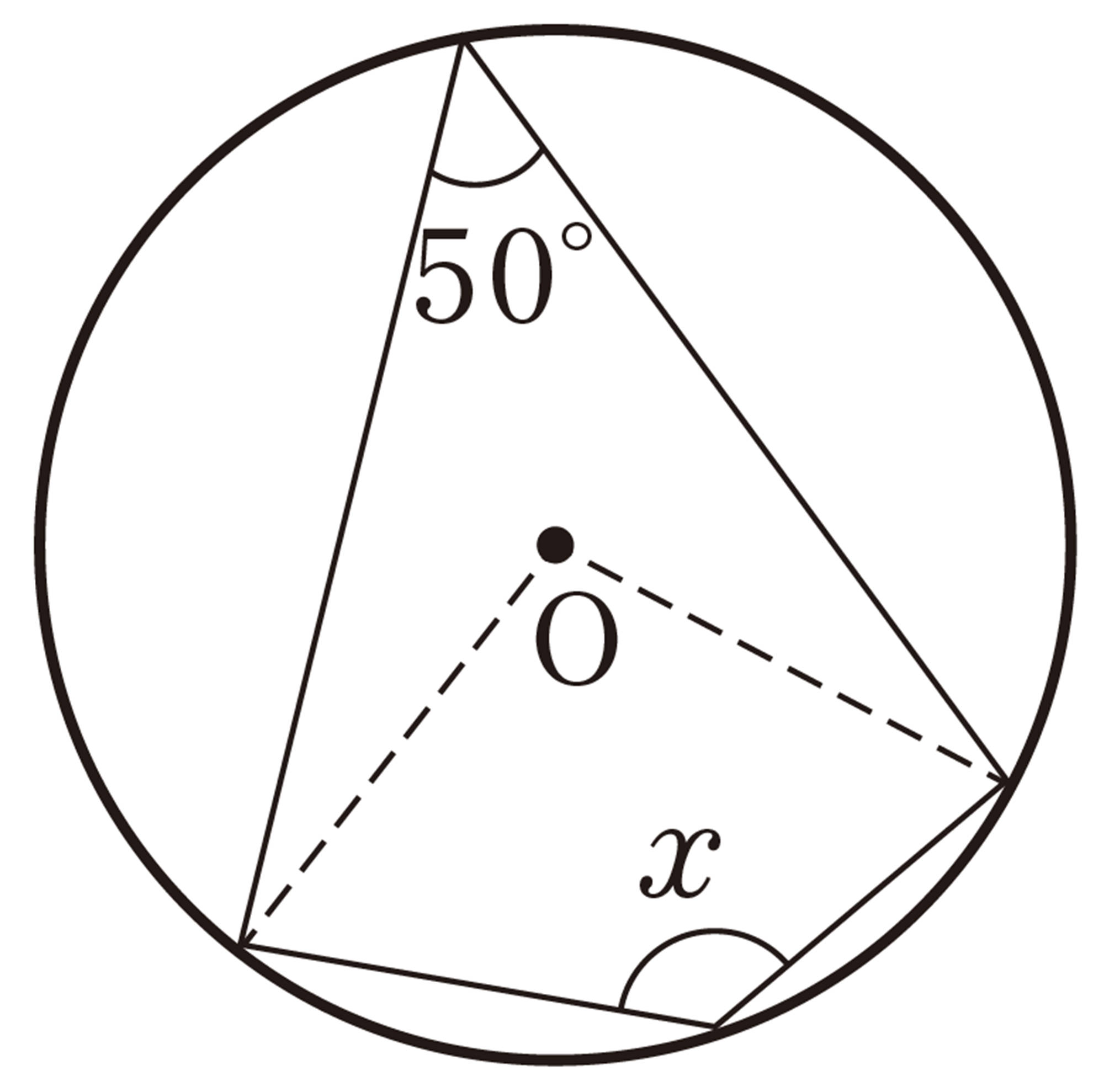
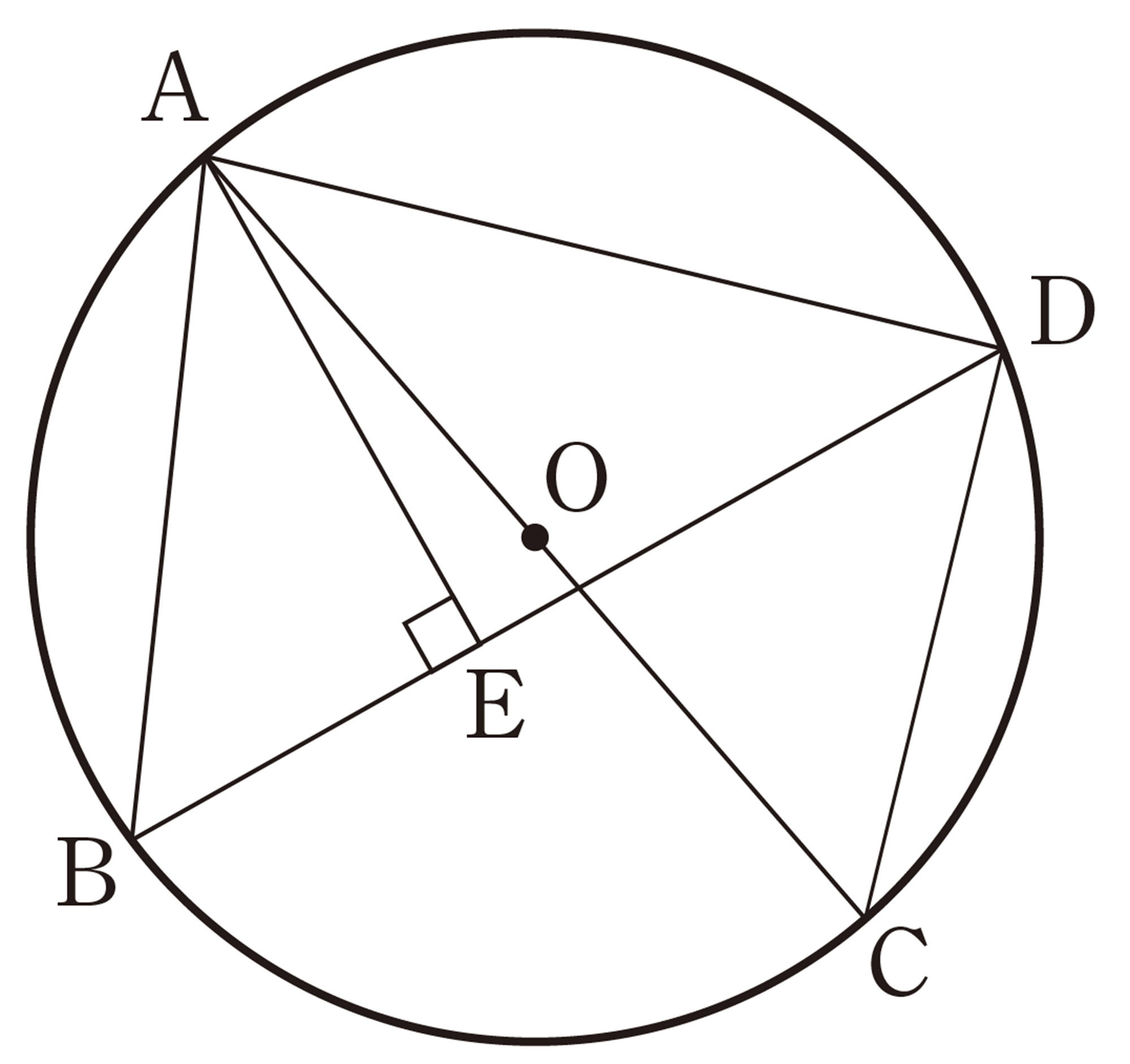
1 次の図で,[mathjax]\(\angle x\)の大きさを求めなさい。
gkt-horizontal-line
<3年p.211>
活用
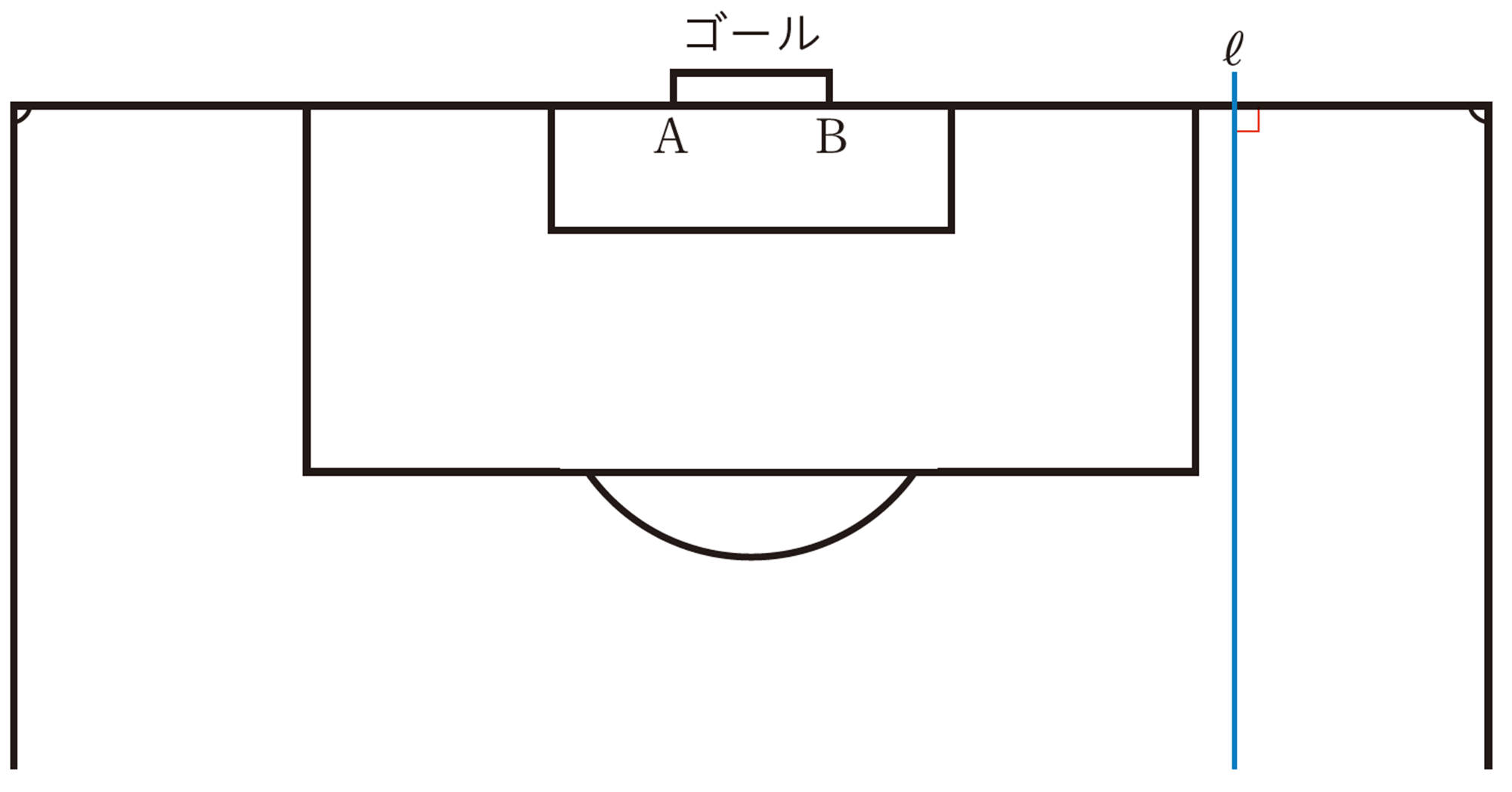
1 拓真さんは,友だちとサッカーゲームをしています。ボールを10回けって,たくさんゴールに入れた人が勝ちです。
下の図のようなサッカー場で,直線ℓ上にボールを置いてけります。直線ℓ上なら,どこからでもボールをけることができるとするとき,どこからボールをければ,ゴールに入れやすいですか。下の⑴,⑵に答えなさい。
⑴ 拓真さんは,
「ボールをけって,ゴールに入る確率が高い場所は,ゴールの両端A,Bを通る円のうち,直線ℓと接する円との接点Pになる。」
と予想しました。点Pを,次の図に作図しなさい。
⑵ ⑴でかいた場所が,ゴールに入る確率がもっとも高くなる理由を説明しなさい。
gkt-horizontal-line
<3年p.212>
深めよう 発展 高等学校
動かして考えよう
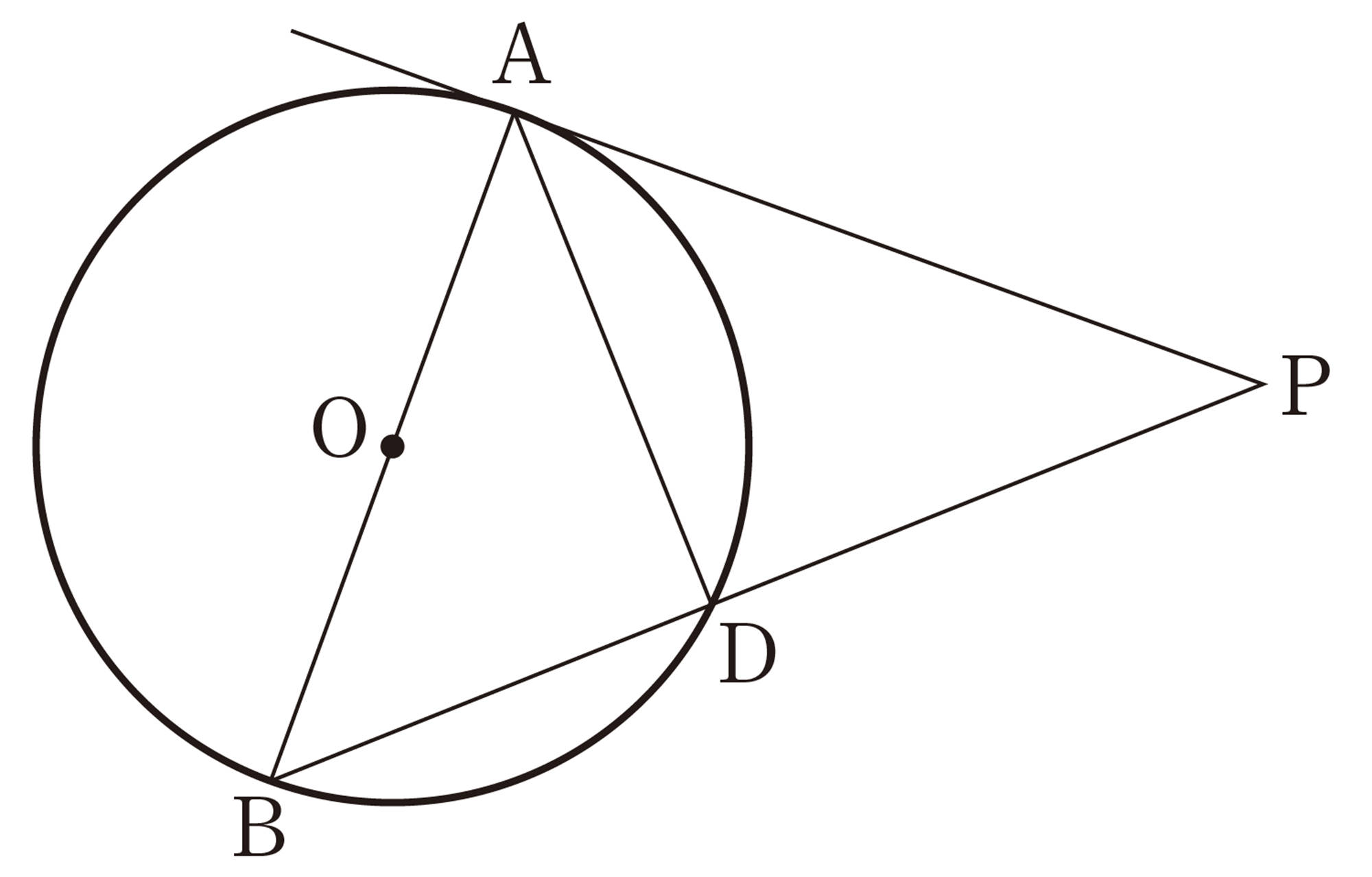
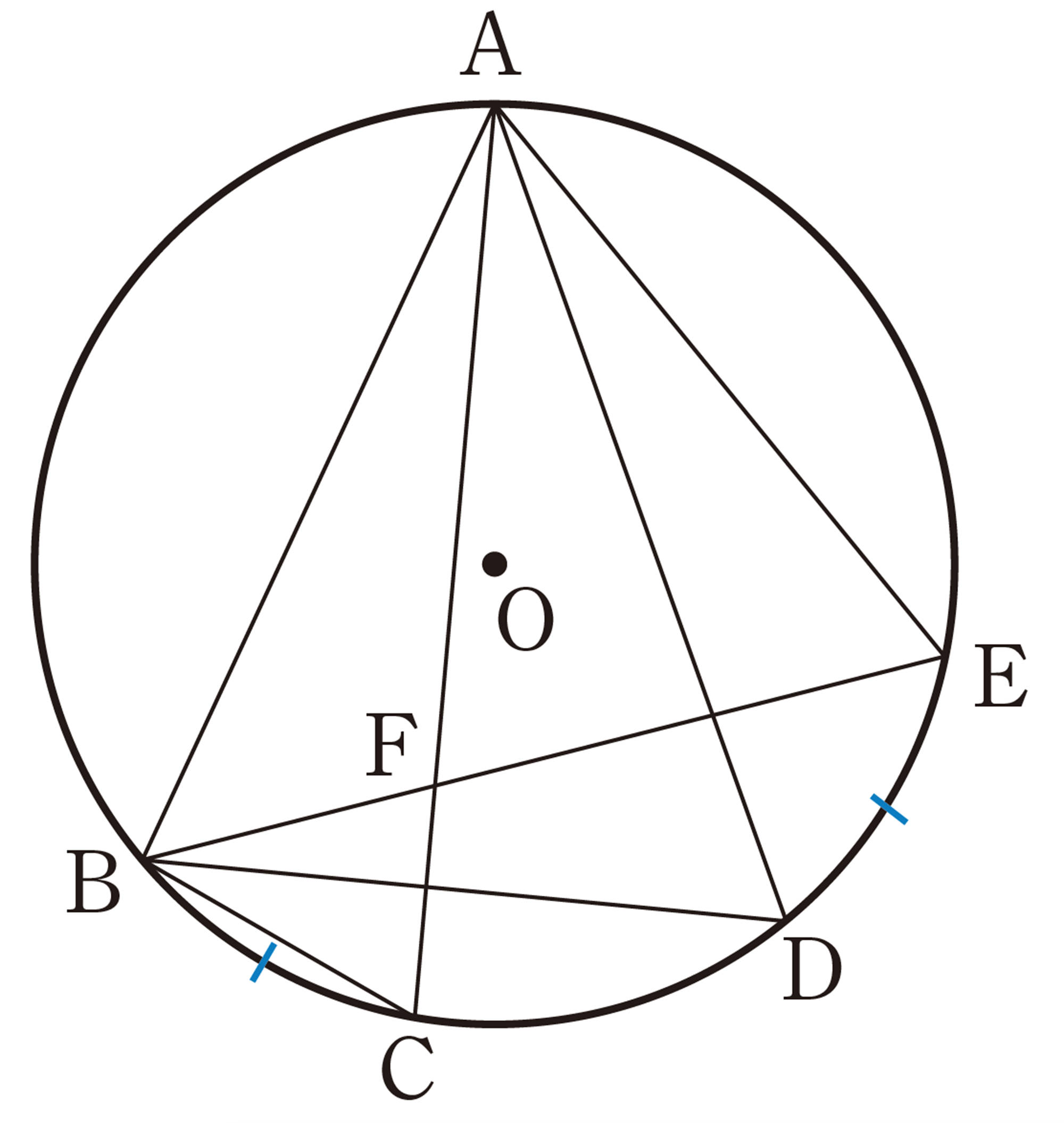
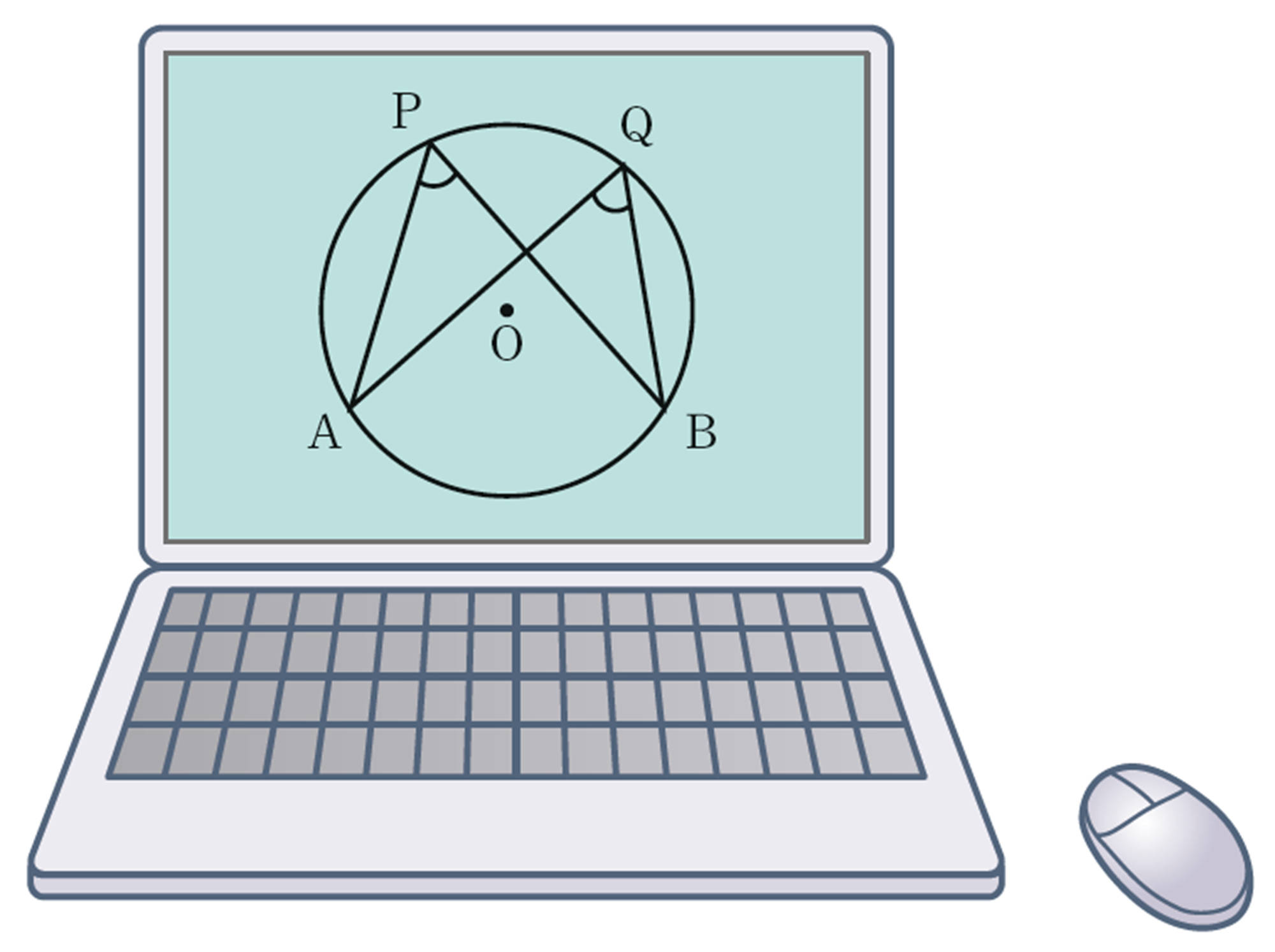
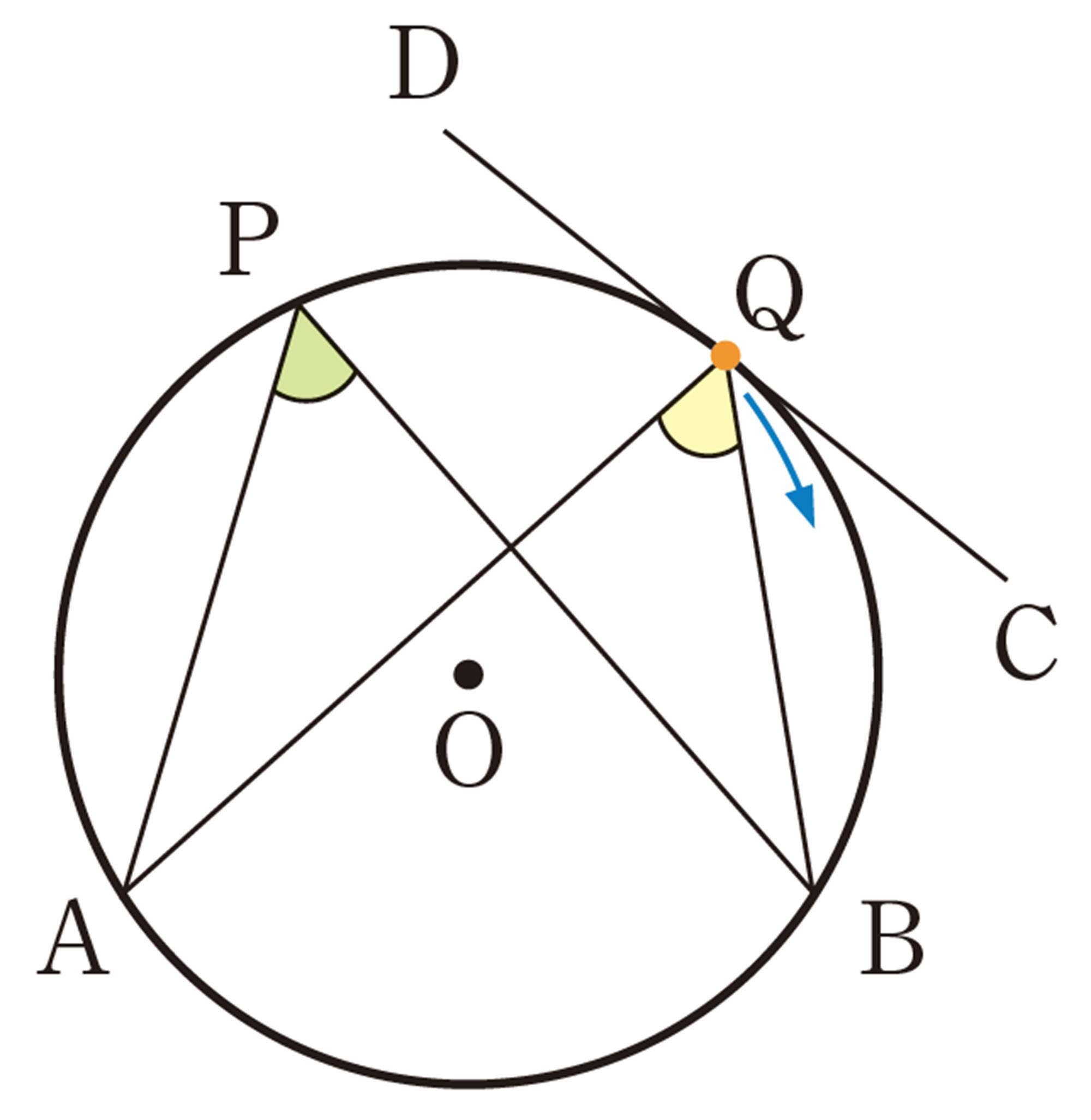
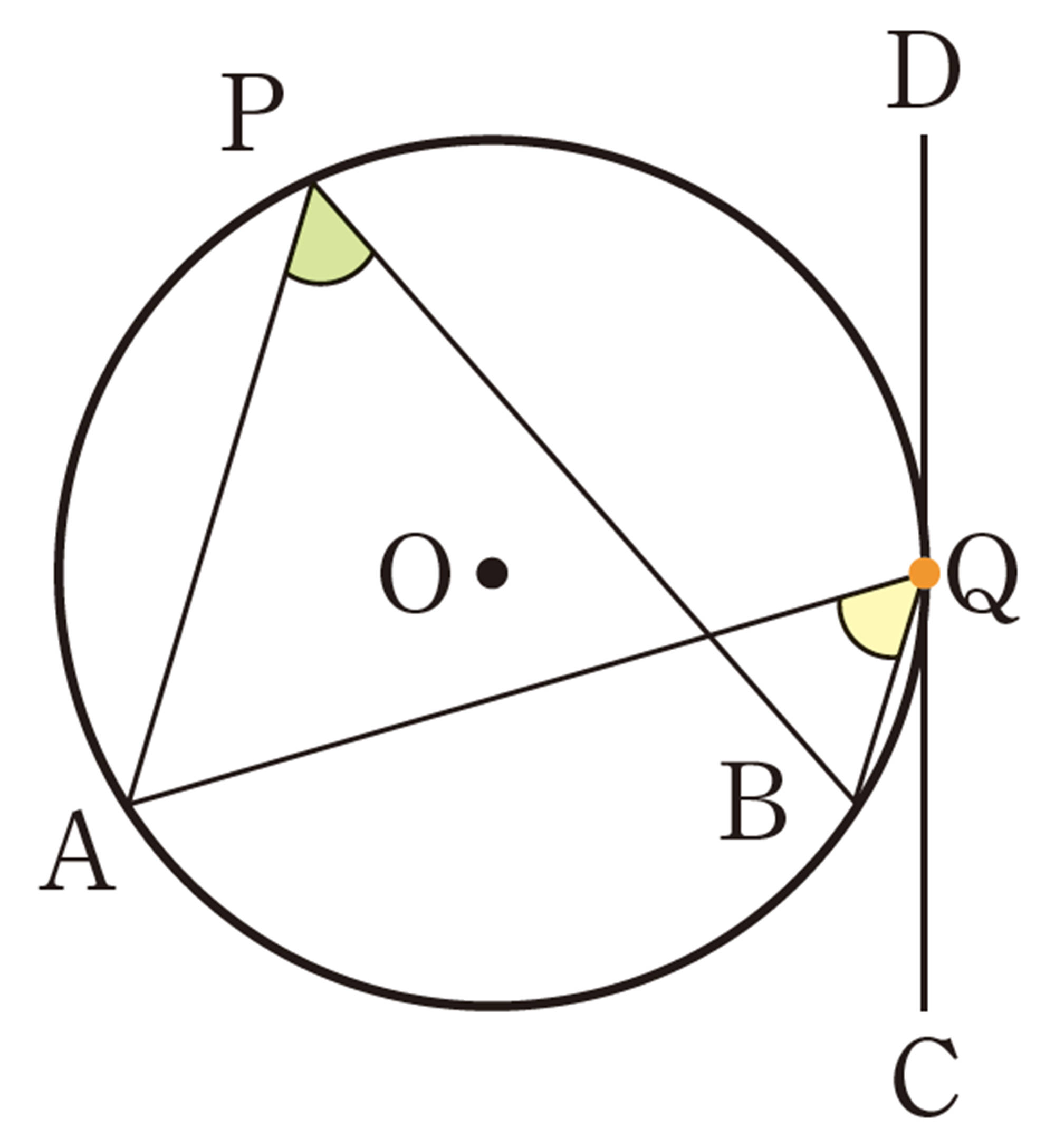
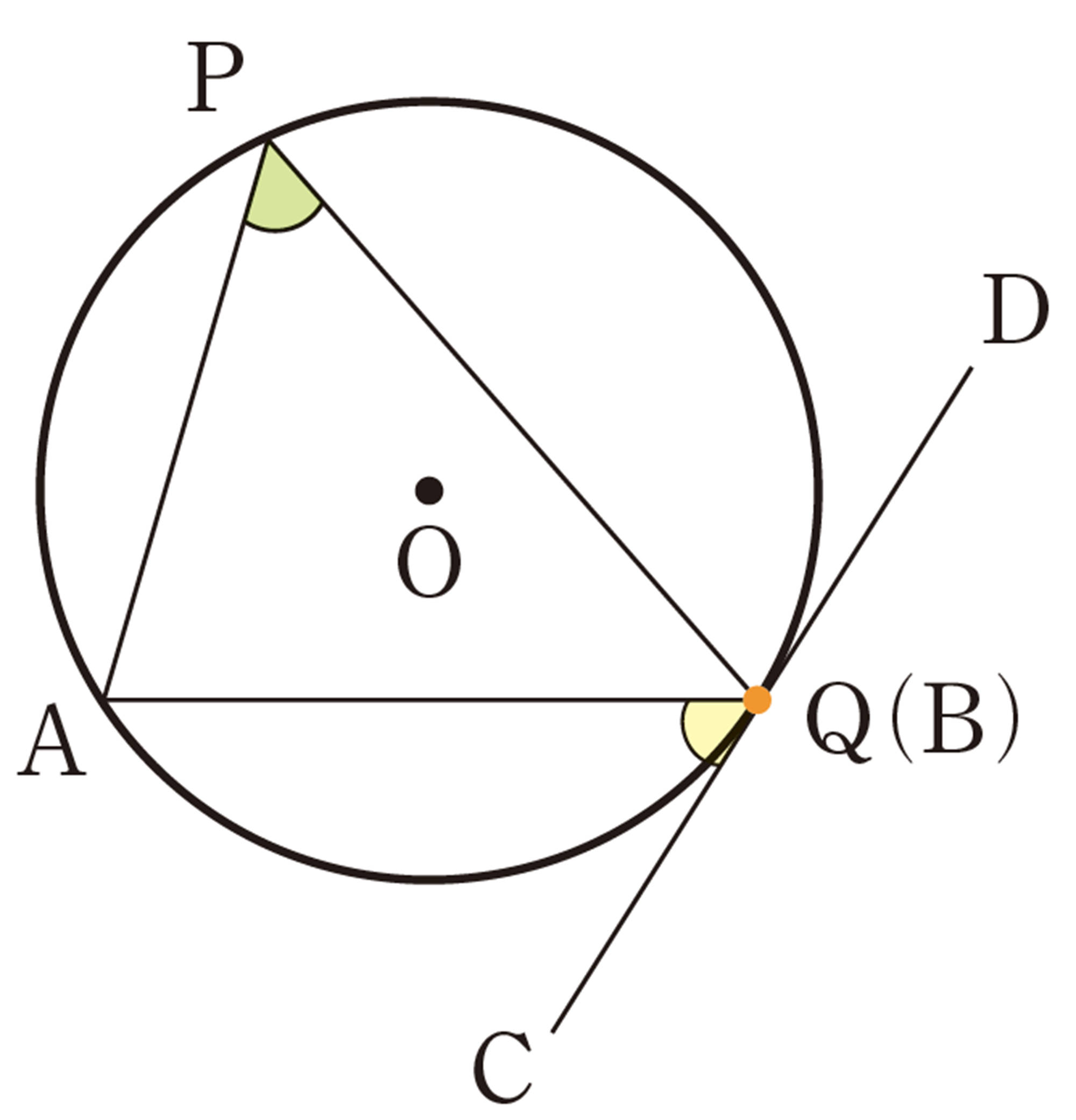
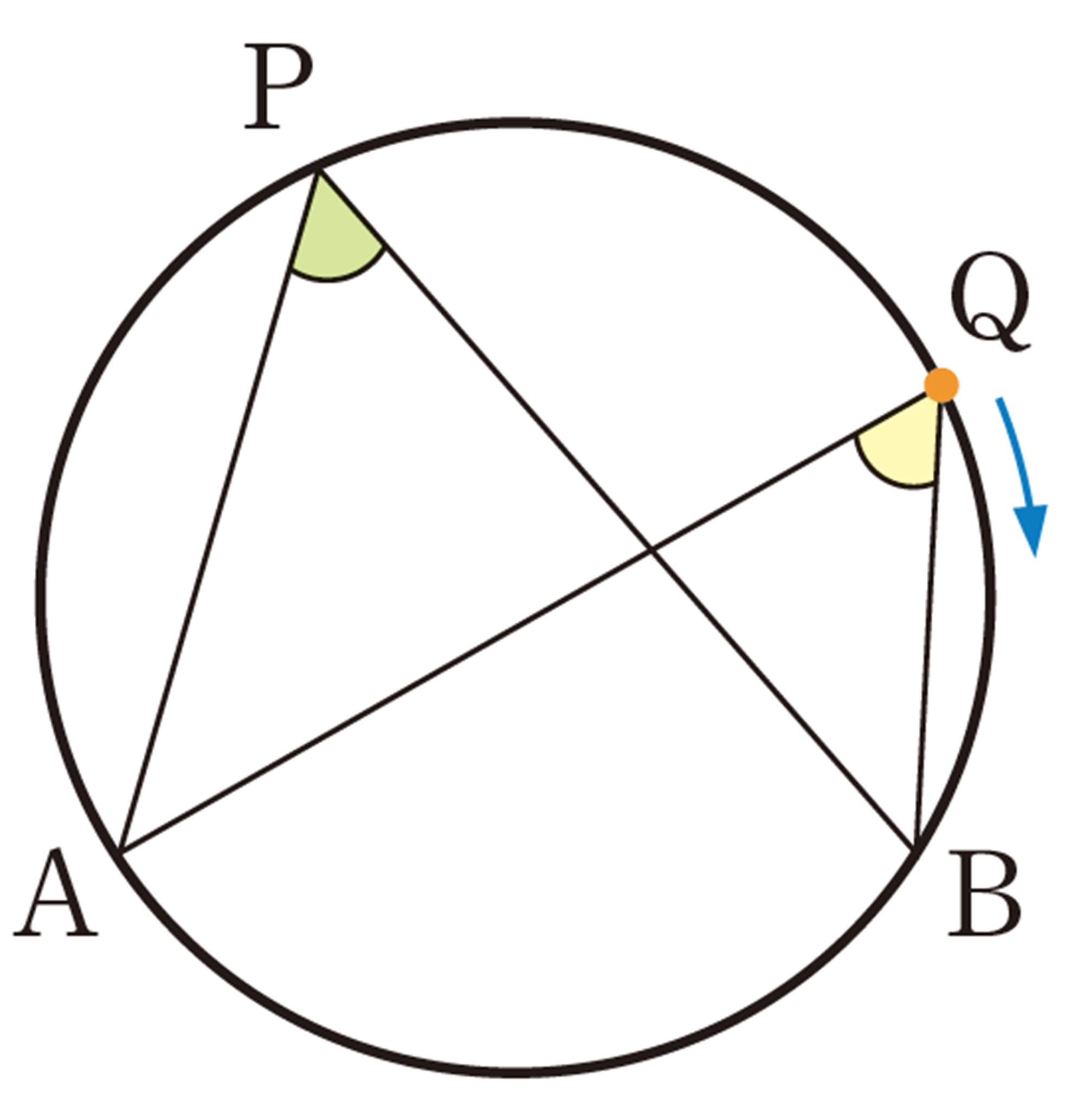
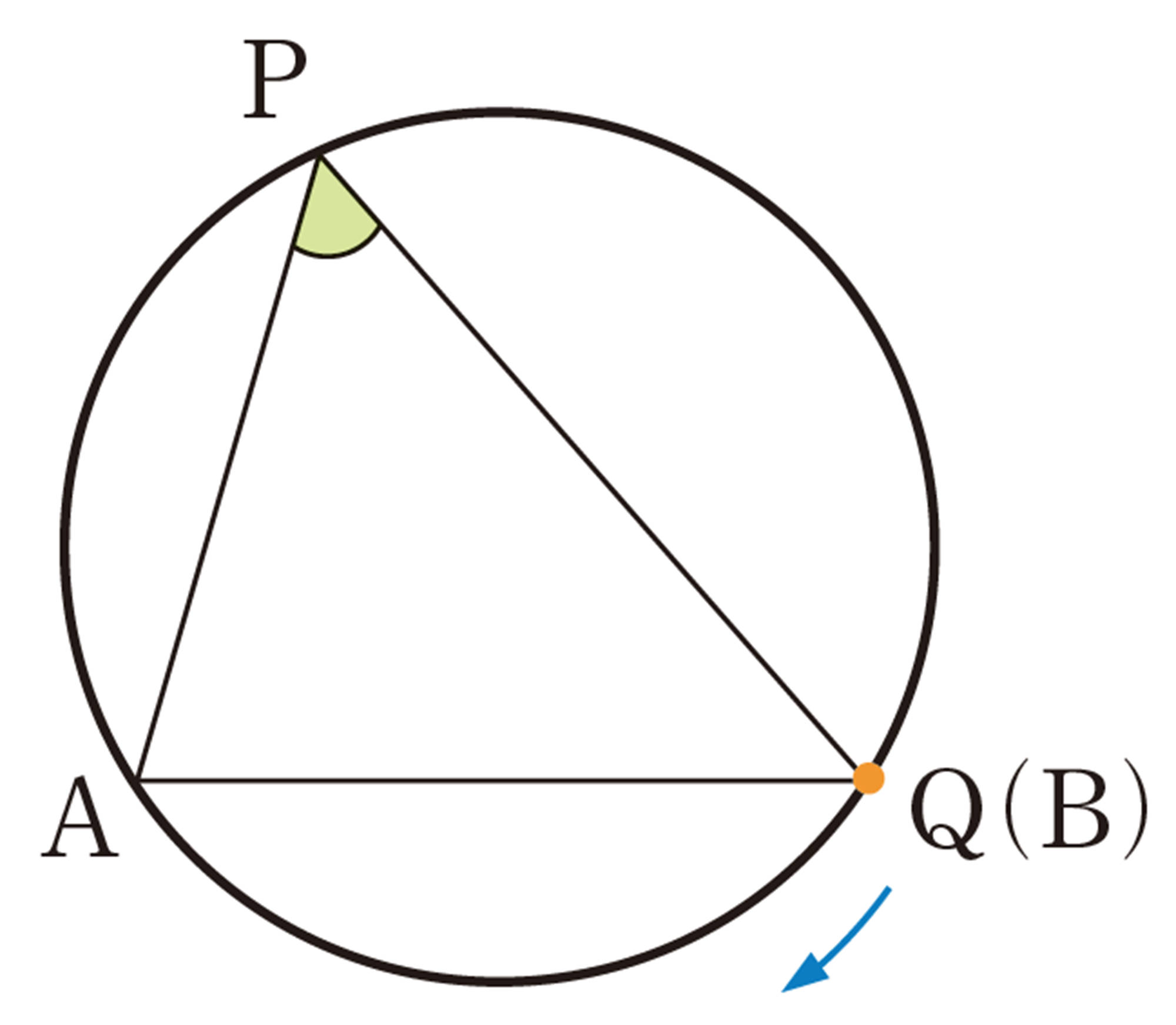
① 次の図で,直線CDは点Qを接点とする円Oの接線です。点Qを円周上で点Bまで動かしたとき,[mathjax]\(\angle APB\)と[mathjax]\(\angle AQC\)の大きさを調べてみましょう。2つの角の間には,どんな関係があるでしょうか。
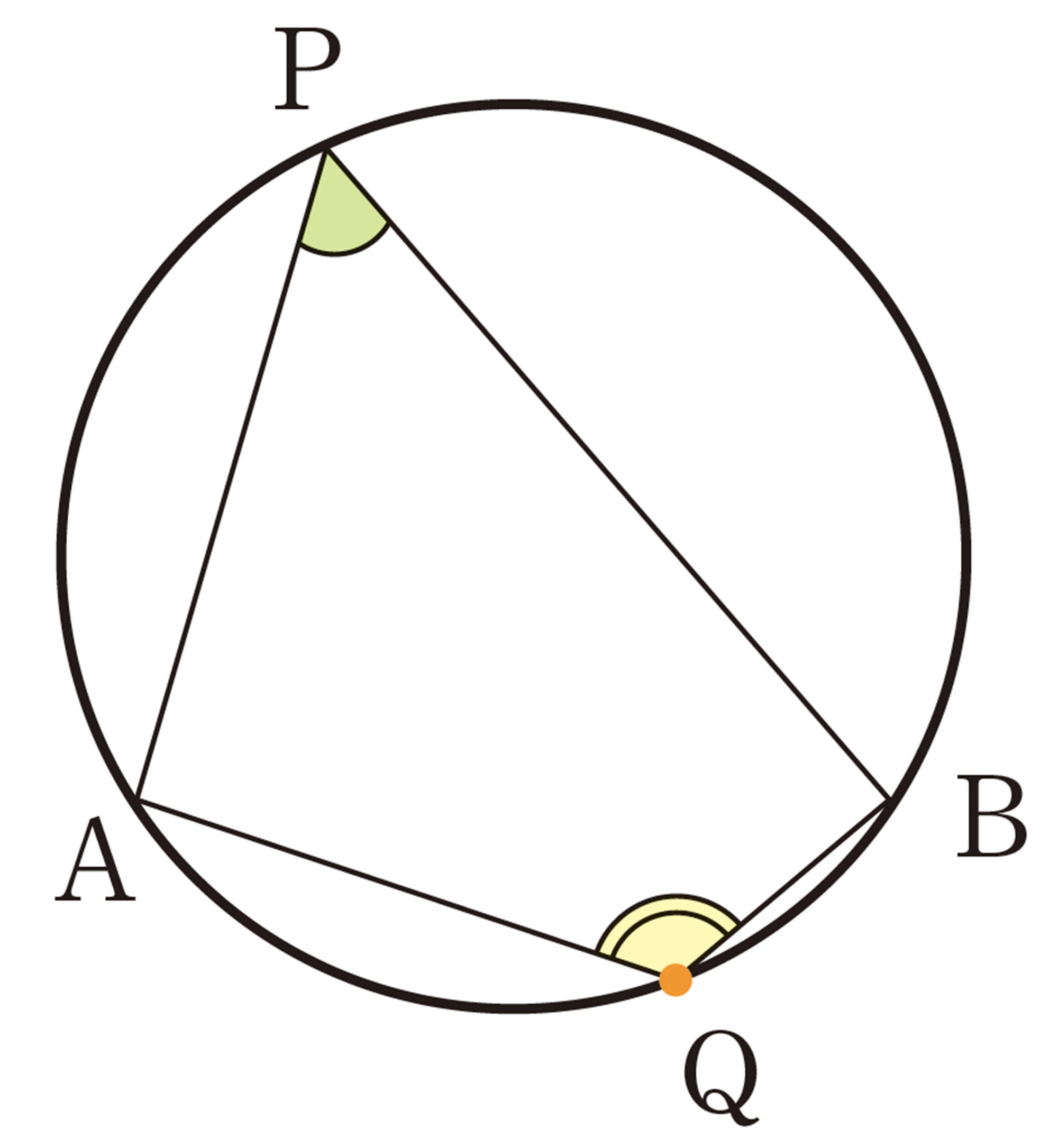
② 次の図で,点Qを[mathjax]\(\stackrel{\huge\frown}{AB}\)上まで動かしたとき,[mathjax]\(\angle APB\)と[mathjax]\(\angle AQB\)の大きさを調べてみましょう。2つの角の間には,どんな関係があるでしょうか。