<3年p.201>
2節 円周角の定理の利用
船の位置を求められるかな？
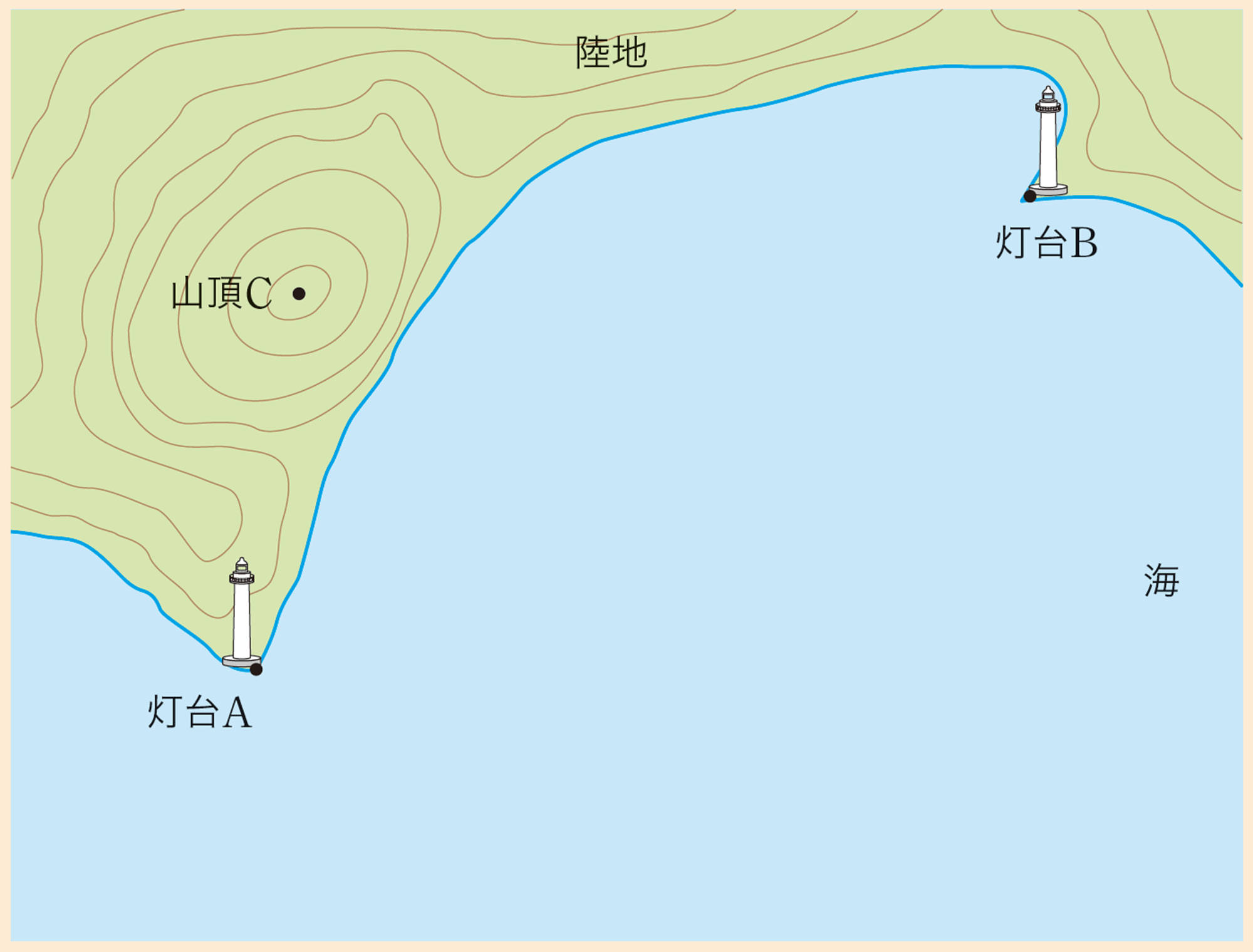
船で沿岸を安全に航海するためには，海図(航海のための地図)上で，自分の位置を知る必要があります。GPS(人工衛星から信号を受け取り，現在位置を知るシステム)などのなかった時代は，自分の位置と陸上の3地点それぞれとを結ぶ線でできる角度を調べて，現在位置を確認していました。
角度を測るだけで，どのようにして位置を知ることができたのでしょうか。
【１】 次のような海図があり，船からは，灯台A，灯台B，山頂Cが見えます。船の位置Pから角度を測定すると，[mathjax]\(\angle APC = 28^{\circ}\)，[mathjax]\(\angle CPB = 60^{\circ}\)でした。コンパスや分度器を使って，船の位置Pを求める方法を考えましょう。
[mathjax]\(\angle APC = 28^{\circ}\)となる点Pは，どこになるのかな。
2点A，Cを通る円の円周角を考えればいいのかな。
次の課題へ！
円周角の定理を，どのように利用しているのかな？
P.202
<3年p.202>
１ 円周角の定理の利用
Q Question
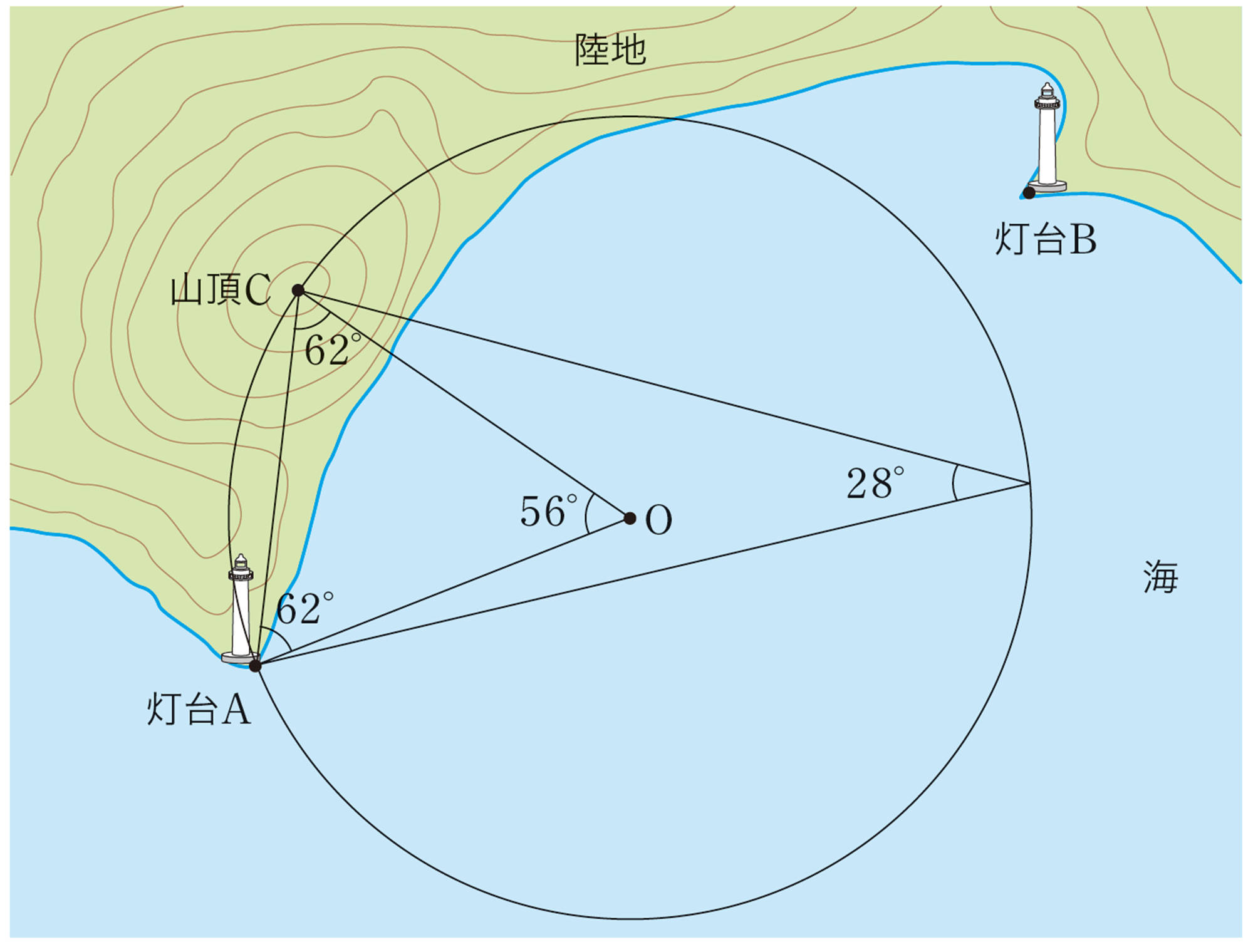
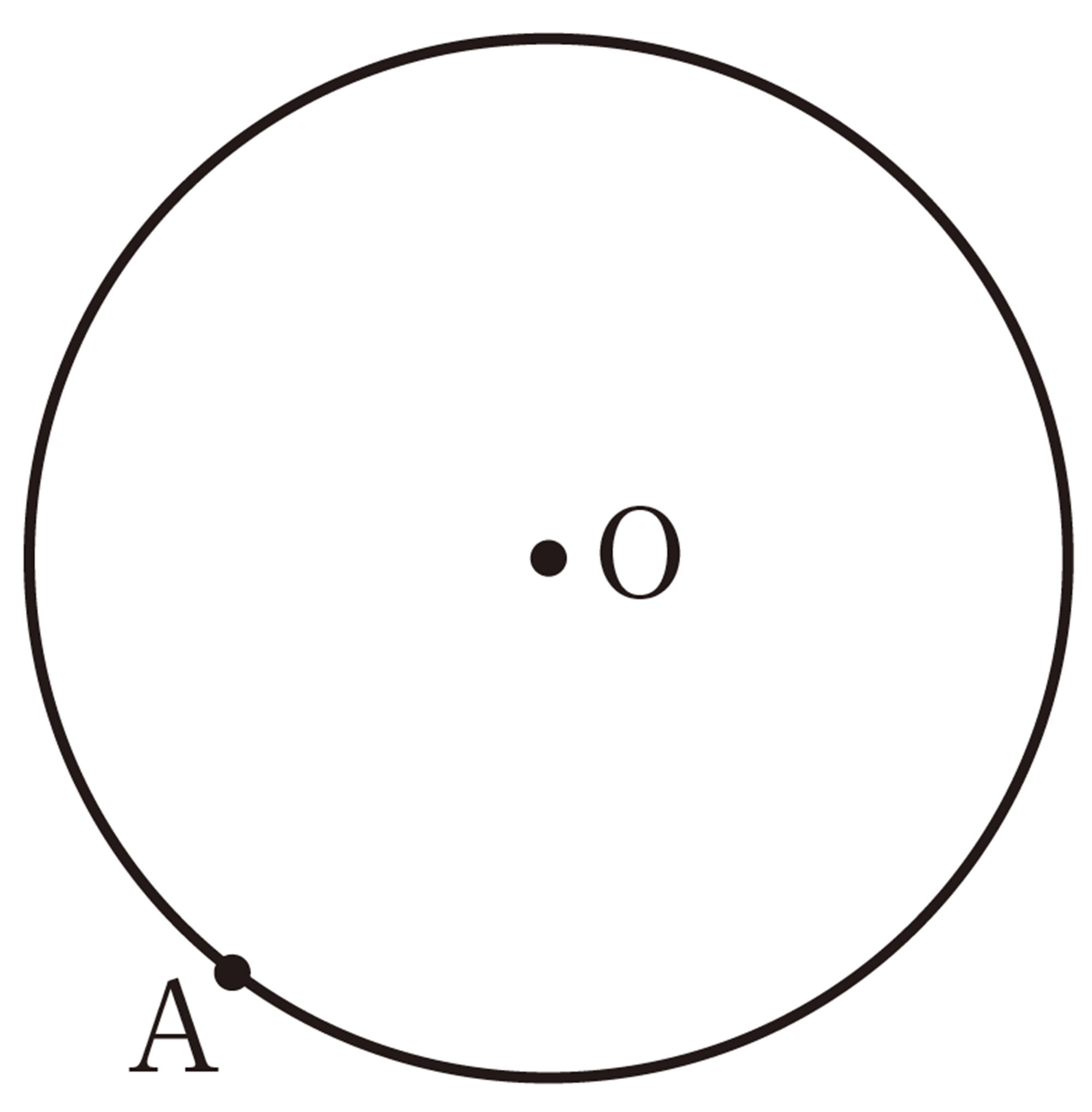
真央さんは，前ページの 1 で，[mathjax]\(\angle APC=28^{\circ}\) となる点Pは，次の図のように，2点A，Cを通り[mathjax]\(\stackrel{\huge\frown}{AC}\)に対する円周角が[mathjax]\(28^{\circ}\)となる円Oの円周上にあると考えました。そして，中心Oを求めるために，ACを底辺として底角が[mathjax]\(62^{\circ}\)の二等辺三角形をかきました。なぜ，真央さんはこのような二等辺三角形をかいたのでしょうか。その理由を説明してみましょう。
どうして底角が[mathjax]\(62^{\circ}\)の二等辺三角形をかいたのかな。
[mathjax]\(\stackrel{\huge\frown}{AC}\)に対する円周角が[mathjax]\(28^{\circ}\)だから，中心角は…。
見方・考え方
根拠を明らかにして，説明できるかな。
問 １ 真央さんの考え方で，上の図に，[mathjax]\(\angle CPB = 60^{\circ}\)となる点Pを求めるための円[mathjax] \(O´\)をかきなさい。また，2つの円[mathjax] \(O\)，[mathjax] \(O´\)をもとにして，船の位置Pを求めなさい。
どんなことがわかったかな
円周角の定理を利用すると，船の位置を知ることができました。
次の課題へ！
これまでに学んだ円と角の関係は，どんなところで使えるのかな？
P.203，205
<3年p.203>
円周角と図形の証明
目標 ▷ 円周角に関する定理を使って，図形の性質を証明しよう。
例 １ 右の図のように，円Oの2つの弦AB，CDの交点をPとするとき，[mathjax]\(\triangle ACP \backsim \triangle DBP\)であることを証明しなさい。
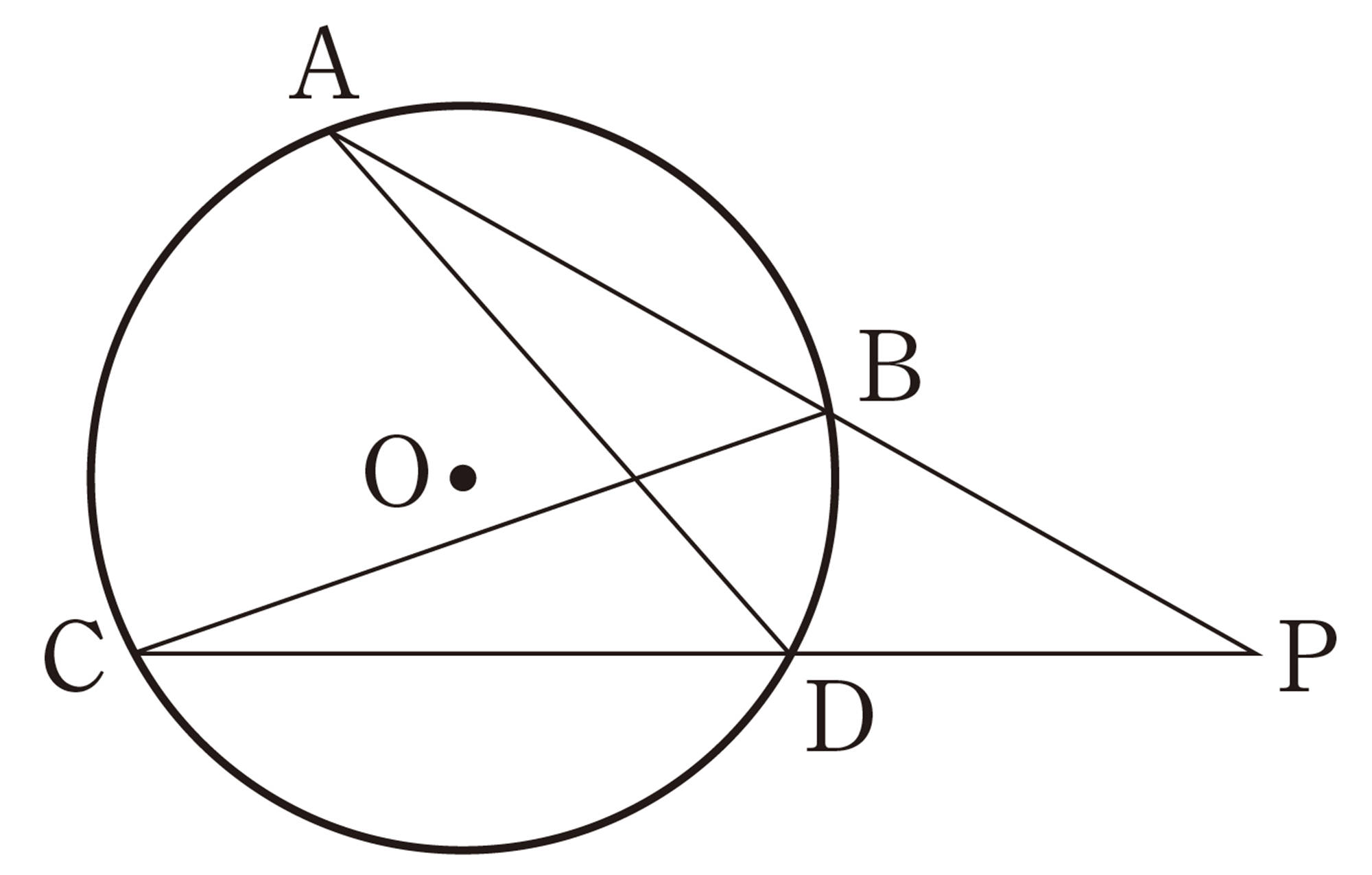
証明
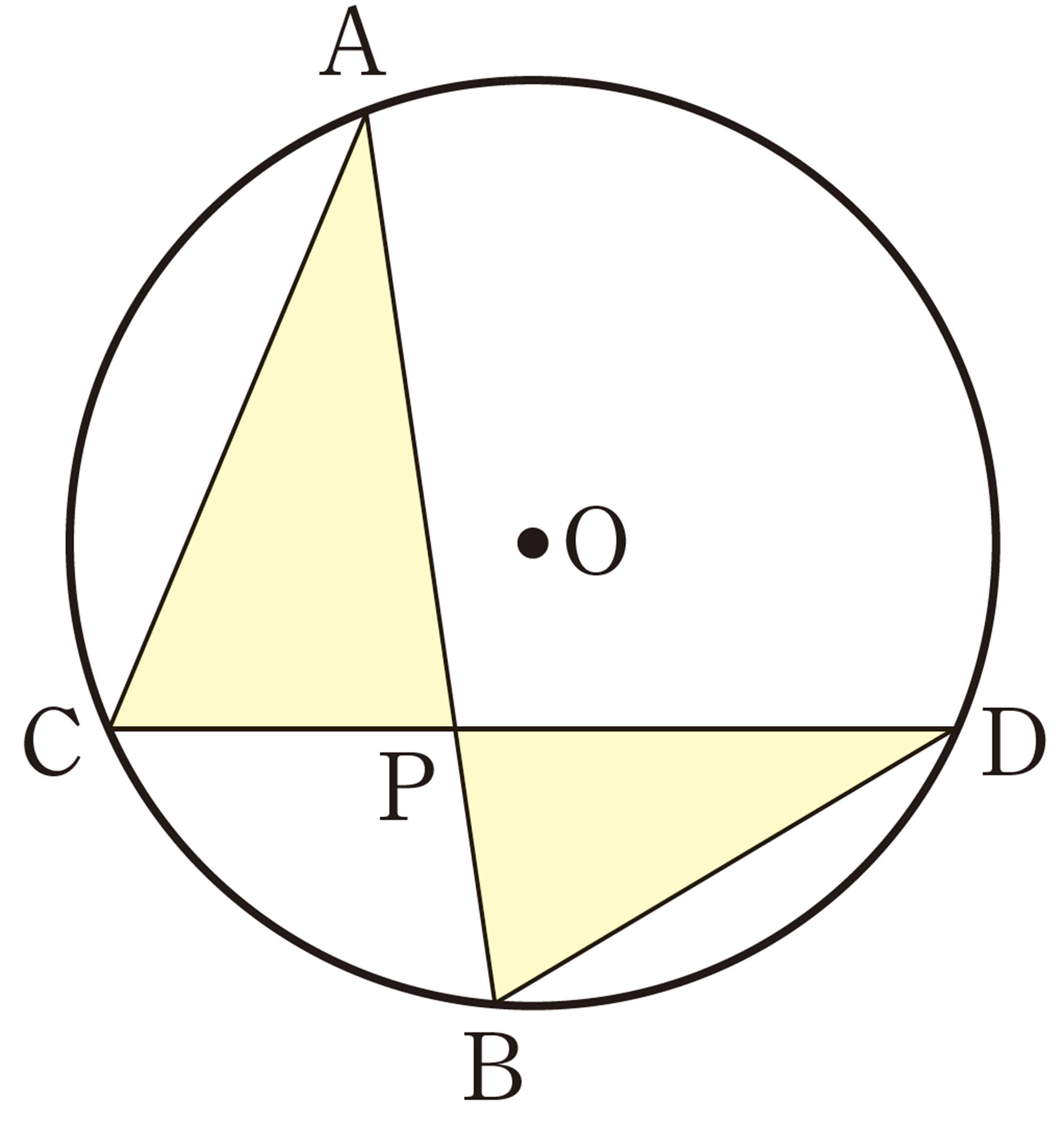
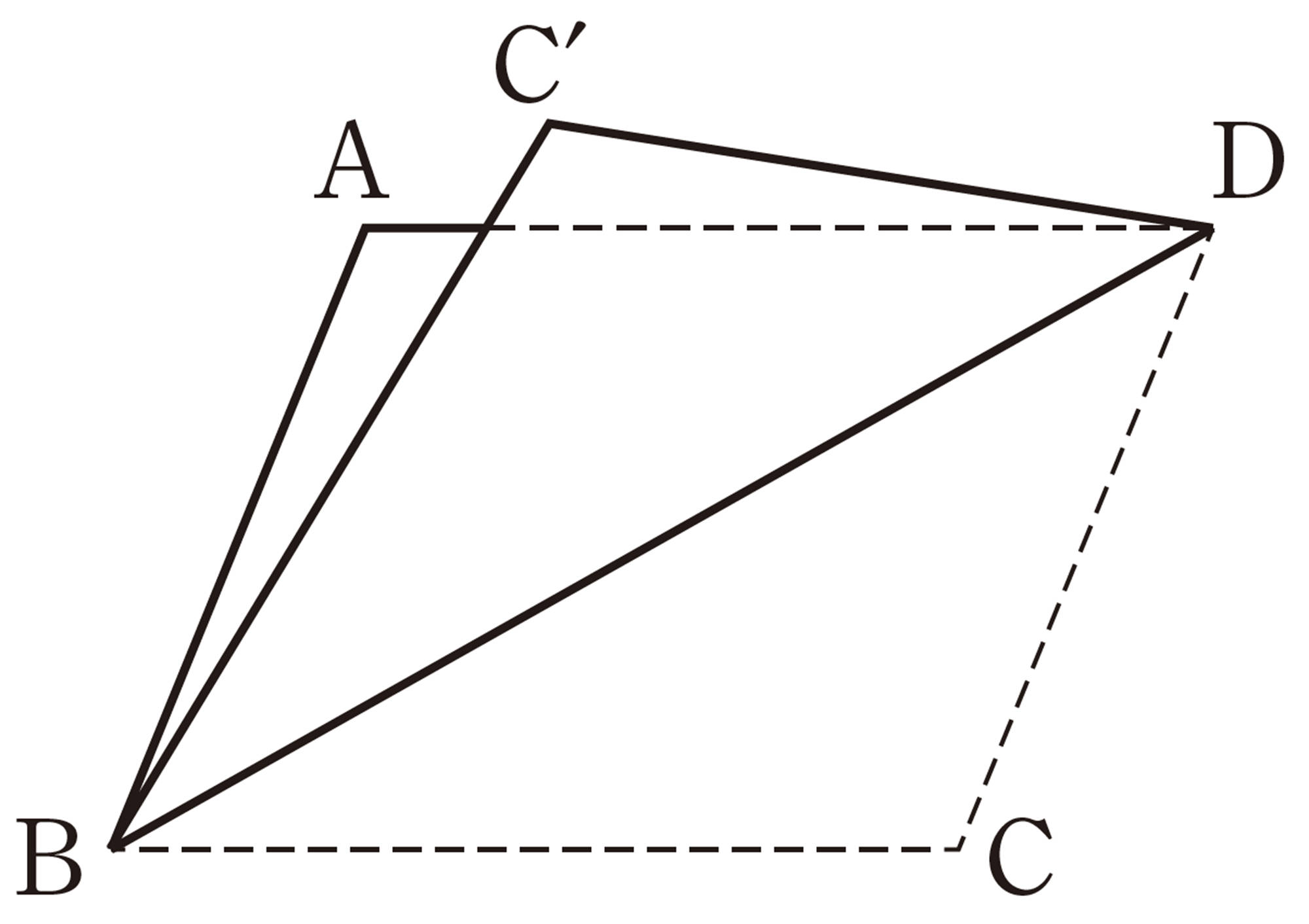
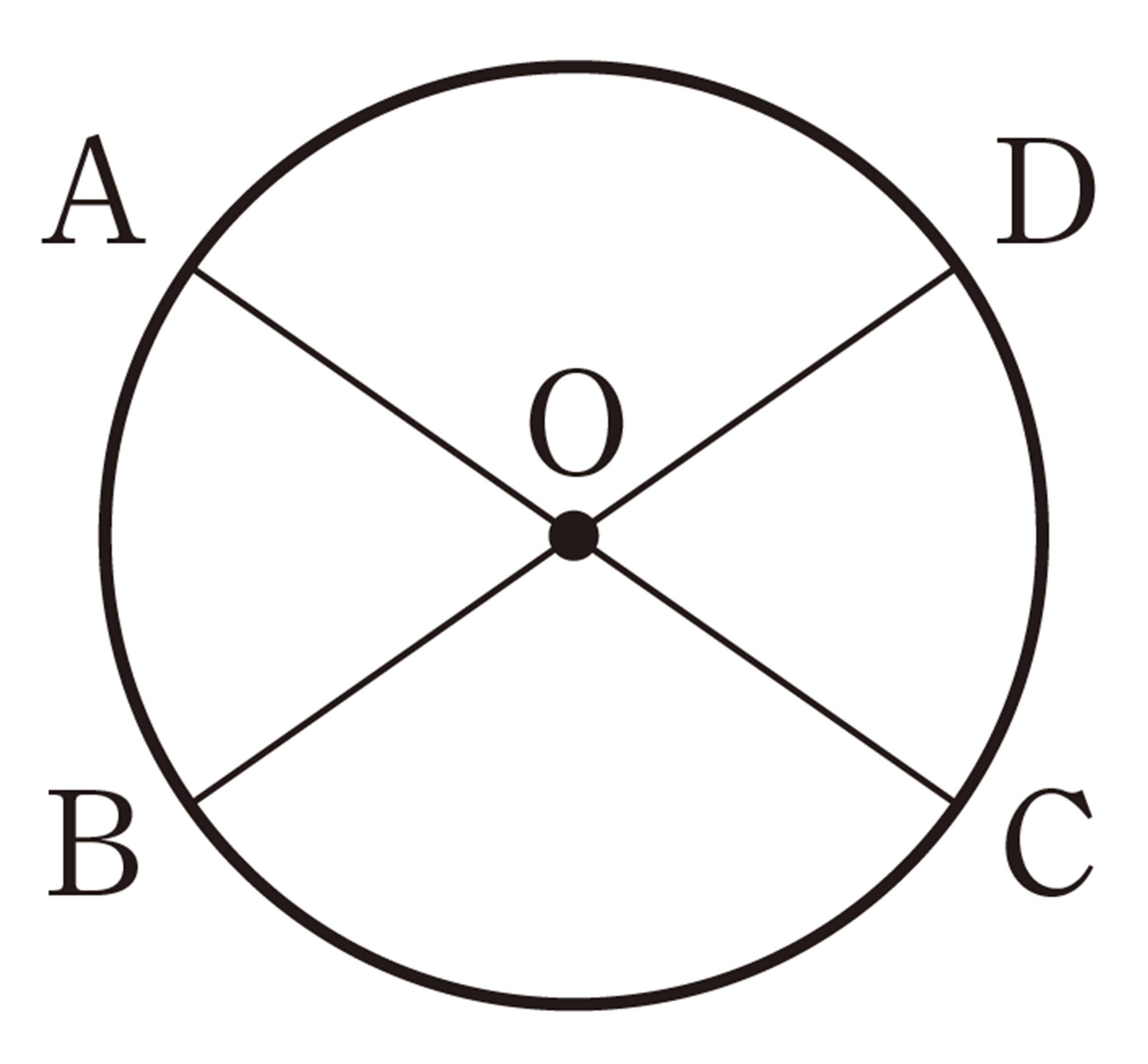
[mathjax]\(\triangle ACP\)と[mathjax]\(\triangle DBP\)において，
[mathjax]\(\stackrel{\huge\frown}{CB}\)に対する円周角は等しいから，
[mathjax]\(\hspace{20pt}\angle A=\angle D \quad \cdots \cdots \mathsf{①}\)
同様にして，
[mathjax]\(\hspace{20pt}\angle C=\angle B \quad \cdots \cdots \mathsf{②}\)
①，② より，2組の角がそれぞれ等しいから，
[mathjax]\(\triangle ACP \backsim \triangle DBP\)
問 ２ 例1の図で，[mathjax]\(AP=9\)cm，[mathjax]\(BP=4\)cm，[mathjax]\(CP=5\)cmのとき，DPの長さを求めなさい。
問 ３ 右の図のように，円Oの2つの弦AB，CDを延長し，その交点をPとするとき，[mathjax]\(\triangle ADP \backsim \triangle CBP\)であることを証明しなさい。
<3年p.204>
例 ２ 右の図のように，円Oの円周上に4点A，B，C，Dがあります。円Oの弦AB，CDについて，
[mathjax]\(AB /\!/CD\)ならば，
[mathjax]\(\stackrel{\huge\frown}{AC} = \stackrel{\huge\frown}{BD}\)であることを証明しなさい。
証明
2点B，Cを結ぶ。
平行線の錯角は等しいから，
[mathjax]\(AB/\!/CD\)より，[mathjax]\(\angle ABC = \angle DCB\)
等しい円周角に対する弧は等しいから，
[mathjax]\(\stackrel{\huge\frown}{AC} = \stackrel{\huge\frown}{BD}\)
問 ４ 例2で証明したことがらの逆をいいなさい。また，それが成り立つことを証明しなさい。
問 ５
右の図のように，4点A，B，C，Dは円Oの円周上の点，弦AC，BDの交点をEとします。[mathjax]\(\stackrel{\huge\frown}{AD} = \stackrel{\huge\frown}{DC}\)のとき，[mathjax]\(\triangle ABE \backsim \triangle DBC\)であることを証明しなさい。
問 ６ 右の図のように，▱ABCDの紙を対角線BDで折ります。点 C が移った点を[mathjax] \( C´\)とするとき，4点[mathjax] \(A\)，[mathjax] \(B\)，[mathjax] \(D\)，[mathjax] \(C´\)が1つの円周上にあることを証明しなさい。
どんなことがわかったかな
円周角の定理を利用すると，いろいろな図形の性質を証明することができます。
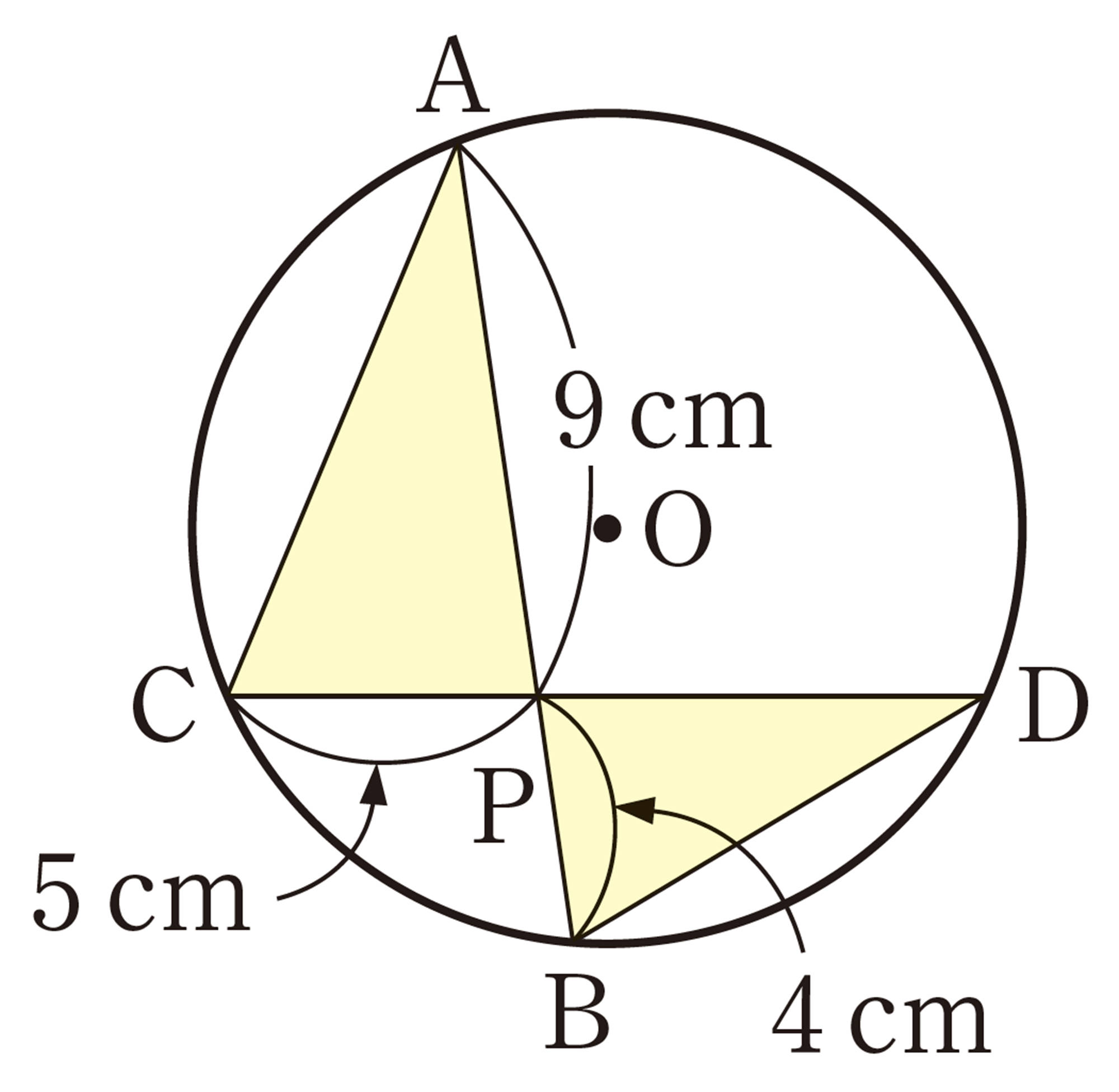
注意 [mathjax]\(AP \times BP\)は，線分AP，BPの長さの積を表している。
<3年p.205>
円周角と円の接線
問 ７ 右の図で，点Aを接点とする円Oの接線を作図しなさい。また，その作図は，接線のどんな性質を利用しているか説明しなさい。
ふりかえり
▷1年
円と1点だけを共有する直線を接線という。
Q Question
右の図のように，円Oの外部に点Pがあるとき，点Pを通る円Oの接線は，何本引けるでしょうか。また，どのように作図すればよいでしょうか。
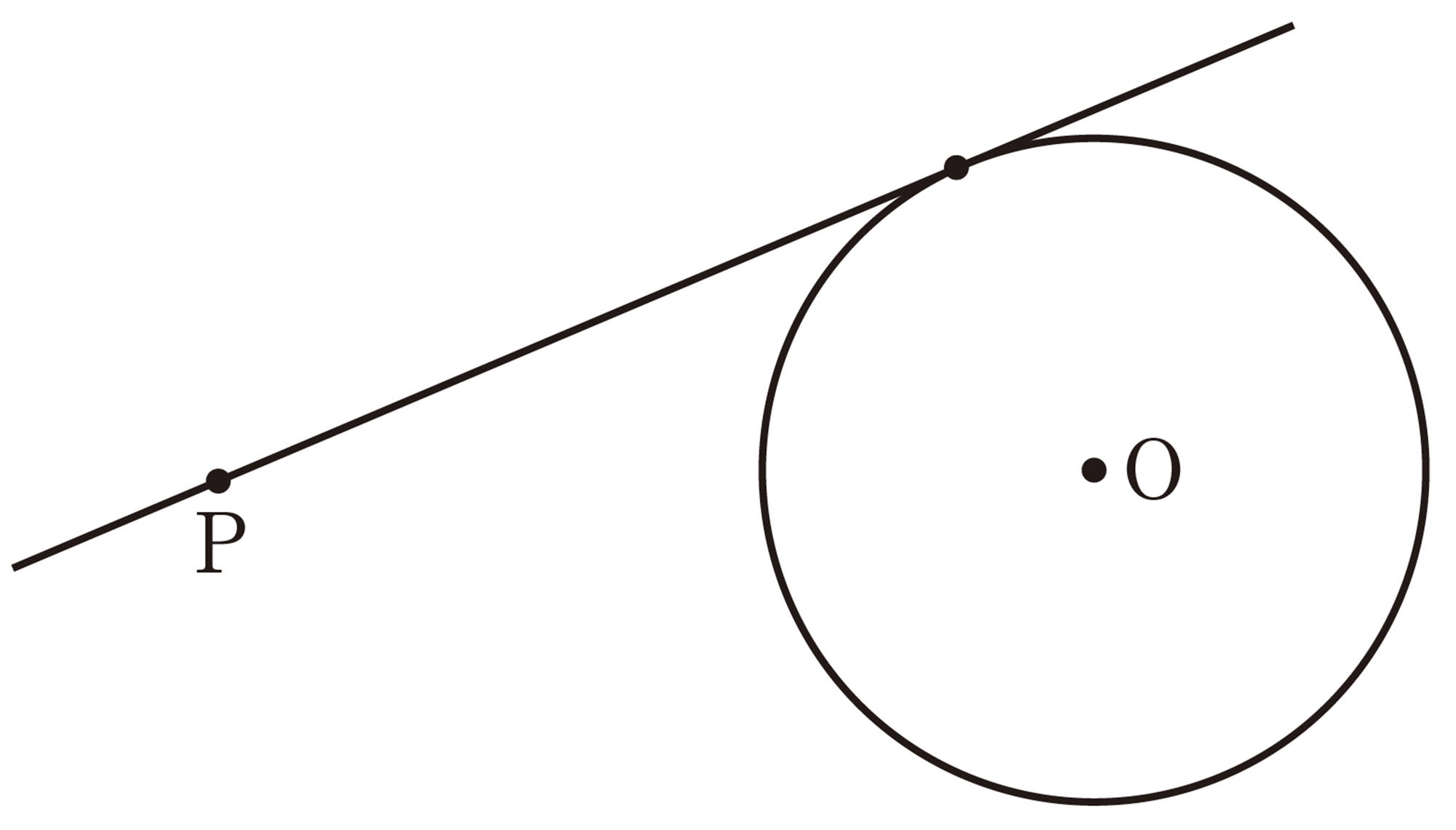
1年のときに円周上の点を通る接線の作図をしたね。
円周上以外に点をとったとき，接線はどうなるのかな。
見方・考え方
条件を変えるとどうなるかな。
目標 ▷ 円の外部にある1 点を通る円の接線の作図のしかたを 考えよう。
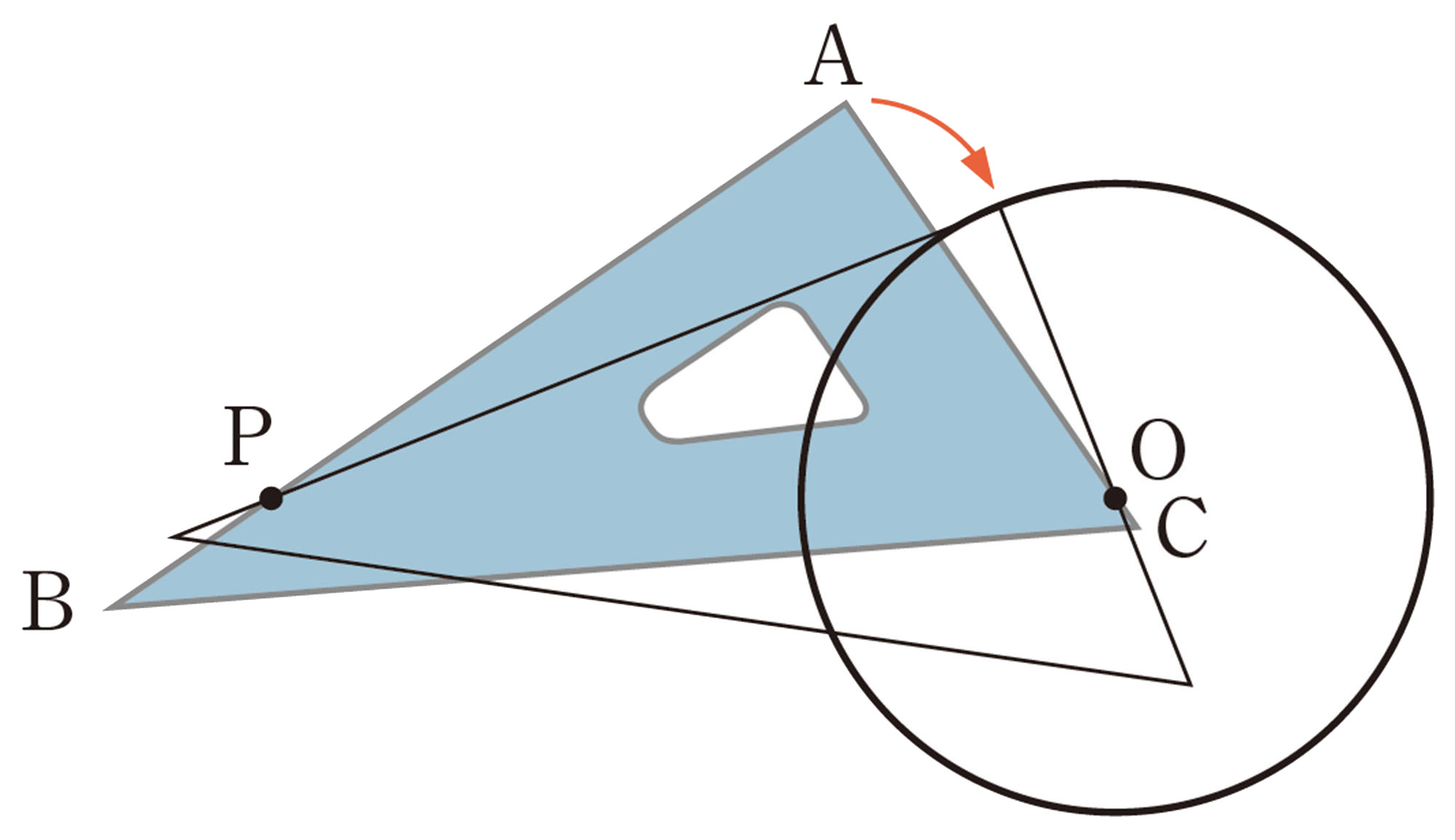
１ 美月さんは，Qの図で，三角定規を使って，次のような方法で接線が引けると考えました。
美月さんの考え
右の図のように，三角定規の2辺AB，ACが，それぞれ点P，Oを通るように三角定規を置く。その状態を保ったまま三角定規をずらし，頂点Aが円Oの円周上にくるようにして，直線PAを引く。
このとき，直線PAが円Oの接線となる理由を説明してみましょう。
<3年p.206>
前ページの美月さんの考えをもとにして，円Oの外部の点Pを通る円Oの接線の作図の方法を考えてみよう。
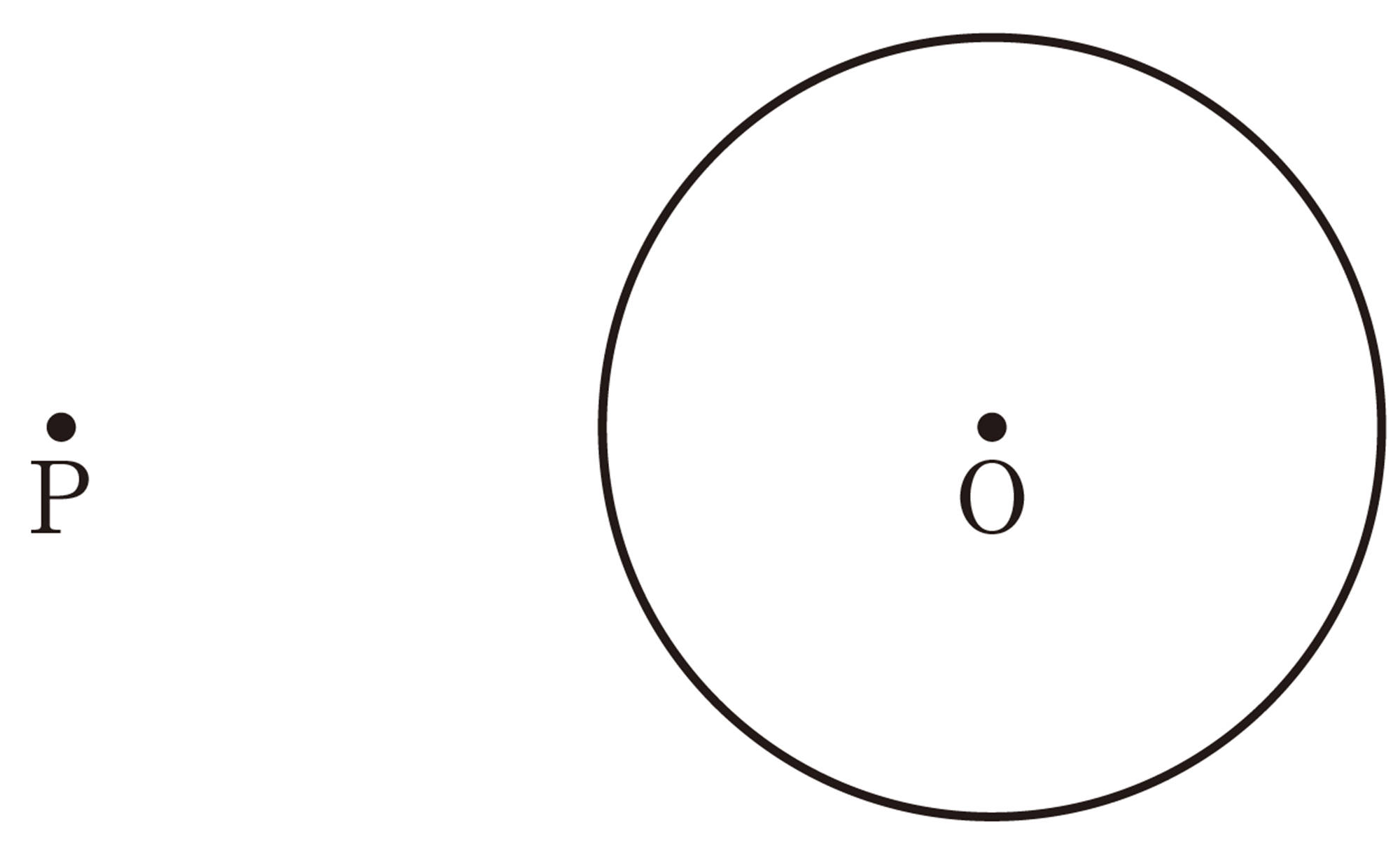
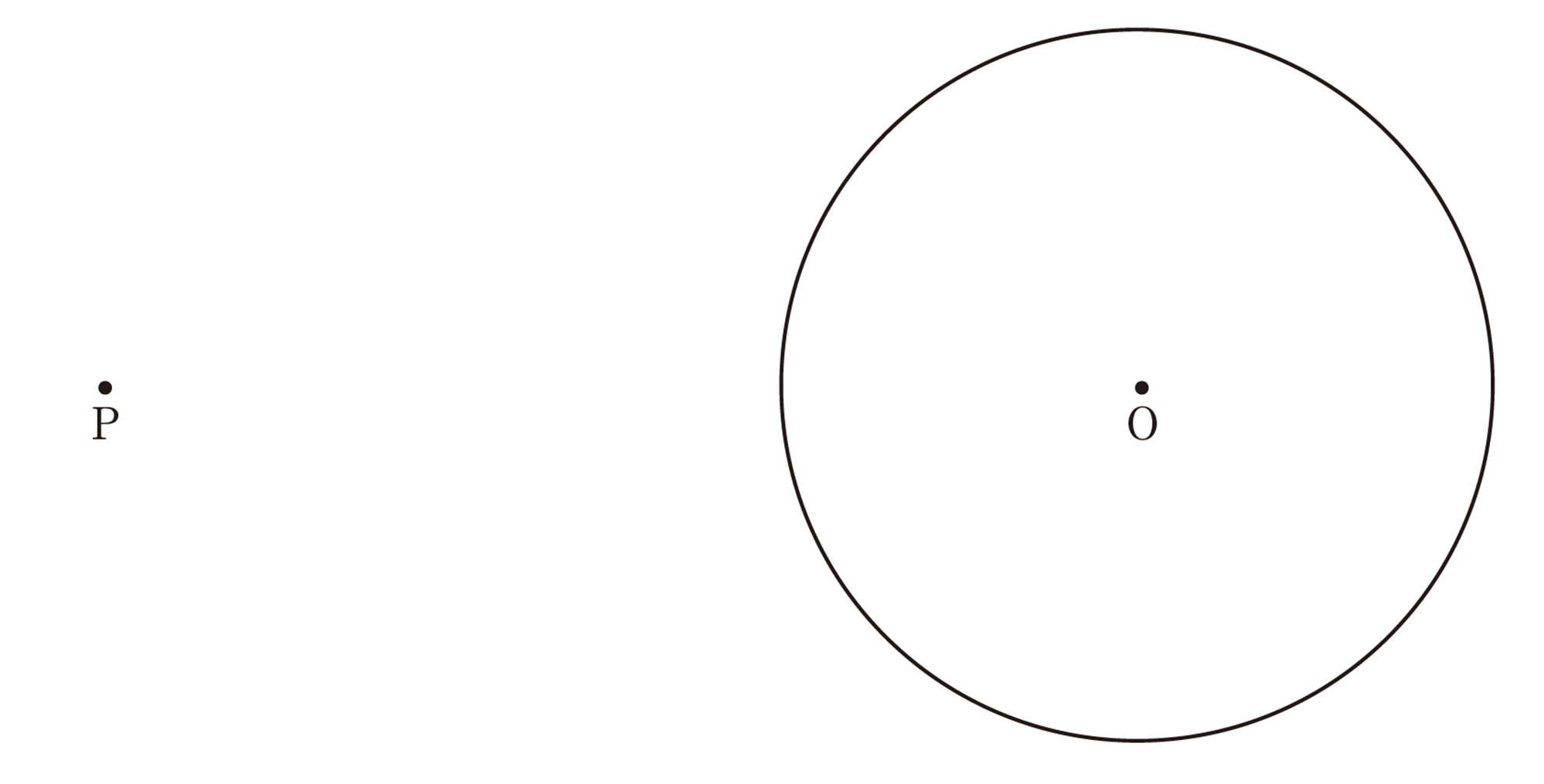
２ 拓真さんは，次の手順で，円Oの外部の点Pを通る円Oの接線を作図しました。この手順にしたがって，作図をしてみましょう。
手順
① 点P，Oを結び，線分POの中点[mathjax] \(O´\)を求める。
② [mathjax] \(O´\)を中心として半径[mathjax] \(O´P\)の円をかき，円Oとの交点をそれぞれA，Bとする。
③ 直線 PA，PB を引く。
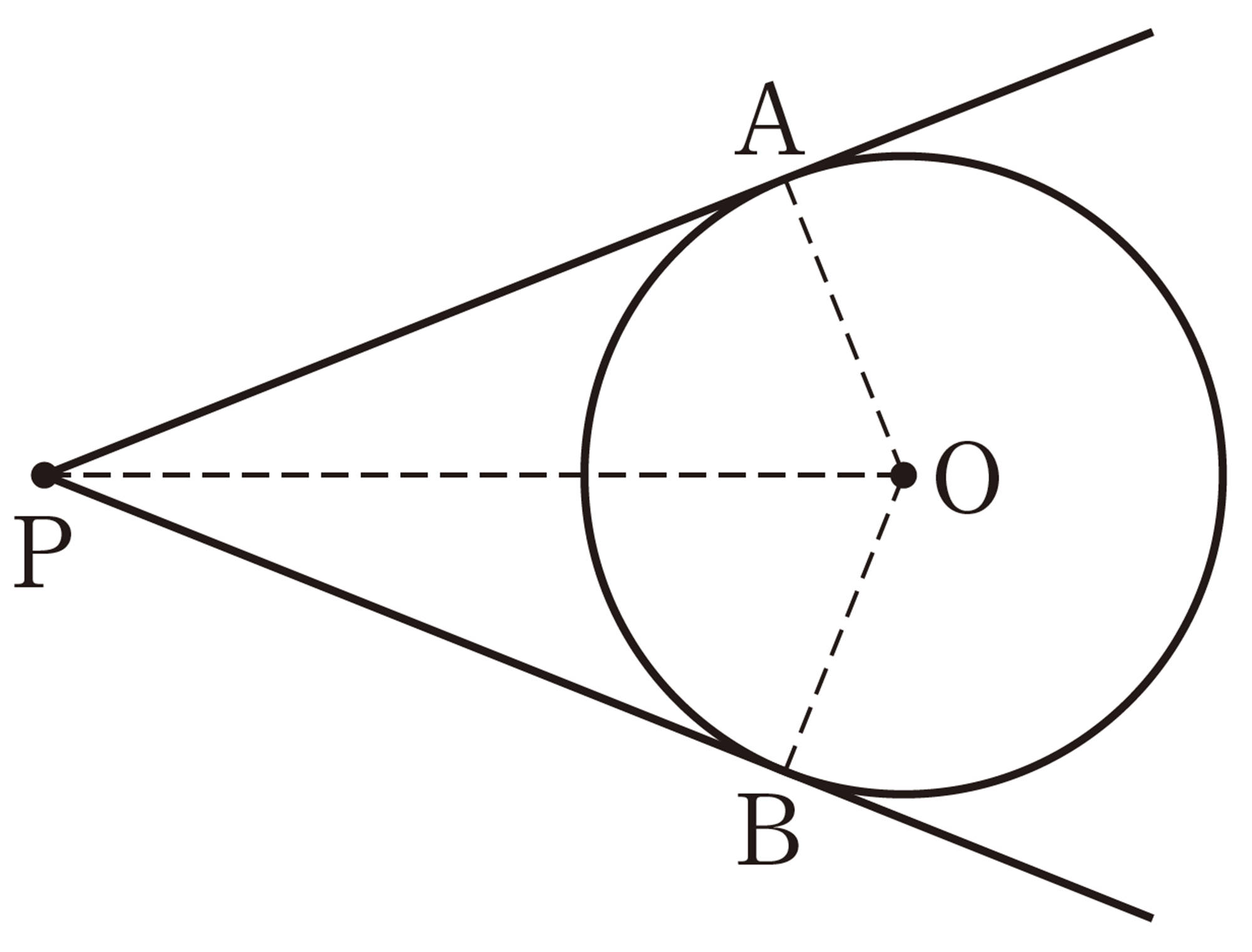
３ 2の図で，OとA，OとBを，それぞれ結んでみましょう。このとき，円[mathjax] \(O´\)において，[mathjax]\(\angle PAO\)や[mathjax]\(\angle PBO\)はどんな角といえるでしょうか。また，そのことをもとにして，拓真さんの方法で接線が作図できる理由を説明してみましょう。
2で作図した線分PAとPBは，長さが等しく見えるよ。
[mathjax]\(\triangle APO\)と[mathjax]\(\triangle BPO\)について調べてみたらわかるかな。
<3年p.207>
問 ８ 円Oの外部の点Pから円Oに接線PA，PBを引くとき，[mathjax]\(PA=PB\)であることを証明しなさい。
円Oの外部の点Pから円Oに接線を引き，接点をA，Bとするとき，線分PA，PBの長さのことを，接線の長さという。
[mathjax]\(\triangle APO\)と[mathjax]\(\triangle BPO\)は合同なので，問8から，接線の長さについて，次のことがいえる。
円の外部にある1点から，この円に引いた2本の接線の長さは等しい。
どんなことがわかったかな
円周角と中心角の関係を利用して，円の外部にある1点を通る円の接線を作図することができます。
確かめよう 2節 円周角の定理の利用
１ 右の図のように，円Oの2つの直径をAC，BDとする。このとき，四角形ABCDは長方形になることを証明しなさい。
２ 三角定規を使って，右の円の中心Oを求めなさい。また，その方法で中心を求めることができる理由を説明しなさい。
<3年p.208>
6章 「円」を学んで
できるようになったこと 身のまわりの課題へ ▷ P.211
円周角と中心角の関係から，円周角の定理を見つけ，それを証明することができる。
身のまわりや数学の中から見つけた問題を，円周角の定理や円周角の定理の逆を使って解決することができる。
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
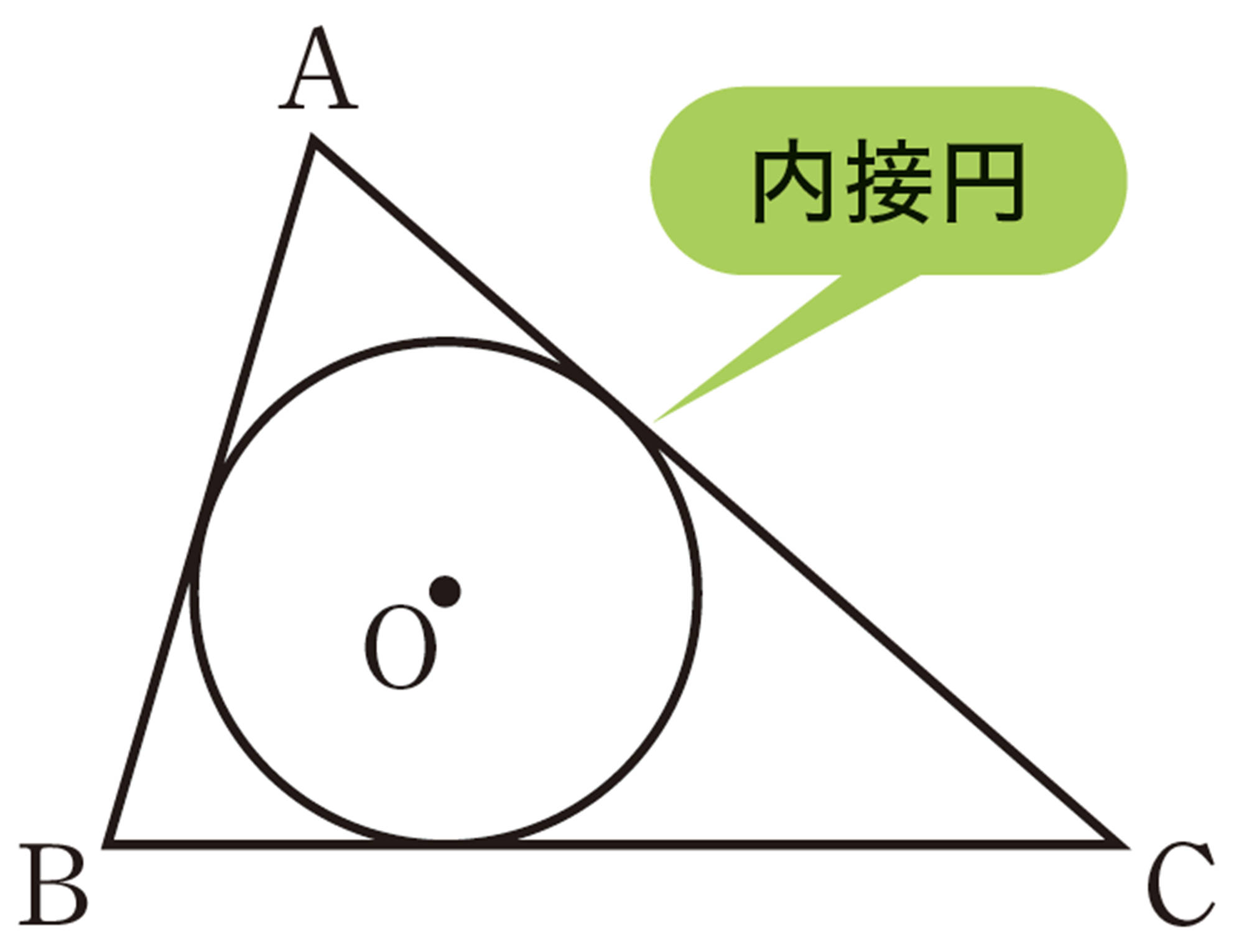
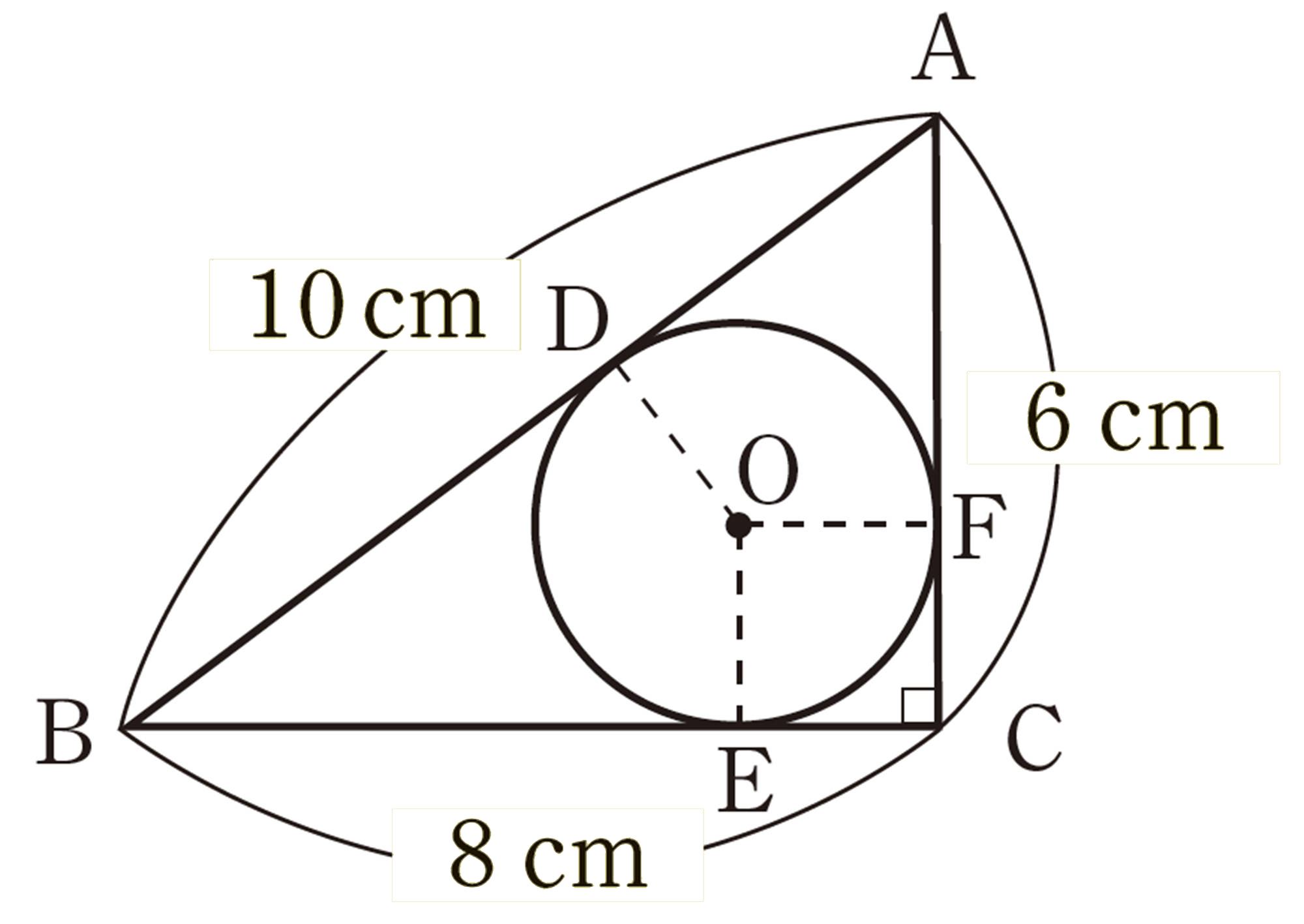
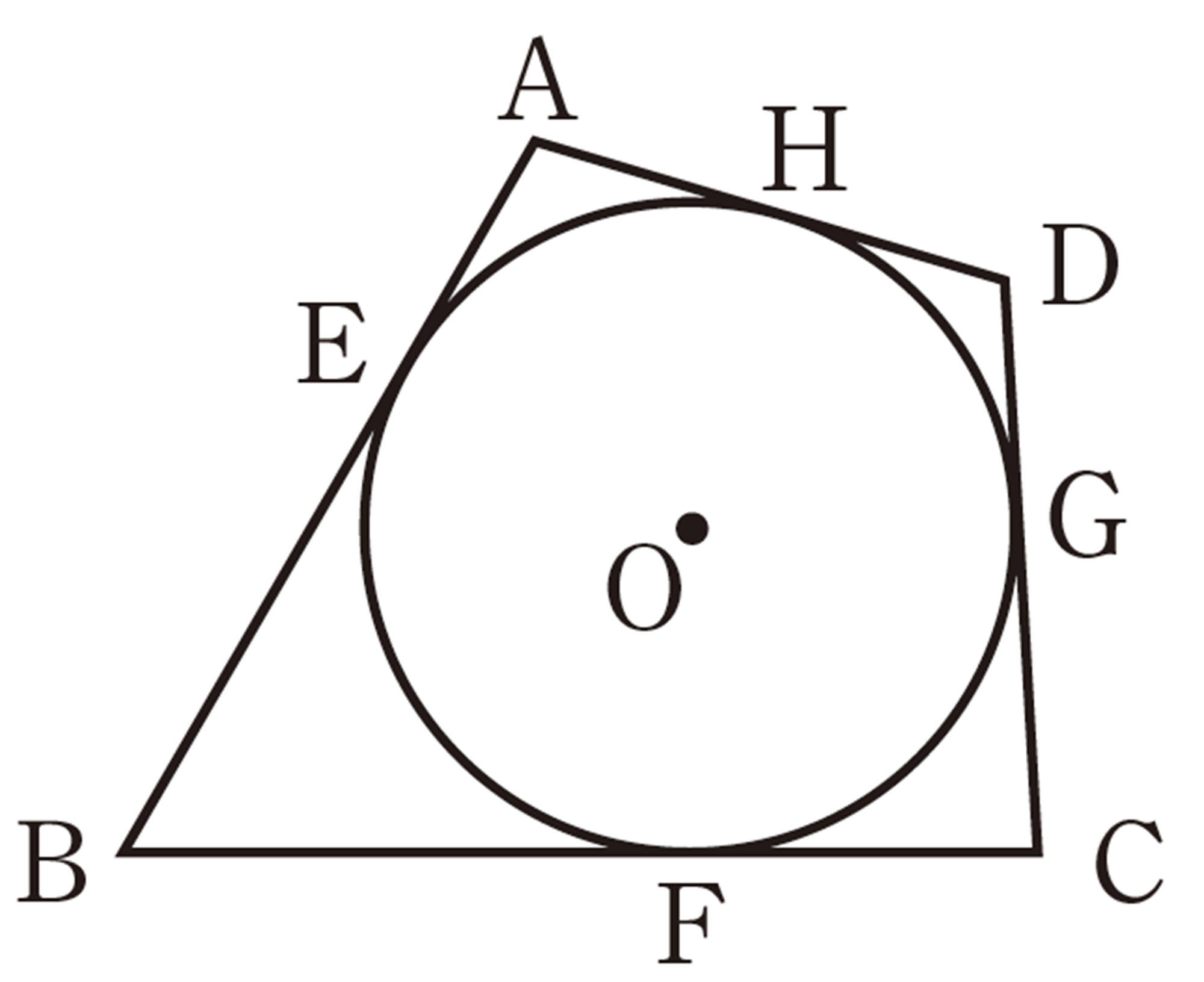
数学へのいざない 内接円 発展 高等学校
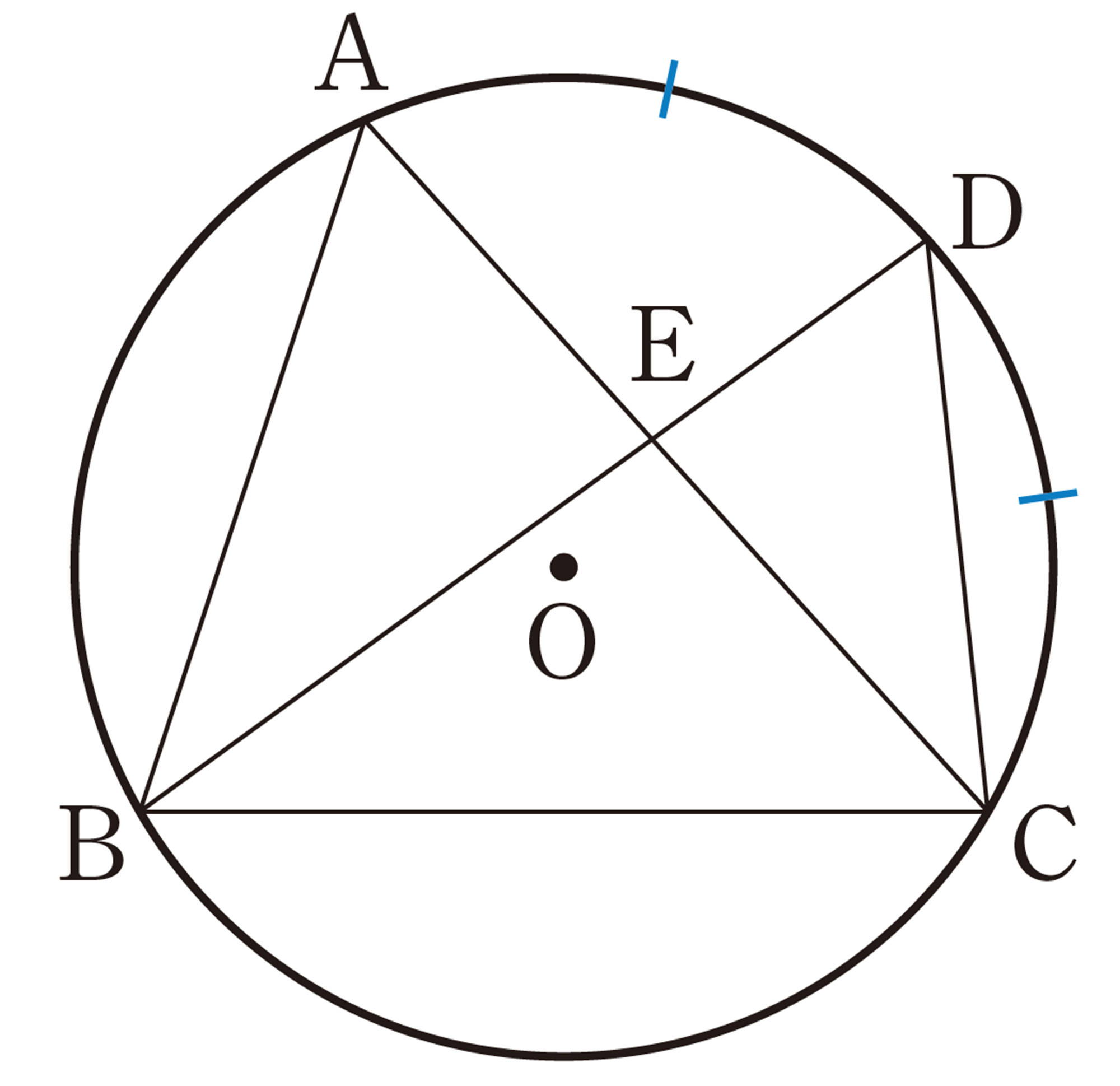
長さが等しい線分はどれとどれかな。
右の図のように，円Oが [mathjax]\(\triangle ABC\) の3辺に接しているとき，円Oを [mathjax]\(\triangle ABC\) の内接円といいます。
❶ 右の図で，円Oは [mathjax]\(\triangle ABC\) の内接円で，点D，E，Fは接点です。[mathjax]\(\angle C=90^{\circ}\)，[mathjax]\(AB=10\)cm，[mathjax]\(BC=8\)cm，[mathjax]\(CA=6\)cmのとき，円Oの半径の長さを求めてみましょう。
❷ 右の図で，円Oは，四角形ABCDと各辺上の点 E， F，G，Hで接しています。このとき，[mathjax]\(AB+CD=BC+DA\) であることを，接線の性質を使って証明してみましょう。
