<3年p.187>
６章 Chapter 6 円
1節 円周角と中心角
2節 円周角の定理の利用
これまでに，三角形や四角形の性質を学んだね。
合同や相似という図形どうしの関係も学んだよ。
これまでに，円の性質についても学んだね。
円には，ほかにどんな性質があるのかな。調べてみたいな。
？ 円にはどんな性質があるのかな？
<3年p.188>
1節 円周角と中心角
何かきまりがあるのかな？
左の写真は，「糸かけ曼荼羅」と呼ばれているものです。
円周上にピンを等間隔に立てて，そこに糸をかけることで美しい図形をえがいています。
円周上にピンを等間隔に立て，そこに糸をかけて模様をつくってみましょう。
【１】 拓真さんは，ピンAを通る糸がつくる角を見て，あることに気づきました。どんなことに気づいたのか，話し合ってみましょう。
<3年p.189>
【２】 美月さんは，ピンA，Bを通る糸がつくる角について，あることに気づきました。どんなことに気づいたのか，話し合ってみましょう。
【３】 [mathjax] \(1\)，[mathjax] \(2\)で，角について気づいたことは，ピンが10本のときでもいえるでしょうか。次の図に，線を引いて確かめてみましょう。
となりどうしのピンじゃなくても，いえるのかな。
ピンが等間隔になっていない場合は，どうなるのかな。
次の課題へ！
円の中にできる角には，何かきまりがあるのかな？
P.190
<3年p.190>
１ 円周角の定理
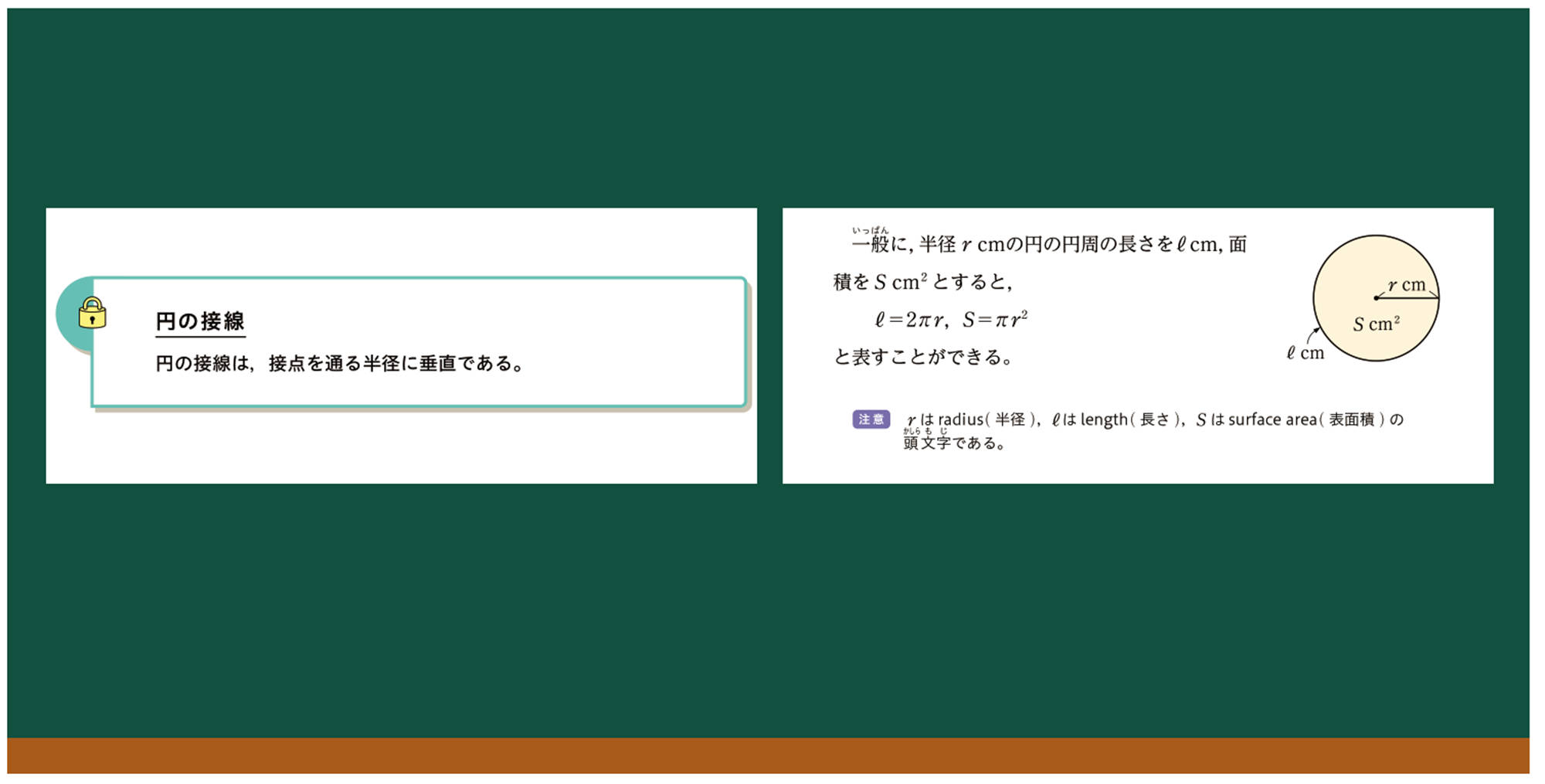
円周角
Q Question
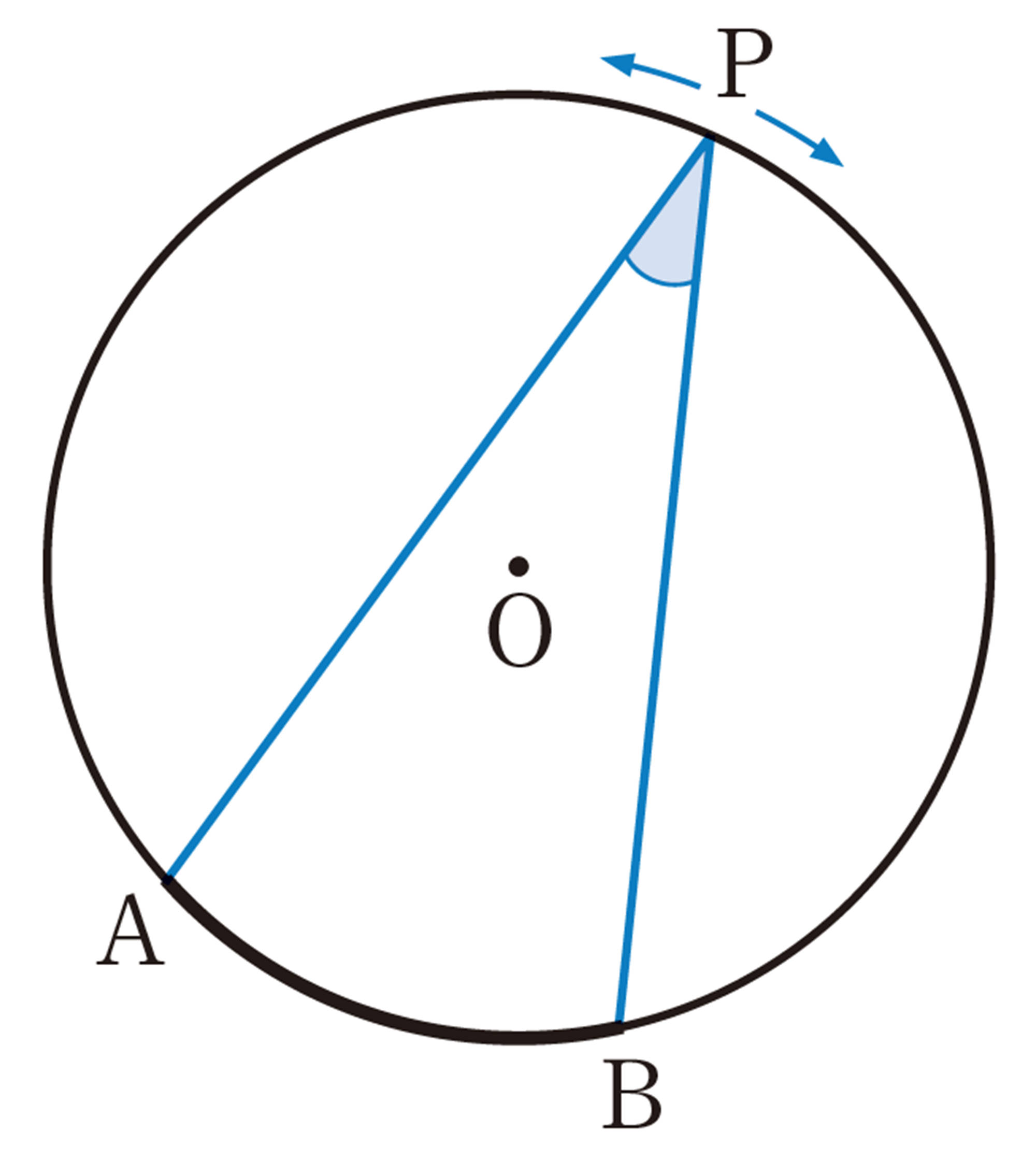
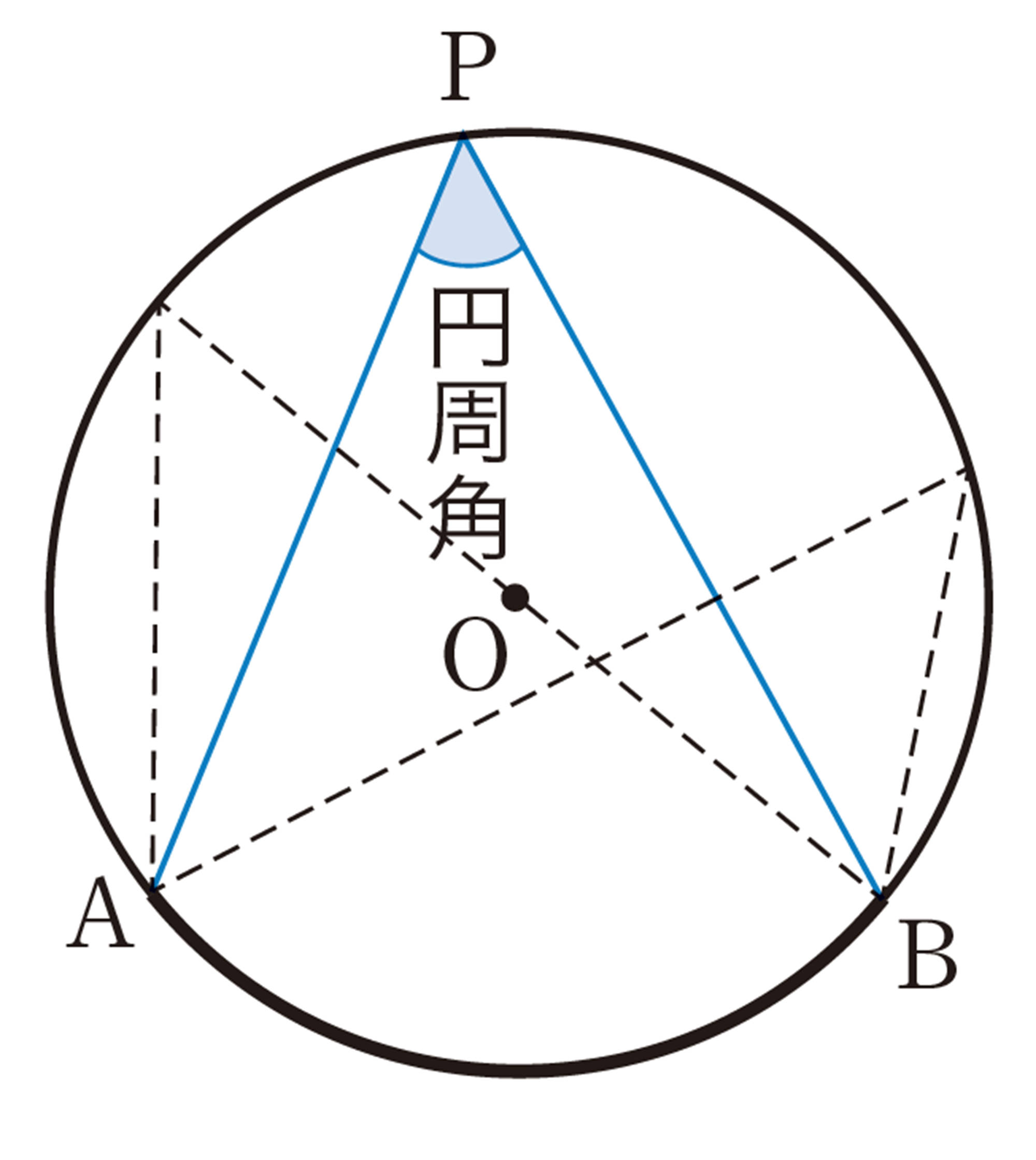
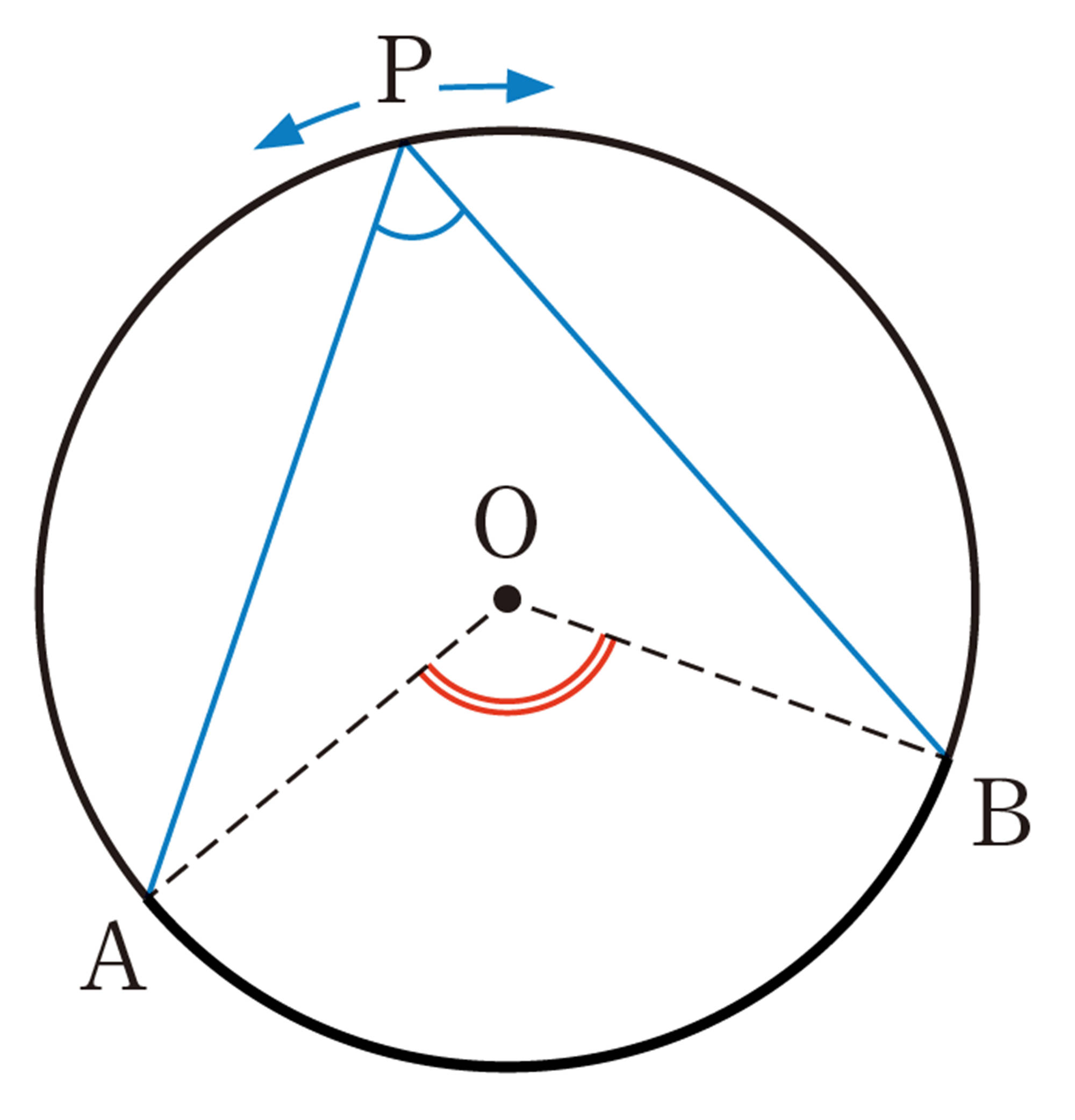
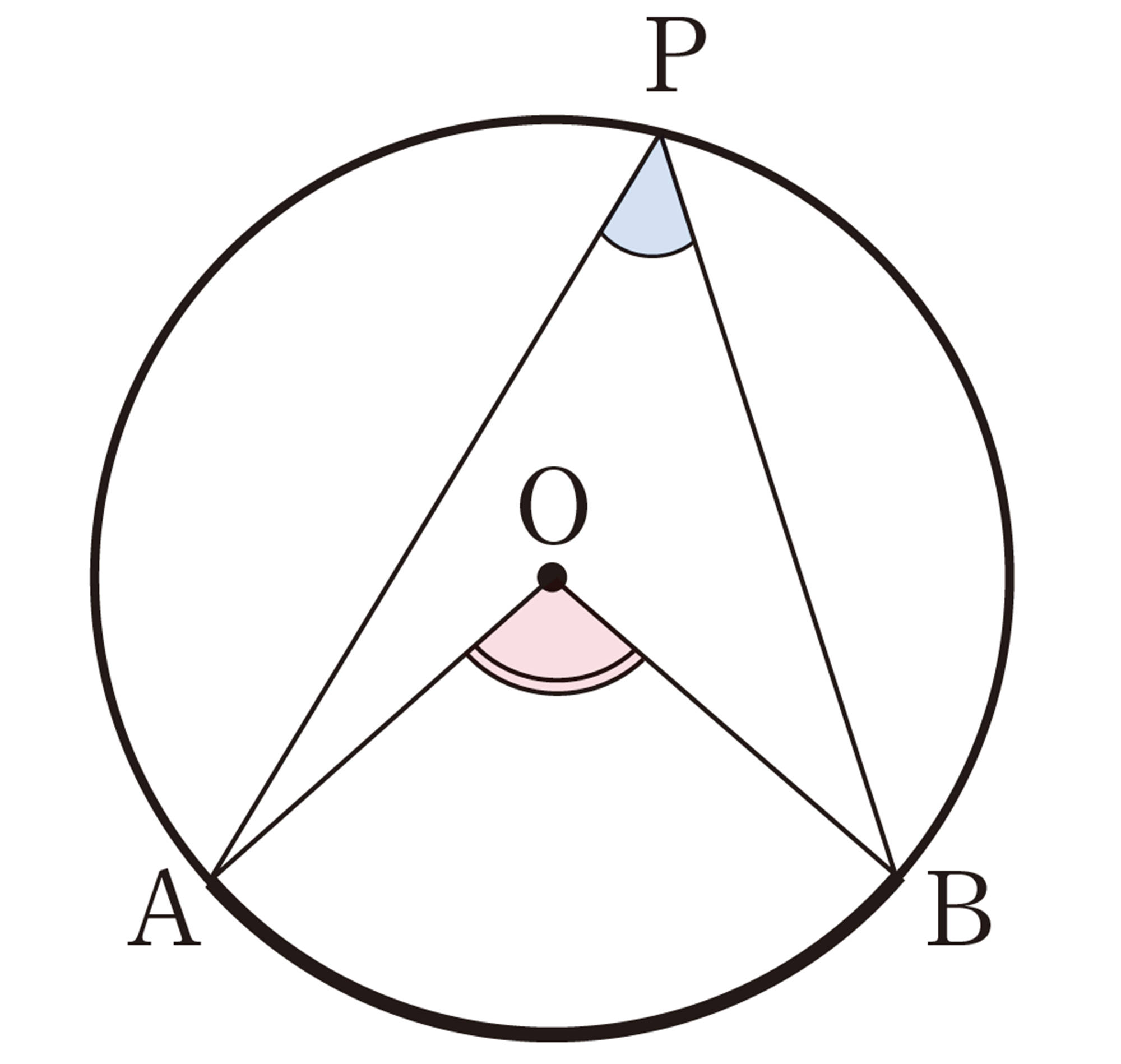
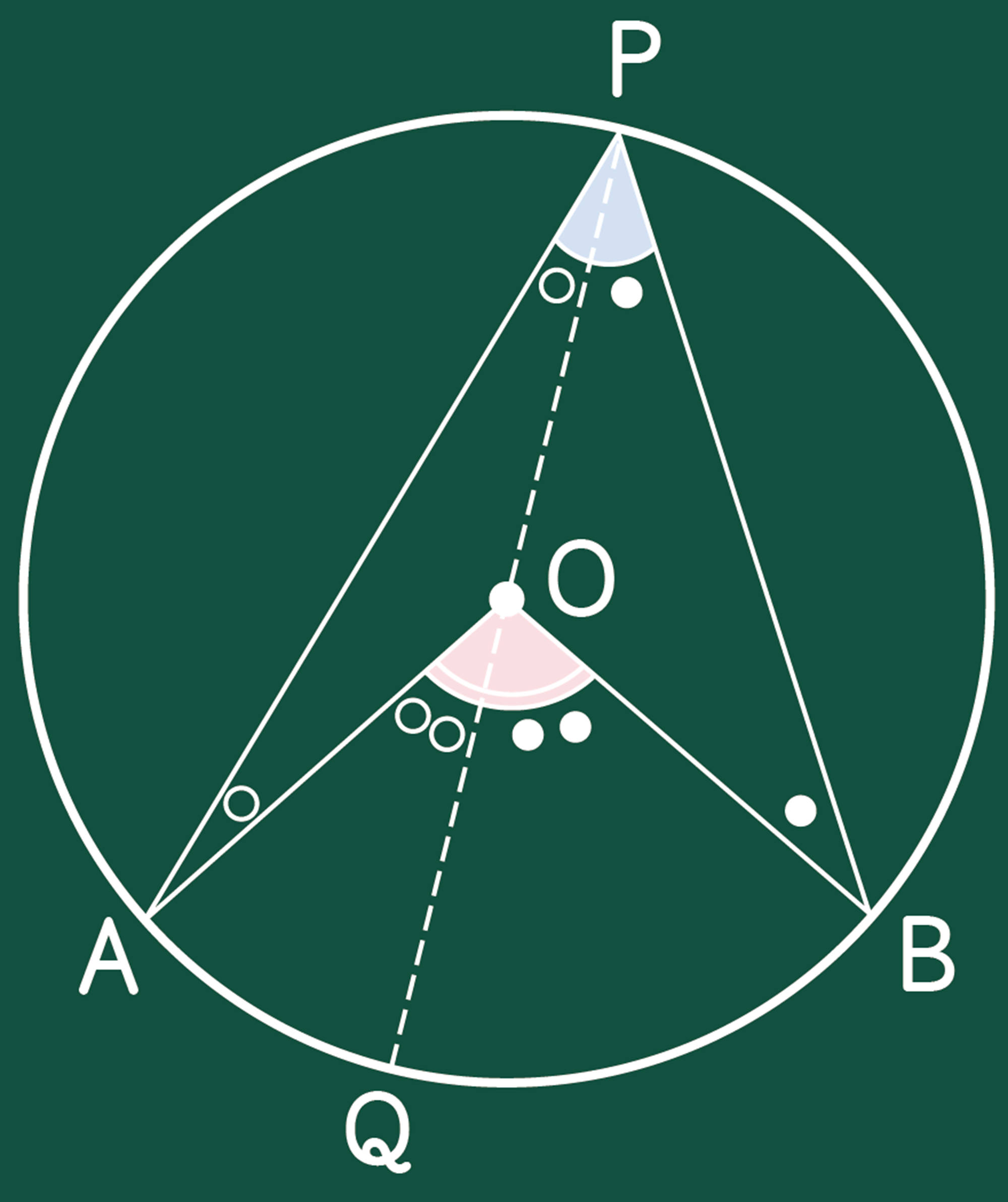
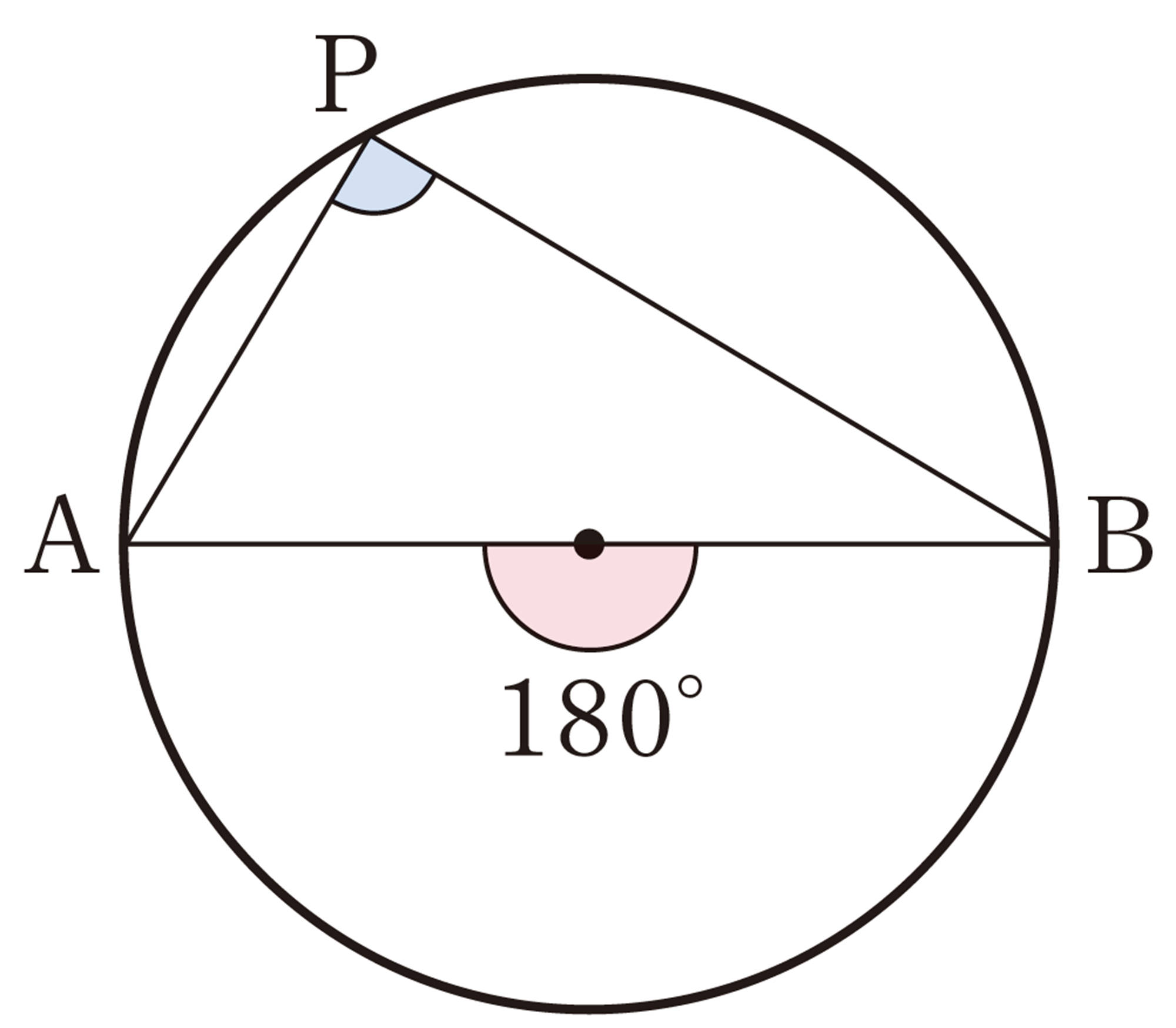
次の図のように，円Oの[mathjax]\(\stackrel{\huge\frown}{AB}\)を除いた円周上に点Pをとり，[mathjax]\(\angle APB\)をつくります。点Pの位置をいろいろ変えて，[mathjax]\(\angle APB\)の大きさを調べてみましょう。
見方・考え方
点Pをいろいろな位置にとって，どんなきまりがあるか見つけられるかな。
点Pの位置がどこでも[mathjax]\(\angle APB\)は同じ角度になるといえるのかな。
右の図のように，円Oの[mathjax]\(\stackrel{\huge\frown}{AB}\)に対して，[mathjax]\(\stackrel{\huge\frown}{AB}\)を除いた円周上に点Pをとるとき，[mathjax]\(\angle APB\)を[mathjax]\(\stackrel{\huge\frown}{AB}\)に対する円周角という。
目標 ▷ 円周角について調べよう。
円周角と中心角
問 １ 適当な半径の円Oをかき，中心角[mathjax]\(\angle AOB\)の大きさを決め，[mathjax]\(\stackrel{\huge\frown}{AB}\)を除いた円周上に点Pをとったときの円周角[mathjax]\(\angle APB\)の大きさを調べなさい。また，その結果から，円周角と中心角の間にはどんな関係があるかを予想しなさい。
中心角が[mathjax]\(180^{\circ}\)や[mathjax]\(180^{\circ}\)より大きい場合も調べてみよう。
<3年p.191>
前ページのQや問1から，[mathjax]\(\stackrel{\huge\frown}{AB}\)に対する円周角[mathjax]\(\angle APB\)の大きさは一定で，その弧に対する中心角[mathjax]\(\angle AOB\)の半分であることが予想できる。
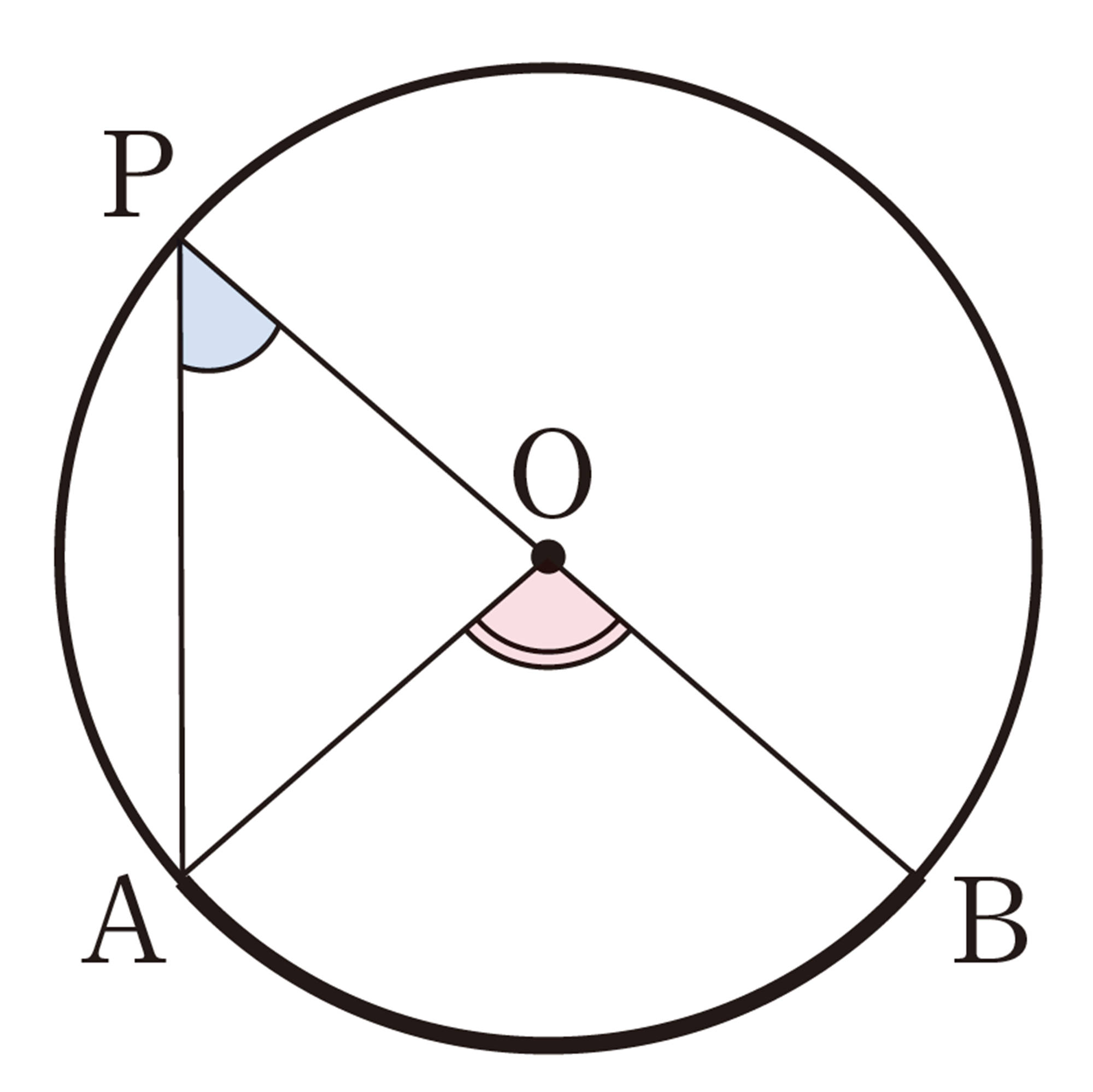
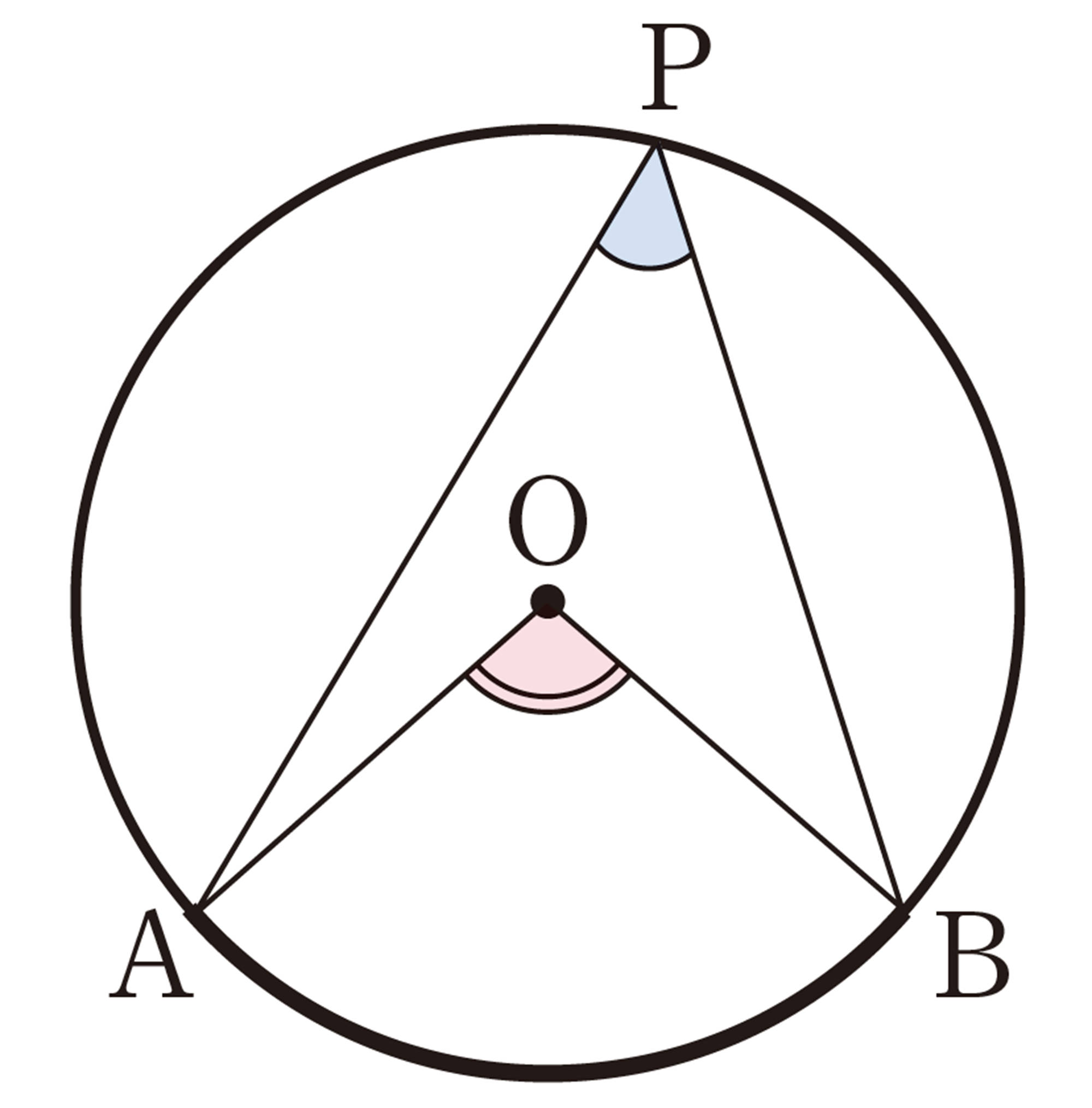
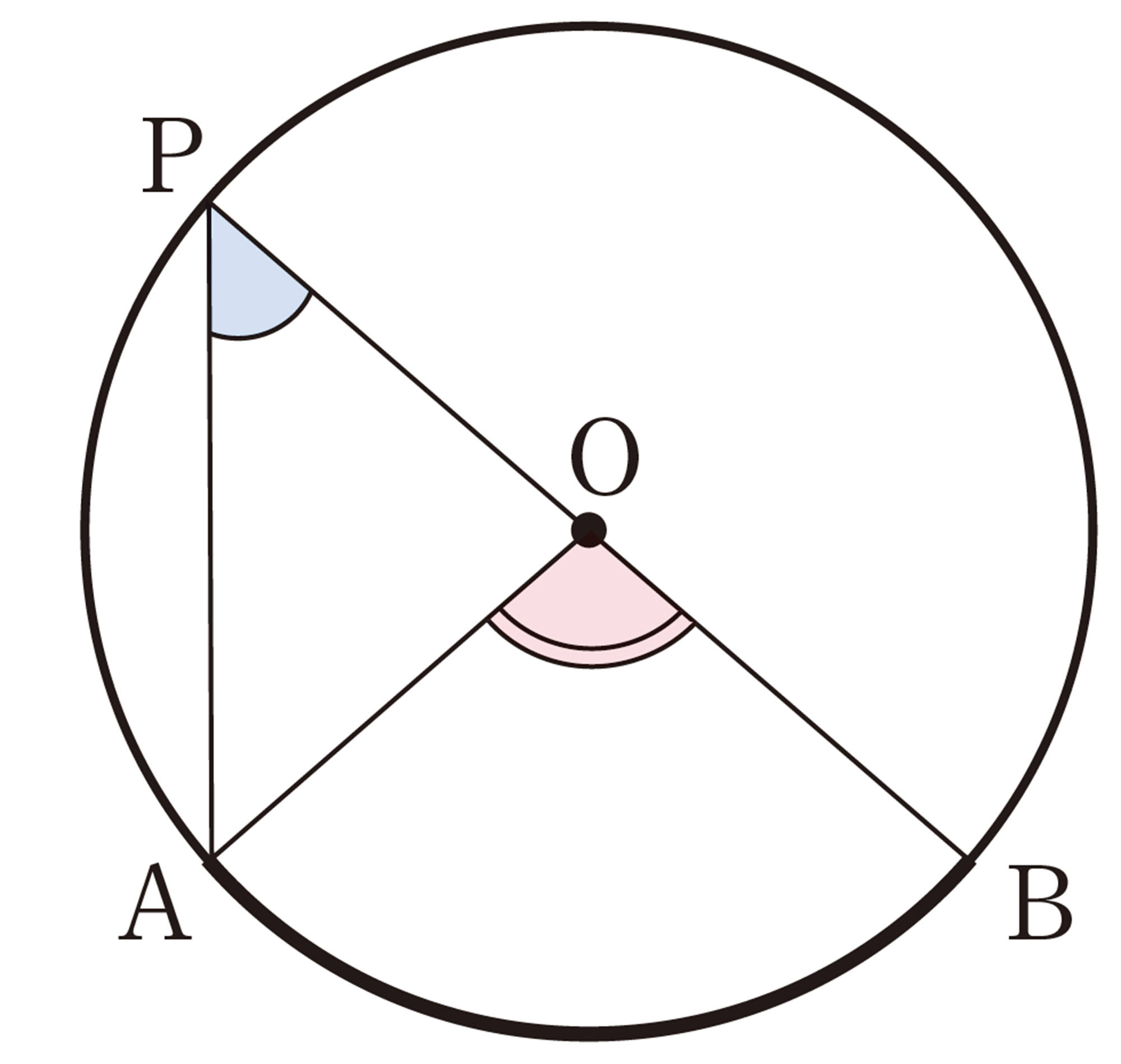
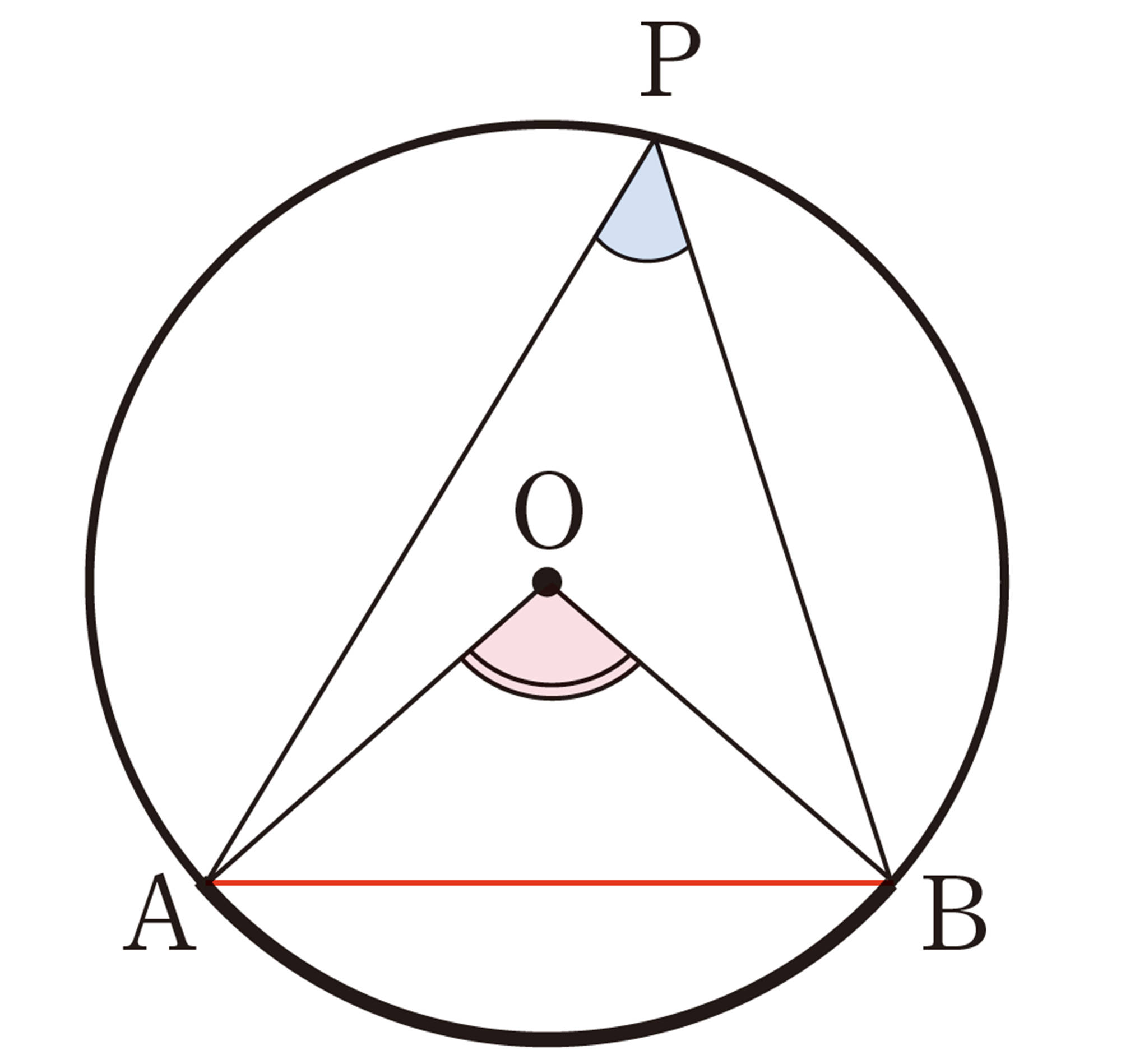
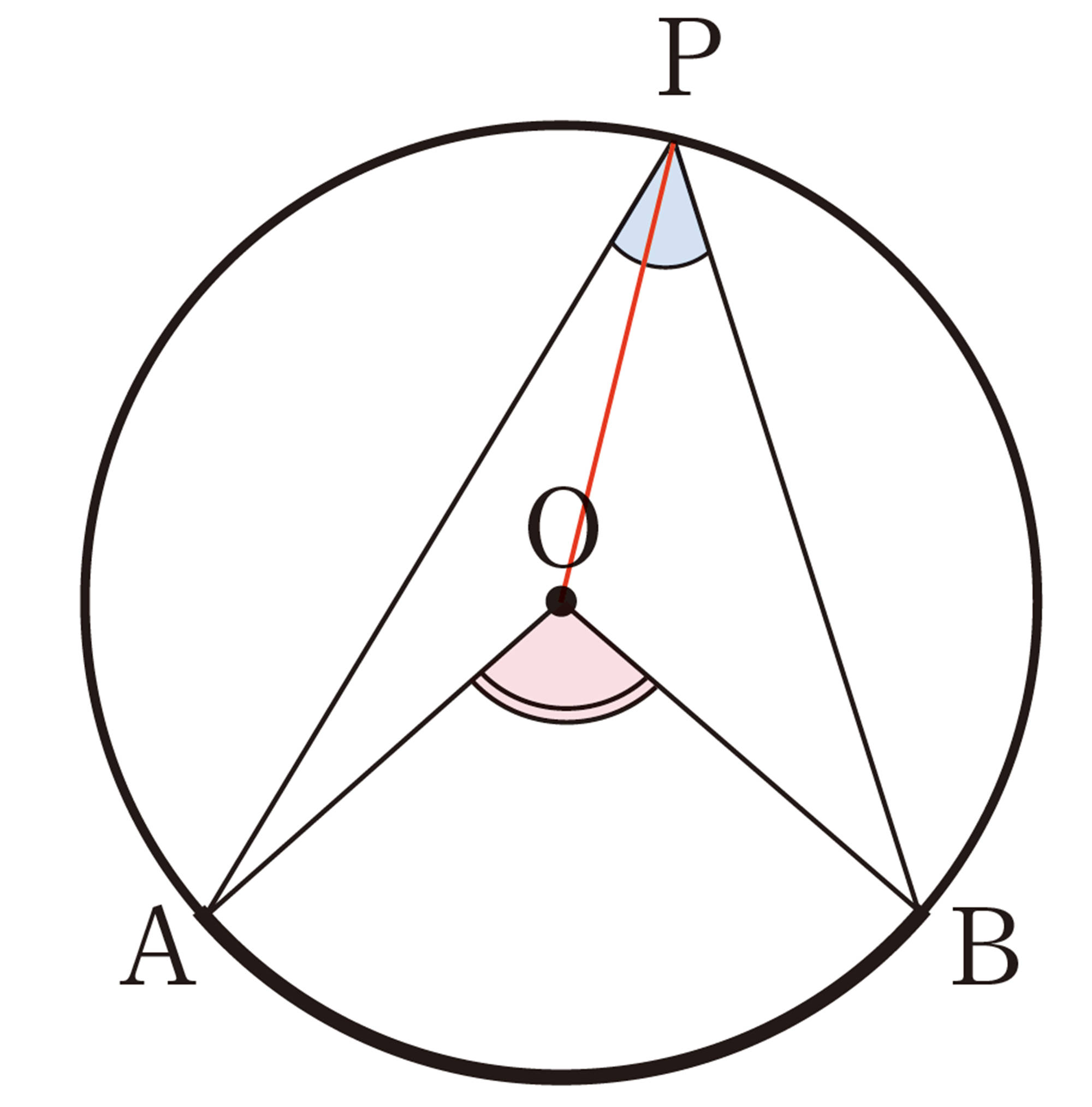
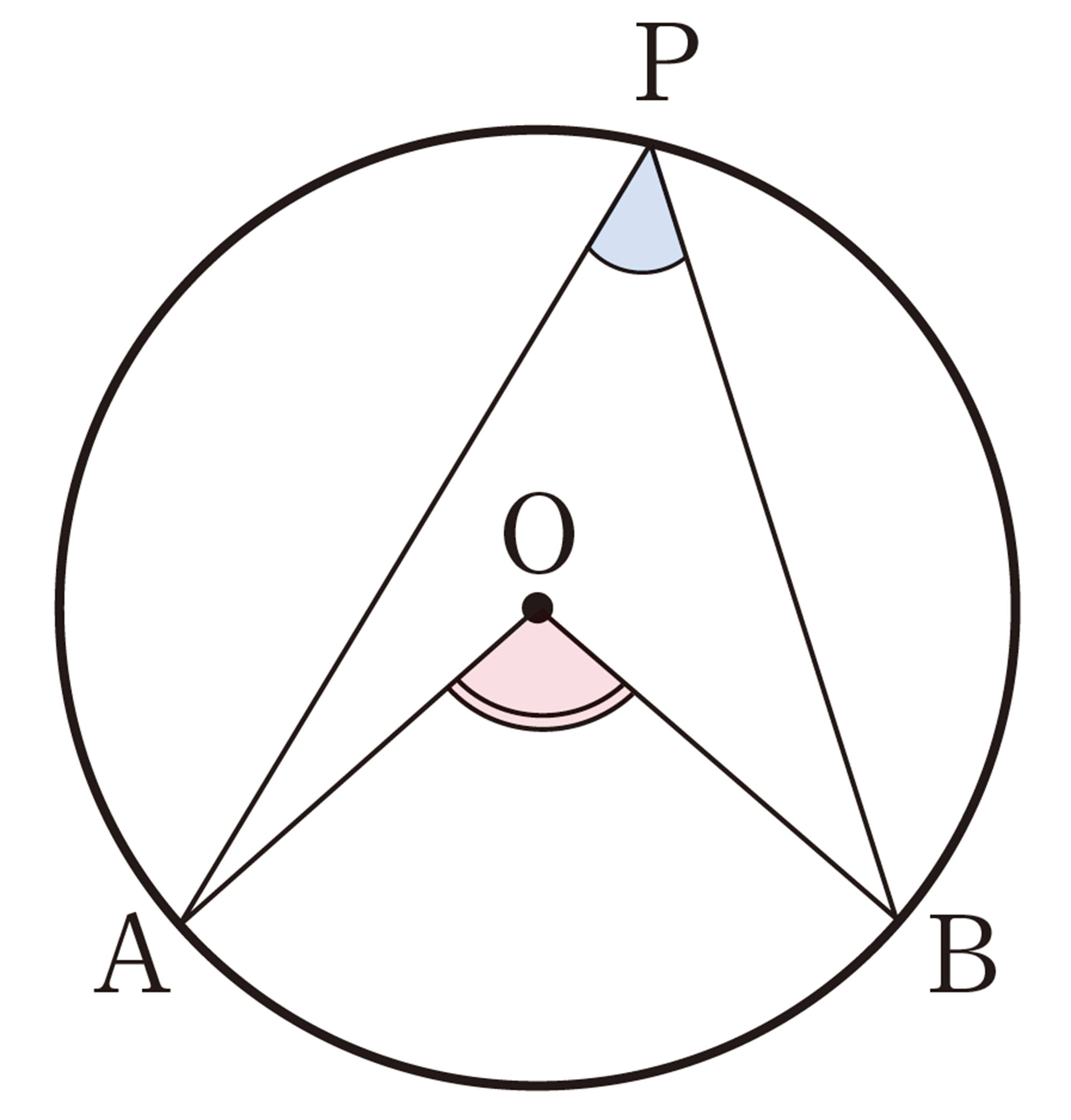
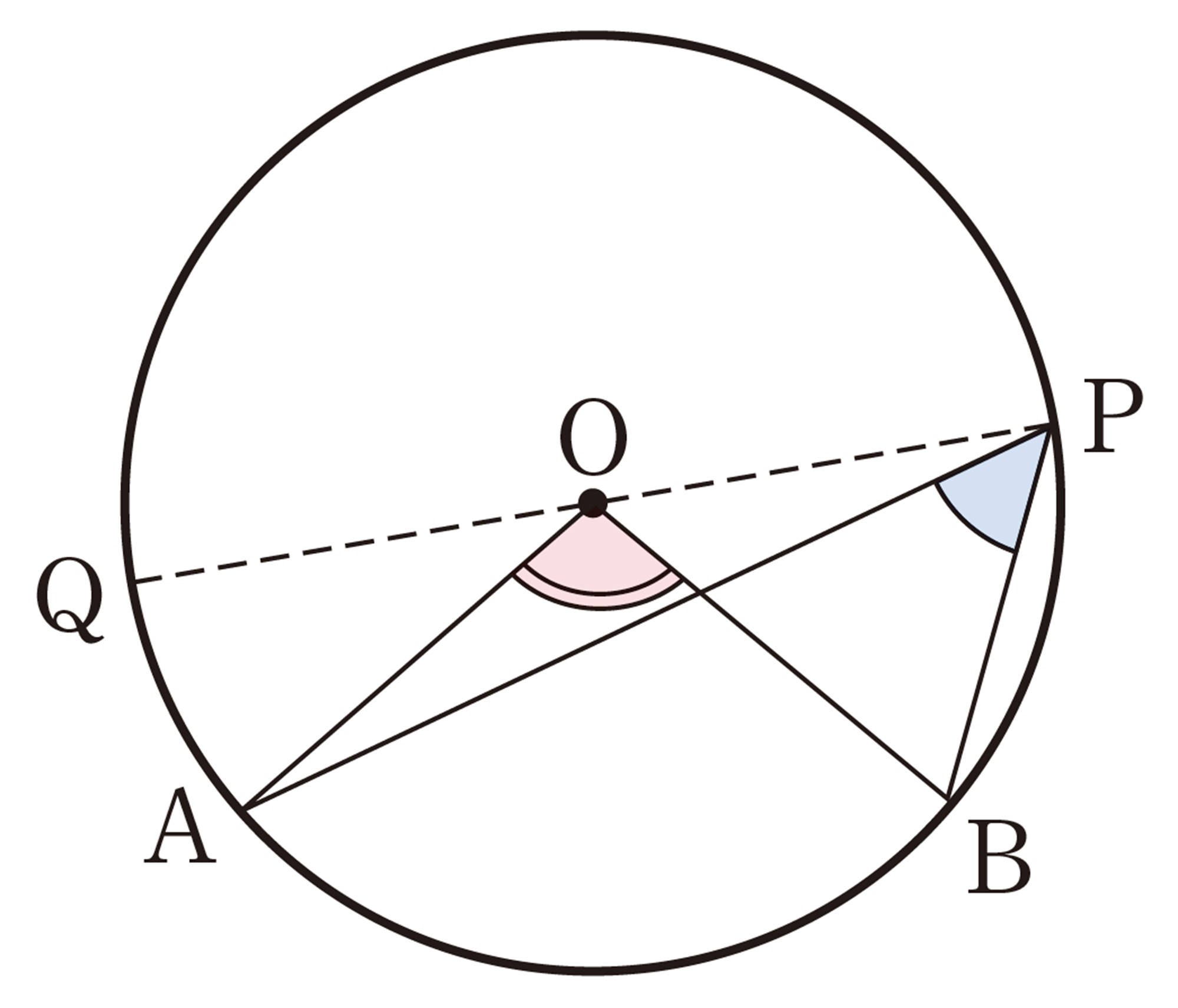
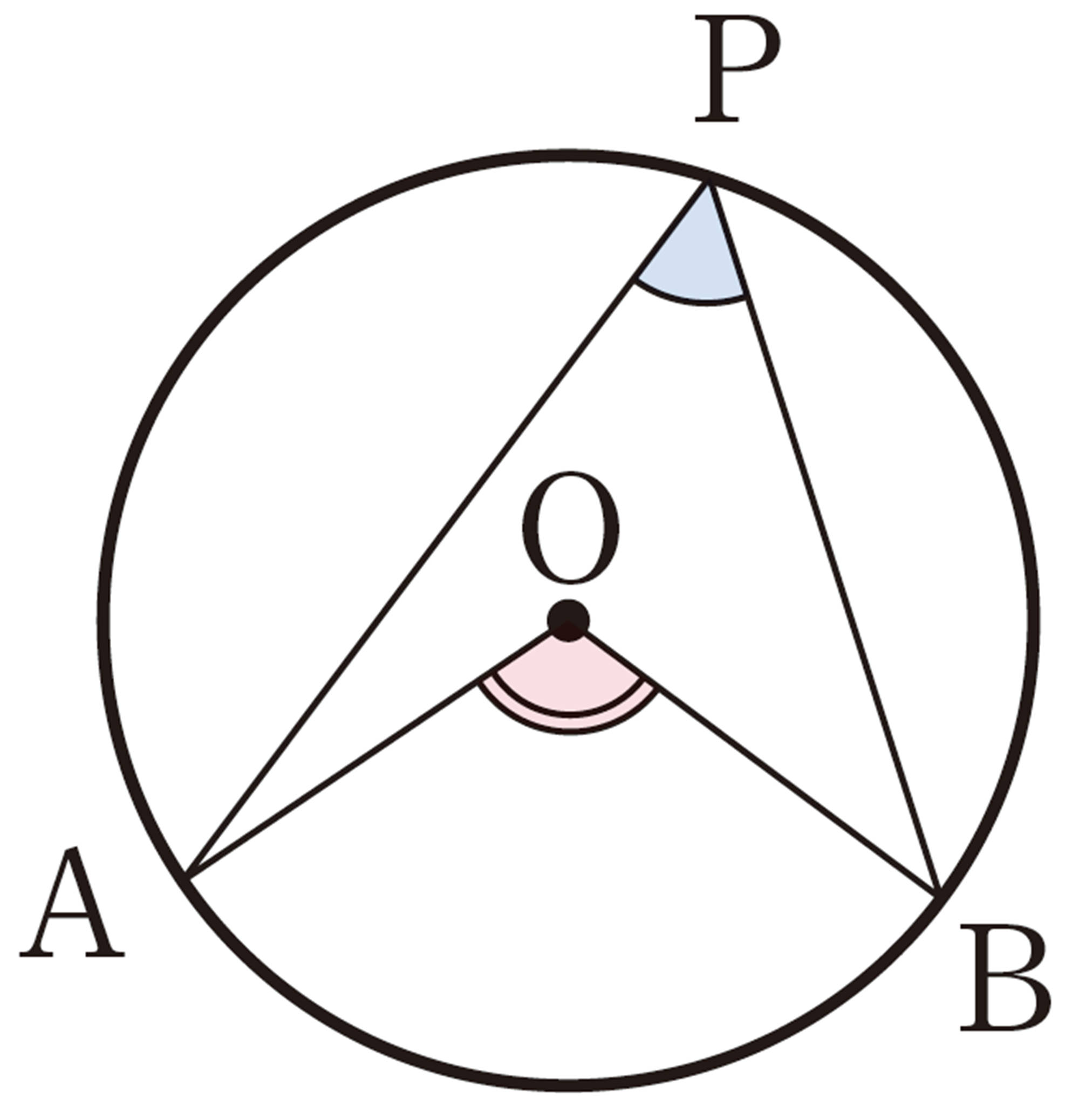
円周角[mathjax]\(\angle APB\)と中心角[mathjax]\(\angle AOB\)の位置関係は，次の図のように，3つの場合に分けることができる。
㋐ 中心Oが[mathjax]\(\angle APB\)の辺上にある。
㋑ 中心Oが[mathjax]\(\angle APB\)の内部にある。
㋒ 中心Oが[mathjax]\(\angle APB\)の外部にある。
上の㋐，㋑，㋒のそれぞれの場合について，[mathjax]\(\angle APB = \dfrac{1}{2} \angle AOB\)であることが証明できれば，[mathjax]\(\angle AOB\)は一定なので，[mathjax]\(\stackrel{\huge\frown}{AB}\)に対する円周角 [mathjax]\(\angle APB\) の大きさはすべて等しいことが証明されたことになる。
最初に，中心Oが[mathjax]\(\angle APB\)の辺上にある特別な場合の㋐から考えてみよう。 [mathjax]\(\angle APB = \dfrac{1}{2} \angle AOB\)を証明するには，どのようにすればよいだろうか。
[mathjax]\(\triangle OPA\)に着目したらどうかな。
三角形の内角と外角についての性質が使えそうだね。
三角形の内角や外角について，2年で学習したね。
[mathjax]\(\angle OPA + \angle OAP = \angle AOB\)になるけど，このあとはどうすればいいのかな。
問 ２ 上の㋐の場合について，次のことを証明しなさい。
[mathjax]\(\angle APB = \dfrac{1}{2} \angle AOB\)
<3年p.192>
次に，前ページの㋑の場合について，考えてみよう。
[mathjax]\(\angle APB = \dfrac{1}{2} \angle AOB\)を証明するには，どのようにすればよいだろうか。
これまでにわかっていることを使って，考えられるといいね。
問2で証明した，特別な場合の㋐の証明が使えないかな。
でも，このままだと㋐の場合の証明は，使えないよ。
補助線を引いたら，どうかな。
なぜ，補助線を引くの？
補助線を引くことで，㋐の場合の証明が使えるようになるかもしれないから。
なるほど，㋐の場合の証明が使えるようにするために，補助線を引くんだね。
どんな補助線を引けばいいかな。
点AとBを直線で結んだらどうかな。
それだと，㋐の場合の図が見えないね。
点PとOを直線で結んだらどうかな。
それでも，㋐の場合の図が見えないね。
補助線を引いて，特別な場合の㋐の証明を活用して証明してみよう。
<3年p.193>
問 ３ 191ページの㋑の場合について，次のように，[mathjax]\(\angle APB = \dfrac{1}{2} \angle AOB\)であることを証明しました。[mathjax]\(\boxed{\phantom{000}}\)をうめて，証明を完成させなさい。
［証明］
点Pを通る直径PQを引き，
[mathjax]\(\angle APQ = \angle a\)とする。
[mathjax]\(\triangle OPA\)は二等辺三角形であるから，
[mathjax]\(\hspace{40pt}\angle OPA = \angle \boxed{\phantom{0000}} = \angle a\)
[mathjax]\(\angle AOQ\)は [mathjax]\(\triangle OPA\)の外角であるから，
[mathjax]\(\angle BPQ = \angle b\)とすると，同様にして，
[mathjax]\(\hspace{43pt}\angle\boxed{\phantom{0000}} = 2 \angle b \quad \cdots \cdots\mathsf{②}\)
①，② から，
したがって，[mathjax]\(\angle APB = \dfrac{1}{2} \angle AOB\)
191ページの㋒の場合についても，問3と同じようにして，[mathjax]\(\angle APB ＝ \dfrac{1}{2} \angle AOB\)であることを証明することができる。
補助線PQを引くと，191ページの㋐の証明が利用できるね。
▲トライ 191ページの㋒の場合について，[mathjax]\(\angle APB ＝ \dfrac{1}{2} \angle AOB\)であることを証明してみよう。
<3年p.194>
これまで調べたことは，次のように定理としてまとめることができる。
定理
円周角の定理
❶ 1つの弧に対する円周角は，その弧に対する中心角の半分である。
[mathjax]\(\angle APB = \dfrac{1}{2} \angle AOB\)
❷ 1つの弧に対する円周角はすべて等しい。
[mathjax]\(\angle APB = \angle AQB\)
例 １ ある弧に対する中心角が[mathjax]\(180^{\circ}\)のとき，その弧に対する円周角の大きさは，[mathjax]\(90^{\circ}\)である。
円周角の定理の特別な場合として，次のことが成り立つ。
半円の弧に対する円周角は[mathjax]\(90^{\circ}\)である。
ターレスの定理と呼ばれているよ。
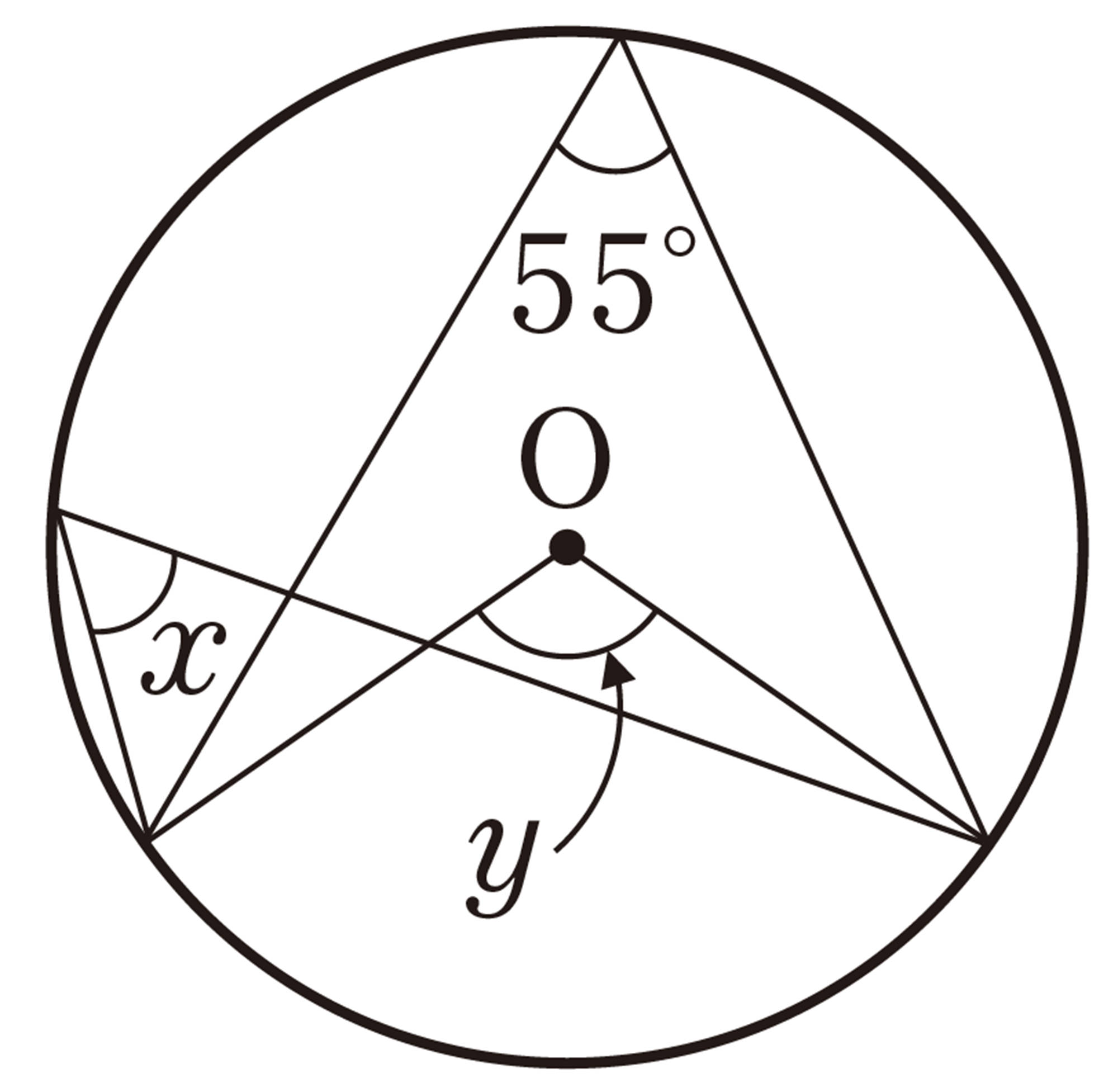
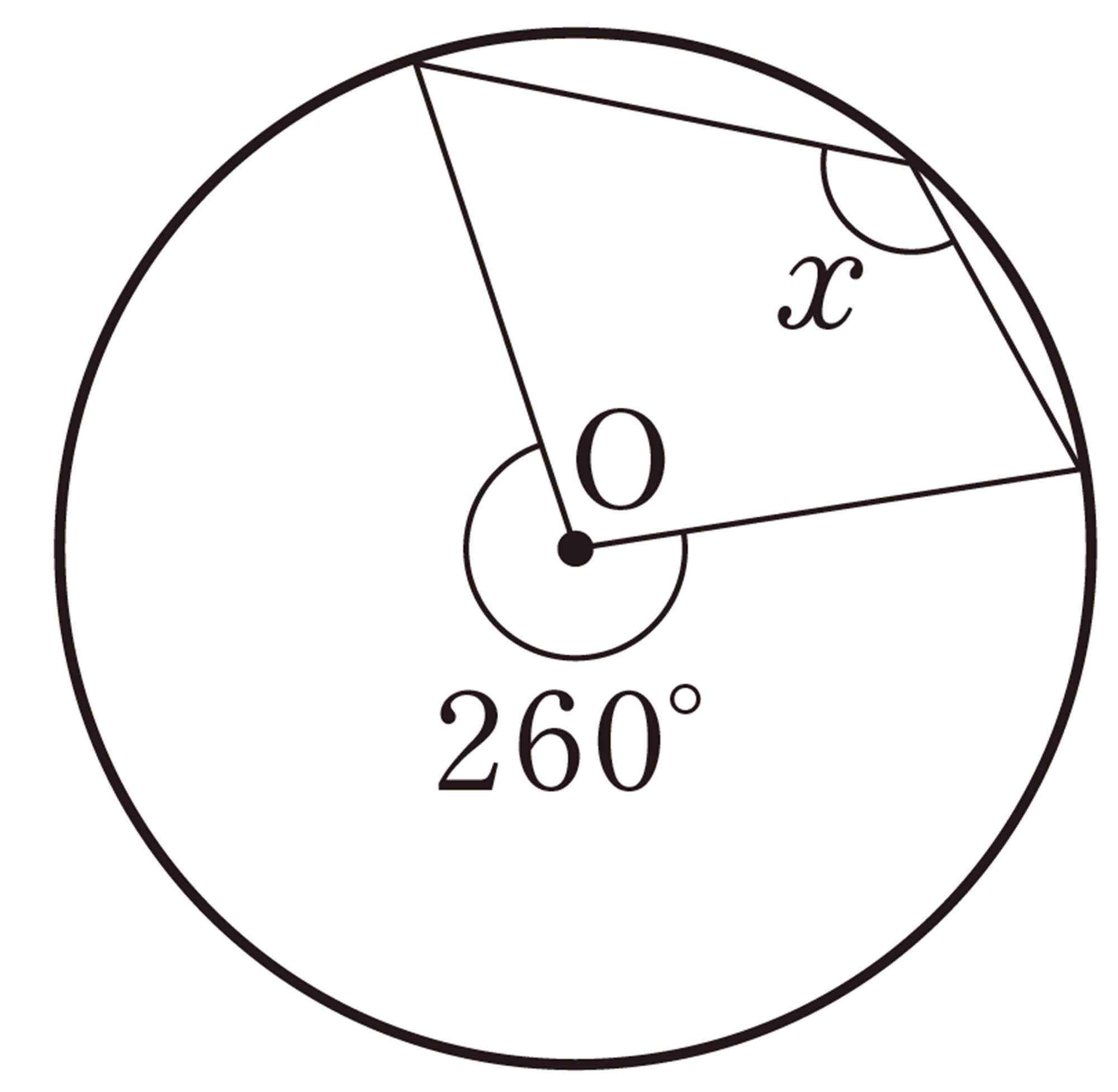
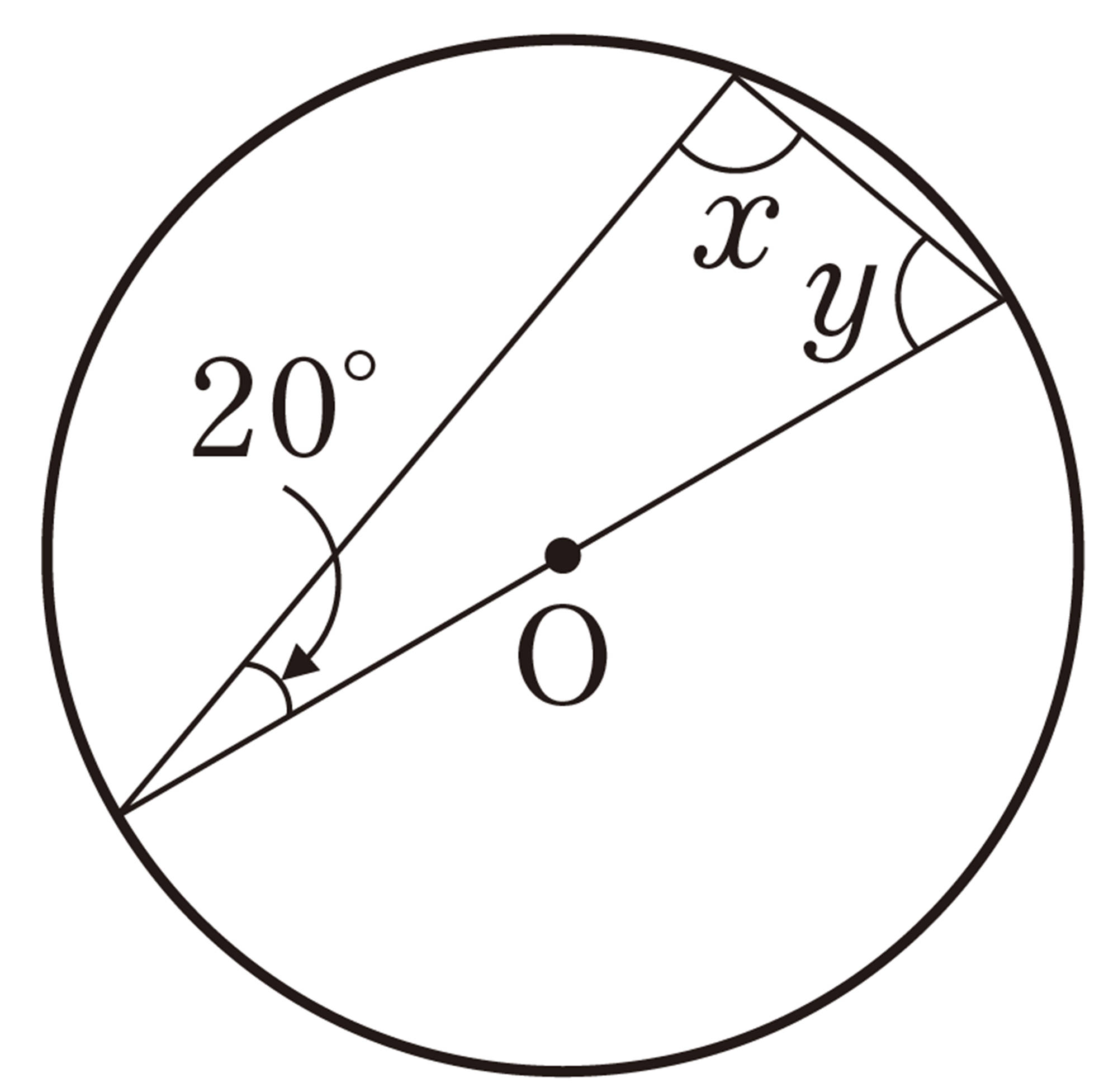
問 ４ 次の図で，[mathjax]\(\angle x\)，[mathjax]\(\angle y\)の大きさを求めなさい。
⑴
⑵
⑶
どんなことがわかったかな
円周角の定理が成り立つことから，いろいろな円周角や中心角を求めることができます。
次の課題へ！
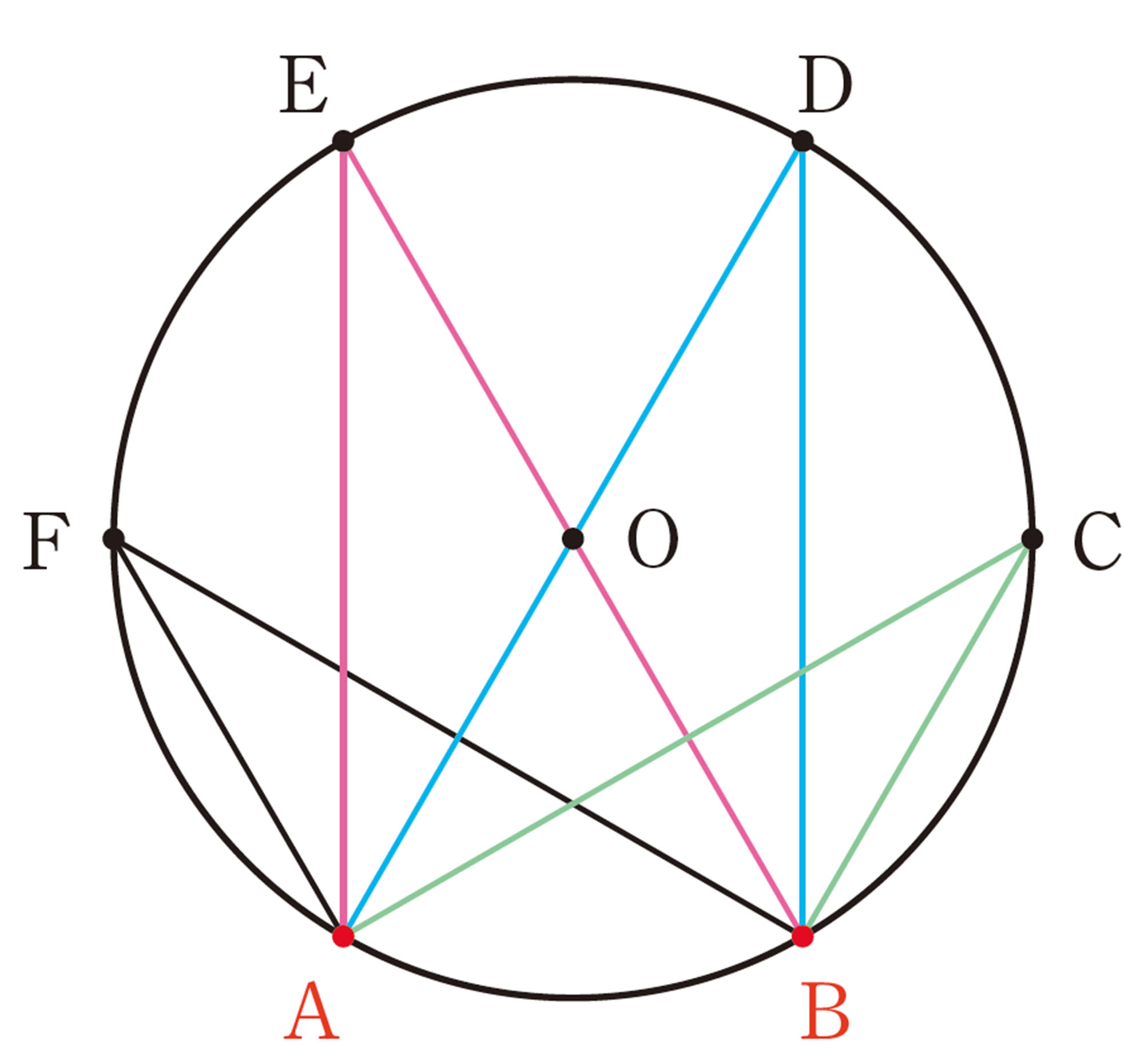
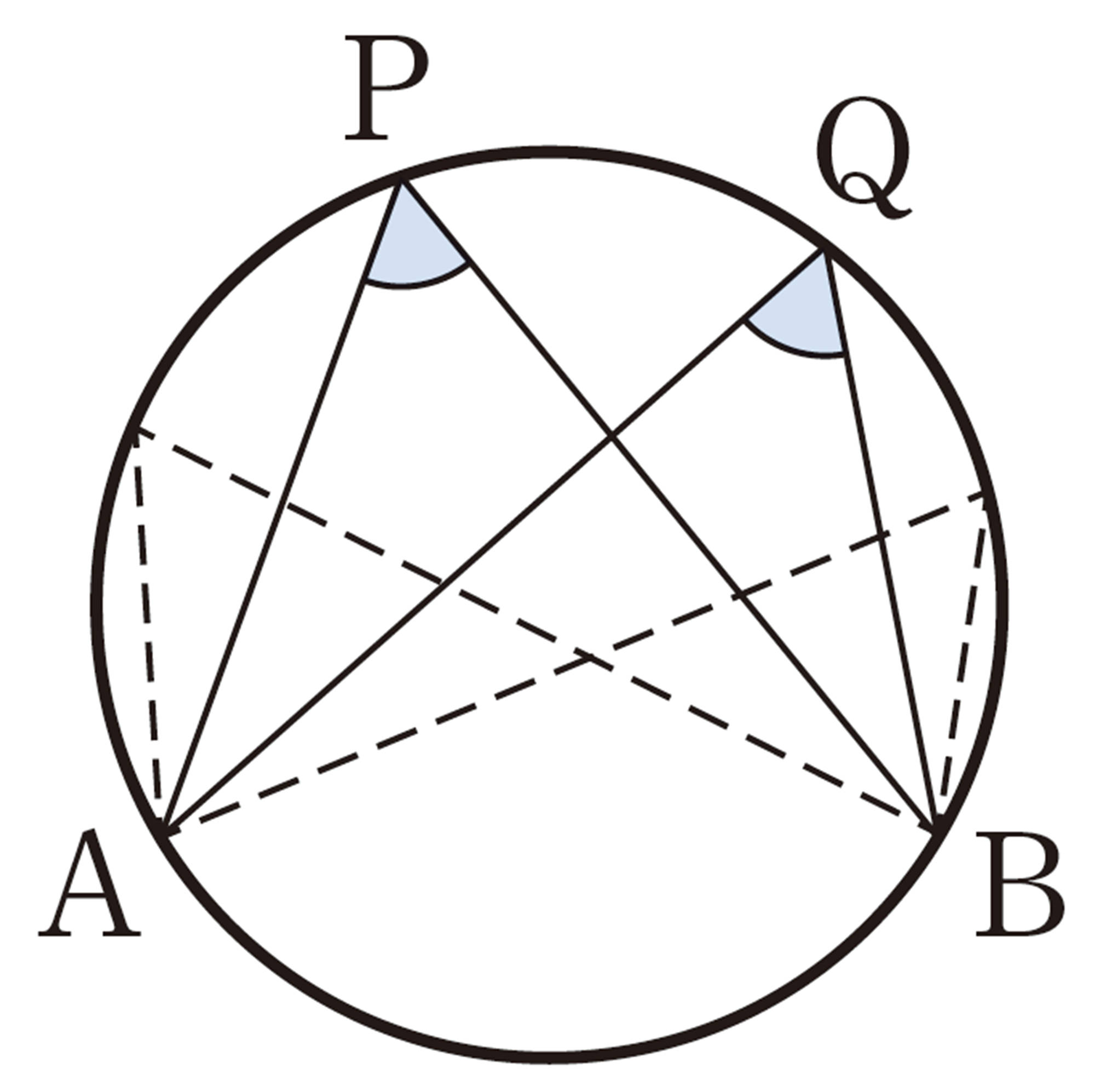
1つの円周上では，1つの弧ではなくても，弧の長さが等しければ，その円周角も等しくなるのかな？
P.195
