<3年p.177>
２ 相似な立体の表面積比と体積比
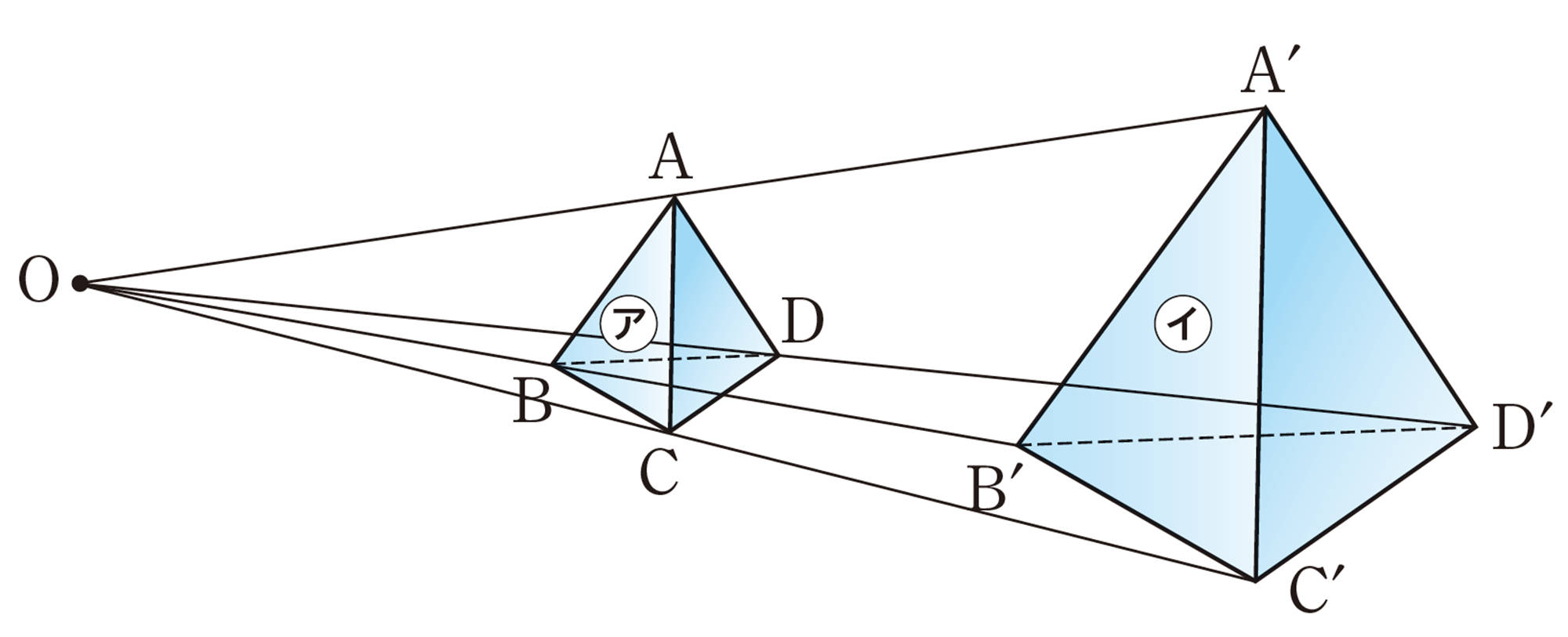
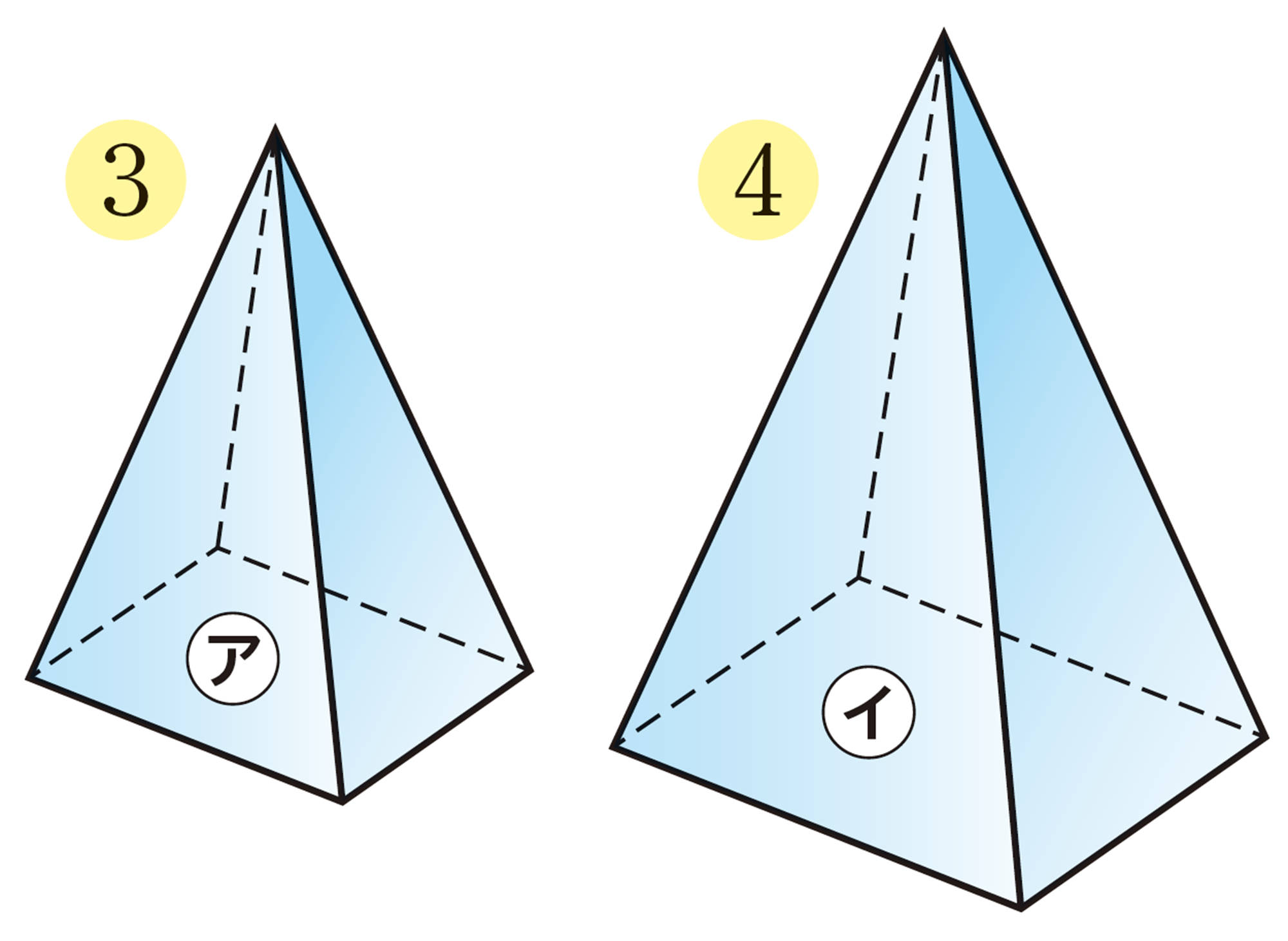
次の図で，三角錐㋑は，三角錐㋐を2倍に拡大したものであり，点Oを中心として，
[mathjax]\(OA´:OA=OB´:OB=OC´:OC=OD´:OD=2:1\)
となるように4点 [mathjax] \(A´\)，[mathjax] \(B´\)，[mathjax] \(C´\)，[mathjax] \(D´\)をとっている。
このように，1つの立体を一定の割合で拡大または縮小して得られる立体は，もとの立体と相似であるという。
相似な立体では，対応する線分の長さの比はすべて等しく，この比を相似比という。上の三角錐㋑と三角錐㋐の相似比は[mathjax]\(2:1\)である。
相似な立体では，対応する角の大きさもそれぞれ等しい。
問 １ 次の各組の立体は，つねに相似であるといえますか。
⑴ 2つの立方体
⑵ 2つの直方体
⑶ 2つの円錐
⑷ 2つの球
Q Question
立方体の1辺の長さを2倍，3倍にすると，表面積や体積は，それぞれ何倍になるでしょうか。また，そのことから，立体の相似比と表面積比，相似比と体積比の関係を予想してみましょう。
相似な立体の表面積比や体積比にも，相似な平面図形のような関係があるのかな。
見方・考え方
平面図形の相似の面積比を考えたときと同じように考えられるかな。
注意 表面積の比のことを表面積比，体積の比のことを体積比という。
<3年p.178>
目標 ▷ 2つの立体の表面積比や体積比を調べよう。
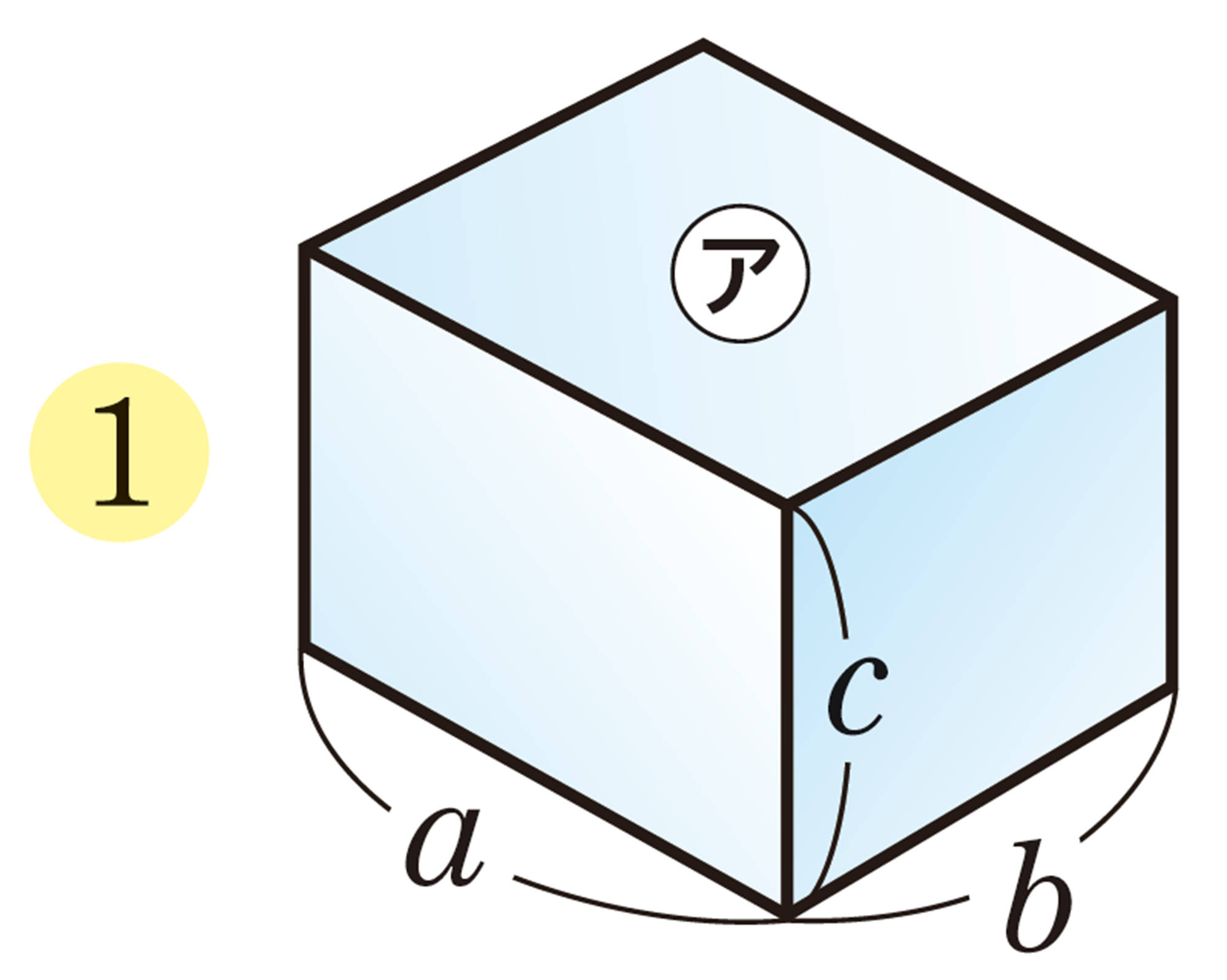
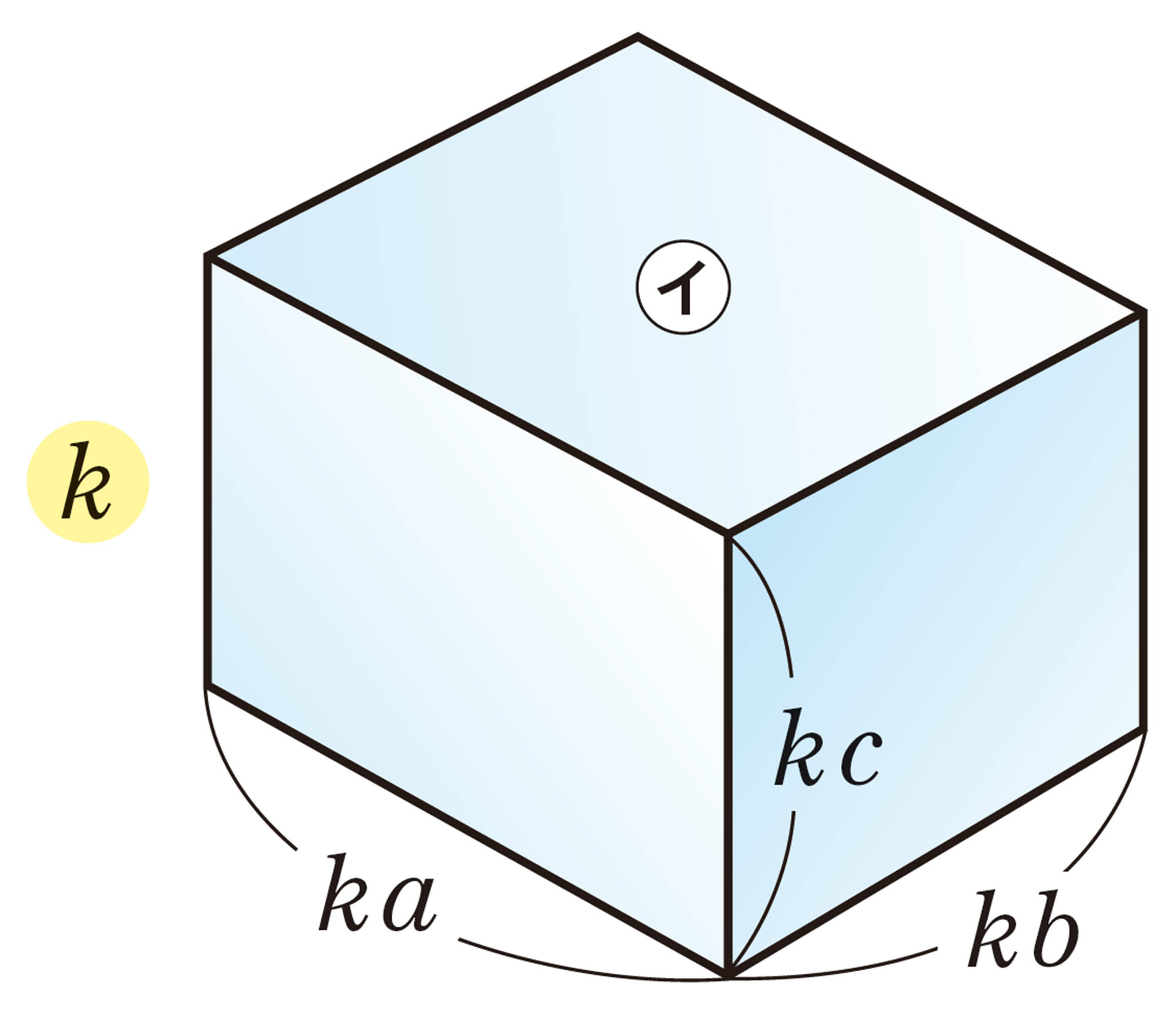
直方体㋐と直方体㋑が相似で，相似比が [mathjax]\(1:k\) であるとき，各辺の長さを右下の図のようにし，その表面積を[mathjax] \(S\)，[mathjax] \(S´\)，体積を[mathjax] \(V\)，[mathjax] \(V´\)とすると，
このように，相似な直方体では，対応する部分の長さがk倍になると，表面積は[mathjax] \(k²\)倍，体積は[mathjax] \(k³\)倍になることがわかる。
一般に，相似な立体の表面積や体積について，次の定理が成り立つ。
定理
相似な立体の表面積比と体積比
❶ 相似な立体の表面積比は，相似比の2乗に等しい。
❷ 相似な立体の体積比は，相似比の3乗に等しい。
すなわち，相似比が[mathjax]\(m:n\)ならば，
表面積比は[mathjax]\(m²:n²\)
体積比は[mathjax]\(m³:n³\) となる。
問 ２ 次の2つの図形の相似比，表面積比，体積比を求めなさい。
⑴ 半径がそれぞれ5cm，2cmの球
⑵ 底面の半径が5cmで高さが5cmの円柱と，底面の半径が2cmで高さが2cmの円柱
<3年p.179>
問 ３ 相似比が[mathjax]\(3:4\)の四角錐㋐と四角錐㋑について，次の問いに答えなさい。
⑴ ㋐の表面積が180cm²のとき，㋑の表面積を求めなさい。
⑵ ㋑の体積が256cm³のとき，㋐の体積を求めなさい。
例 １ 右の図のような，底面の直径が16cm，高さが24cmの円錐の形をした容器にコップで水を入れます。コップ1杯で12cmの高さまで水が入りました。このコップであと何杯水を入れれば，容器が満水になりますか。
考え方 容器の水が入っている部分と容器とは，相似になっている。その相似比をもとに体積比を考える。
解答
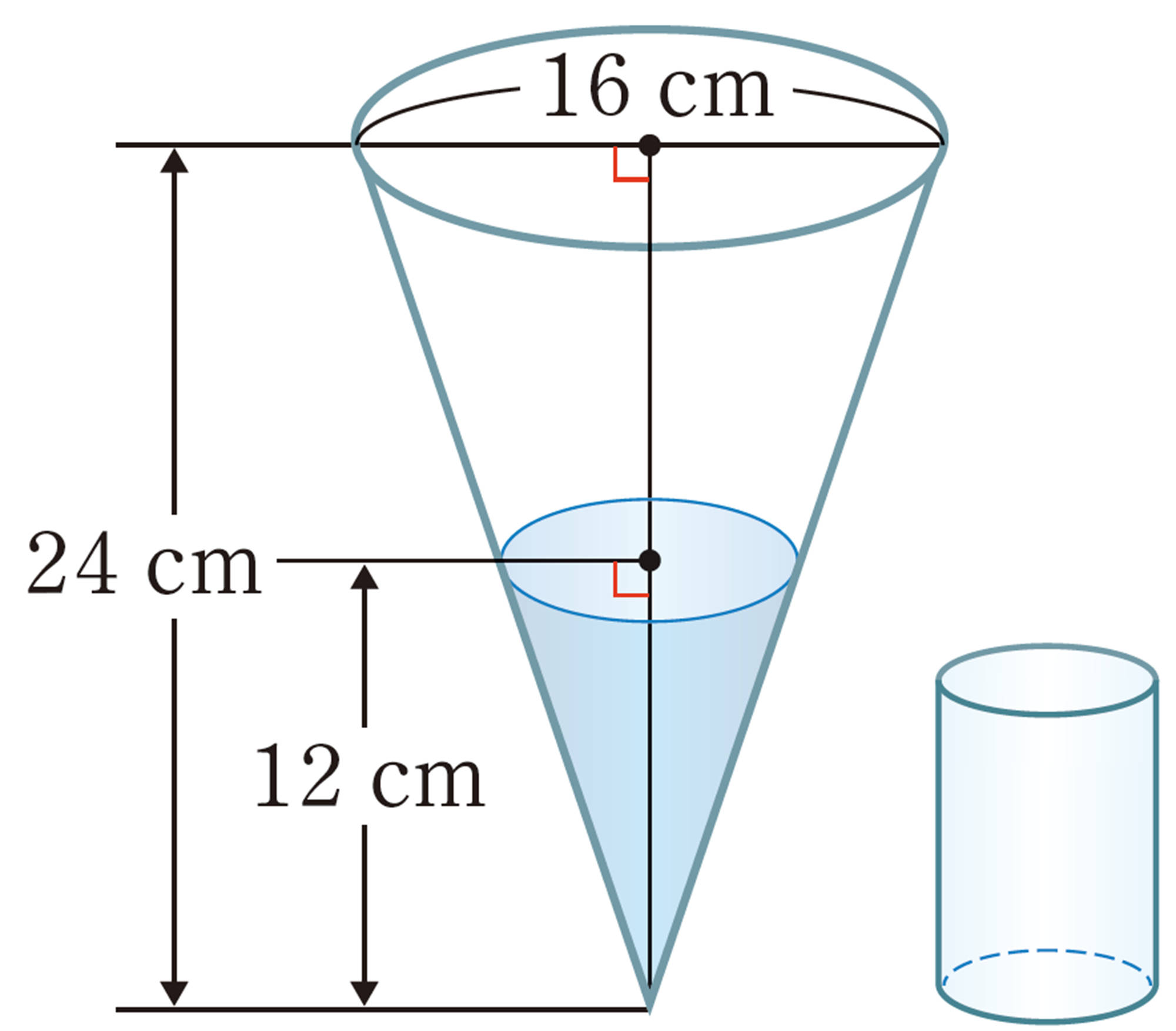
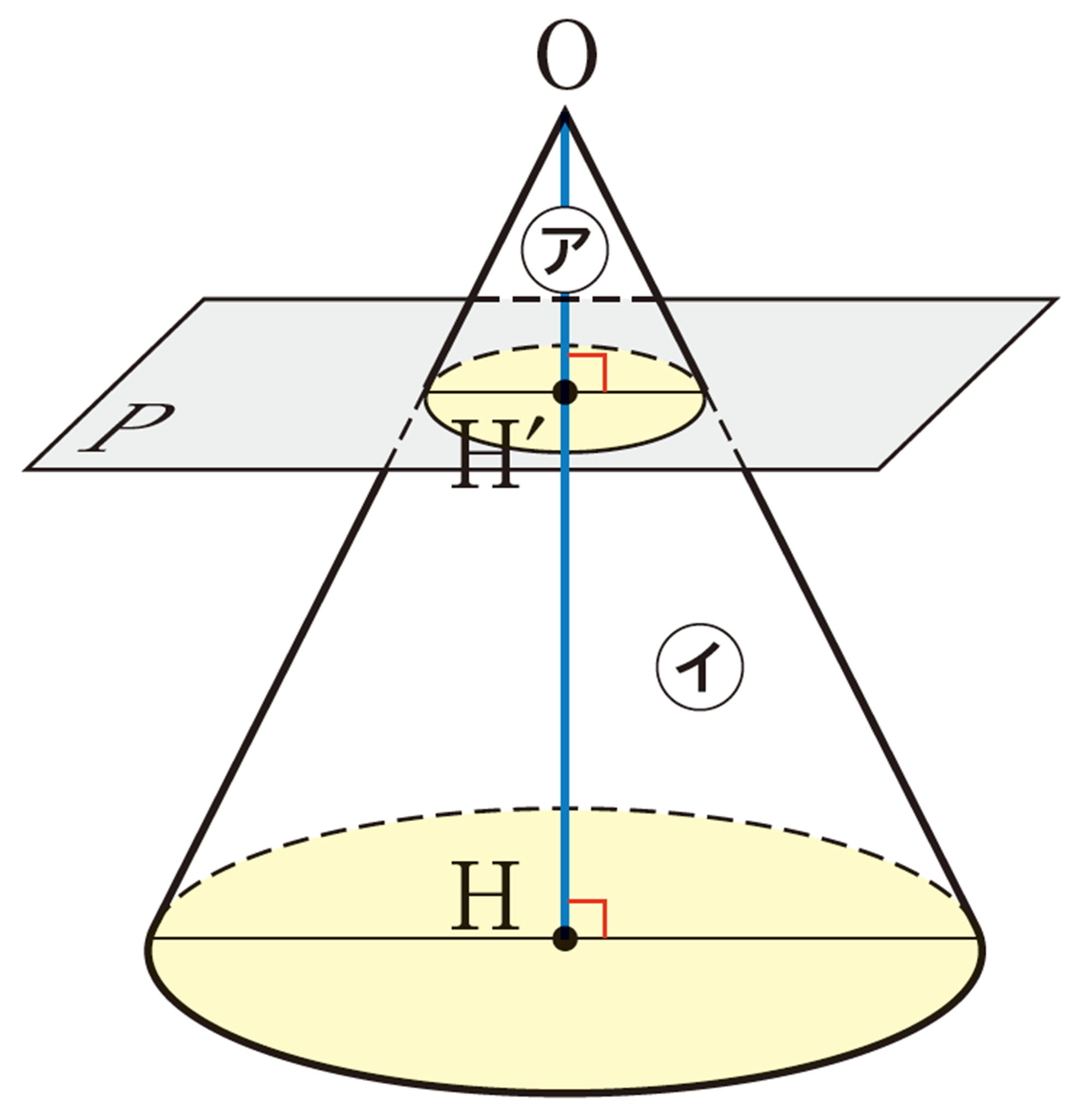
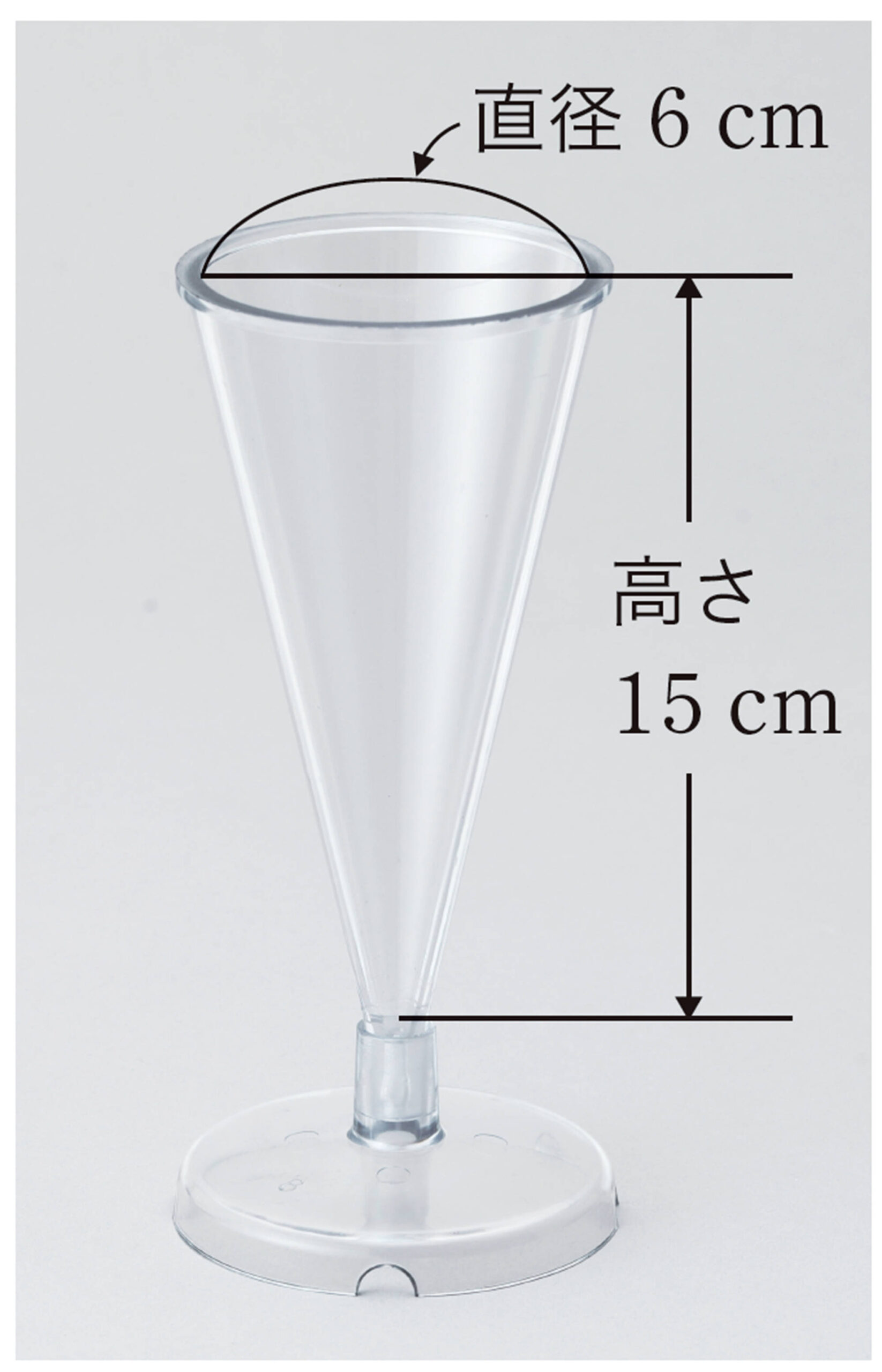
容器の水が入っている部分と容器とは， 相似になっている。
その相似比は，[mathjax] \(1:2\) であるから， 体積比は[mathjax] \(1³:2³=1:8\) である。
よって， 容器の容積は容器に入っている水の量の8 倍となる。
したがって，[mathjax] \(8-1=7\)
答 7 杯
問 ４
右の図の平面 P は円錐の底面に平行で，円錐の高さ OH を，
[mathjax]\(OH´:H´H=1:2\)
の比に分けています。このとき，平面Pで分けられる2つの部分㋐，㋑の体積比を求めなさい。
どんなことがわかったかな
相似な空間図形では，表面積比は相似比の2乗に，体積比は相似比の3乗になっていることをもとにして，相似な図形の表面積や体積を求めることができます。
<3年p.180>
身のまわりのものの体積 Tea Break
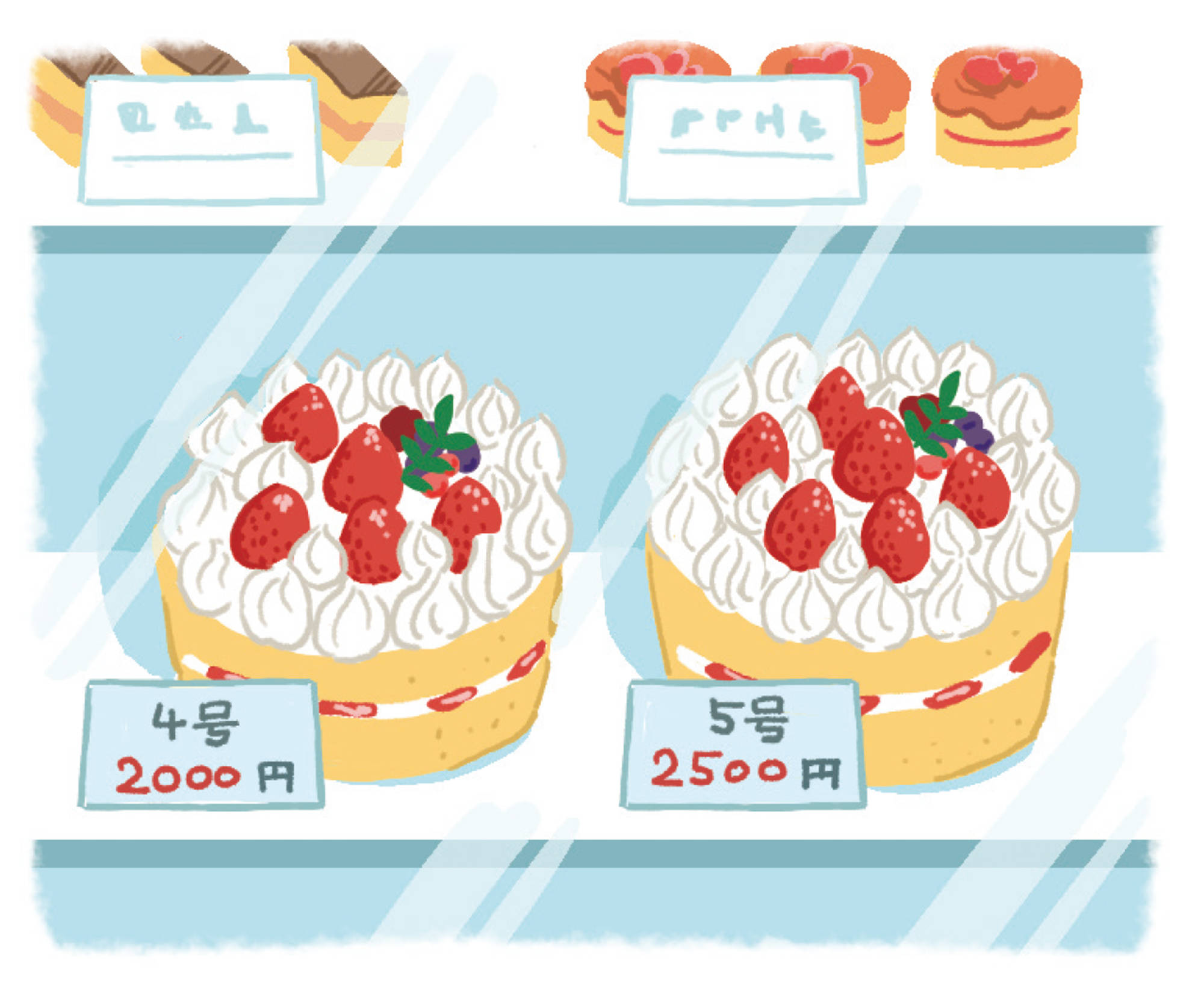
身のまわりのものの体積を，相似な図形の性質を利用して，考えてみましょう。
相似比で考えればいいね。4号と5号の直径の比は[mathjax]\(4:5\)，値段の比も[mathjax]\(4:5\)だから，どちらを買っても同じだね。
体積と値段の関係を比べないといけないから，体積比で考えるんだと思うけど，ちがうかな。
でも，どちらのケーキも高さは6cmで同じだよ。
この問題は，体積比を考えればいいね。
<3年p.181>
確かめよう 3節 相似な図形の面積比・体積比
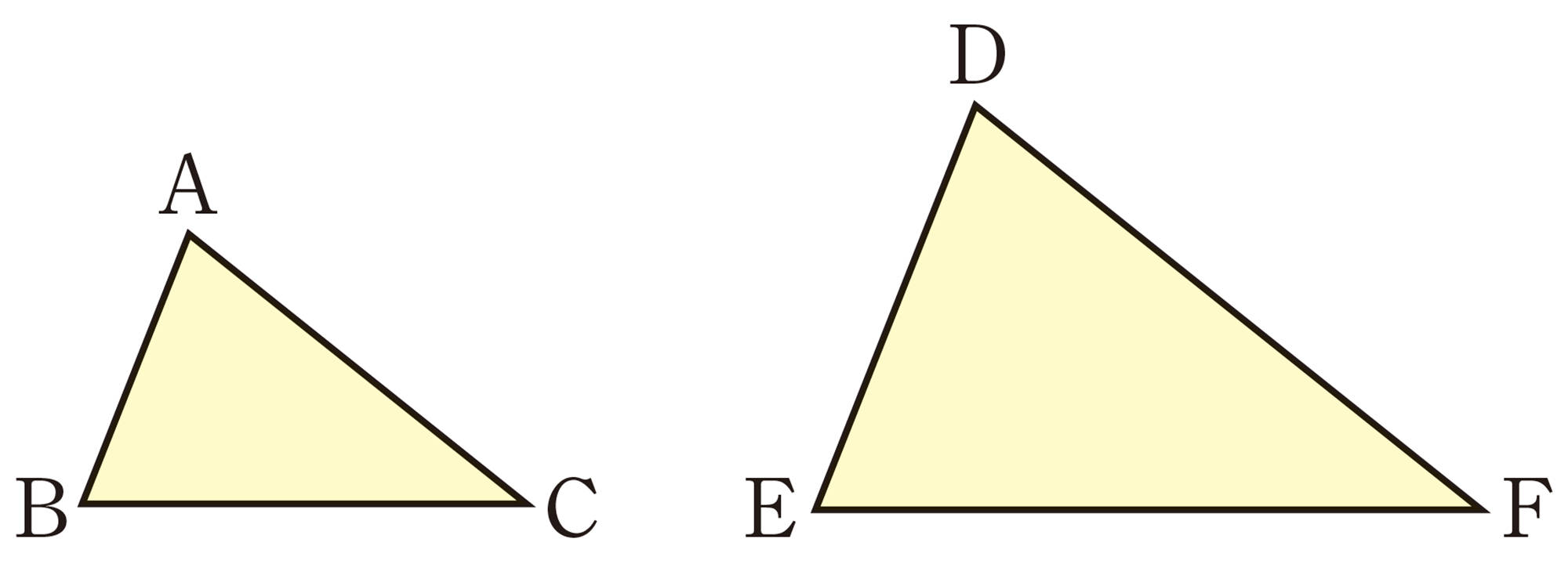
１ 相似比が[mathjax]\(2:3\)の[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle DEF\)があります。次の問いに答えなさい。
⑴ 2つの三角形の面積比を求めなさい。
⑵ [mathjax]\(\triangle ABC\)の面積が32cm²のとき，[mathjax]\(\triangle DEF\)の面積を求めなさい。
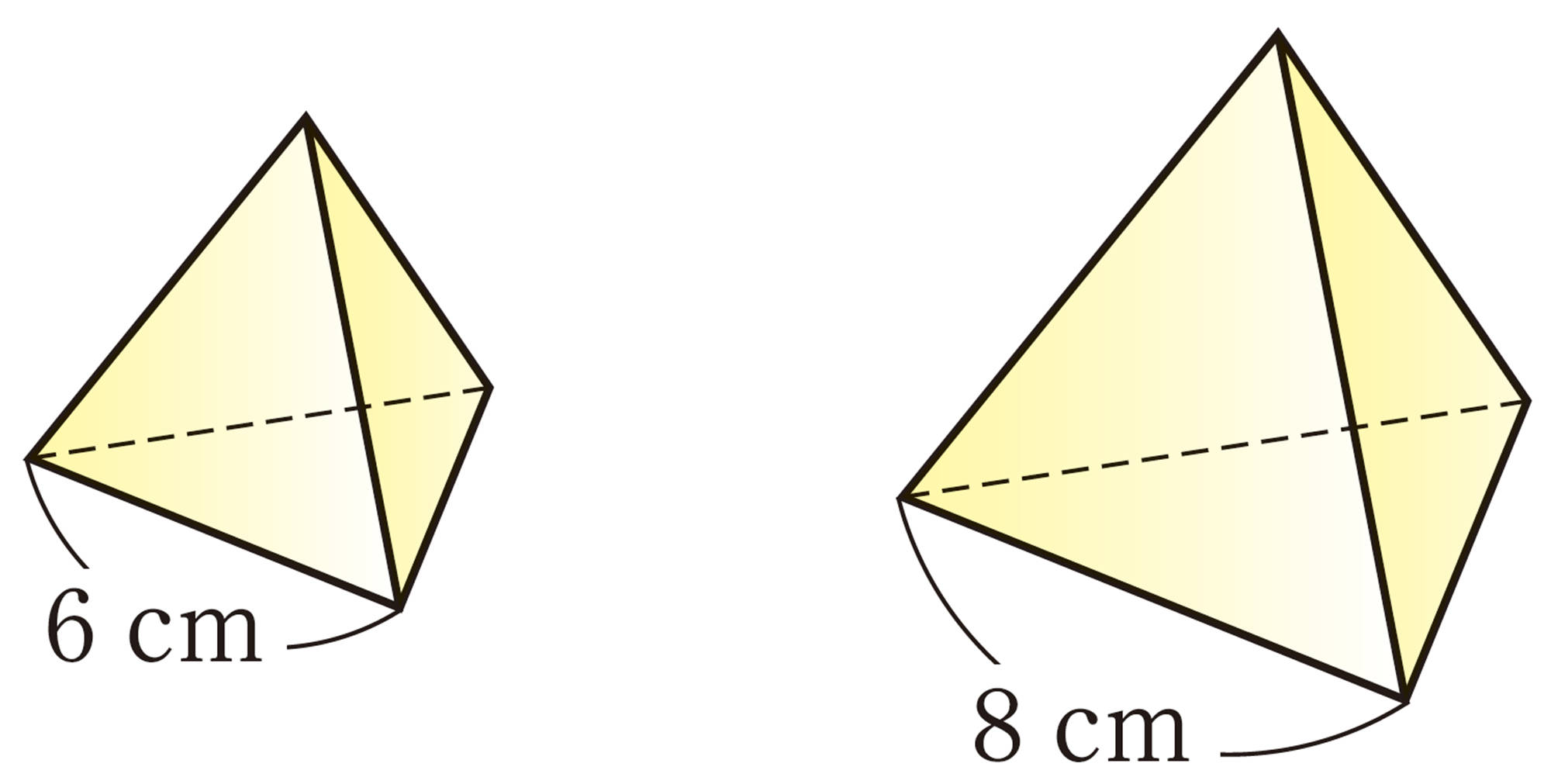
２ 2つの正四面体の1辺がそれぞれ6cm，8cmのとき，相似比，表面積比，体積比を求めなさい。
記号の由来「[mathjax]\(\equiv\)，[mathjax]\(\backsim\)」 Tea Break
合同や相似の記号を最初に使ったのは，ドイツのライプニッツ(1646〜1716)で，17世紀のことです。相似の記号[mathjax]\(\backsim\)は，ラテン語のsimilis(「似ている」の意味)の頭文字sを横にしたものといわれています。また，合同の記号[mathjax]\(\equiv\) は，次のようにして考案されました。
<3年p.182>
5章 「相似な図形」を学んで
できるようになったこと 身のまわりの課題へ ▷P.185
2つの図形が相似の位置にあるとき，その2つの図形は相似であり，その性質を調べることができる。
三角形の相似条件を理解して，図形の性質を証明することができる。
身のまわりや数学の中から見つけた問題を，相似な図形の考えを使って解決することができる。
平行線と線分の比の性質を，相似を使って見つけ，確かめることができる。
相似な図形の面積比，体積比は，それぞれ相似比の2乗，3乗になることを使って，いろいろな立体の表面積や体積を求めることができる。
さらに学んでみたいこと
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない デッサンと相似
デッサンをするとき，腕をのばし鉛筆を使ってデッサンするもの（対象物）の大きさを測ることがあります。
これは，対象物の大きさを測るときに，相似を利用しています。
右の図のように，対象物の一部（BC）を鉛筆で測りとると，目（A）は相似の中心となり，[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle AB´C´\)は，相似の位置にあります。この方法で必要な箇所の長さを測りとってデッサンすることにより，それぞれの測りとった箇所の相似比はすべて等しくなり，正確なデッサンをかくことができます。
関連 美術科
