<3年p.173>
3節 相似な図形の面積比・体積比
辺の長さが2倍になると,面積も2倍になる?
右の図は,[mathjax]\(\triangle ABC \backsim \triangle DEF\)で,相似比は[mathjax]\(1:2\)です。
【1】 上の図で,[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle DEF\)の面積比はどうなっているか考えてみましょう。
注意 面積の比のことを面積比という。

相似比が[mathjax]\(1:2\)だから,面積比も[mathjax]\(1:2\)だと思う。
図を見ると,2倍よりも,もっと大きくなっているみたい。

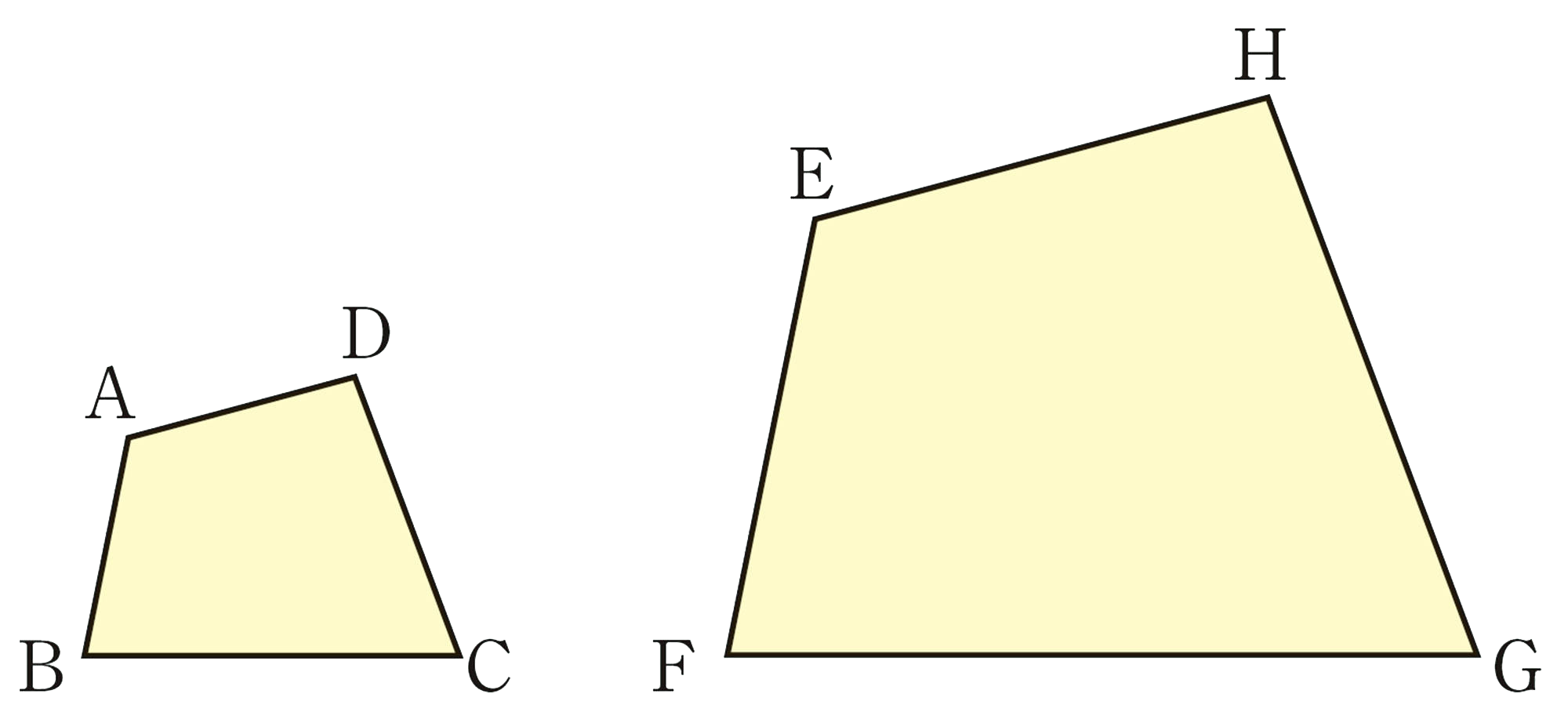
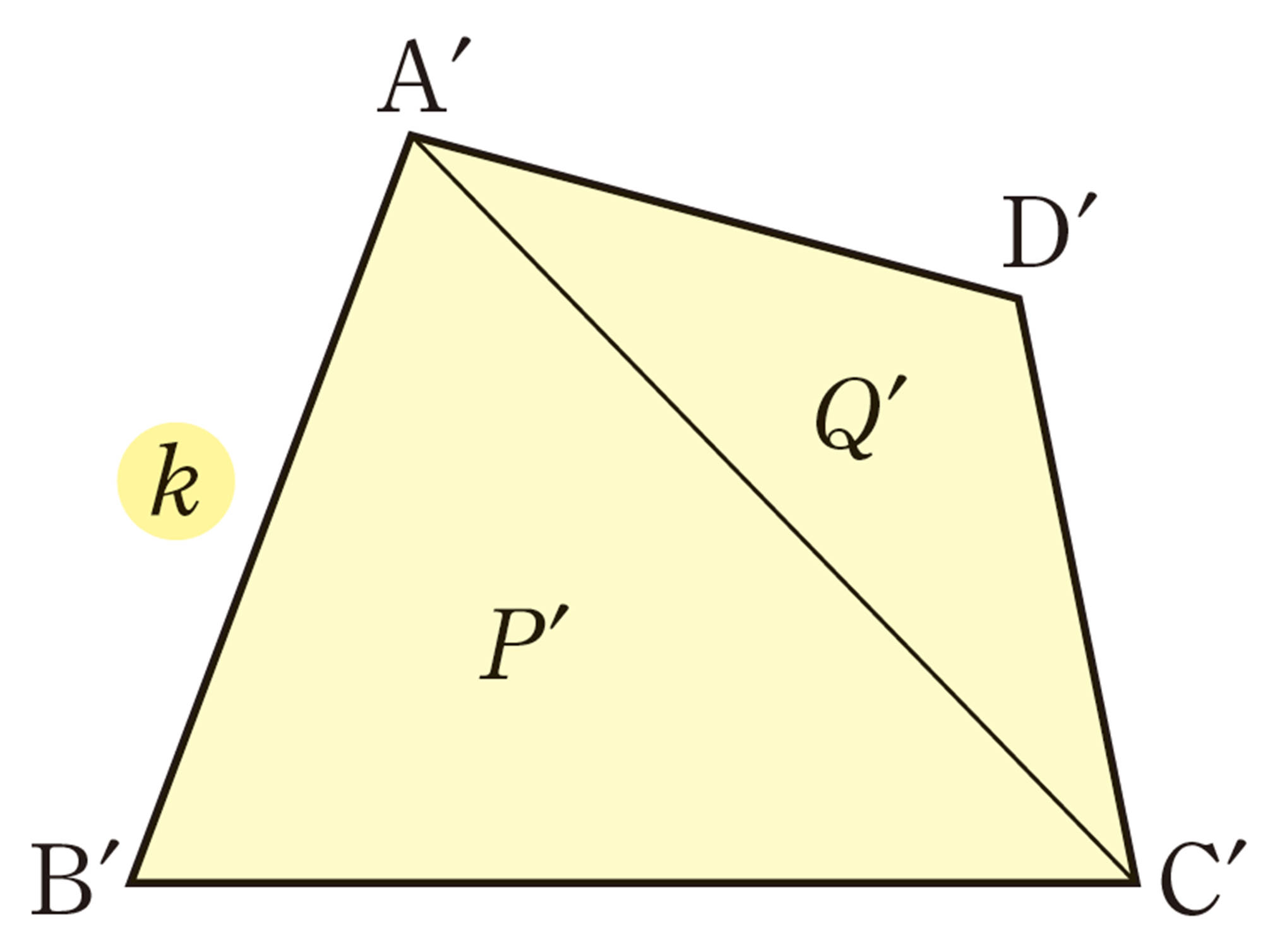
【2】 次の図形は,相似比が[mathjax]\(1:2\)の四角形です。面積比がどうなっているか予想してみましょう。
<3年p.174>
1 相似な図形の面積比
Q Question
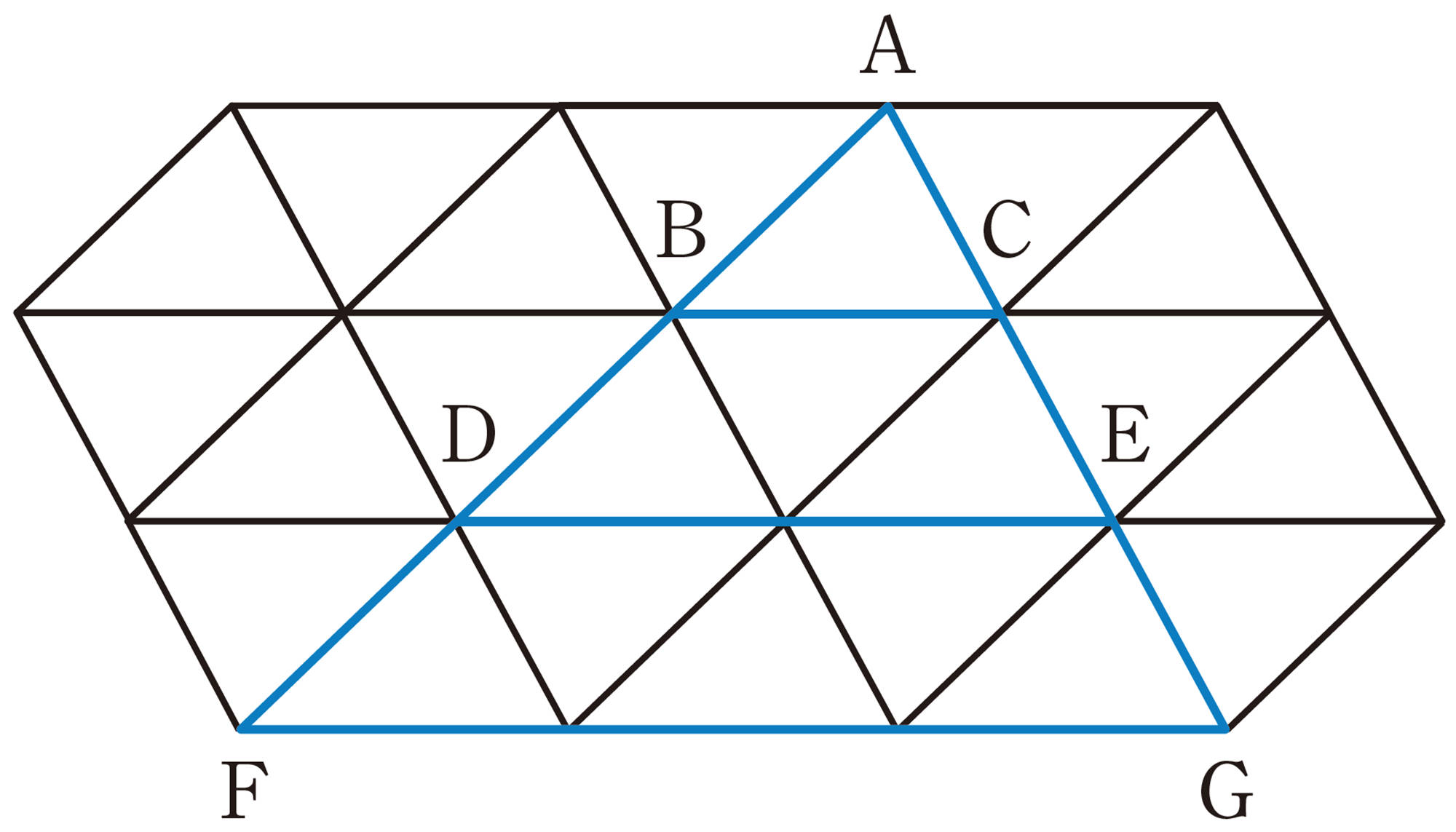
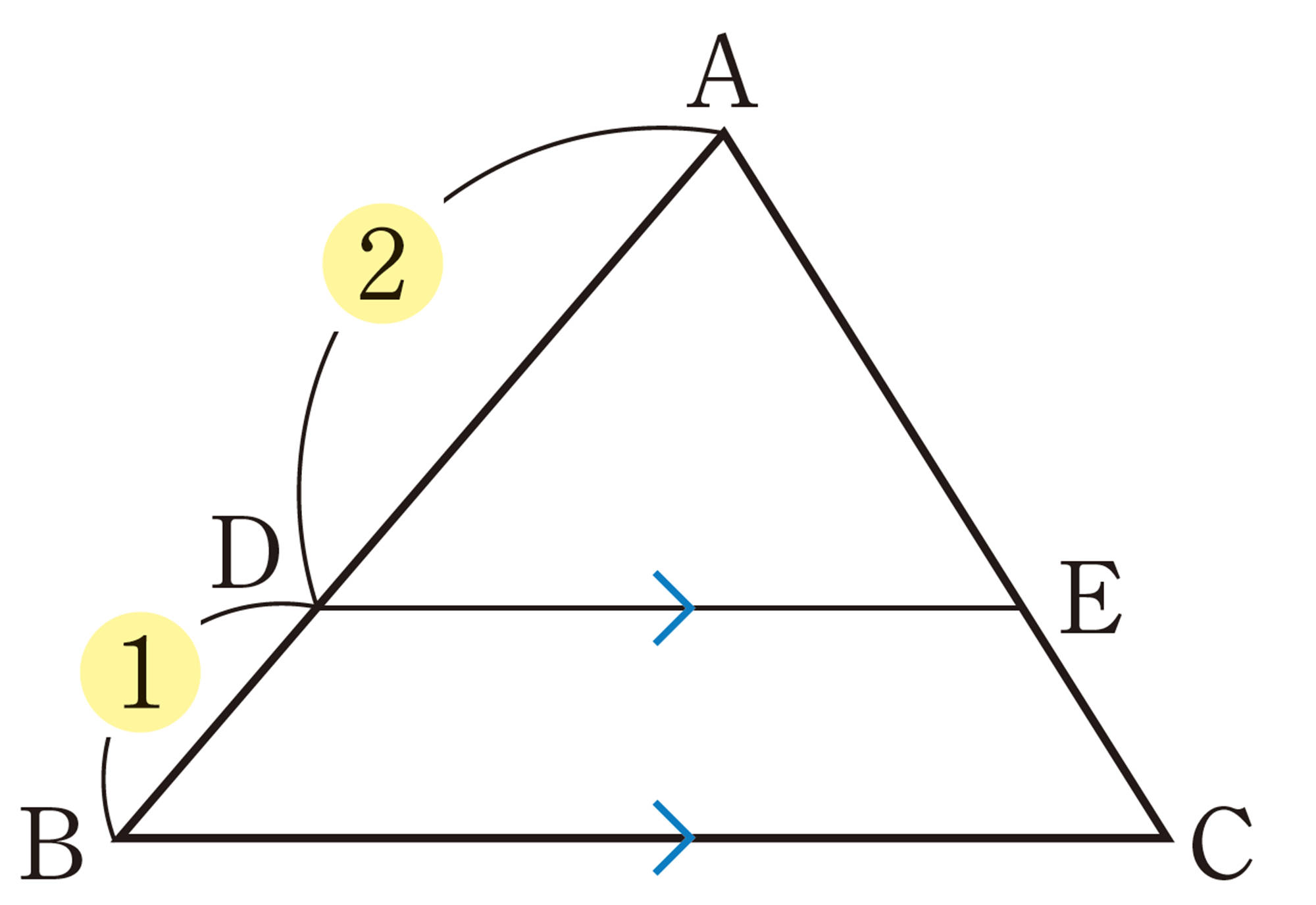
合同な三角形をしきつめた次の図について,下の問いを考えてみましょう。
⑴ [mathjax]\(\triangle ABC\)と[mathjax]\(\triangle ADE\)の相似比と面積比を求めましょう。
⑵ [mathjax]\(\triangle ABC\)と[mathjax]\(\triangle AFG\)の相似比と面積比を求めましょう。
⑶ ⑴,⑵から,相似比と面積比の関係を予想しましょう。

相似比と面積比は同じになるのかな。
いつでも同じことがいえるのかな。

見方・考え方
相似比と面積比の間には どんな関係があるかな。
目標 ▷ 平面図形の相似比と面積比の関係について調べよう。
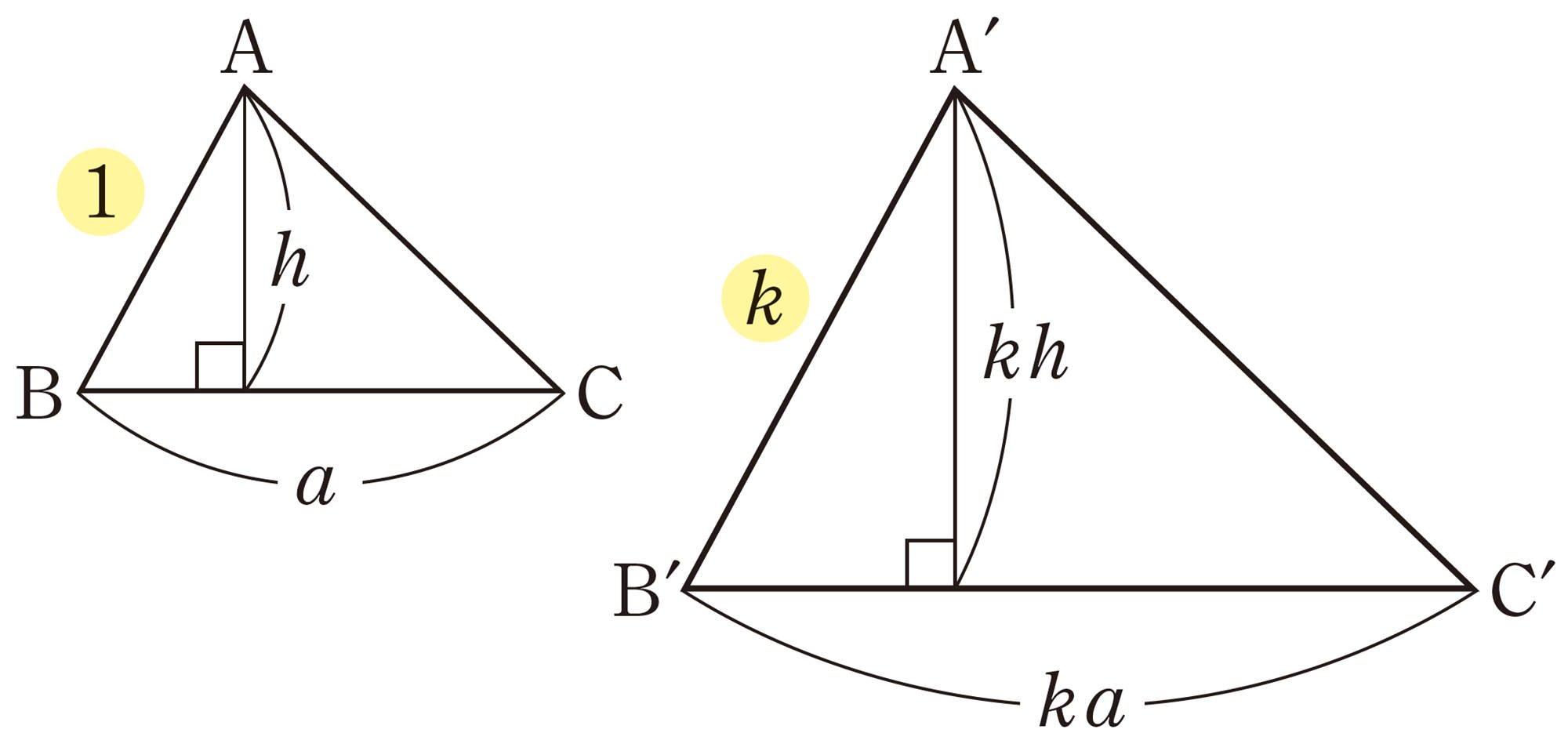
次の図は,[mathjax]\(\triangle ABC \backsim \triangle A´B´C´\)で,相似比が[mathjax]\(1:k\)であることを示している。[mathjax]\(\triangle ABC\),[mathjax]\(\triangle A´B´C´\)の面積をそれぞれ [mathjax] \(S\),[mathjax] \(S´\)とすると,
このことから,相似な三角形では,対応する線分の長さがk倍になると,面積は[mathjax] \(k²\)倍になることがわかる。
<3年p.175>
問 1 [mathjax]\(\triangle ABC\)を5倍に拡大すると,その面積は何倍になりますか。
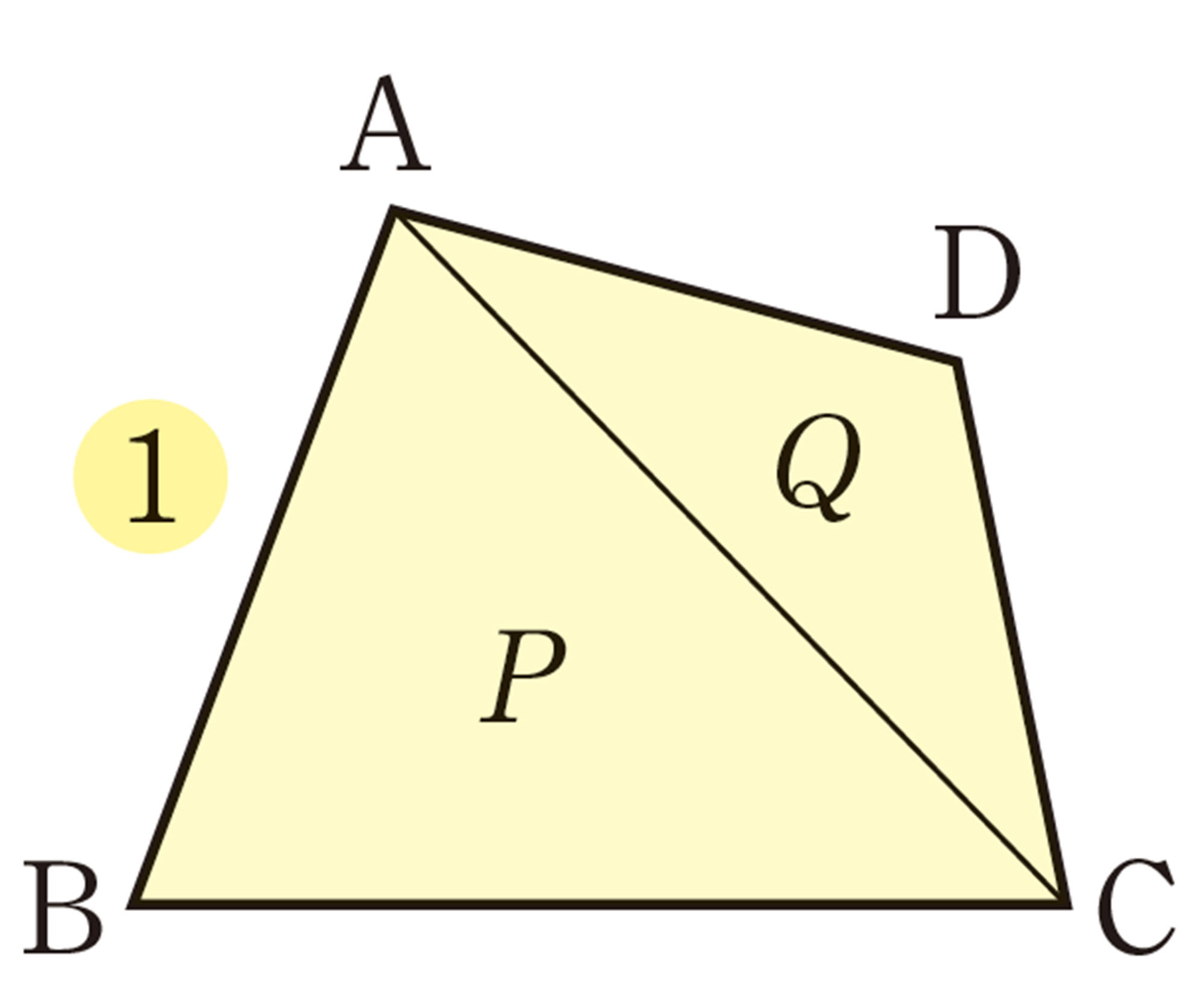
2つの四角形の面積をそれぞれ [mathjax] \(S\),[mathjax] \(S´\)とし,各三角形の面積を右の図のように,それぞれ[mathjax] \(P\),[mathjax] \(Q\),[mathjax] \(P´\),[mathjax] \(Q´\)とすると,
[mathjax]\(P´=k²P\),[mathjax]\(Q´=k²Q\)
これより,
このように考えると,相似な多角形では,対応する部分の長さがk倍になると,面積は[mathjax] \(k²\)倍になることがわかる。
一般に,相似な図形の面積について,次の定理が成り立つ。
定理
相似な図形の面積比
相似な図形の面積比は,相似比の2乗に等しい。
すなわち, 相似比が[mathjax]\(m:n\)ならば,面積比は[mathjax]\(m²:n²\)となる。
<3年p.176>
問 2 2つの円の半径が,それぞれ6cm,10cmのとき,相似比,円周の長さの比,面積比を求めなさい。
解答
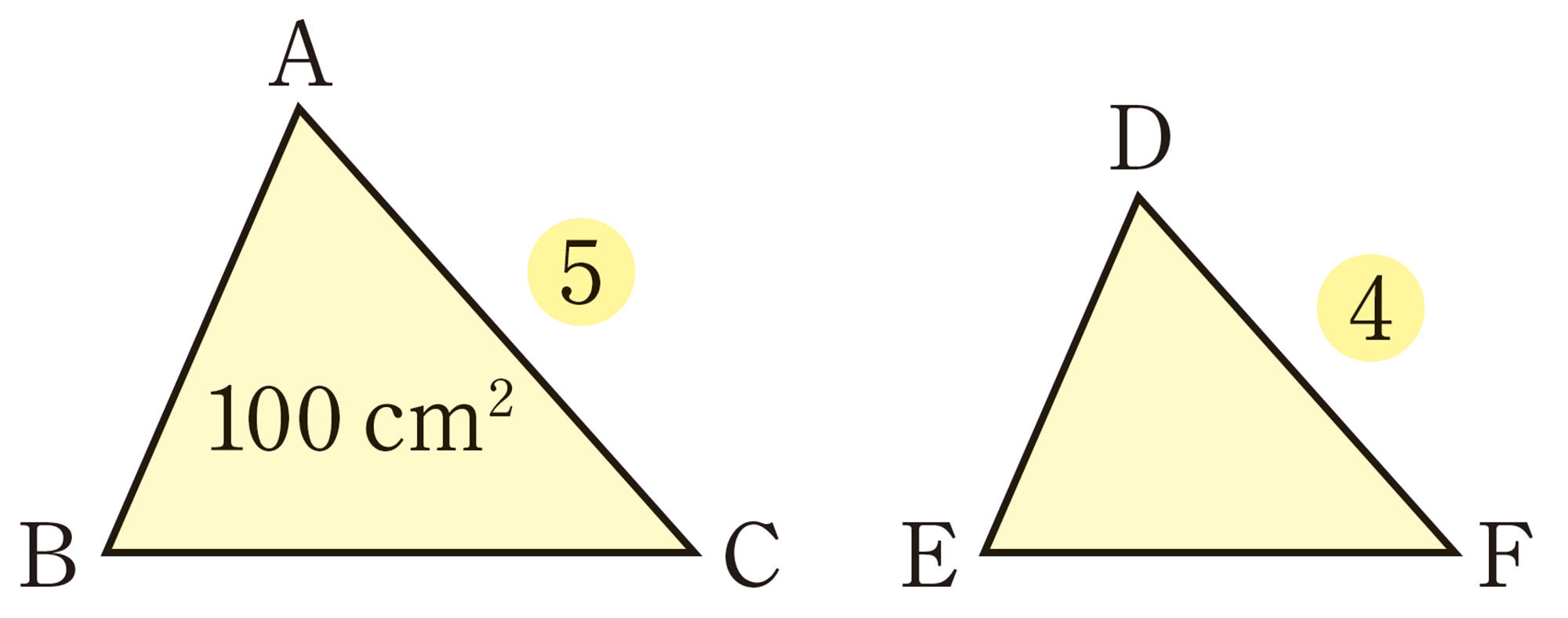
[mathjax]\(\triangle DEF\) の面積を[mathjax] \( x \) cm²とすると, 面積比は相似比の2乗に等しいから,
[mathjax] \(\hspace{41pt}100:x = 5²:4²\)
これを解くと,
答 [mathjax] \( 64 \) cm²
どんなことがわかったかな
相似な平面図形では,面積比は相似比の2乗になっていることをもとにして,相似な図形の面積を求めることができます。
次の課題へ!
空間図形についても,平面図形と同じようなことがいえるのかな?
P.177