<3年p.155>
4 相似の利用
Q Question
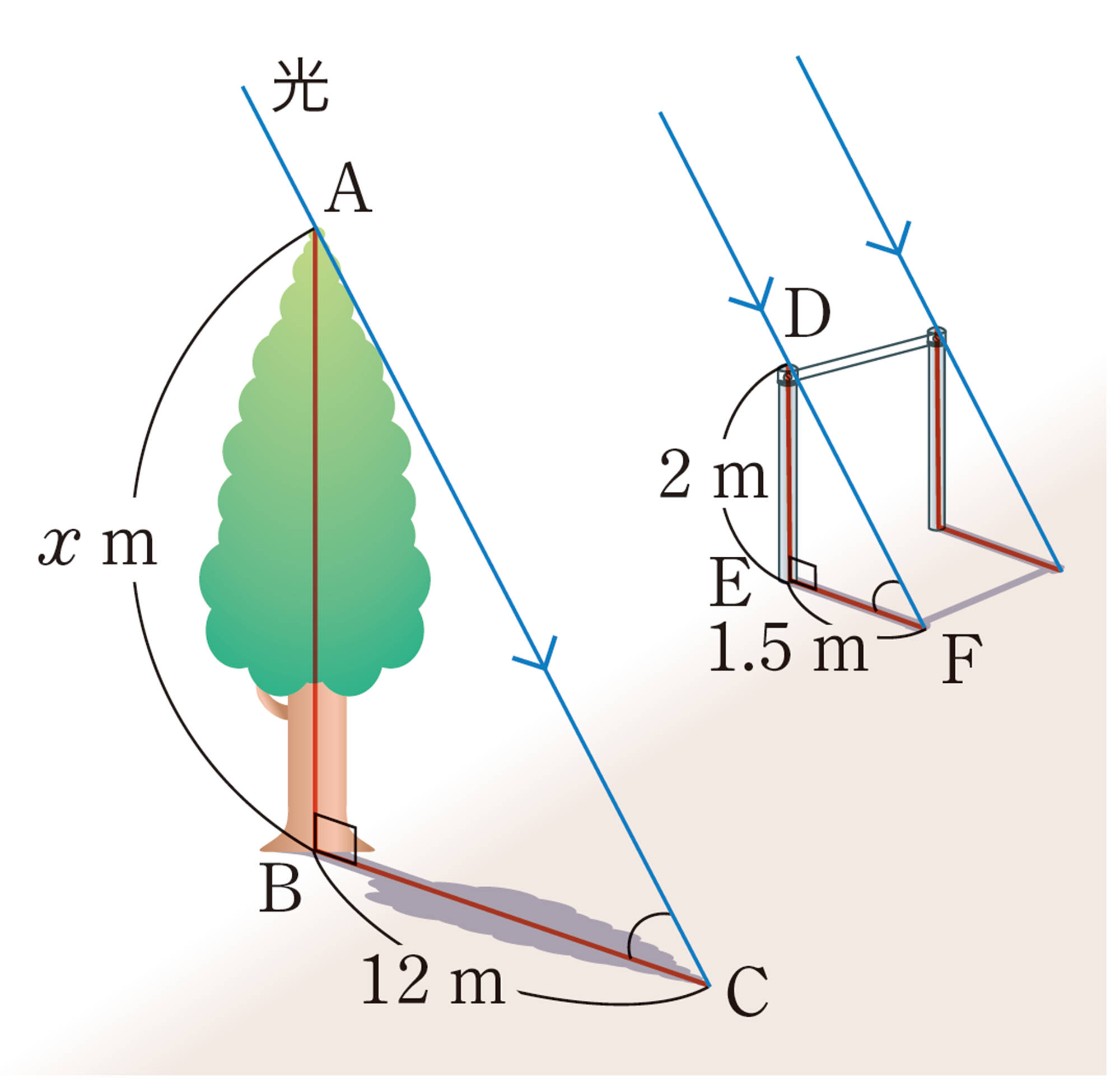
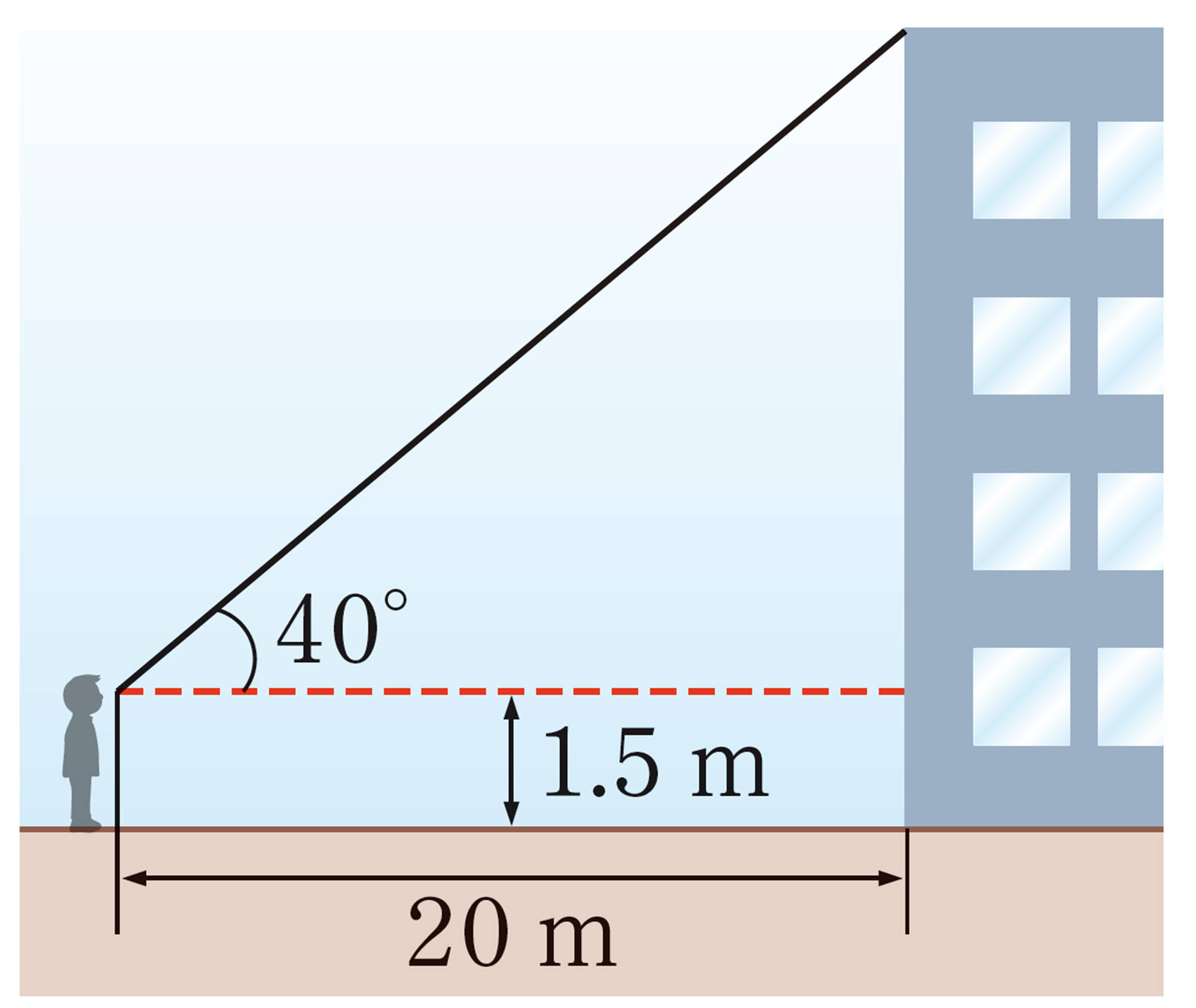
例 1 ある時刻に影の長さを測定したところ,木の影の長さは12m,高さ2mの鉄棒の影の長さは[mathjax]\(1.5\)mでした。この木の高さを求めなさい。
解答
[mathjax] \(\triangle ABC\) と [mathjax] \(\triangle DEF\) において,
[mathjax] \(\angle B= \angle E=90^{\circ}\) ,[mathjax] \(\angle C= \angle F\)
2組の角がそれぞれ等しいから,
[mathjax] \(\hspace{7pt}\triangle ABC \backsim \triangle DEF\)
木の高さを [mathjax] \( x \) m とすると,
答 16 m
<3年p.156>
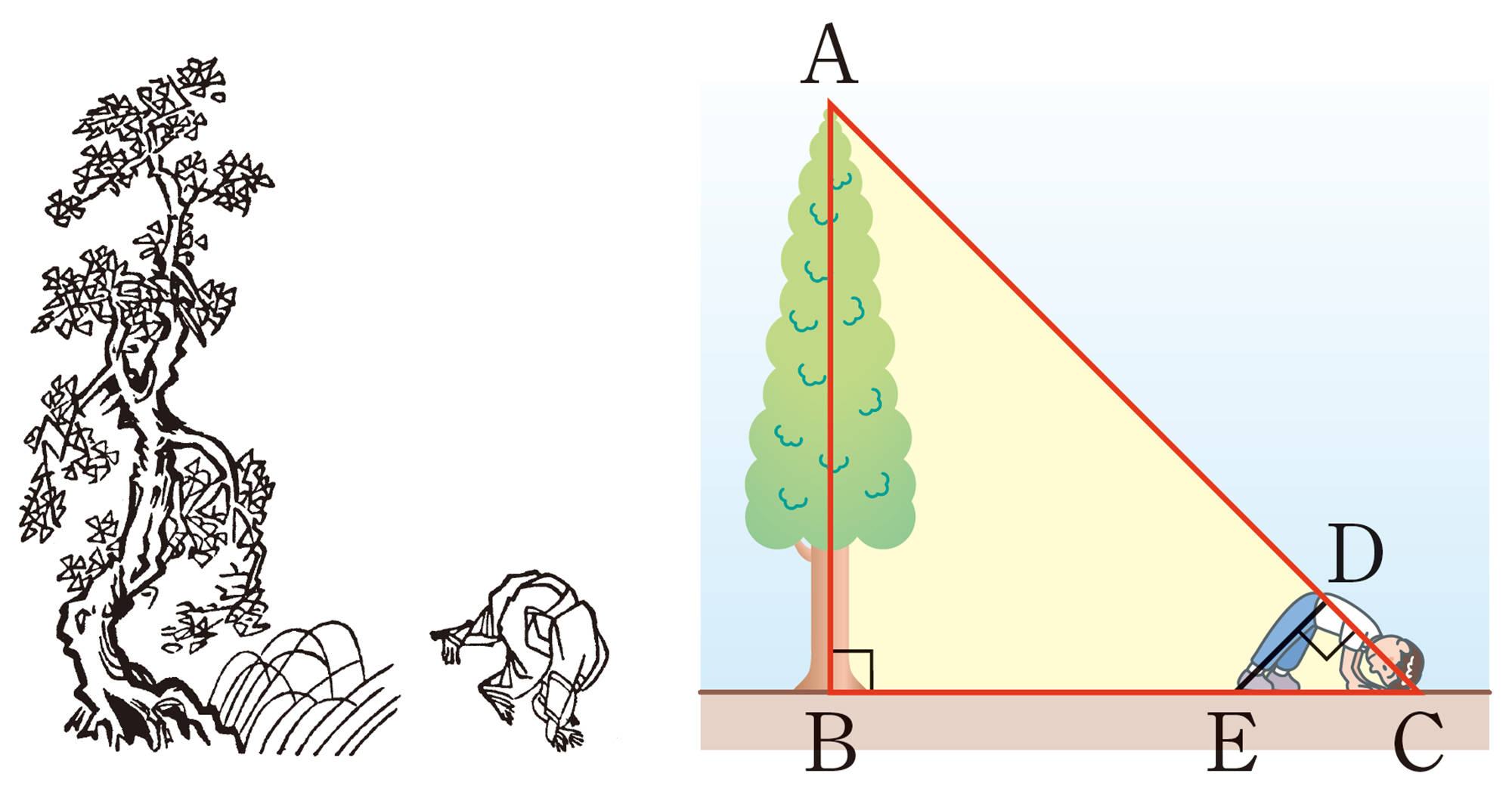
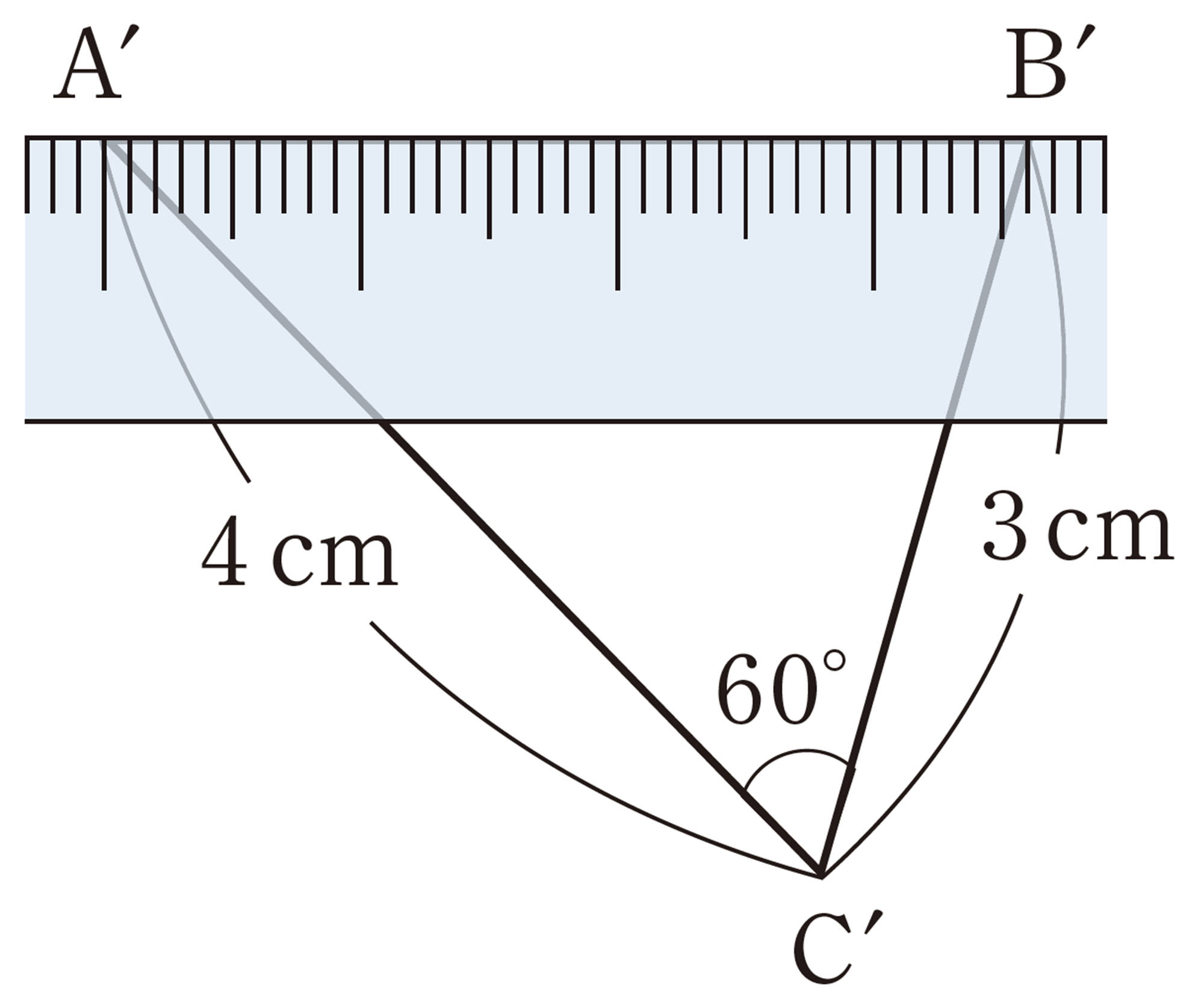
考え方 縮尺を決めて縮図をかき,その縮図上の長さを測り,縮尺をもとに実際の長さを求める。
解答
<3年p.157>
誤差
Q Question
計器を使った量の測定では,真の値は正しく測れないことがあるため,測定値を近似値で表す。
近似値から真の値をひいた差を誤差という。
[mathjax]\((\textsf{誤差})=(\textsf{近似値})-(\textsf{真の値})\)
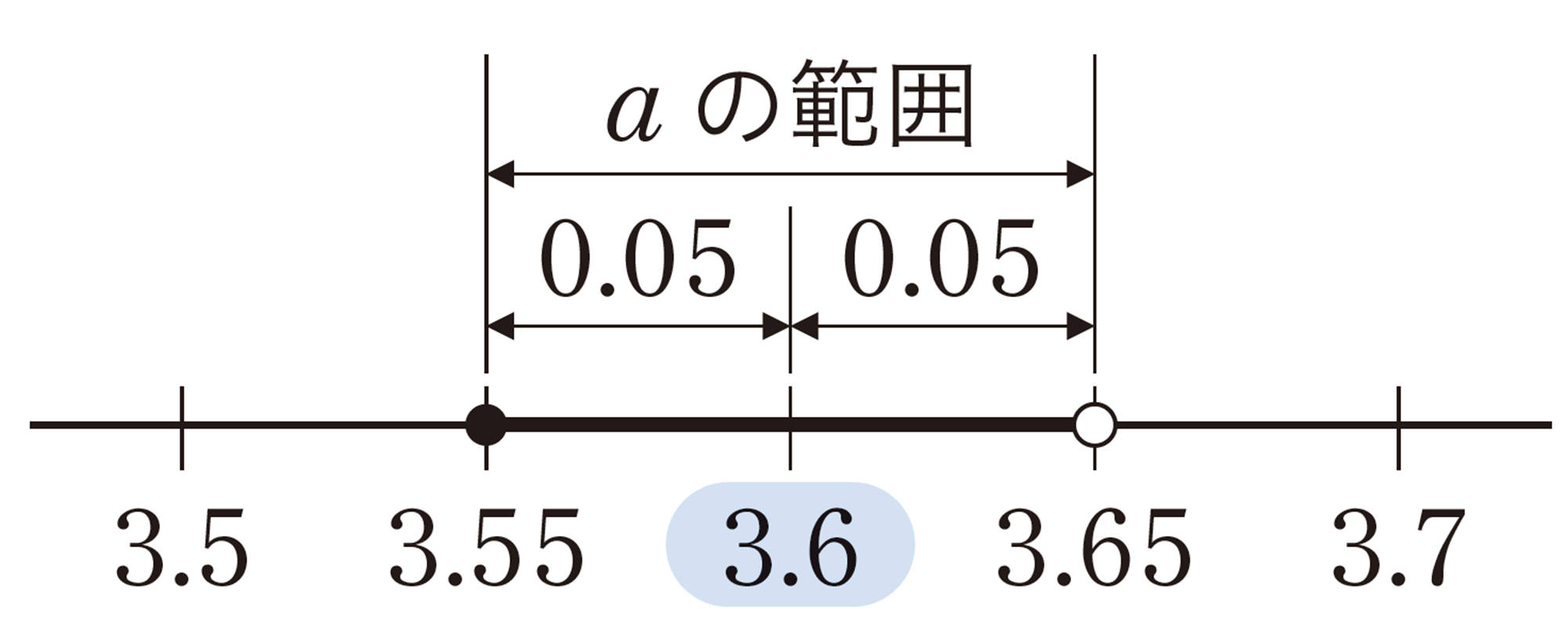
計器を使った量の測定では,真の値が測れなくても真の値がどの範囲にあるのかを知ることはできる。たとえば,測定値[mathjax]\(3.6\)cmは,小数第二位を四捨五入して得られた近似値と考えられる。したがって,その真の値をacmとすると,aの範囲は,
問 3 前ページの例2の答えを約18mとしてもよい理由を説明しなさい。
問 4 次の⑴,⑵は,四捨五入によって得られた近似値です。真の値をそれぞれamとして,aの範囲を不等号を使って表しなさい。また,誤差の絶対値はそれぞれ何m以下となりますか。
⑴ [mathjax]\(25.6\)m
⑵ [mathjax]\(1.83\)m
有効数字
前ページの例2で,辺[mathjax] \(A´B´\)の長さ[mathjax]\(3.6\)cmは近似値であるが,目盛りを読み取って得られた数字なので,3と6は信頼できる数字である。このような信頼できる数字を有効数字という。
<3年p.158>
例 3 札幌市の人口は1972202人です。1970000人と近似値で表したとき,千の位を四捨五入したと考えられるので,[mathjax] \(1\),[mathjax] \(9\),[mathjax] \(7\)は有効数字である。また,万の位を四捨五入すると,近似値は2000000人であり,有効数字は[mathjax] \(2\),[mathjax] \(0\)である。
問 5 ある品物を,最小の目盛りが10g であるはかりで量ったところ,1260gでした。この測定値の有効数字を答えなさい。
「地球から太陽までの距離は149600000km」と近似値で表すことがある。この場合,どこまでが有効数字であるかわからないので,有効数字がはっきりとわかるようにするために,
[mathjax]\((\mathsf{整数部分が}1 \mathsf{桁の小数}) \times (10 \mathsf{の累乗)}\)
[mathjax]\((\mathsf{整数部分が}1 \mathsf{桁の小数}) \times \dfrac{1}{10\mathsf{の累乗}}\)
で表すことがある。たとえば,地球から太陽までの距離の近似値149600000 km の有効数字が[mathjax] \(1\),[mathjax] \(4\),[mathjax] \(9\),[mathjax] \(6\),[mathjax] \(0\)の5桁であるとき,「[mathjax]\(1.4960 \times 10⁸\)km」のように表す。
注意 末位に0がある場合でも,0が有効数字であるときは,省略はしない。
例 4 近似値[mathjax]\(0.047\)g は,有効数字が[mathjax] \(4\),[mathjax] \(7\)の2桁であるとき,次のように表す。
[mathjax]\(4.7 \times \dfrac{1}{10²}\)g
問 6 次の値を,有効数字を2桁として,有効数字がはっきりわかる形で表しなさい。
⑴ 250g
⑵ 6000km
⑶ [mathjax]\(0.80\)m
問 7 四捨五入して,近似値[mathjax]\(3.776 \times 10³\)mが得られました。このとき,誤差の絶対値は何m以下となりますか。
どんなことがわかったかな
相似を利用すると,実際には測れない場合でも,長さを求めることができます。ただし,測定値はふつう誤差があり,有効数字を使って表すことがあります。
<3年p.159>
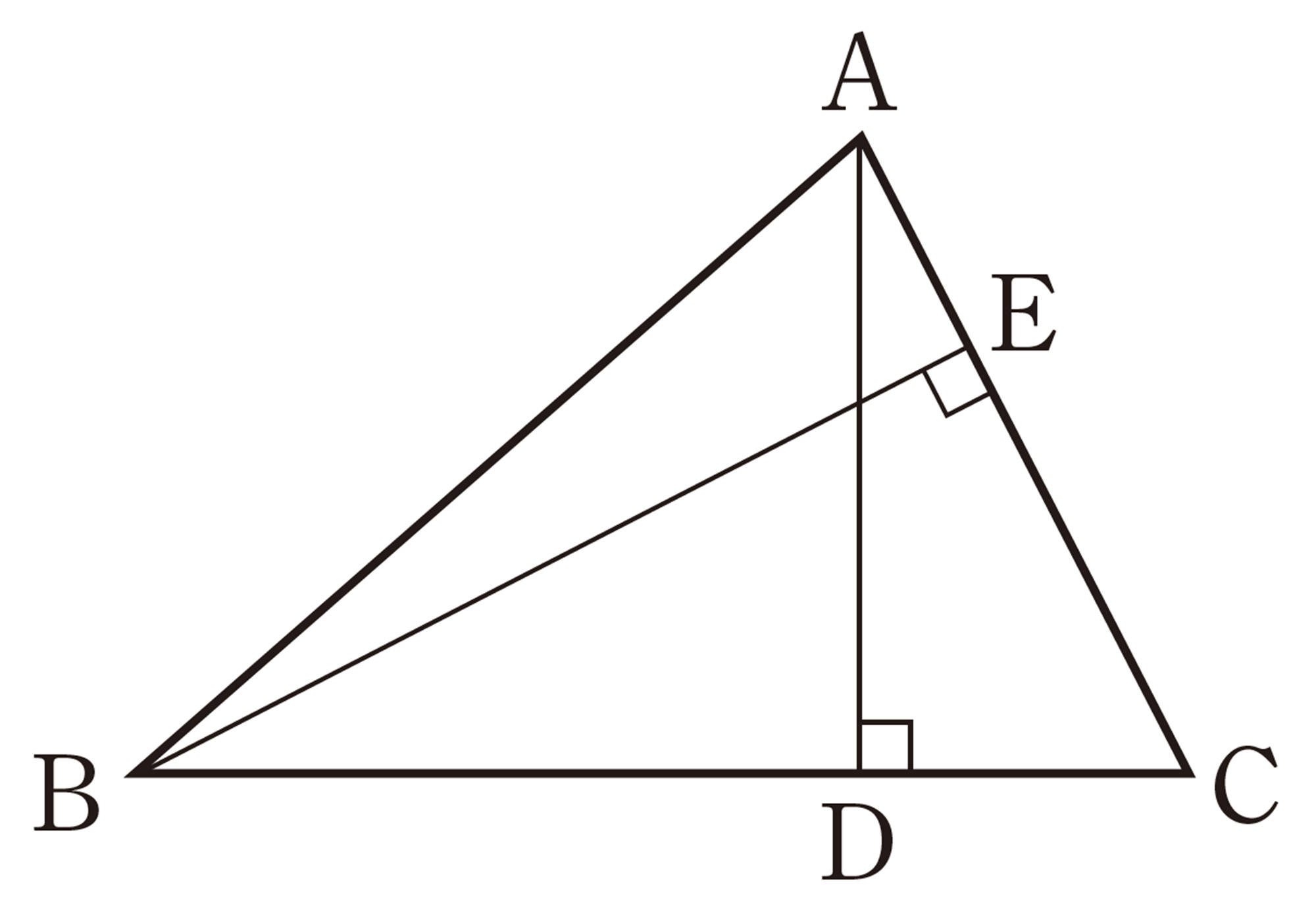
確かめよう 1節 相似な図形
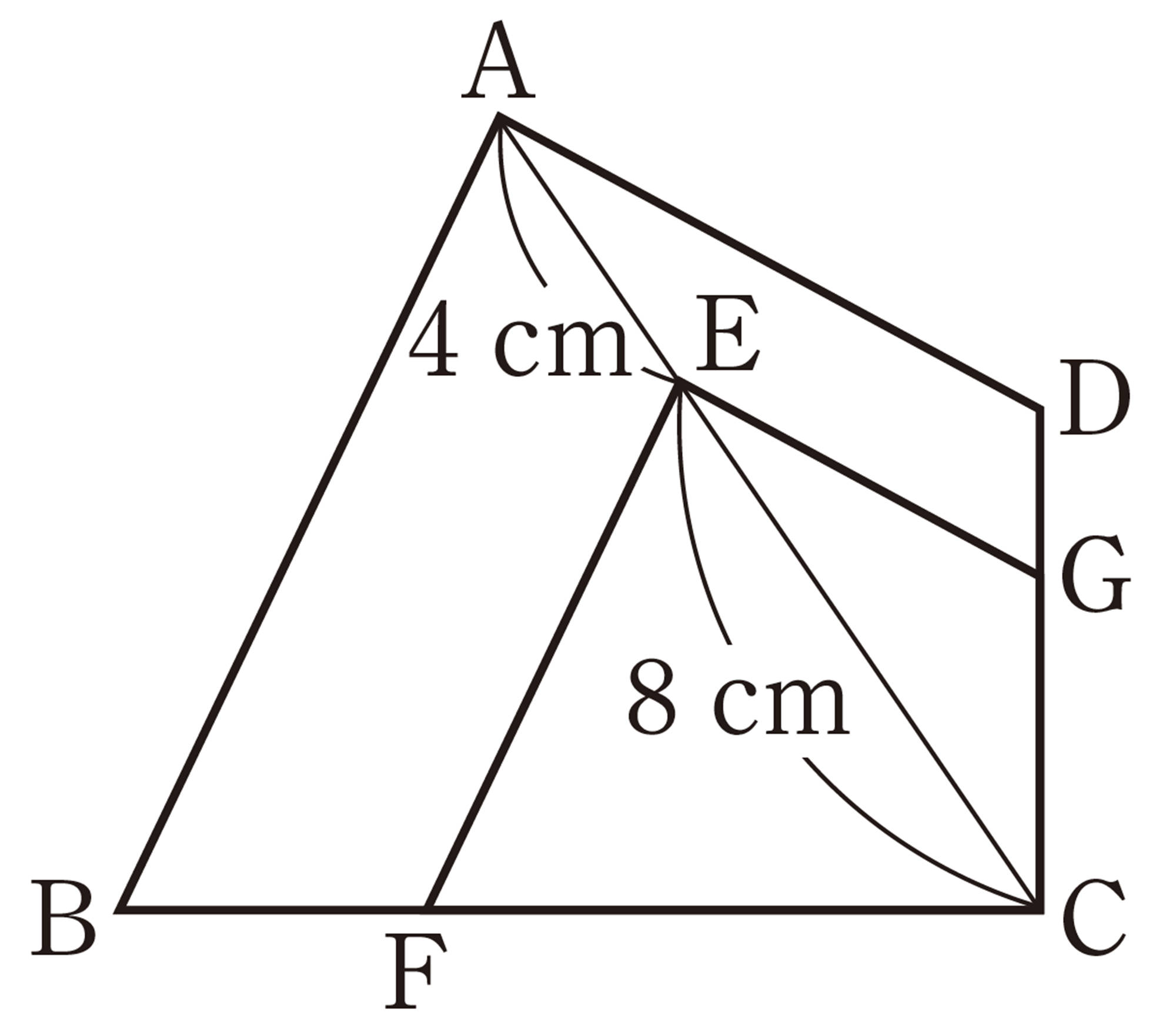
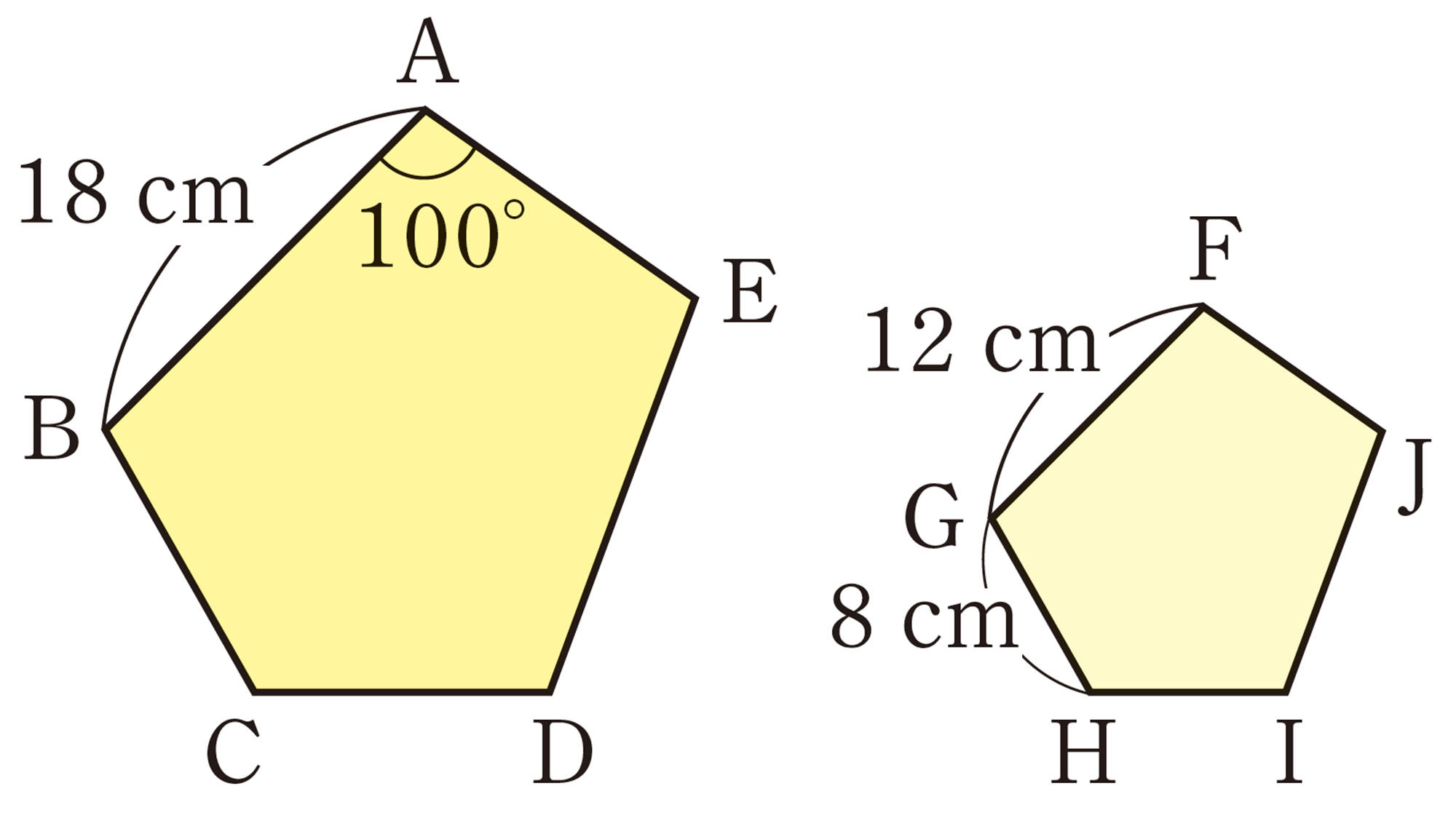
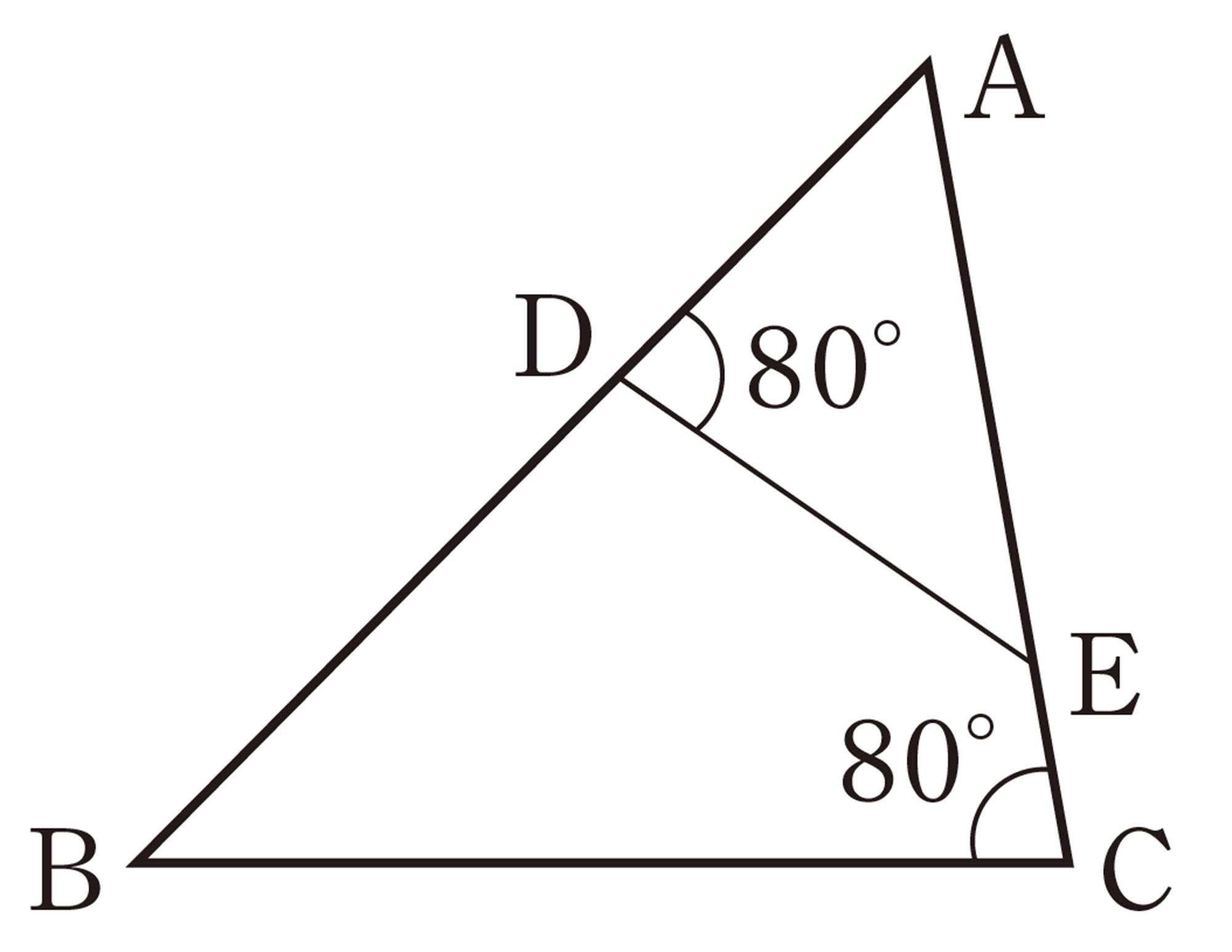
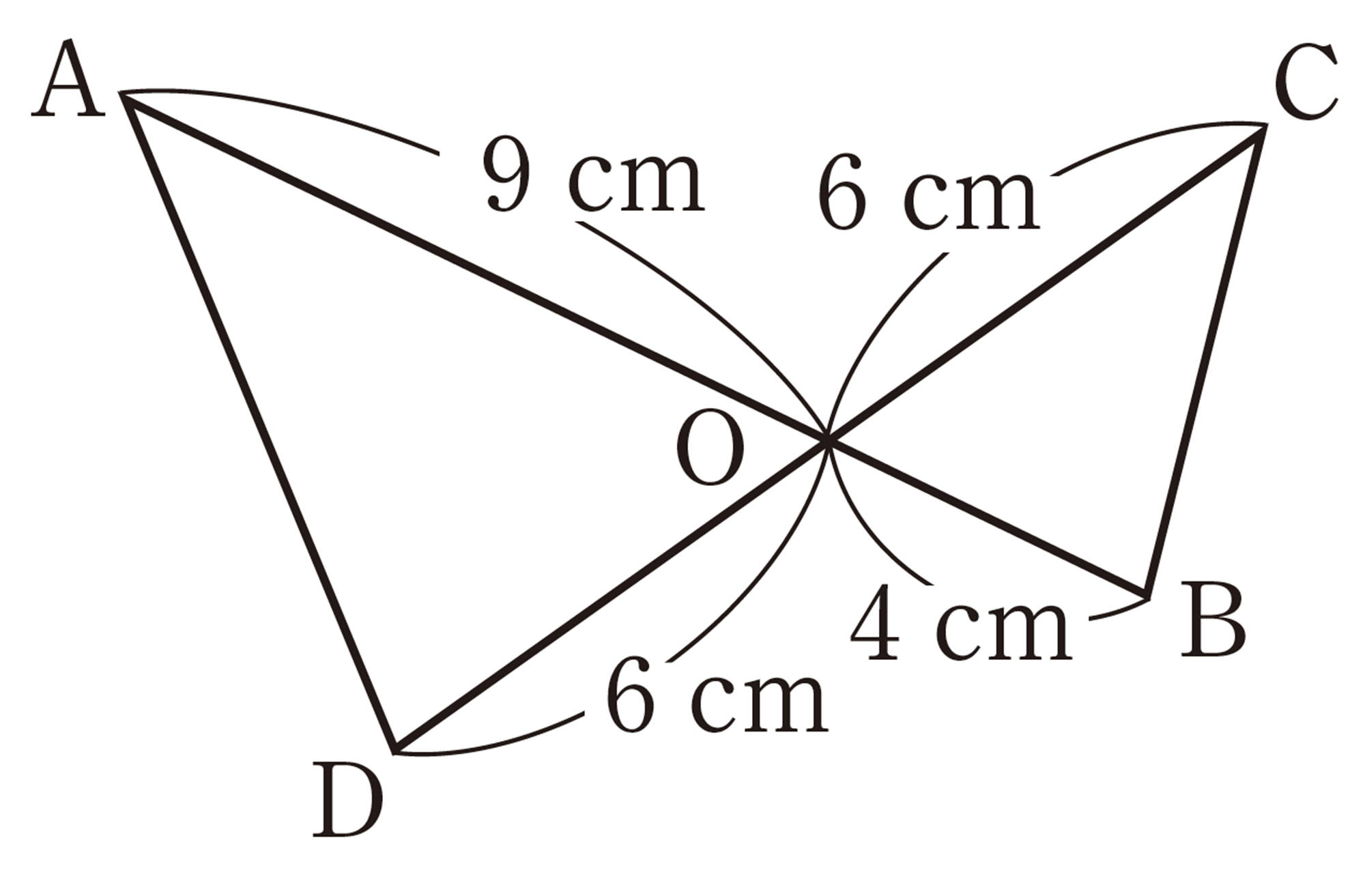
3 次の図で,相似な三角形を記号[mathjax]\(\backsim\)を使って表しなさい。また,そのときの相似条件をいいなさい。
5 次の値を有効数字が3桁の近似値とするとき,有効数字がはっきりわかる形で表しなさい。また,誤差の絶対値はいくら以下と考えられますか。
⑴ 3190m
⑵ [mathjax]\(0.526\)kg