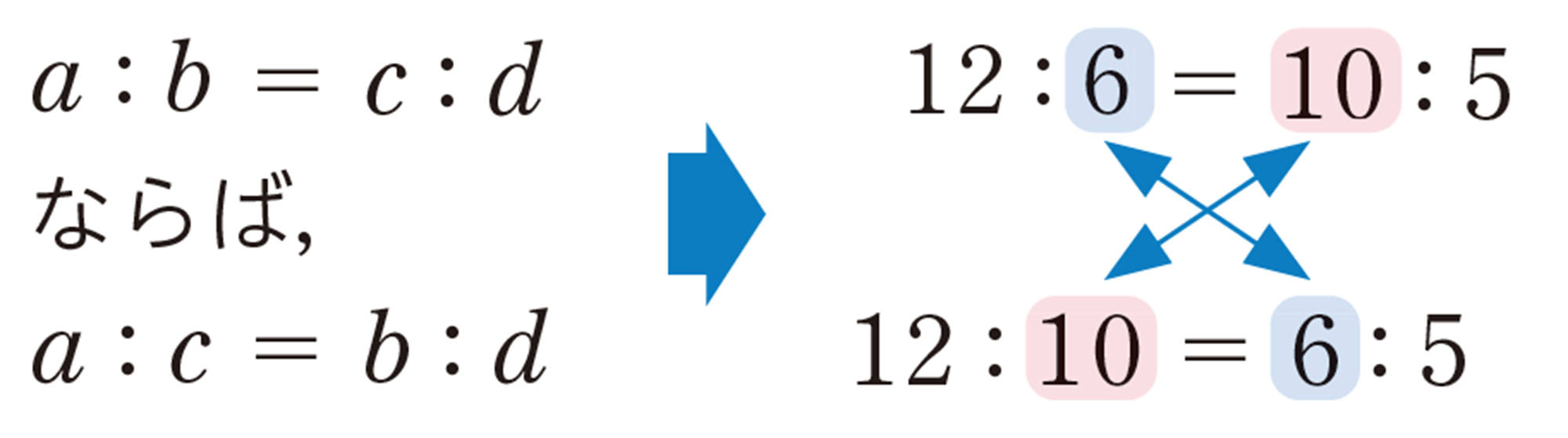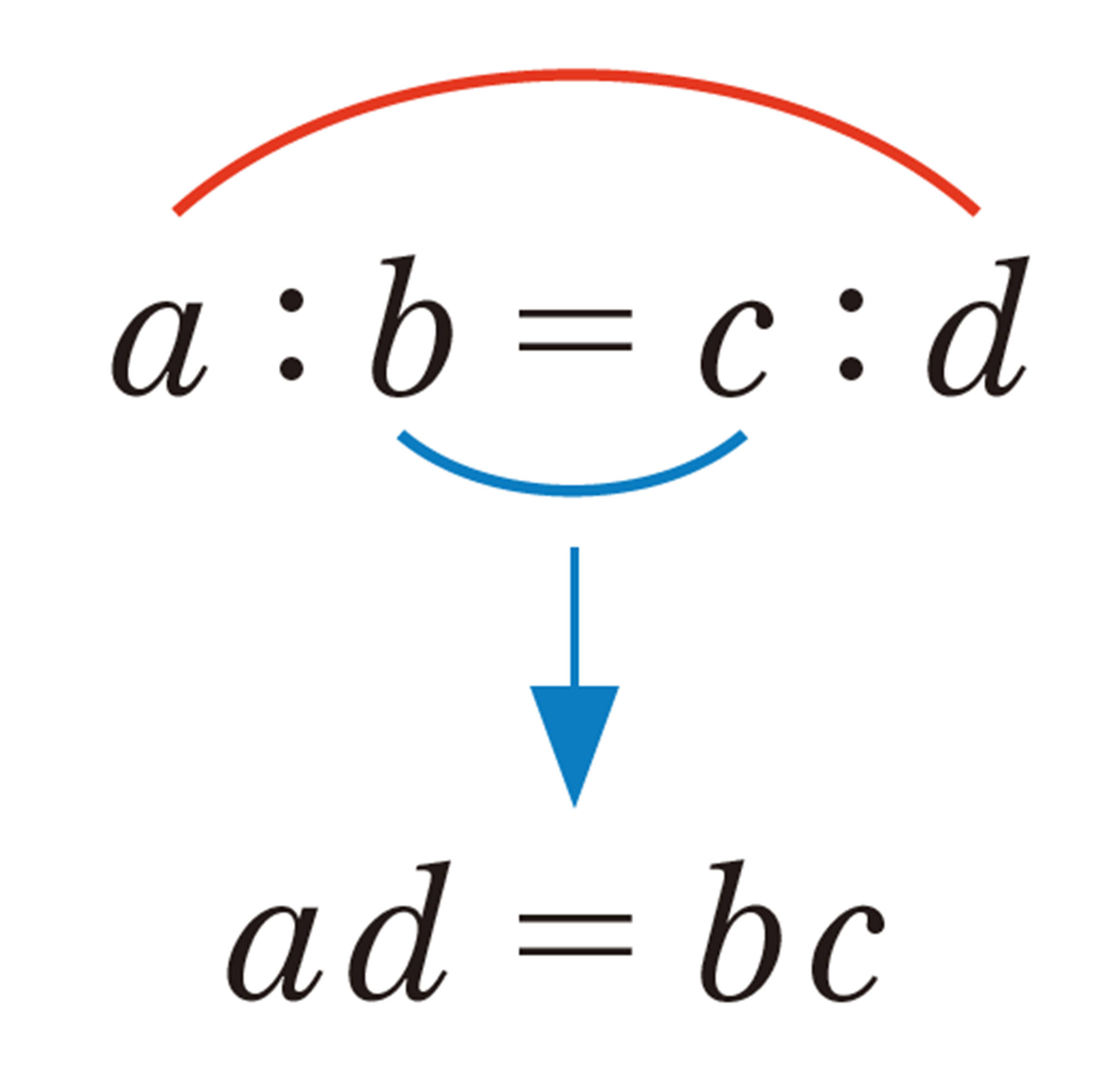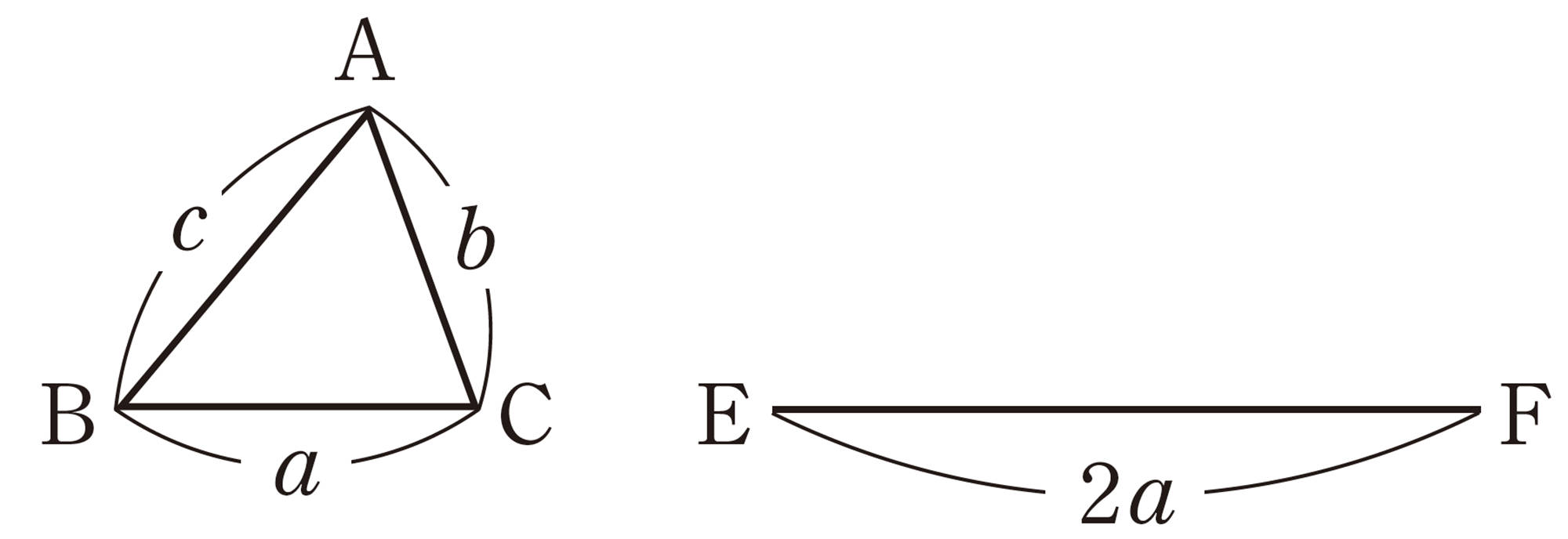<3年p.146>
2 相似な図形の性質
Q Question
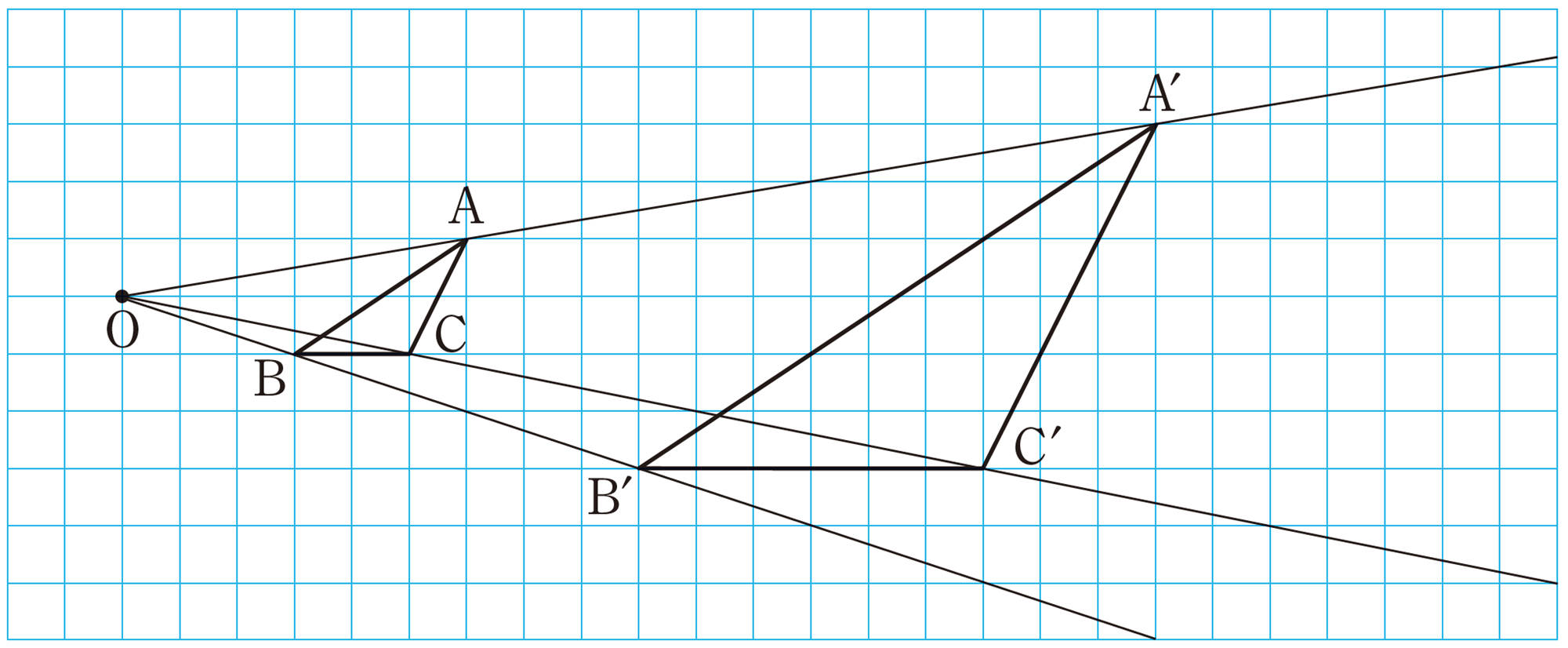
四角形ABCDを3倍に拡大した四角形[mathjax] \(A´B´C´D´\)を,次の図にかきましょう。また,辺の長さや角の大きさについて調べてみましょう。

相似の中心を使わなくてもかけそうだね。
相似な図形について,いつでも同じことがいえるのかな。

見方・考え方
相似な図形には,どんな性質があるか見つけられるかな。
目標 ▷ 相似な図形の性質について調べよう。
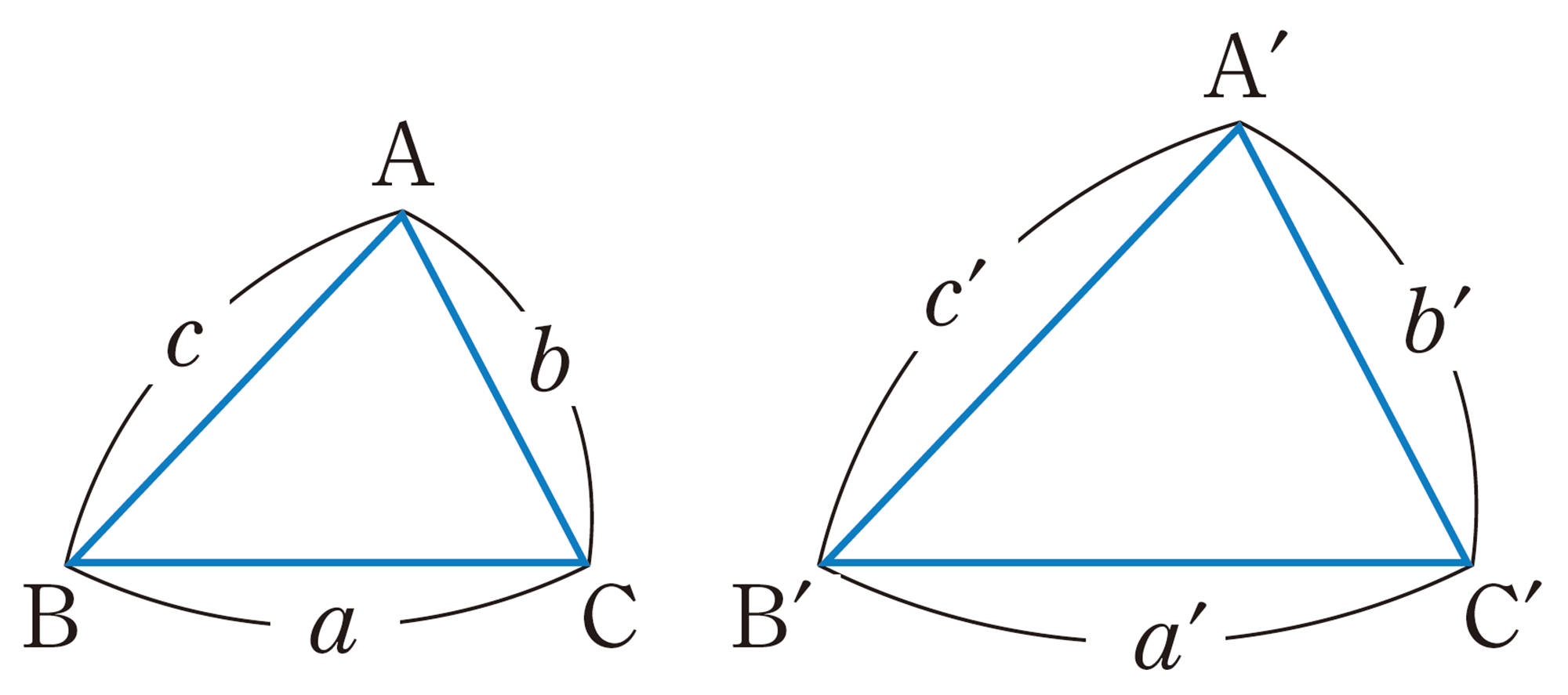
Qの四角形[mathjax] \(A´B´C´D´\)と四角形ABCDの間には,対応する辺の長さと対応する角の大きさについて,次の関係がある。
[mathjax]\(A´B´=3AB\),[mathjax]\(B´C´=3BC\),[mathjax]\(C´D´=3CD\),[mathjax]\(D´A´=3DA\)
[mathjax]\(\angle A´=\angle A\),[mathjax]\(\angle B´=\angle B\),[mathjax]\(\angle C´=\angle C\),[mathjax]\(\angle D´=\angle D\)
また,対応する辺の長さの関係は,次のように表すこともできる。
[mathjax]\(A´B´:AB=B´C´:BC=C´D´:CD=D´A´:DA=3:1\)
問 1 【Q】 の2つの四角形で,対角線[mathjax] \(A´C´\)とAC,[mathjax] \(B´D´\)とBDの長さの関係をそれぞれ調べ,記号を使って表しなさい。
問 2 144ページの 【Q】 の[mathjax]\(\triangle A´B´C´\) と[mathjax]\(\triangle ABC\) について,対応する辺の長さ,対応する角の大きさの関係を,それぞれ記号を使って表しなさい。
<3年p.147>
一般に,相似な図形では,次のことが成り立つ。
相似な図形の性質
❶ 相似な図形では,対応する線分の長さの比はすべて等しい。
❷ 相似な図形では,対応する角の大きさはそれぞれ等しい。
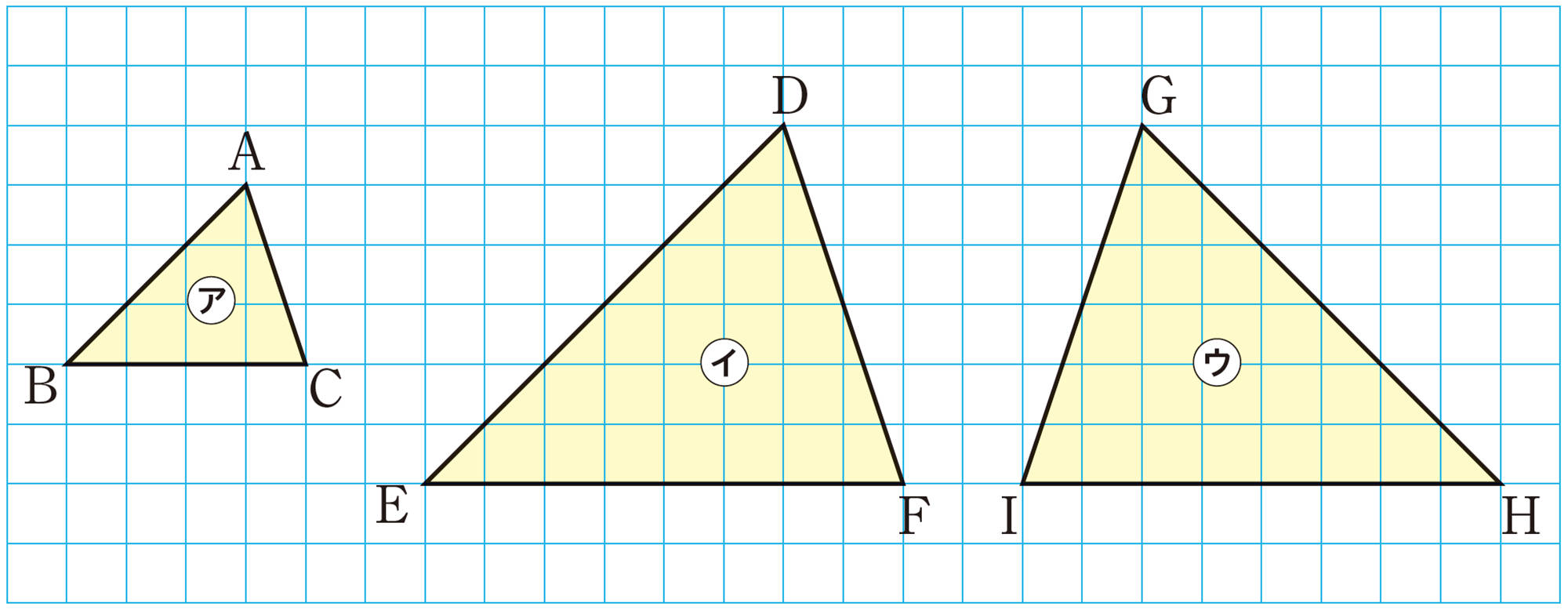
問 3 次の図で,三角形㋐と三角形㋑は相似である。このとき,三角形㋐と三角形㋒も相似といえますか。
問3の図で,三角形㋒は,三角形㋑を対称移動した図形であり,この2つの三角形は合同である。
したがって,三角形㋐と三角形㋒も相似である。
問 4 次の各組の図形は,つねに相似であるといえますか。
⑴ 2つの正五角形
⑵ 2つのひし形
⑶ 2つの円
注意 多角形以外の図形でも,ある図形を拡大,縮小した図形は相似である。
相似な図形で,対応する線分の長さの比を,相似比 という。
前ページの【Q】の四角形[mathjax] \(A´B´C´D´\)と四角形ABCDの相似比は,[mathjax]\(3:1\) である。
<3年p.148>
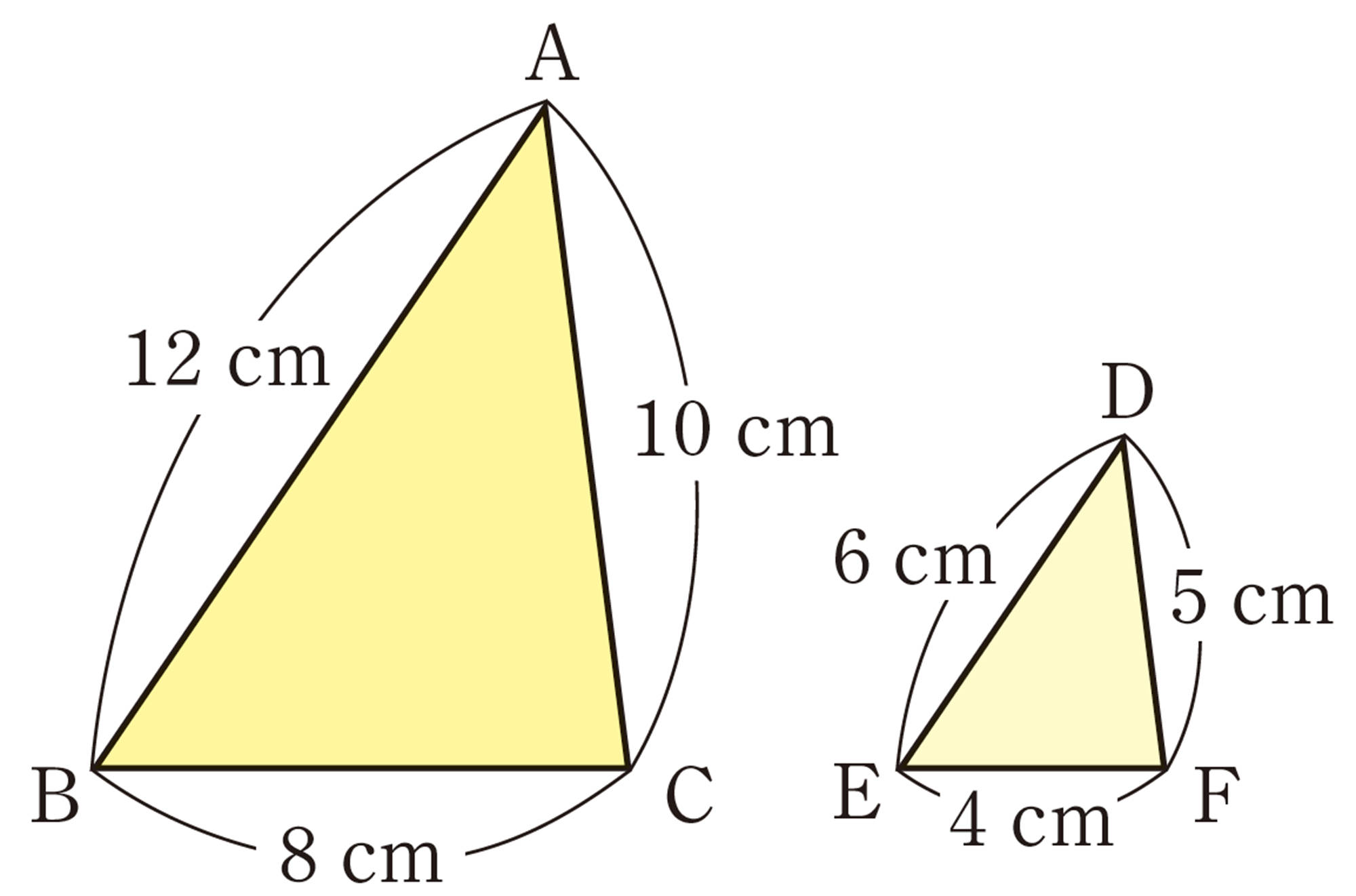
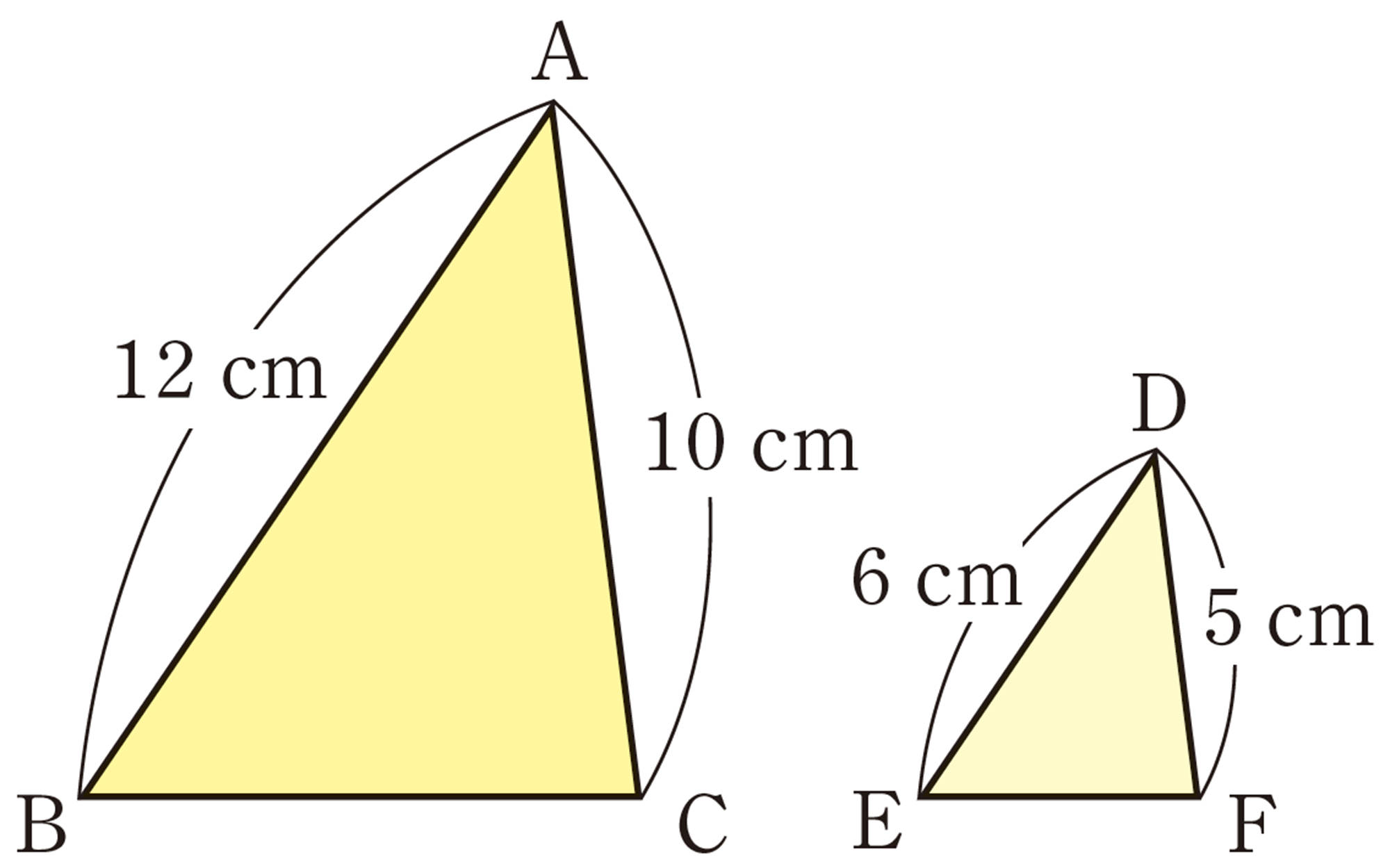
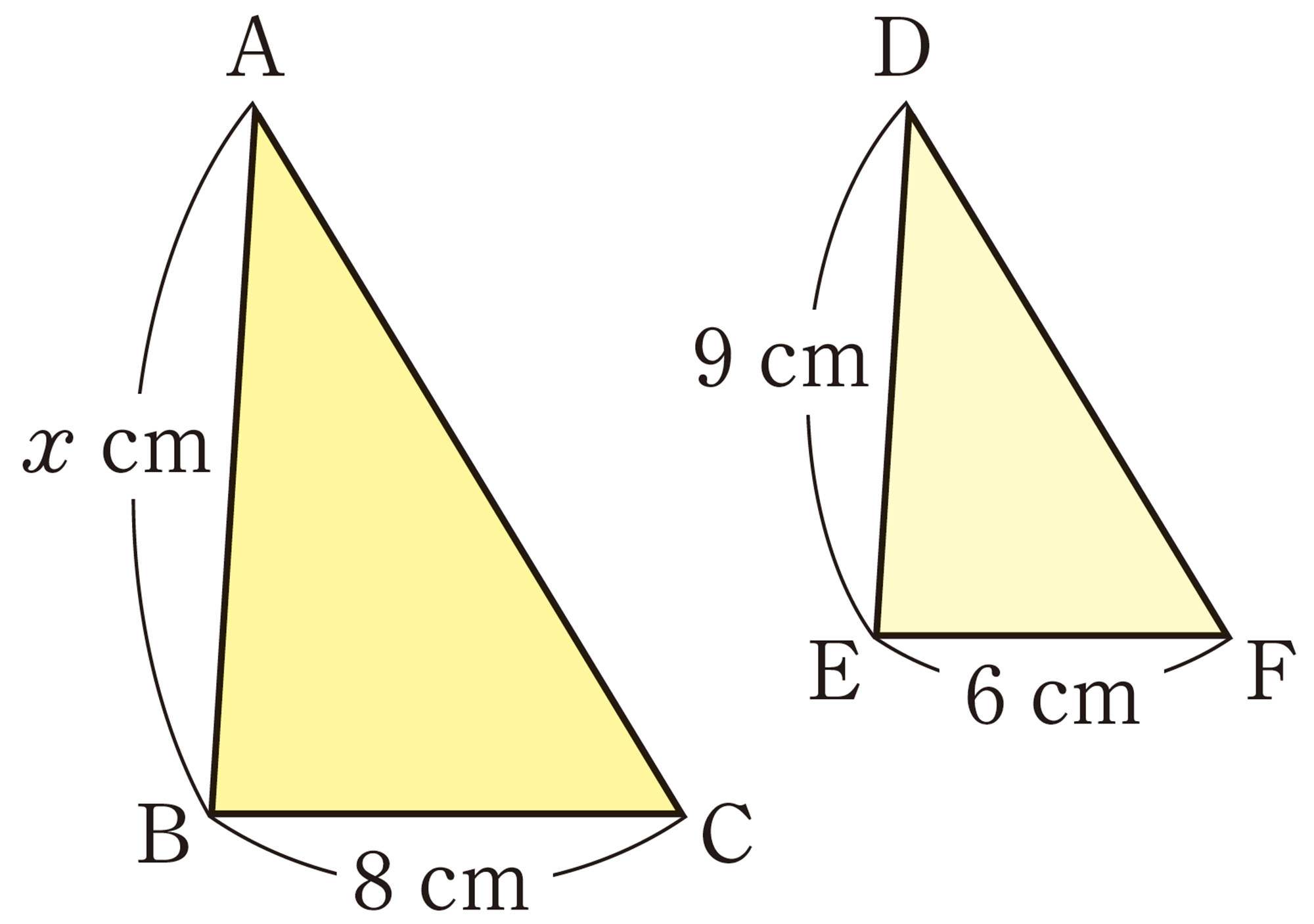
例 1 右の図で,[mathjax]\(\triangle ABC \backsim \triangle DEF\) であるとき,対応する辺の長さの比は,
問 5 次の図で,[mathjax]\(\triangle ABC \backsim \triangle DEF\)であるとき,[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle DEF\)の相似比を求めなさい。
問 6 相似な図形で,相似比が [mathjax]\(1:1\) であるのはどんな場合ですか。
次の課題へ!
相似な2つの三角形の相似比が [mathjax]\(2:1\) のとき,面積の比も [mathjax]\(2:1\) になっているのかな?
P.173

<3年p.149>
相似な図形の性質の利用
<3年p.150>
三角形の相似条件
Q Question

どんな条件のときに,相似な三角形がかけるのかな。
見方・考え方
三角形の合同条件と同じように考えられるかな。
目標 ▷ 2つの三角形が相似になるための条件について調べよう。
問 1 辺の長さや角の大きさに着目して,上の方法以外で,2倍に拡大した図をかく方法を話し合いなさい。
<3年p.151>
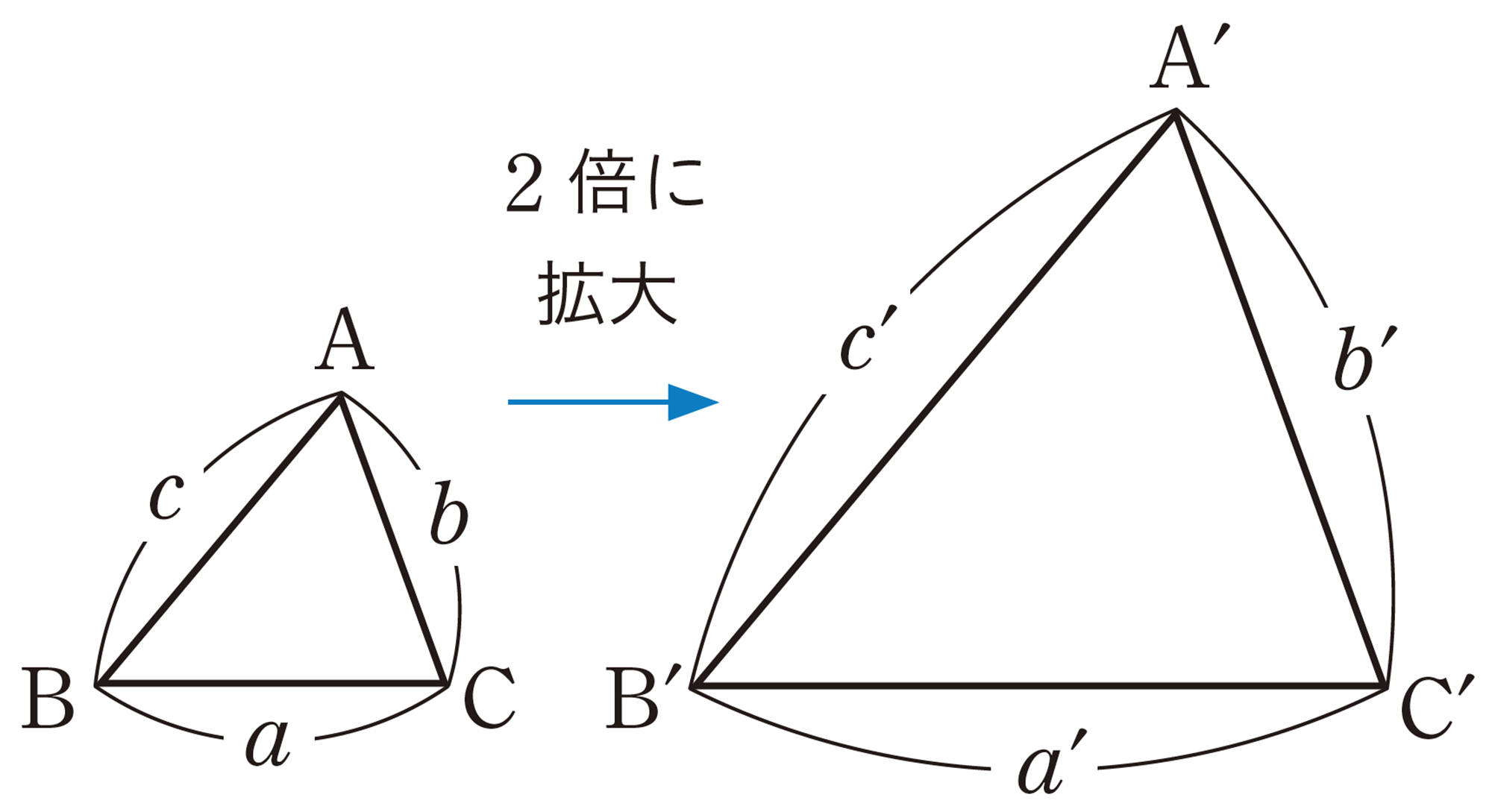
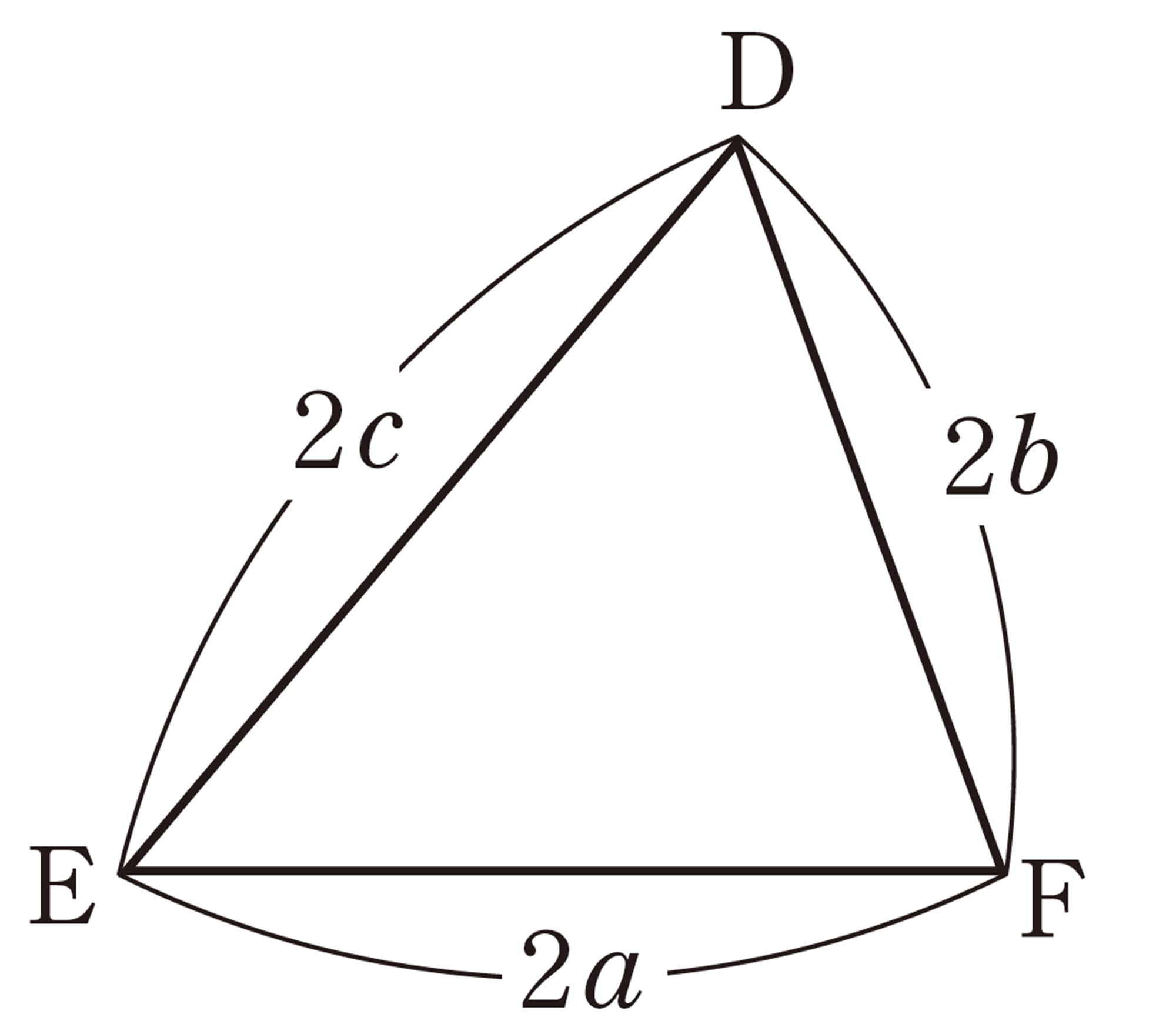
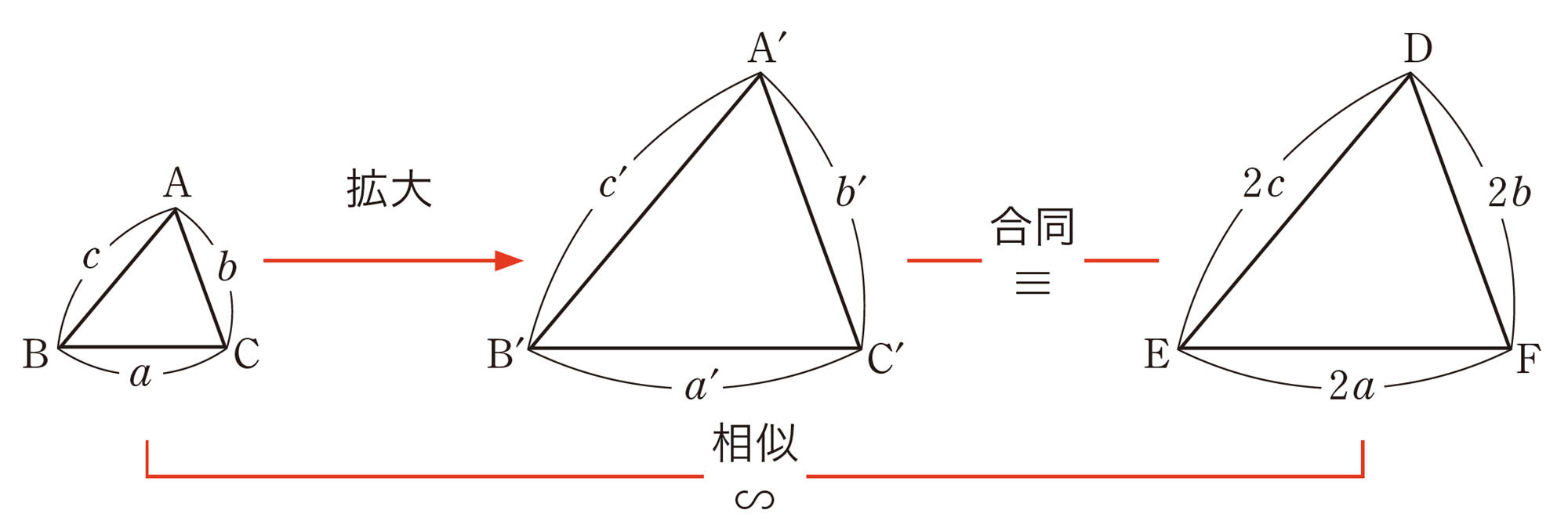
[mathjax]\(\triangle ABC\)を2倍に拡大した[mathjax]\(\triangle A´B´C´\)をかくには,次の3つの方法が考えられる。
① 3辺の長さをそれぞれ2倍にする。
[mathjax]\(a´=2a\),[mathjax]\(b´=2b\),[mathjax]\(c´=2c\)
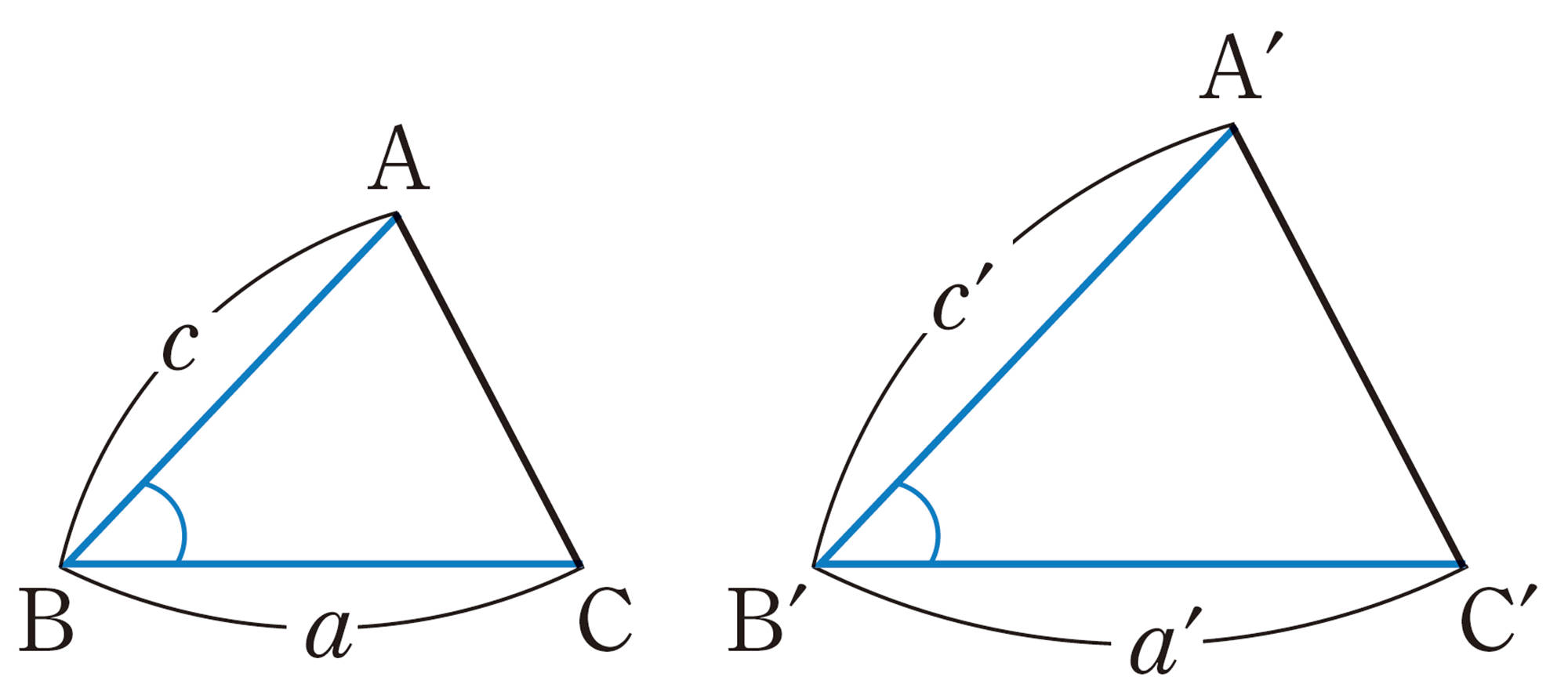
② 2辺の長さをそれぞれ2倍にして,その間の角を等しくする。
たとえば,[mathjax]\(a´=2a\),[mathjax]\(c´=2c\),[mathjax]\(\angle B´=\angle B\)
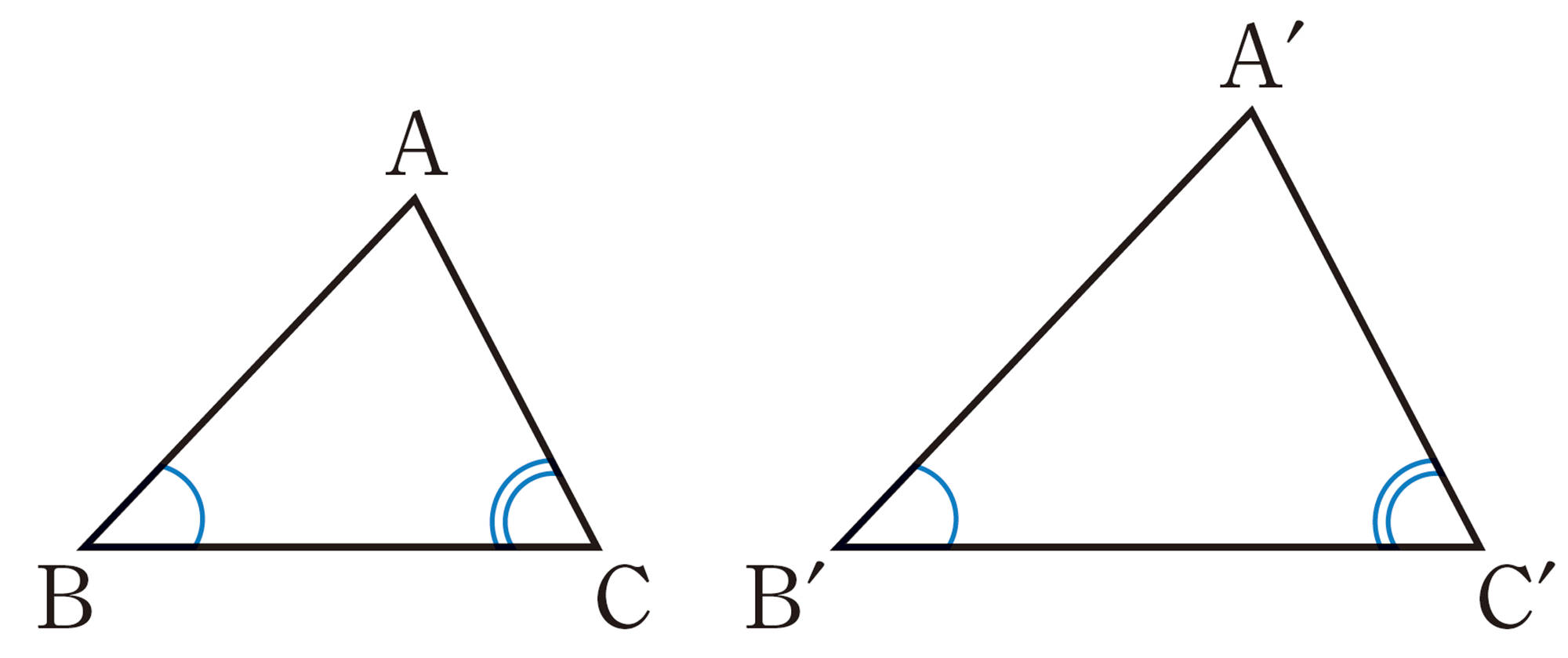
③ 1辺の長さを2倍にして,その両端の角をそれぞれ等しくする。
たとえば,[mathjax]\(a´=2a\),[mathjax]\(\angle B´=\angle B\),[mathjax]\(\angle C´=\angle C\)
問 2 上の②,③の方法で,[mathjax]\(\triangle A´B´C´\)をかきなさい。
三角形の相似条件は,次のようにまとめることができる。
合同条件と比べてみよう。 相似条件③は,辺の比を考えなくていいんだね。

ふりかえり
▷2年
三角形の合同条件
① 3組の辺がそれぞれ等しい。
② 2組の辺とその間の角がそれぞれ等しい。
③ 1組の辺とその両端の角がそれぞれ等しい。
<3年p.152>
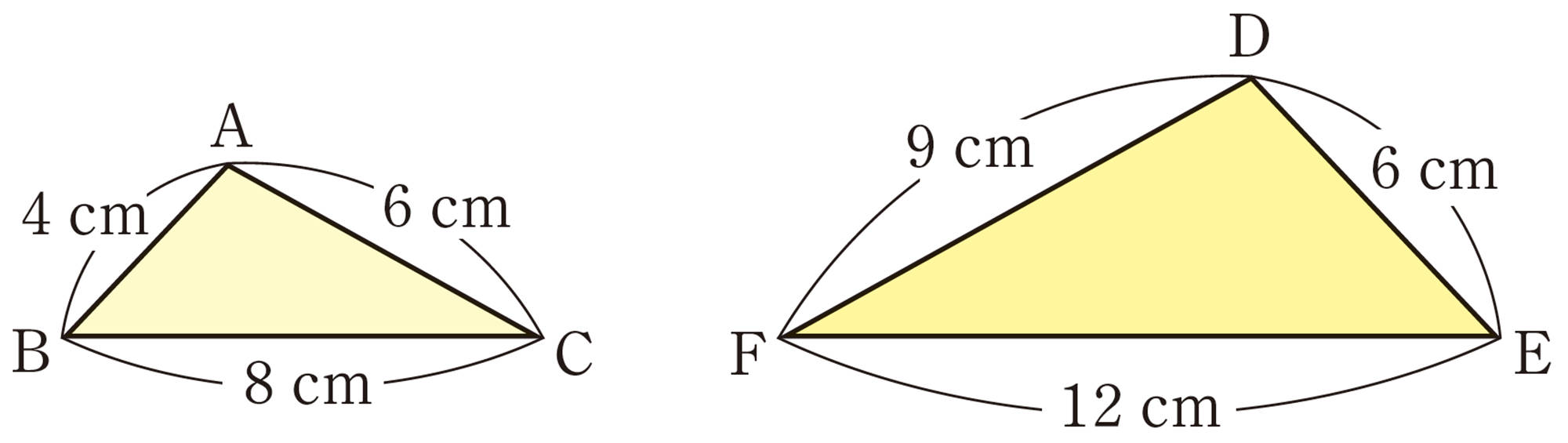
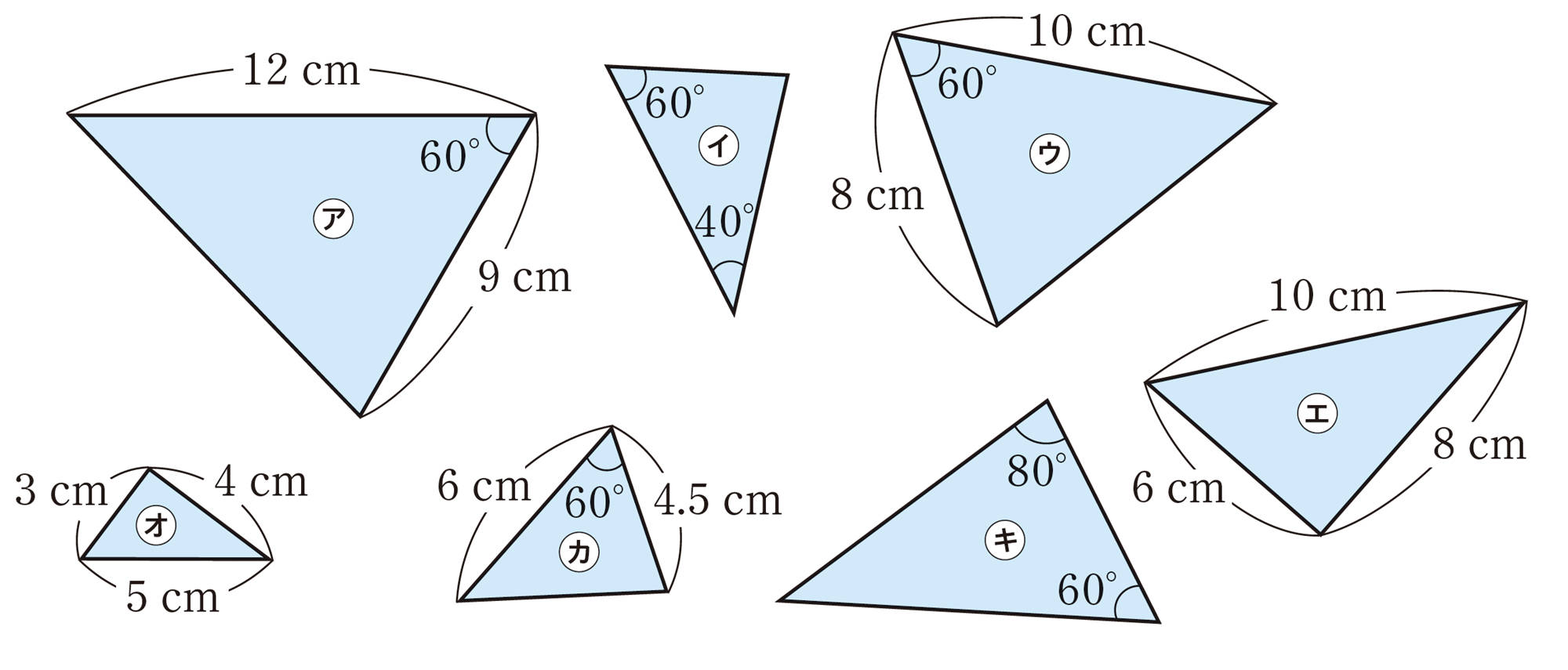
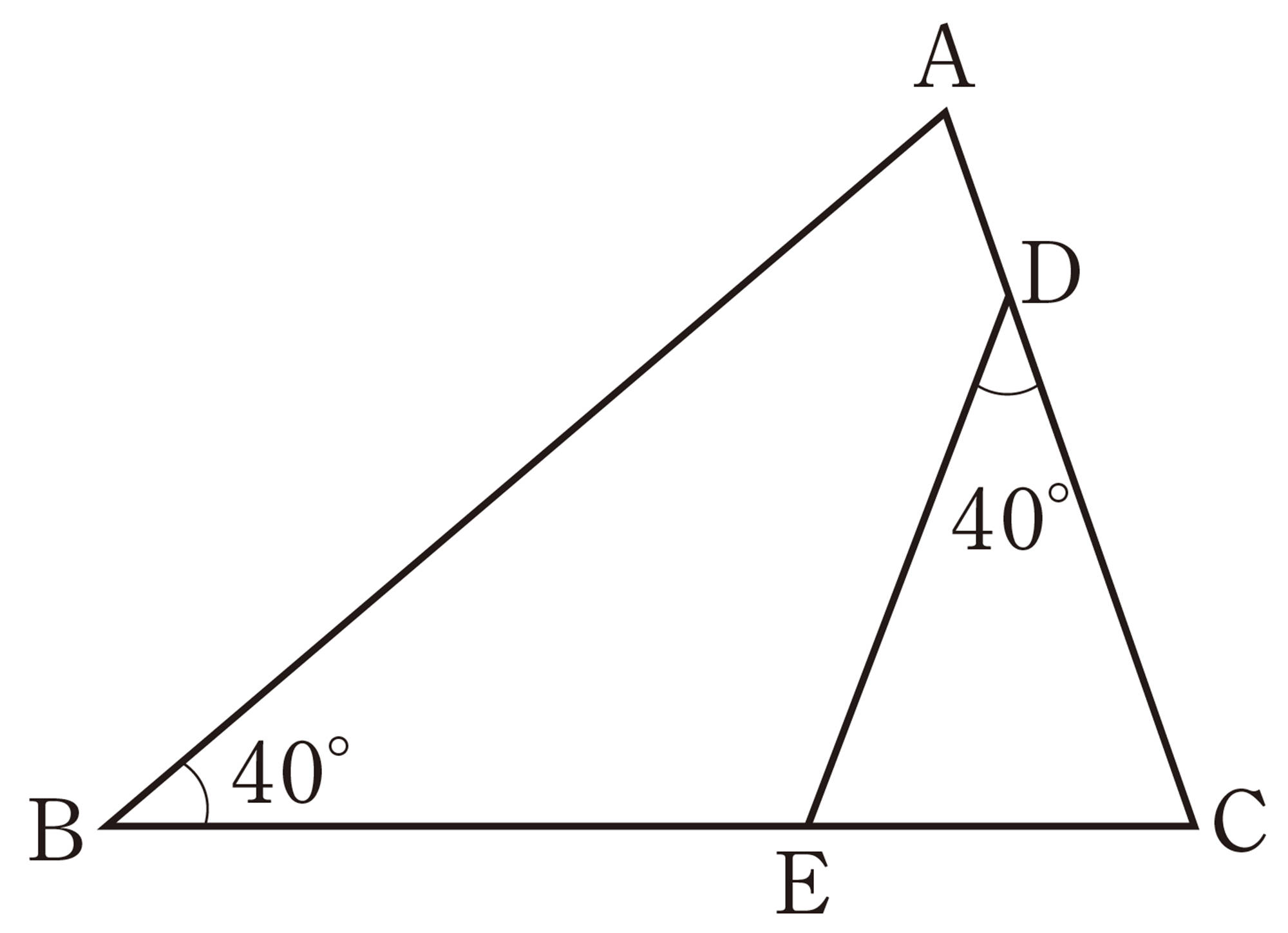
問 3 次の図で,相似な三角形はどれとどれですか。また,そのときの相似条件をいいなさい。
問 4 次の図で,相似な三角形を記号 [mathjax]\(\backsim\) を使って表しなさい。また,そのときの相似条件をいいなさい。
<3年p.153>
三角形の相似条件を使った図形の証明
これからは,「三角形の相似条件」も,証明の根拠として用いることにする。
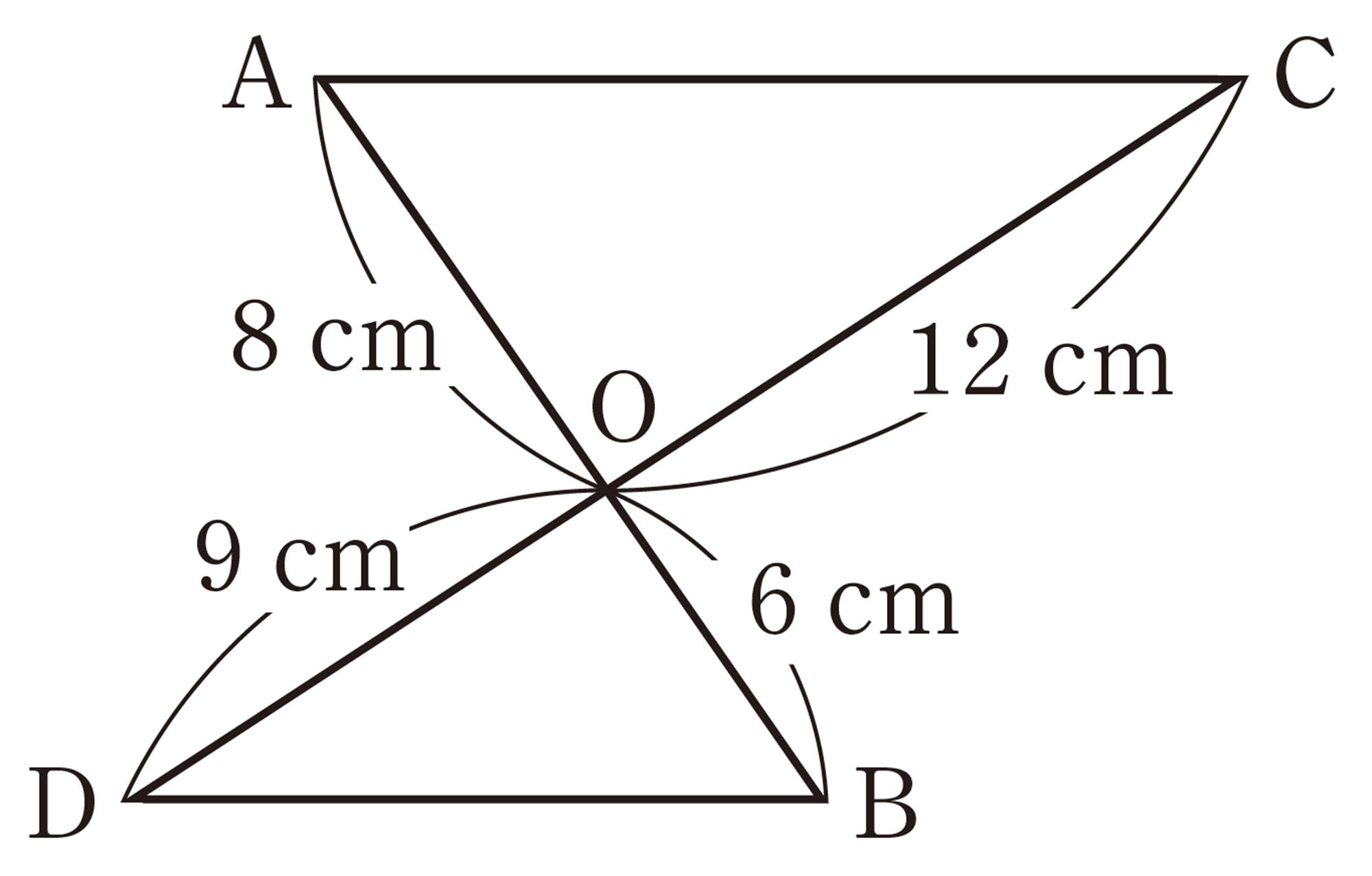
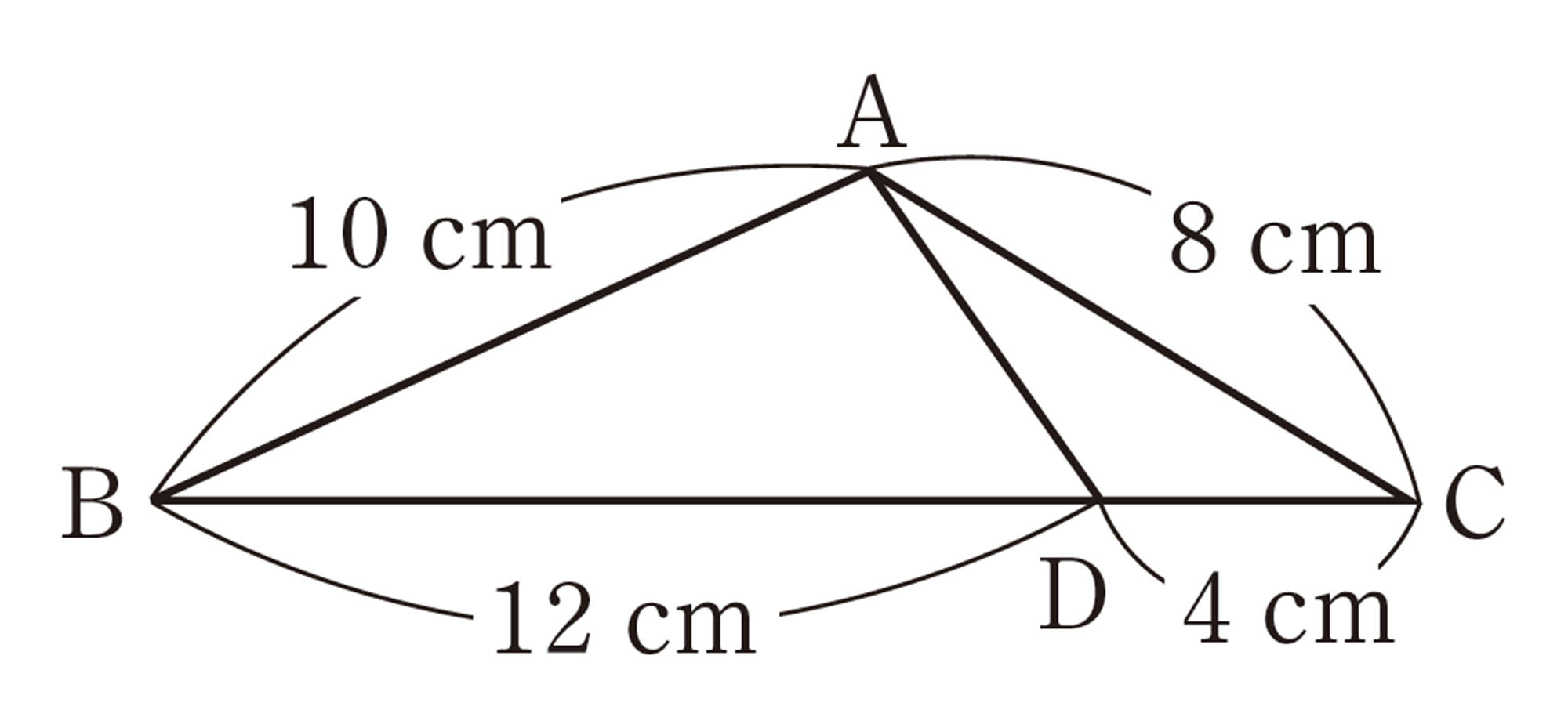
問 5 前ページの問4⑴の図で,[mathjax]\(\triangle AOC \backsim \triangle BOD\)であることを,次のように証明しました。[mathjax]\(\boxed{\phantom{000}}\)をうめて,証明を完成させなさい。
[証明]
[mathjax]\(\triangle AOC\)と[mathjax]\(\triangle BOD\)において,
仮定から, [mathjax]\(\hspace{41pt} AO:BO=8:6=\boxed{\phantom{00}}:\boxed{\phantom{00}} \quad \cdots \cdots\)①
[mathjax]\(\hspace{86pt}CO:DO=12:9=\boxed{\phantom{00}}:\boxed{\phantom{00}} \ \ \cdots \cdots\)②
①,②から,[mathjax]\(\hspace{37pt}AO:BO=CO:DO \hspace{40pt} \cdots \cdots \)③
対頂角は等しいから, [mathjax]\(\boxed{\phantom{0000000}} = \boxed{\phantom{0000000}} \hspace{39pt} \cdots \cdots\)④
③,④より,[mathjax]\(\boxed{\phantom{0000000000000000000}}\)が
それぞれ等しいから,[mathjax]\(\hspace{10pt}\triangle AOC \backsim \triangle BOD\)
証明
<3年p.154>
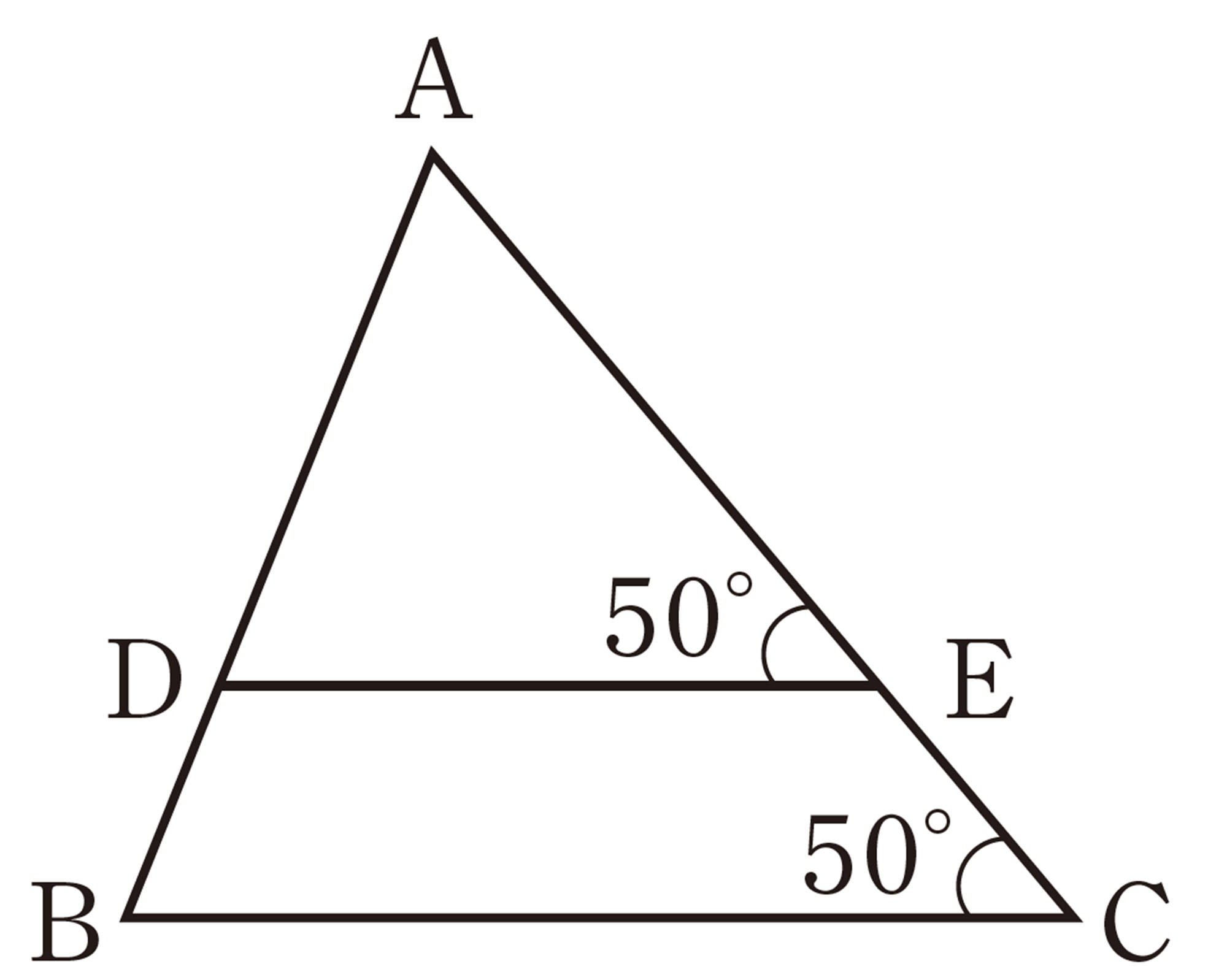
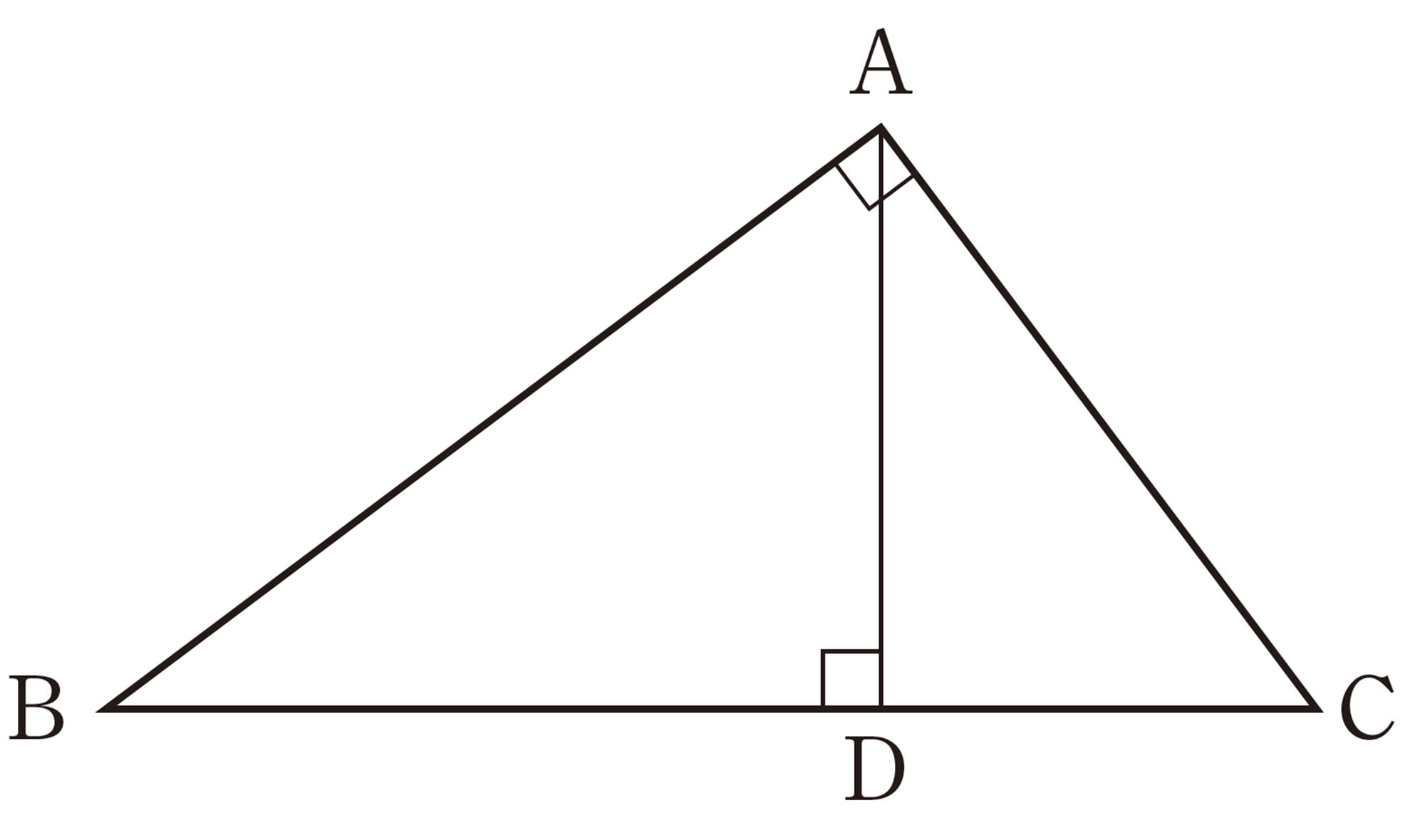
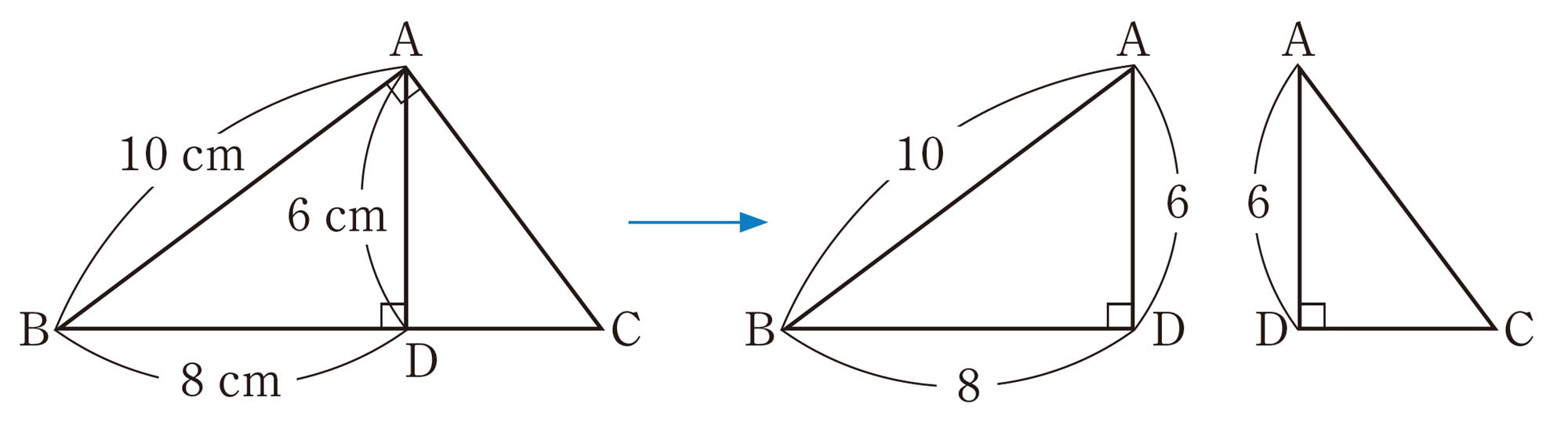
問 6 前ページの例2の図で,[mathjax]\(\triangle ABC \backsim \triangle DAC\) であることを証明しなさい。
例2,問6から,[mathjax]\(\triangle DBA \backsim \triangle DAC\) であることもいえる。すなわち,例2の図で,[mathjax]\(\triangle ABC\),[mathjax]\(\triangle DBA\),[mathjax]\(\triangle DAC\)は,それぞれたがいに相似である。
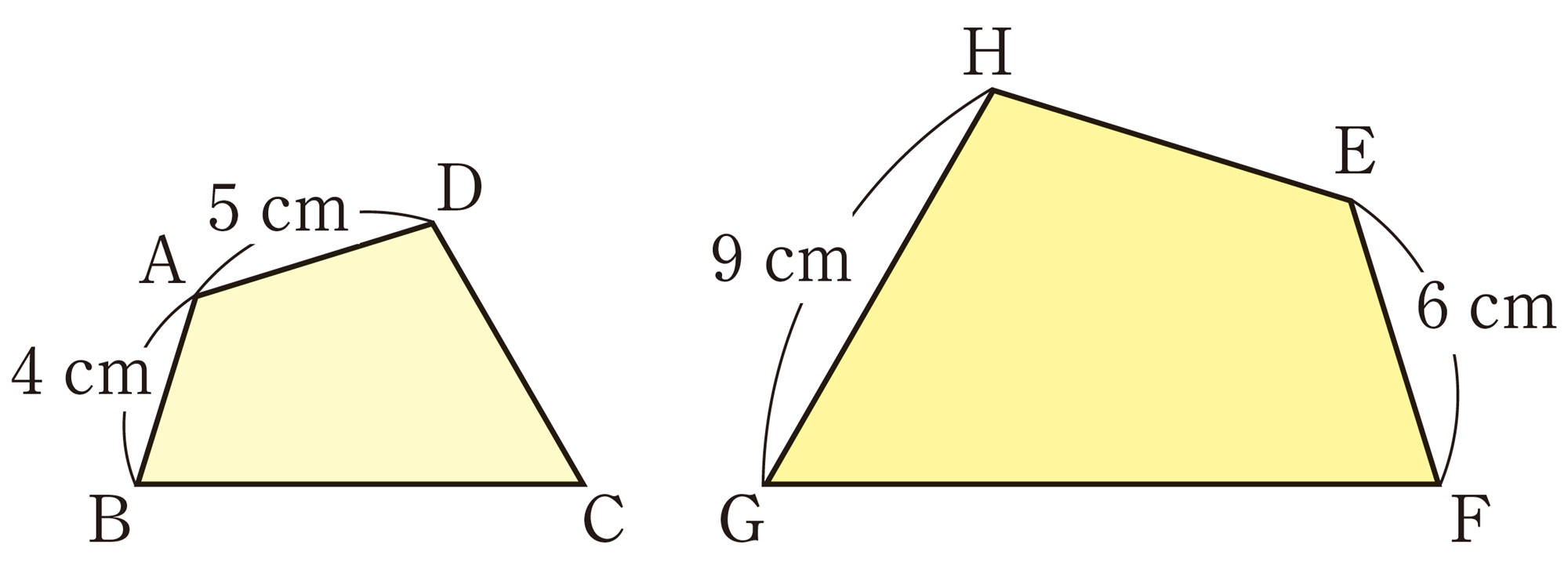
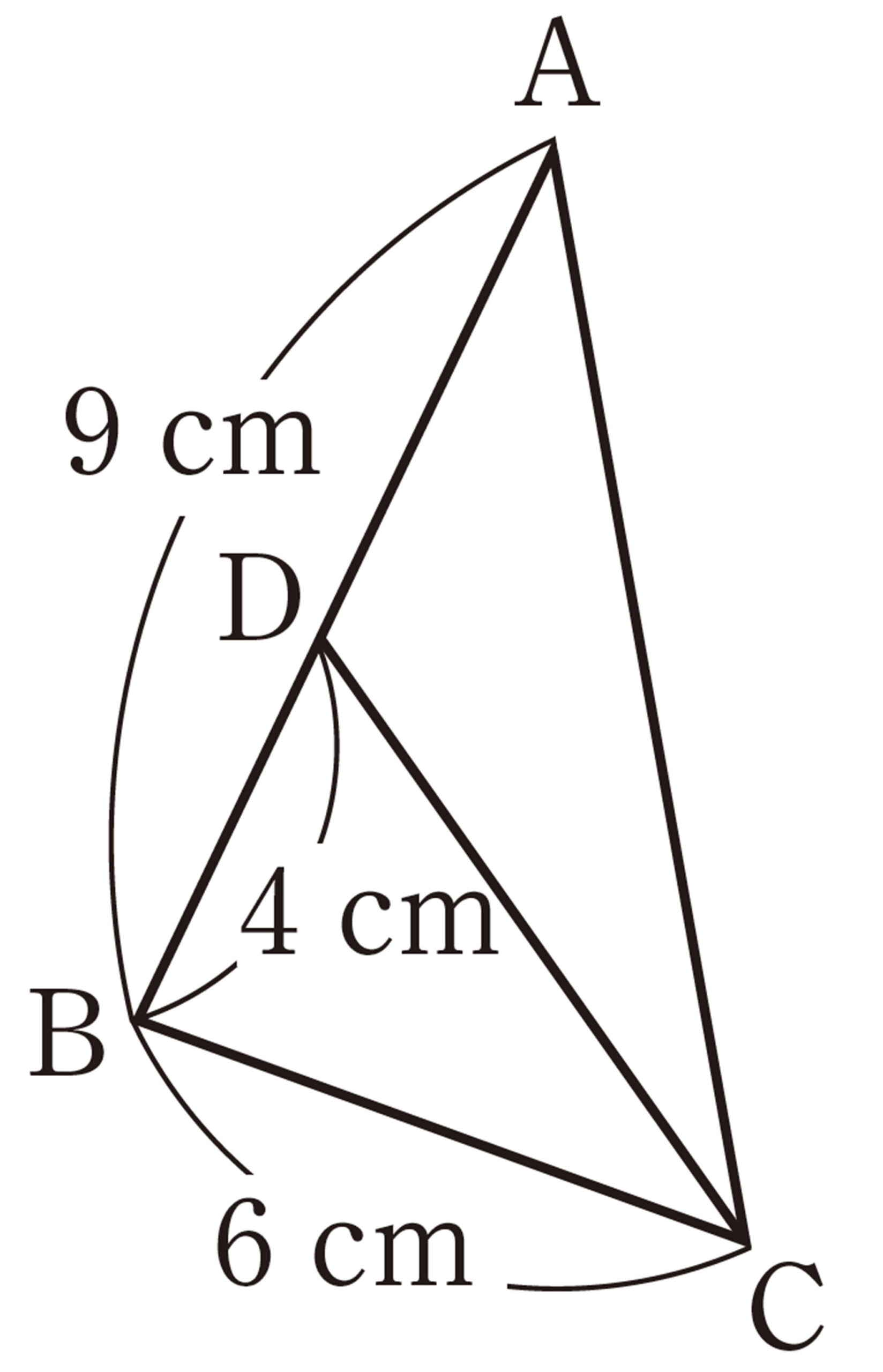
問 7 次の図で,線分AC,DCの長さを求めなさい。
問 9 次の相似の位置にある [mathjax]\(\triangle ABC\) と [mathjax]\(\triangle A´B´C´\) について,下の問いに答えなさい。
⑴ [mathjax]\(\triangle OA´B´ \backsim \triangle OAB\) であることを証明しなさい。
⑵ [mathjax]\(A´B´:AB=3:1\) である理由をいいなさい。
⑶ [mathjax] \(A´B´\)とABの位置関係について,どんなことがいえますか。
⑷ [mathjax]\(\triangle ABC \backsim \triangle A´B´C´\) であることを,三角形の相似条件を使って証明しなさい。
どんなことがわかったかな
2つの三角形が相似であるかどうかは,三角形の相似条件を使えば確かめることができます。
次の課題へ!
相似の考えは,どんなところで使えるのかな?
P.155