<3年p.140>
ふりかえり
【拡大図・縮図】
対応する角の大きさがそれぞれ等しく，対応する辺の長さの比がすべて等しくなるようにのばした図を拡大図といい，縮めた図を縮図という。
拡大図や縮図，合同な図形は，辺の長さや角の大きさを考えてかくことができたね。
【三角形の合同条件】
2つの三角形は，次のどれか1つが成り立てば合同である。
① 3組の辺がそれぞれ等しい。
② 2組の辺とその間の角がそれぞれ等しい。
③ 1組の辺とその両端の角がそれぞれ等しい。
【おうぎ形と中心角】
2つの半径と弧で囲まれた図形をおうぎ形という。おうぎ形で 2 つの半径のつくる角を中心角という。
【円の接線】
円の接線は，接点を通る半径に垂直である。
【角錐・円錐の体積】
底面積Scm²，高さhcmの角錐，円錐の体積をVcm³とすると，
[mathjax]\(V =\dfrac{1}{3}Sh\)
いくつかの場合を考えることで，三角形の合同条件が3つにまとめられることがわかったね。
<3年p.141>
５章 Chapter ５ 相似な図形
1節 相似な図形
2節 平行線と相似
3節 相似な図形の面積比・体積比
地図は，実際の地形の縮図だったね。
縮尺がわかれば，実際の長さもわかったね。
拡大図や縮図を使って，地図をつくってみたいな。
拡大図や縮図の性質を確かめておくといいね。
？ 拡大図や縮図にはどんな性質があるのかな？
<3年p.142>
1節 相似な図形
形は変わる？
タブレットでは，写真を大きくしたり小さくしたりすることができます。
写真を大きくしても，小さくしても映っているものの形は変わりません。
【１】 タブレットで，写真を大きくしても小さくしても，形は変わらないとは，どのようなことか考えてみましょう。
<3年p.143>
【２】 次の図のように，輪ゴムを使って絵をかくと，どんな図形がかけるでしょうか。
方法
① 画用紙に，好きな絵をはる。
② 同じ大きさの輪ゴムを2本つなぐ。
③ 画用紙に画びょうをさし，輪ゴムの一方を画びょうにかけて固定し，反対側の輪ゴムに鉛筆をかける。
④ 輪ゴムの結び目が絵に合うようにして，鉛筆を動かしていく。
【３】 【２】の方法②で，つなぐ輪ゴムの本数を3本，4本，…と変えて，画びょうから1つ目の結び目が絵に合うようにして鉛筆を動かすと，かける絵の大きさはどのように変わるでしょうか。
次の課題へ！
上の方法でかいた図ともとの図は，拡大図と縮図の関係になっているのかな？
P.144
<3年p.144>
１ 相似な図形
相似の位置
Q Question
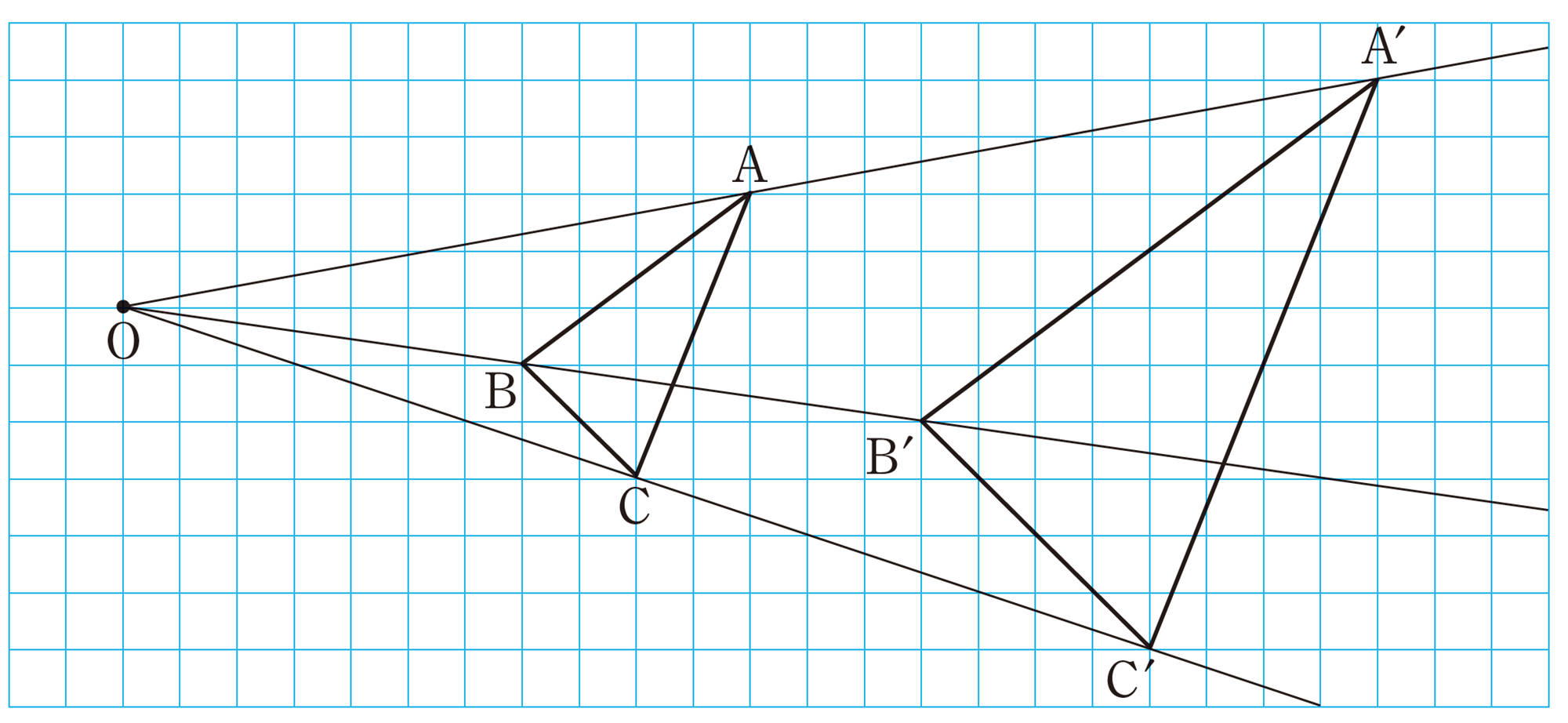
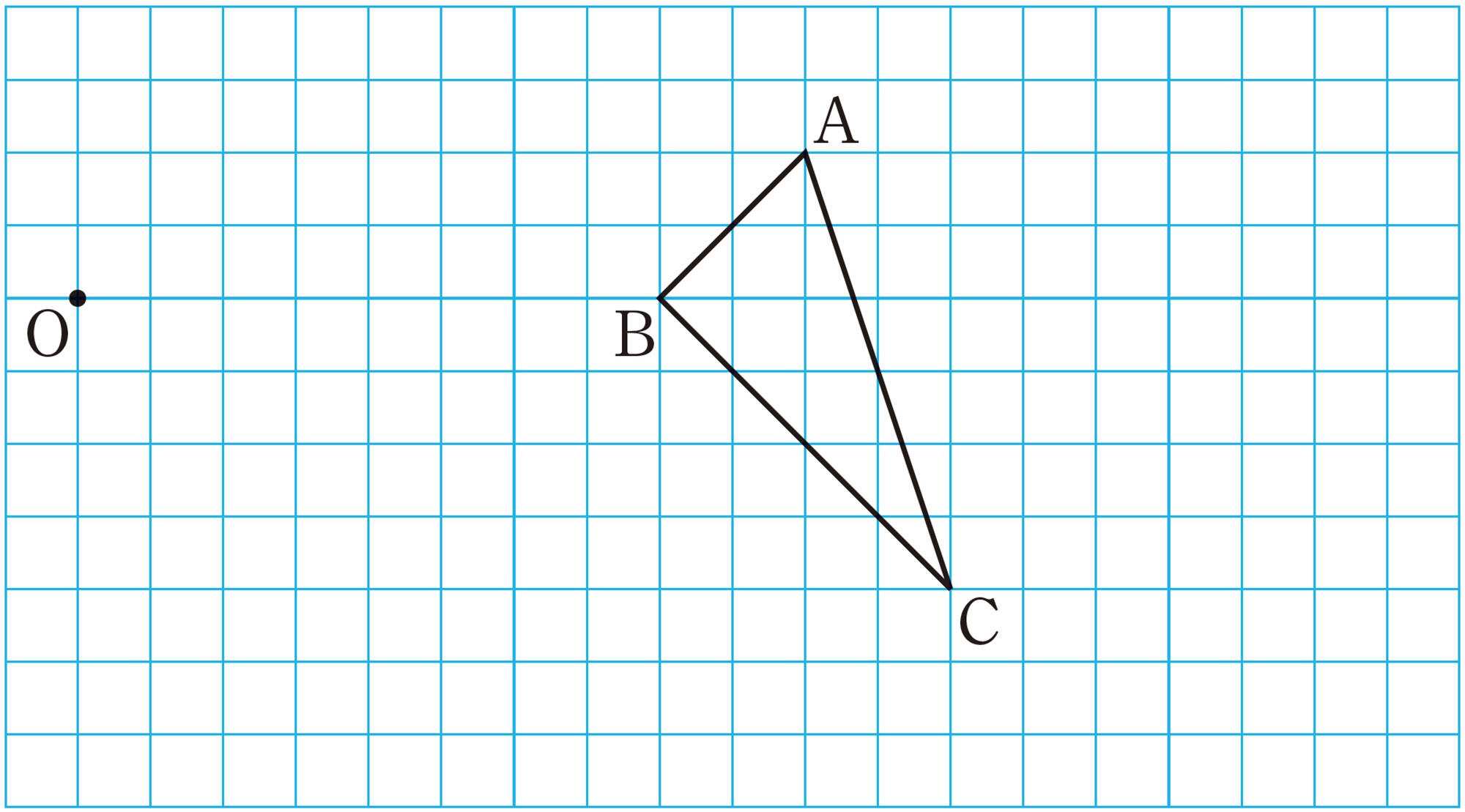
次の図のように，[mathjax]\(\triangle ABC\)があるとき，適当な点Oを決め，[mathjax]\(OA´ =2OA\)となるように点[mathjax] \(A´\)をとり，同じ方法で，点[mathjax] \(B´\)，点 [mathjax] \(C´\)をとって， [mathjax]\(\triangle A´B´C´\)をかきました。
[mathjax]\(\triangle A´B´C´\)は[mathjax]\(\triangle ABC\)の何倍の拡大図になっているでしょうか。
方眼のマスを使うと，辺の長さが何倍になっているかわかるね。
角の大きさはどうなっているかな。
見方・考え方
図のどこに着目して考えればいいかな。
目標 ▷ 適当な点を決めてかいた拡大図と縮図の関係について調べよう。
【Q】 のように図形をかくと，[mathjax]\(\triangle ABC\) と[mathjax]\(\triangle A´B´C´\)は拡大図と縮図の関係になっている。このように，一方の図形を拡大または縮小すると，他方の図形と合同になるとき，2つの図形は相似であるという。
相似な[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle A´B´C´\)で，点Aと点[mathjax] \(A´\)などを対応する点，辺ABと辺[mathjax] \(A´B´\)などを対応する辺，[mathjax]\(\angle A\)と[mathjax]\(\angle A´\)などを対応する角という。
<3年p.145>
[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle A´B´C´\)が相似であることを，記号 [mathjax]\(\backsim\) を使って
[mathjax]\(\triangle ABC \backsim \triangle A´B´C´\)
と表し，「三角形ABC相似三角形[mathjax] \(A´B´C´\)」と読む。
注意 相似の記号[mathjax]\(\backsim\)を使うときは，対応する点が同じ順序になるように表す。
また，前ページの Q の[mathjax]\(\triangle ABC\) と[mathjax]\(\triangle A´B´C´\)のように，2つの図形の対応する点を通る直線がすべて1点Oを通り，点Oから対応する点までの距離の比がすべて等しいとき，この2つの図形は相似の位置にあるといい，点Oを相似の中心という。
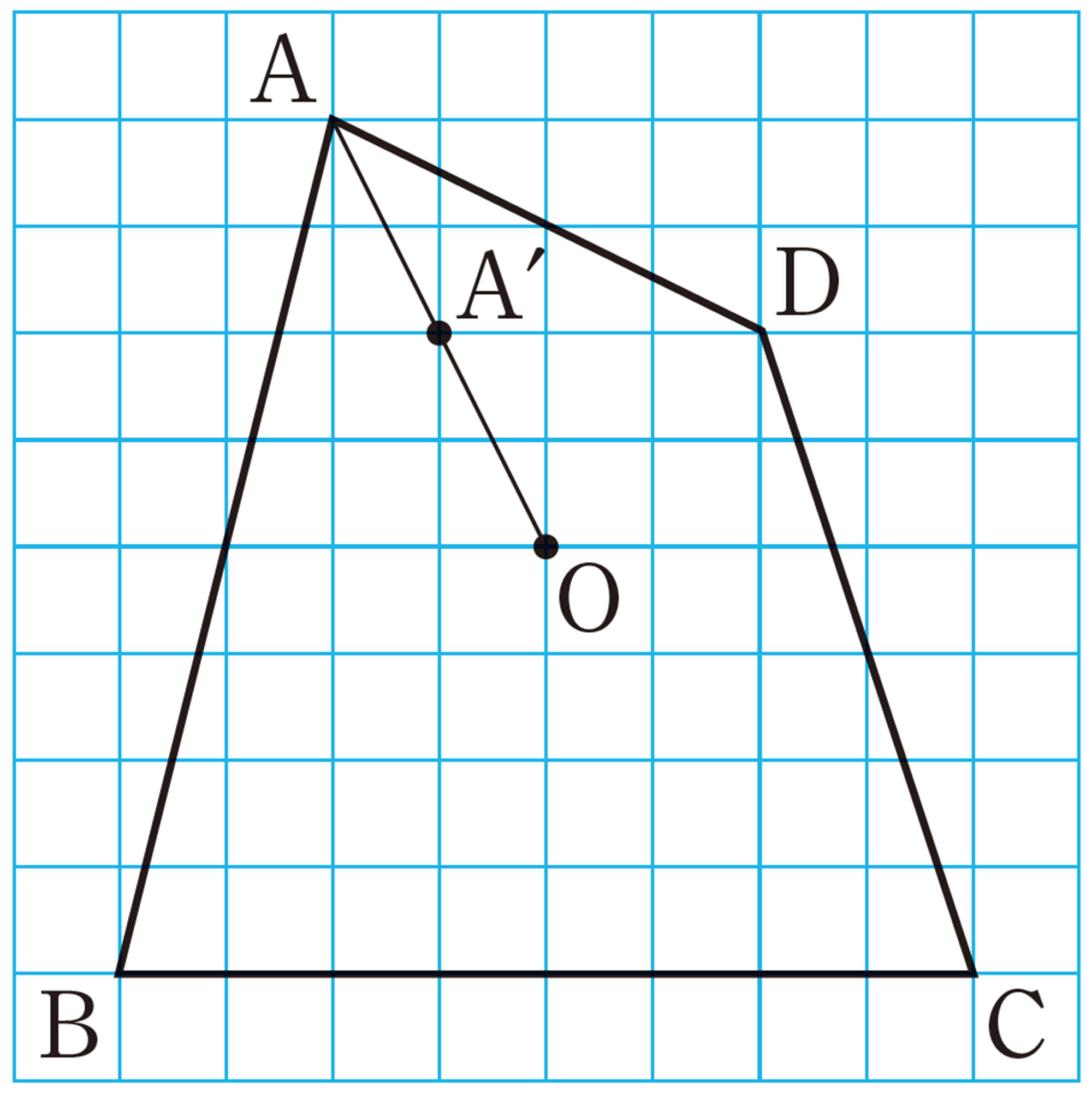
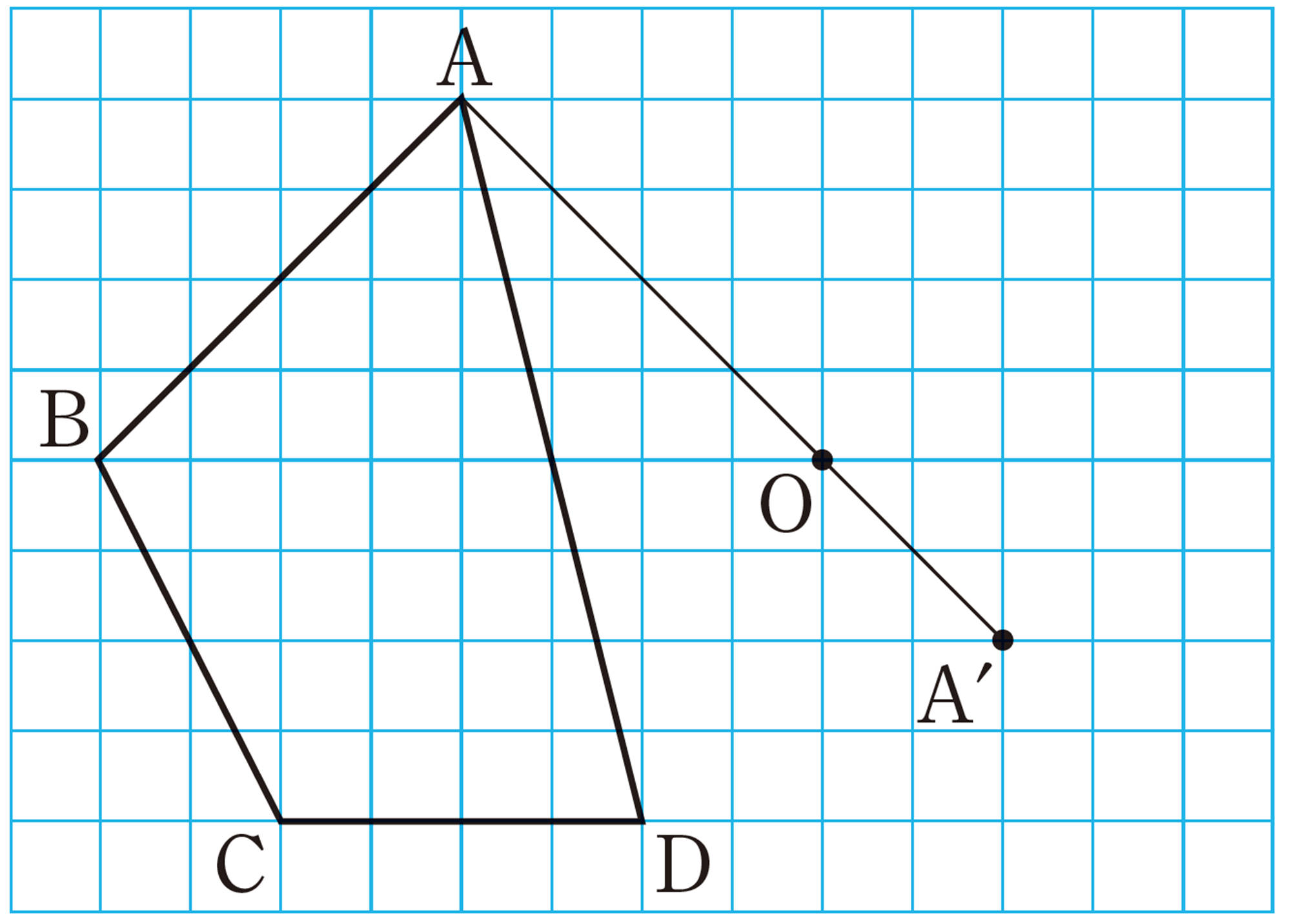
問 １ 次の⑴，⑵の図で，点Oを相似の中心として，四角形ABCDを[mathjax]\(\dfrac{1}{2}\)に縮小した四角形[mathjax] \(A´B´C´D´\)を完成させなさい。
⑵は，向きを逆にした四角形になるね。
⑴
⑵
問 ２ 右の図で，点Oを相似の中心として，[mathjax]\(\triangle ABC\)を[mathjax]\(\dfrac{3}{2}\)倍に拡大した[mathjax]\(\triangle A´B´C´\)をかきなさい。
問 ３ 143ページの【２】 について，相似の中心がどこか答えなさい。
どんなことがわかったかな
拡大図や縮図の関係になっている2つの図形を，相似であるといいます。
次の課題へ！
相似な図形にはどんな性質があるのかな？
P.146
