<3年p.116>
3 関数 [mathjax]\(y=ax²\) の値の変化
Q Question
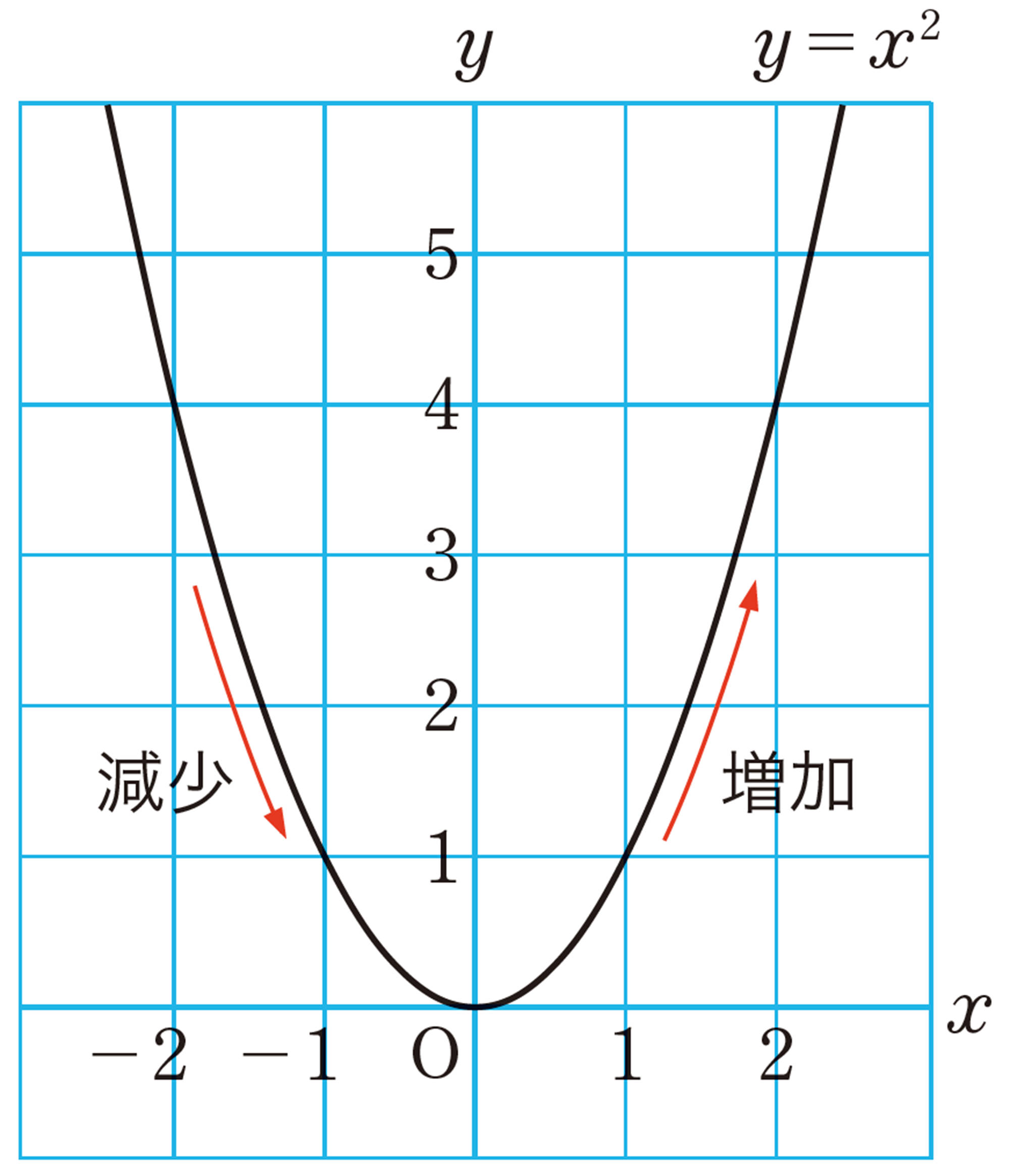
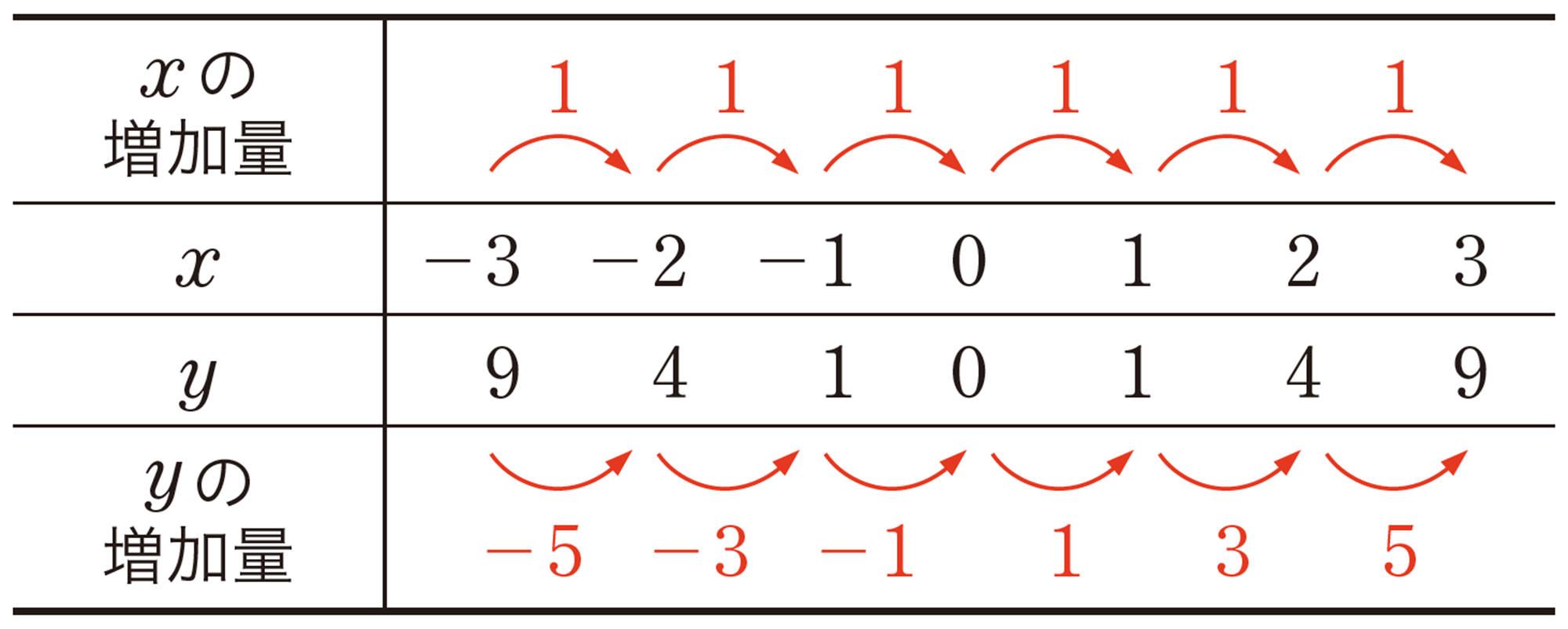
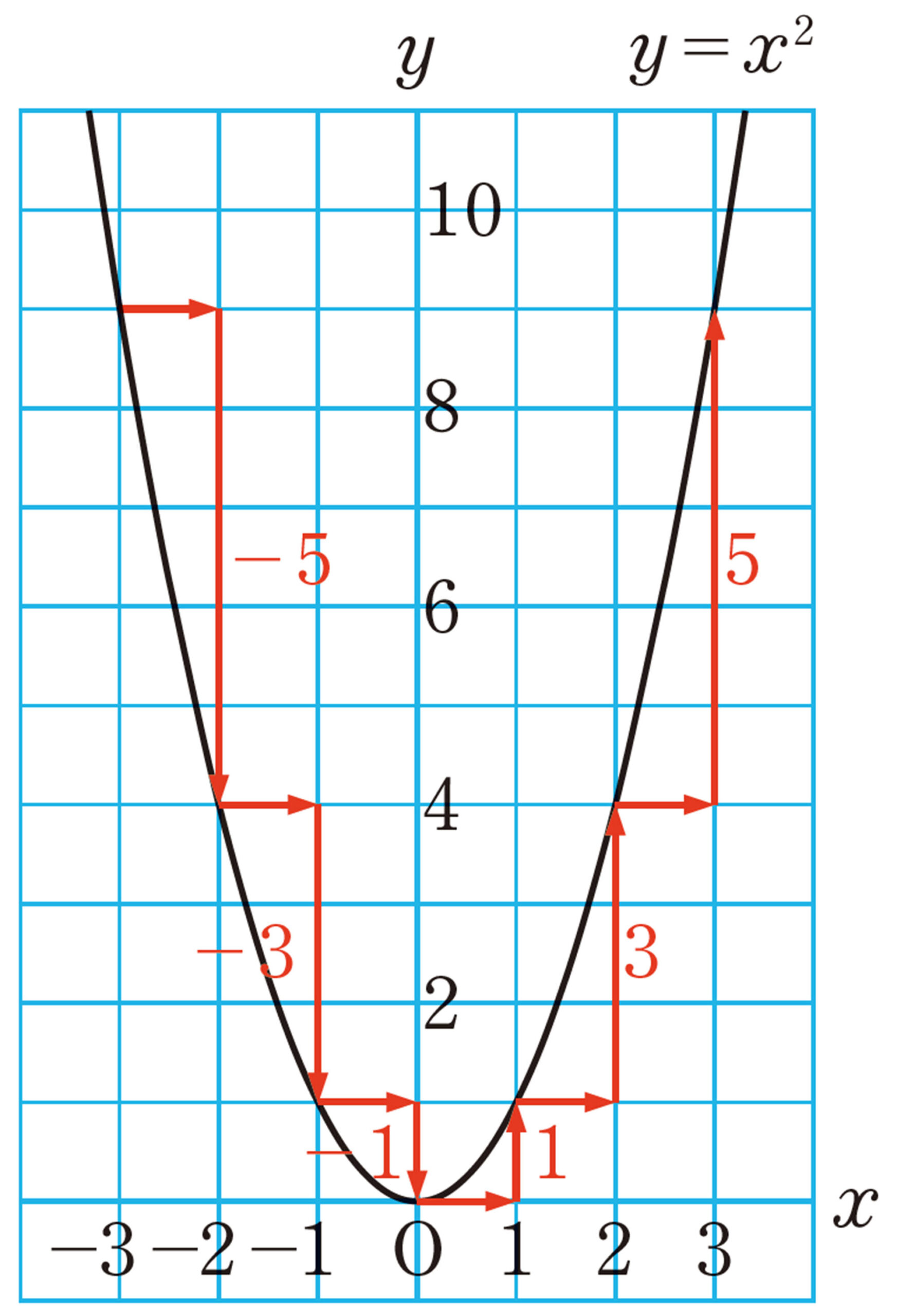
関数 [mathjax]\(y=x²\) では,xの値が増加するにつれて,それに対応するyの値はどのように変化しているでしょうか。109ページのグラフを使って調べてみましょう。

1次関数のグラフとは,どんなところがちがうのかな。
見方・考え方
グラフのどこに着目して考えればいいかな。
目標 ▷ グラフをもとにして,関数 [mathjax]\(y=ax²\) の値の変化について調べよう。
問 1 関数[mathjax]\(y=\dfrac{1}{2}x²\)では,xの値が増加するにつれて,それに対応するyの値はどのように変化しますか。109ページの図にかき入れたグラフを使って調べなさい。
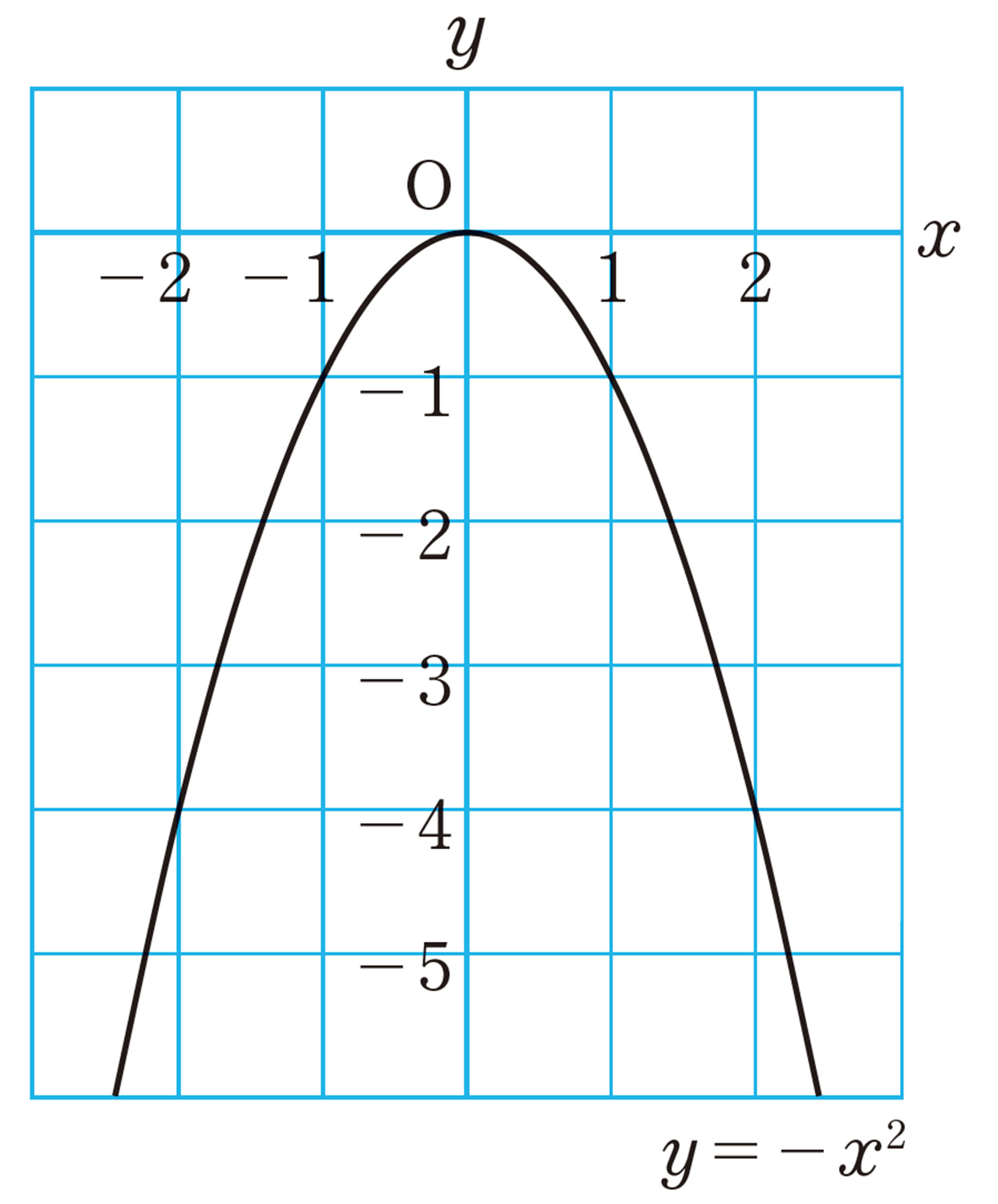
[mathjax]\(y=-x²\) では,[mathjax]\(x=0\) のとき [mathjax]\(y=0\) となり,yの値は増加から減少に変わる。このとき,yは最大値0をとる。
<3年p.117>
関数[mathjax]\(y=ax²\)で,xの変域が限られている場合のyの変域を調べてみよう。
例 1 関数[mathjax]\(y=\dfrac{1}{4}x²\)で,xの変域が[mathjax]\(-2 \leqq x \leqq 4\)のときのyの変域を求めなさい。
考え方 グラフを使って,xの変域におけるyの値の変化を調べる。
解答
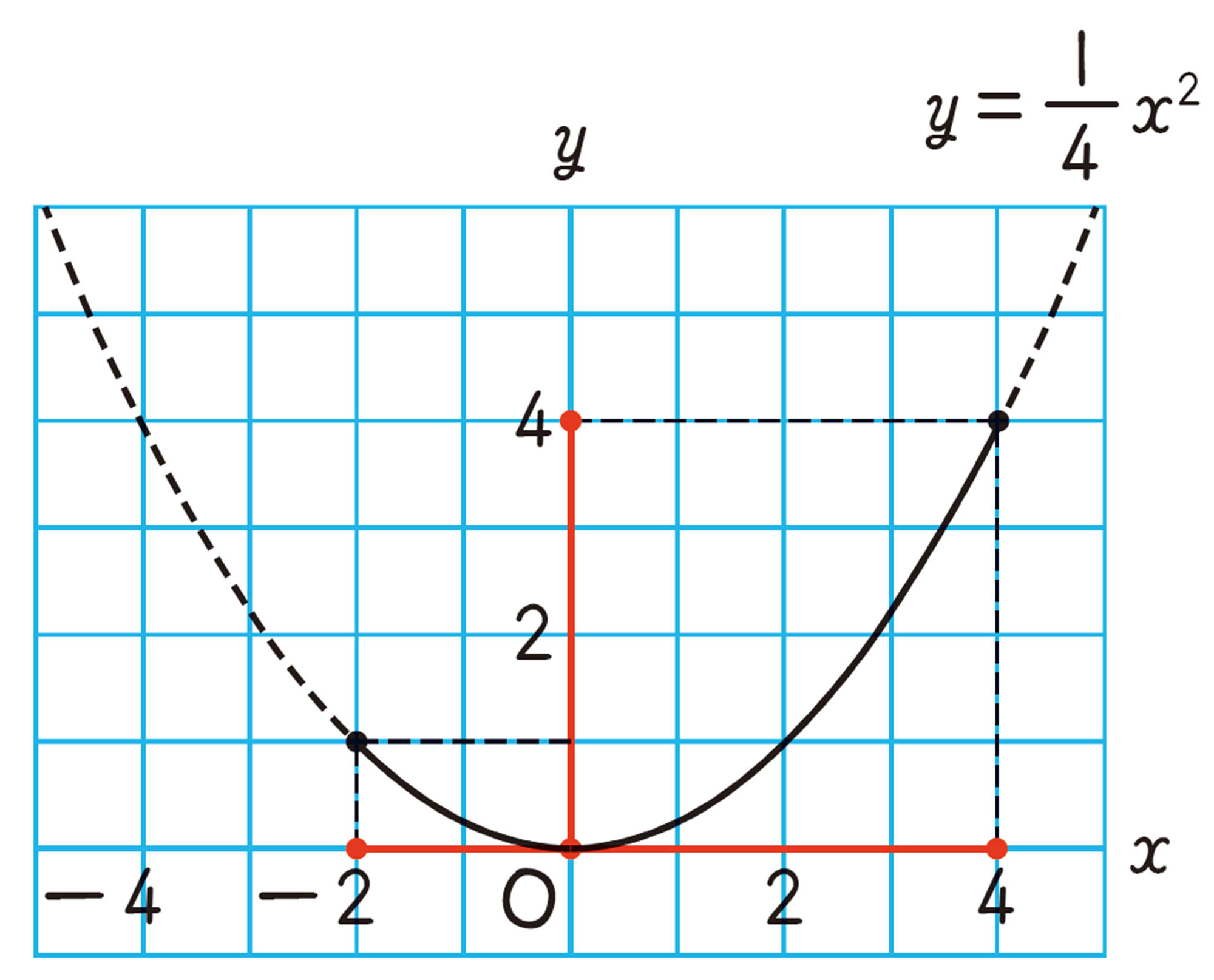
[mathjax] \( x \) の変域が [mathjax] \( -2 \leqq x \leqq 4 \) のとき,
[mathjax] \( y=\dfrac{1}{4}x² \) のグラフは右の図の実線の部分になる。
[mathjax] \(-2 \leqq x \leqq 0\) のとき,[mathjax] \( y \) の値は1 から0まで減少する。
[mathjax] \( 0 \leqq x \leqq 4\) のとき,[mathjax] \( y \) の値は
0から4 まで増加する。
したがって, [mathjax] \( y \) の変域は,
[mathjax] \(0 \leqq y \leqq 4\)
答 [mathjax] \( 0 \leqq y \leqq 4\)
[mathjax]\(x=-2\)のときのyの値は,最小値にはならないね。

問 3 [mathjax]\(y=\dfrac{1}{4}x²\)で,xの変域が次の⑴,⑵のときのyの変域を求めなさい。
⑴ [mathjax]\(-4 \leqq x \leqq 2\)
⑵ [mathjax]\(2 \leqq x \leqq 6\)
問 4 次の関数で,xの変域が [mathjax]\(-2 \leqq x \leqq 3\) のときのyの変域を求めなさい。
⑴ [mathjax]\(y=3x²\)
⑵ [mathjax]\(y=-\dfrac{1}{2}x²\)
[mathjax] \(109\),[mathjax] \(112\)ページにかき入れたグラフを利用しよう。

<3年p.118>
変化の割合
Q Question

1次関数と同じように,つねに変化の割合は一定になるのかな。
ふりかえり▷2年
[mathjax]\((\mathsf{変化の割合})=\dfrac{(y \mathsf{の増加量})}{(x \mathsf{の増加量})}\)
問 5 [mathjax]\(y=x²\) について,次の問いに答えなさい。
⑴ [mathjax]\(x \lt 0\)のときと[mathjax]\(x \gt 0\)のときでは,変化の割合にどんなちがいがありますか。
⑵ xの値の絶対値が大きくなるにつれて,yの値の変化のしかたはどのように変わりますか。
問 6 関数[mathjax]\(y=-x²\)について対応の表をつくり,問5と同じことを調べなさい。
<3年p.119>
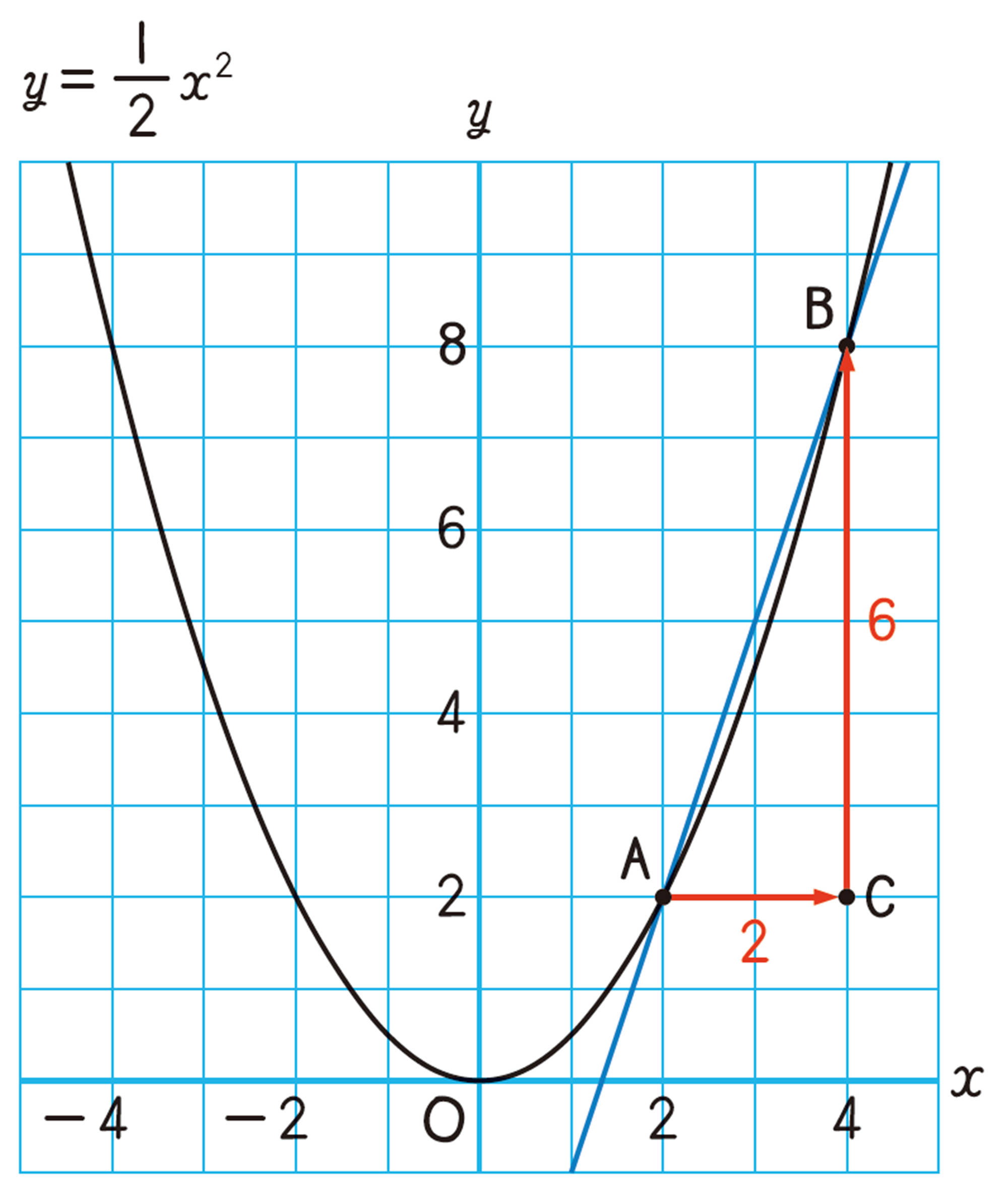
例 2 関数[mathjax]\(y=\dfrac{1}{2}x²\)で,xの値が2から4まで増加するときの変化の割合を求めなさい。
解答
[mathjax] \(x=2\) のとき,
[mathjax] \(x=4\) のとき,
したがって, 変化の割合は,
答 3
例2の図で,2点 A[mathjax] \((2,2)\),B[mathjax] \((4,8)\)を通る直線の傾きは[mathjax]\(\dfrac{CB}{AC}\)である。すなわち,xの値が2から4まで増加するときの変化の割合が,この直線の傾きを表している。
問 7 [mathjax]\(y=\dfrac{1}{2}x²\)で,xの値が次のように増加するときの変化の割合を求めなさい。
⑴ 4から6まで
⑵ [mathjax] \(-4\)から[mathjax] \(-2\)まで
問 8 関数[mathjax]\(y=-2x²\)で,xの値が次のように増加するときの変化の割合を求めなさい。
⑴ 2から5まで
⑵ [mathjax] \(-3\)から0まで
これまで調べてきたように,関数[mathjax]\(y=ax²\)の変化の割合は,1次関数と異なり,一定ではない。
どんなことがわかったかな
関数[mathjax]\(y=ax²\)の変化の割合は一定ではなく,[mathjax]\(x=0\)を境としてyの値は増加と減少が変わります。
次の課題へ!
関数[mathjax]\(y=ax²\)の変化の割合には,どんな意味があるのかな?
P.120

<3年p.120>
平均の速さ
Q Question
左の写真のように,空中で物を落下させたとき,落下した距離は時間の2乗に比例し,落下し始めてからx秒間にym 落下したとすると, xとyの間には,[mathjax]\(y=4.9x²\)の関係があることが知られています。
次の表のxの値に対応するyの値を求め,表を完成させましょう。また,変化の割合はどんなことを表しているか話し合ってみましょう。

時間の経過とともに,同じ時間に落下する距離は増えるけど,変化の割合と何か関係があるのかな。
見方・考え方
いろいろな場合を調べて考えられるかな。
目標 ▷ 物が落下するときの関数[mathjax]\(y=4.9x²\)の変化の割合が,どんな意味をもつのかを考えよう。
物が落下するときの平均の速さは,次の式で求めることができる。
[mathjax]\((\mathsf{平均の速さ})= \dfrac{(\mathsf{落下した距離})}{(\mathsf{落下した時間})}= \dfrac{(y\mathsf{の増加量})}{(x\mathsf{の増加量})}\)
したがって,[mathjax]\(y=4.9x²\)の変化の割合は,平均の速さを表している。平均の速さを求めると,次のようになる。
0秒後~1秒後 [mathjax]\(\dfrac{4.9-0}{1-0}=4.9\) [mathjax]\(4.9\)m/s
1秒後~2秒後 [mathjax]\(\dfrac{19.6-4.9}{2-1}=14.7\) [mathjax]\(14.7\)m/s
問 9 【Q】について,次の平均の速さを求めなさい。
⑴ 2秒後 ~3秒後
⑵ 3秒後 ~4秒後
⑶ 4秒後 ~5秒後
発展 高等学校
▲トライ 上のように,1秒後 ~2秒後の平均の速さは[mathjax]\(14.7\)m/sでしたが,
1秒後~[mathjax]\(1.1\)秒後,1秒後 ~[mathjax]\(1.01\)秒後,…
と時間の幅を短くしていくと,平均の速さはどのように変化するかを調べよう。また,その結果から1秒後の瞬間の速さを予想してみよう。