<3年p.107>
2 関数[mathjax]\(y=ax²\)のグラフ
[mathjax]\(y=x²\)のグラフ
Q Question
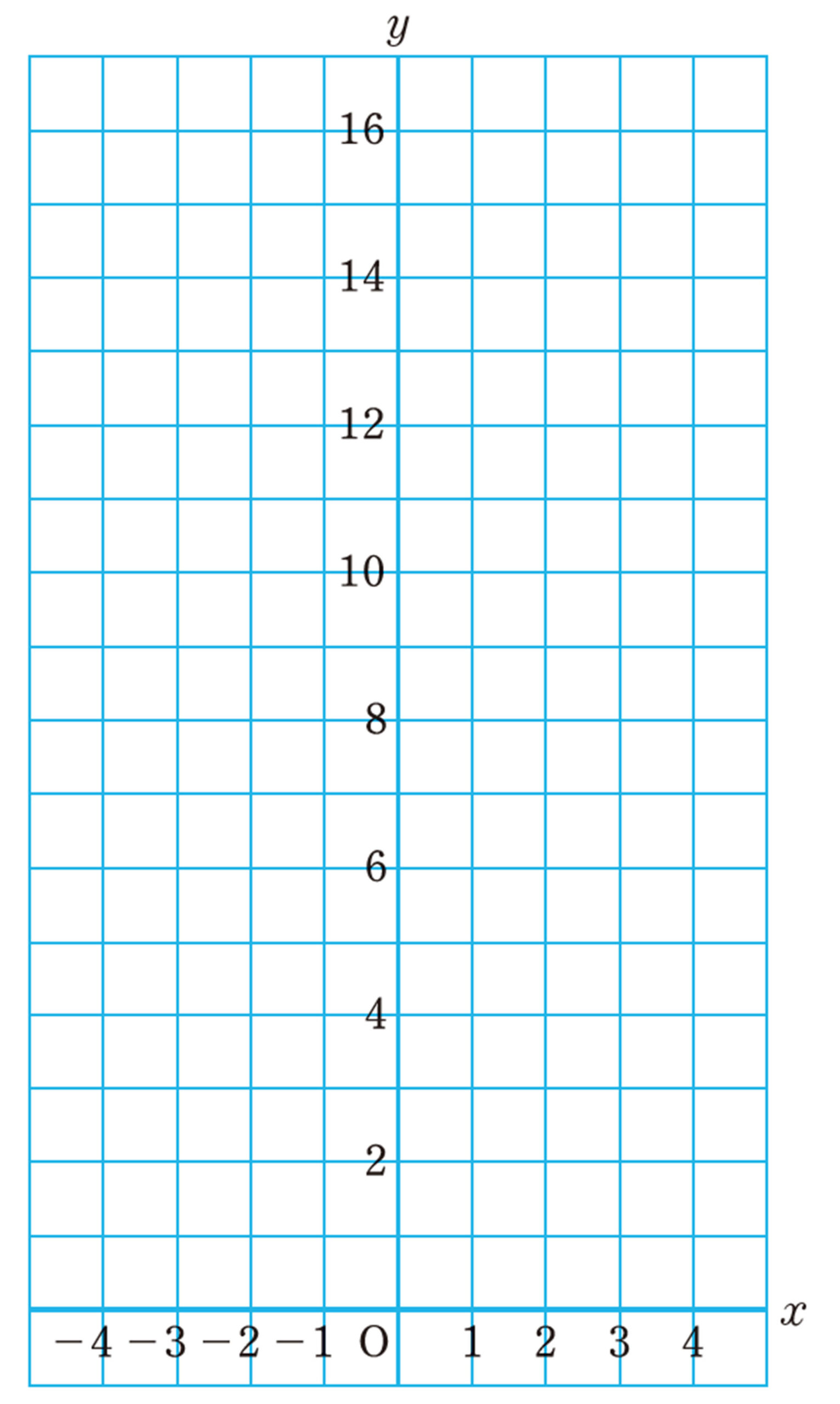
関数[mathjax]\(y=x²\)について,次の表を完成させて,対応するx,yの値の組を座標とする点を,下の図にかき入れてみましょう。
また,グラフがどんな形になるか考えてみましょう。
目標 ▷ 関数[mathjax]\(y=ax²\)のグラフや,その特徴について調べよう。
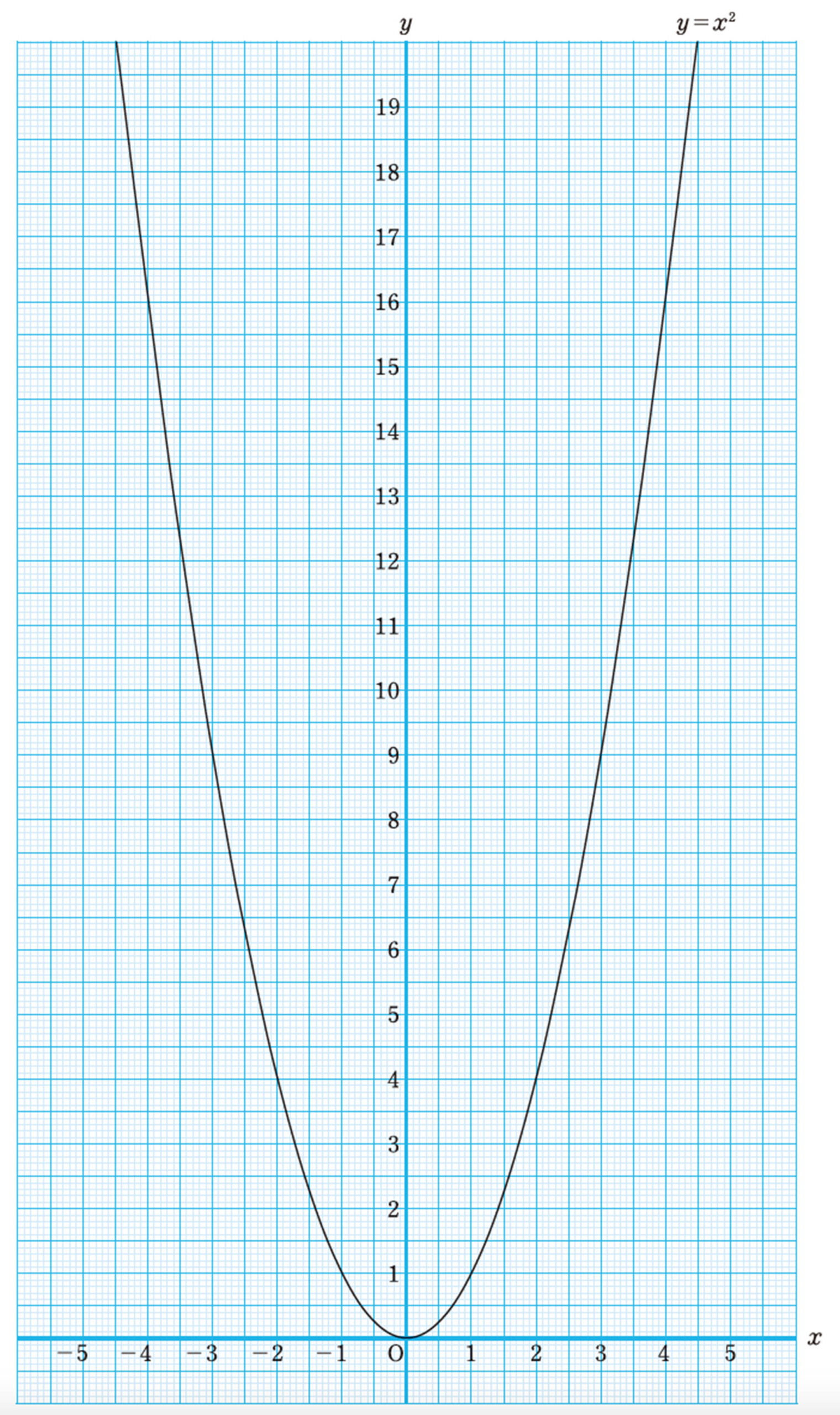
【Q】 でかき入れた点は,一直線上には並ばない。さらに多くの点をとり,どんなグラフになるかを調べてみよう。
<3年p.108>
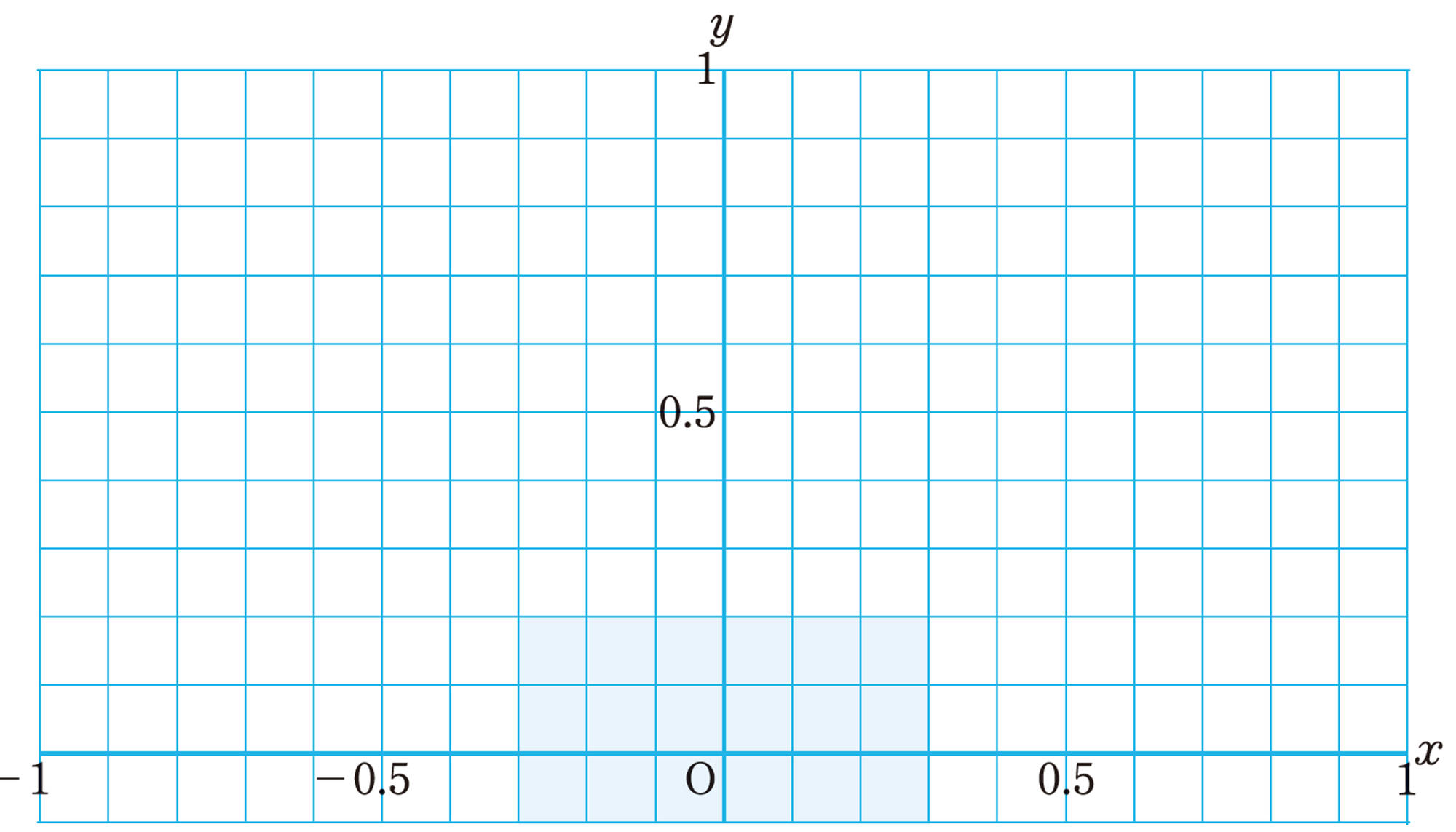
問 1 [mathjax]\(y=x²\)で,xの値を[mathjax] \(-1\)から1まで[mathjax]\(0.1\)おきにとってyの値を求め,次の表を完成させなさい。また,対応するx,yの値の組を座標とする点を下の図にかき入れなさい。
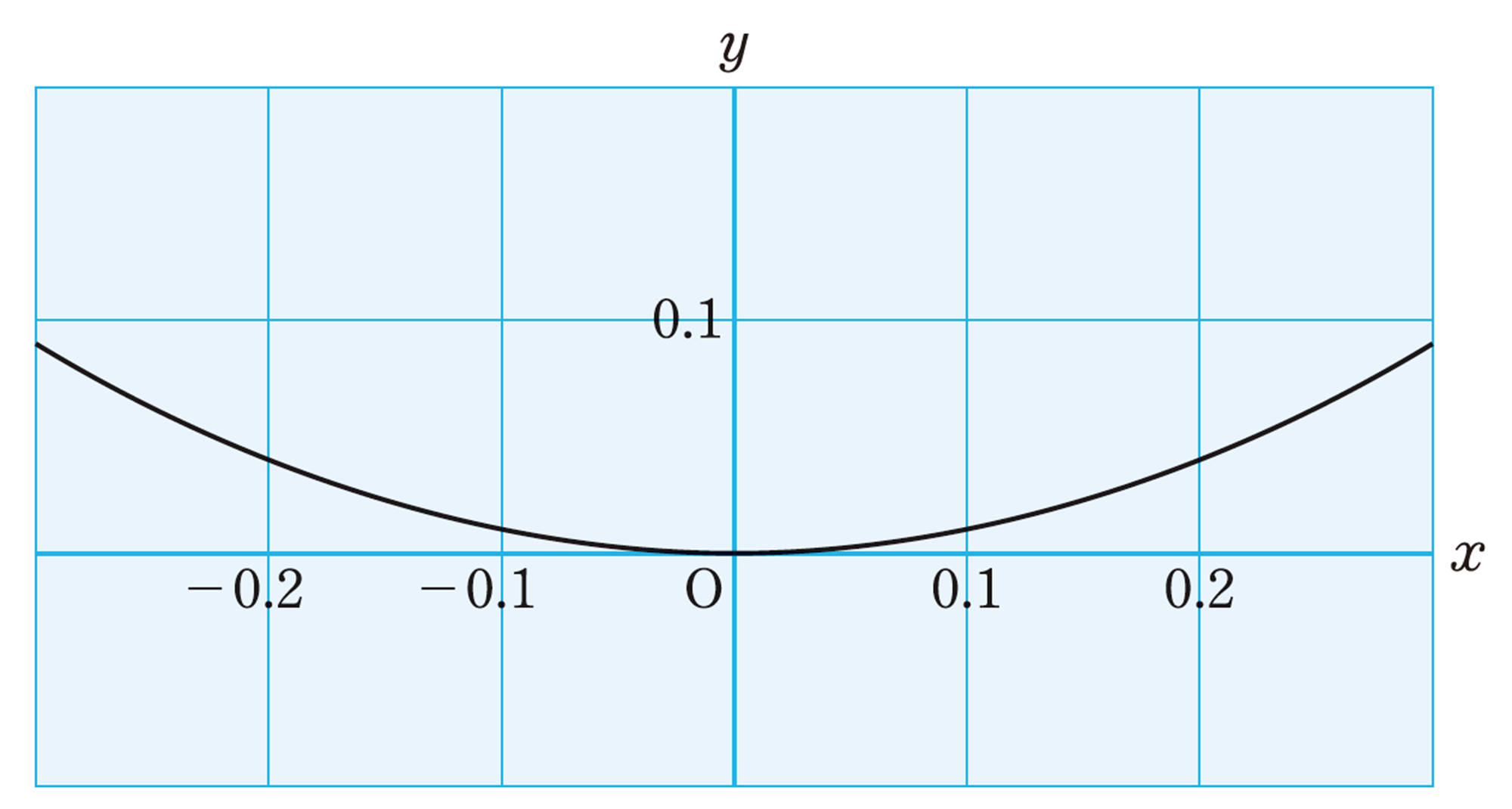
[mathjax]\(y=x²\)で,さらに多くの点をとっていくと,点の集合は1つのなめらかな曲線になる。原点の付近をさらに拡大すると,次の図のようになる。
<3年p.110>
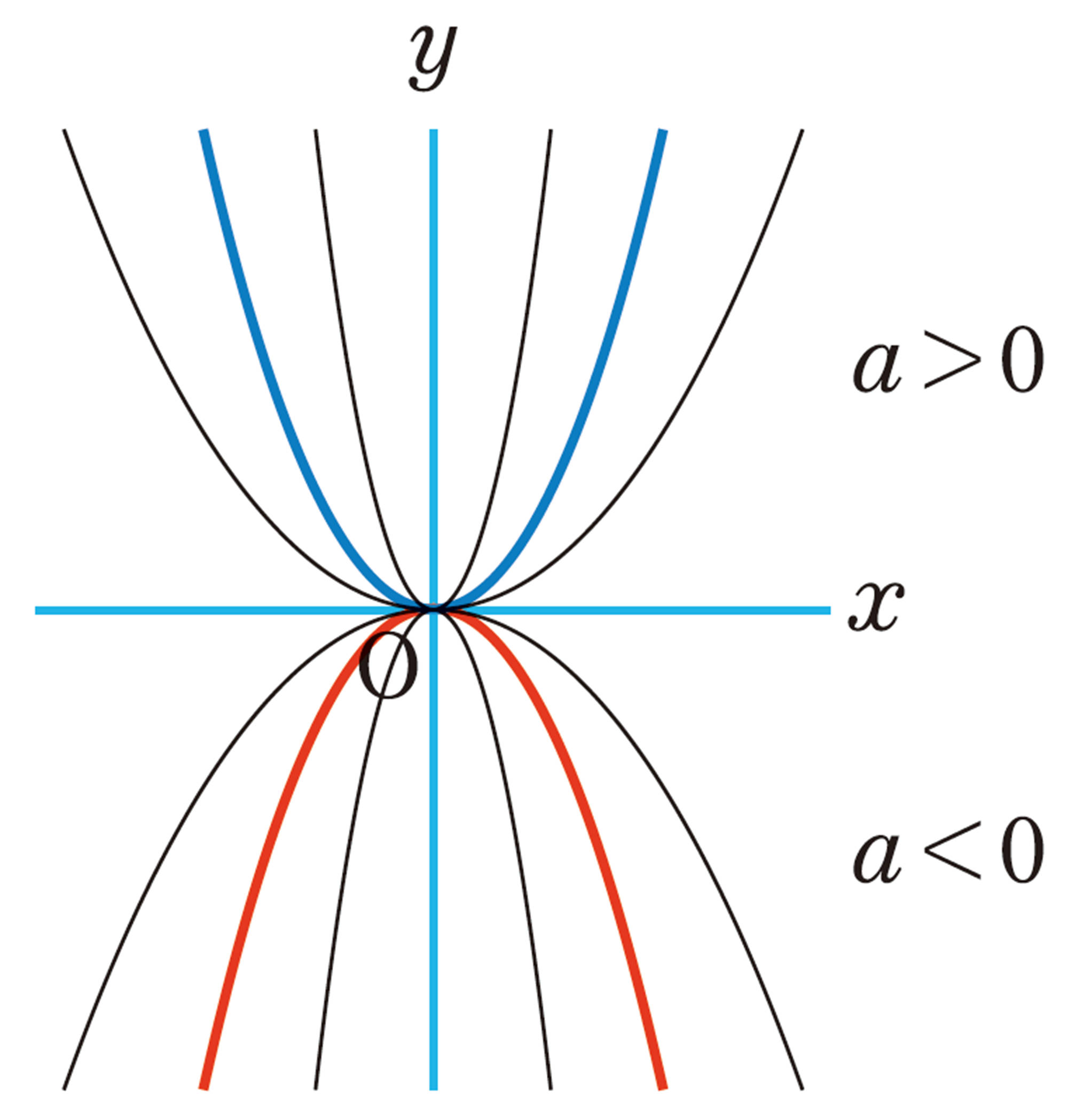
[mathjax]\(a\gt 0\)のときの[mathjax]\(y=ax²\)のグラフ
Q Question
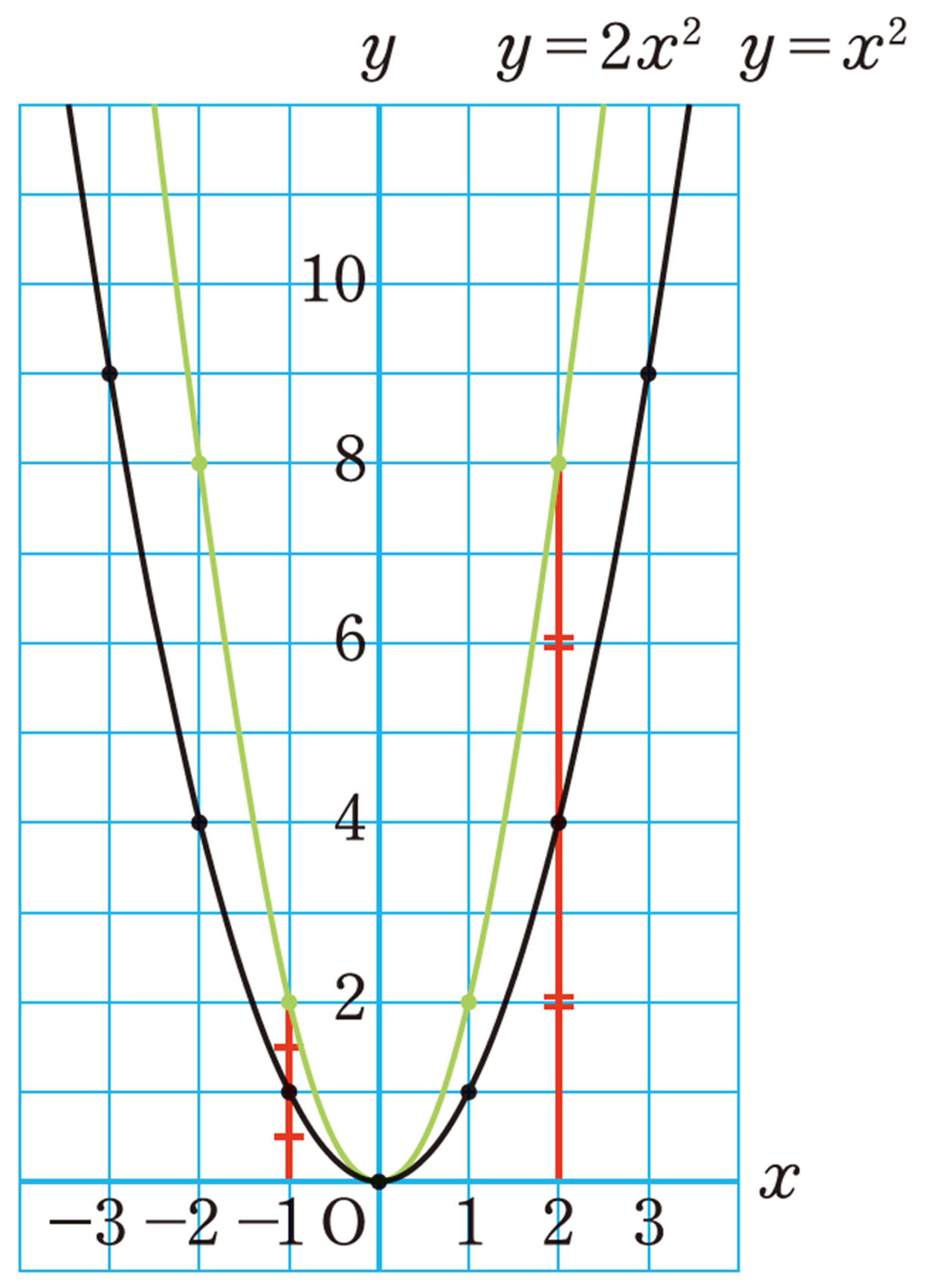
関数[mathjax]\(y=2x²\)について,次の問いに答えましょう。
⑴ 次の表を完成させましょう。
⑵ 上の表をもとに,[mathjax]\(y=2x²\)のグラフを,前ページの図にかき入れ,[mathjax]\(y=x²\)のグラフと比べてみましょう。

比例[mathjax]\(y=ax\)のグラフは,比例定数aが変わると傾きが変わったね。
関数[mathjax]\(y=ax²\)のグラフは,比例定数aが変わると何が変わるのかな。

見方・考え方
比例定数が1でないときは,どんなグラフになるかな。
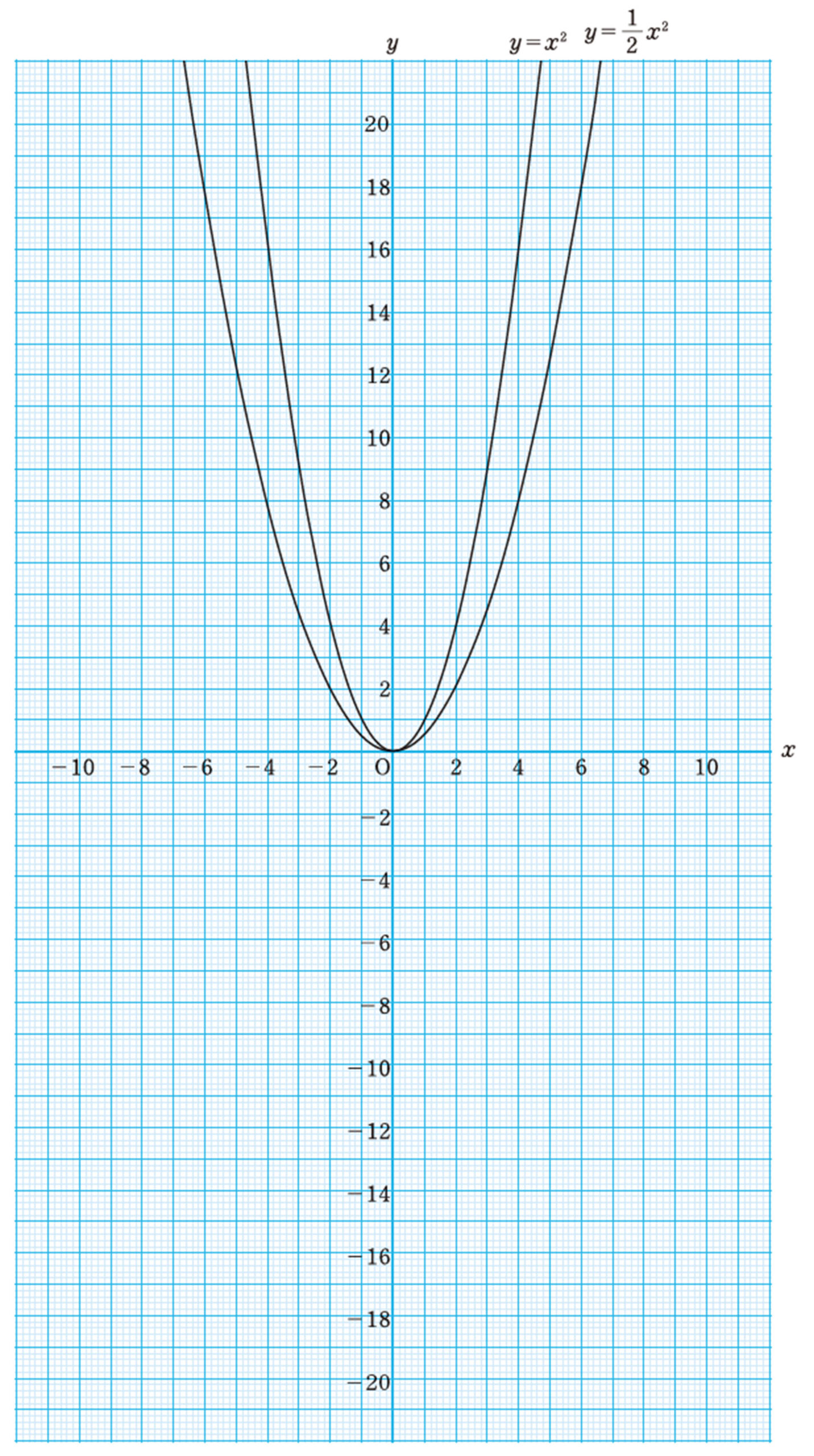
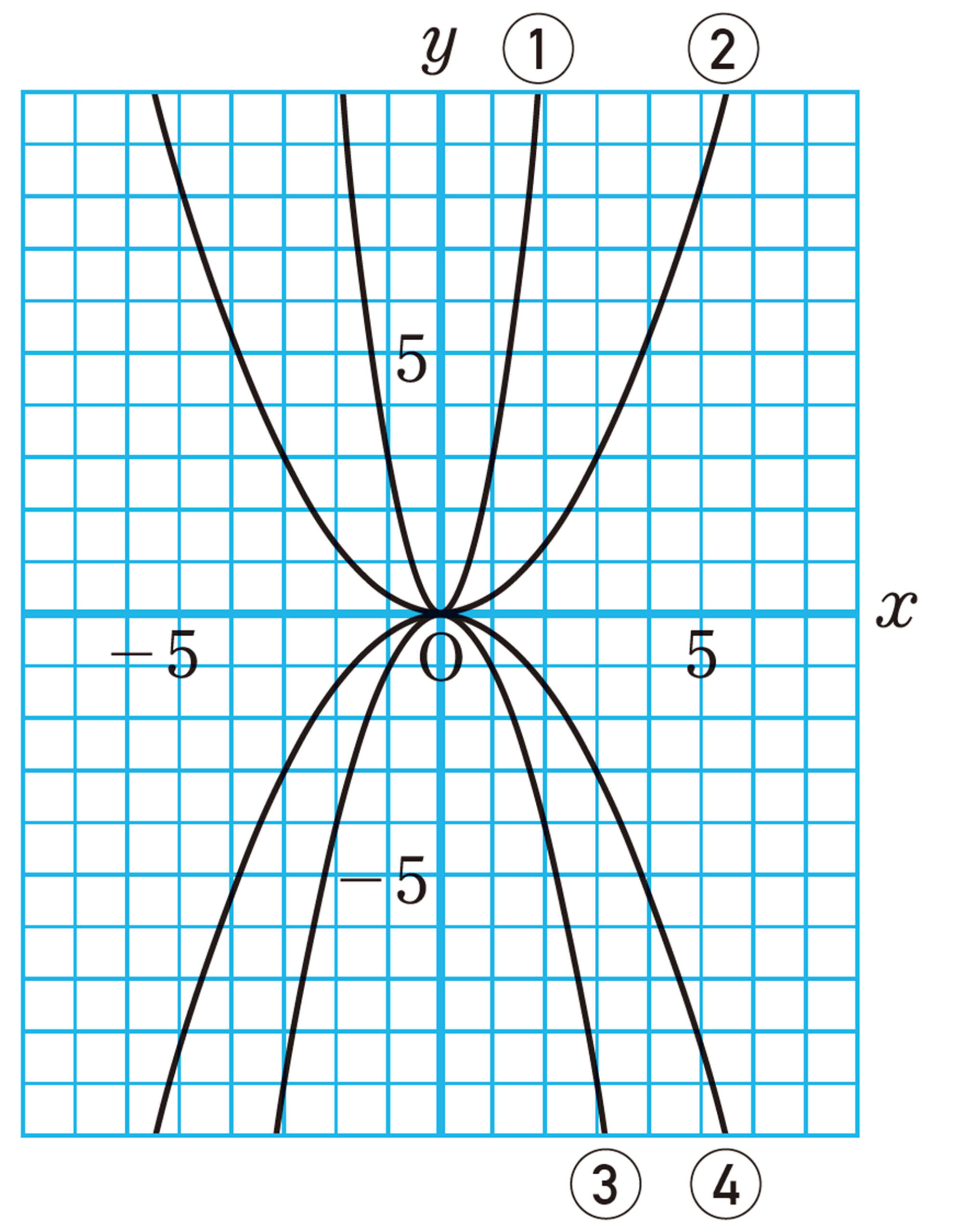
問 2 [mathjax]\(y=x²\)のグラフをもとにして,次の関数のグラフを,前ページの図にかき入れなさい。
⑴ [mathjax]\(y=3x²\)
⑵ [mathjax]\(y=\dfrac{1}{2}x²\)
問 3 [mathjax]\(a \gt 0\)のとき,関数[mathjax]\(y=ax²\)のグラフにはどんな特徴があるといえるか話し合いなさい。
どのグラフにも共通することは何かな。

<3年p.111>
[mathjax]\(a \lt 0\)のときの[mathjax]\(y=ax²\)のグラフ
Q Question
関数[mathjax]\(y=-x²\)について,次の問いに答えましょう。
⑴ 次の表を完成させましょう。
⑵ 上の表をもとに,[mathjax]\(y=-x²\)のグラフを,次ページの図にかき入れ,[mathjax]\(y=x²\)のグラフと比べてみましょう。

どちらのグラフも原点を通っているね。
2つのグラフはどんな関係にあるのかな。

見方・考え方
比例定数が負の数のときは,どんなグラフになるかな。
【Q】 の表で,それぞれの[mathjax]\(x\)の値に対応する[mathjax]\(y\)の値は,[mathjax]\(x²\)の値と絶対値が等しく,符号が反対になっている。
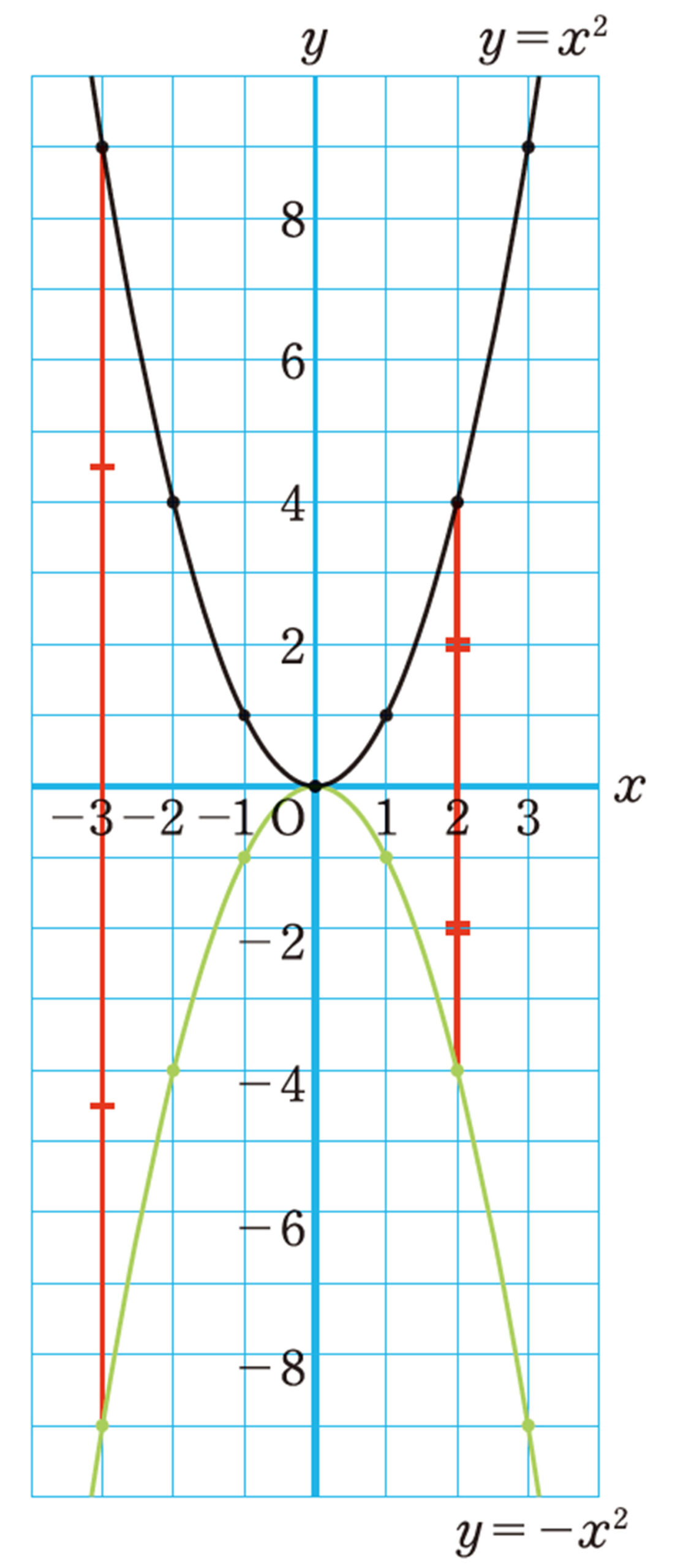
[mathjax]\(y=-x²\)のグラフは右の図のようになり,このグラフ上の点は, [mathjax]\(y=x²\)のグラフ上の各点とx軸について対称な点である。
したがって,[mathjax]\(y=x²\)のグラフと [mathjax]\(y=-x²\)のグラフは,x軸について対称な曲線となる。
問 4 [mathjax]\(y=\dfrac{1}{2}x²\)のグラフをもとにして,[mathjax]\(y=-\dfrac{1}{2}x²\)のグラフを,次ページの図にかき入れなさい。
問 5 [mathjax]\(a \lt 0\)のとき, 関数[mathjax]\(y=ax²\)のグラフにはどんな特徴があるといえるか話し合いなさい。また,[mathjax]\(a \gt 0\)のときのグラフと比べなさい。
どんなことがわかったかな
関数[mathjax]\(y=ax²\)のグラフは,原点を通り,y軸について対称な放物線になります。
次の課題へ!
グラフをもとにして,関数[mathjax]\(y=ax²\)の変化のしかたについて,もっと調べられるかな?
P.116

<3年p.114>
逆関数 発展 高等学校 Tea Break
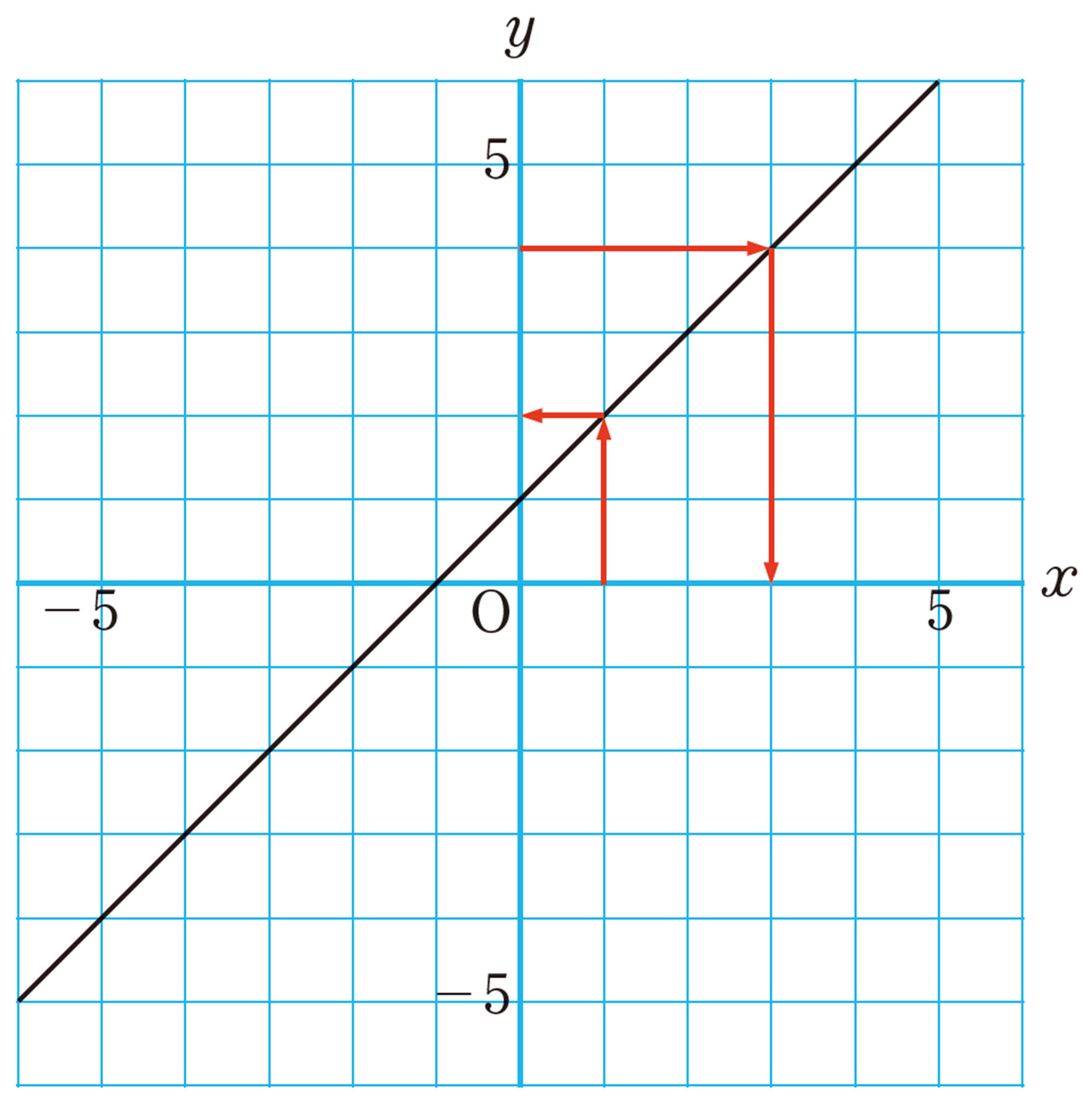
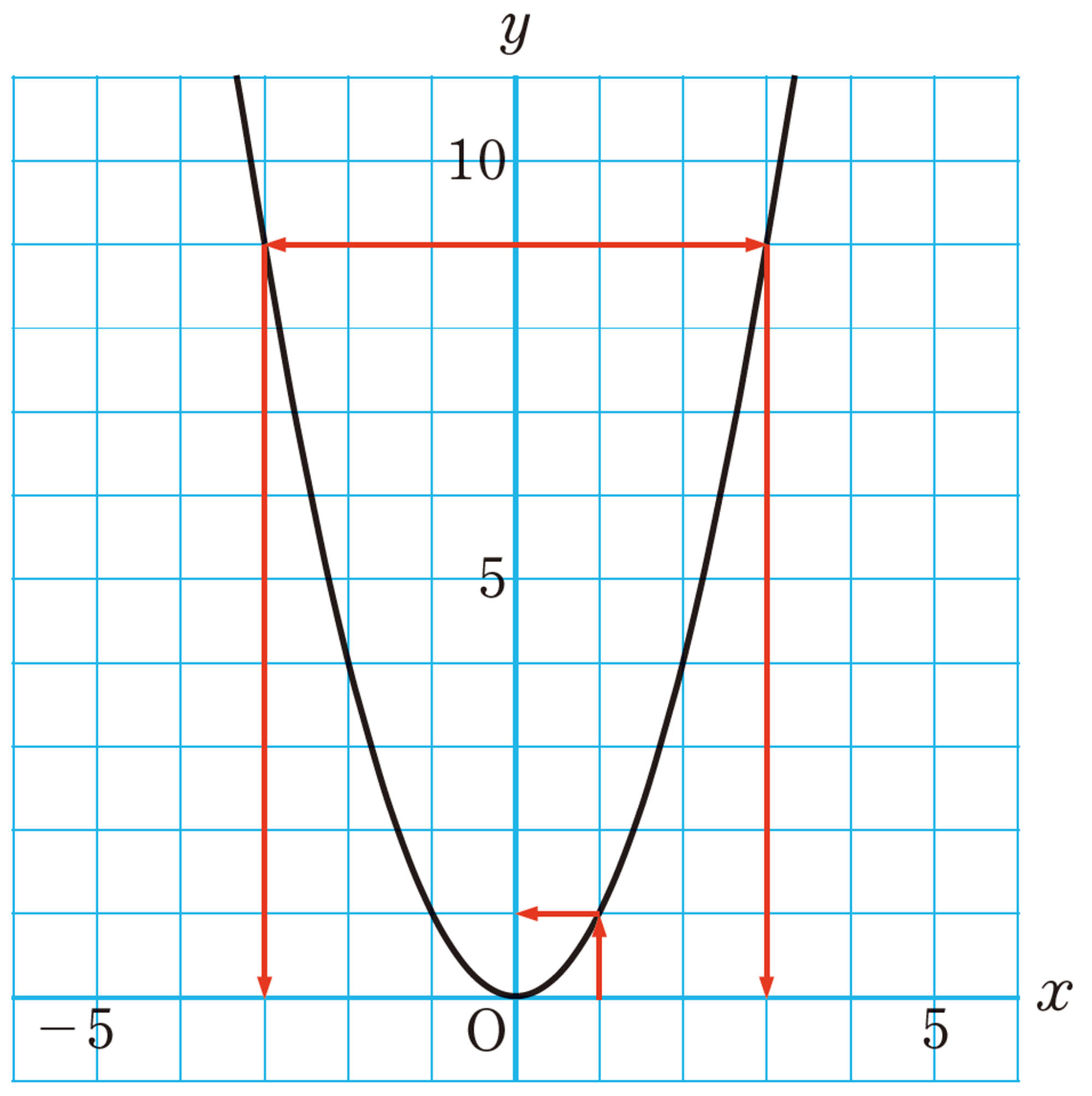
右下のグラフからもわかるように,関数[mathjax]\(y=x²\)では,yの値を決めても,それに対応するxの値がただ1つに決まりません。
1次関数[mathjax]\(y=x+1\)のように,yの値を決めると,それに対応するxの値もただ1つに決まるとき,逆関数が存在するといいます。関数[mathjax]\(y=x²\)の場合,yの値を決めても,それに対応するxの値がただ1つに決まらないので,逆関数は存在しません。
<3年p.115>
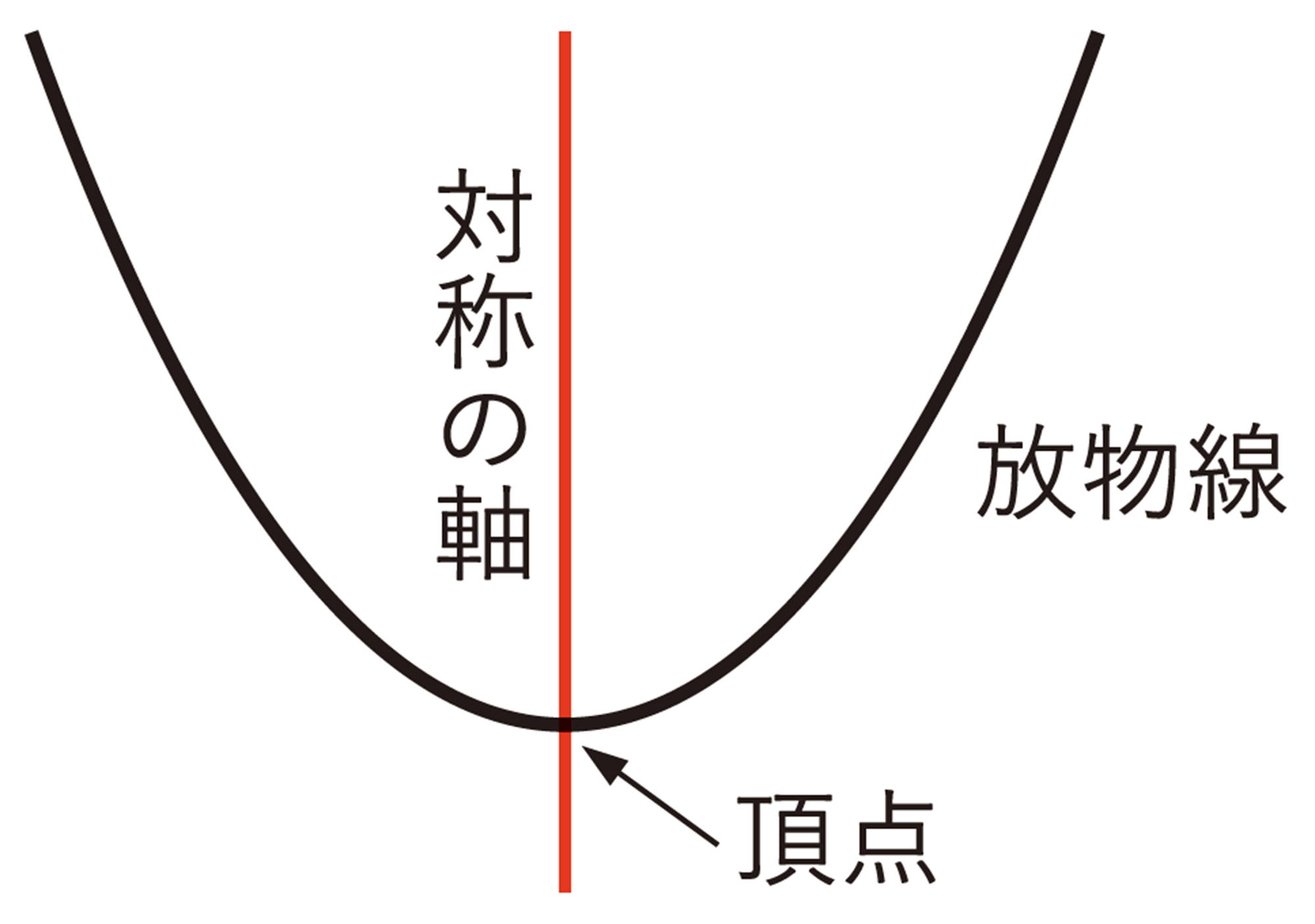
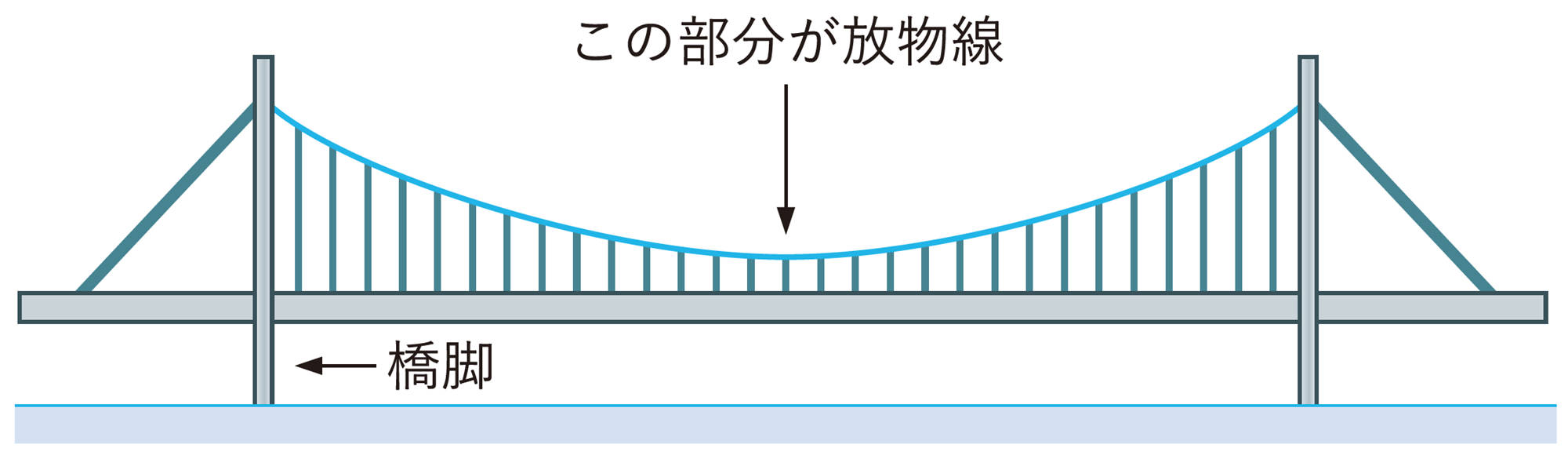
身近に見られる放物線 Tea Break
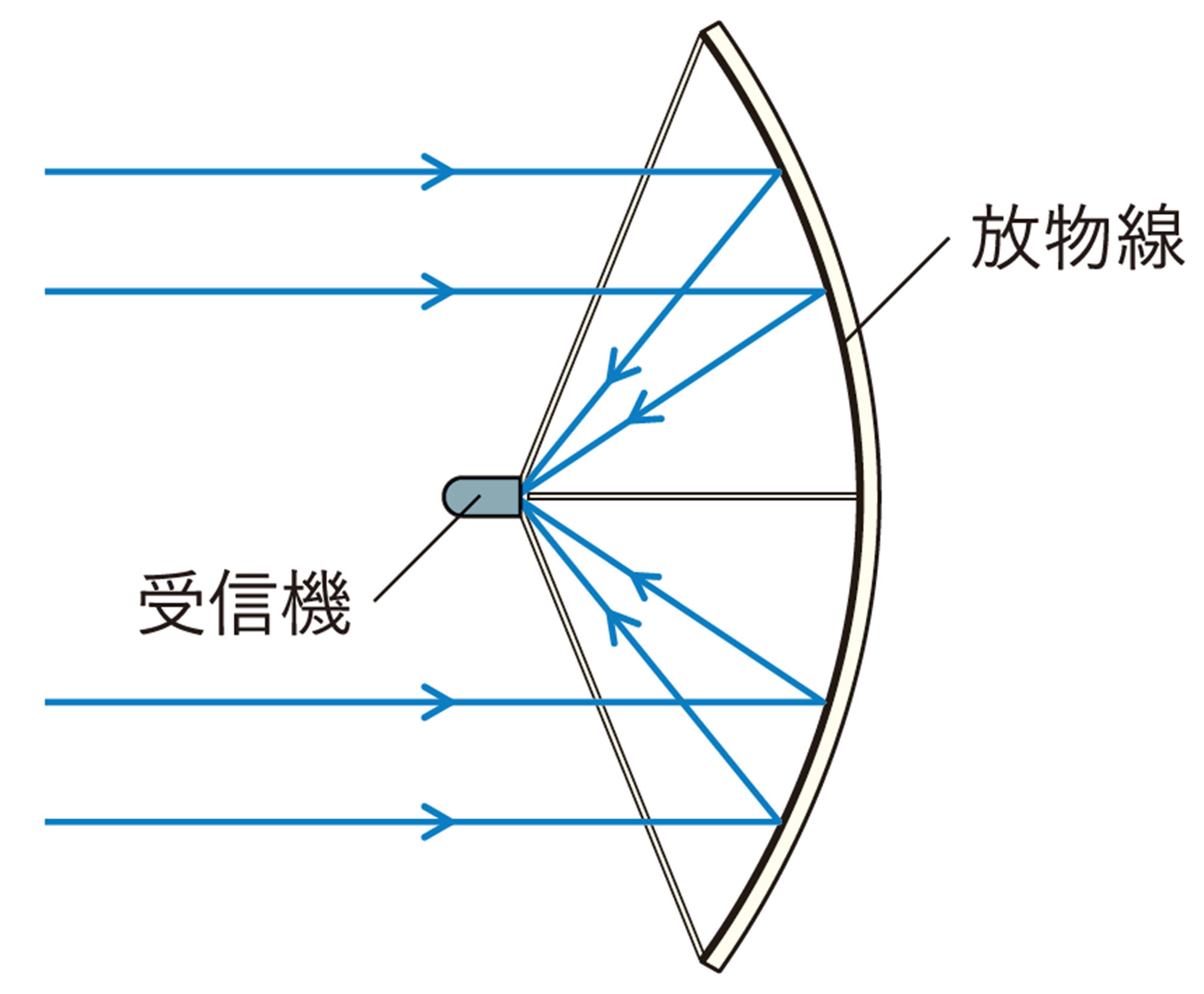
衛星放送を受信するパラボラアンテナの「パラボラ」( parabola )は,「放物線」を意味しています。パラボラアンテナは,放物線が対称の軸のまわりを回転してできた面(放物面)を利用しています。遠方から対称の軸に平行に届いた電波はこの面に当たって反射し,1点に集められます。そこに受信機を設置することにより,効率よく電波を集めることができます。
![]() 身のまわりから放物線を探してみましょう。
身のまわりから放物線を探してみましょう。