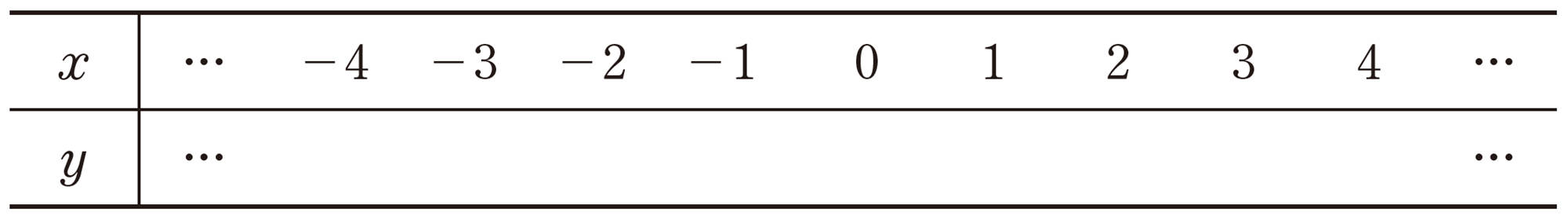<3年p.100>
ふりかえり
【関数】
ともなって変わる2 つの変数 [mathjax]\( x \) , [mathjax]\( y \) があって, [mathjax]\( x \) の値を決めると,それに対応する [mathjax]\( y \) の値がただ1つ決まるとき, [mathjax]\( y \) は [mathjax]\( x \) の関数である。
関数の特徴は, ・式 ・グラフ ・変化の割合 などを比べて考えたね。

【比例】
yがxの関数であり,次のような式で表されるとき,yはxに比例するという。
[mathjax]\(y=ax\)
ただし,aは0でない定数で,このaを比例定数という。
【反比例】
yがxの関数であり,次のような式で表されるとき,yはxに反比例するという。
[mathjax]\(y=\dfrac{a}{x}\)
ただし,aは0でない定数で,このaを比例定数という。
【1次関数】
yがxの関数で,yがxの1次式で表されるとき,yはxの1次関数であるという。
身のまわりのことがらを1次関数とみなすと,問題を解決できることがあったね。

関数を利用すると,未来のことが予測できることもあるね。

1次関数は,変化の割合が一定で,グラフは直線になったね。 反比例は,変化の割合が一定ではなく,グラフは曲線だったね。

<3年p.102>
1節 関数 [mathjax]\(y=ax²\)
時間と距離の関係は?
スキージャンプは,ジャンパーがスタート地点から斜面を滑り降りる勢いを利用して,踏み切り台から飛び出し,美しく遠くへ飛ぶスポーツです。
<3年p.103>

yの増え方は一定じゃないよ。
xの値が2倍,3倍になったら,yの値はどうなるのかな。

比例や反比例のグラフはどんな形だったかな。

⑵ ⑴の表の対応するx,yの値の組を座標とする点を,上の図にかき入れてみましょう。また,グラフはどんな形になるでしょうか。
⑶ yはxに比例する,または,yはxに反比例するといえるでしょうか。その理由も説明しましょう。
次の課題へ!
ジャンパーが斜面を滑り始めてからの時間と距離の間にはどんな関係があるのかな?
P.104

次の課題へ!
時間の経過とともに速さはどのように変化しているのかな?
P.120

<3年p.104>
1 関数[mathjax]\(y=ax²\)
Q Question

xの値が決まるとyの値がただ1つ決まるから,yはxの関数といえそうだね。
xの値が増えたとき,yの値はどんな増え方をしているのかな。

見方・考え方
これまでと同じように,2つの数量を関数として考えられるかな。
目標 ▷ ボールが転がり始めてからの時間と転がる距離の関係について調べよう。
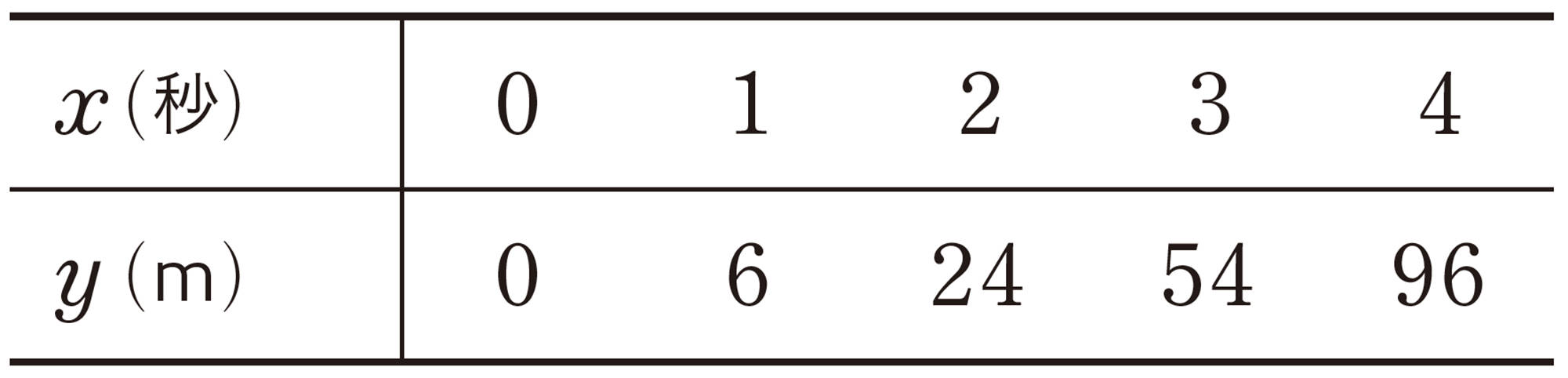
問 1 【Q】について,[mathjax]\(x²\)の値を求め,次の表を完成させなさい。また,[mathjax]\(x²\)と[mathjax]\(y\)の関係を調べなさい。
問1の表から,yの値はどこでも[mathjax]\(x²\)の値の[mathjax]\(0.5\)倍になっていることがわかる。すなわち,xとyの間には,次の関係がある。
[mathjax]\(y=0.5x²\)
<3年p.105>
関数[mathjax]\(y=ax²\)
yがxの関数であり,次のような式で表されるとき,yはxの2乗に比例するという。
[mathjax]\(y=ax²\)
ただし,aは0でない定数で,このaを比例定数という。
これまでの関数と同じように,比例定数や変域を負の数まで広げたときについて考えよう。
問 3 次の関数について,表を完成させなさい。また,yの値について気づいたことをいいなさい。
⑴ 関数[mathjax]\(y=x²\)
⑵ 関数[mathjax]\(y=-x²\)
関数[mathjax]\(y=ax² \)で,[mathjax]\(a>0 \)のとき,[mathjax]\(y≧0 \)であり,[mathjax]\(a<0 \)のとき,[mathjax]\(y\leqq 0 \)である。
<3年p.106>
例 2 yはxの2乗に比例し,[mathjax]\(x=-2\)のとき[mathjax]\(y=12\)です。yをxの式で表しなさい。また,[mathjax]\(x=5\)のときのyの値を求めなさい。
解答
yはxの2乗に比例するから,[mathjax]\(y=ax²\)
[mathjax]\(x=-2\)のとき[mathjax]\(y=12\)であるから,これらを代入すると,
したがって,[mathjax]\(y=3x²\)
この式に[mathjax]\(x=5\)を代入すると,
答 [mathjax]\(y=3x²,y=75\)
問 4 yがxの2乗に比例するとき,次の⑴,⑵について,yをxの式で表しなさい。また,[mathjax]\(x=-2\)のときのyの値を求めなさい。
⑴ [mathjax]\(x=-4\)のとき[mathjax]\(y=8\)
⑵ [mathjax]\(x=3\)のとき[mathjax]\(y=-36\)
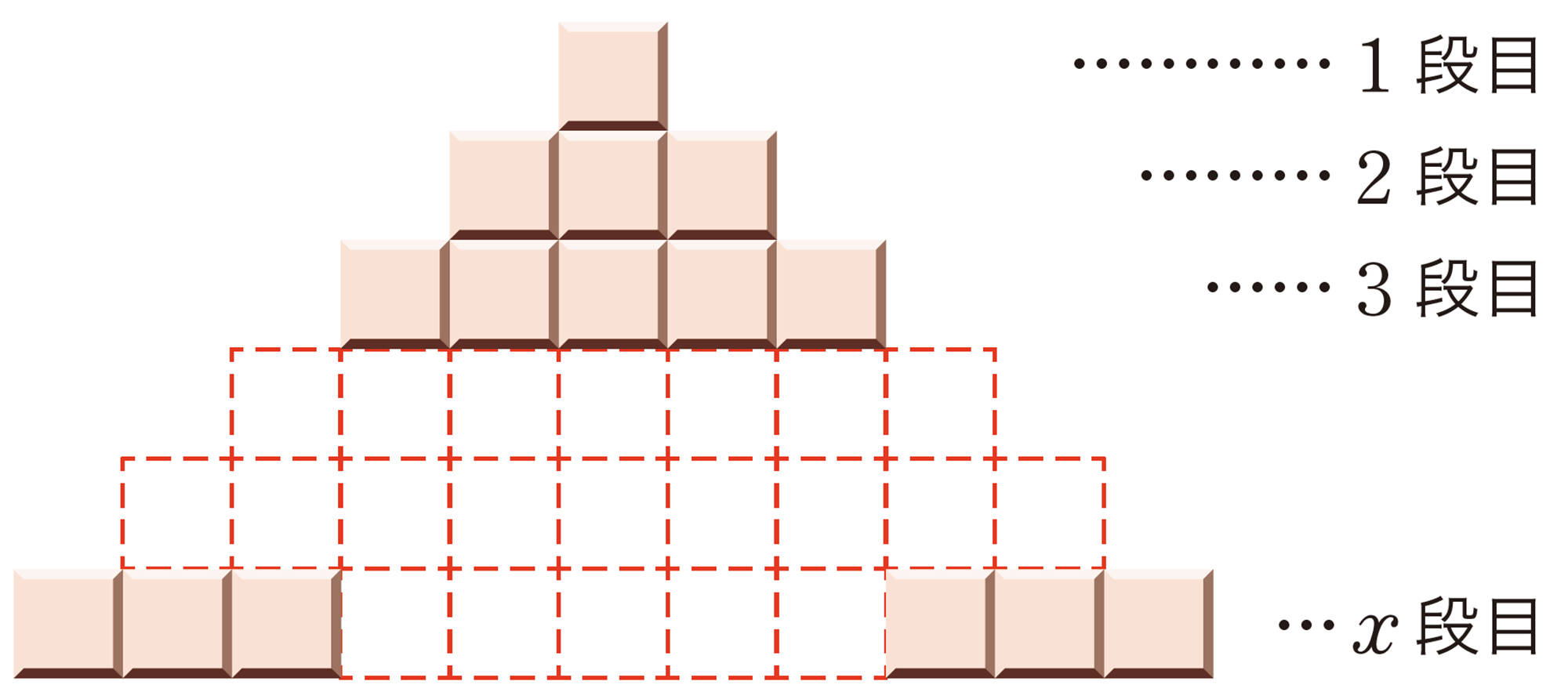
⑴ x段目のタイルの枚数をy枚としたとき,yをxの式で表しなさい。また, 12段目のタイルの枚数を求めなさい。
⑵ x段目までのタイルの総数をy枚としたとき,yをxの式で表しなさい。また,12段目までのタイルの総数を求めなさい。
⑶ ⑴,⑵は,それぞれどんな関数といえばよいですか。
どんなことがわかったかな
ボールが斜面を転がるときの時間と距離の関係のように,身のまわりには関数[mathjax]\(y=ax²\)の式で表せるものがあります。
次の課題へ!
関数[mathjax]\(y=ax²\)は,どんなグラフになるのかな?
P.107