<3年p.67>
計算力を高めよう 3
家庭学習や計算練習で利用しましょう。
根号をふくむ式の計算
解答 ▷ P.301
1 乗法・除法
⑴ [mathjax]\(\sqrt{2} \times \sqrt{13}\)
⑵ [mathjax]\(\sqrt{42} \div \sqrt{7}\)
⑶ [mathjax]\(\sqrt{24} \times \sqrt{6}\)
⑷ [mathjax]\(\sqrt{50} \div \sqrt{2}\)
⑸ [mathjax]\(2\sqrt{5} \times 4\sqrt{2}\)
⑹ [mathjax]\(4\sqrt{3} \times (-\sqrt{15})\)
⑺ [mathjax]\(3\sqrt{5} \times \sqrt{\dfrac{5}{2}}\)
⑻ [mathjax]\(9\sqrt{6} \div 3\sqrt{2}\)
⑼ [mathjax]\(8\sqrt{15} \div 2\sqrt{10}\)
⑽ [mathjax]\(\dfrac{\sqrt{21}}{3} \div \dfrac{\sqrt{7}}{6}\)
2 加法・減法
⑴ [mathjax]\(3\sqrt{5}+4\sqrt{5}\)
⑵ [mathjax]\(\sqrt{7}-6\sqrt{7}\)
⑶ [mathjax]\(-2\sqrt{2}+9\sqrt{2}-3\sqrt{2}\)
⑷ [mathjax]\(5\sqrt{2}+4\sqrt{6}-8\sqrt{2}+\sqrt{6}\)
⑸ [mathjax]\(\sqrt{63}+\sqrt{7}\)
⑹ [mathjax]\(\sqrt{50}-\sqrt{18}\)
⑺ [mathjax]\(\sqrt{18}-7\sqrt{2}+\sqrt{32}\)
⑻ [mathjax]\(\sqrt{45}+4\sqrt{5}-\sqrt{20}\)
⑼ [mathjax]\(\dfrac{6}{\sqrt{2}}+\sqrt{8}\)
⑽ [mathjax]\(\sqrt{24}-\dfrac{18}{\sqrt{6}}\)
⑾ [mathjax]\(\dfrac {9\sqrt{15}}{5}+\sqrt{\dfrac{3}{5}}\)
⑿ [mathjax]\(\sqrt{32}-\dfrac{4}{\sqrt{2}}+\sqrt{50}\)
3 いろいろな計算
⑴ [mathjax]\(\sqrt{24}+\sqrt{2} \times \sqrt{3}\)
⑵ [mathjax]\(\sqrt{8} \times \sqrt{6}-\sqrt{18} \div \sqrt{6}\)
⑶ [mathjax]\(\sqrt{2}(5\sqrt{3}-\sqrt{2})\)
⑷ [mathjax]\((\sqrt{72}-\sqrt{56}) \div \sqrt{8}\)
⑸ [mathjax]\((\sqrt{7}+2)(\sqrt{7}+5)\)
⑹ [mathjax]\((8-\sqrt{3})(7+\sqrt{3})\)
⑺ [mathjax]\((\sqrt{5}-1)(\sqrt{5}-6)\)
⑻ [mathjax]\((\sqrt{10}+9)(\sqrt{10}-9)\)
⑼ [mathjax]\((\sqrt{19}-\sqrt{13})(\sqrt{19}+\sqrt{13})\)
⑽ [mathjax]\((\sqrt{5}-\sqrt{2})(\sqrt{2}+\sqrt{5})\)
⑾ [mathjax]\((\sqrt{7}+3)²\)
⑿ [mathjax]\((\sqrt{6}-\sqrt{2})²\)
⒀ [mathjax]\((2\sqrt{3}-1)(2\sqrt{3}+4)\)
⒁ [mathjax]\((3\sqrt{2}-5)²\)
⒂ [mathjax]\((2\sqrt{6}+\sqrt{2})(2\sqrt{6}-\sqrt{2})\)
⒃ [mathjax]\(\require{physics} \left(\dfrac{4}{\sqrt{3}}+\sqrt{3}\right)\require{physics} \left(\dfrac{4}{\sqrt{3}}-\sqrt{3}\right)\)
⒄ [mathjax]\((\sqrt{2}+3)(\sqrt{2}-1)+1\)
⒅ [mathjax]\(\sqrt{3}(\sqrt{6}-\sqrt{3})-\dfrac{8}{\sqrt{2}}\)
⒆ [mathjax]\((\sqrt{5}-1)²+\dfrac{10}{\sqrt{5}}\)
<3年p.68>
2章 「平方根」を学んで
できるようになったこと 身のまわりの課題へ ▷ P.71,72
2乗してある数になるものをある数の平方根という。平方根は根号を使って表すことができる。
根号のついた数も,これまで学んできた数と同じように,数直線上の点として表すことができる。
根号のついた数の計算ができる。
身のまわりや数学の中から見つけた問題を,平方根を使って解決することができる。
これからもっと学んでみたいことや,疑問に思ったことを書いておこう。
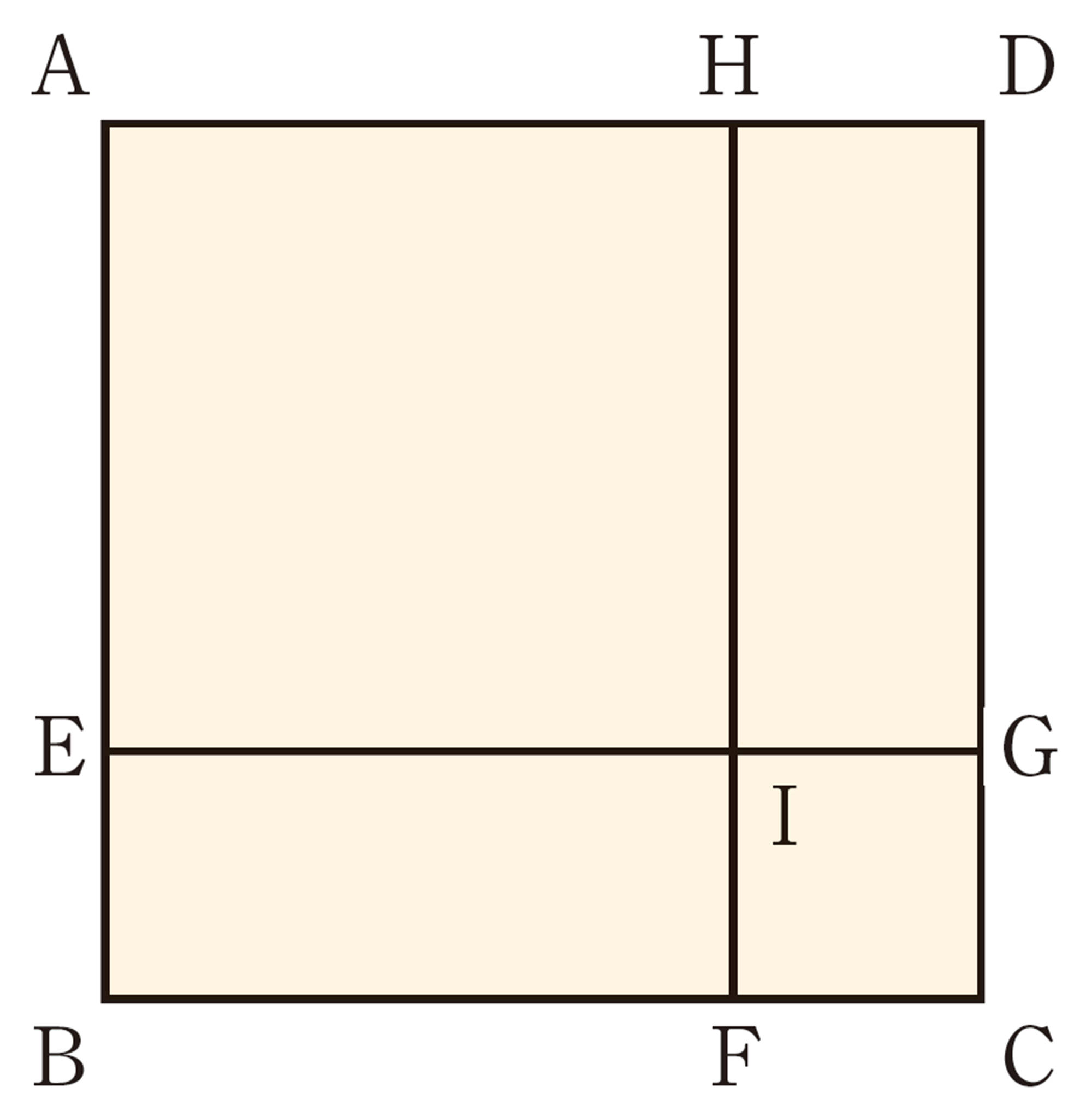
数学へのいざない 日本人に好まれやすい白銀比
64ページで学んだように,教科書やコピー用紙の2辺の長さの比は[mathjax]\(1:\sqrt{2}\)になっており,白銀比と呼ばれています。
現存する最古の木造建築物である法隆寺には,いたるところに白銀比を見つけることができます。室町時代後期の雪舟や江戸時代中期の菱川師宣の作品の中にも白銀比が存在します。このように,白銀比は,昔から日本の美の中に潜んでいます。
そのため,日本人は自然と白銀比を好む傾向にあり,人気のキャラクターの縦と横の長さの比は,白銀比になっていることが多いといわれています。
縦と横の長さを測ってみてね。白銀比になっているかな。

>> 関連する職業・仕事 [イラストレーター,デザイナー]
関連 P.270
<3年p.69>
2章のまとめの問題 解答 P.301〜302 基本
1 次の数の平方根を求めなさい。
⑴ 25
⑵ 19
⑶ [mathjax]\(0\)
⑷ [mathjax]\(0.16\)
2 次のことがらは正しいですか。誤りがあるものは,下線部を正しく書き直しなさい。
⑴ [mathjax]\(\sqrt{49}=\underline{\pm 7}\)である。
⑵ [mathjax]\((-\sqrt{6})²=\underline{6}\)である。
⑶ [mathjax]\(\sqrt{(-2)}²=\underline{-2}\)である。
⑷ [mathjax]\(-\sqrt{14}\) は [mathjax]\(-\sqrt{15}\)より小さい。
3 次の各組の数の大小を,不等号を使って表しなさい。
⑴ [mathjax]\(4\sqrt{3}\),7
⑵ [mathjax]\(-\sqrt{17}\),[mathjax]\(-3\sqrt{2}\)
4 次の計算をしなさい。
⑴ [mathjax]\(3\sqrt{2} \times \sqrt{14}\)
⑵ [mathjax]\(\dfrac{\sqrt{2}}{3} \div \dfrac{\sqrt{3}}{6}\)
⑶ [mathjax]\(7 \sqrt{3} – \sqrt{27}\)
⑷ [mathjax]\(5\sqrt{3} + \sqrt{18} + 2\sqrt{2} – \sqrt{48}\)
⑸ [mathjax]\(\dfrac{10}{\sqrt{5}} + 4\sqrt{5}\)
⑹ [mathjax]\(\sqrt{24} + \sqrt{42} \div \sqrt{7}\)
⑺ [mathjax]\((3 + \sqrt{11})²\)
⑻ [mathjax]\((2\sqrt{2} + 5)(5 – 2\sqrt{2})\)
<3年p.70>
2章のまとめの問題 応用
1 次の4つの数の大小を,不等号を使って表しなさい。
[mathjax]\(\dfrac{3}{7}\),[mathjax]\(\dfrac{\sqrt{3}}{7}\),[mathjax]\(\dfrac{3}{\sqrt{7}}\),[mathjax]\(\sqrt{\dfrac{3}{7}}\)
2 次の数の分母を有理化しなさい。
⑴ [mathjax]\(\dfrac{\sqrt{3}+1}{\sqrt{2}}\)
⑵ [mathjax]\(\dfrac{\sqrt{10}-\sqrt{2}}{\sqrt{5}}\)
3 次の計算をしなさい。
⑴ [mathjax]\(8 \sqrt{3}-\dfrac{6}{\sqrt{3}}+\sqrt{48}\)
⑵ [mathjax]\(6 \sqrt{15} \div \sqrt{3} \times \sqrt{5}\)
⑶ [mathjax]\(3\sqrt{6} \times \sqrt{2}-\dfrac{15}{\sqrt{3}}\)
⑷ [mathjax]\((\sqrt{7}+3)(\sqrt{7}-4)+\sqrt{63}\)
⑸ [mathjax]\((\sqrt{2}-\sqrt{6})(\sqrt{2}+\sqrt{6})+(\sqrt{3}+1)²\)
4 次の問いに答えなさい。
⑴ [mathjax]\(\sqrt{24n}\)が自然数となるような,もっとも小さい自然数nを求めなさい。
⑵ [mathjax]\(\sqrt{180}\)を小数で表したときの整数部分の数を求めなさい。
⑶ [mathjax]\(x=\dfrac{\sqrt{5}+1}{3}\)のとき,[mathjax]\(9x²-6x+1\)の値を求めなさい。
⑷ [mathjax]\(\sqrt{5}\) の小数部分をaとするとき,[mathjax]\(\dfrac{a-3}{a+2}\) の値を求めなさい。
<3年p.71>
活用
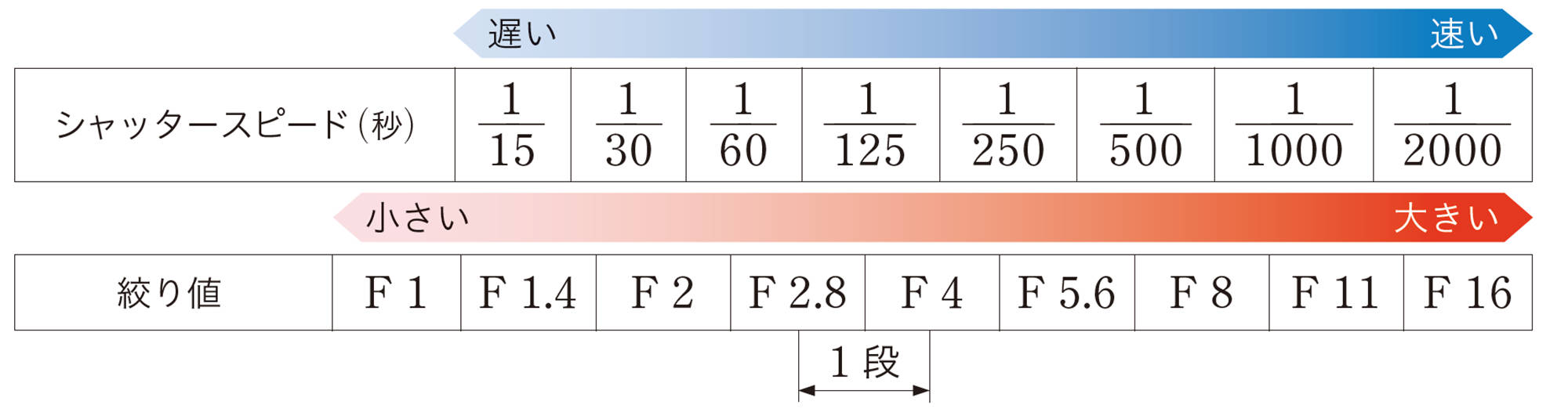
〔シャッタースピード〕シャッターがあいている時間のことで,この時間が短いほど,シャッタースピードが速いという。シャッタースピードを[mathjax]\(\dfrac{1}{15}\)から[mathjax]\(\dfrac{1}{30}\)にすると,シャッターがあいている時間が半分になるので,取り込める光の量も半分になる。
〔絞り値〕光の入る穴の大きさのことで,絞り値を小さくすると,穴の大きさは大きくなる。穴を円と考えたとき,絞り値をF16からF11のように1段小さくすると,穴の直径は[mathjax]\(\sqrt{2}\)倍になり,取り込める光の量は2倍になる。
1 絞り値をF4からF[mathjax]\(1.4\)に3段小さくすると,光の入る穴の直径は何倍になりますか。
2 適正露出が,絞り値 F4,シャッタースピード[mathjax]\(\dfrac{1}{250}\)であるとき,シャッタースピードを[mathjax]\(\dfrac{1}{1000}\)にすると,絞り値をいくつにすれば同じ露出になりますか。
>> 関連する職業・仕事 [写真家]
<3年p.72>
深めよう
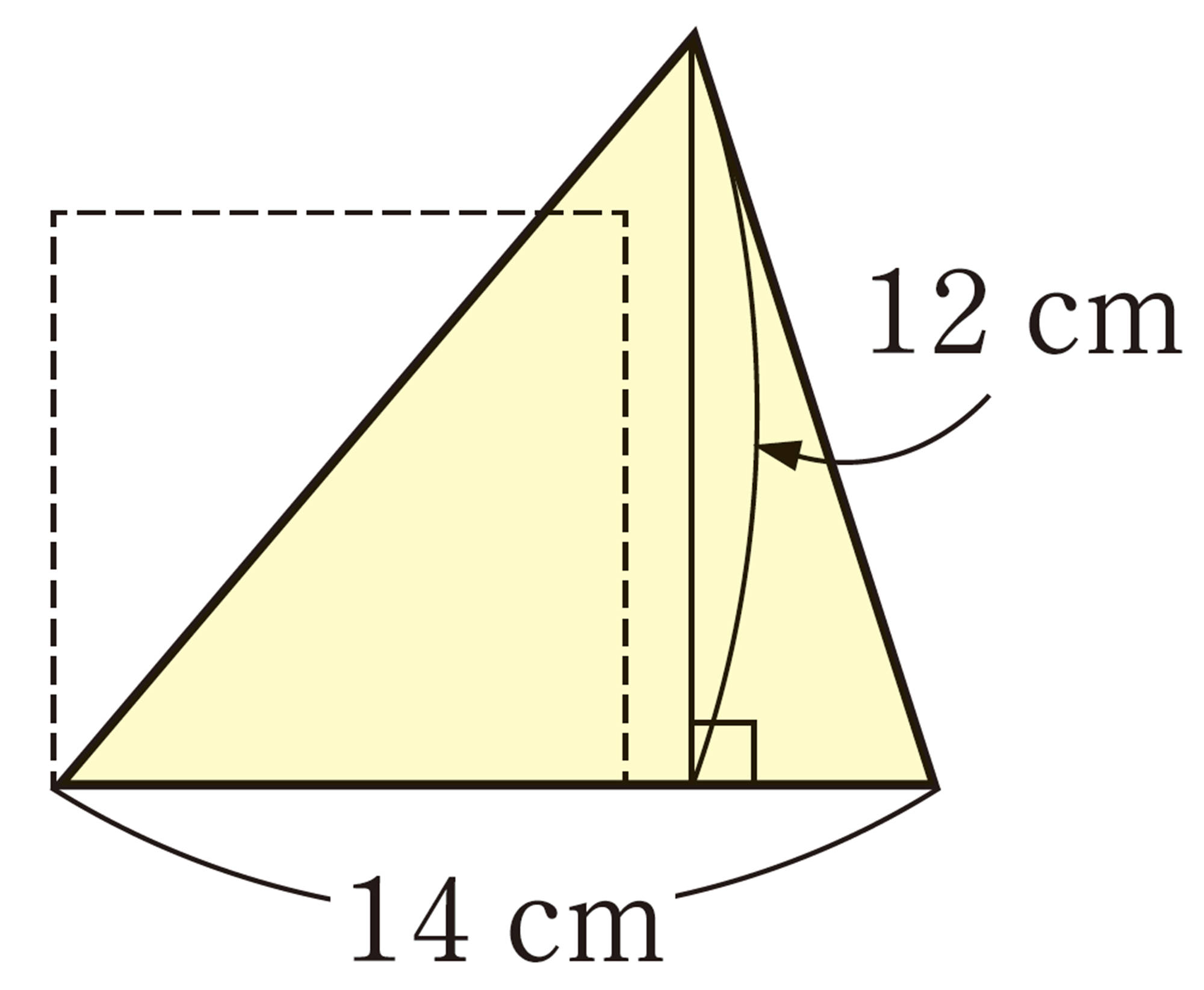
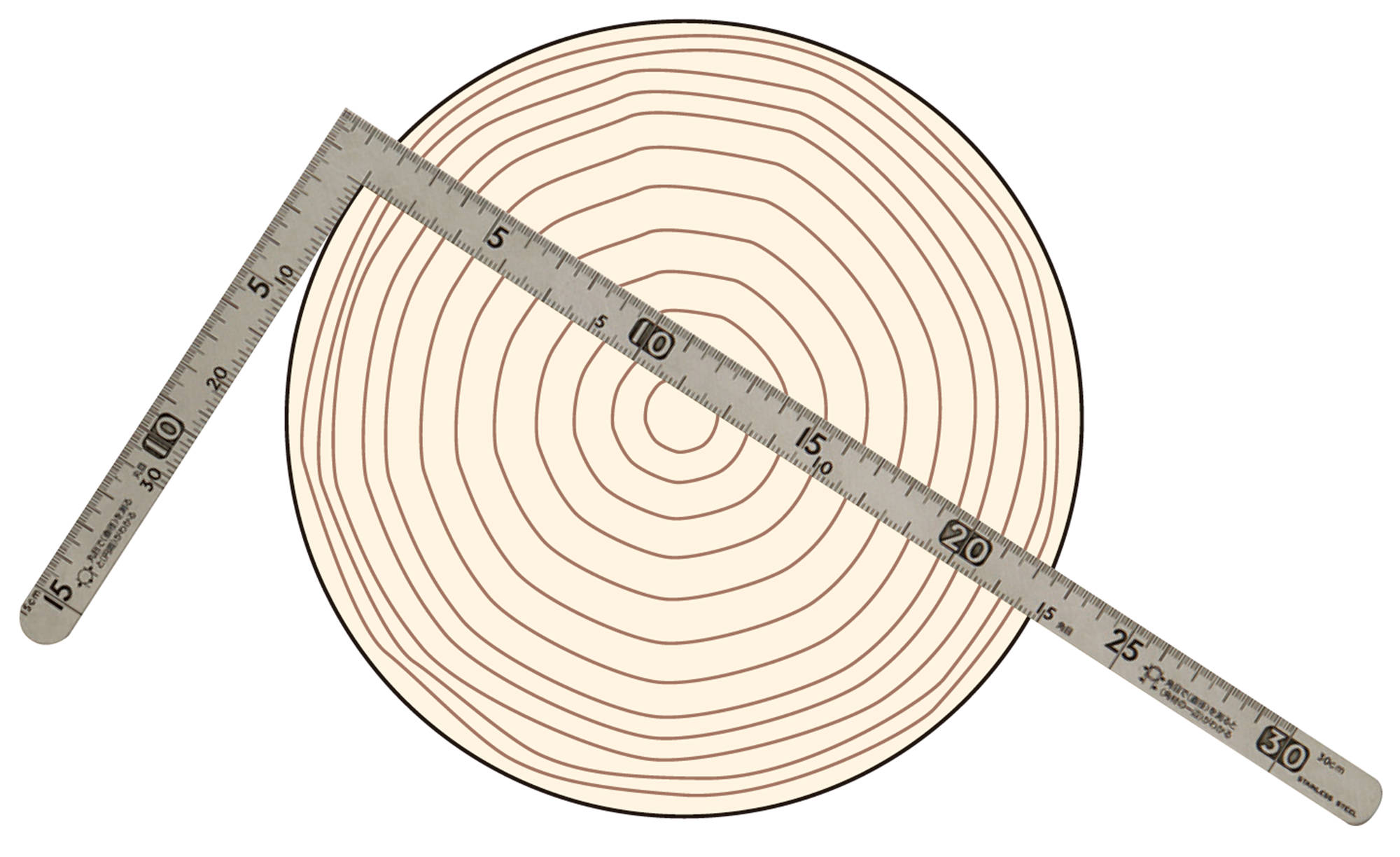
丸太からとれる角材は?
>> 関連する職業・仕事 [建築士 , 大工 , 林業]