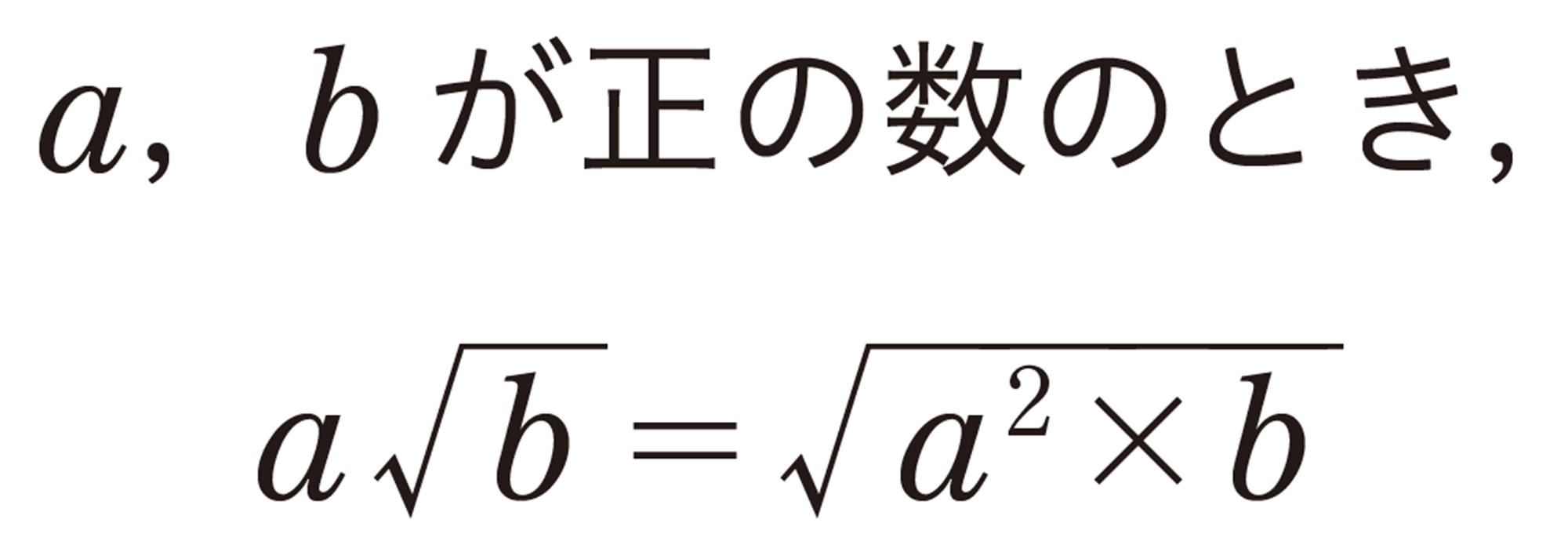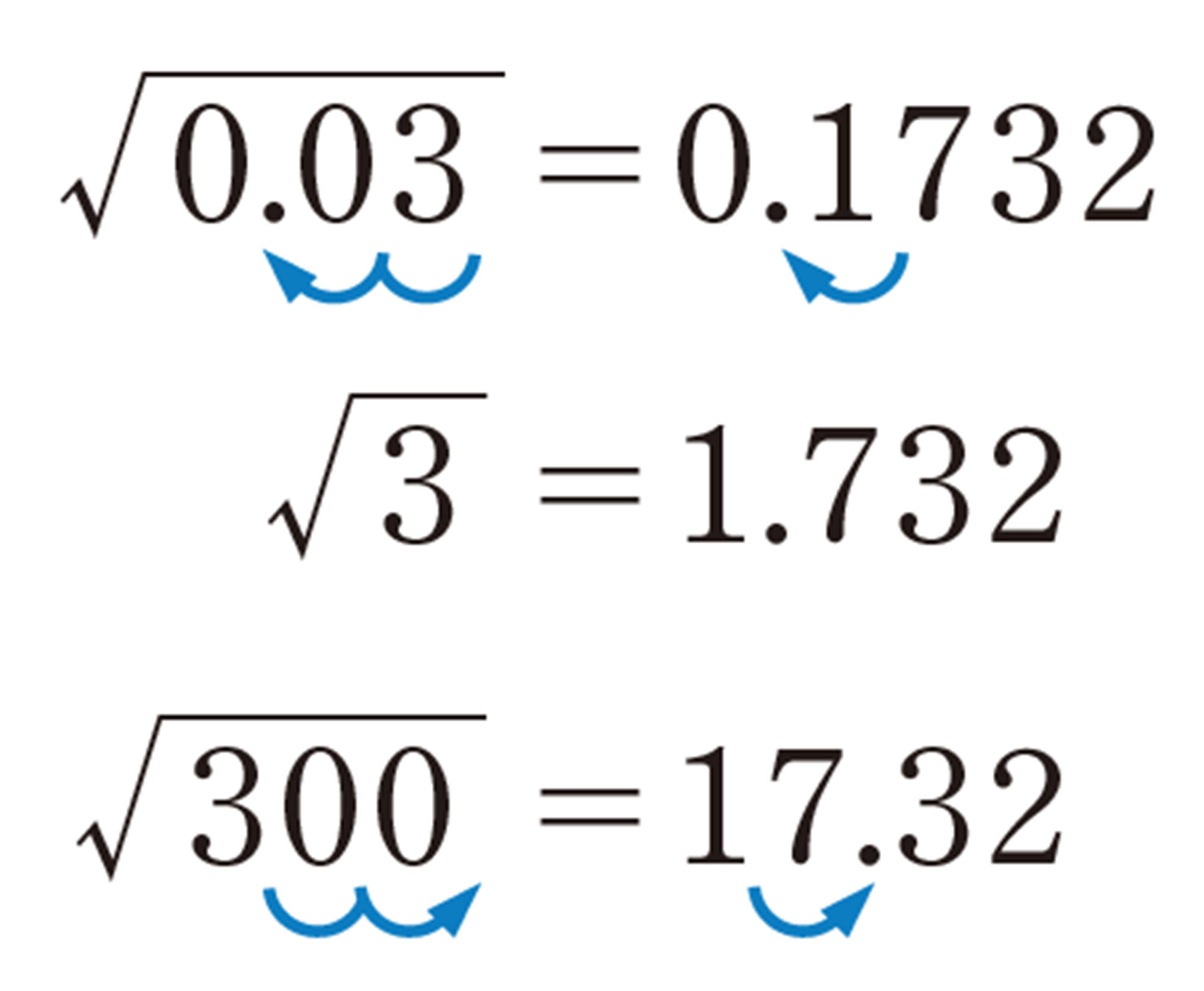<3年p.54>
2節 根号をふくむ式の計算
根号をふくむ数の計算はできるの?
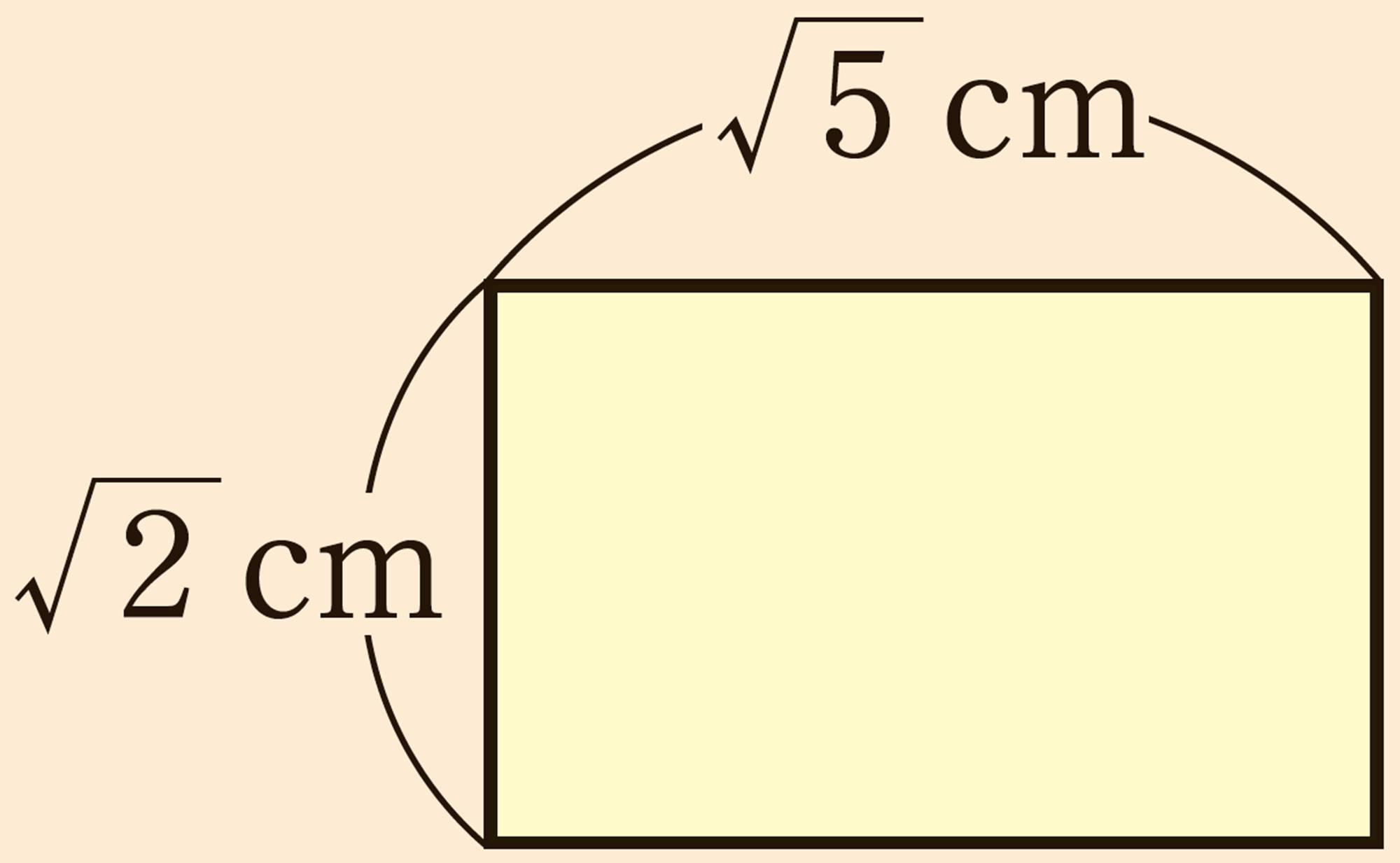
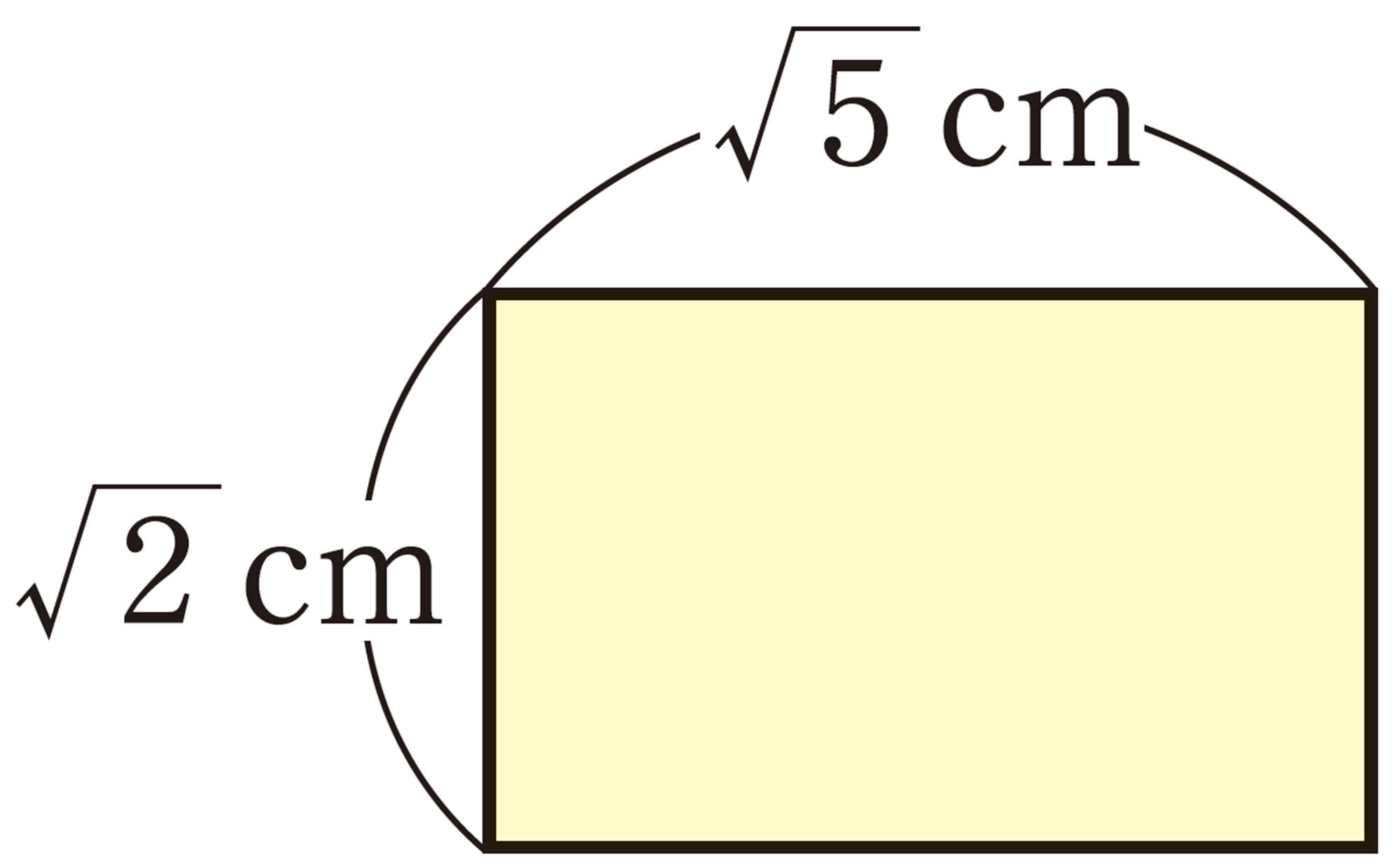
根号をふくむ数の乗法や除法,加法や減法の計算のしかたを,面積や長さをもとにして考えてみましょう。
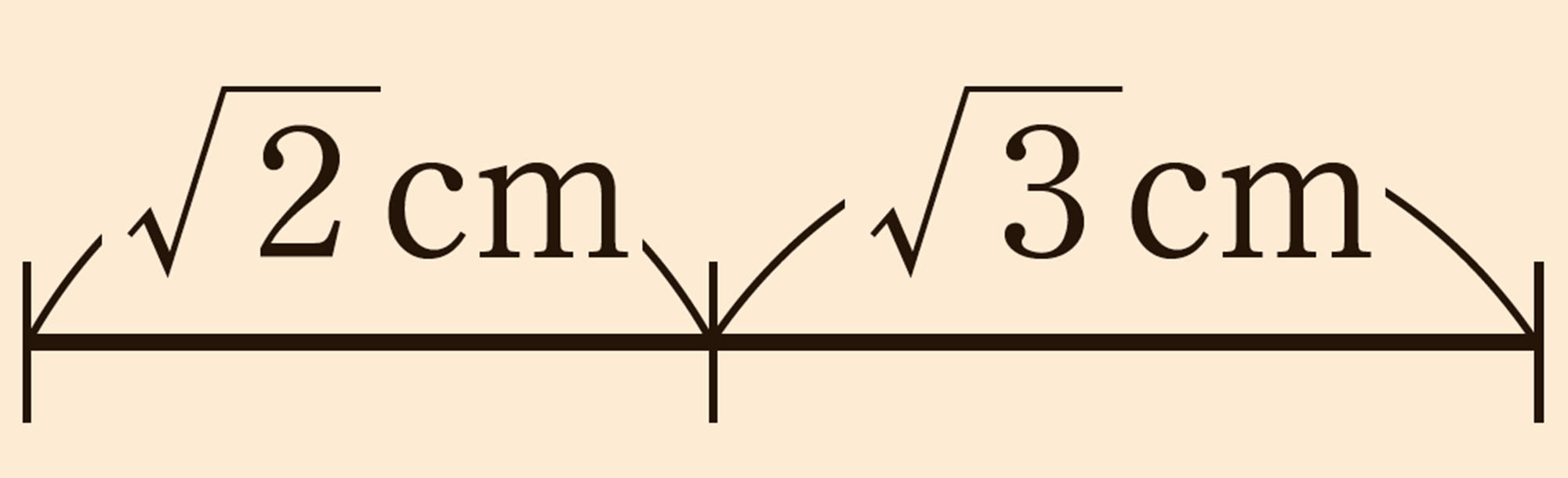
[mathjax]\(\sqrt{2} + \sqrt{3}\)は,これまでの計算と同じように考えると,[mathjax]\(\sqrt{5}\)になるのかな。

次の課題へ!
根号をふくむ数の計算も,これまでの数と同じようにできるのかな?
P.54,59

1 根号をふくむ式の乗法・除法
根号をふくむ数の積や商
Q Question

[mathjax]\(\sqrt{2}=1.414\),[mathjax]\(\sqrt{5}=2.236\)で考えてみればいいね。。
図や近似値を使って確かめられるかな。

見方・考え方
およその値で考えられるかな。
目標 ▷ 根号をふくむ式の乗法・除法を考えよう。
<3年p.55>
[mathjax]\(\sqrt{2} \times \sqrt{5}\)と[mathjax]\(\sqrt{2 \times 5}\)が等しいといえるか,確かめてみよう。
[mathjax]\(\sqrt{2} \times \sqrt{5}\)は,正の数であり,2乗すると次のようになる。
したがって,[mathjax]\(\sqrt{2} \times \sqrt{5}\)は,[mathjax]\(2 \times 5\)の正の平方根である。すなわち,
[mathjax]\(\sqrt{2} \times \sqrt{5} = \sqrt{2 \times 5}\)
問 1 [mathjax]\(\dfrac{\sqrt{2}}{\sqrt{3}} = \sqrt{\dfrac{2}{3}}\)であることを,上と同じようにして確かめなさい。
[mathjax]\(\dfrac{\sqrt{2}}{\sqrt{3}}\)は[mathjax]\(\sqrt{2} \div \sqrt{3}\)のことだね。

一般に,根号をふくむ数の積や商について,次のことが成り立つ。
根号をふくむ数の積と商
a,bが正の数のとき,次の式が成り立つ。
[mathjax]\(\sqrt{a} \times \sqrt{b}=\sqrt{ab}\),[mathjax]\(\dfrac{\sqrt{a}}{\sqrt{b}}=\sqrt{\dfrac{a}{b}}\)
注意 [mathjax]\(\sqrt{a} \times \sqrt{b}\)は,[mathjax]\(\sqrt{a}\sqrt{b}\)と表すこともある。
例 1
⑴
⑵
問 2 次の計算をしなさい。
⑴ [mathjax]\(\sqrt{3} \times \sqrt{5}\)
⑵ [mathjax]\(\sqrt{13} \times \sqrt{7}\)
⑶ [mathjax]\(\sqrt{6}\sqrt{11}\)
⑷ [mathjax]\(\sqrt{6} \div \sqrt{3}\)
⑸ [mathjax]\(\sqrt{35} \div \sqrt{5}\)
⑹ [mathjax]\(\sqrt{150} \div \sqrt{30}\)
<3年p.56>
根号をふくむ数の変形
[mathjax]\(a \times \sqrt{b}\) や [mathjax]\(\sqrt{b} \times a\) は,乗法の記号 [mathjax]\(\times\) を省いて,ふつう [mathjax]\(a\sqrt{b}\) と表す。
問 3 次の数を[mathjax]\(\sqrt{a}\) の形に表しなさい。
⑴ [mathjax]\(2\sqrt{3}\)
⑵ [mathjax]\(3\sqrt{2}\)
⑶ [mathjax]\(4\sqrt{5}\)
⑷ [mathjax]\(3\sqrt{7}\)
例 3
⑴
⑵
根号の中の数がある数aの2乗を因数にもっているとき,[mathjax]\(a \sqrt{b}\)の形に変形して,根号の中を簡単な数にすることができる。
問 4 例3にならって,次の数を根号の中ができるだけ小さい自然数になるように,[mathjax]\(a \sqrt{b}\)の形に表しなさい。
⑴ [mathjax]\(\sqrt{28}\)
⑵ [mathjax]\(\sqrt{54}\)
⑶ [mathjax]\(\sqrt{48}\)
⑷ [mathjax]\(\sqrt{300}\)
例 4
⑴
⑵
問 5 例4にならって,次の数を変形しなさい。
⑴ [mathjax]\(\sqrt{\dfrac{2}{9}}\)
⑵ [mathjax]\(\sqrt{\dfrac{13}{25}}\)
⑶ [mathjax]\(\sqrt{0.02}\)
⑷ [mathjax]\(\sqrt{0.37}\)
<3年p.57>
分母の有理化
例 5
⑴
⑵
⑶
例5のように,分子と分母に同じ数をかけて,分母に根号をふくまない形にすることを,分母を有理化するという。
問 6 次の数の分母を有理化しなさい。
⑴ [mathjax]\(\dfrac{1}{\sqrt{5}}\)
⑵ [mathjax]\(\dfrac{\sqrt{2}}{\sqrt{7}}\)
⑶ [mathjax]\(\dfrac{6}{5\sqrt{3}}\)
⑷ [mathjax]\(\dfrac{12}{\sqrt{45}}\)
問 7 [mathjax]\(\sqrt{3}=1.732\)として,[mathjax]\(\dfrac{6}{\sqrt{3}}\)の値を求めなさい。
分母を有理化すると,近似値を求めやすくなることがある。
根号をふくむ式の乗法・除法
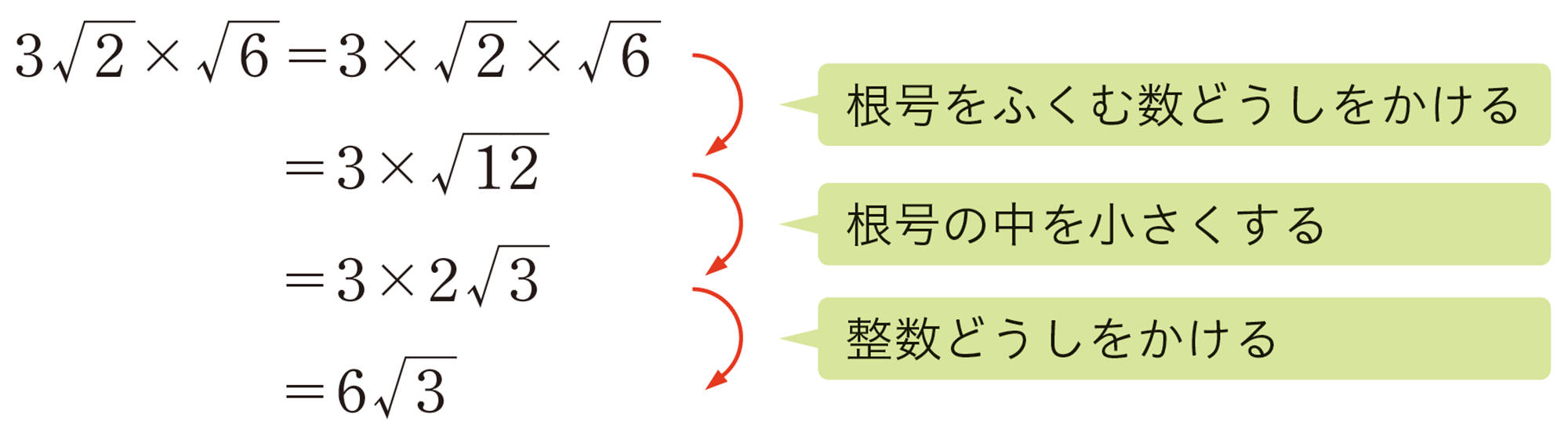
例 6
根号をふくむ数どうしをかける
根号の中を小さくする
整数どうしをかける
注意 計算の結果は,根号の中をできるだけ小さい自然数にしておく。
問 8 拓真さんは,例6の[mathjax]\(3\sqrt{2} \times \sqrt{6}\)の計算を,右のように行いました。拓真さんの考え方を説明しなさい。
問 9 次の計算をしなさい。
⑴ [mathjax]\(5 \sqrt{3} \times \sqrt{5}\)
⑵ [mathjax]\(4 \sqrt{2} \times 6 \sqrt{7}\)
⑶ [mathjax]\(\sqrt{6} \times 4 \sqrt{3}\)
⑷ [mathjax]\(2 \sqrt{2} \times (-3 \sqrt{10})\)
<3年p.58>
例 7
⑴
⑵
注意 計算の結果の分母に根号があるときは,分母を有理化しておく。
問 10 次の計算をしなさい。
⑴ [mathjax]\(8 \sqrt{14} \div \sqrt{7}\)
⑵ [mathjax]\((-12 \sqrt{6}) \div 3 \sqrt{2}\)
⑶ [mathjax]\(2 \sqrt{10} \div \sqrt{6}\)
⑷ [mathjax]\(\dfrac{3 \sqrt{2}}{8} \div \dfrac{\sqrt{5}}{4}\)
やってみよう
計算力を高めよう3-1
P.67
平方根の近似値
Q Question
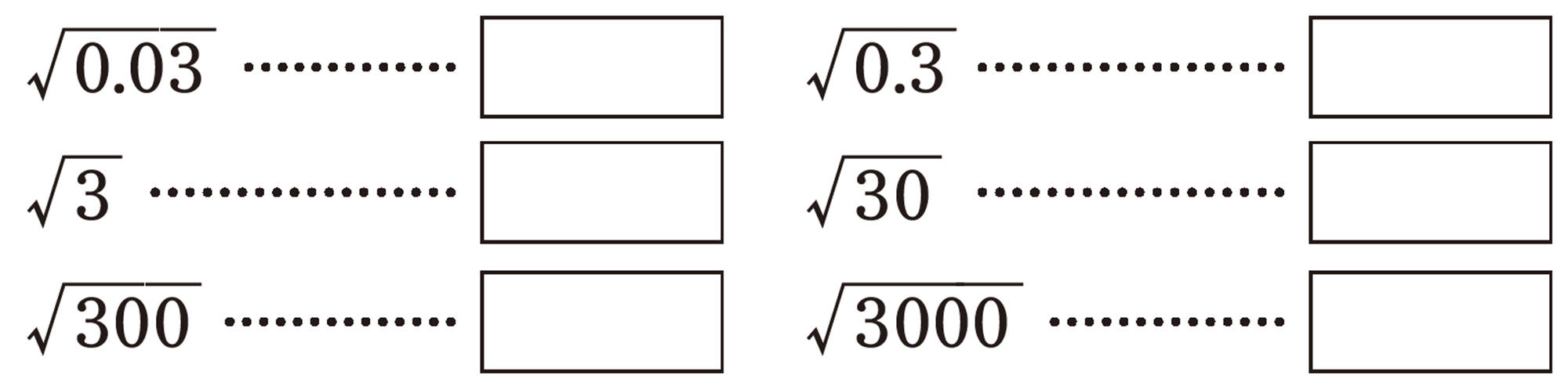
次の数の近似値を4桁まで求めてみましょう。また,その結果を見て気づいたことをいいましょう。

近似値が似ているものがあるけど,共通することがあるのかな。
見方・考え方
いろいろな数で調べて,どんな性質があるか見つけられるかな。
次のように考えると,根号の中の数の小数点の位置が2桁移ると,その数の平方根の小数点の位置は,同じ向きに1桁移ることがわかる。
問 11 [mathjax]\(\sqrt{5}=2.236\),[mathjax]\(\sqrt{50}=7.071\)として,次の数の近似値を求めなさい。
⑴ [mathjax]\(\sqrt{500}\)
⑵ [mathjax]\(\sqrt{5000}\)
⑶ [mathjax]\(\sqrt{0.5}\)
⑷ [mathjax]\(\sqrt{0.05}\)
どんなことがわかったかな
根号をふくむ式の乗法や除法は,根号の中の数をかけたりわったりして計算することができます。