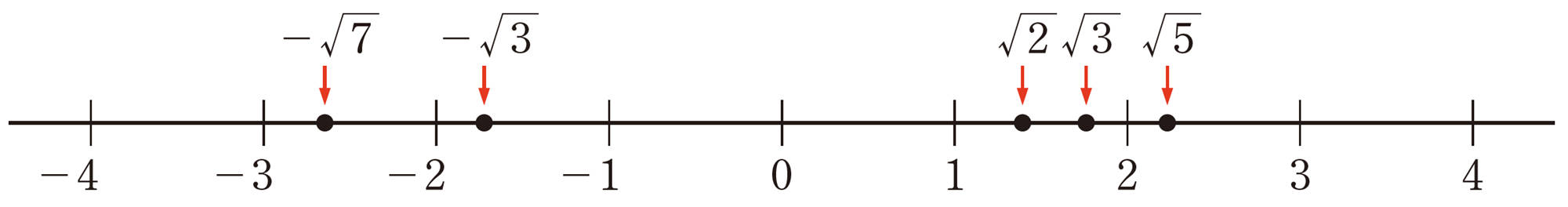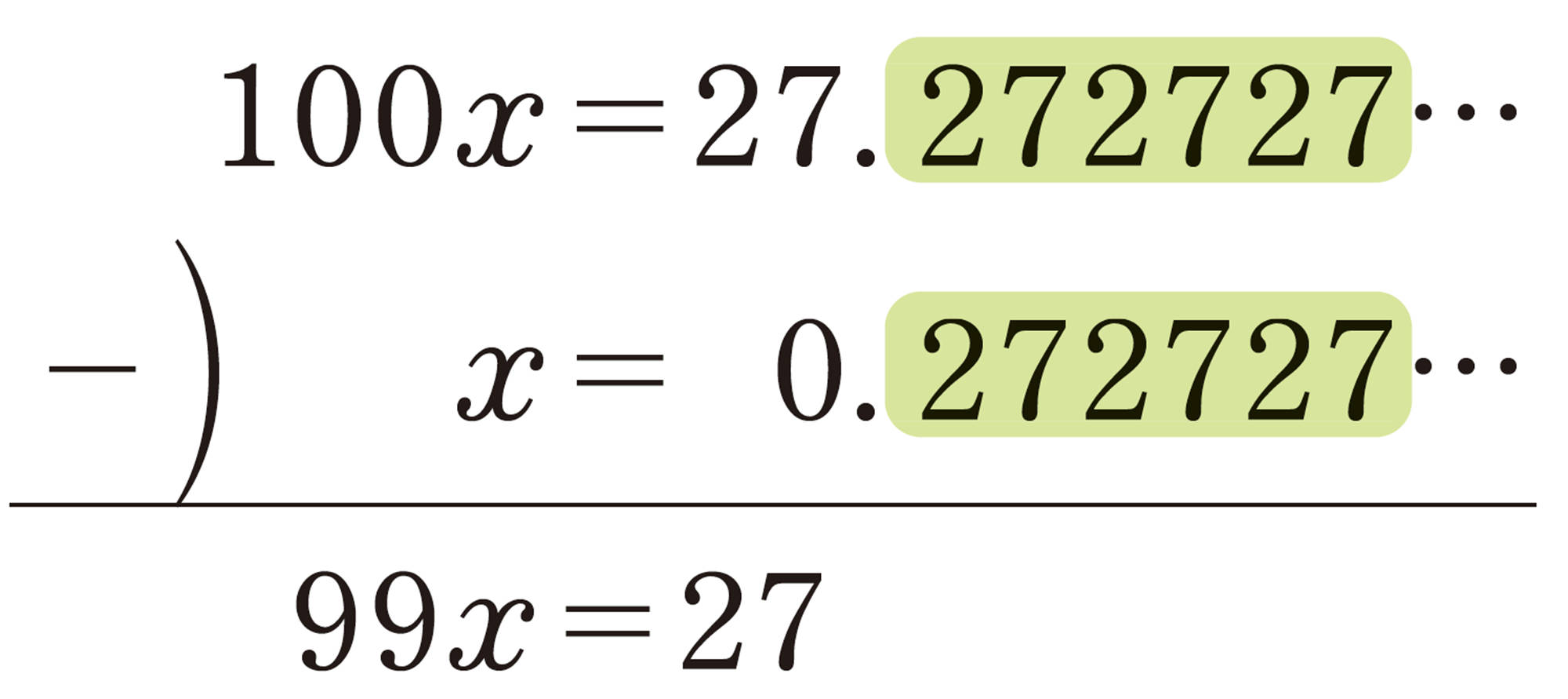<3年p.49>
２ 平方根の大小
Q Question
右の図㋐は，面積2の正方形で，図㋑は，面積5の正方形です。
この図について，次のことを調べてみましょう。
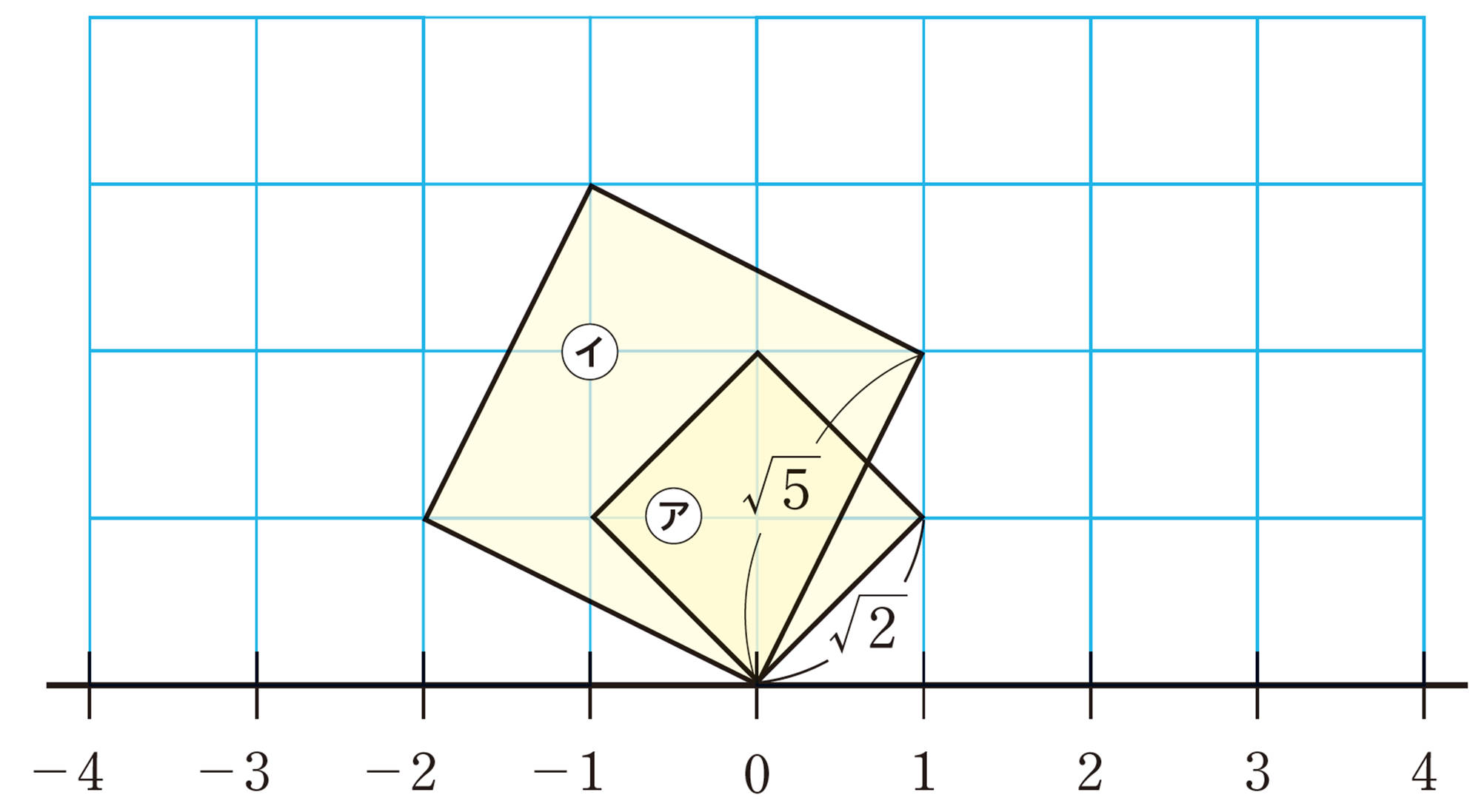
⑴ 上の2つの正方形㋐，㋑の1辺の長さをもとにして，[mathjax]\(\sqrt{2}\)，[mathjax]\(\sqrt{5}\)に対応する点を上の数直線上にとりましょう。また，[mathjax]\(\sqrt{2}\)と[mathjax]\(\sqrt{5}\)ではどちらが大きいか比べましょう。
⑵ [mathjax]\(-\sqrt{2}\)，[mathjax]\(-\sqrt{5}\)に対応する点はどこでしょうか。上の数直線上にとりましょう。
1年で，正の数，負の数の大小を比べるときに数直線を使ったよ。
平方根を数直線上に表すにはどうすればいいのかな。
見方・考え方
これまでの数と同じように，大小について考えられるかな。
目標 ▷ 平方根の大小を比べよう。
正方形の面積をxとすると，xの値が大きくなるにつれて，正方形の1辺の長さ[mathjax]\(\sqrt{x}\)の値も大きくなる。また，Qからわかるように，平方根も数直線上の点に対応させることができる。
このことから，平方根を数直線上に表したときも，右にある数ほど大きく，左にある数ほど小さい。
<3年p.50>
一般に，平方根の大小について，次のことが成り立つ。
平方根の大小
a，bが正の数のとき，[mathjax]\(a \lt b\)ならば，[mathjax]\(\sqrt{a} \lt \sqrt{b}\)
例 １
⑴ [mathjax]\(\sqrt{13}\)，[mathjax]\(\sqrt{15}\)
[mathjax]\(13 \lt 15\)であるから，
[mathjax]\(\sqrt{13} \lt \sqrt{15}\)
⑵ 5，[mathjax]\(\sqrt{24}\)
[mathjax]\(5 = \sqrt{5²} = \sqrt{25}\)
[mathjax]\(25 \gt 24\)であるから，
[mathjax]\(\sqrt{25} \gt \sqrt{24}\)
したがって，[mathjax]\(5 \gt \sqrt{24}\)
⑶ [mathjax]\(-\sqrt{2}\)，[mathjax]\(-\sqrt{5}\)
[mathjax]\(\sqrt{2} \lt \sqrt{5}\)であるから，
[mathjax]\(-\sqrt{2} \gt -\sqrt{5}\)
問 １ 次の各組の数の大小を，不等号を使って表しなさい。
⑴ [mathjax]\(\sqrt{17}\)，[mathjax]\(\sqrt{12}\)
⑵ 6，[mathjax]\(\sqrt{32}\)
⑶ [mathjax]\(\sqrt{120}\)，11
⑷ [mathjax]\(-\sqrt{6}\)，[mathjax]\(-\sqrt{7}\)
⑸ [mathjax] \(-3\)，[mathjax]\(-\sqrt{8}\)
⑹ 4，[mathjax]\(\sqrt{14}\)，[mathjax]\(\sqrt{19}\)
どんなことがわかったかな
平方根も，これまでに学んだ数と同じように，数直線上に表して大小を比べることができます。
次の課題へ！
根号のついた数の計算も，これまでの数と同じようにできるのかな？
P.54
用語の由来「平方根，[mathjax]\(\sqrt{\phantom{0}}\)」 Tea Break
平方根は，英語ではsquare rootといいます。squareは正方形や平方，rootは根っこを意味しています。square rootを直訳すれば，「平方をつくる根っこ，もとになるもの」すなわち「平方根」となります。rootの語源はラテン語のradix（植物の根）ですが，これはアラビア語のal-jidrを翻訳したものです。アラビアで発展した数学の研究が，ヨーロッパに伝えられ，このような用語が生まれました。
平方根の記号は，ドイツの数学者ルドルフが，著書「代数」（1525）の中で使ったのが最初といわれ，radixの頭文字rを図案化したものと考えられています。
ルドルフの『代数』 根号として[mathjax]\(\sqrt{\phantom{0}}\)が使われている
<3年p.51>
３ 有理数と無理数
目標 ▷ 平方根までふくめた，数の範囲についてまとめよう。
問 １ 次の数を分数で表してみましょう。
⑴ 3
⑵ [mathjax] \(-5\)
⑶ [mathjax]\(0.25\)
⑷ [mathjax] \(-1.7\)
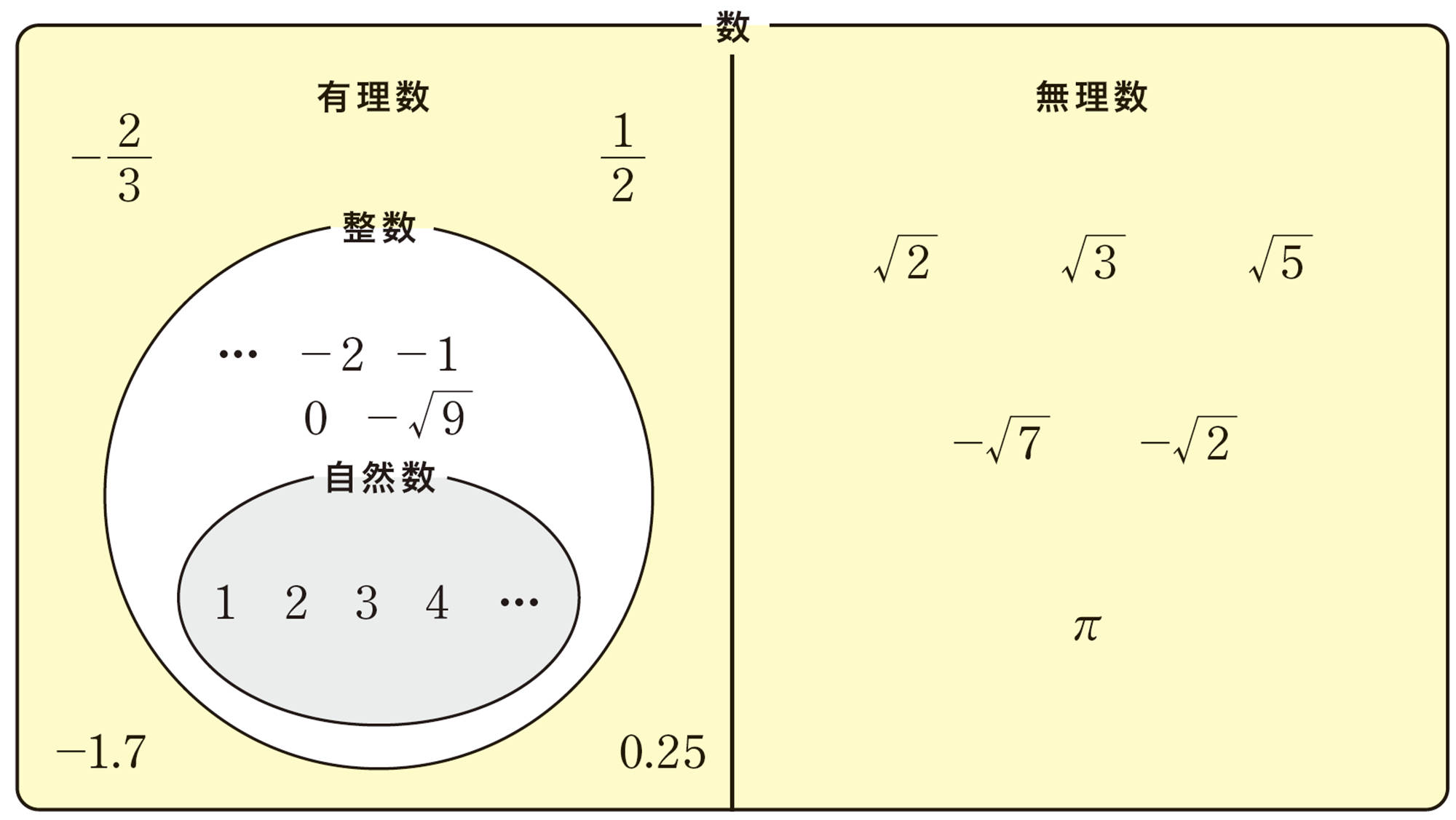
mを整数，nを0でない整数とするとき，[mathjax]\(\dfrac{m}{n}\)のように，分数で表すことができる数を有理数という。たとえば，3は[mathjax]\(\dfrac{3}{1}\)，[mathjax]\(0.25\)は[mathjax]\(\dfrac{1}{4}\)と表すことができるので，3や[mathjax]\(0.25\)は有理数である。
これに対して，[mathjax]\(\sqrt{2}\)や[mathjax]\(\sqrt{3}\)，[mathjax]\(\sqrt{5}\)などは，分数で表すことができないことがわかっている。このような数を無理数という。
円周率[mathjax]\(\pi\)も無理数である。
[mathjax]\(\pi\)などの平方根以外の無理数も，平方根や有理数と同じように数直線上の点を対応させることができる。
問 ２ 次の数は有理数ですか，それとも無理数ですか。
[mathjax]\(\dfrac{12}{7}\)，[mathjax] \(-0.09\)，[mathjax]\(\sqrt{6}\)，[mathjax]\(\sqrt{25}\)，[mathjax]\(-\sqrt{3}\)，[mathjax]\(\sqrt{\dfrac{9}{4}}\)
<3年p.52>
有理数や無理数を小数で表したときの特徴を考えてみよう。
問 ３ 次の分数を，小数で表しなさい。
⑴ [mathjax]\(\dfrac{2}{5}\)
⑵ [mathjax]\(\dfrac{7}{8}\)
⑶ [mathjax]\(\dfrac{5}{11}\)
⑷ [mathjax]\(\dfrac{4}{7}\)
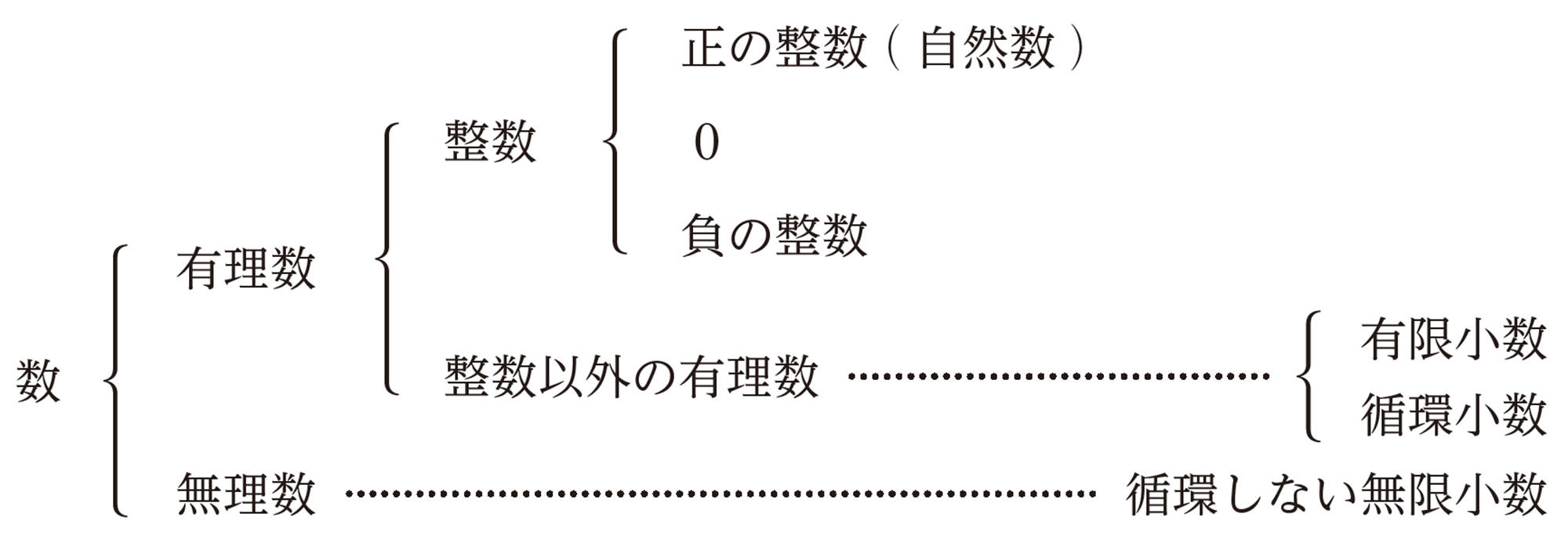
小数第何位かで終わる小数を有限小数といい，小数部分が限りなく続く小数を無限小数という。無限小数のうち，小数部分に同じ数字の並びがくりかえし現れるものを循環小数という。
整数以外の有理数を小数で表すと，有限小数か循環小数になる。
これに対して， 無理数を小数で表すと，
[mathjax]\(\sqrt{3}=1.73205080756887729352\cdots\)
[mathjax]\(\sqrt{5}=2.23606797749978969640\cdots\)
のように，循環しない無限小数になることがわかっている。
有限小数
[mathjax]\(\dfrac{2}{5} = 0.4\)
[mathjax]\(\dfrac{7}{8} = 0.875\)
循環小数
[mathjax]\(\dfrac{5}{11} = 0.454545454545\cdots\)
[mathjax]\(\dfrac{4}{7} = 0.571428571428\cdots\)
関連▷p.53
どんなことがわかったかな
mを整数，nを0でない整数とするとき，[mathjax]\(\dfrac{m}{n}\)で表すことができる数は有理数，[mathjax]\(\dfrac{m}{n}\)で表すことができない数は無理数といいます。数は有理数と無理数に分類することができます。
<3年p.53>
確かめよう 1節 平方根
１ 次の数の平方根を求めなさい。
⑴ 36
⑵ 17
⑶ [mathjax]\(\dfrac{9}{25}\)
⑷ [mathjax]\(0.6\)
２ 次の数を，根号を使わずに表しなさい。
⑴ [mathjax]\(\sqrt{81}\)
⑵ [mathjax]\(-\sqrt{4}\)
⑶ [mathjax]\((\sqrt{5})²\)
⑷ [mathjax]\((-\sqrt{2.4})²\)
３ 次の各組の数の大小を，不等号を使って表しなさい。
⑴ [mathjax]\(\sqrt{15}\)，[mathjax]\(\sqrt{14}\)
⑵ [mathjax]\(-\sqrt{12}\)，[mathjax]\(-\sqrt{10}\)
⑶ [mathjax]\(\sqrt{35}\)，[mathjax]\(\sqrt{37}\)，6
４ 次の数を，有理数と無理数に分けなさい。
[mathjax]\(\sqrt{5}\)，[mathjax]\(-\sqrt{9}\)，[mathjax]\(\dfrac{3}{2}\)，[mathjax] \(-0.7\)，[mathjax]\(-\sqrt{30}\)
循環小数 Tea Break
有理数を小数で表すと，有限小数か循環小数になることを学びました。たとえば， [mathjax]\(\dfrac{1}{3}\)や[mathjax]\(\dfrac{4}{7}\)は，循環小数になります。循環小数は，くりかえされる並びの最初と最後の数字の上に・をつけて，次のように表すことがあります。
[mathjax]\(\dfrac{1}{3} = 0.333333 \dots = 0.\dot{3}\)
[mathjax]\(\dfrac{4}{7} = 0.571428571428571428 \dots =0.\dot{5}7142\dot{8}\)
次に，[mathjax]\(0.\dot{2}\dot{7}\)を例として，循環小数を分数に直す方法を考えてみましょう。
[mathjax]\(x = 0.\dot{2}\dot{7}\)とすると，[mathjax]\(x = 0.272727\dots\) ①
両辺を100倍すると，[mathjax]\(100x = 27.272727\dots\) ②
②の両辺から①の両辺をそれぞれひくと，
上の方法で，循環小数[mathjax]\(0.\dot{1}\dot{4}\)，[mathjax]\(0.\dot{7}2\dot{9}\)を分数に直してみましょう。
