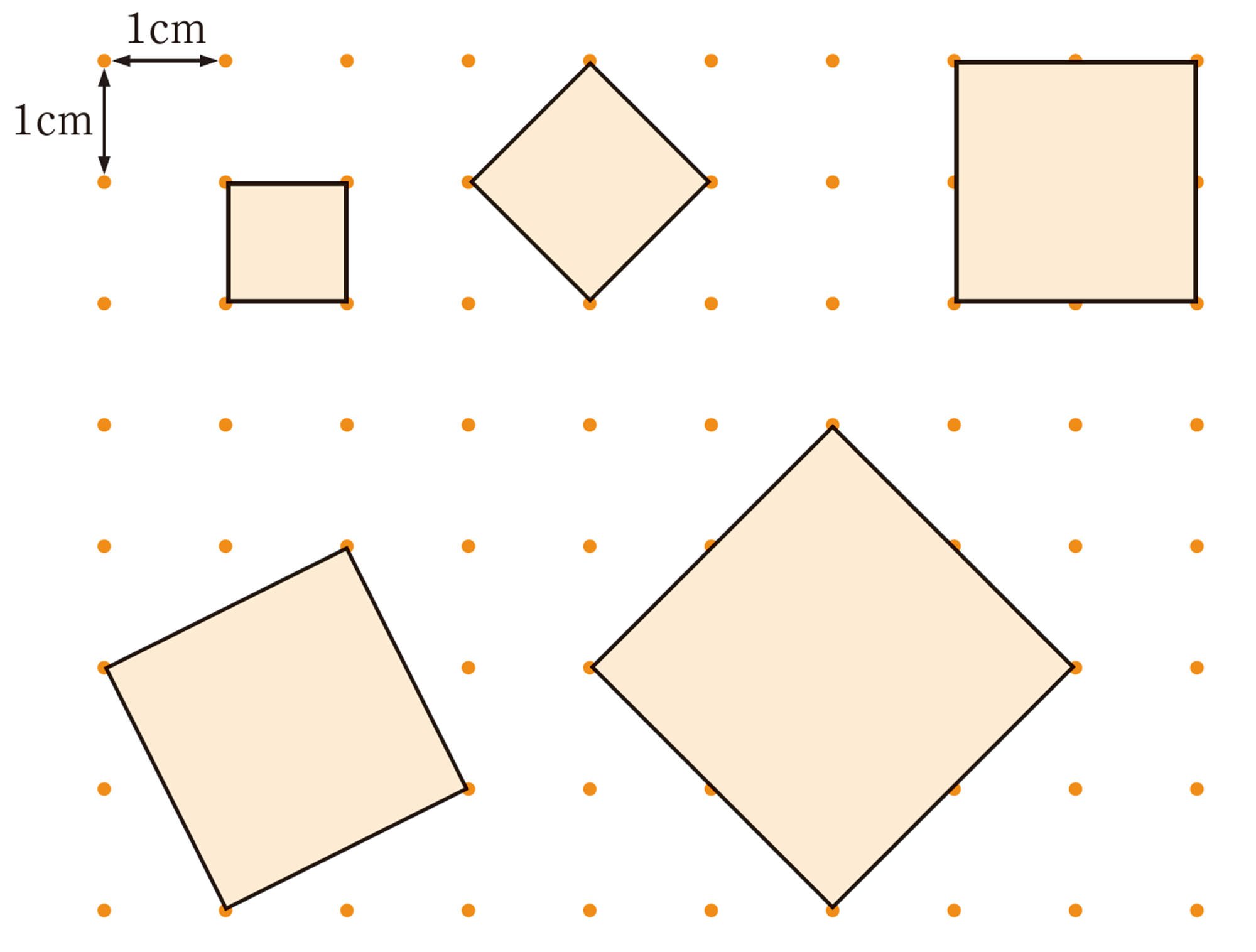
<3年p.45>
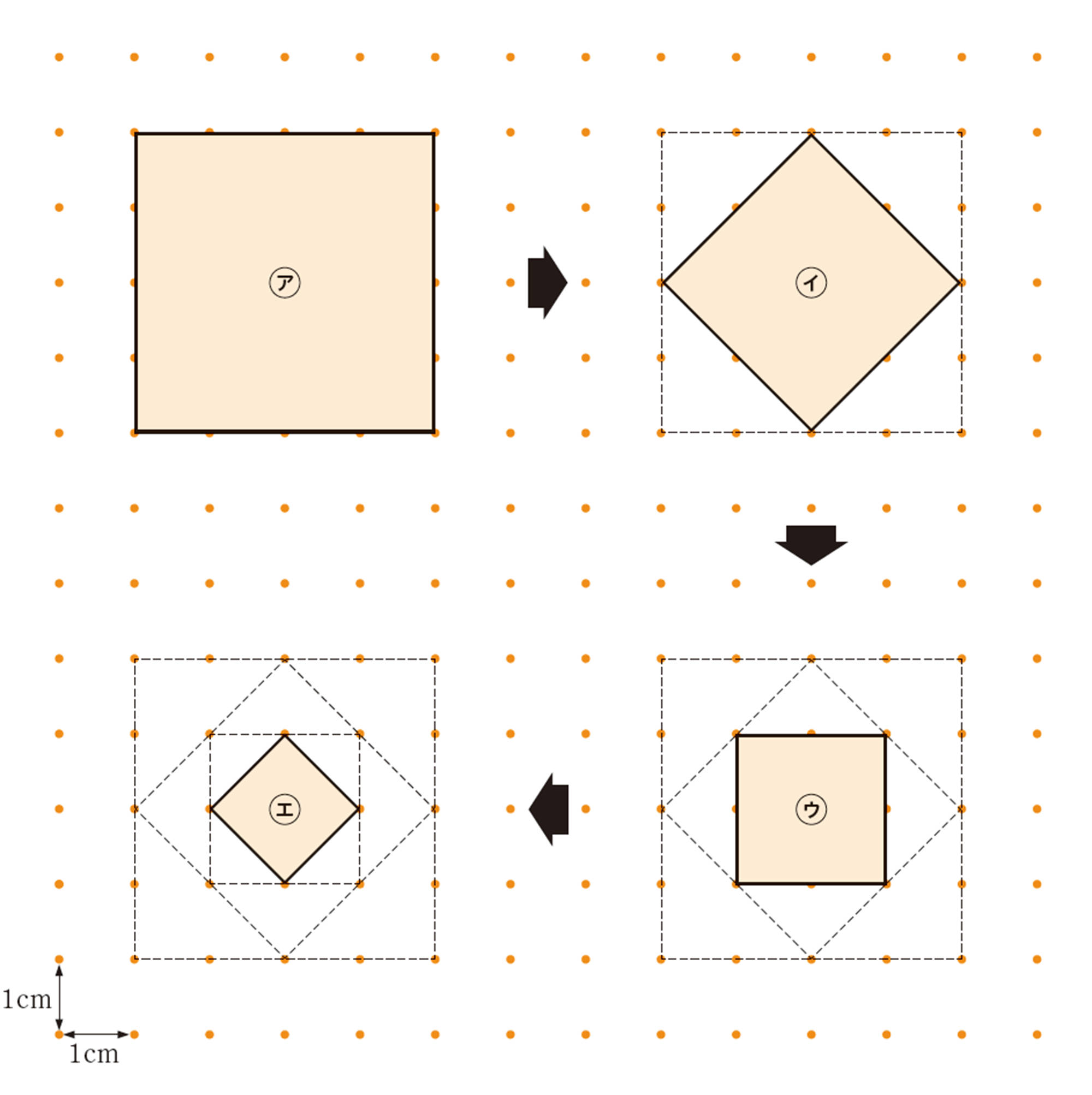
【1】 前ページの正方形㋐,㋒の面積を求めましょう。また,それぞれの正方形の1辺の長さを求めましょう。
【2】 前ページの正方形㋑,㋓の面積は,いくらになるでしょうか。また,正方形の1辺の長さを求められるか考えてみましょう。
正方形㋑の面積は,正方形㋐の面積の半分になっているね。
正方形㋑の面積と同じように考えれば,正方形㋓の面積もわかるね。
面積がわかっているのに,1辺の長さがわからないよ。
1辺の長さを測ってみたらどうかな。
【3】 前ページの正方形㋑,㋓の1辺の長さを,それぞれ測ってみましょう。また,測った長さから正方形㋑,㋓の面積を計算で求め, 2 で考えた面積と比べてみましょう。
正方形㋑,㋓の面積は整数値になるね。でも,測った1辺の長さを2乗してもぴったり同じにならないよ。

次の課題へ!
面積が2cm²や8cm²になる正方形の1辺の長さは,どのくらいになるのかな?
P.46

<3年p.46>
1 平方根
根号
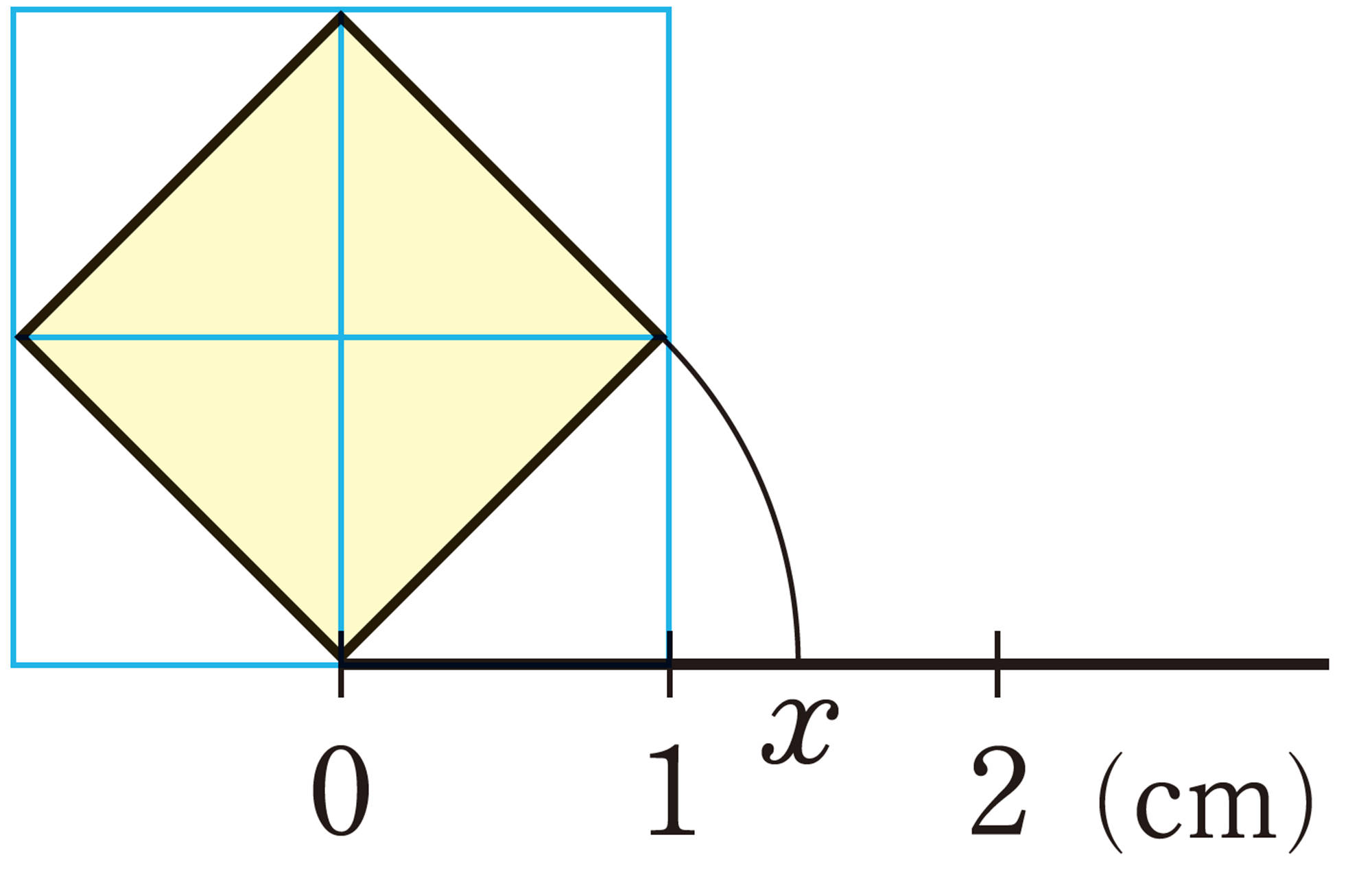
Q Question

1cmと2cmの間になりそうだね。
正方形の1辺の長さを正確に測れるかな。

見方・考え方
具体的な数を使って,考えられるかな。
目標 ▷ 2乗すると2になる数は,どのくらいの大きさになるのか調べよう。
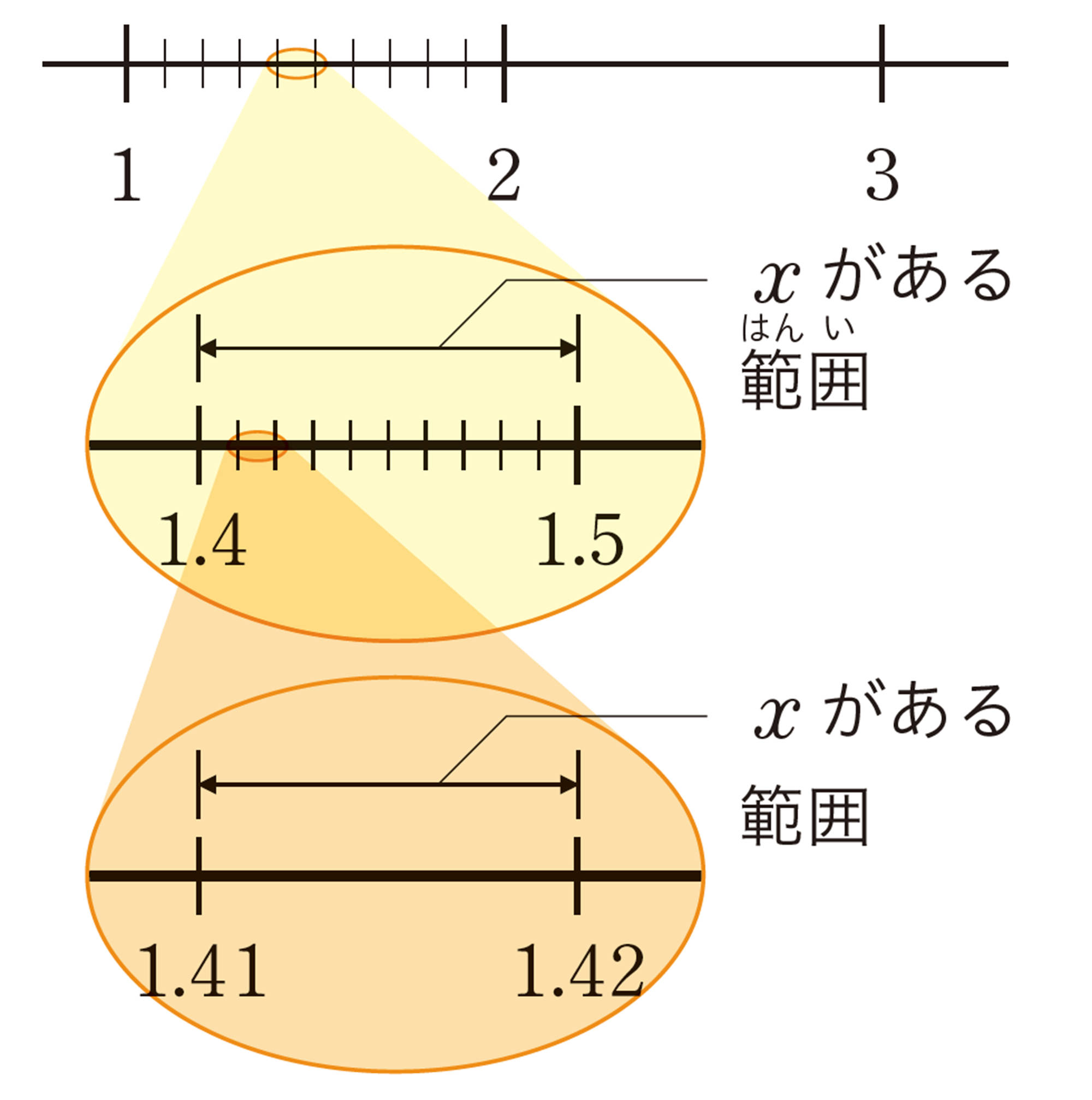
問 1 上のようにして,【Q】 のxの値の小数第三位を求めなさい。
上のようにして計算していくと, Q のxの値は,
1.414213562373095048801688724209…
となり,限りなく続く小数となる。
「2乗すると2になる正の数」を記号[mathjax]\(\sqrt{\phantom{0}}\)を使って[mathjax]\(\sqrt{2}\)と表す。
この記号[mathjax]\(\sqrt{\phantom{0}}\)を根号といい,[mathjax]\(\sqrt{2}\)を「ルート2」と読む。
面積が2cm²の正方形の1辺の長さは,[mathjax]\(\sqrt{2}\)cmと表すことができる。
<3年p.47>
近似値
長さや重さなどを測定したとき,真の値と多少のちがいがあっても,それに近い値が得られる。このように,真の値に近い値を近似値という。
たとえば,円周率として使われる[mathjax]\(3.14\)は,円周率[mathjax]\(\pi\)の近似値である。
[mathjax]\(\bbox[lemonchiffon, 5pt]{\sqrt{2}}\)の近似値は,電卓の[mathjax]\(\bbox[lemonchiffon, 5pt]{\sqrt{\phantom{0}}}\)キーを使って求めることもできる。[mathjax]\(2 \sqrt{\phantom{0}}\)の順に押せば,右のように表示される。
また,近似値として小数第三位までの値が必要なときは,小数第四位を四捨五入すればよい。
問 2 電卓の[mathjax]\(\bbox[lemonchiffon, 5pt]{\sqrt{\phantom{0}}}\)キーを使って,次の数の近似値を小数第三位まで求めなさい。
⑴ [mathjax]\(\sqrt{3}\)
⑵ [mathjax]\(\sqrt{7}\)
⑶ [mathjax]\(\sqrt{10}\)
⑷ [mathjax]\(\sqrt{30}\)
2乗するとaになる数
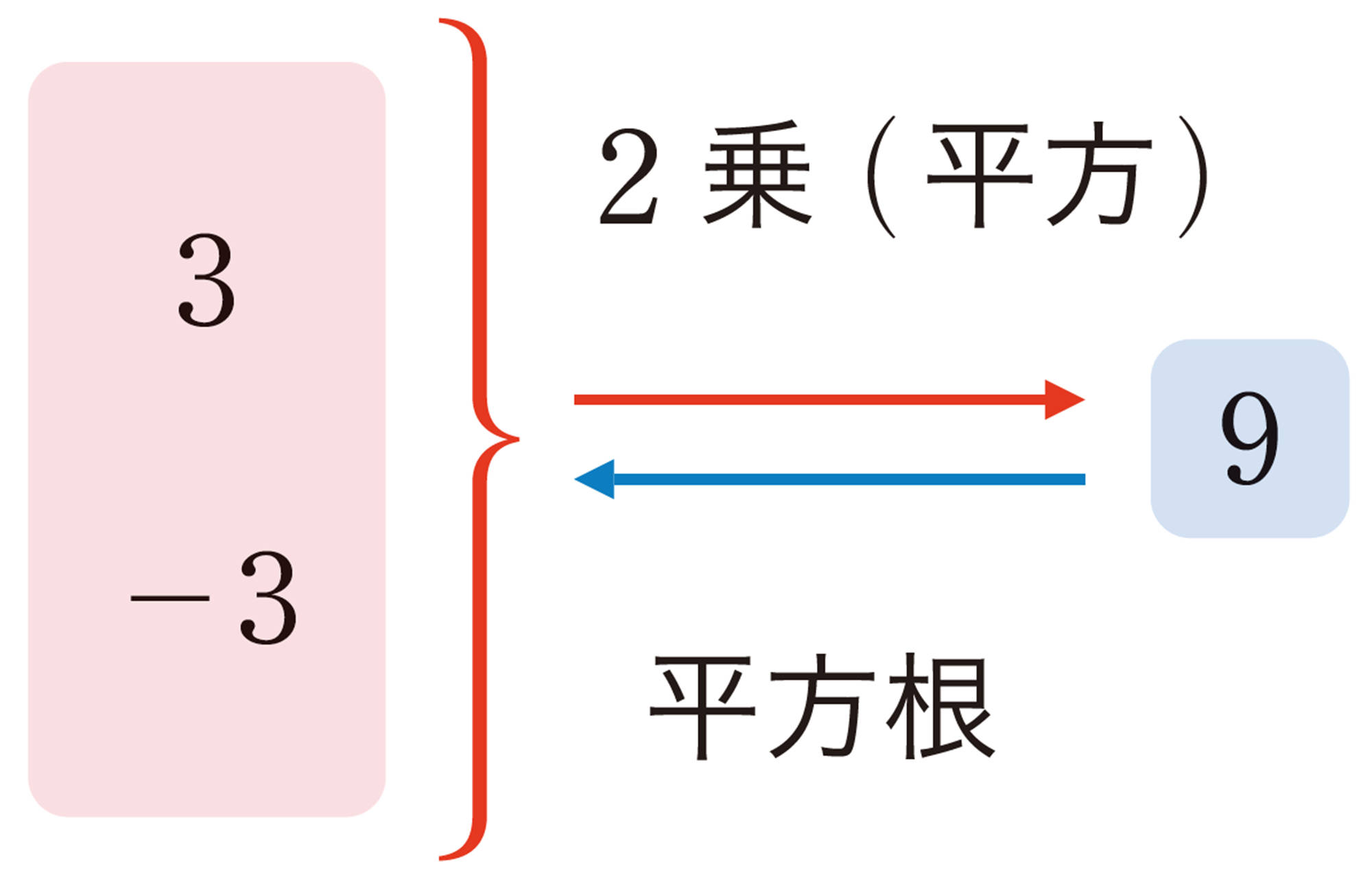
例 1 「2乗すると9になる数」は,[mathjax]\(x²=9\)を成り立たせるxの値である。
[mathjax]\(3² = 9\),[mathjax]\((-3)² = 9\)
したがって,2乗すると9になる数は,正の数3と負の数[mathjax]\(-3\)の2つである。
問 3 次の数の平方根を求めなさい。
⑴ 1
⑵ 16
⑶ 81
⑷ [mathjax]\(\dfrac{9}{100}\)
⑸ [mathjax]\(0.25\)
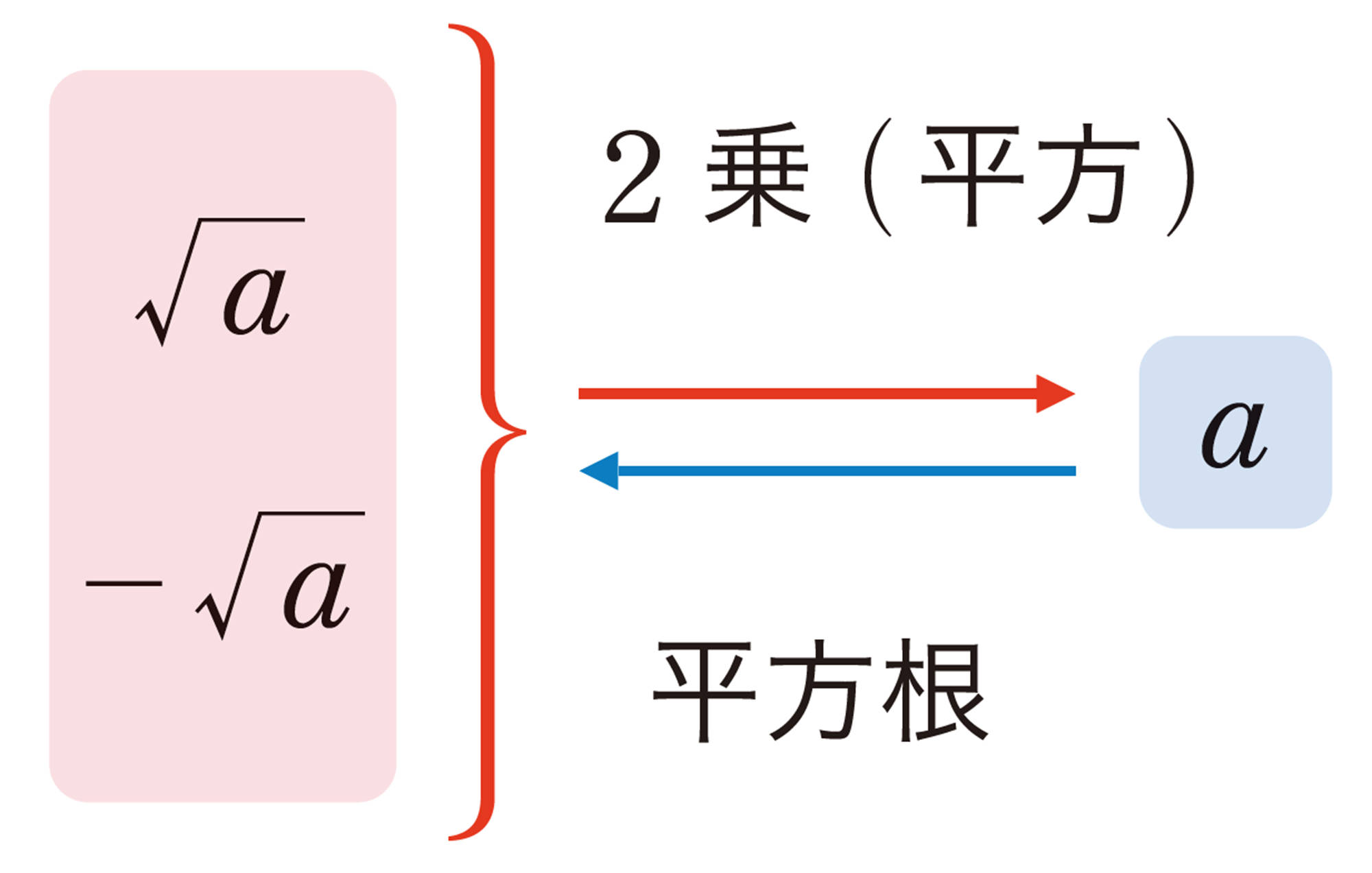
aが正の数のとき,aの平方根を,根号を使って,次のように表す。
正の方を[mathjax]\(\sqrt{a}\),負の方を[mathjax]\(-\sqrt{a}\)
例 2 2の平方根は,[mathjax]\(\sqrt{2}\)と[mathjax]\(-\sqrt{2}\)である。
注意 [mathjax]\(\sqrt{2}\)と[mathjax]\(-\sqrt{2}\)をまとめて, [mathjax]\(\pm \sqrt{2}\)と表すことがある。[mathjax]\( \pm \sqrt{2}\)は,「プラスマイナス ルート2」と読む。
[mathjax]\( \sqrt{2} = 1.414\cdots\)
[mathjax]\(-\sqrt{2} = -1.414\cdots\)
<3年p.48>
問 4 次の数の平方根を,根号を使って表しなさい。
⑴ 3
⑵ 7
⑶ [mathjax]\(0.8\)
⑷ [mathjax]\(\dfrac{5}{3}\)
どんな数を2乗しても負の数にならないから,負の数には平方根はない。また,2乗すると0になる数は0だけである。
平方根
① 正の数の平方根は正,負の2つあり,その絶対値は等しい。
② 0の平方根は0だけである。
9の平方根は,根号を使うと[mathjax]\(\sqrt{9}\),[mathjax]\(-\sqrt{9}\)と表すことができるが,これらはそれぞれ,[mathjax] \(3\),[mathjax] \(-3\)のことである。このように,根号を使って表した数の中には,根号を使わずに表すことのできる数がある。
また,0の平方根は0であるから,[mathjax]\(\sqrt{0}=0\)である。
例 3
⑴
⑵
問 5 次の数を,根号を使わずに表しなさい。
⑴ [mathjax]\(\sqrt{4}\)
⑵ [mathjax]\(-\sqrt{64}\)
⑶ [mathjax]\(\sqrt{\dfrac{4}{9}}\)
⑷ [mathjax]\(\sqrt{(-5)²}\)
問 6 次の数を求めなさい。
⑴ [mathjax]\((\sqrt{7})²\)
⑵ [mathjax]\((-\sqrt{10})²\)
⑶ [mathjax]\((\sqrt{0.5})²\)
⑷ [mathjax]\(\require{physics}\left(-\sqrt{\dfrac{5}{6}}\right)^{2}\)
どんなことがわかったかな
aが正の数のとき,aの平方根を[mathjax]\(\sqrt{a}\) ,[mathjax]\(-\sqrt{a}\)と表すことができます。
次の課題へ!
これまでに学んだ数と同じように,平方根の大小も比べられるのかな?また,どんなところがちがうのかな?
P.49,51