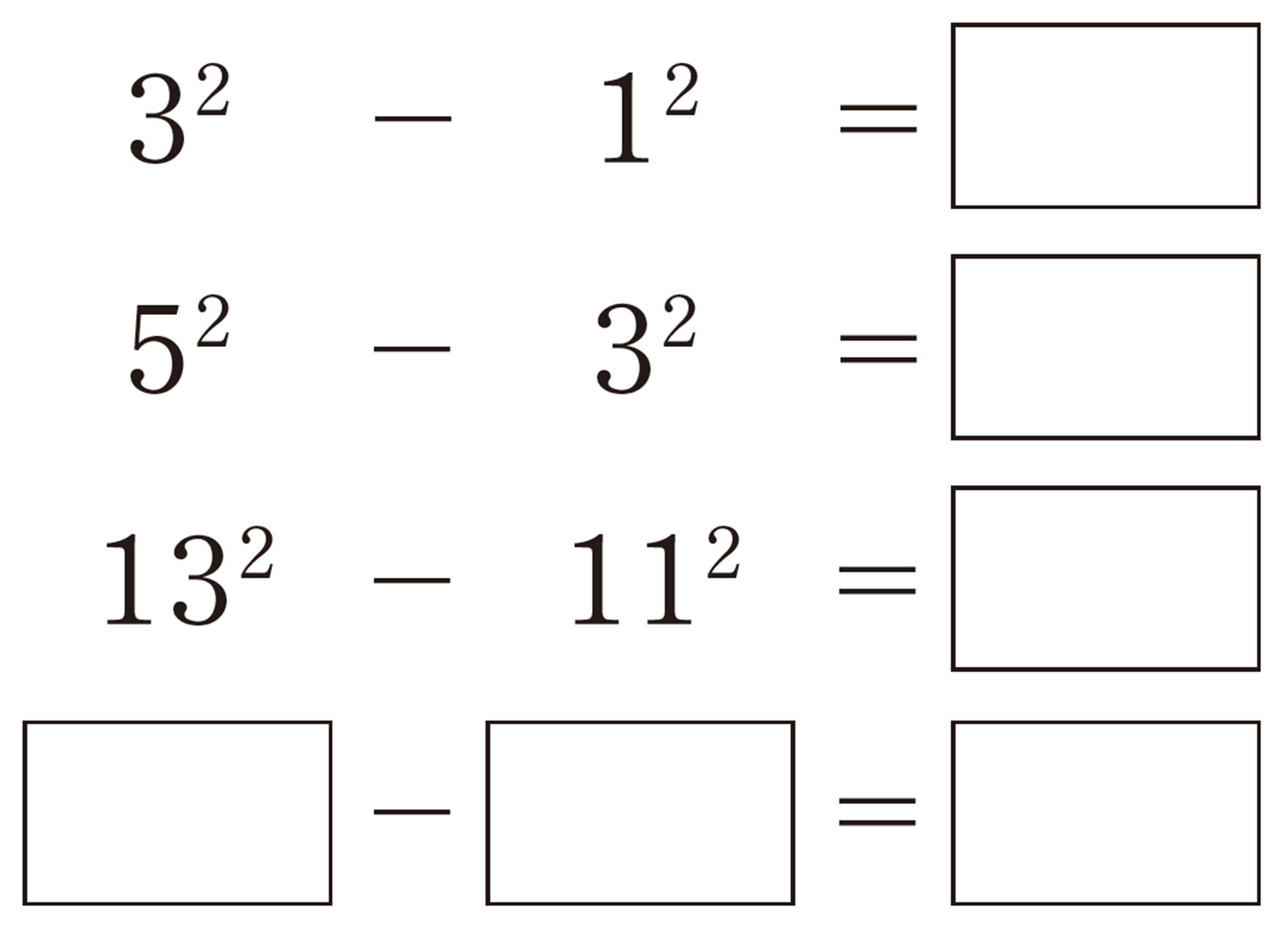教科書アドバイザー「マスマス！」

gkt-horizontal-line

<3年p.32>

3節　式の利用

乗法公式や因数分解を利用できるかな？

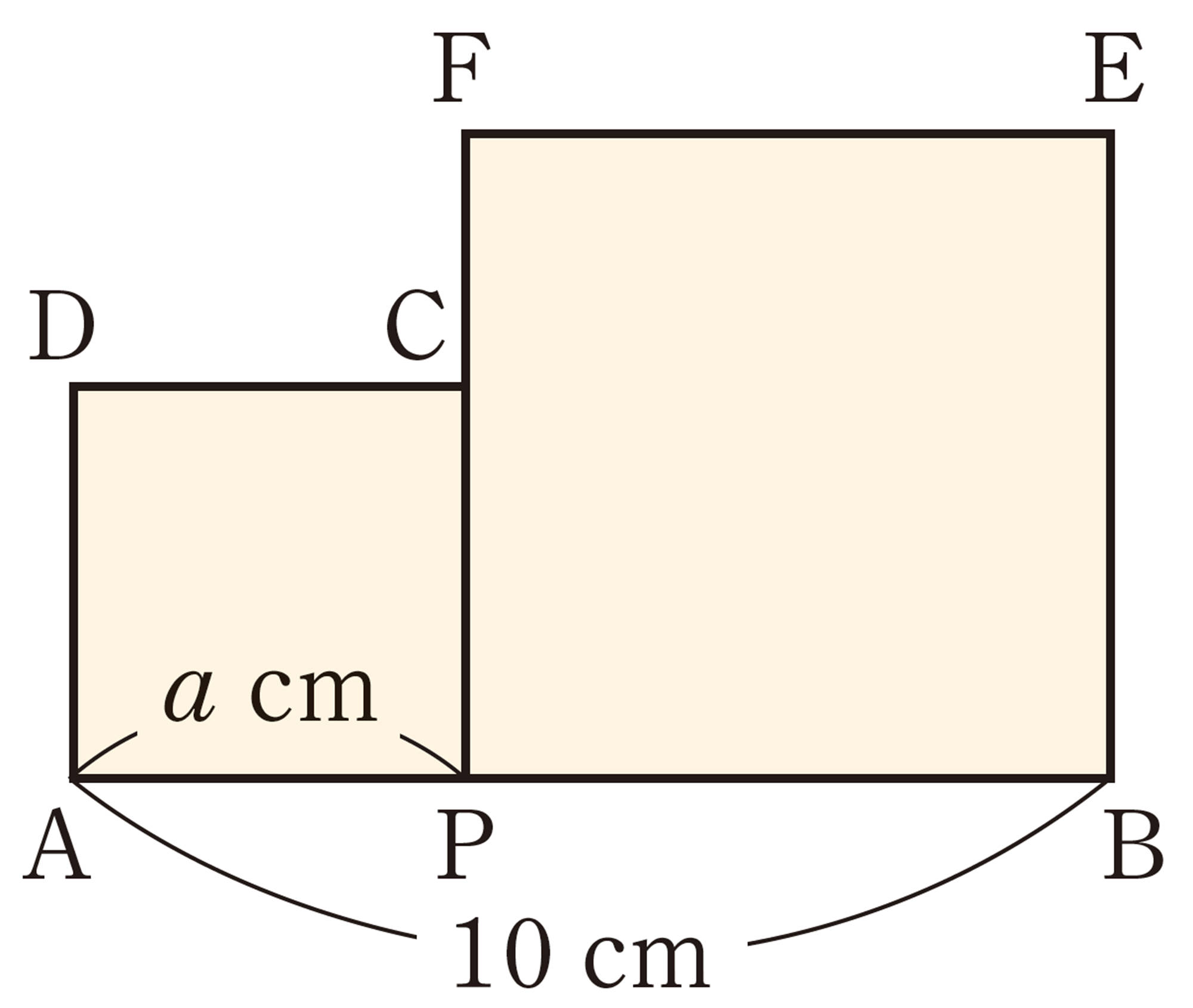
美月さんは，連続する2つの偶数の積に1を加えた結果がどうなるかについて，いろいろな数で調べたところ，おもしろいことに気づきました。
どんなことに気づいたのでしょうか。

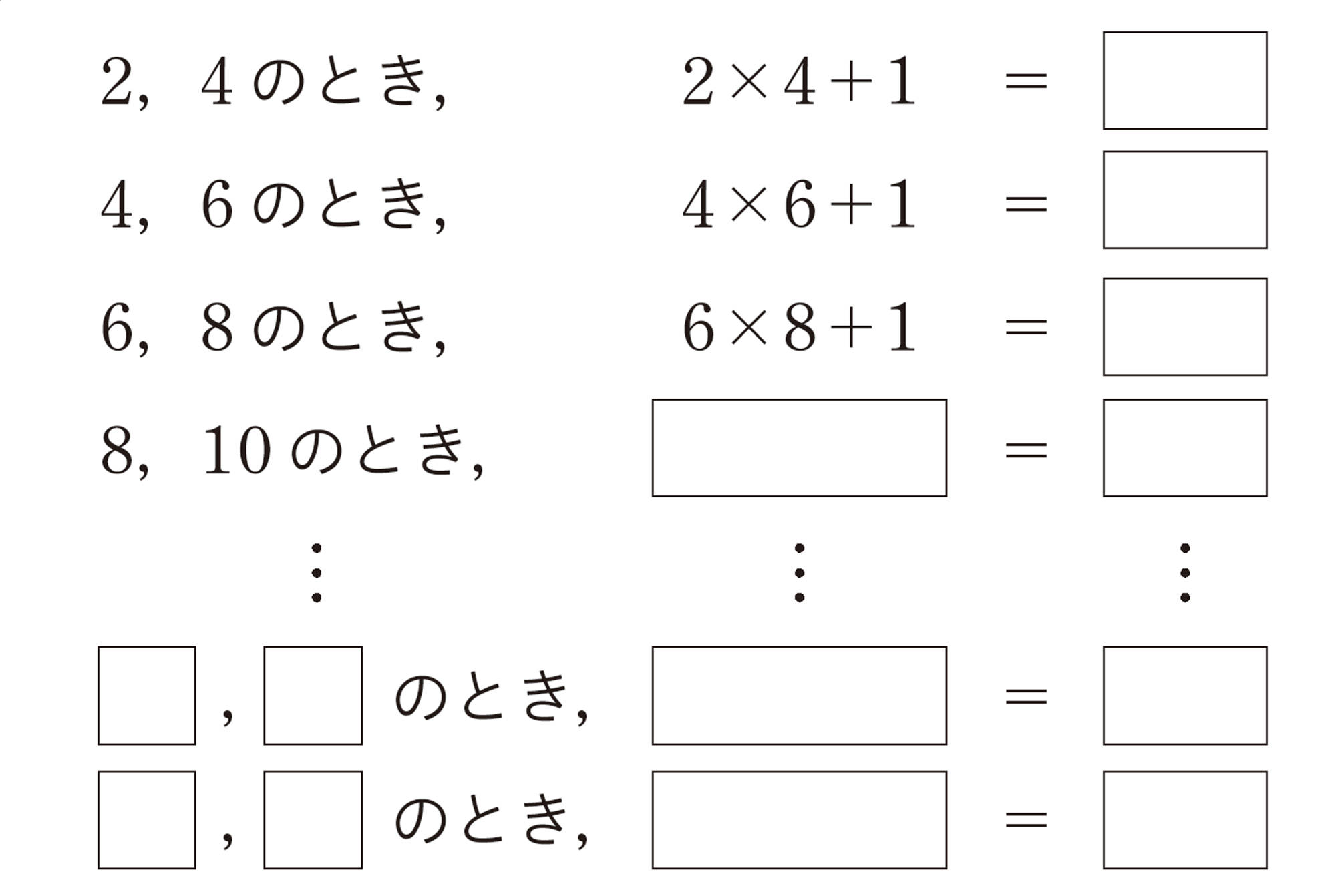
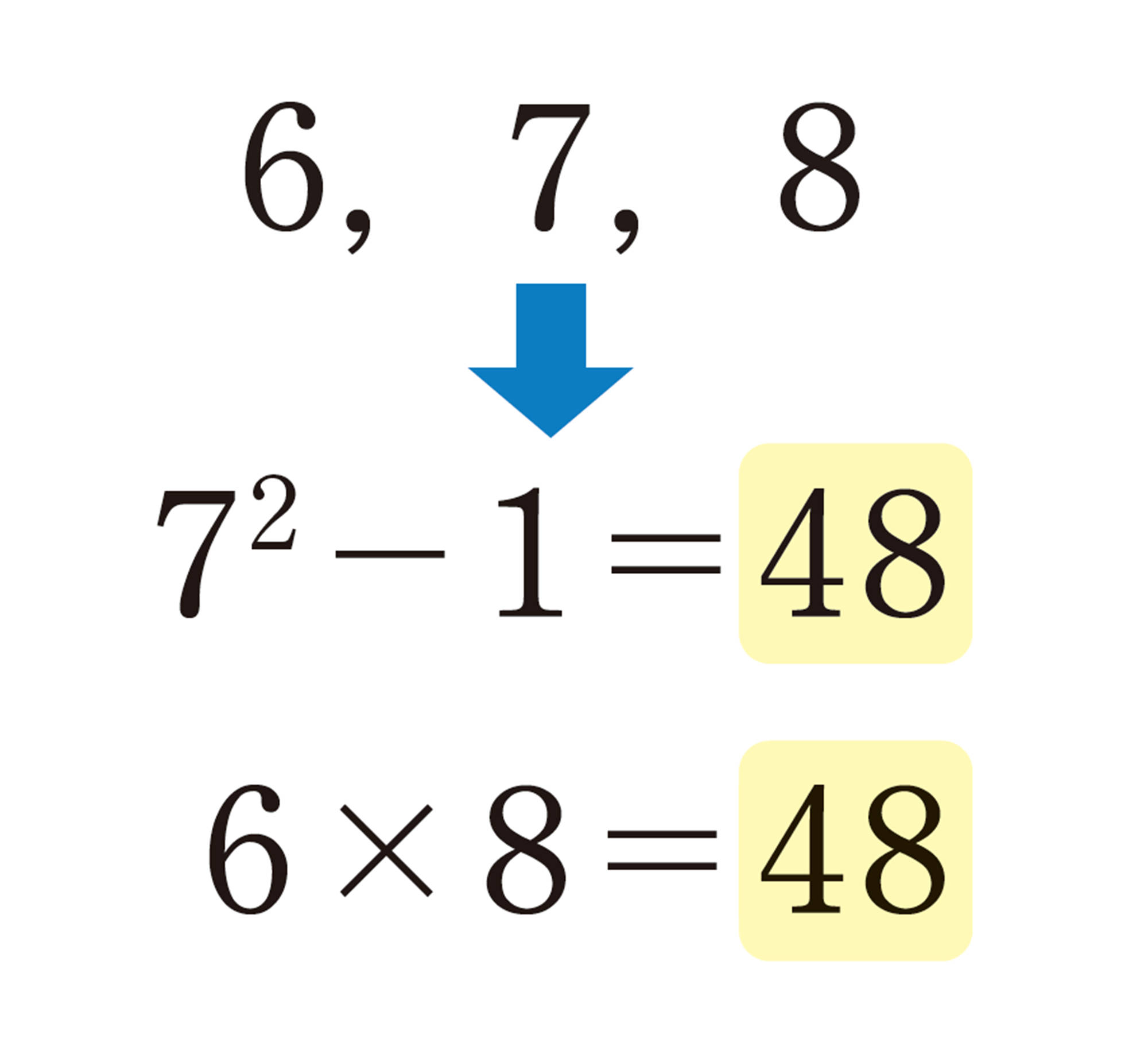
【１】　[mathjax] \(2\)，[mathjax] \(4\)や[mathjax] \(6\)，[mathjax] \(8\)のような連続する2つの偶数の積に1を加えると，計算の結果はどんな数になるでしょうか。
いろいろな場合について調べてみましょう。

avatar

[mathjax]\(9\)や[mathjax]\(25\)，[mathjax]\(49\)は，[mathjax]\(3\)や[mathjax]\(5\)，[mathjax]\(7\)の2乗になっているね。

[mathjax]\(\begin{array}{lcr} 2，4\mathsf{のとき，}& 2 \times 4+1&=\boxed{\phantom{000}}\\ 4，6\mathsf{のとき，}&4 \times 6 + 1&=\boxed{\phantom{000}}\\ 6，8\mathsf{のとき，}&6 \times 8 + 1&=\boxed{\phantom{000}}\\ 8，10\mathsf{のとき，}&\boxed{\phantom{0000000}} &=\boxed{\phantom{000}}\\ \phantom{00000}\vdots &\vdots &\vdots\phantom{00}\\ \boxed{\phantom{00}}，\boxed{\phantom{00}}\mathsf{のとき，}&\boxed{\phantom{0000000}}&=\boxed{\phantom{000}}\\ \boxed{\phantom{00}}，\boxed{\phantom{00}}\mathsf{のとき，}&\boxed{\phantom{0000000}}&=\boxed{\phantom{000}}\end{array}\)

ほかの数ではどうなっているのかな。

avatar

どうすれば，奇数の2乗になっていることを確認できるのかな。

avatar

次の課題へ！
数の性質を証明するには，どうすればいいのかな？
P.33

gkt-horizontal-line

<3年p.33>

１　式の利用

　数の性質

Q Question

美月さんは，前ページの【１】で「連続する2つの偶数の積に1を加えると，奇数の2乗になる」と予想しました。このことをどのように証明すればよいでしょうか。

avatar

2年で，数を文字におきかえて，文字式を使って説明したよ。

見方・考え方　

根拠を明らかにして，説明できるかな。

　目標　▷　式の計算を利用して，数や図形の性質を証明しよう。

　例１　　連続する2つの偶数の積に1を加えると，奇数の2乗になります。このことを証明しなさい。

証明

連続する2つの偶数は，[mathjax]\(n\)を整数とすると，[mathjax]\(2n\)，[mathjax]\(2n+2\)と表される。

[mathjax]\(\begin{eqnarray} & & 2n(2n+2)+1\\ &=& 4n²+4n+1\\ &=& (2n+1)²\end{eqnarray}\)

nは整数だから，[mathjax]\(2n+1\)は奇数である。
したがって，連続する2つの偶数の積に1を加えると，奇数の2乗になる。

　問１　　例1の証明から，計算の結果が「奇数の2乗になる」こと以外に，どんなことを読み取ることができますか。

avatar

式の計算を利用すると，いろいろな数の性質を見つけることができるね。

「連続する2つの偶数」を「連続する2つの奇数」に変えると，どんな性質が見つけられるかな。

avatar

　問２　　連続する3つの整数では，中央の数の2乗から1をひいた差は，残りの2数の積に等しくなります。このことを，中央の数をnとして証明しなさい。

gkt-horizontal-line

<3年p.34>

Q Question

連続する2つの奇数では，大きい方の数の2乗から小さい方の数の2乗をひいた差は，どんな数の倍数になるかを予想しましょう。

[mathjax]\(\begin{eqnarray}3^{2}-1^{2}&=&\boxed{\phantom{000}}\\ 5^{2}-3^{2}&=&\boxed{\phantom{000}}\\ 13^{2}-11^{2}&=&\boxed{\phantom{000}}\\ \boxed{\phantom{000}}-\boxed{\phantom{000}}&=&\boxed{\phantom{000}}\end{eqnarray}\)

avatar

計算の結果は，8の倍数になりそうだね。

いつでも8の倍数になっているかを，文字式を使って証明できるかな。

avatar

見方・考え方　

いろいろな数で調べて，どんな性質があるか見つけられるかな。

　説明する力をつけよう　

１　Qで予想したことを証明します。どのように証明すればよいか話し合ってみましょう。

avatar

いくつかの数で確かめてみると，どれも8の倍数になるね。だから差は，8の倍数になると思う。

数学の予想らしく，仮定と結論をはっきりさせて，文章に表してみるといいね。

avatar

予想を文章にしてみると，「連続する2つの奇数では，大きい方の数の2乗から小さい方の数の2乗をひいた差は，8の倍数になる」となるね。

avatar

この予想が成り立つかどうかを，考えてみよう。奇数を2つ考えるから，[mathjax]\(2n+1\)，[mathjax]\(2m+1\)だね。

それだと「連続する」かどうかわからないから，同じ文字を使わないといけないね。 [mathjax]\(2n+1\)，[mathjax]\(2n+3\)になるのかな。

avatar

拓真さんは，予想が成り立つかどうかを，次のように証明しました。

証明

これでいいのかな？

連続する2つの奇数は，nを整数とすると，[mathjax]\(2n+1\)，[mathjax]\(2n+3\)と表される。

[mathjax]\(\begin{eqnarray} & & (2n+3)²-(2n+1)²\\ &=& (4n²+12n+9)-(4n²+4n+1)\\ &=& 8n+8\end{eqnarray}\)

したがって，連続する2つの奇数の大きい方の数の2乗から小さい方の数の2乗をひいた差は，8の倍数になる。

gkt-horizontal-line

<3年p.35>

avatar

差が [mathjax]\(8n+8\) で [mathjax]\(8n\) は8の倍数，それに8をたすから，[mathjax]\(8n+8\) も8の倍数ということかな。もっと，はっきりわかる表現にできないかな。

8の倍数は [mathjax]\(8\times (\textsf{整数})\) と表される数のことだから，この形にすると8の倍数であることがはっきりするね。

avatar

２　前ページの証明の [mathjax]\(8n+8\) を [mathjax]\(8\times (\textsf{整数})\) の形に直して，予想がいつでも成り立つことをわかりやすく説明しましょう。

３　前ページの　Qで，問題の条件を変えて「連続する2つの偶数」とした場合には，計算の結果がどうなるかを予想し，そのことを証明しましょう。

　問３　　11ページで，③の面積がもっとも大きくなることや，①と②，②と③の面積の差が一定になる理由を，①〜③の式を展開してことばで説明しなさい。

　計算のくふう

乗法公式や因数分解を，数の計算に利用してみよう。

　例２　　[mathjax]\(x=23\)，[mathjax]\(y=77\)のとき，[mathjax]\(x²+2xy+y²\)の値を求めなさい。

解答

もとの式にそのまま代入する。

[mathjax]\(\begin{eqnarray} & & x²+2xy+y²\\ &=& 23²+2\times23\times77+77²\\ &=& 529+3542+5929\\ &=& 10000\end{eqnarray}\)

答　10000

因数分解してから代入する。

[mathjax]\(\begin{eqnarray} & & x²+2xy+y²\\ &=& (x+y)²\\ &=& (23+77)²\\ &=& 100²\\ &=& 10000\end{eqnarray}\)

答　10000

　問４　　[mathjax]\(x=13\)のとき，次の式の値を求めなさい。

⑴　[mathjax]\(x²-3x\)

⑵　[mathjax]\(x²-8x+15\)

　例３　　

⑴

[mathjax]\(\begin{eqnarray} & & 55²-45²\\ &=& (55+45)\times(55-45)\\ &=& 100\times10\\ &=& 1000\end{eqnarray}\)

⑵

[mathjax]\(\begin{eqnarray} & & 98²\\ &=& (100-2)²\\ &=& 100²-2\times100\times2+2²\\ &=& 9604\end{eqnarray}\)

　問５　　式の展開や因数分解を使って，次の計算をしなさい。

⑴　[mathjax]\(28²-22²\)

⑵　[mathjax]\(103\times97\)

⑶　[mathjax]\(101²\)

gkt-horizontal-line

<3年p.36>

　図形の性質

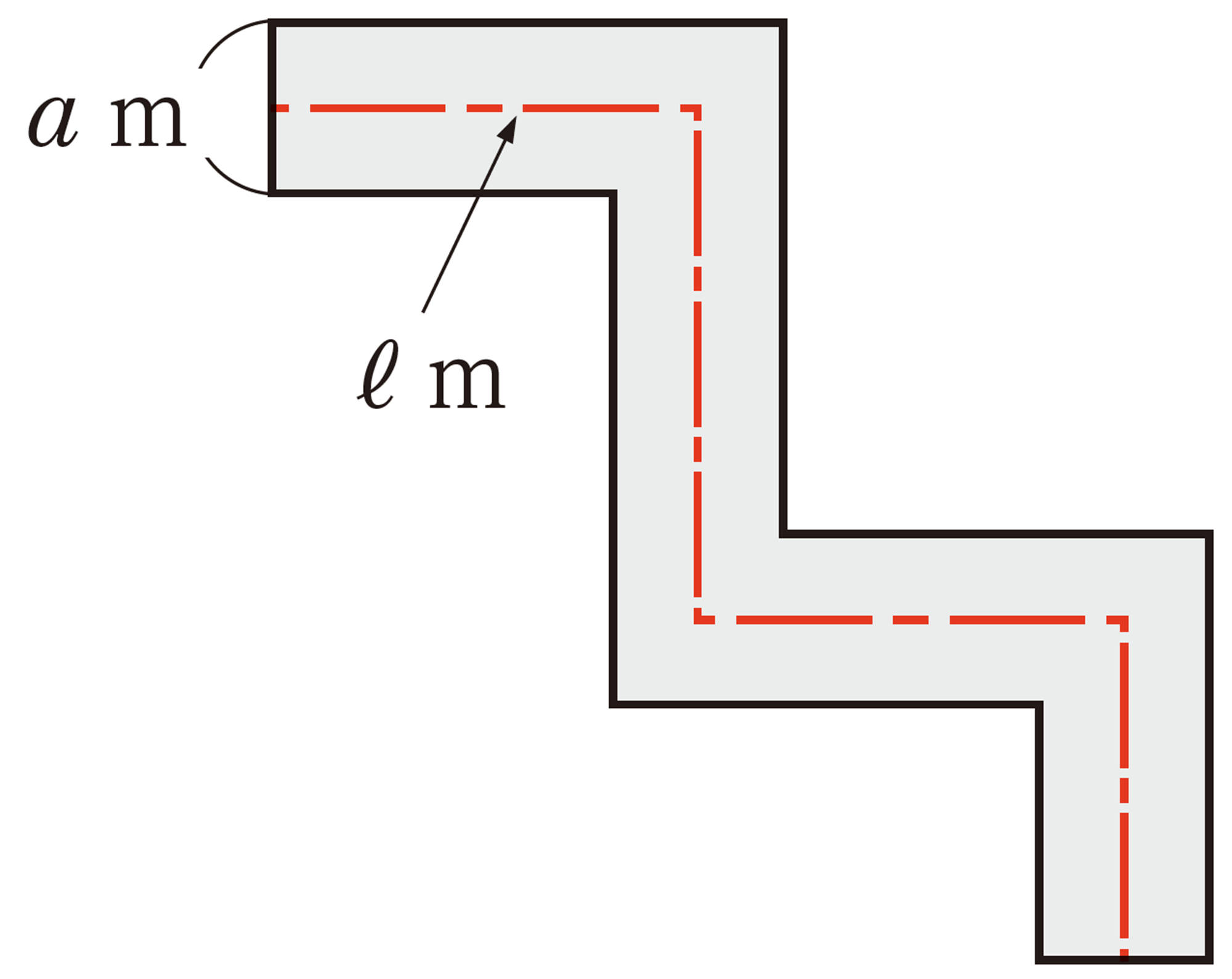
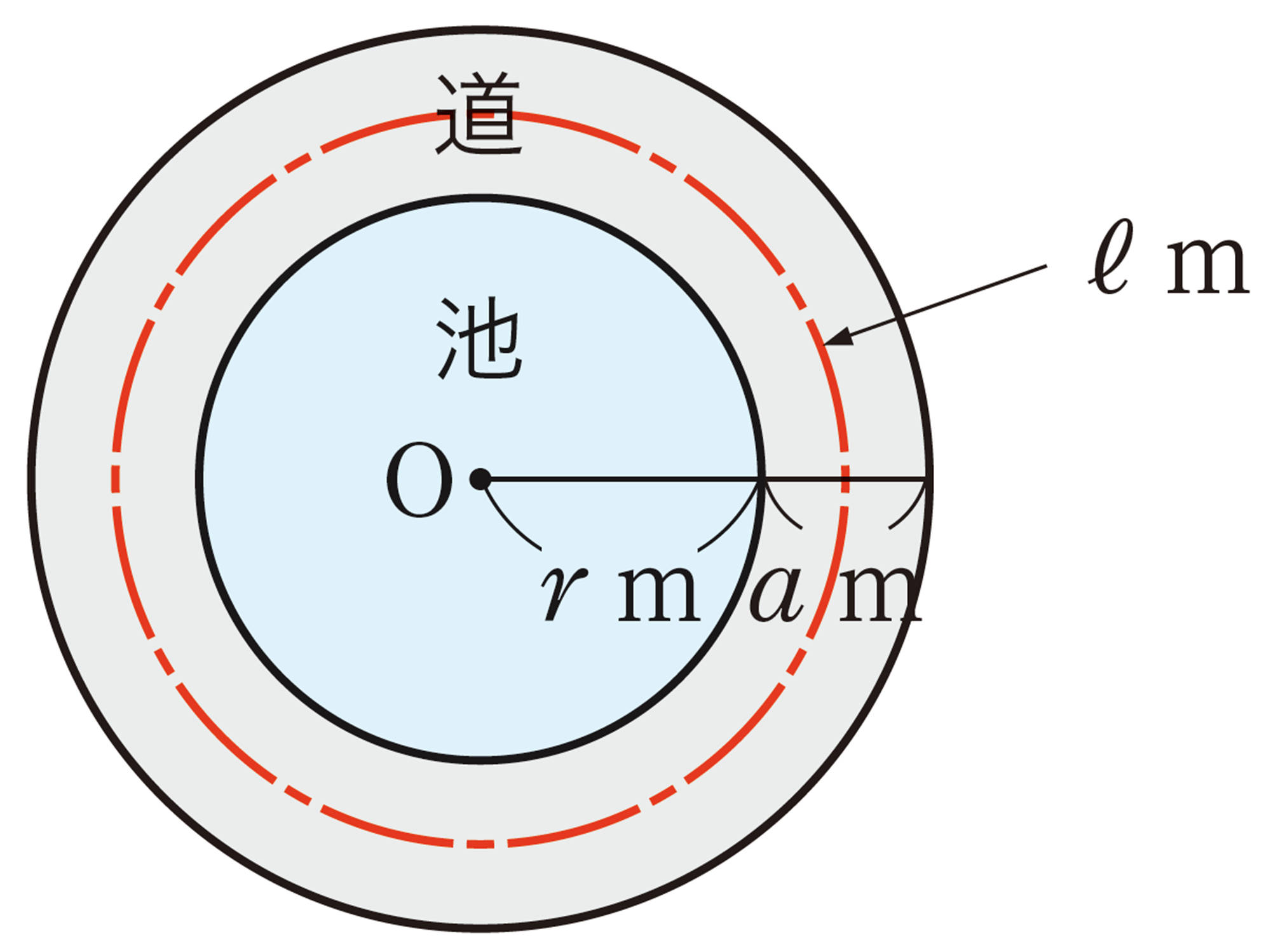
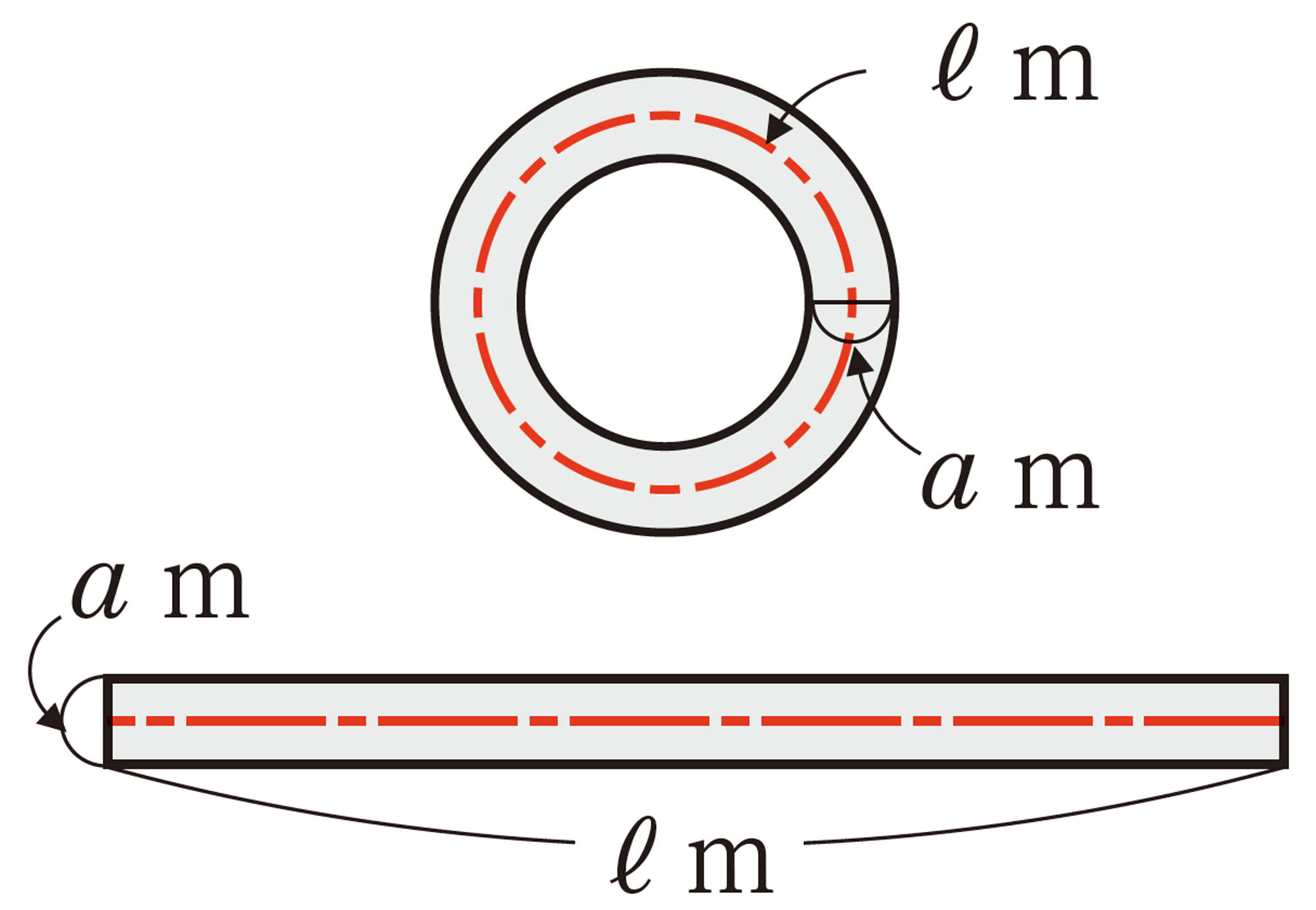
Q Question

次の図のように，幅a ｍの2つの道があります。この道の中央を通る線全体の長さをℓｍとします。また，池の半径はrｍです。このとき，2つの道の面積を比べてみましょう。

㋐

㋑

avatar

㋐は，直線の道として考えられないかな。

見方・考え方　

文字式を使って，説明できるかな。

　例４　　【Q】の㋑の道の面積をSｍ²とするとき，[mathjax]\(S=aℓ\)であることを証明しなさい。

　考え方　　[mathjax]\(S\)と[mathjax]\(aℓ\)をそれぞれ計算して，文字を使って表す。

証明

道の面積[mathjax]\(S\)m²は，

[mathjax]\(\begin{eqnarray}S&=&\pi(r+a)²-\pi r²\\ &=&\pi(r²+2ar+a²)-\pi r²\\ &=&2\pi ar+\pi a²\\ &=&\pi a(2r+a)\quad\cdots\cdots\text{①}\end{eqnarray}\)

また，道の中央を通る円の半径は
[mathjax]\(\require{physics}\left(r+\dfrac{a}{2}\right)\)mであるから，

円周の長さℓmは，

[mathjax]\(\begin{eqnarray}ℓ &=& 2\pi\require{physics}\left(r+\dfrac{a}{2}\right)\\ &=& \pi(2r+a)\end{eqnarray}\)

したがって，
[mathjax]\(aℓ=\pi a(2r+a)\quad\cdots\cdots\text{②}\)
①，②から，[mathjax]\(S=aℓ\)

分数は2行使って書こう。

ふりかえり
▷1年
円の半径をrとすると，
　[mathjax]\(\mathsf{(円周)}=2\pi r\)
　[mathjax]\(\mathsf{(円の面積)}=\pi r²\)

左の証明から，縦aｍ，横ℓｍの長方形の面積と道の面積は等しいことがわかるね。

avatar

gkt-horizontal-line

<3年p.37>

　問６　　右の図のように，1辺がh mの正方形の池の周囲に，幅a mの道があります。この道の面積をS m²，道の中央を通る線全体の長さをℓ mとして，次の問いに答えなさい。

⑴　ℓをaとhを使って表しなさい。
⑵　[mathjax]\(S= aℓ\)であることを証明しなさい。

▲トライ　　右のような図形でも，[mathjax]\(S= aℓ\)が成り立つかどうかを調べてみよう。

どんなことがわかったかな

式の展開や因数分解を利用すると，数や図形の性質について証明することができます。

gkt-horizontal-line

確かめよう　3節　式の利用

□　文字式を利用して，数の性質を証明することができる。　▷　数の性質　・P.33　例1

１　連続する2つの整数では，大きい方の数の2乗から小さい方の数の2乗をひいた差は，はじめの2数の和に等しいことを証明しなさい。

□　因数分解を利用して，式の値を求めることができる。　▷　計算のくふう　・P.35　例2

２　[mathjax]\(x=-15\)のとき，次の式の値を求めなさい。

⑴　[mathjax]\(x²-5x\)

⑵　[mathjax]\(x²+x-20\)

□　乗法公式や因数分解を利用して，数の計算をすることができる。　▷　計算のくふう　・P.35　例3

３　次の式をくふうして計算しなさい。

⑴　[mathjax]\(65²-15²\)

⑵　[mathjax]\(4.8 \times 5.2\)

□　文字式を利用して，問題を解くことができる。　▷　図形の性質　・P.36　例4

４　右の図のように，長さ10 cmの線分AB上に，点Pを[mathjax]\(AP=a\)cmとなるようにとり，AP，PBをそれぞれ1辺とする正方形をつくります。[mathjax]\(AP \lt PB\)のとき，正方形PBEFの面積は，正方形APCDの面積よりどれだけ広いですか。

gkt-horizontal-line

<3年p.38>

1章「式の計算」を学んで

　できるようになったこと　　身のまわりの課題へ　▷P.41

単項式と多項式の乗法・除法の計算ができる。

2年までに学んできた式の計算と同じように考えることで，式の展開や因数分解の公式を導くことができる。

数や図形の性質について見つけた問題を，式の展開や因数分解を使って解決することができる。

　さらに学んでみたいこと　

これからもっと学んでみたいことや，疑問に思ったことを書いておこう。

gkt-horizontal-line

数学へのいざない　因数分解で売り上げアップ！

経営者は，売上を伸ばすために売上だけを見るのではなく，いろいろな要素を細かく分析する必要があります。たとえば，コンビニエンスストアの売上は次のような要素に分解することができます。
[mathjax]\((\textsf{売上})=(\textsf{客の数}) \times (\textsf{1人当たりの客の購入額})\)
さらに細かく分解してみると，次のように分解することもできます。
[mathjax]\((\textsf{売上})=(\textsf{客の数}) \times (\textsf{商品の価格}) \times (\textsf{購入数})\)
細かくなった要素をそれぞれ分析することで，売上アップにつなげることができます。
世の中のいろいろな場面では，小さな要素が集まってできていると考えることができます。ものごとを分解して小さな要素を一つひとつ洗い出していくことこそ，因数分解の考え方です。要素が集まっている状態では見えなかったことが，小さな
要素では見えることがあります。
　このように，因数分解の考え方は，ビジネスの世界でも大いに役立っています。

　関連　　裏見返し

3節　式の利用