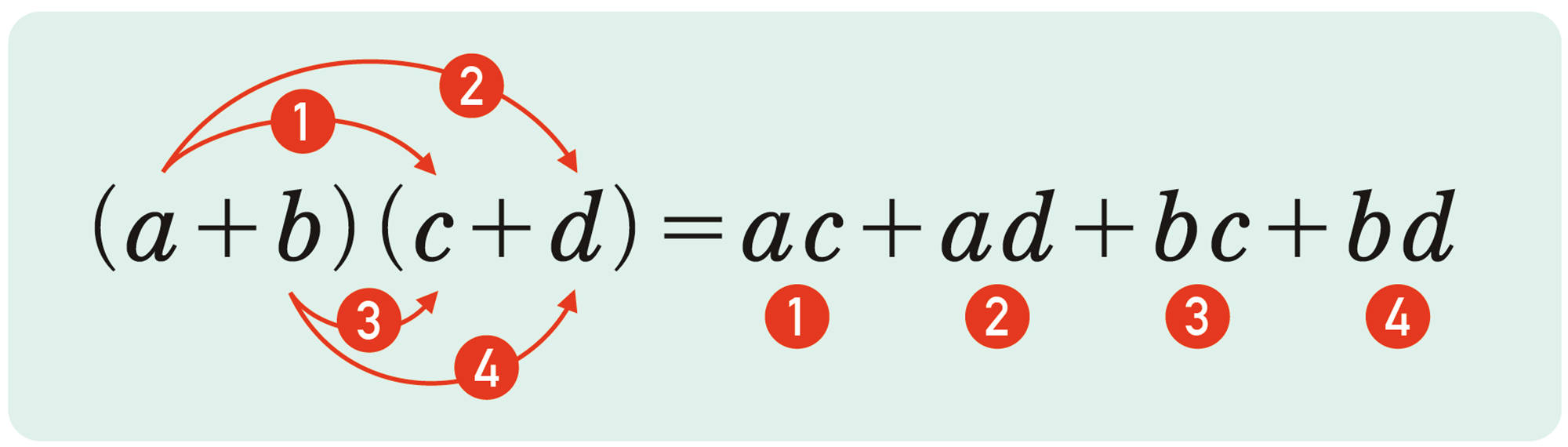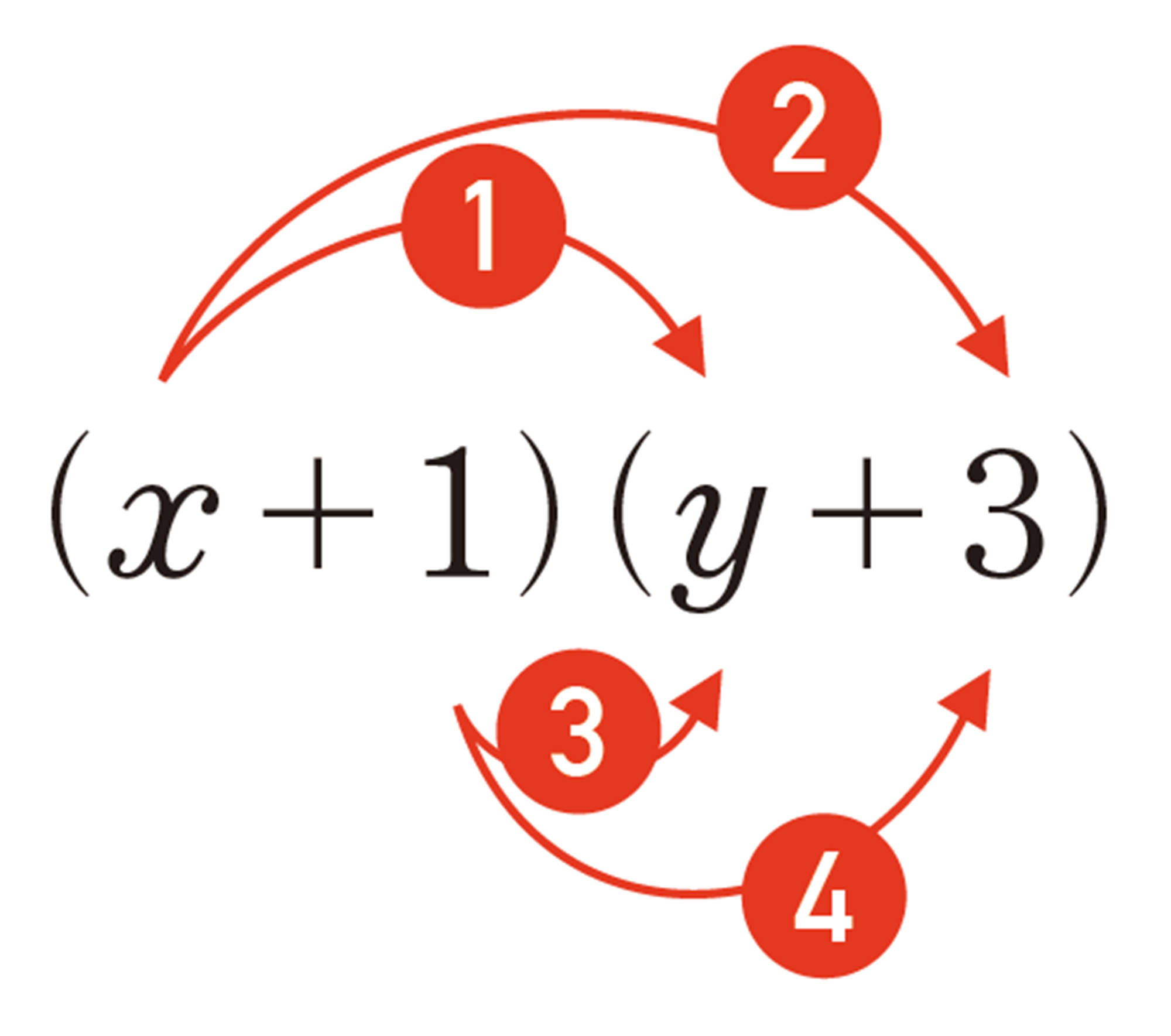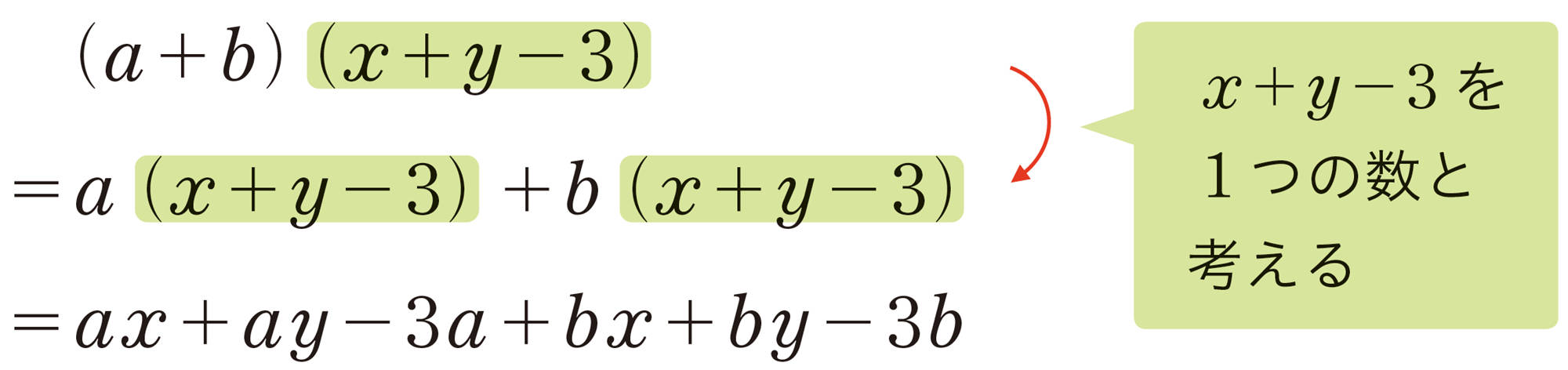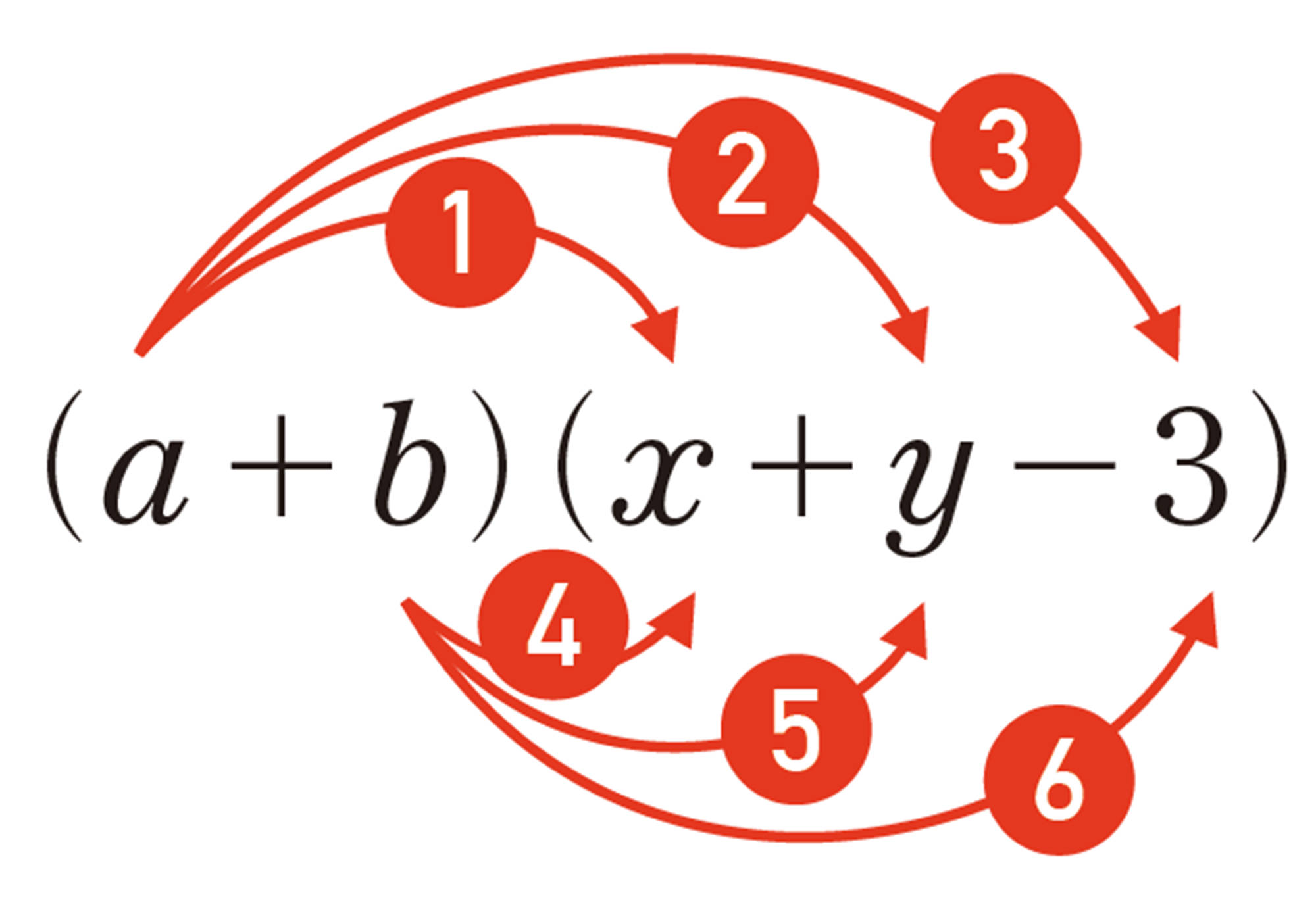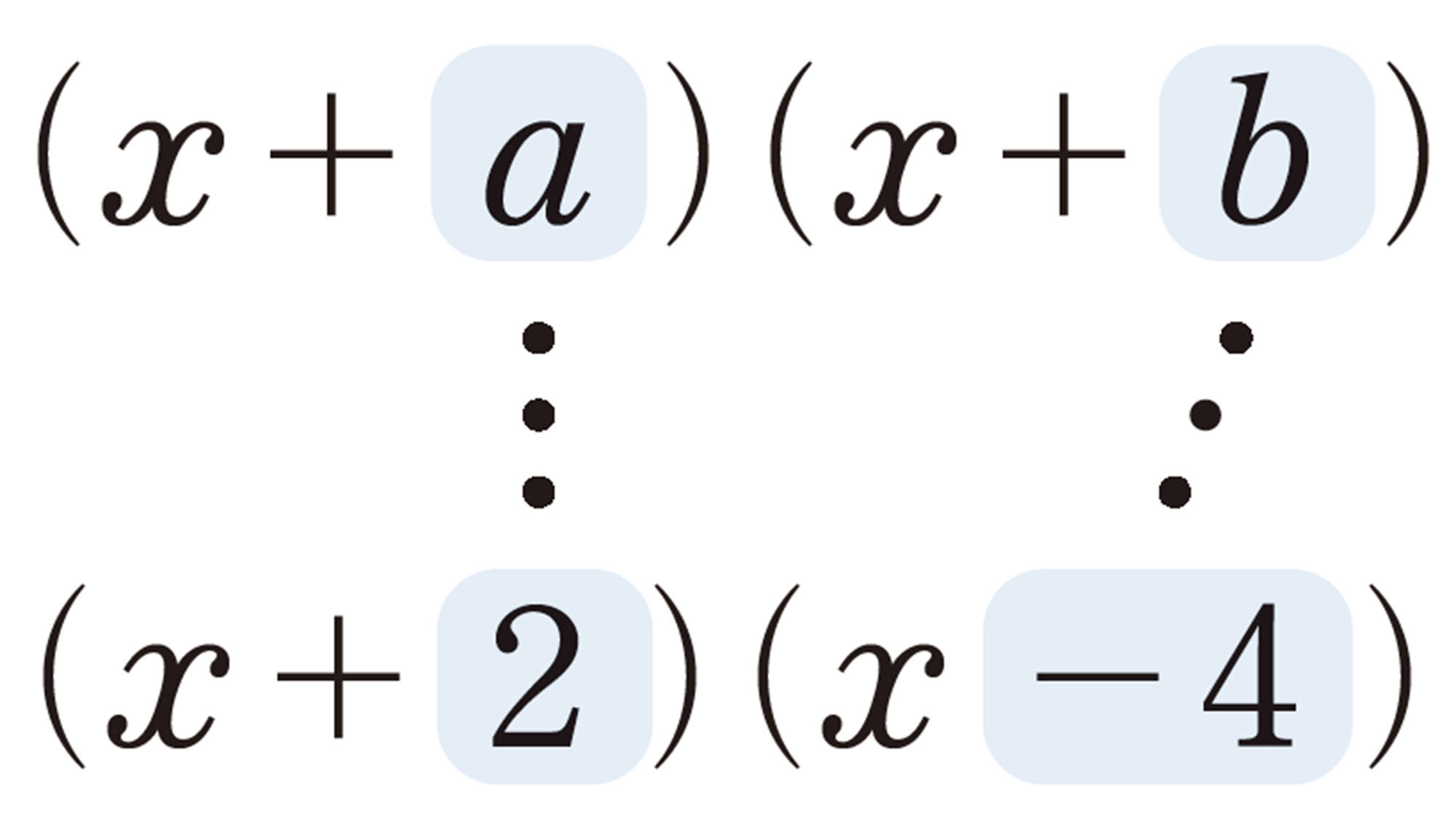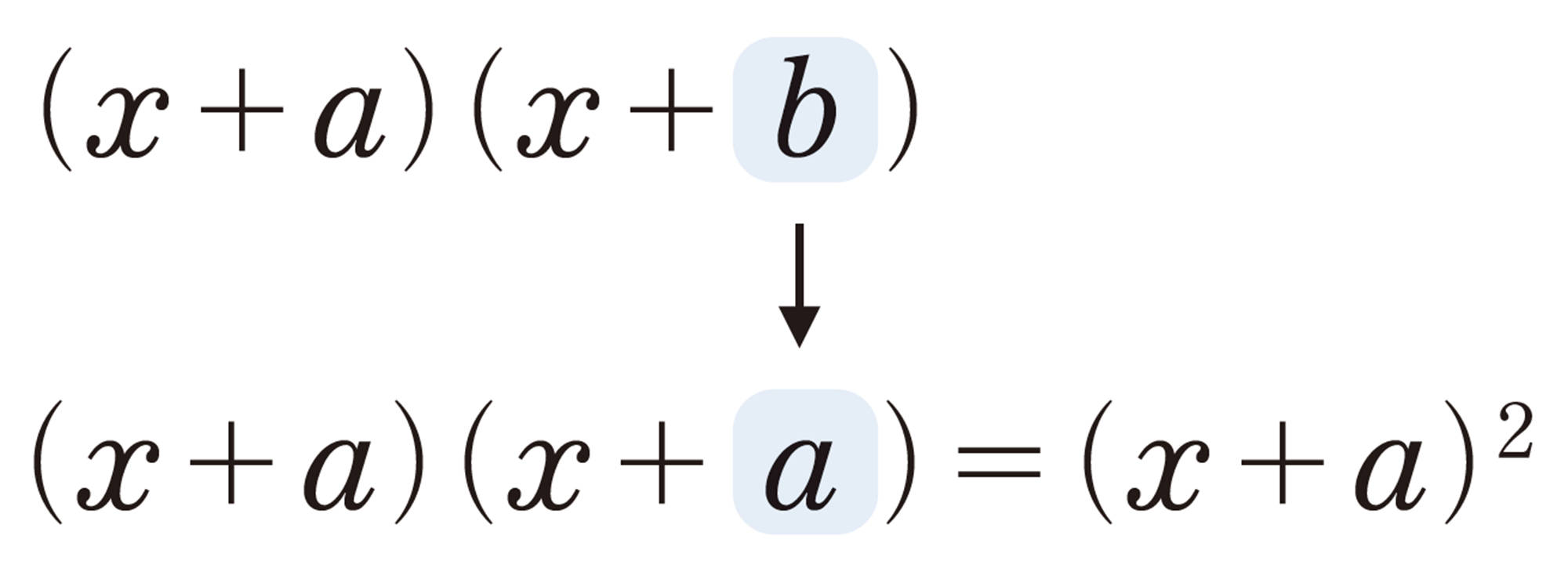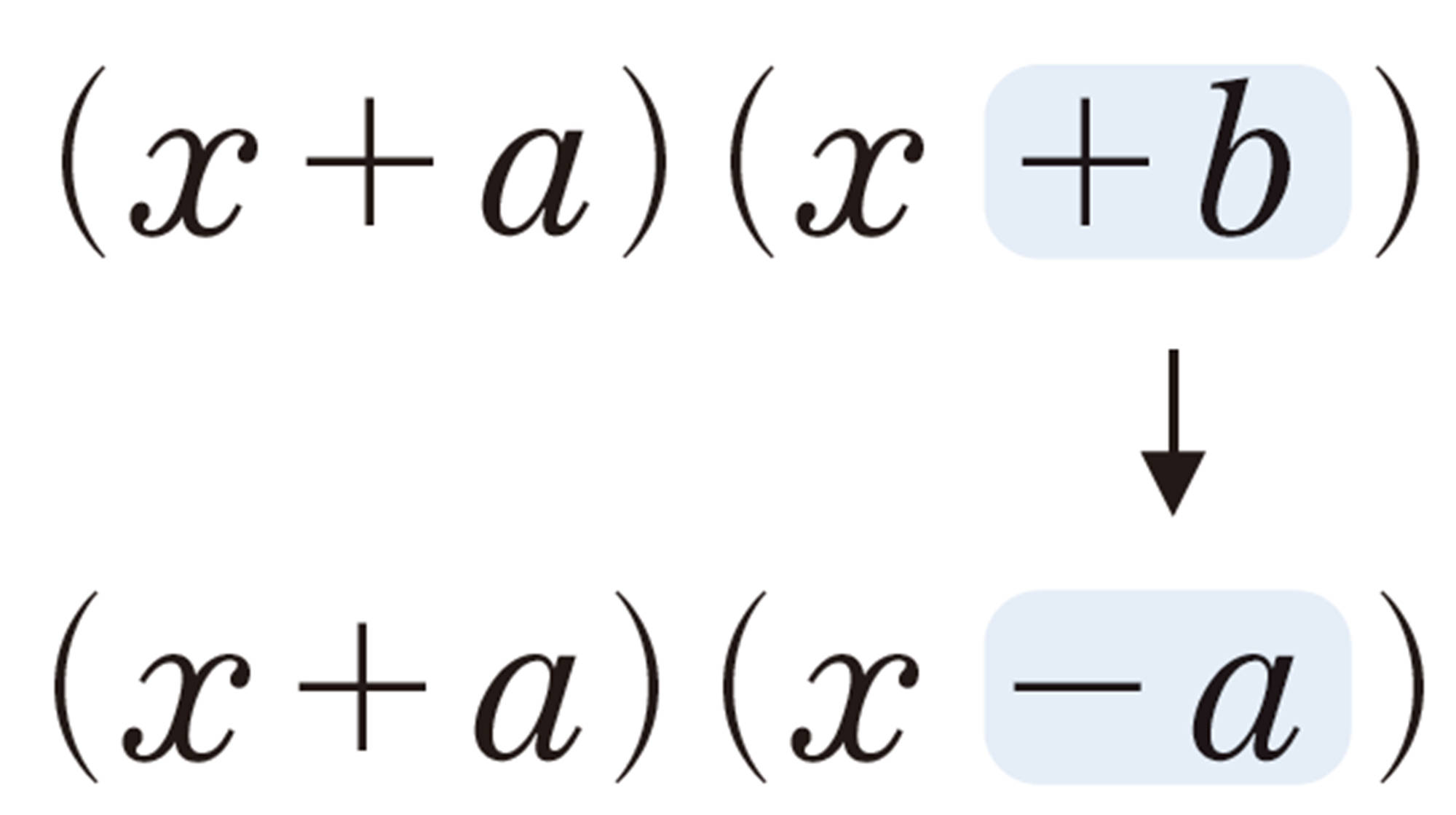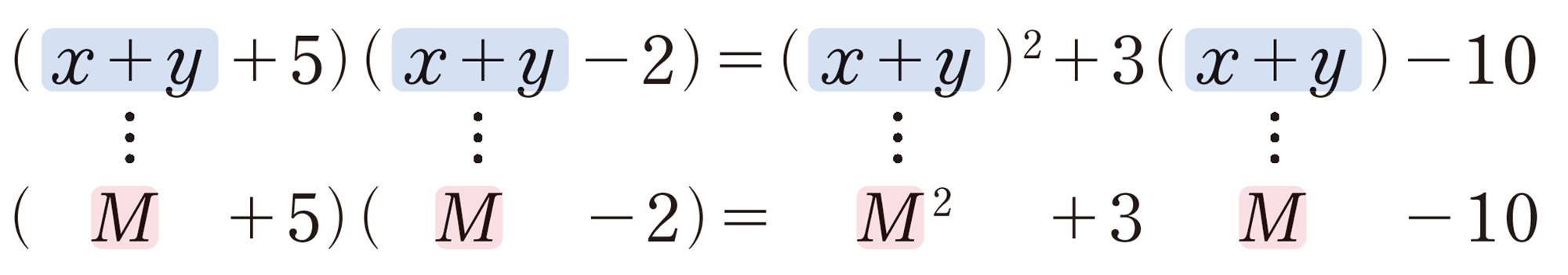<3年p.14>
２ 式の展開
Q Question
縦 [mathjax]\(a\) m，横 [mathjax]\(c\) mの長方形の土地があります。この土地の縦を [mathjax]\(b\) m，横を [mathjax]\(d\) m長くすると，全体の面積はどのように表せるでしょうか。
今度は縦も横も，長くしているね。
面積を[mathjax]\((\textsf{縦}) \times (\textsf{横})\)や，㋐〜㋓の合計で表せば，式の関係がわかるかな。
見方・考え方
図を式におきかえて考えられるかな。
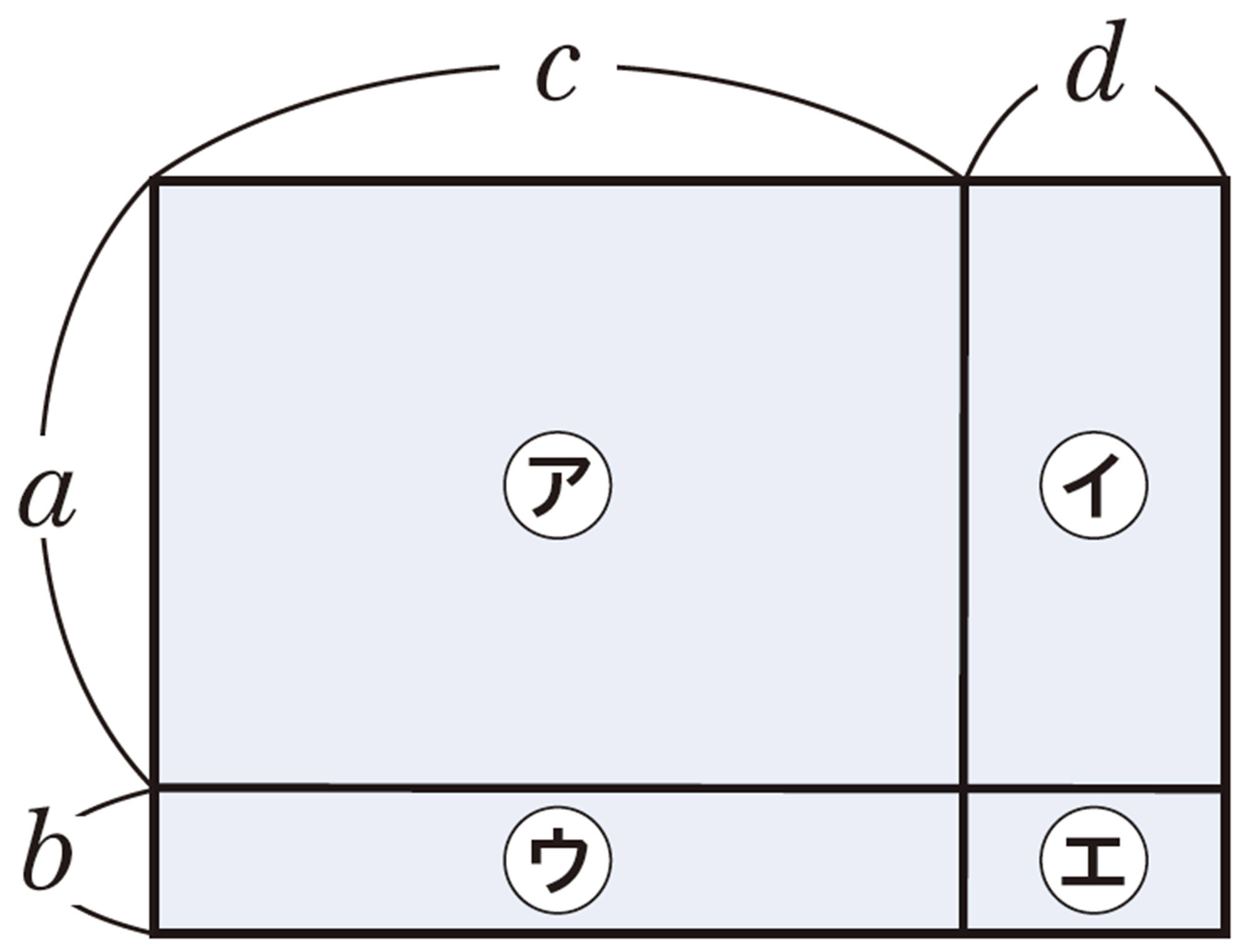
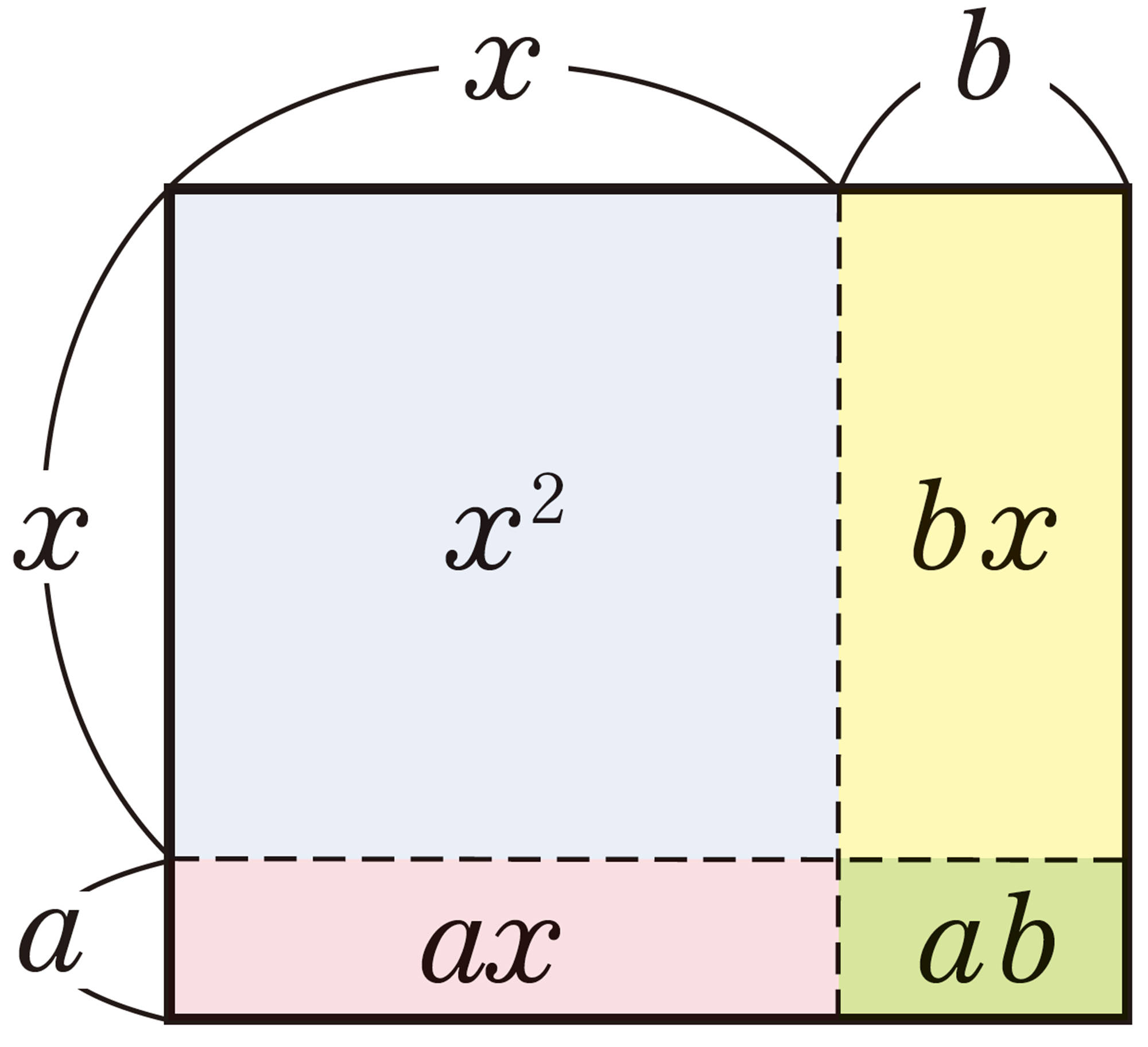
Q で，全体の面積を表す式は，[mathjax]\((\textsf{縦}) \times (\textsf{横})\)や，[mathjax]\(\textsf{㋐}+\textsf{㋑}+\textsf{㋒}+\textsf{㋓}\)で表すことができるから，次の式が成り立つ。
[mathjax]\((a + b)(c + d) = ac\textsf{㋐} + ad\textsf{㋑} + bc\textsf{㋒} + bd\textsf{㋓}\)
目標 ▷ 多項式どうしの乗法を考えよう。
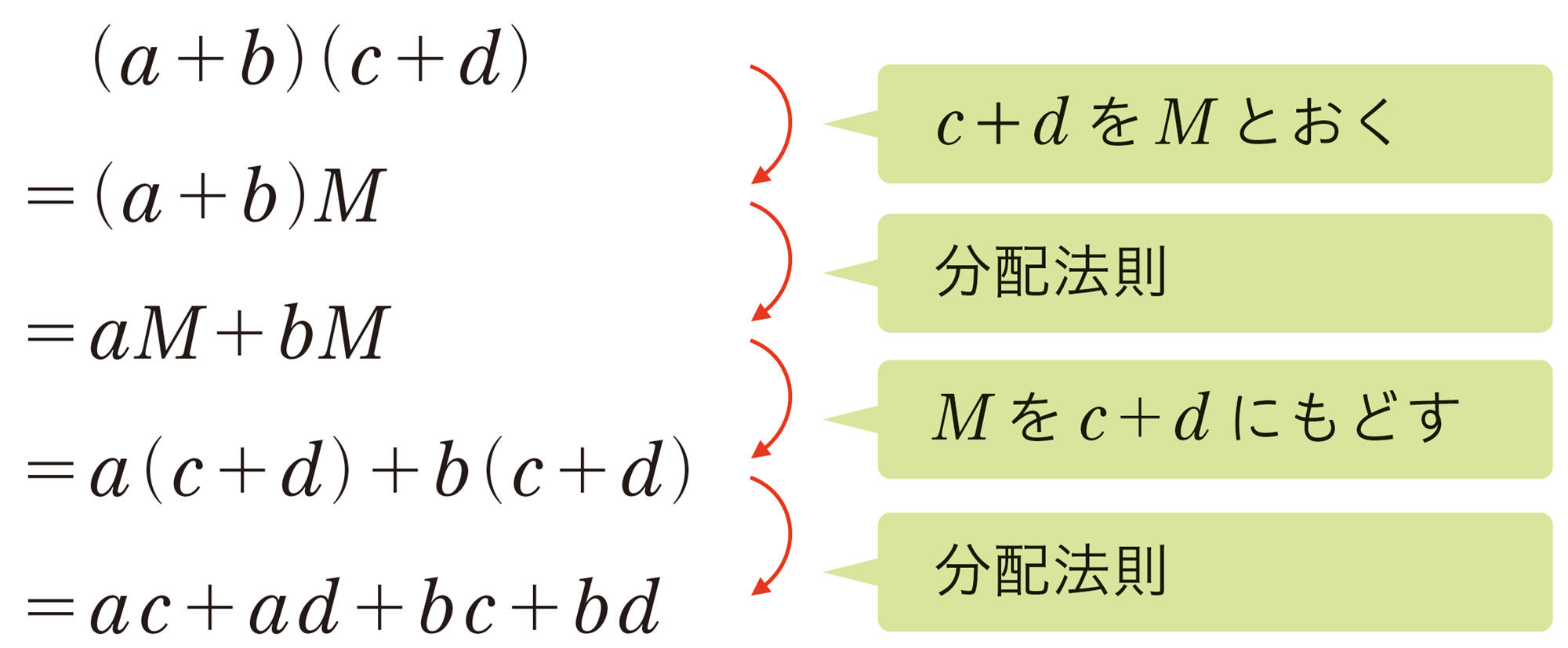
例 １ [mathjax]\((a+b)(c+d)\)で，[mathjax]\(c+d\)を1つの数と考えて，[mathjax]\(c+d=M\)とおくと，分配法則を使って，次のように計算できる。
[mathjax]\(c+d\)をMとおく
分配法則
Mを[mathjax]\(c+d\)にもどす
分配法則
問 １ [mathjax]\((a+b)(c+d)\)を，[mathjax]\(a+b=N\)とおいて計算し，例1の計算の結果と比べなさい。
一般に，[mathjax]\((a + b)(c + d)\)は，右のように計算することができる。
単項式と多項式や，多項式どうしの積の形をした式のかっこをはずして，単項式の和の形で表すことを，もとの式を 展開 するという。
<3年p.15>
例 ２
⑴
⑵
問 ２ 次の式を展開しなさい。
⑴ [mathjax]\((a+3)(b+5)\)
⑵ [mathjax]\((x-2)(y+6)\)
⑶ [mathjax]\((a+b)(c-d)\)
⑷ [mathjax]\((x-a)(y-b)\)
例 ３
⑴
⑵
展開した式に同類項があるときは，それらをまとめておく。
問 ３ 次の式を展開しなさい。
⑴ [mathjax]\((x+1)(x+6)\)
⑵ [mathjax]\((x+2)(x-7)\)
⑶ [mathjax]\((x+6)(x-6)\)
⑷ [mathjax]\((3x-1)(x-5)\)
⑸ [mathjax]\((-a+4)(2a-5)\)
⑹ [mathjax]\((5x-y)(x+2y)\)
例 ４
[mathjax]\(x+y-3\)を1つの数と考える
問 ４ 次の式を展開しなさい。
⑴ [mathjax]\((a-b)(x-y+2)\)
⑵ [mathjax]\((x+y+1)(x-y)\)
やってみよう
計算力を高めよう1-2
▷P.22
どんなことがわかったかな
多項式どうしの乗法は，分配法則を使って展開することができます。
次の課題へ！
展開すると，同類項がまとめられる式があるけど，もっと簡単に展開する方法はあるのかな？
P.16
<3年p.16>
３ 乗法公式
[mathjax]\((x+a)(x+b)\)の公式
Q Question
次の式を展開して，気づいたことを話し合ってみましょう。
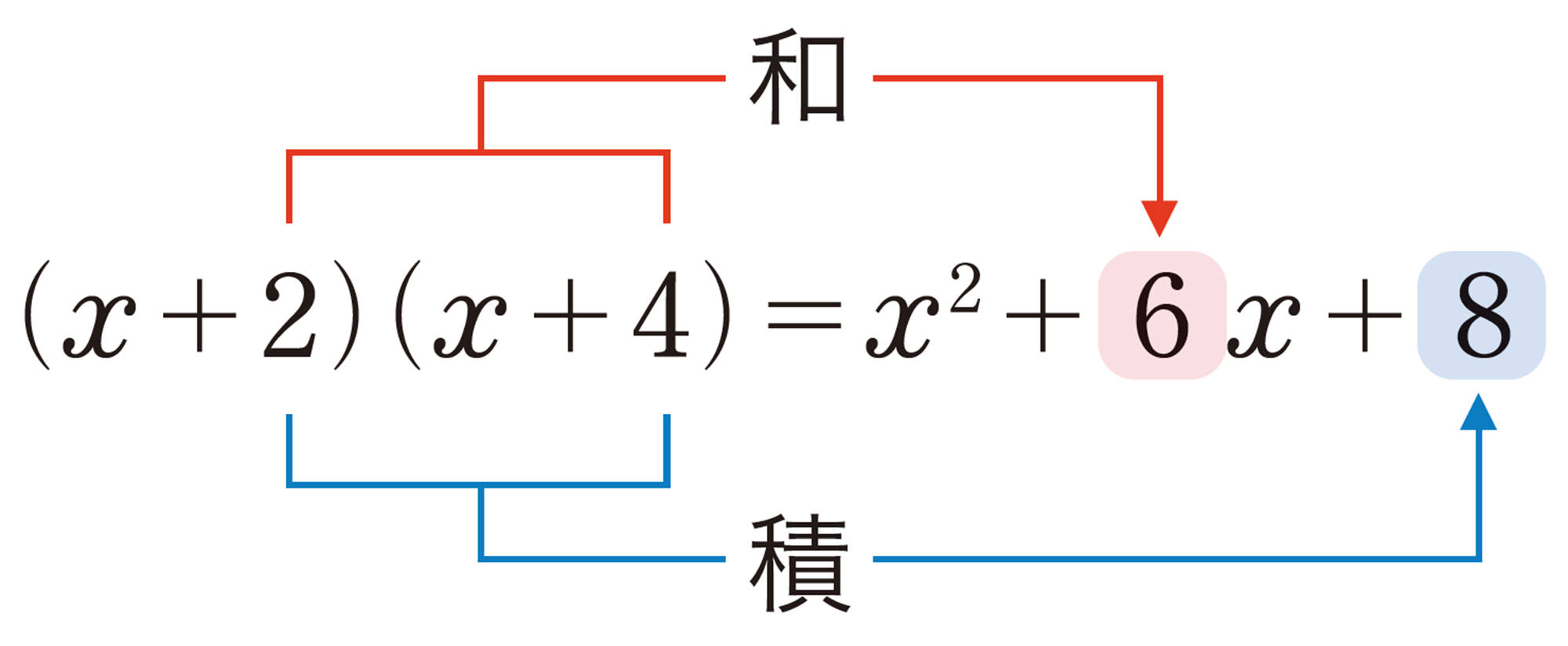
⑴ [mathjax]\((x+2)(x+4)\)
⑵ [mathjax]\((x+2)(x-4)\)
⑶ [mathjax]\((x-2)(x+4)\)
⑷ [mathjax]\((x-2)(x-4)\)
似ているところやちがうところはどこかな。
見方・考え方
どこに着目して考えればいいかな。
目標 ▷ 多項式どうしの乗法で，計算のしかたをくふうしよう。
[mathjax]\((x+a)(x+b)\)を展開すると，次のようになる。
公式❶ [mathjax]\((x+a)(x+b)=x²+(a+b)x+ab\)
例 １
⑴
⑵
問 １ 次の式を展開しなさい。
⑴ [mathjax]\((x+2)(x+1)\)
⑵ [mathjax]\((a-5)(a+3)\)
⑶ [mathjax]\((a-7)(a-2)\)
⑷ [mathjax]\((x+8)(x-6)\)
⑸ [mathjax]\((x+3)(x-3)\)
⑹ [mathjax]\((x+3)²\)
⑺ [mathjax]\(\require{physics}\left(x+\dfrac{2}{3}\right)\require{physics}\left(x+\dfrac{1}{3}\right)\)
⑻ [mathjax]\(\require{physics}\left(x-\dfrac{1}{3}\right)\require{physics}\left(x+\dfrac{1}{2}\right)\)
<3年p.17>
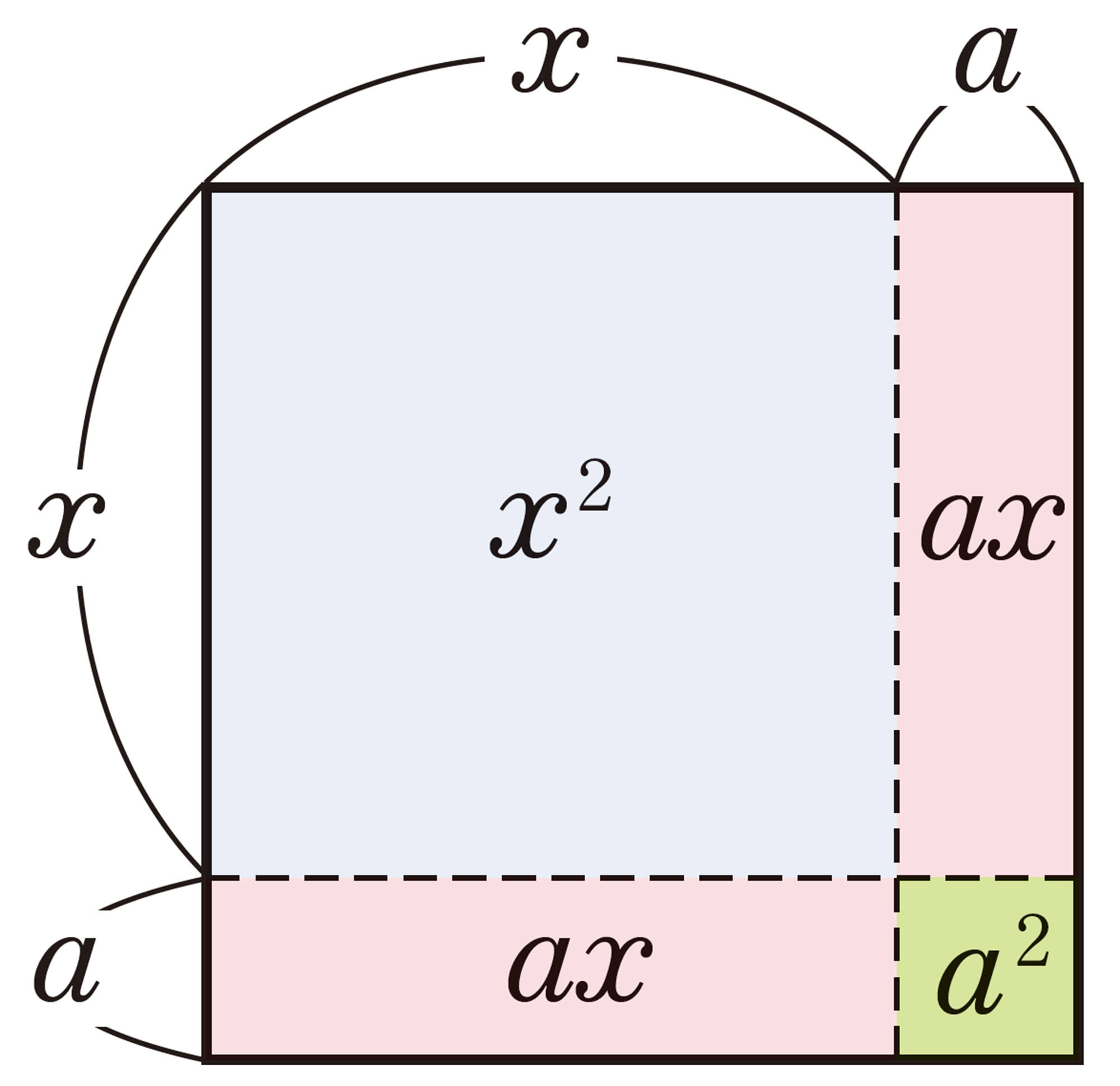
平方の公式
問 ２ 前ページの[mathjax]\((x + a)(x + b)\)の式で，bをaに変えました。次の[mathjax]\(\boxed{\phantom{00}}\)にあてはまるものを書き入れなさい。
問2と同様に，[mathjax]\((x-a)²\)も次のように展開できる。
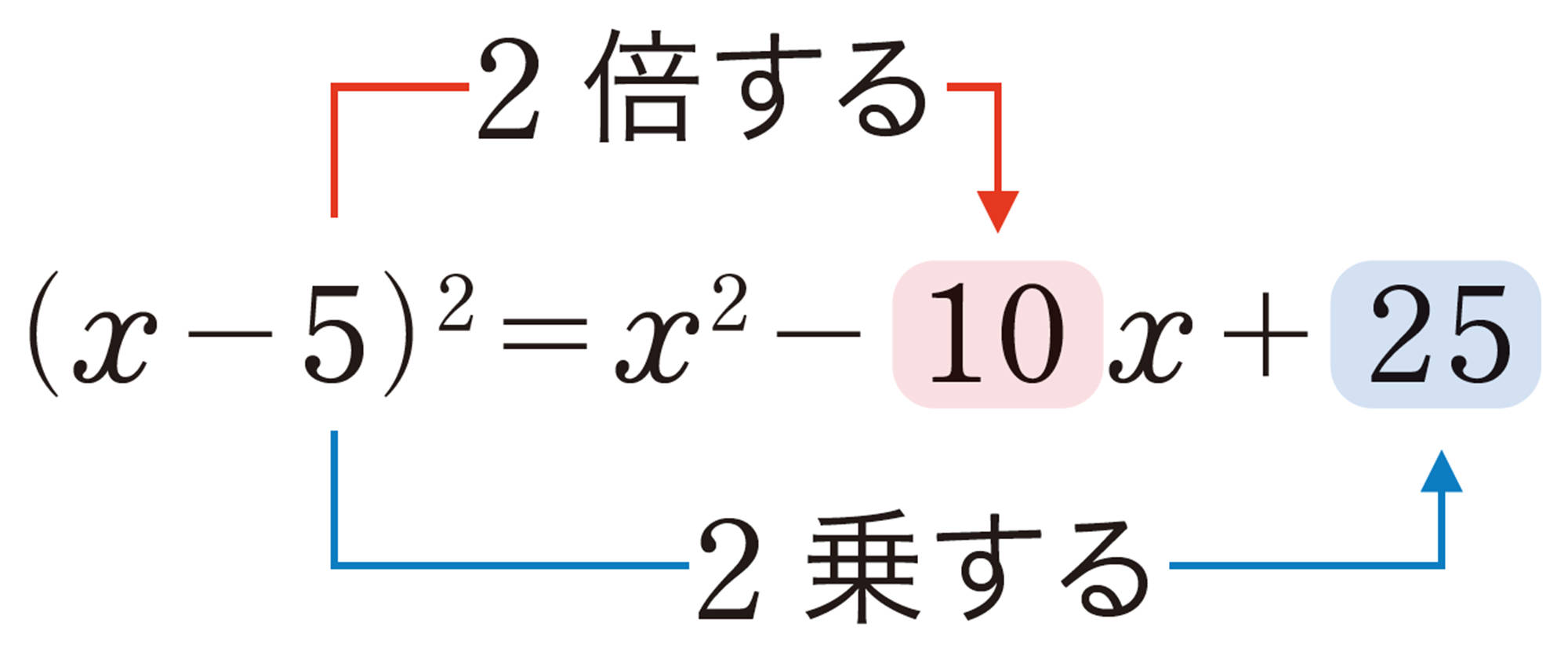
公式❷ [mathjax]\((x+a)²=x²+2ax+a²\) (和の平方)
公式❸ [mathjax]\((x-a)²=x²-2ax+a²\) (差の平方)
例 ２
⑴
⑵
問 ３ 次の式を展開しなさい。
⑴ [mathjax]\((x+1)²\)
⑵ [mathjax]\((y+7)²\)
⑶ [mathjax]\((x-2)²\)
⑷ [mathjax]\((a-9)²\)
⑸ [mathjax]\((a+b)²\)
⑹ [mathjax]\(\require{physics}\left(x-\dfrac{1}{2}\right)^{2}\)
<3年p.18>
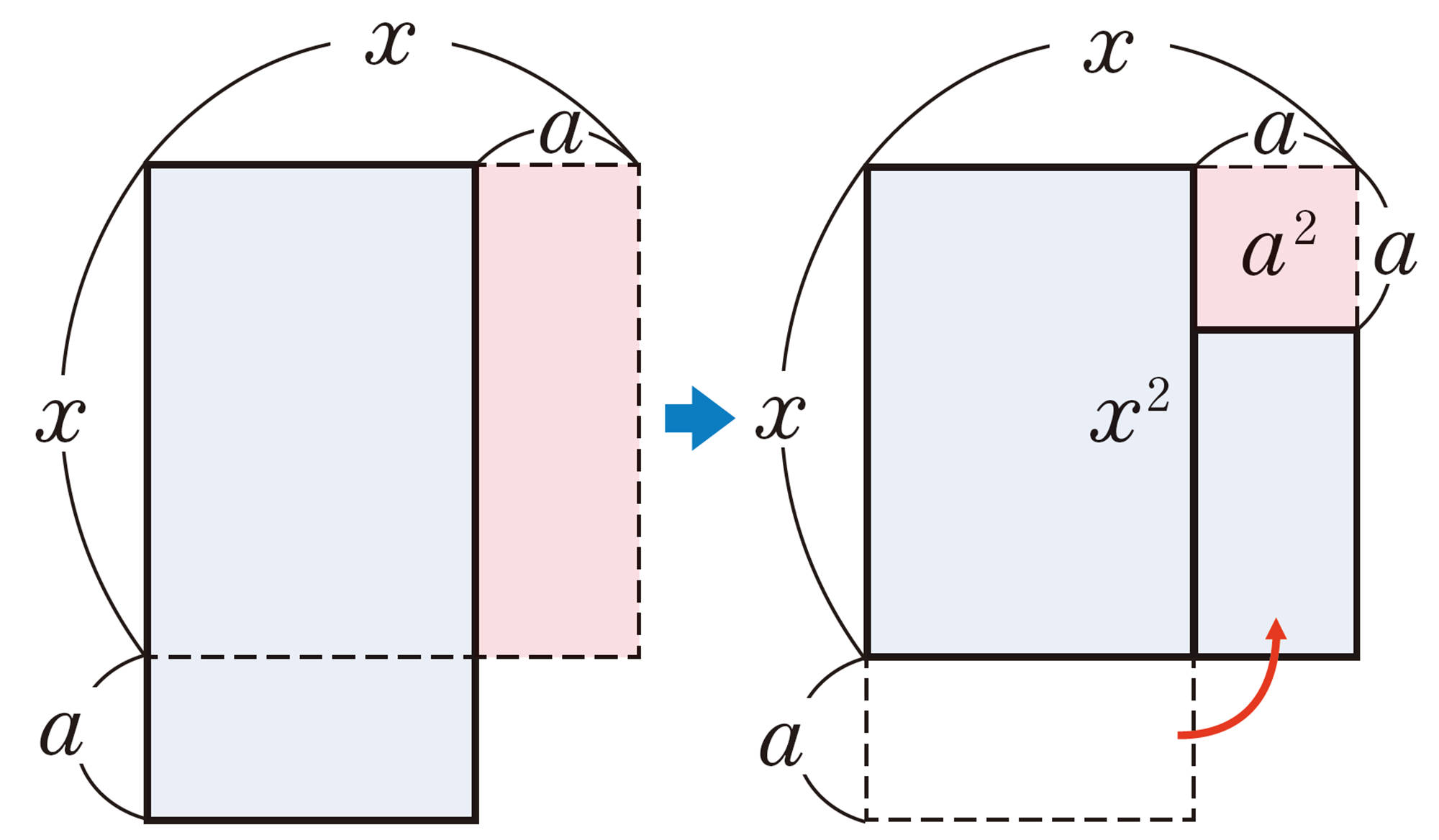
和と差の積の公式
問 ４ 16ページの[mathjax]\((x + a)(x + b)\)の式で，[mathjax]\(+b\)を[mathjax]\(-a\)に変えました。次の[mathjax]\(\boxed{\phantom{00}}\)にあてはまるものを書き入れなさい。
公式❹ [mathjax]\((x+a)(x-a)=x²-a²\)
例 ３
問 ５ 次の式を展開しなさい。
⑴ [mathjax]\((x+2)(x-2)\)
⑵ [mathjax]\((x-8)(x+8)\)
⑶ [mathjax]\((3+y)(3-y)\)
⑷ [mathjax]\((a-b)(a+b)\)
⑸ [mathjax]\((x-5)(5+x)\)
⑹ [mathjax]\(\require{physics} \left(x+\dfrac{1}{3}\right)\require{physics}\left(x-\dfrac{1}{3}\right)\)
やってみよう
計算力を高めよう1-3
▷P.22
これまで学んだ❶〜❹の公式を乗法公式という。
乗法公式
❶ [mathjax]\((x+a)(x+b)=x²+(a+b)x+ab\)
❷ [mathjax]\((x+a)²=x²+2ax+a²\)
❸ [mathjax]\((x-a)²=x²-2ax+a²\)
❹ [mathjax]\((x+a)(x-a)=x²-a²\)
❷，❸，❹は❶の特別な場合と見ることができるね。それぞれどんな場合か説明してみよう。
<3年p.19>
いろいろな計算
乗法公式を使って，いろいろな計算をしてみよう。
次の式のように，xの係数が1でないときは，3xを1つの数と考えて，[mathjax]\(3x = A\)とおくと，乗法公式❶を利用して，次のように計算できる。
[mathjax]\(3x\)をAとおく
展開する
Aを[mathjax]\(3x\)にもどす
[mathjax]\(3x + 1 = M\)とおいてもできるかな。
例 ４ [mathjax]\((4x – 3y)²\)で，[mathjax]\(4x = A\)，[mathjax]\(3y = B\)とおくと，次のように展開することができる。
おきかえは省略することができるね。
問 ６ 次の式を展開しなさい。
⑴ [mathjax]\((3a+2)(3a+5)\)
⑵ [mathjax]\((5a-4)(5a+6)\)
⑶ [mathjax]\((2x+5)²\)
⑷ [mathjax]\((4x-y)²\)
⑸ [mathjax]\((3x-1)(3x+1)\)
⑹ [mathjax]\((6a+7b)(6a-7b)\)
問 ７ 大和さんは，[mathjax]\((5x – 3)²\)の展開を，右のように行いました。この展開は正しいですか。誤りがあれば，正しく直しなさい。
<3年p.20>
例 ５ [mathjax]\((x+y+5)(x+y-2)\)を展開しなさい。
考え方 [mathjax]\(x + y\)をMとおいて，乗法公式❶を利用して展開する。
解答
[mathjax] \(x+y=M\)とおくと，
答 [mathjax] \( x²+2xy+y²+3x+3y-10 \)
例5のように，式を展開するとき，式の一部をひとまとめにして1つの文字におきかえると，乗法公式が使える場合がある。
問 ８ 次の式を展開しなさい。
⑴ [mathjax]\((x+y+4)(x+y+1)\)
⑵ [mathjax]\((x-y-3)(x-y-6)\)
⑶ [mathjax]\((a-b+3)²\)
⑷ [mathjax]\((a+b-7)(a+b+7)\)
例 ６
⑴
⑵
問 ９ 次の計算をしなさい。
⑴ [mathjax]\(x²+(x+5)(x+1)\)
⑵ [mathjax]\((a+4)²-(a-2)(a+2)\)
⑶ [mathjax]\((y+2)(y-7)-y(y-4)\)
⑷ [mathjax]\(2(x-1)²-(2x-1)²\)
やってみよう
計算力を高めよう1-4
P.22
どんなことがわかったかな
乗法公式を利用すると，手際よくいろいろな式を展開することができます。
次の課題へ！
式の展開とは逆に，単項式の和の形を，単項式や多項式の積の形にできるのかな？
P.23
<3年p.21>
確かめよう １節 多項式の計算
１ 次の計算をしなさい。
⑴ [mathjax]\(x(2x + 5y)\)
⑵ [mathjax]\(2x(3x – 4y)\)
⑶ [mathjax]\((6a² – 7a) \div a\)
⑷ [mathjax]\((12a² + 9a) \div 3a\)
２ 次の式を展開しなさい。
⑴ [mathjax]\((x + 2)(y + 5)\)
⑵ [mathjax]\((2x + 1)(x – 4)\)
３ 次の式を展開しなさい。
⑴ [mathjax]\((a + 5)(a + 9)\)
⑵ [mathjax]\((x – 7)(x + 3)\)
⑶ [mathjax]\((y – 1)(y – 8)\)
⑷ [mathjax]\((a + 8)²\)
⑸ [mathjax]\((x – 3)²\)
⑹ [mathjax]\((y – 4)(y + 4)\)
４ [mathjax]\((x + 1)² + (2 + x)(2 – x)\)を計算しなさい。
筆算の計算と式の展開 Tea Break
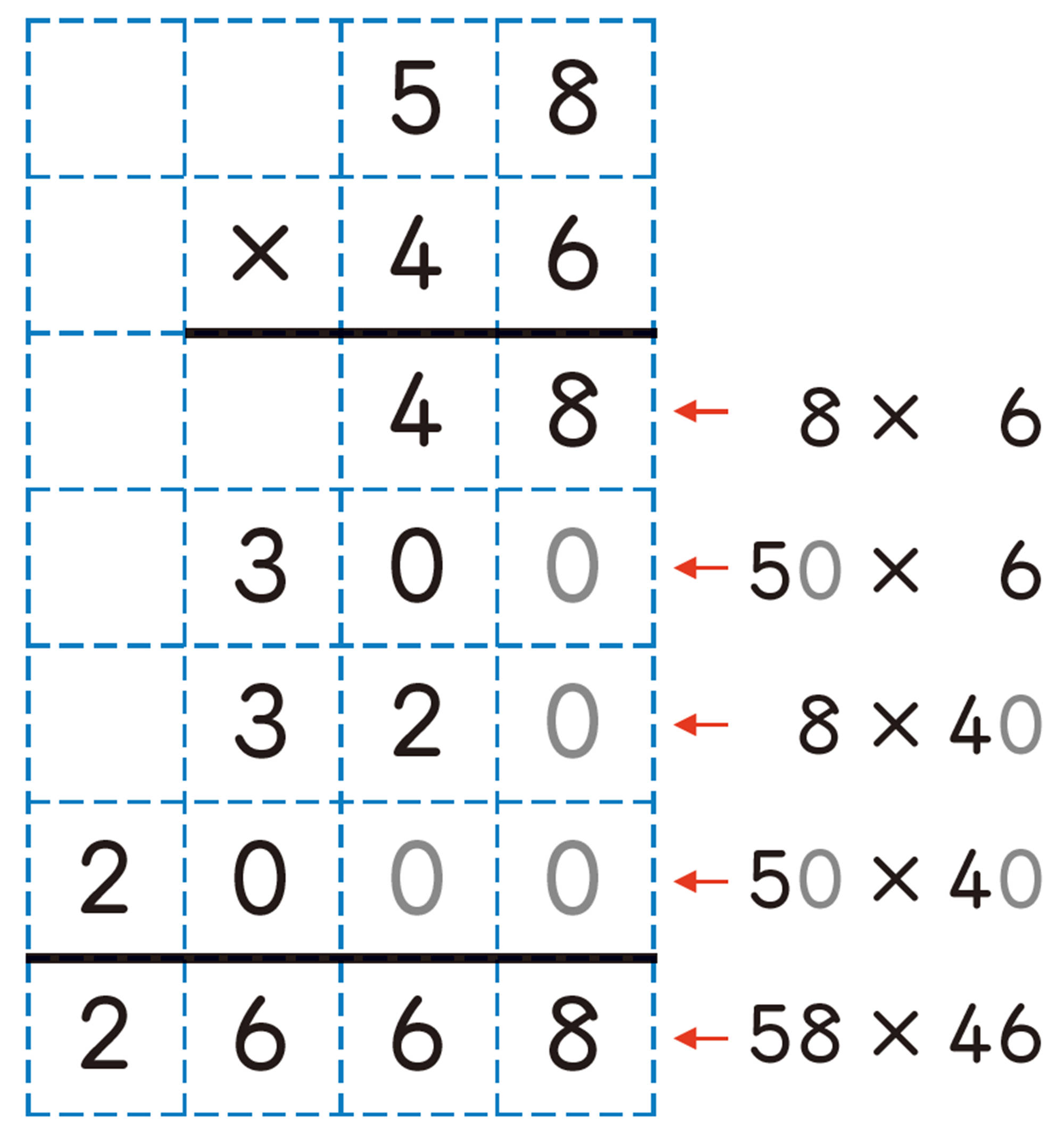
小学校のときに学習したかけ算の筆算は，乗法公式を利用しているといえます。筆算では，[mathjax]\(\textsf{2桁} \times \textsf{2桁}\)の計算も，1桁どうしのかけ算をしています。
たとえば，[mathjax]\(58 \times 46\)をすると，右のようになります。
順に，[mathjax]\(8 \times 6\)，[mathjax]\(50 \times 6\)，[mathjax]\(8 \times 40\)，[mathjax]\(50 \times 40\)の計算をし，位取りに気をつけて筆算をしています。
これは，
[mathjax]\(58 \times 46=(8+50) \times (6+40)\)
と考えて，式を展開していることになります。
<3年p.22>
計算力を高めよう 1
家庭学習や計算練習で利用しましょう。
多項式の計算 解答P.300
⑴ [mathjax]\(2x(x+4)\)
⑵ [mathjax]\(-x(6-3x)\)
⑶ [mathjax]\((-5a+8) \times 2a\)
⑷ [mathjax]\((7x-2) \times (-4x)\)
⑸ [mathjax]\(-3a(a-5b+1)\)
⑹ [mathjax]\((12a+8) \times \dfrac{3}{4}a\)
⑺ [mathjax]\((2x²-9x) \div x\)
⑻ [mathjax]\((15a²+3ab) \div 3a\)
⑼ [mathjax]\((4a²b-ab²) \div ab\)
⑽ [mathjax]\((8x²+6xy) \div (-2x)\)
⑾ [mathjax]\((-3xy+2x) \div \require{physics} \left(-\dfrac{x}{3}\right)\)
２ 式の展開
⑴ [mathjax]\((a+8)(b+2)\)
⑵ [mathjax]\((x-7)(y+6)\)
⑶ [mathjax]\((2a-1)(a-8)\)
⑷ [mathjax]\((4+2x)(3x+1)\)
⑸ [mathjax]\((2a-5b)(-a+6b)\)
⑹ [mathjax]\((7x+2y)(-7x+3y)\)
⑺ [mathjax]\((a+b)(x-y+5)\)
⑻ [mathjax]\((a-2b)(x+2y-3)\)
⑼ [mathjax]\((x+y-3)(x-y)\)
⑽ [mathjax]\((2a-b-4)(a+3b)\)
３ 乗法公式
⑴ [mathjax]\((x+3)(x+7)\)
⑵ [mathjax]\((x-4)(x-5)\)
⑶ [mathjax]\((x+9)(x-10)\)
⑷ [mathjax]\((x-1)(x+6)\)
⑸ [mathjax]\((x+4)²\)
⑹ [mathjax]\((x-10)²\)
⑺ [mathjax]\(\require{physics} \left(x+ \dfrac{1}{3}\right)^{2}\)
⑻ [mathjax]\((x+1)(x-1)\)
⑼ [mathjax]\((a-9)(a+9)\)
⑽ [mathjax]\((x+6)(6-x)\)
⑾ [mathjax]\(\require{physics} \left(x+ \dfrac{5}{4}\right)\require{physics} \left(x-\dfrac{5}{4}\right)\)
４ いろいろな計算
⑴ [mathjax]\((2x-7)(2x+7)\)
⑵ [mathjax]\((3a+5)²\)
⑶ [mathjax]\((5x-2y)²\)
⑷ [mathjax]\((2a+6)(2a+3)\)
⑸ [mathjax]\((x-y+8)(x-y-8)\)
⑹ [mathjax]\((a+b-2)(a+b-5)\)
⑺ [mathjax]\((a+b-4)(a-b+4)\)
⑻ [mathjax]\((x-3)(x+3)-x(x-4)\)
⑼ [mathjax]\(b²+(a+b)(a-b)\)
⑽ [mathjax]\((x+3)(x+4)-(x-2)²\)
⑾ [mathjax]\((2a+b)²-(2a-b)²\)
