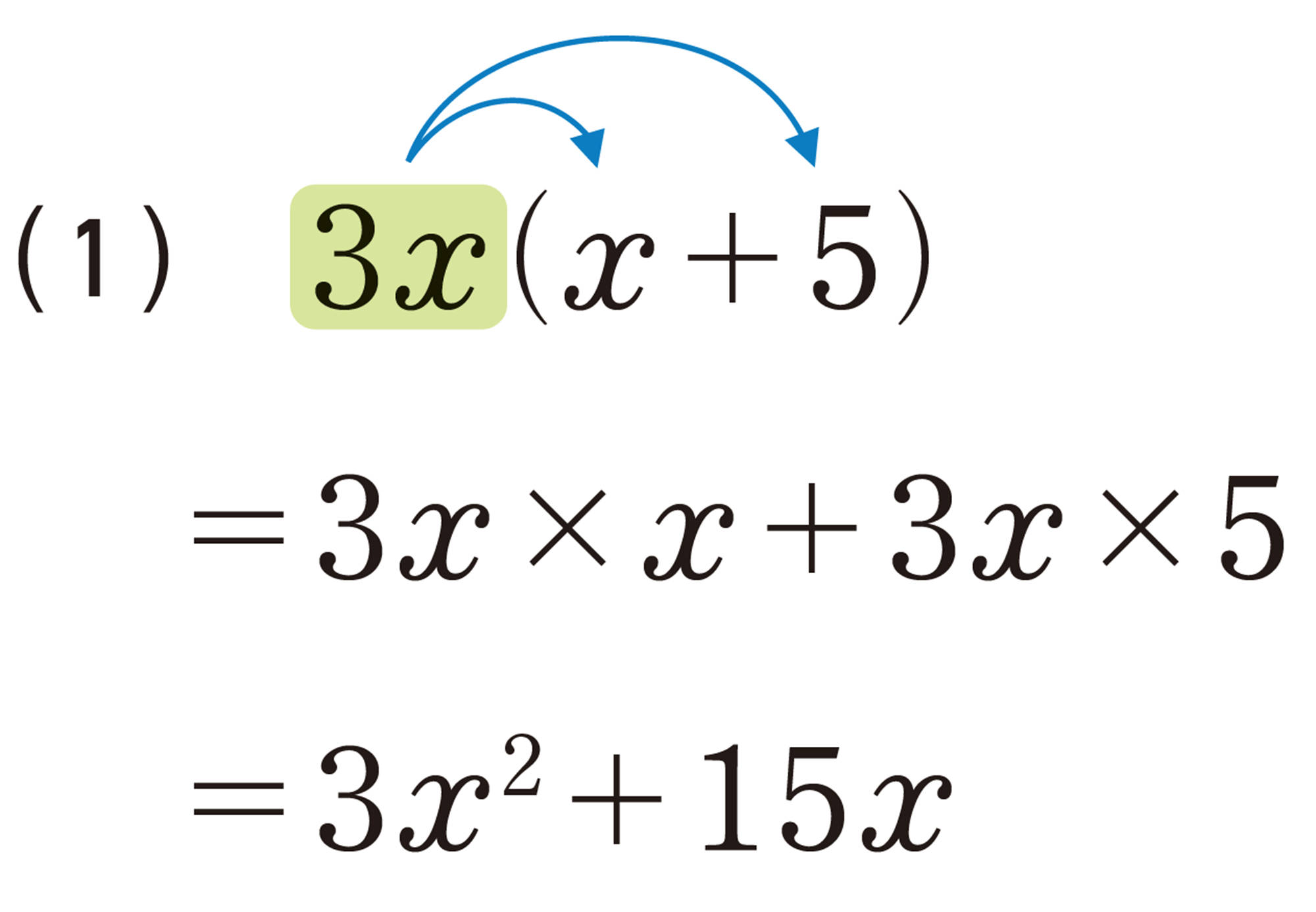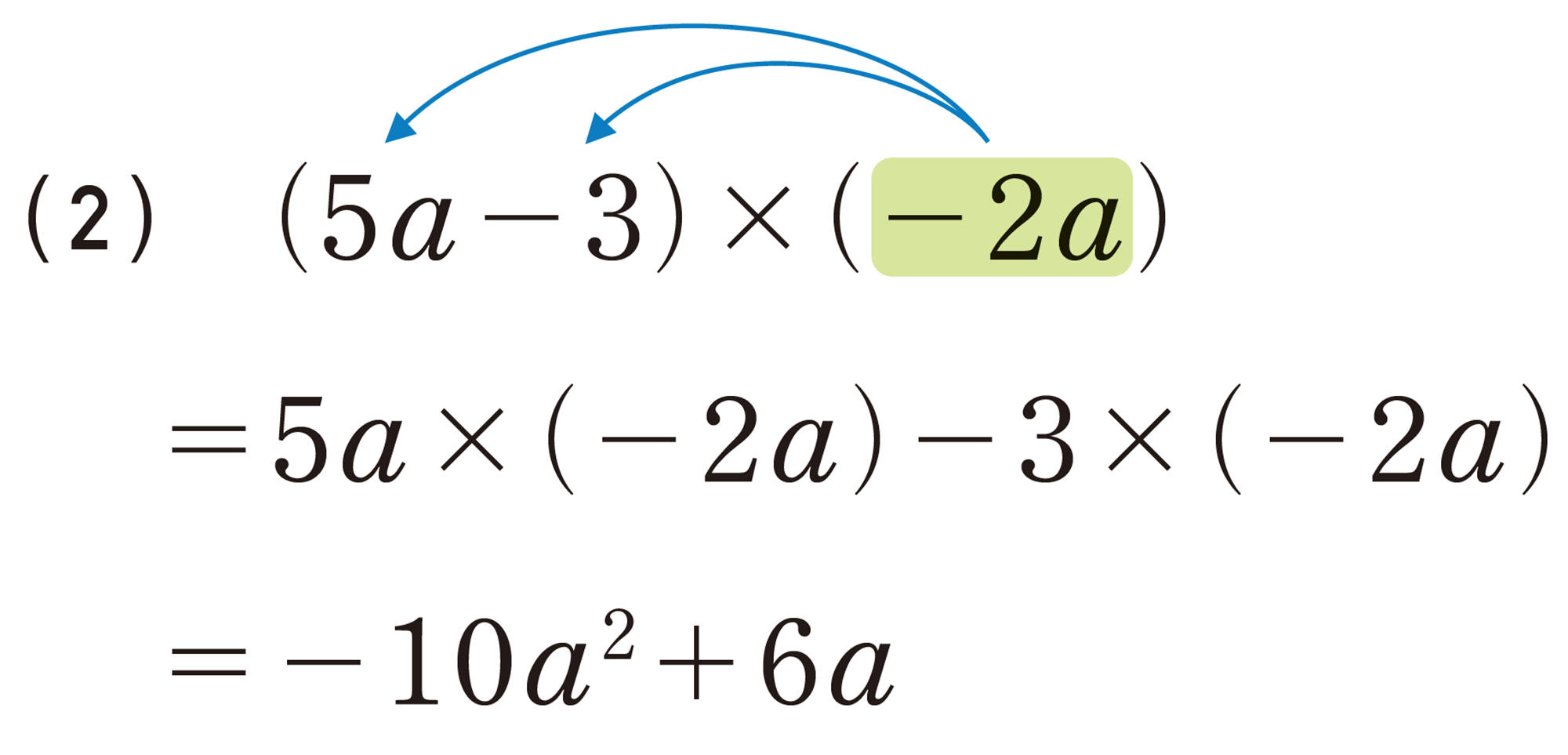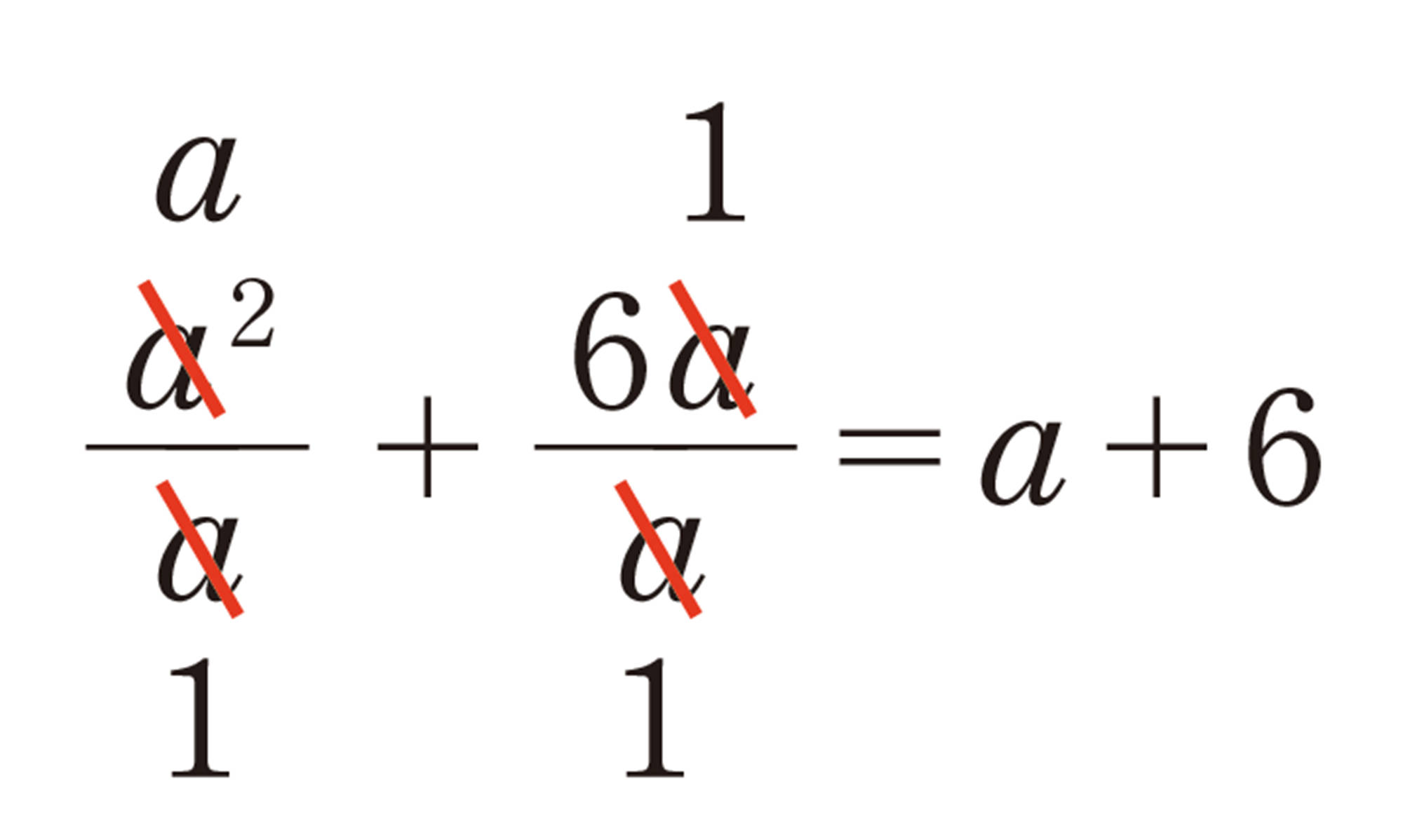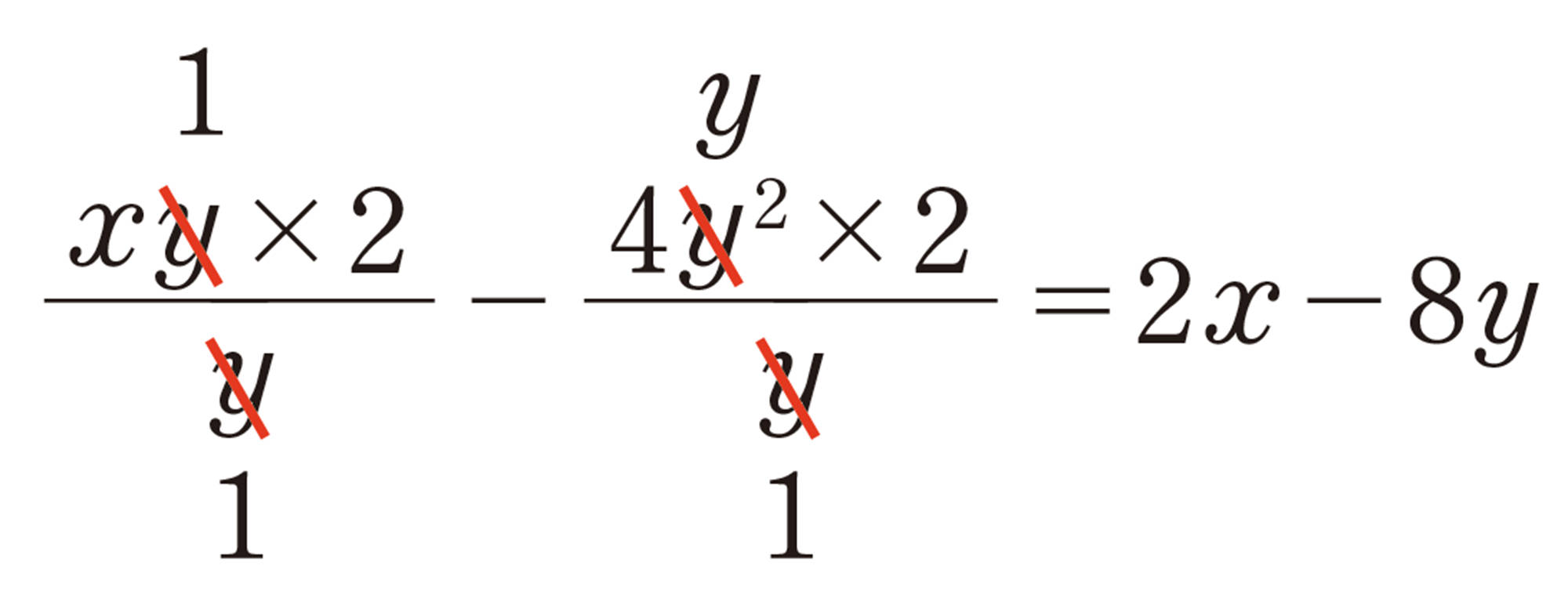<3年p.9>
１章 Chapter １ 式の計算
1節 多項式の計算
2節 因数分解
3節 式の利用
2年生までにどんな文字式の計算ができるようになったかな。
加法や減法は単項式でも多項式でもできるようになったね。
単項式と多項式の乗法や，多項式どうしの乗法も，計算できるのかな。
？ 多項式の乗法も，２年の文字式と同じようにできるのかな？
<3年p.10>
1節 多項式の計算
長方形の面積は？
1辺の長さが10cmの正方形があります。
この正方形の縦と横の長さの和が4cm増えるように長さを加えて，長方形をつくったときの面積について調べてみましょう。
【１】 正方形に，次の①〜③のように長さを加えて長方形をつくりました。
① 縦はそのまま，横に4cm加える。
② 縦に1cm，横に3cm加える。
③ 縦に2cm，横に2cm加える。
①〜③の面積の大小関係は，どのようになるでしょうか。
縦，横に加える長さの合計は同じだね。
形は長方形になったり，正方形になったりするね。
<3年p.11>
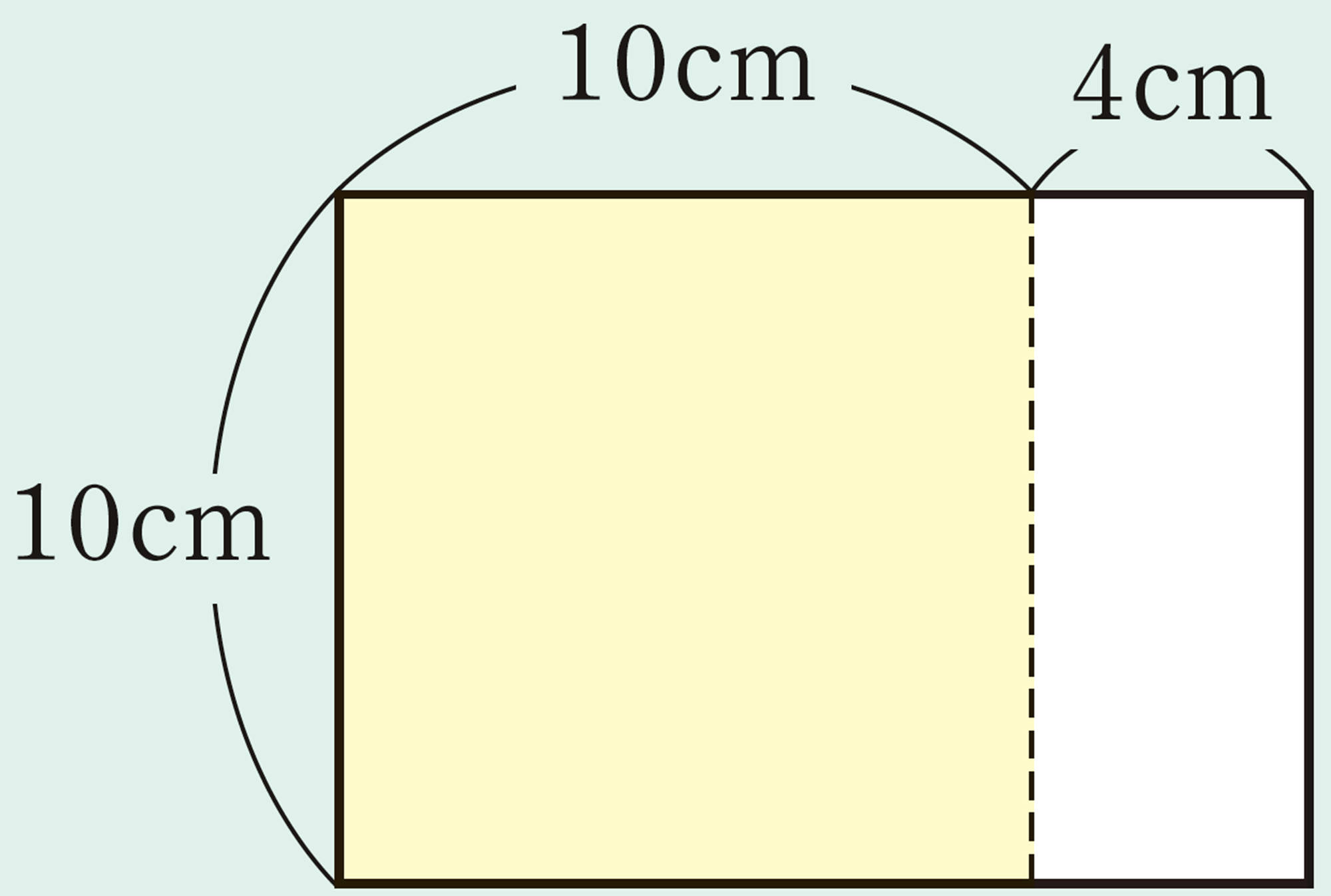
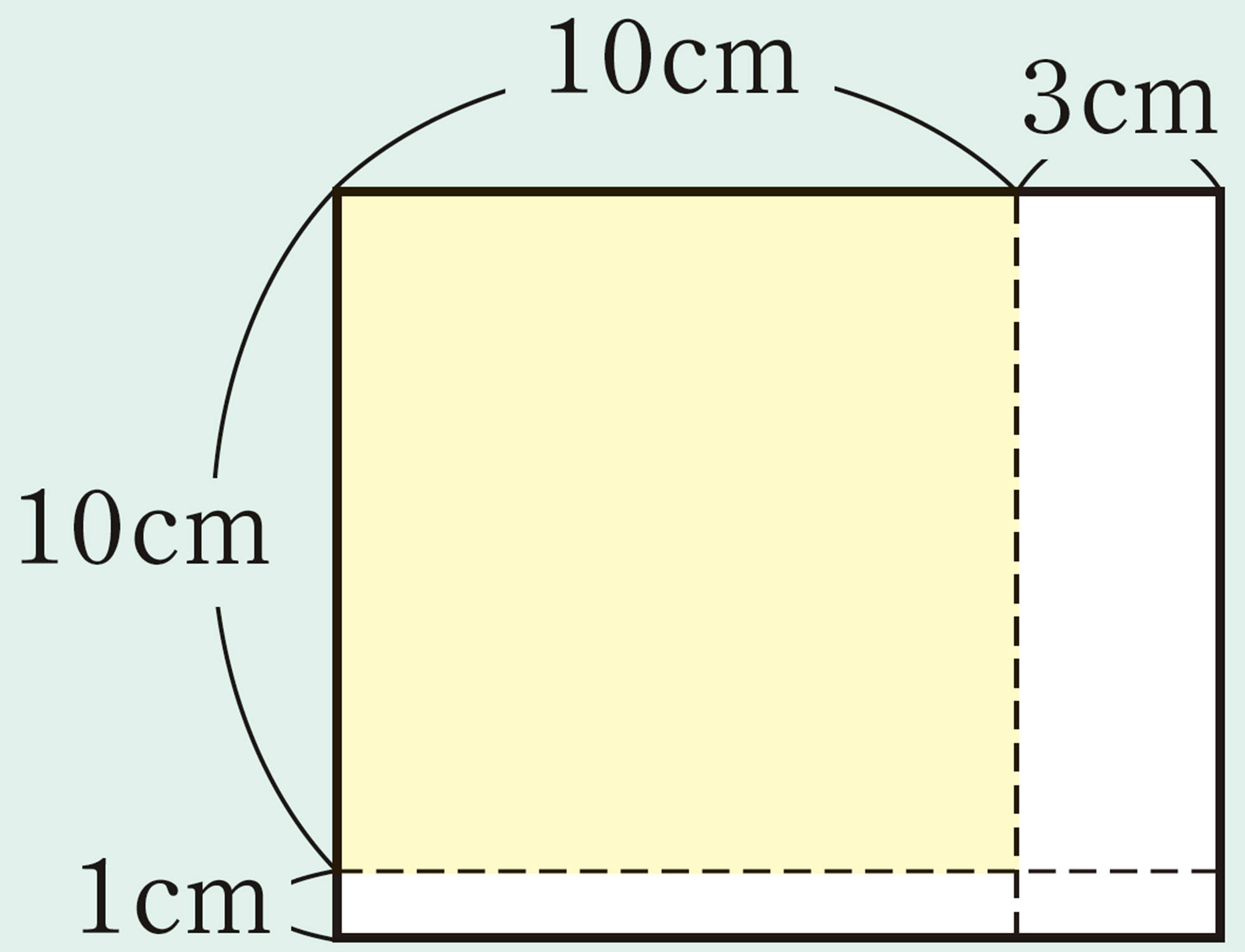
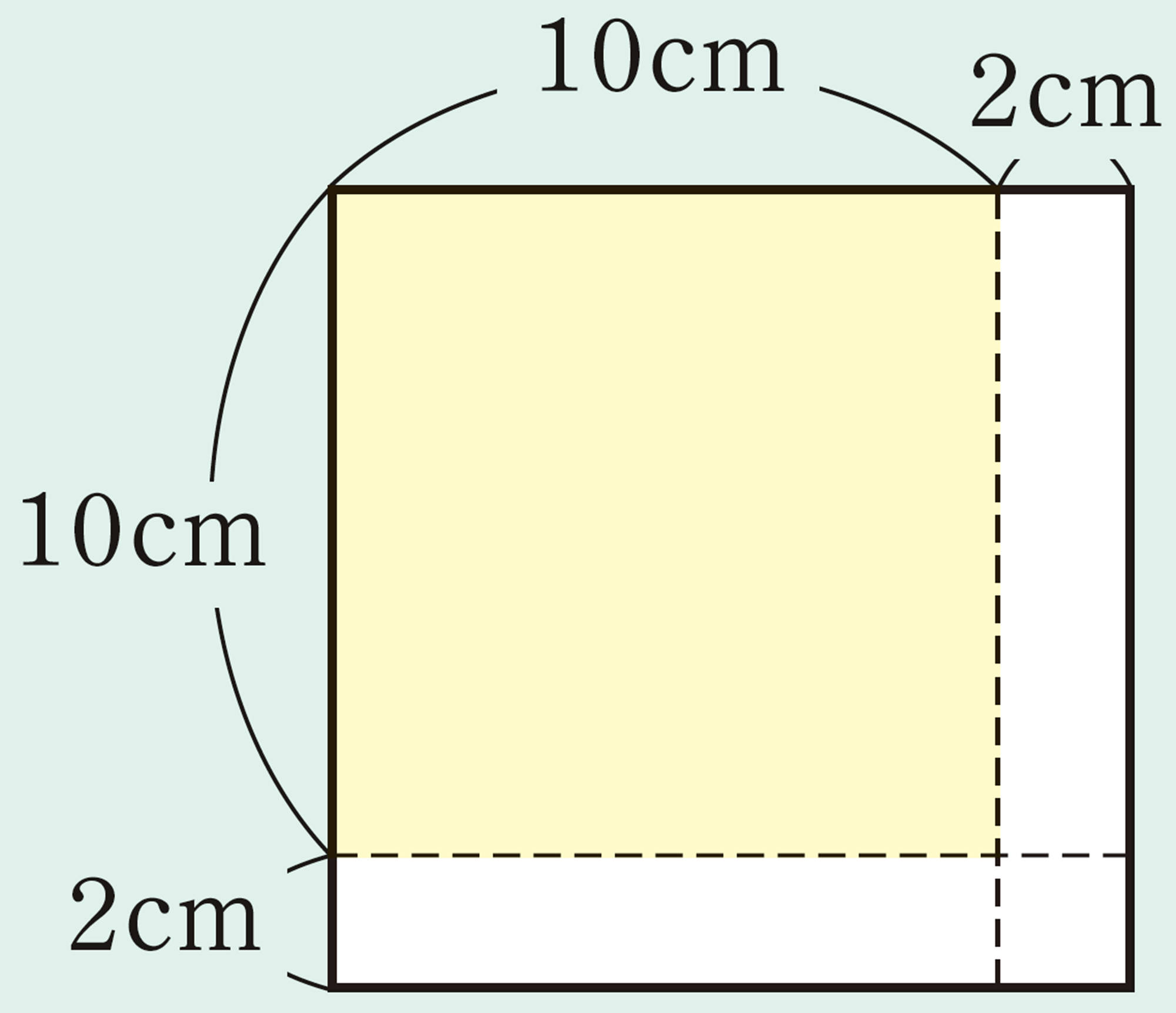
【２】 前ページの【１】①〜③で，もとの正方形の1辺の長さを10cm，20cm，30cmと変えたときの面積について，次の表にまとめてみましょう。また，もとの正方形の1辺の長さを自由に決めて，同じように面積を求めてみましょう。
注意 ①では，縦の長さはそのままなので，「縦0cm」と表すことにする。
【３】 【２】から，面積についてどんなことがわかるか話し合ってみましょう。
①〜③のどの形の面積がいちばん大きくなるのかな。
それぞれどれだけ面積が増えたのかな。
【４】 もとの正方形の1辺の長さがどんな数でも，【３】で見つけたことは成り立つでしょうか。もとの正方形の1辺の長さをxcmとして，①〜③の面積を式で表してみましょう。
もとの正方形の1辺の長さをxcmとしたとき，①〜③の面積を式で表すと，次のようになります。
① [mathjax]\(x(x + 4)\)
② [mathjax]\((x + 1)(x + 3)\)
③ [mathjax]\((x + 2)(x + 2)\)
次の課題へ！
①の単項式と多項式の計算や，②，③の多項式どうしの計算も，これまでの計算と同じようにできるのかな？
P.12，14
<3年p.12>
１ 式の乗法・除法
単項式と多項式の乗法
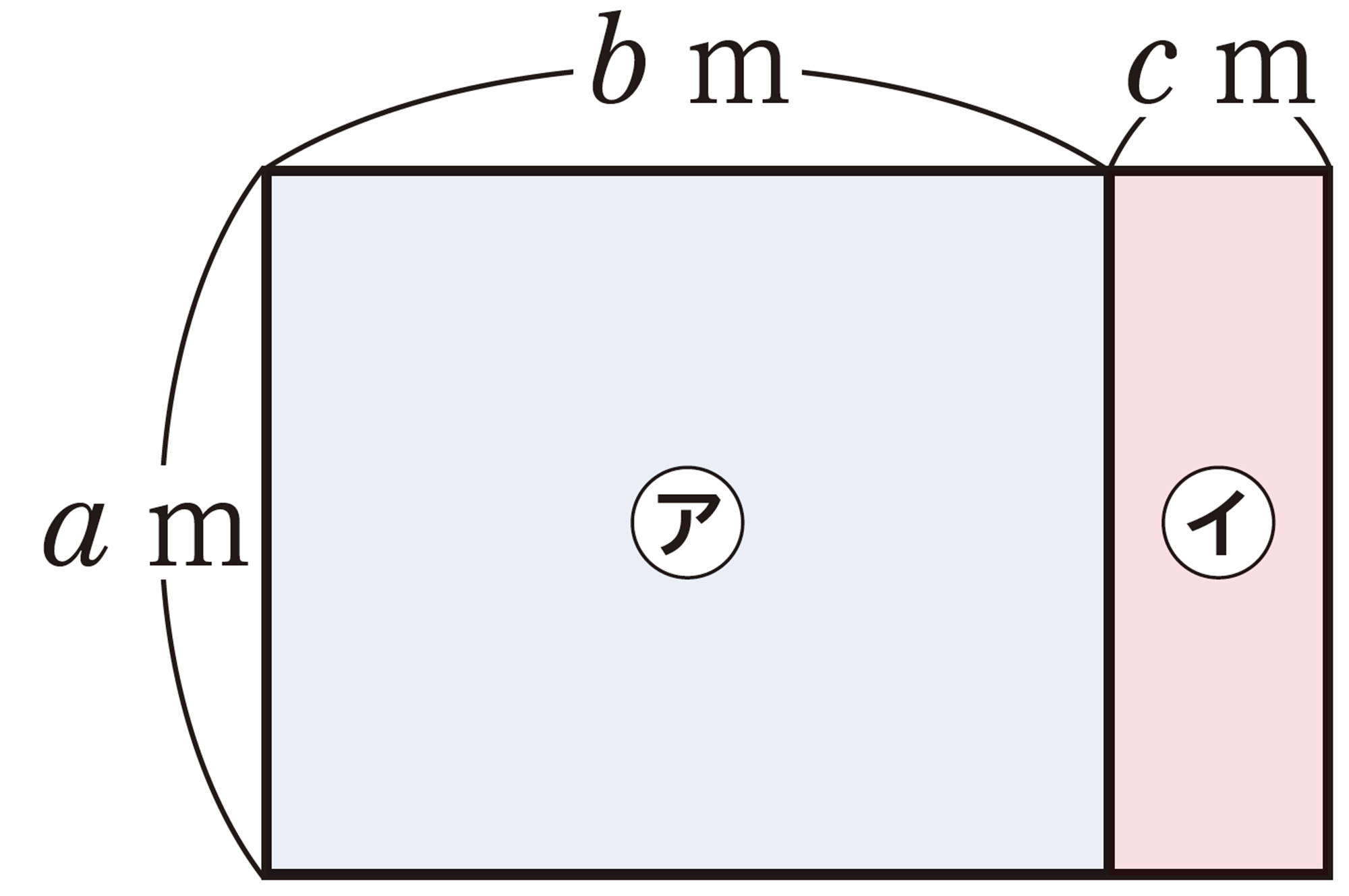
Q Question
縦 [mathjax]\(a\) m，横 [mathjax]\(b\) mの長方形の土地があります。
この土地の横の長さだけを [mathjax]\(c\) m長くすると， 全体の面積は何m²になるでしょうか。次の2通りの式で表してみましょう。
⑴ [mathjax]\((\textsf{縦}) \times (\textsf{横})\)で表す。
⑵ ㋐，㋑の面積の和で表す。
⑴と⑵の式は，同じ面積を表しているね。
単項式と多項式の乗法でも，分配法則を使っていいのかな。
見方・考え方
これまでの文字式の計算と同じように考えられるかな。
目標 ▷ 単項式と多項式の乗法を考えよう。
単項式と多項式の乗法は，分配法則を使って，かっこをはずすことができる。
ふりかえり ▷1年
分配法則
[mathjax]\(a(b + c) = ab + ac\)
[mathjax]\((b + c)a = ab + ac\)
例 １
⑴
⑵
⑴ [mathjax]\(a(a + 3)\)
⑵ [mathjax]\(-4x(2x – 5)\)
⑶ [mathjax]\((-3a + 1) \times 6a\)
⑷ [mathjax]\((2x + 4y) \times (-y)\)
⑸ [mathjax]\(2a(a² + 2a – 3)\)
⑹ [mathjax]\((6x – 9) \times \dfrac{2}{3}x\)
<3年p.13>
多項式と単項式の除法
Q Question
面積が[mathjax]\((a² + 6a)\)m²の長方形の土地があります。この土地の縦の長さが[mathjax]\(a\)mのとき，横の長さは何mでしょうか。
単項式でわる除法も，数でわる除法と同じように計算できるのかな。
見方・考え方
これまでの文字式の計算と同じように考えられるかな。
例 ２
⑴
⑵
[mathjax]\(\dfrac{1}{2}y = \dfrac{y}{2}\)だから，[mathjax]\(\dfrac{1}{2}y\)の逆数は[mathjax]\(\dfrac{2}{y}\)だね。
多項式を単項式でわる除法は，式を分数の形で表して計算するか，乗法に直して計算すればよい。
注意 文字aでわる場合，[mathjax]\(a \neq 0\)でなければならない。
問 ２ 次の計算をしなさい。
⑴ [mathjax]\((10x² + 7x) \div x\)
⑵ [mathjax]\((8a²b – 2ab²) \div 2ab\)
⑶ [mathjax]\((4x² – 6xy) \div \dfrac{2}{3}x\)
⑷ [mathjax]\((-2ab + a) \div \require{physics} \left(-\dfrac{a}{4}\right)\)
⑸ [mathjax]\((2x²y – 3xy² + y³) \div y\)
やってみよう
計算力を高めよう1-1
▷P.22
どんなことがわかったかな
単項式と多項式の乗法や除法も，これまでの文字式と同じように分配法則を使って計算できます。
次の課題へ！
多項式どうしの乗法も，分配法則を使って計算できるのかな？
P.14
