<2年p.206>
２ データの傾向の読み取り方
Q Question
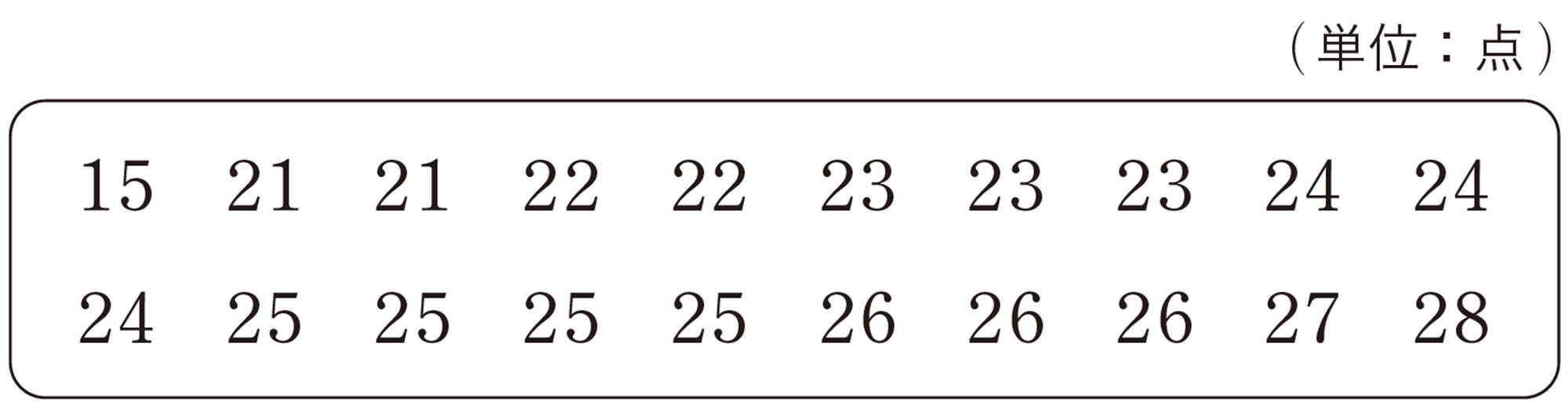
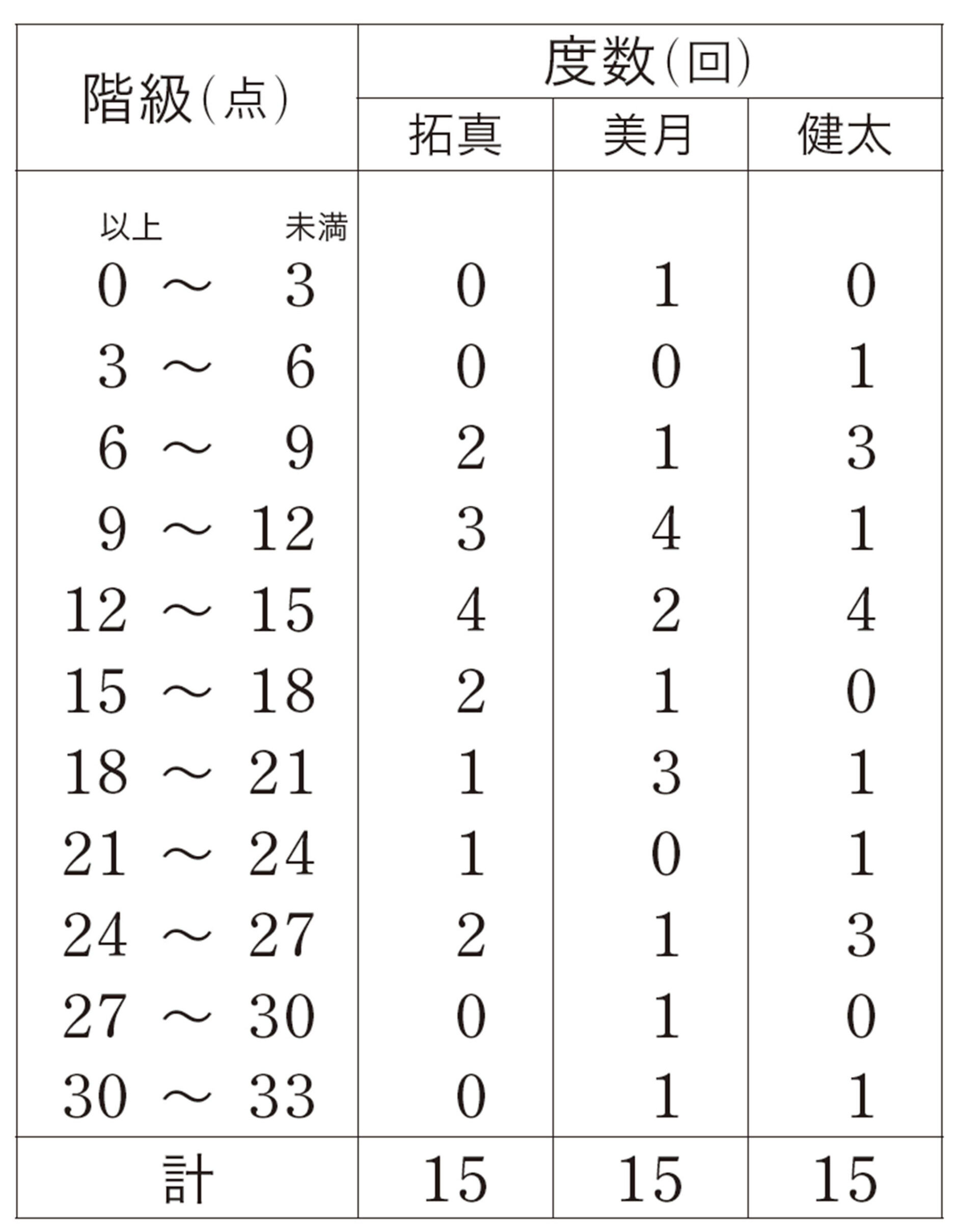
次のデータは，バスケットボールの最近20試合での大和さんの得点のデータを，少ない順に並べかえたものです。このデータを箱ひげ図に表すと，下のようになりました。これらのデータから，どんなことがわかるか話し合ってみましょう。
（単位：点）
箱ひげ図からは，どんなことが読み取れるのかな。
箱の部分は，何を表しているかな。
見方・考え方
これまで学習してきた用語を用いて説明できないかな。
目標 ▷ 箱ひげ図から，どんなことが読み取れるか考えよう。
箱ひげ図では，中央値付近の約半分のデータが箱の中に収まっている。
箱の中には，全体の約50％のデータがふくまれているから，約50％の確率で，1試合当たり23～25点が取れるとみなして考えられるね。
<2年p.207>
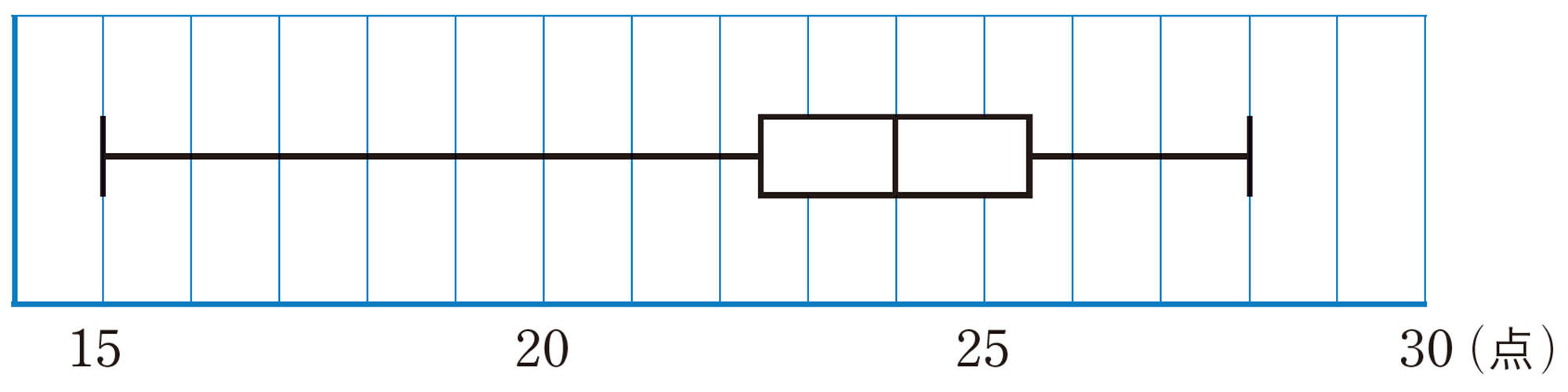
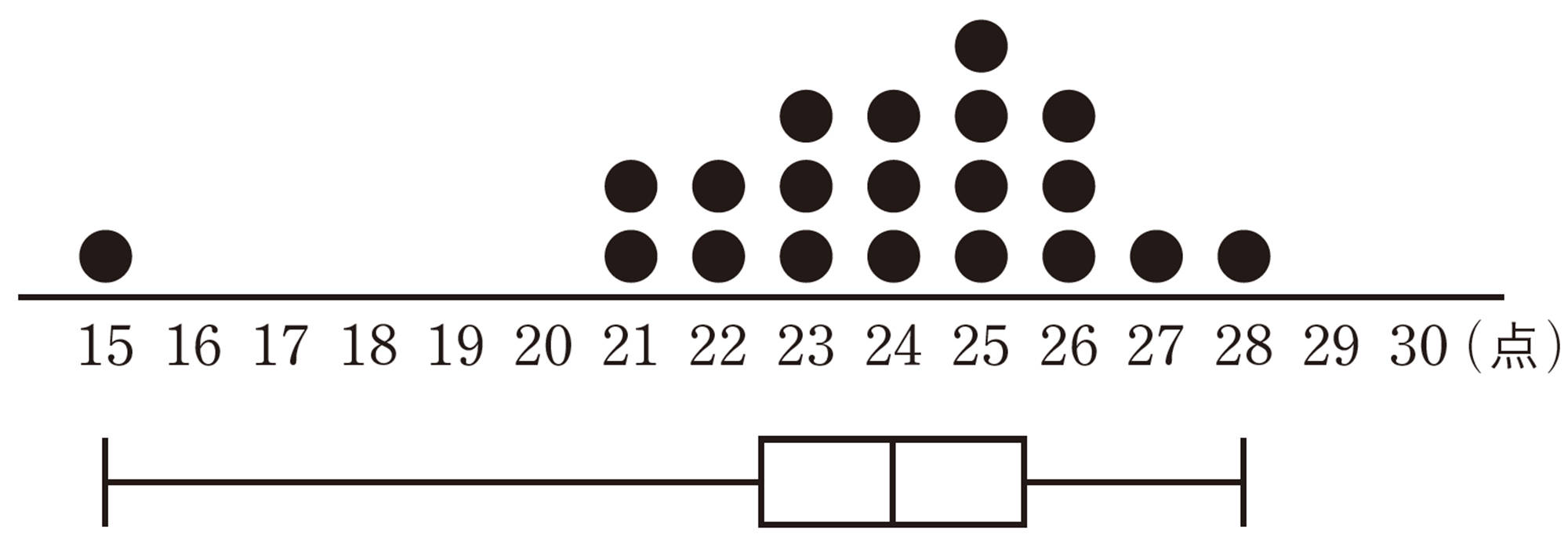
問 １ 拓真さんは，前ページの【Q】の箱ひげ図の左のひげの長さから，15点以上
箱ひげ図の左右のひげの部分には，ひげの長短に関係なく，それぞれ全体の25％のデータがふくまれていると考えられる。また，ヒストグラムでは中央値がわかりにくいが，箱ひげ図ならば中央値がすぐに判断できる。
しかし，前ページで調べたように，箱ひげ図では，最小値や最大値に極端にかけ離れた値がある場合，ひげの長さが長くなることがある。
したがって，データの分布を調べるには，極端にかけ離れた値が大きく影響しない四分位範囲で判断したり，さらにくわしく調べたりする必要がある。
複数のデータを比較する場合について調べよう。
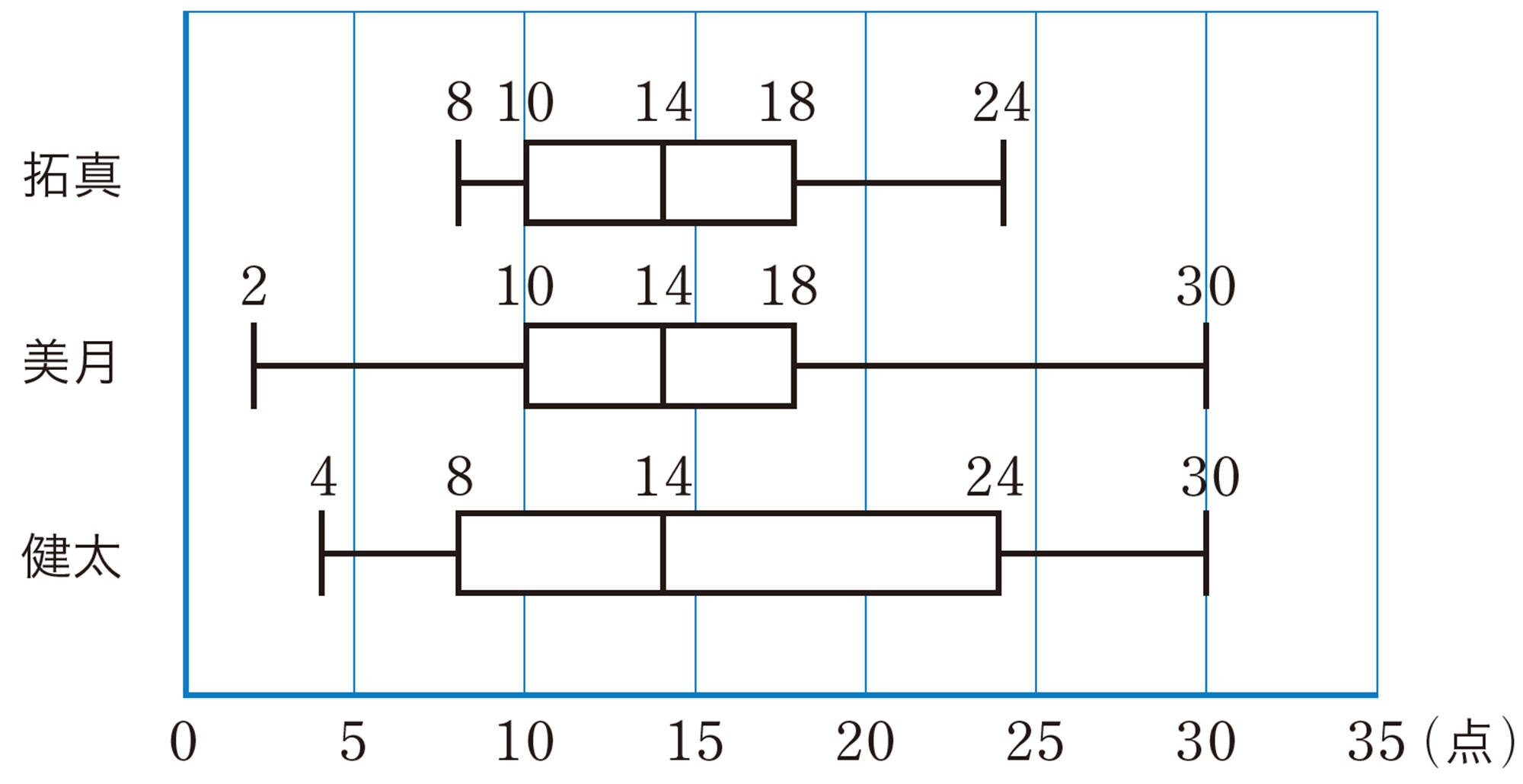
Q Question
次の箱ひげ図は，バスケットボールの試合を15 回行ったときの拓真さん，美月さん，健太さんの3 人の得点を表したものです。次の試合の選手を1人選ぶとすると，誰を選べばよいか話し合ってみましょう。
見方・考え方
どこに着目して考えればいいかな。
中央値はどのデータも同じだね。
3人のデータが並べられていて比較はしやすいけど，細かいところはわかりにくいね。
おおまかなちがいはわかるけど，分布のしかたも調べたいね。
<2年p.208>
問 ２ 前ページの【Q】の3人の記録について，度数分布表で表すと，右のようになりました。前ページの箱ひげ図や，右の度数分布表から，次の試合の選手に誰を選べばよいか話し合いなさい。
この表をヒストグラムに表すと，もっと見やすくなるね。
Q Question
これまでに学んだことをもとにして，203ページの降水量が1日50 mm以上の日数の箱ひげ図から，どんなことがわかるか話し合ってみましょう。
1日の降水量が50 mm以上の日数は増えているのかな。
どの地域も，②の方が箱が少し右にずれているみたいだね。
見方・考え方
どこに着目して考えればいいかな。
<2年p.209>
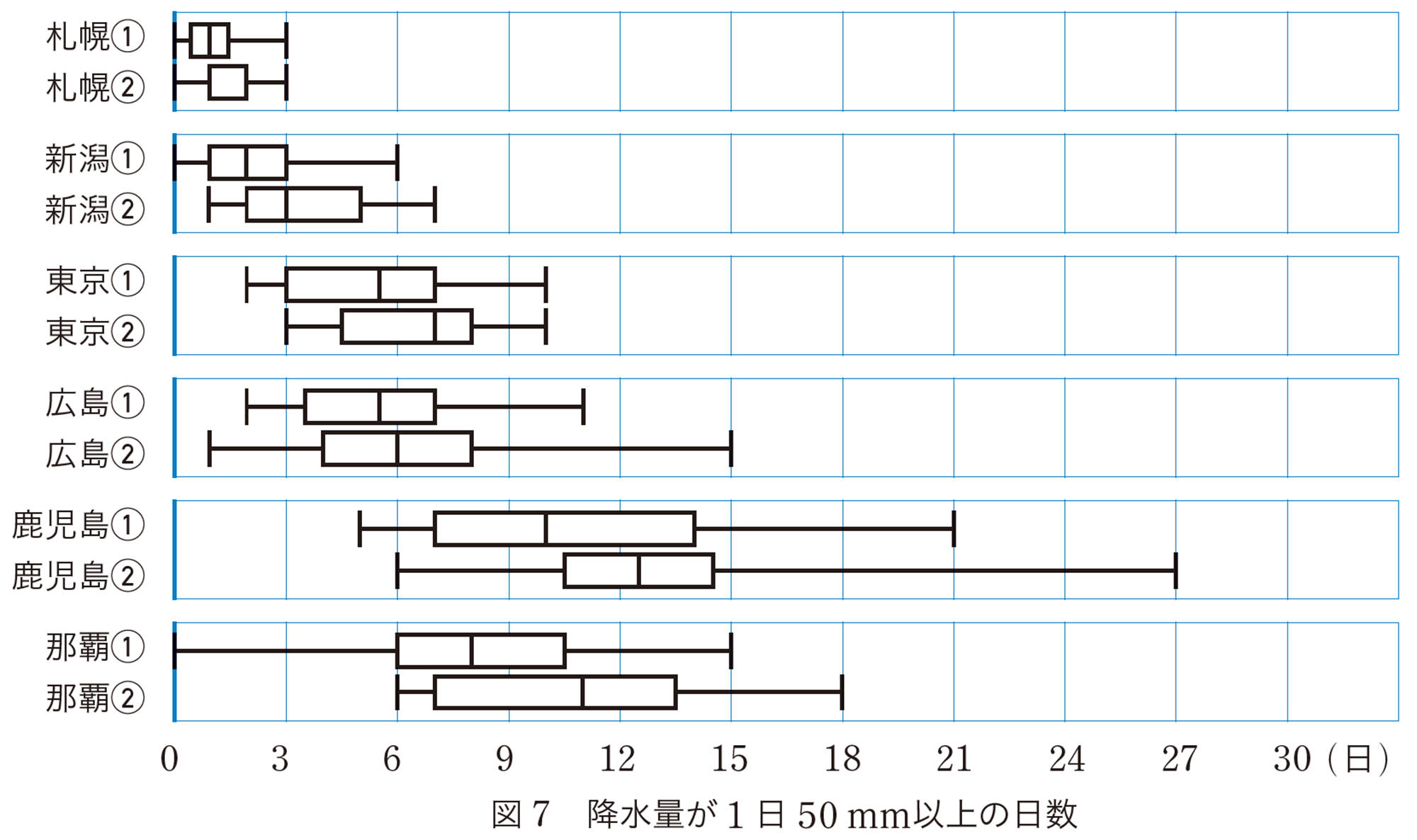
問 ３ 前ページの【Q】から，ほかにどんなことを調べたいか話し合い，実際に調べなさい。
どんなことがわかったかな
箱ひげ図では，複数のデータのおおまかな分布の傾向はわかりますが，くわしいことはわからない場合があります。目的に応じて，表現のしかたをくふうする必要があります。
次の課題へ！
これまで学んだデータの整理のしかたを使って，身のまわりの問題に利用できないかな？
P.210
平均値と外れ値 発展 高等学校 Tea Break
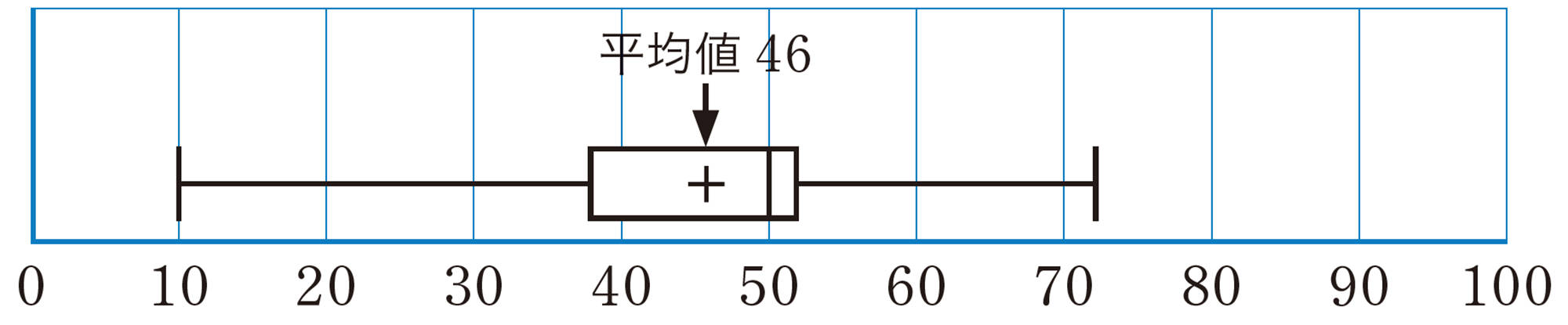
次の10個のデータについて，箱ひげ図の表し方を考えてみましょう。
●平均値
箱ひげ図では，平均値を次の図のように，
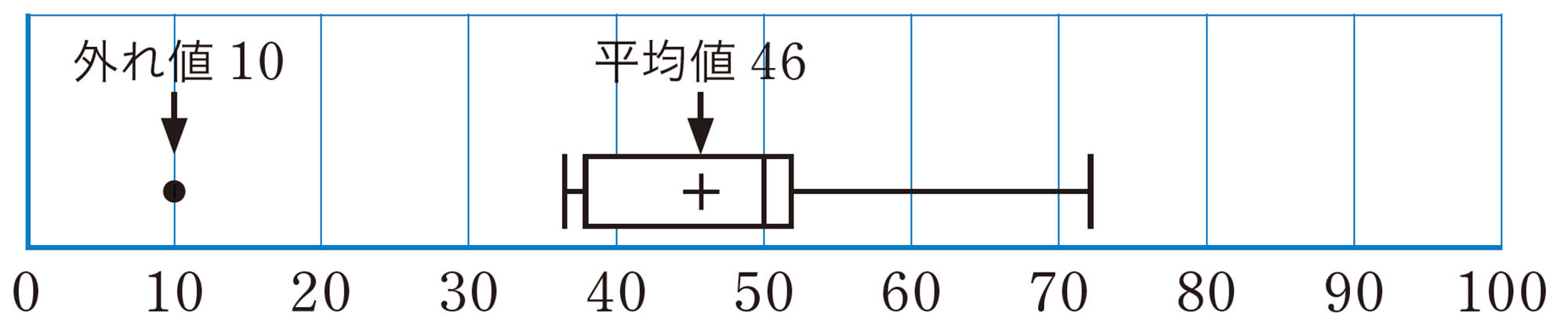
●外れ値
データの中で，ほかのデータに比べて極端にかけ離れた値があるとき，そのデータのことを外れ値といいます。たとえば，第1四分位数から四分位範囲の
上のデータで，四分位範囲は14で，その
とみなすことができ，次のように表すことがあります。
<2年p.210>
３ データの活用
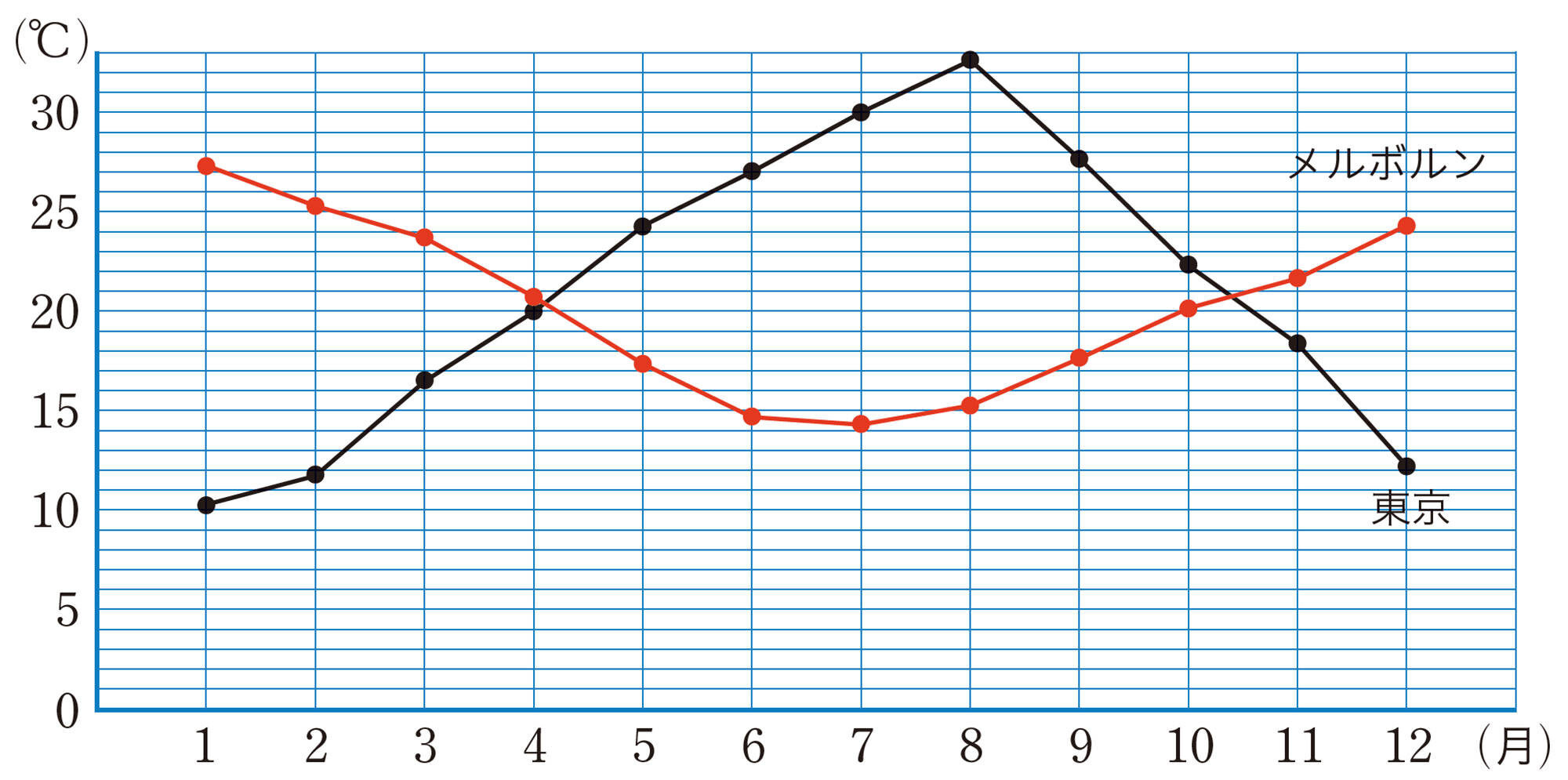
今度，1月から3月まで兄がオーストラリアのメルボルンに留学するの。どんな服が必要かな。
メルボルンの気温は，日本と比べると寒いのかな，暑いのかな。
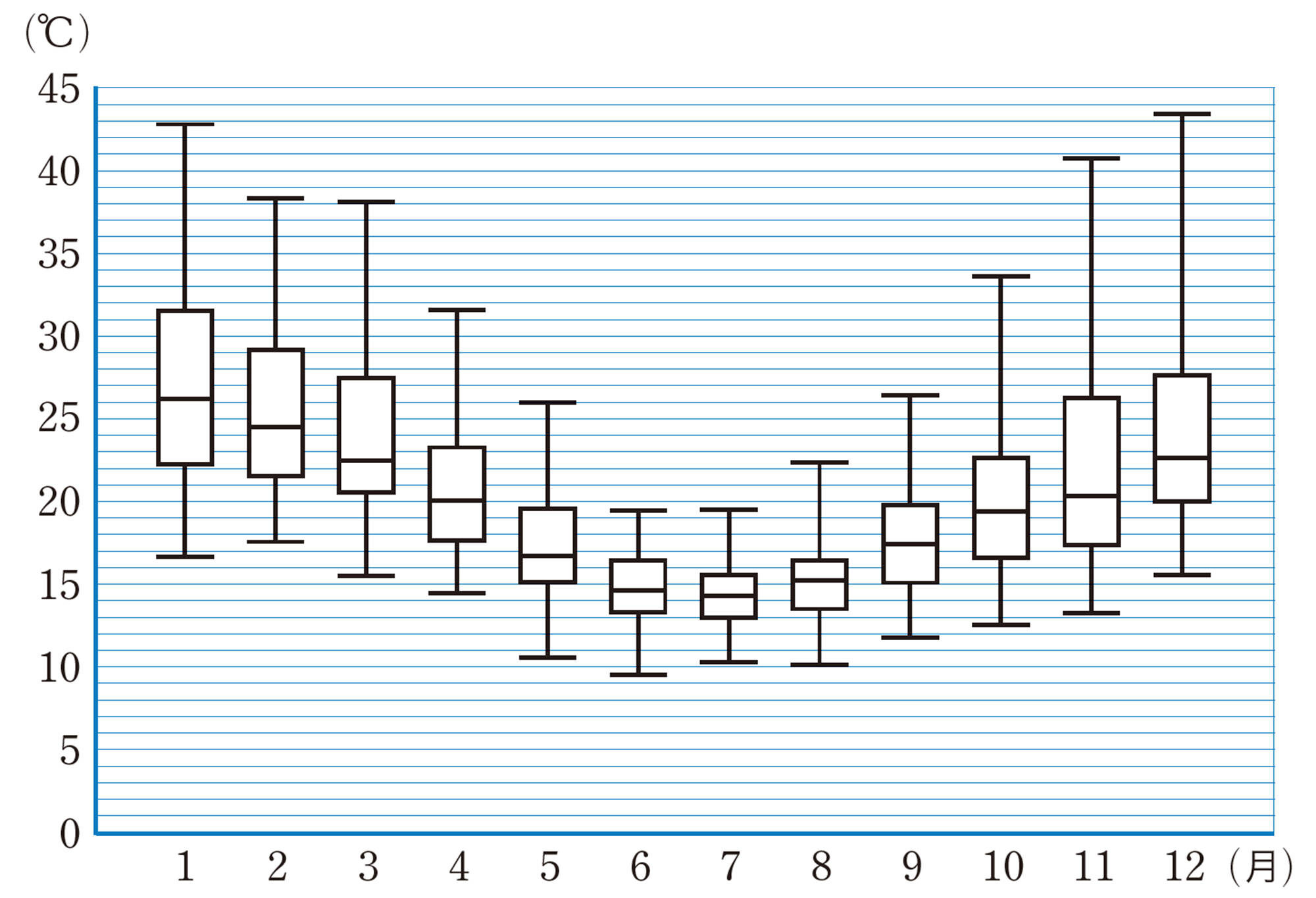
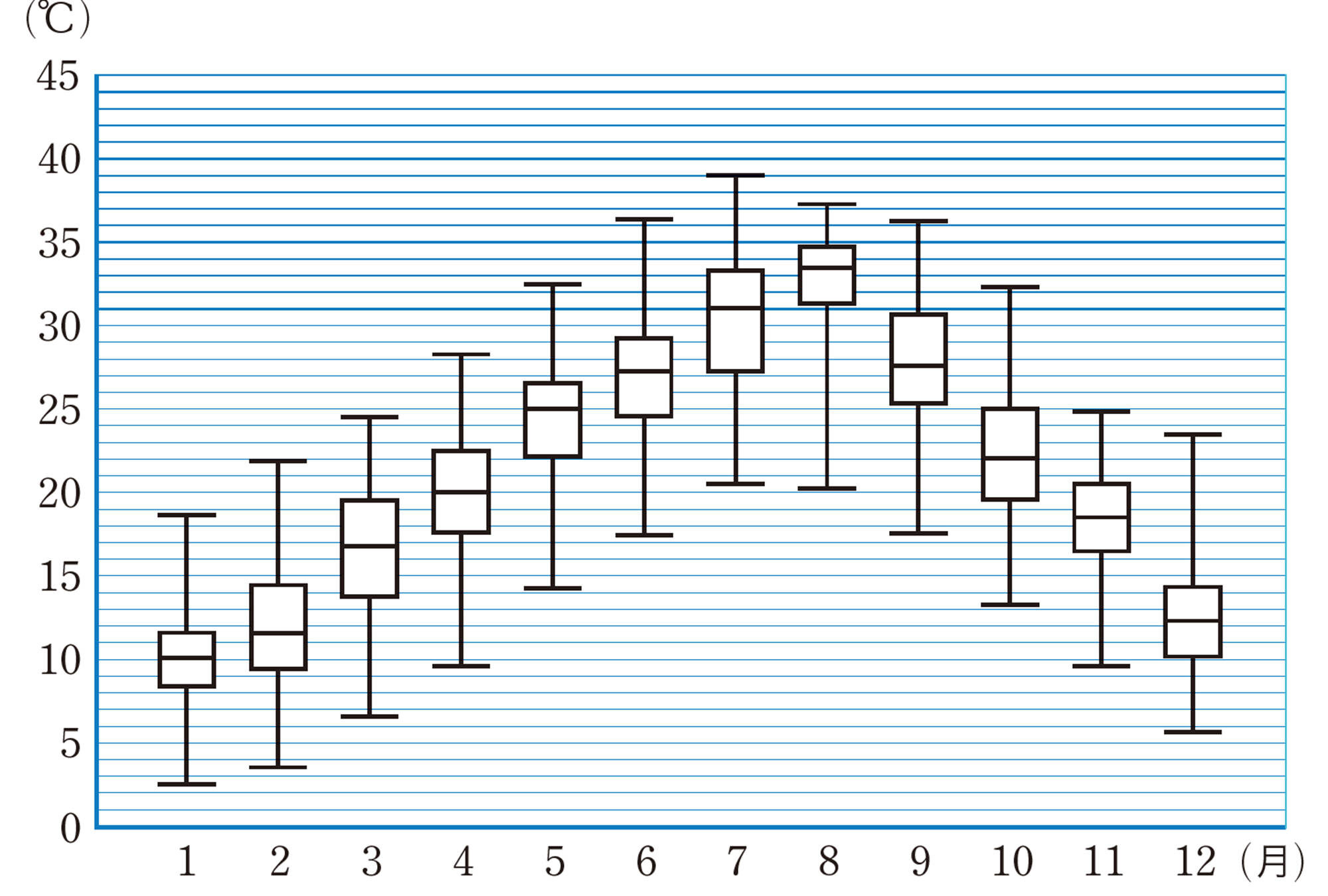
Q Question
1月から3月の間にメルボルンに行く場合，どんな服を準備すればよいか調べるために，5年間の日ごとの最高気温のデータから月ごとの平均値を求め折れ線グラフに表すと，次のようになりました。このグラフから，どんなことがわかりますか。
東京とは夏と冬が逆になっているけど，東京の夏ほど暑くはなさそうだね。
最高気温の平均値で比べるだけでいいのかな。
暑い日や寒い日があるかもしれないから，最高気温の分布も調べた方がいいんじゃないかな。
見方・考え方
どこに着目して考えればいいかな。
目標 ▷ データの傾向を読み取り，問題を解決しよう。
<2年p.211>
１ メルボルンと東京の5年間の日ごとの最高気温のデータを月ごとに集めて箱ひげ図をつくると，次のようになりました。このグラフから，どんな服を準備すればよいか話し合ってみましょう。
箱ひげ図を縦にかくこともあるよ。
メルボルンには，極端に暑い日があるよ。
極端に暑い日がどのくらいあるのかどうすればわかるのかな。
<2年p.212>
２ メルボルンの5年間の1月から3月の日ごとの最高気温を，次のような度数分布表に整理しました。累積度数や相対度数，累積相対度数を求めて，どんな服を用意すればよいか話し合ってみましょう。
1月から3月の間に20℃未満になる確率はどのくらいといえるかな。
どんなことがわかったかな
過去のデータを箱ひげ図やヒストグラムで表すと，未来のことを予測したり，どんな傾向があるかを調べたりすることができます。
確かめよう 1節 データの分布
１ 男子17人のハンドボール投げの記録を調べたところ，次のようになりました。これらのデータについて，次の問いに答えなさい。
（単位：m）
⑴ 四分位数，四分位範囲をそれぞれ求めなさい。
⑵ 次の図に，箱ひげ図で表しなさい。
<2年p.213>
7章 「データの分布」を学んで
できるようになったこと 身のまわりの課題へ ▷P.215
データの傾向を，四分位範囲や箱ひげ図を使って比較することができる。
データを調べるとき，これまで学んできた表し方の中から適切なものを選び，その傾向について考えることができる。
身のまわりや数学の中から見つけた問題を，四分位範囲や箱ひげ図を使って解決することができる。また，調べた結果が，本当に正しいといえるかどうか確かめることができる。
さらに学んでみたいこと
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない グラフの読み取りの注意点
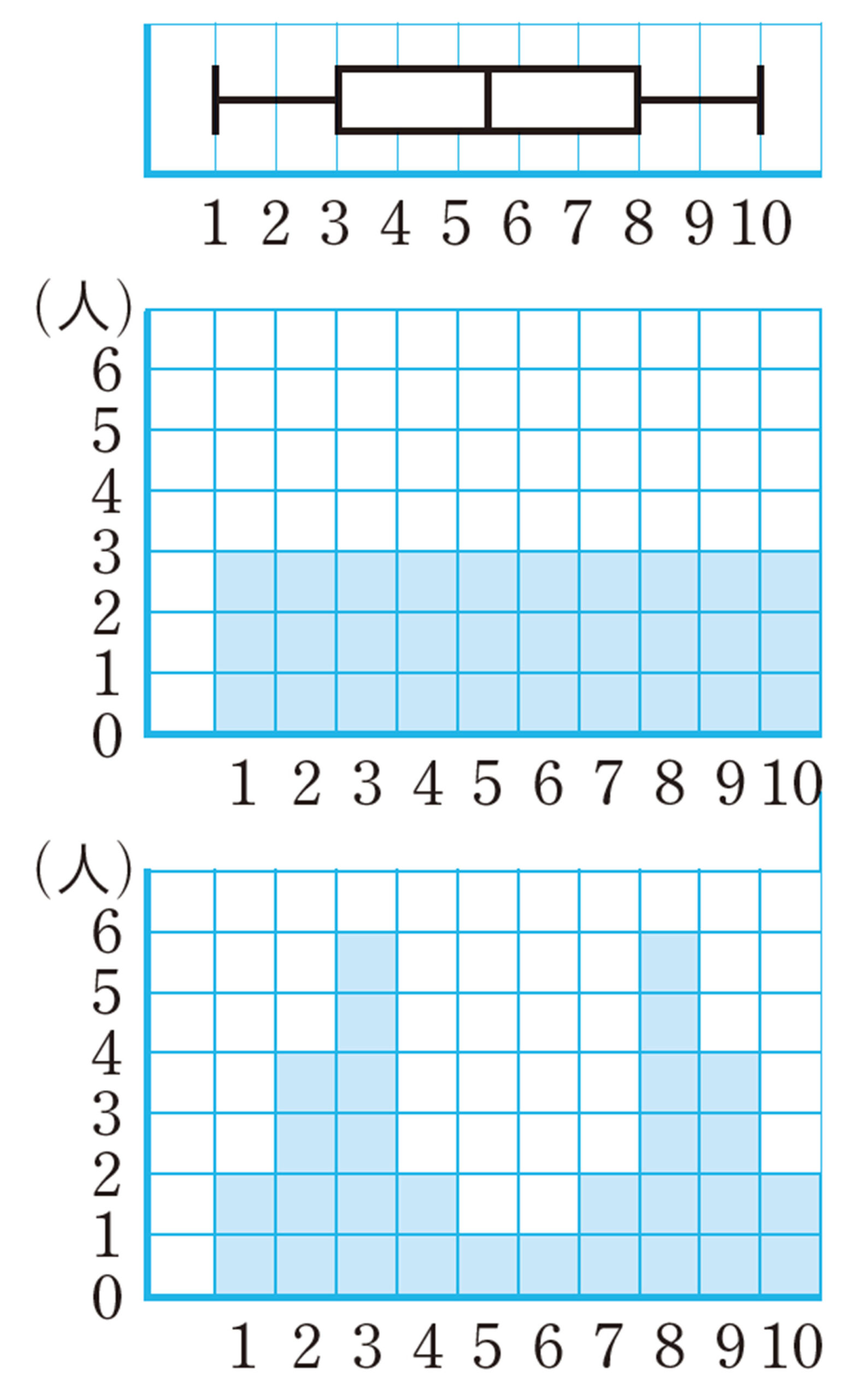
右の箱ひげ図は，30人に対してある商品が好きか嫌いかを10段階で評価してもらい，その結果をまとめたものです。もしもこのグラフを示されて，「1から10までどこにもかたよっていない」という結果になったといわれたとき，あなたはその情報をそのまま信じるでしょうか。
この箱ひげ図から，分布のようすを考えたとき，右のようなヒストグラムを考えてしまいそうです。しかし，右下のヒストグラムを箱ひげ図にしても，同じ箱ひげ図になります。
したがって，箱ひげ図だけでは実際の分布を必ずしも読み取れるとは限りません。箱ひげ図だけで判断しようとすると，結果的に誤った解釈をしてしまうことがあります。
これまで学習したグラフの読み取り方を知っておくことで，データを誤って解釈することを減らすことができます。
