<2年p.195>
確かめよう 1節 確率
2 次の確率を求めなさい。
⑴ 1枚の硬貨を2回続けて投げるとき,少なくとも1回は表が出る確率
⑵ 2つのさいころを同時に投げるとき,同じ目が出る確率
<2年p.196>
6章 「確率」を学んで
できるようになったこと 身のまわりの課題へ P.199,200
相対度数と確率の関係をもとにして,起こり得る場合がすべて同様に確からしいときは,実験をしなくても確率が求められることを理解することができる。
同様に確からしいことがらについて,いろいろな確率を求めることができる。
身のまわりや数学の中から見つけた問題を,確率を使って解決することができる。
これからもっと学んでみたいことや,疑問に思ったことを書いておこう。
数学へのいざない 迷惑メールの判別法
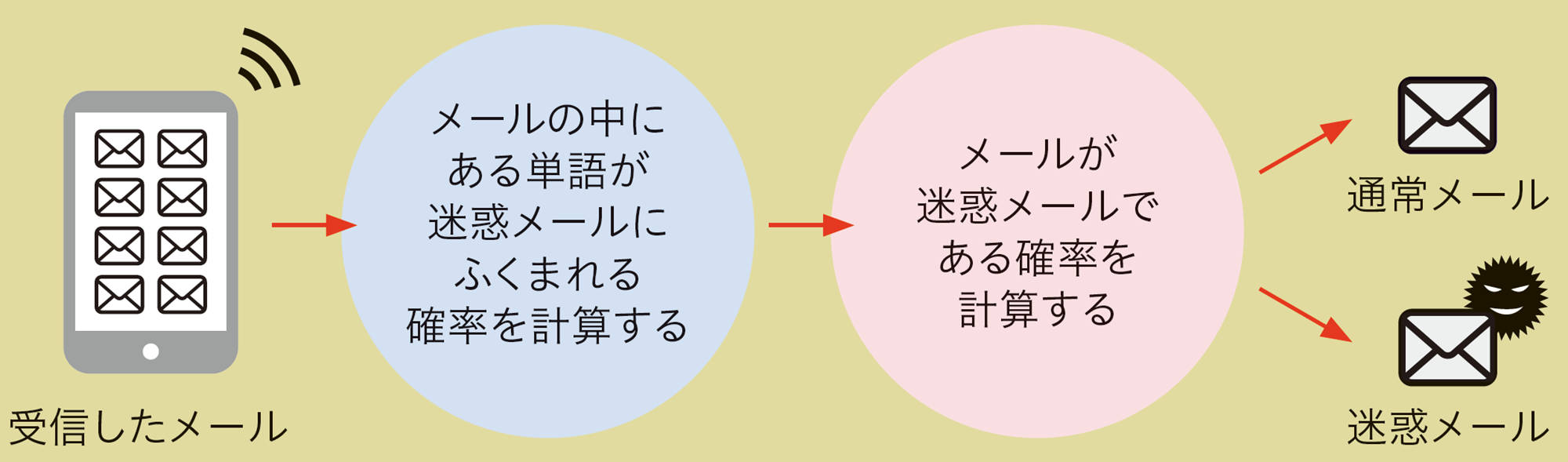
電子メールを受信したとき,迷惑メールであることがあります。しかし,最近のメールソフトでは,迷惑メールであると初めから判別して,別の場所に格納しています。このような機能には,メールの中にある単語が迷惑メールにふくまれる確率によって,迷惑メールかどうかを判定する統計的な手法などが用いられています。
たとえば,過去の受信メールを通常のメールと迷惑メールに分類して,データベースに格納しておきます。そして,新たに受信したメールについて,その内容を単語に分割し,データベースの情報を利用して,「該当単語をふくむメールが迷惑メールである確率」を求め,この確率が大きければ,受信メールは迷惑メールに分類されます。さらに,分類されたメールの情報は,新たに受信したメールを迷惑メールかどうか判別する際に利用されます。
受信したメール → メールの中にある単語が迷惑メールにふくまれる確率を計算する → メールが迷惑メールである確率を計算する → 通常メール/ 迷惑メール
<2年p.197>
6章のまとめの問題 解答 P.251〜252 基本
1 次のことがらは正しいですか。
⑴ 1つのさいころを投げるとき,1から6までのどの目が出ることも同様に確からしい。
⑵ 1つのさいころを60 回投げるとき,4の目は必ず10回出る。
⑶ 1枚の硬貨を3回続けて投げる実験をしたところ,1回目,2回目と続けて表が出たから,3回目は表の出る確率より裏の出る確率の方が大きい。
⑷ 2枚の硬貨を同時に投げるとき,2枚とも表になる確率と,1枚が表でもう1枚が裏になる確率は等しい。
2 1から30までの整数を1つずつ書いた30枚のカードの中から1枚を取り出すとき,次の確率を求めなさい。
⑴ 4の倍数である確率
⑵ 5の倍数か7の倍数である確率
⑶ 3の倍数でない確率
⑷ 4の倍数か6の倍数である確率
3 次の確率を求めなさい。
⑴ 20本のうち,当たりが4本入っているくじを1回引くとき,当たる確率
⑵ 1つのさいころを2回投げるとき,目の和が6になる確率
⑶ 2つのさいころを同時に投げるとき,目の和が奇数になる確率
⑷ 1枚の硬貨を3回投げるとき,3回続けて裏が出る確率
<2年p.198>
6章のまとめの問題 応用
1 A,B,C,Dの4 人でリレーのチームを組むとき,走る順番は全部で何通りありますか。また,Aが第3走者になる場合は何通りありますか。
3 A,B,Cの3人で190ページの問3のカードを1セットずつ使って1回だけじゃんけんをするとき,次の問いに答えなさい。
⑴ 3人のグー,チョキ,パーの出方は,全部で何通りありますか。
⑵ 3人があいこ[mathjax]\((\)引き分け[mathjax]\()\)になる確率を求めなさい。
⑶ Bが1人だけ勝つ確率を求めなさい。
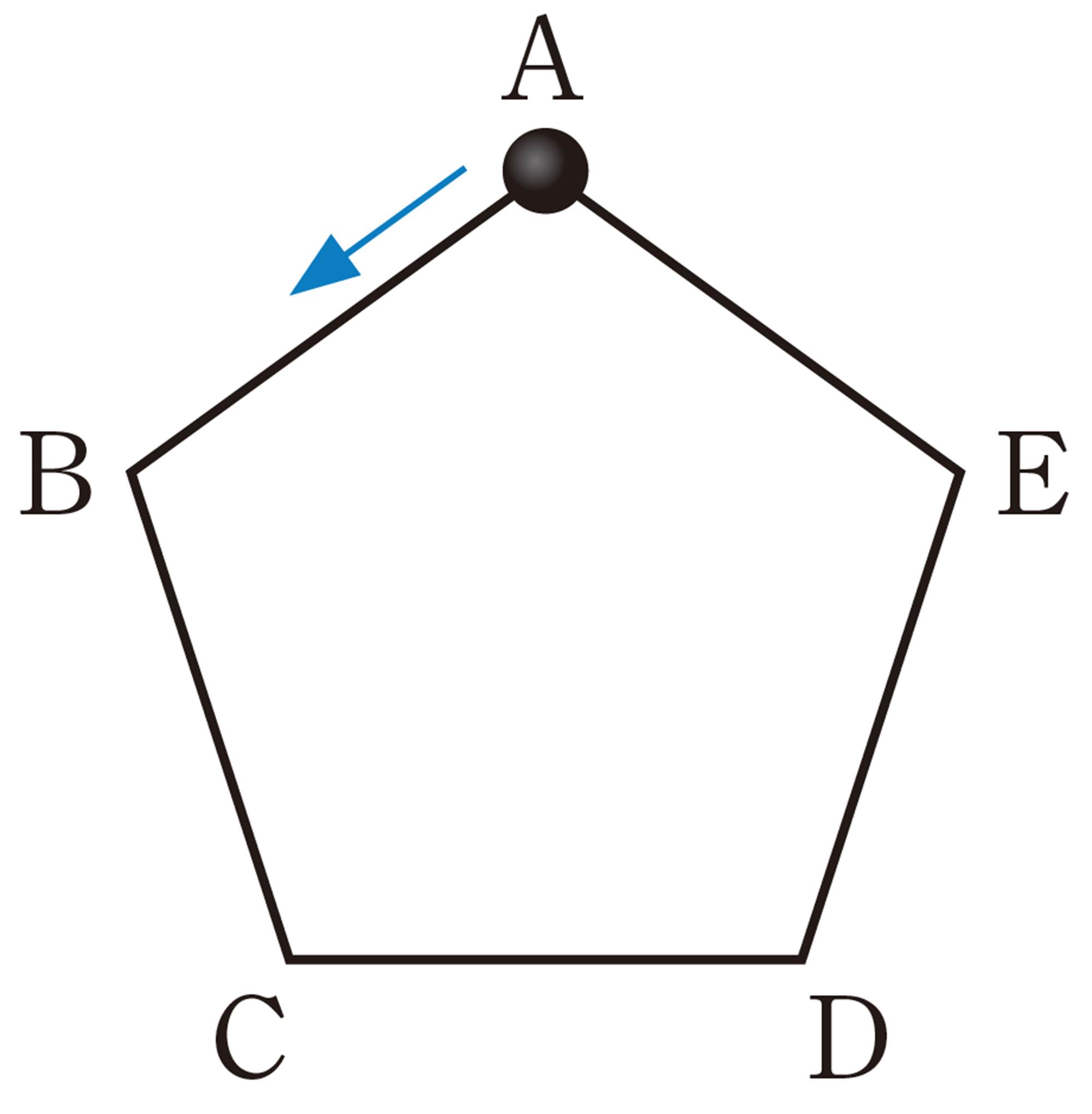
⑴ 碁石が1回目に動いたとき,頂点Bにある確率を求めなさい。
⑵ 碁石が2回目に動いたとき,頂点Bにある確率を求めなさい。
<2年p.199>
活用
1 美月さんは,テレビで賞品当てゲームを見ています。このゲームは,司会者と挑戦者[mathjax]\((\) 賞品を当てる人 [mathjax]\()\) で,次のように進められます。
賞品当てゲーム
挑戦者の前に3つの箱が置かれており,そのうちの1つは当たりの箱です。司会者はどれが当たりの箱であるか知っています。
[進め方]
① 挑戦者は,最初に箱を1つ選びます。
② 司会者は,残った2つの箱のうち,はずれの箱を1つ開けて見せます。
③ 挑戦者は,最初に選んだ箱を「変更する」か「変更しない」のいずれかを選択します。
このゲームについて,次の問いに答えなさい。
⑴ 最初から「箱を変更しない」と決めて挑戦すると,進め方の①で当たるかどうかが決まります。それが当たりの箱である確率を求めなさい。
⑵ 美月さんは,最初から「箱を変更する」と決めてゲームを行う場合について,次のように考えました。□に,あてはまることばを入れて,説明を完成させなさい。
 美月さんの説明
美月さんの説明
最初に選んだ箱が当たりだとすると,残りの2つの箱ははずれだから,司会者がどちらの箱を開けても,残った箱は必ずはずれである。
したがって,箱を変更すると必ずはずれる。
最初に選んだ箱がはずれだとすると,
□
したがって,箱を変更すると必ず当たる。
⑶ 最初から「箱を変更する」と決めてゲームを行う方が当たりやすくなります。このことを実験で確かめる方法を考えなさい。
<2年p.200>
深めよう どちらにかける?
① 多くの人たちは,3つのさいころの目の和が9になる場合は6通り,10になる場合も6通りあるので,どちらにかけても有利,不利はないと考えていました。
9になる場合,10になる場合の目の出方をすべてあげてみましょう。