<2年p.180>
ふりかえり
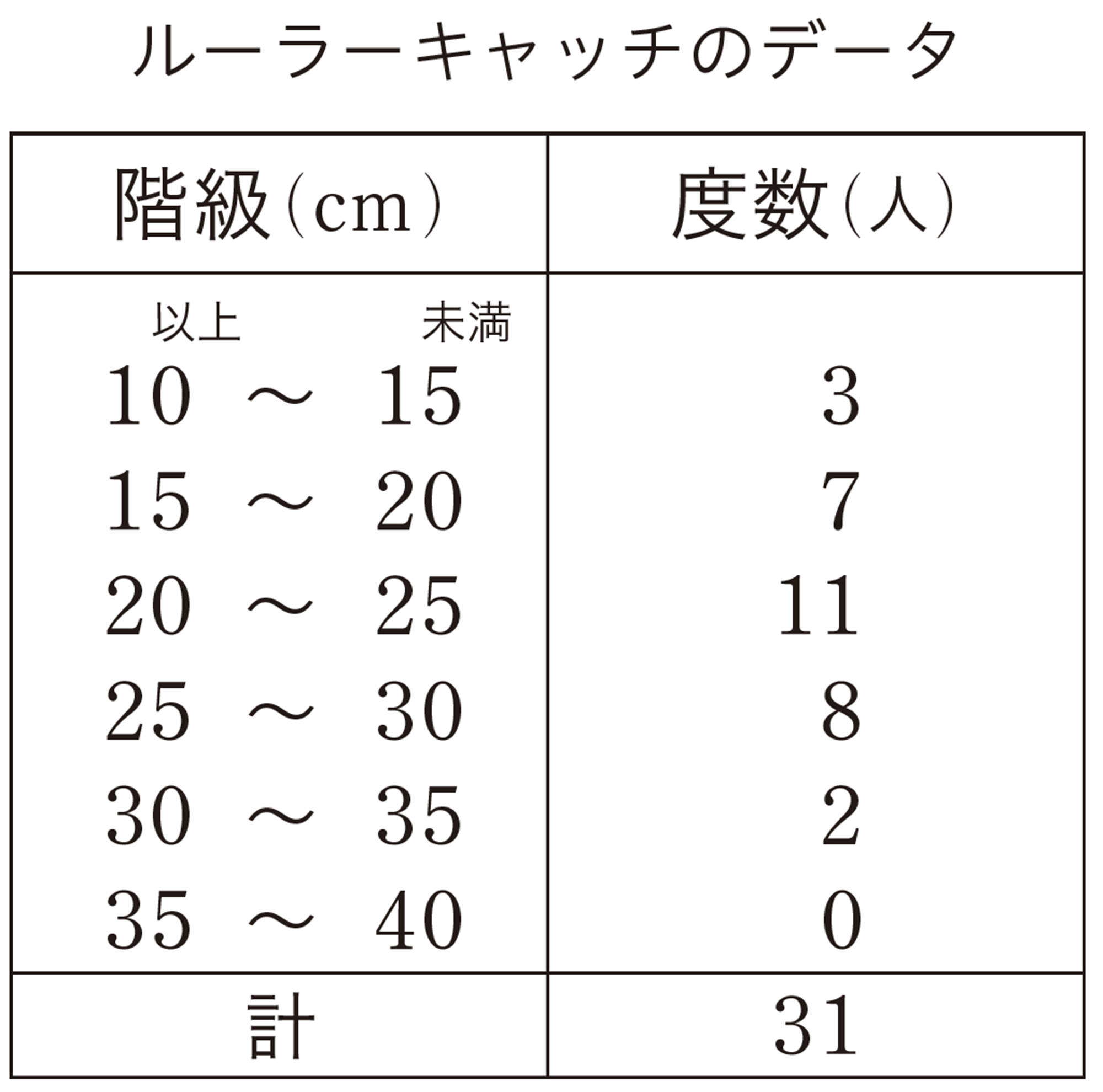
【度数分布表】
階級と度数で資料の分布を示している表を度数分布表という。
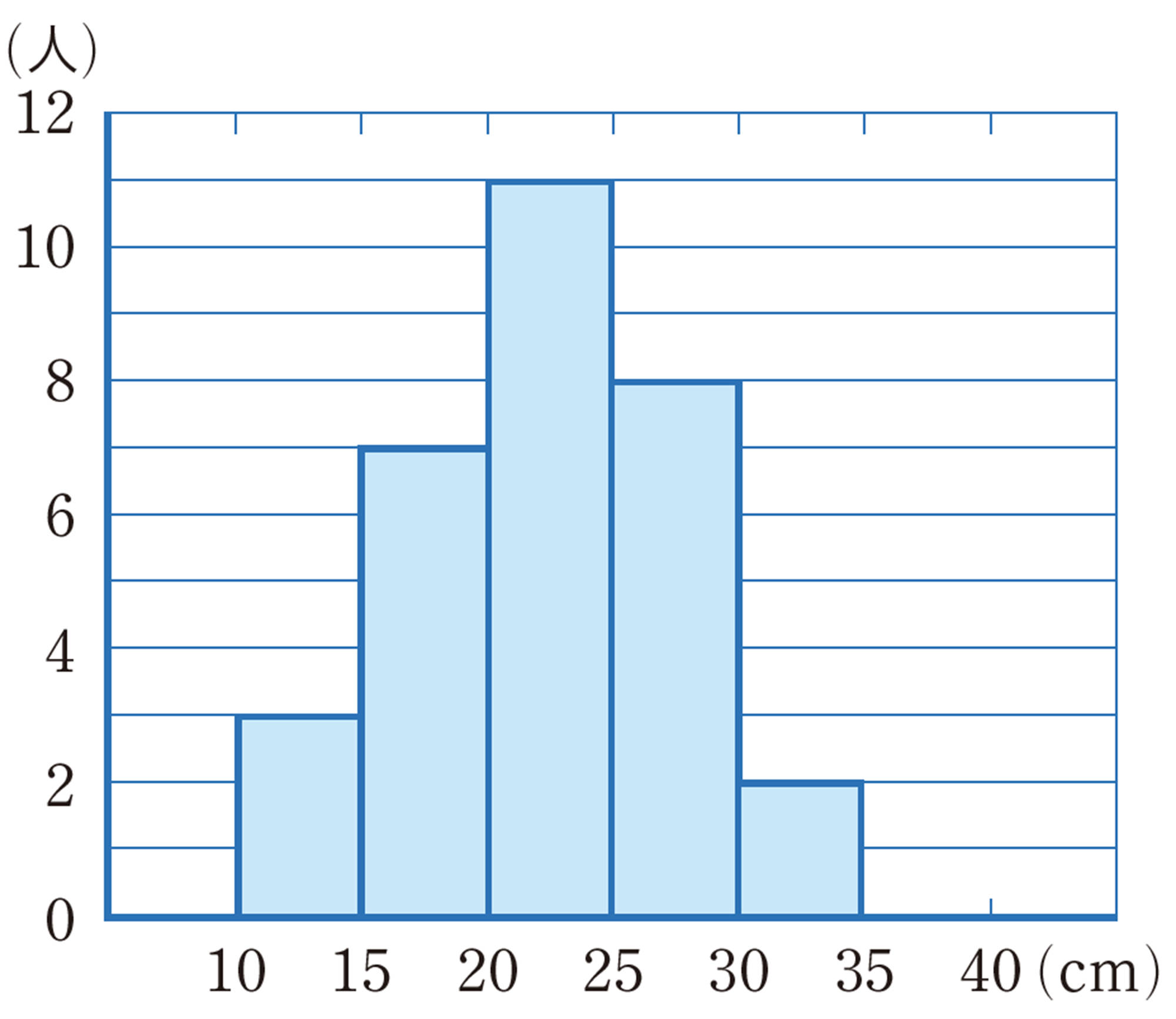
ルーラーキャッチのデータ
【ヒストグラム】
度数分布表を用い，階級の幅を横，度数を縦とする長方形を順に並べてかいたグラフをヒストグラムという。
データの傾向は，表にまとめたり図に表したりして調べたね。
PPDACサイクルを使って，いろいろなことを調べたね。
【中央値】
データを大きさの順に並べたとき，中央にくる値。
【相対度数】
各階級の度数を総度数でわった値を，その階級の相対度数という。
【確率】
多数回の実験の結果，あることがらの起こる相対度数が一定の数値に近づくとき，その数値でことがらの起こりやすさを表すことができる。その数をそのことがらの起こる確率という。
ペットボトルのキャップを投げる実験をすると，どの向きが出る相対度数も，一定の数値に近づくことを確かめたね。
<2年p.181>
６章 Chapter 6 確率
1節 確率
ペットボトルのふたを投げたとき，表向きと裏向きは，どちらが出やすかったかな。
たくさん実験すれば，確率が求められたよ。
いつも実験するのは，たいへんだね。
もっと簡単に確率を求められないかな。
？ 実験をしないで確率を求められる？
<2年p.182>
1節 確率
出やすいのはどれ？
次の図のような展開図を組み立てたさいころがあります。
このさいころを 2つ使って，景品を当てるゲームをしようと思います。さいころを2つ同時に投げたとき，もっとも出にくい目を「1等」，もっとも出やすい目を「はずれ」とするとき，どんな目の出方を「1等」と「はずれ」にすればよいか考えてみましょう。
<2年p.183>
【１】 前ページのさいころを2つ同時に投げたとき，「1 等」と「はずれ」は次の㋐～㋕のうちのどれにすればよいでしょうか。それぞれ予想してみましょう。
㋐ [mathjax]\(\large{\boxed{A} \ \boxed{A}}\)
㋑ [mathjax]\(\large{\boxed{A} \ \boxed{B}}\)
㋒ [mathjax]\(\large{\boxed{A} \ \boxed{C}}\)
㋓ [mathjax]\(\large{\boxed{B} \ \boxed{B}}\)
㋔ [mathjax]\(\large{\boxed{B} \ \boxed{C}}\)
㋕ [mathjax]\(\large{\boxed{C} \ \boxed{C}}\)
1つのさいころには，面が6つあって，どの面の出やすさも同じといえそうだね。
1年のときのように，何回も実験すれば，面の出やすさを数で表せそうだね。
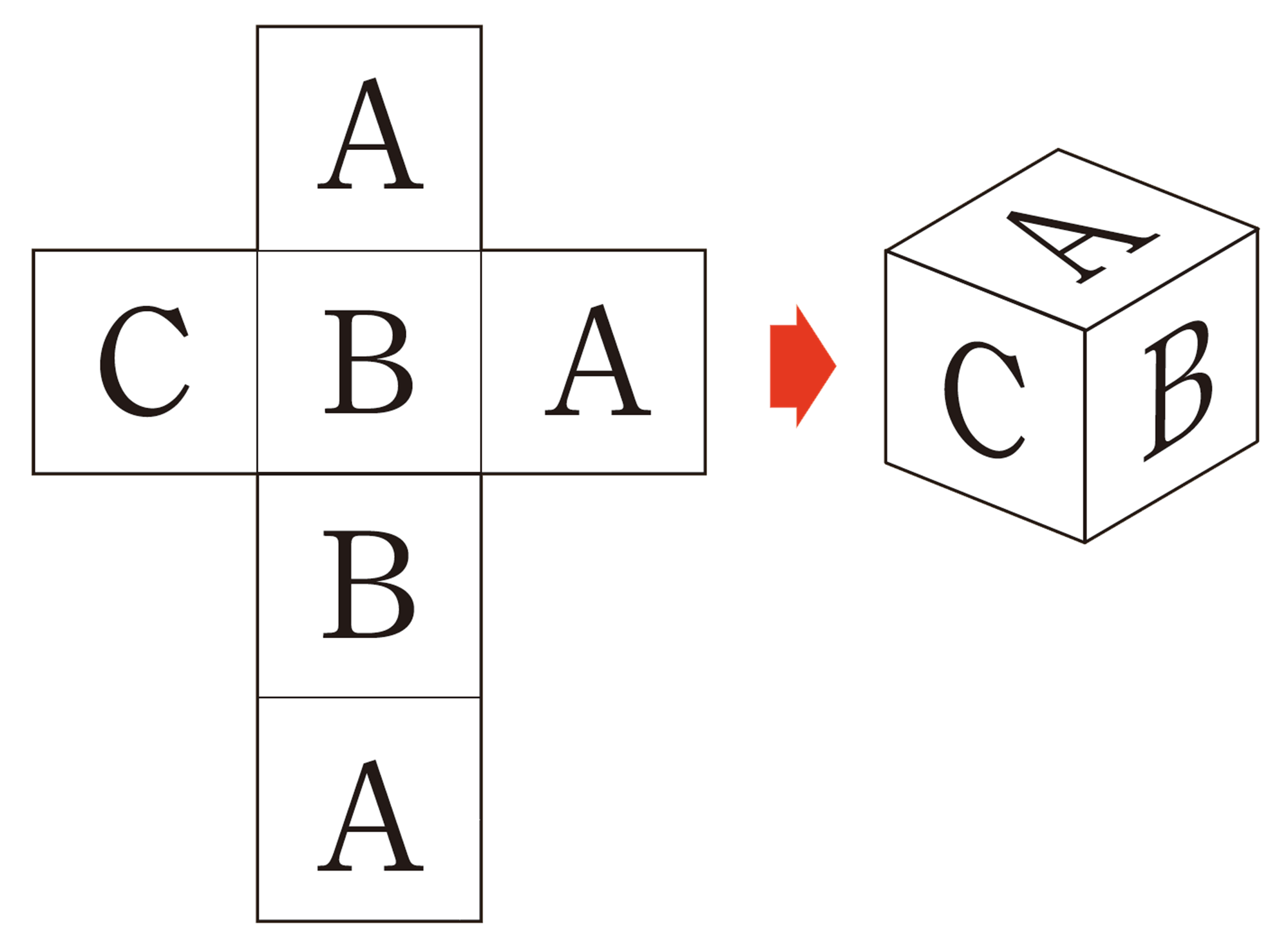
巻末④の展開図を組み立ててさいころを作り，実験してみよう。
【２】 1つのさいころで，6つの面がそれぞれ同じ確率で出ると仮定してよいでしょうか。また，そのように仮定した場合，「1 等」と「はずれ」は決められるか，話し合ってみましょう。
1つのサイコロなら，Cが出る確率はもっとも小さそうだよ。
さいころが2つあるときは，どう決めたらいいのかな。
次の課題へ！
実験をしなくても，確率は求められるのかな？
P.184
<2年p.184>
１ 確率の求め方
Q Question
さいころを投げたとき，それぞれの目が出る確率はすべて等しくなると考えてもよいでしょうか。また，その理由を話し合ってみましょう。
どの目の出やすさも同じだと思うよ。
1年のときのように，実験すれば確かめられるかな。
見方・考え方
どこに着目して考えればいいかな。
次の図は，実際にさいころを50回，100回，…と投げて，3の目が出た相対度数をグラフに表した1つの例である。
上のグラフで，はじめ大きく変動していた相対度数は，さいころを投げる回数が増えるにつれてあまり変動しなくなり，一定の数値[mathjax]\(0.17\)に近づいていく。この数値は，3の目が出ることの起こりやすさを表していると考えられる。したがって，3の目が出る確率は[mathjax]\(0.17\)と考えられる。
目標 ▷ 実験をせずに，確率を求める方法を考えよう。
<2年p.185>
正しくつくられたさいころを投げるとき，1から6までのどの目が出ることも，同じ程度に期待される。このようなとき，1から6までのどの目が出ることも同様に確からしいという。
1つのさいころを投げるとき，起こり得るすべての場合は6通りあるから，1から6までのどの目が出る確率も，それぞれ[mathjax]\(\dfrac{1}{6}\)である。
前ページの実験で得られた3の目の出る確率0.17は，[mathjax]\(\dfrac{1}{6}\)とほぼ等しい。
例 １ ジョーカーを除く52枚のトランプを裏返しにしてよく混ぜ，その中から 1 枚を引くとき，どのカードを引くことも同様に確からしいといえる。このとき，どのカードを引く確率も，それぞれ[mathjax]\(\dfrac{1}{52}\)である。
問 １ さいころを6回投げたとき，1の目は必ず1回出るといってよいですか。
問 ２ 次のことがらについて，同様に確からしいといえるものを選びなさい。
㋐ 右の写真のようなさいころを投げたとき， 1 から 6 のそれぞれの目が出ること。
㋑ 10 円硬こう貨か を投げたとき，表と裏が出ること。
㋒ 明日，雨が降ることと降らないこと。
問 ３ 身のまわりのことがらの中で，同様に確からしいといえる例をあげなさい。
同様に確からしいことがらの起こる確率を求めてみよう。
さいころを投げるとき，偶数の目が出る確率は，次のように考えればよい。
右の図のように，目の出方は全部で6通りあり，どの目が出ることも同様に確からしい。そのうち，偶数の目は，右の図のように3通りあるから，
[mathjax]\(\text{(偶数の目が出る確率)}=\dfrac{3}{6}=\dfrac{1}{2}\)
となる。
<2年p.186>
起こり得るすべての場合が同様に確からしいとするとき，あることがらが起こる確率は，次のようにして求めることができる。
確率の求め方
起こり得る場合が全部でn通りあり，そのどれが起こることも同様に確からしいとする。
そのうち，あることがらの起こる場合がa通りあるとき，そのことがらの起こる確率pは次のようになる。
[mathjax]\(p=\dfrac{a}{n}\)
注意 pはprobability（確率）の頭文字である。
例 ２ ジョーカーを除く52枚のトランプを裏返しにしてよく混ぜ，その中から1枚を引くとき，カードのマークが♥である確率を求めなさい。
考え方 52枚のトランプのどのカードを引くことも同様に確からしい。52枚のうち，♥のマークのカードは13枚あることから，確率を求める。
解答
起こり得る場合が全部で 52 通りあり， どのカードを引くことも同様に確からしい。
このうち，♥のマークのカードを引く場合は 13 通りであるから， 求める確率は
次のようになる。
[mathjax]\(\dfrac{13}{52}=\dfrac{1}{4}\)
答 [mathjax]\(\dfrac{1}{4}\)
問 ４ ジョーカーを除く52枚のトランプを裏返しにしてよく混ぜ，その中から1枚を引くとき，次の確率を求めなさい。
⑴ カードのマークが♦
⑵ カードの数が8
⑶ カードが絵札
⑷ カードのマークが♥または♦
問 ５ 1から5までの番号が1つずつ書かれた同じ大きさの玉が，袋の中に入っています。この袋の中から1個の玉を取り出すとき，その番号が偶数である確率と奇数である確率を，それぞれ求めなさい。
<2年p.187>
Q Question
右の図のように，A～Eのどの袋にも，赤玉や白玉が合わせて4個入っています。袋の中から1個の玉を取り出すとき，白玉の出る確率を，それぞれ求めてみましょう。
白玉が出ないときや，白玉しか出ないときがあるね。
確率はどう表せばいいのかな。
見方・考え方
具体的な場面で考えられるかな。
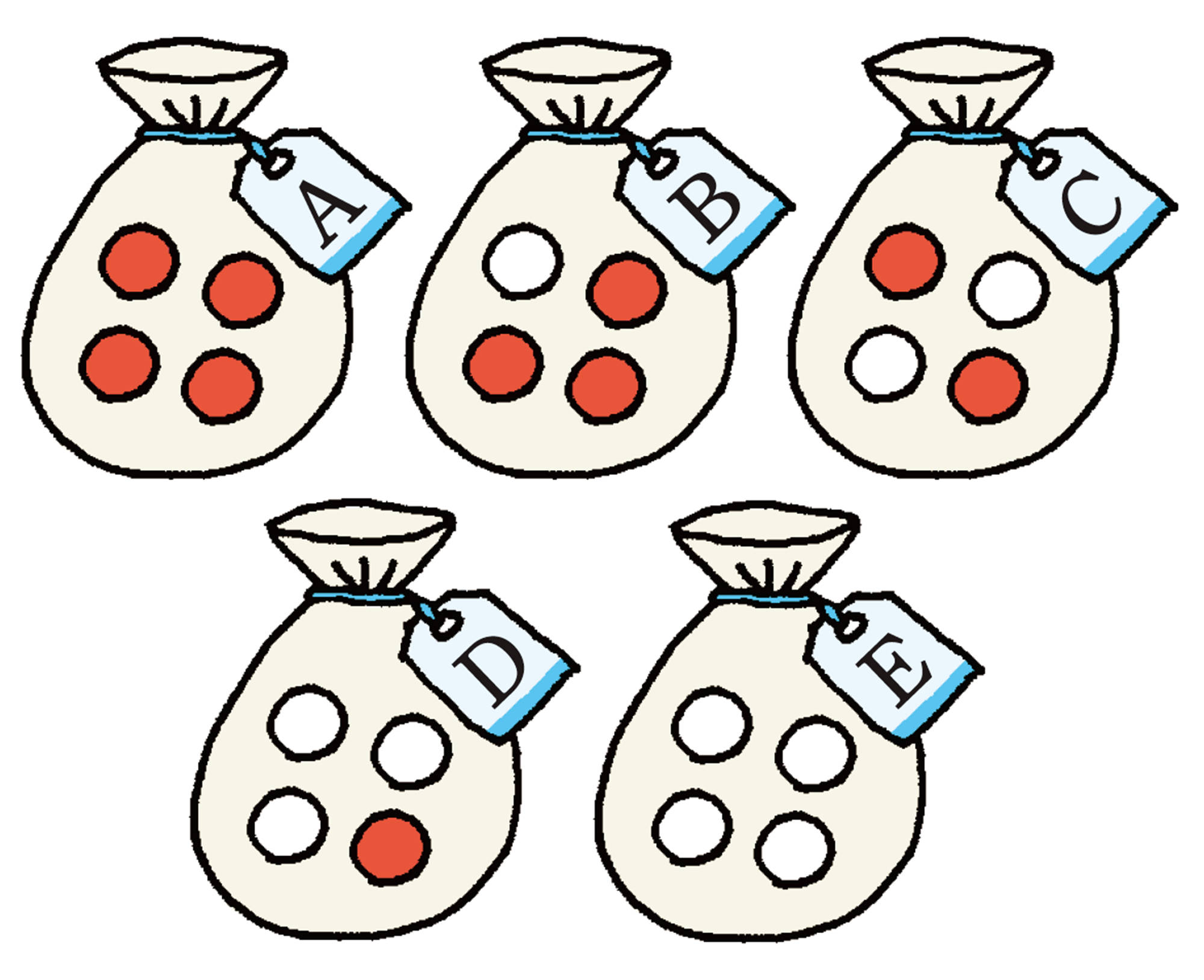
【Q】で，Aの袋では，どの玉を取り出しても決して白玉は出ないから，白玉の出る確率は [mathjax]\(\dfrac{0}{4}=0\)である。
また，Eの袋では，どの玉を取り出しても必ず白玉が出るから，白玉の出る確率は [mathjax]\(\dfrac{4}{4}=1\) である。
それ以外の袋では，白玉の出る確率は0から1の間の数で表される。
あることがらの起こる確率をpとすると，pの範囲は次のようになる。
[mathjax]\(0 \leqq p \leqq 1\)
また，[mathjax]\(p=0\)のとき，そのことがらは決して起こらない。
[mathjax]\(p=1\)のとき，そのことがらは必ず起こる。
問 ６ 確率が[mathjax] \(0\)，[mathjax] \(1\)になることがらの例を，それぞれあげなさい。
Q Question
さいころを投げるとき，次の確率を求めてみましょう。また，その結果から，どのようなことがわかるか話し合ってみましょう。
⑴ 6の目が出る確率
⑵ 6の目が出ない確率
6の目が出る場合は1通りで，出ない場合は5通りだね。
そのほかの場合はあるのかな。
見方・考え方
確率には，どんな性質があるか見つけられるかな。
<2年p.188>
1個のさいころを投げるとき，6の目が出る場合は，「６」の1通りであるから，6の目が出る確率は[mathjax]\(\dfrac{1}{6}\)である。一方，6の目が出ない場合は，「１」「２」「３」「４」「５」の5通りであるから，6の目が出ない確率は[mathjax]\(\dfrac{5}{6}\)である。
したがって，6の目が出る確率と6の目が出ない確率の和は，
[mathjax]\(\dfrac{1}{6}+\dfrac{5}{6}=1\)
である。すなわち，次のことがいえる。
[mathjax]\(\text{(6の目が出ない確率)}=1-\text{(6の目が出る確率)}\)
あることがらAの起こる確率がpであるとき，Aの起こらない確率は，[mathjax]\(1-p\)である。
問 ７ あるくじを1本引くとき，当たる確率は[mathjax]\(\dfrac{3}{20}\)です。このくじを1本引くとき，はずれる確率を求めなさい。
問 ８ 1から50までの整数を1つずつ書いた50枚のカードの中から1枚を取り出すとき，カードの数が素数である確率と素数でない確率を，それぞれ求めなさい。
▲トライ 拓真さんは，美月さんとじゃんけんをするとき，次のようにいいました。
「じゃんけんは，グー，チョキ，パーの3通りだから，美月さんは[mathjax]\(\dfrac{1}{3}\)の確率でグーを出す。」
この考え方は正しいといえるかどうか説明してみよう。
どんなことがわかったかな
起こり得るすべての場合が同様に確からしいとするとき，全部の数と場合の数を求めることで，実験をしなくても確率を求めることができます。また，確率の範囲は，0以上1以下になります。
次の課題へ！
さいころを2つ投げた場合や硬貨を2枚投げた場合の確率も求められるのかな？
P.189
