<2年p.162>
1 平行四辺形の性質
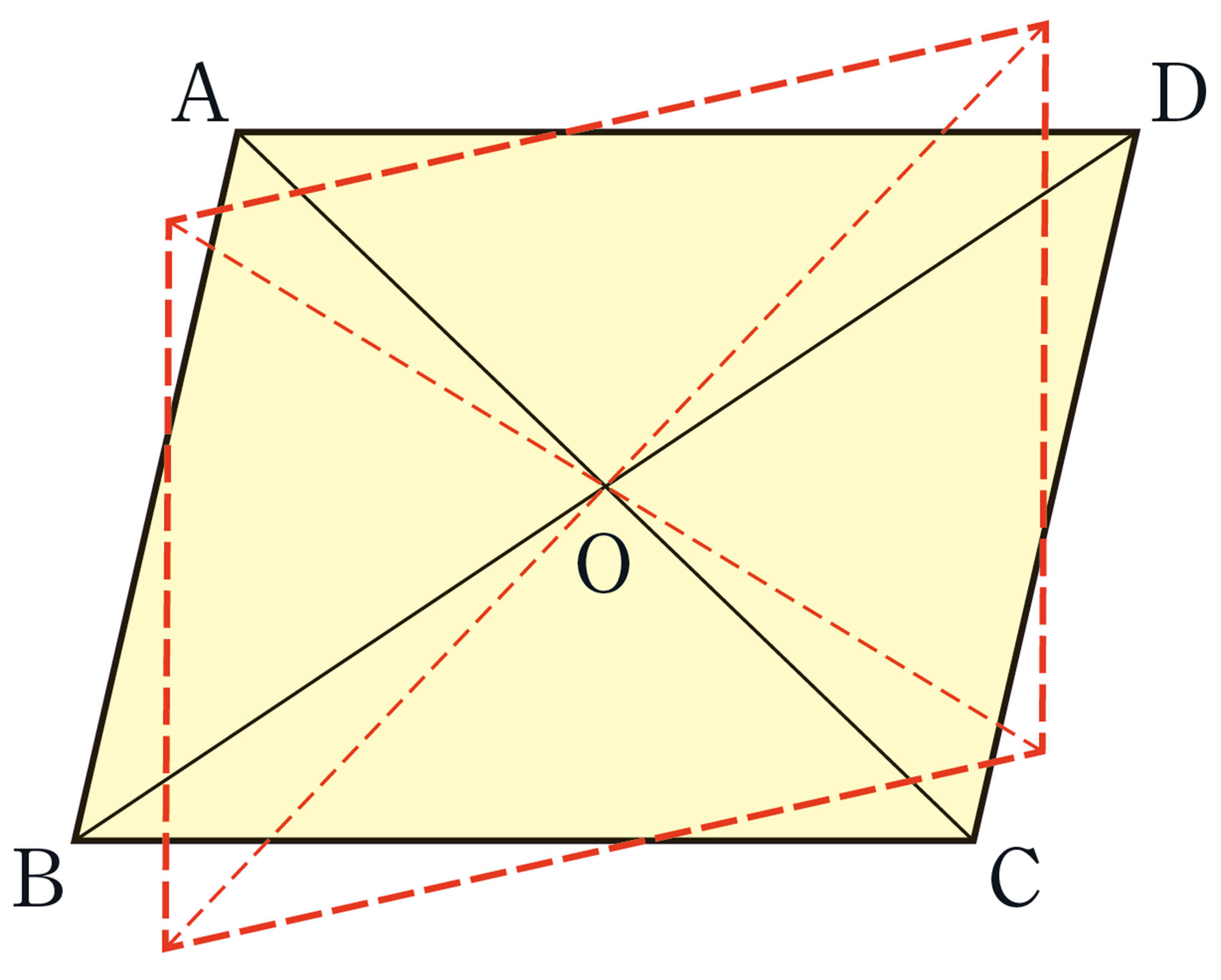
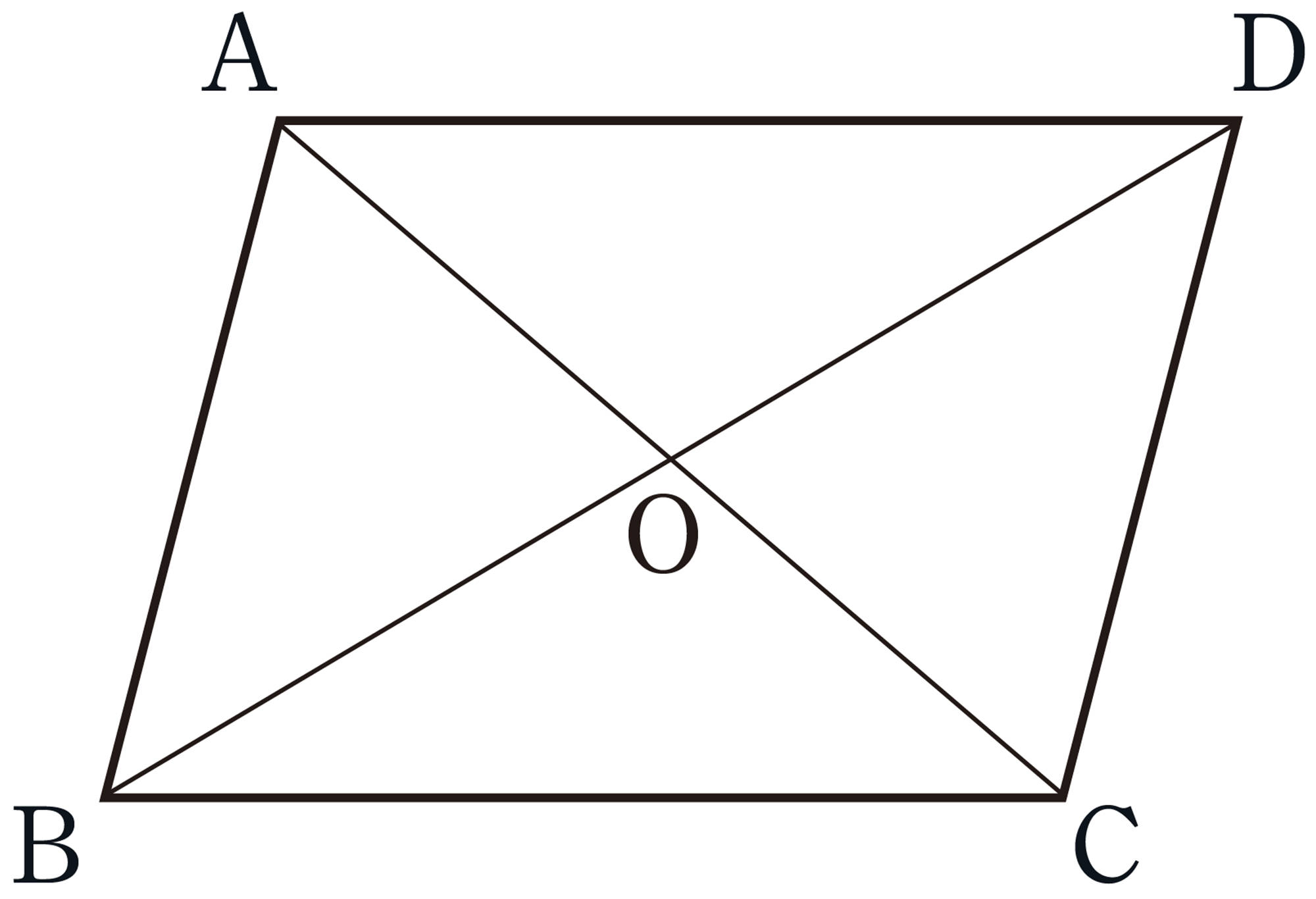
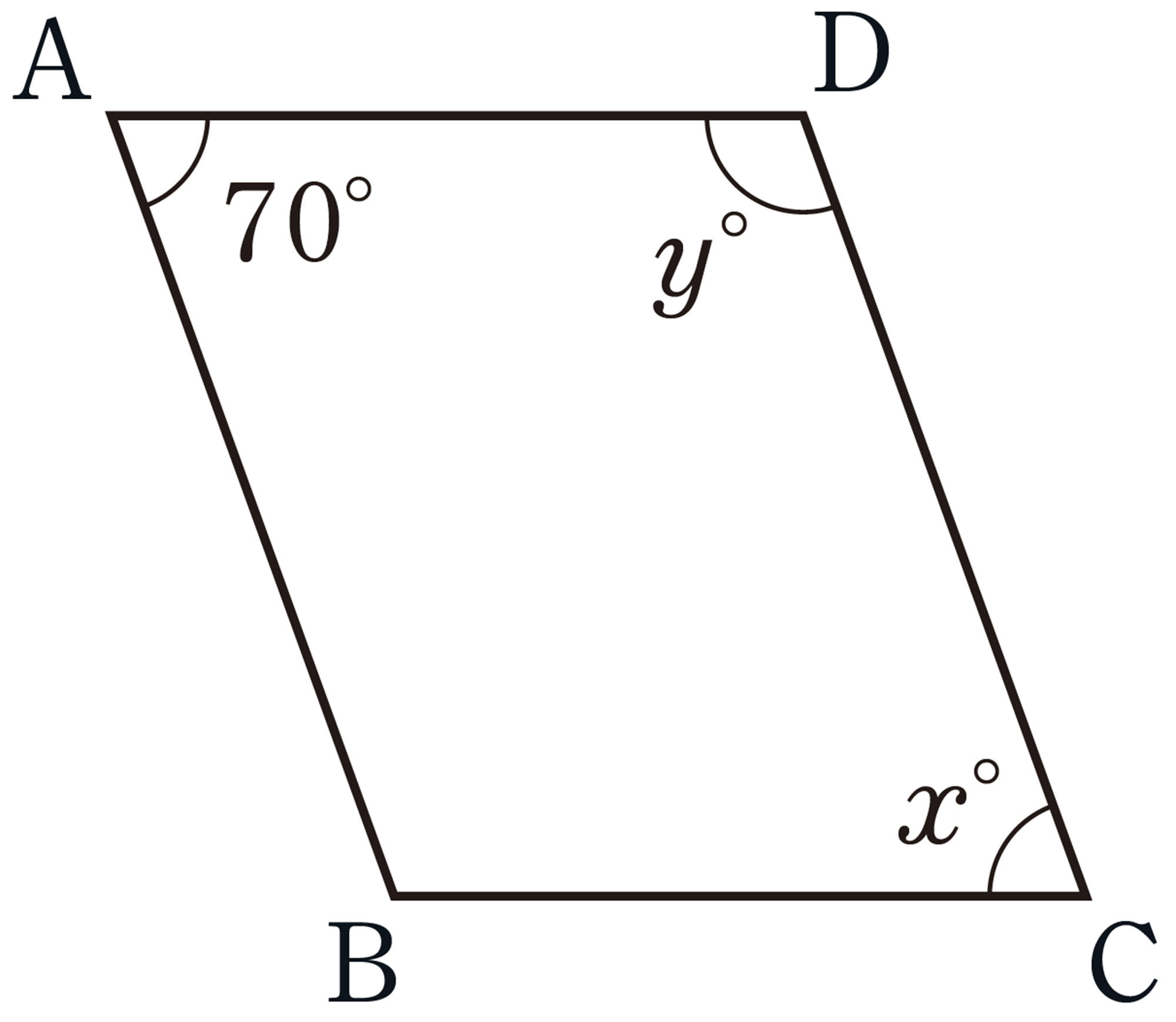
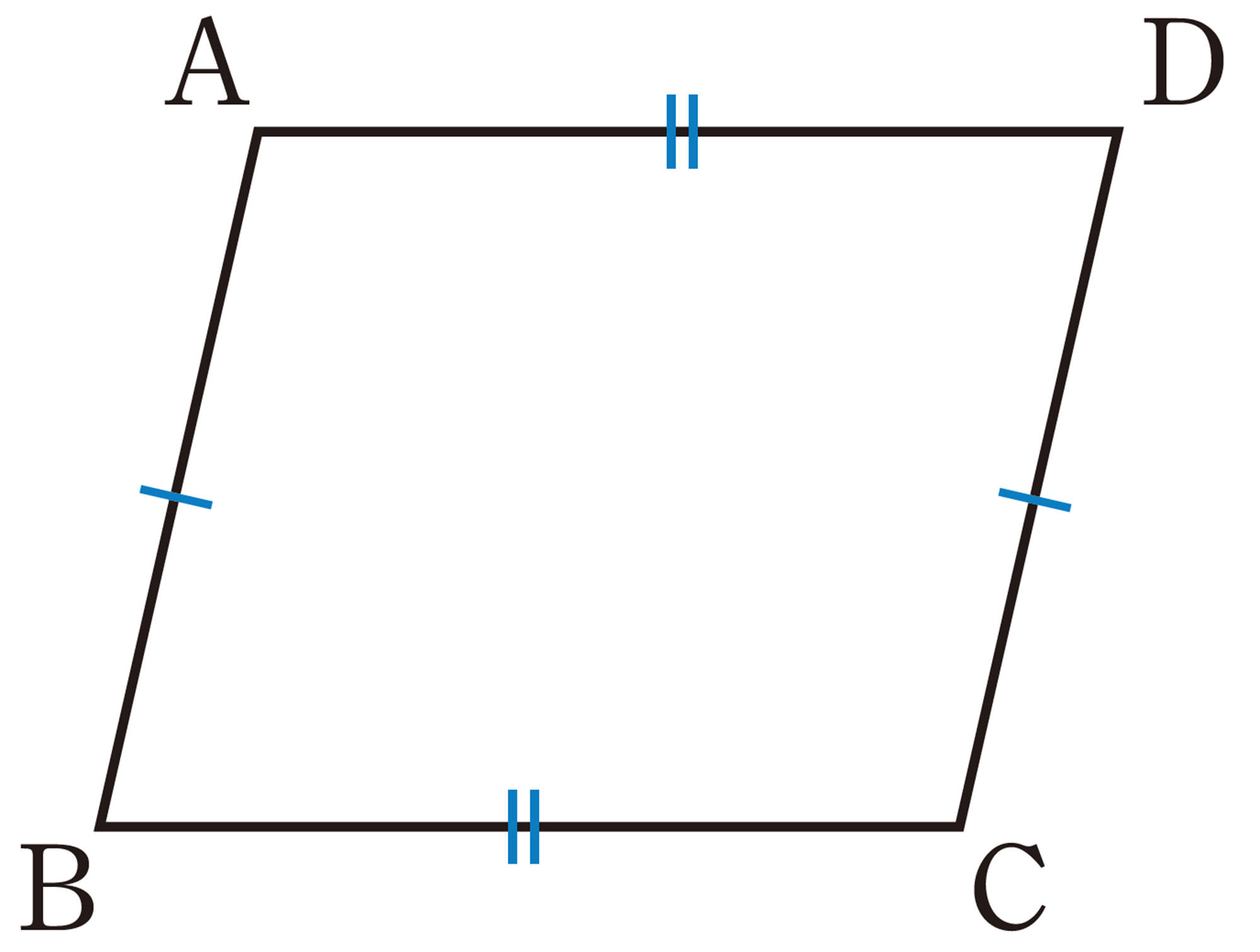
Q Question
<2年p.163>
目標 ▷ 特別な四角形として,平行四辺形の性質について調べよう。
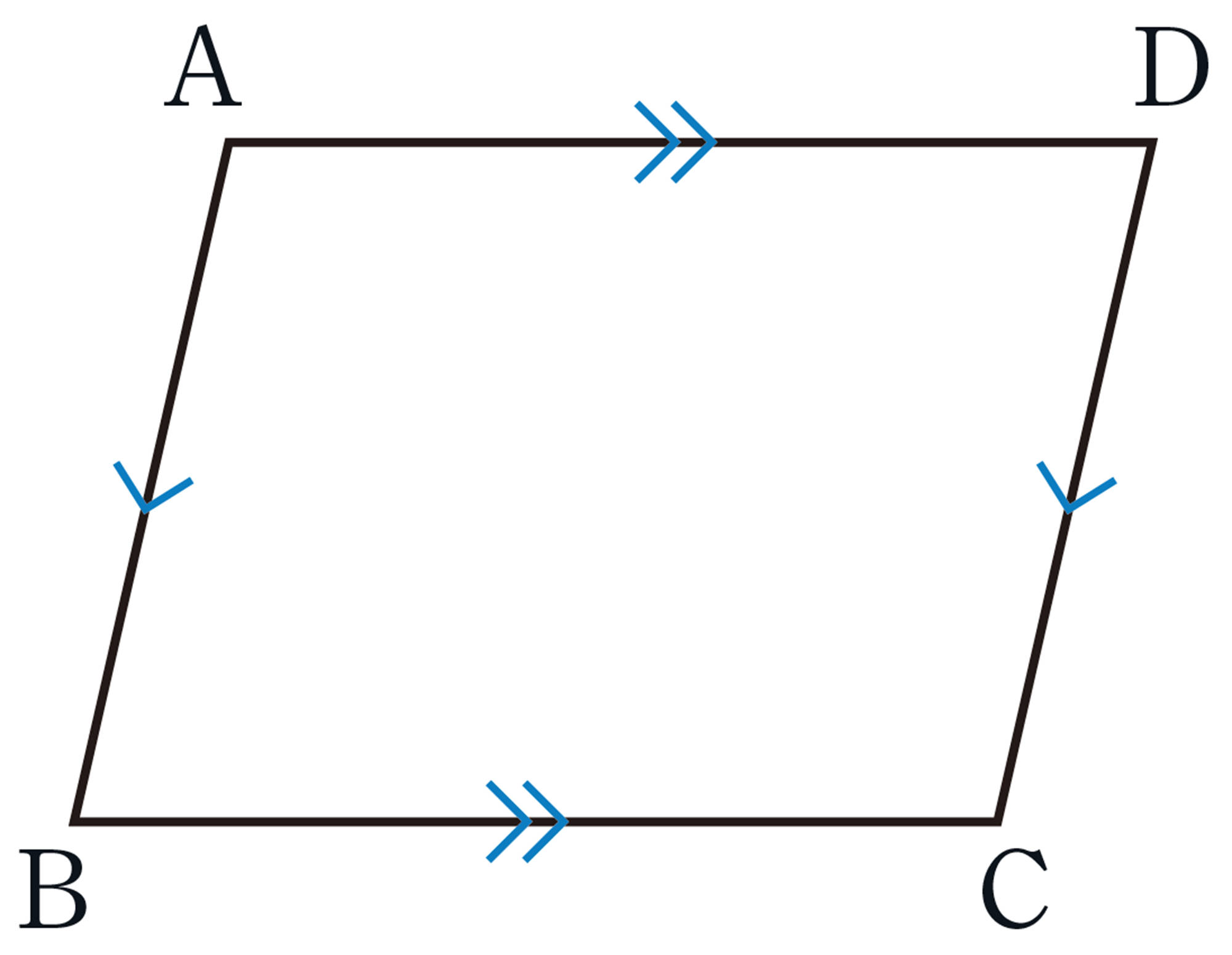
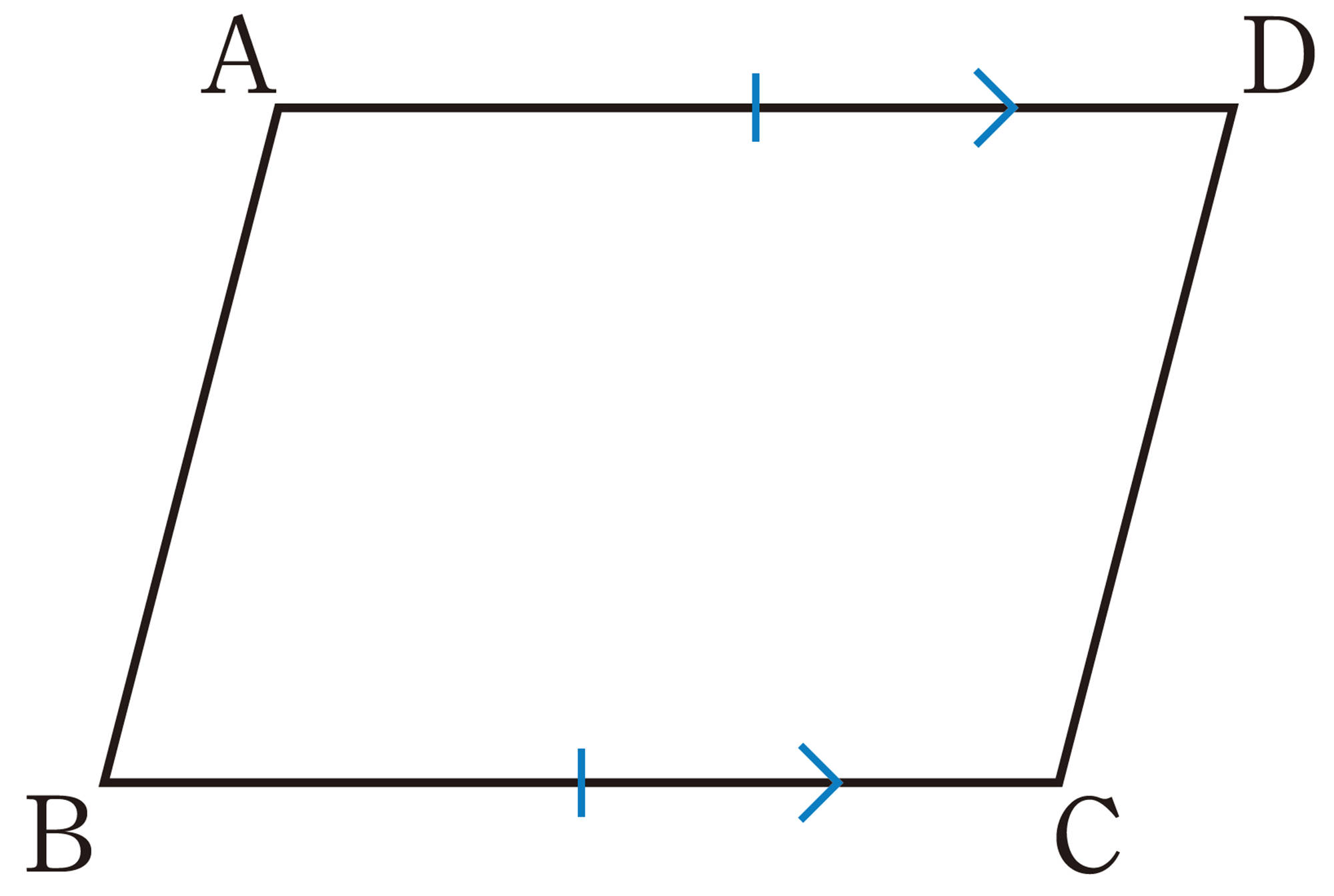
四角形の向かい合う辺を対辺,向かい合う角を対角という。平行四辺形は,次のように定義される。
平行四辺形[mathjax]\(ABCD\)を記号▱を使って▱ABCDと表し,「平行四辺形ABCD」と読む。
問 1 前ページの【Q】から,平行四辺形の辺や角,対角線には,それぞれどんな性質があるといえますか。
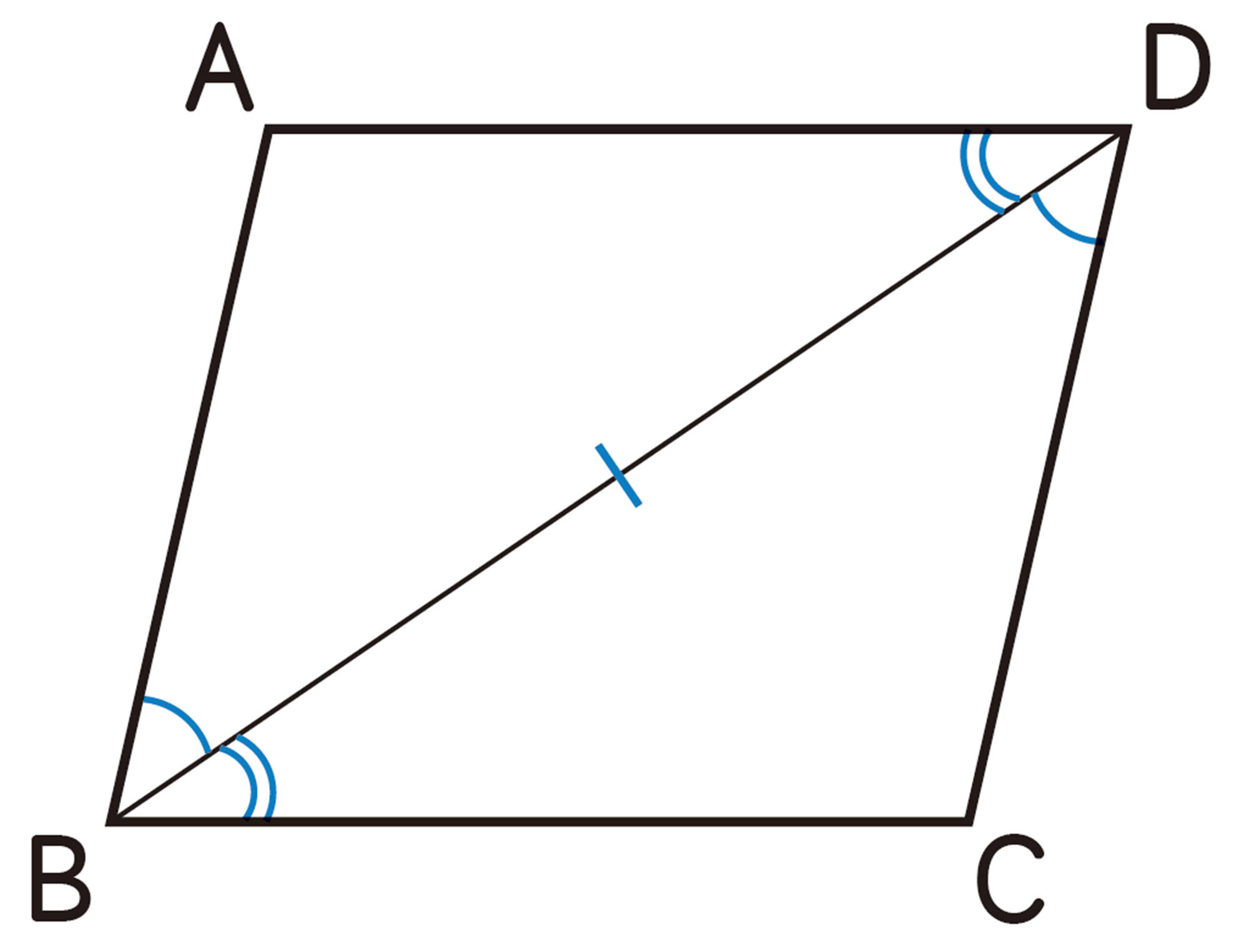
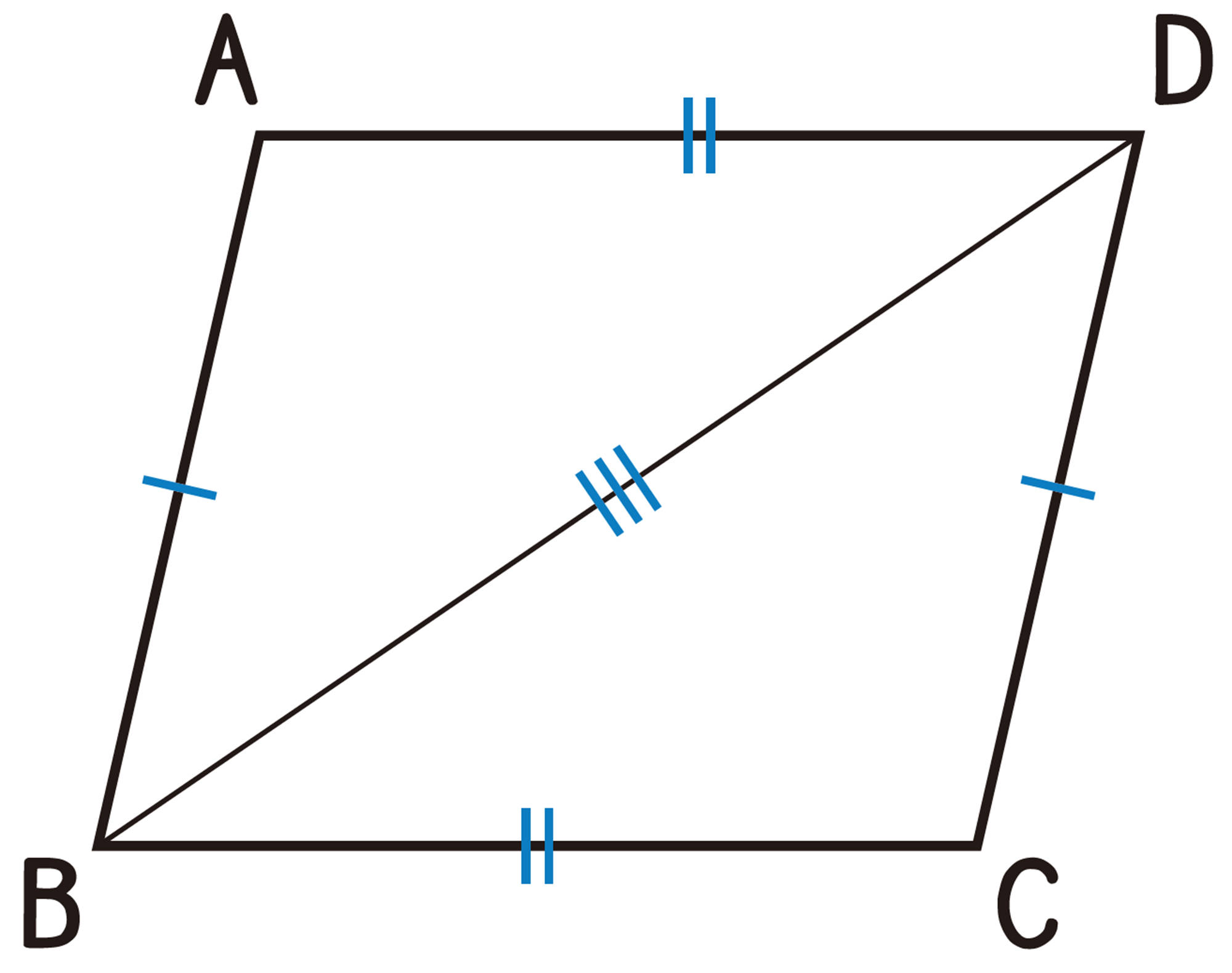
例 1 ▱ABCDで,[mathjax]\(AB=DC\),[mathjax]\(AD=BC\)であることを証明しなさい。
証明
対角線BD を引く。
[mathjax]\(\triangle ABD\) と[mathjax]\(\triangle CDB\)において,
平行線の錯角は等しいから,
[mathjax]\(AB/\!/DC\)より,[mathjax]\(\angle ABD=\angle CDB\cdots\cdots\text{①}\)
[mathjax]\(AD/\!/BC\)より,[mathjax]\( \angle ADB=\angle CBD\cdots\cdots\text{②}\)
また,[mathjax]\(\hspace{40pt}BD\)は共通[mathjax]\(\hspace{35pt}\cdots\cdots\text{③}\)
①, ②, ③より, 1 組の辺とその両端の角がそれぞれ等しいから,
[mathjax] \(\hspace{64pt}\triangle ABD\equiv \triangle CDB\)
したがって, [mathjax]\(AB=DC\),[mathjax]\( AD=BC\)
<2年p.164>
前ページの例1の証明の中で示された,[mathjax]\(\triangle ABD\equiv \triangle CDB\)から,[mathjax]\(\angle A=\angle C\)であることも導くことができる。
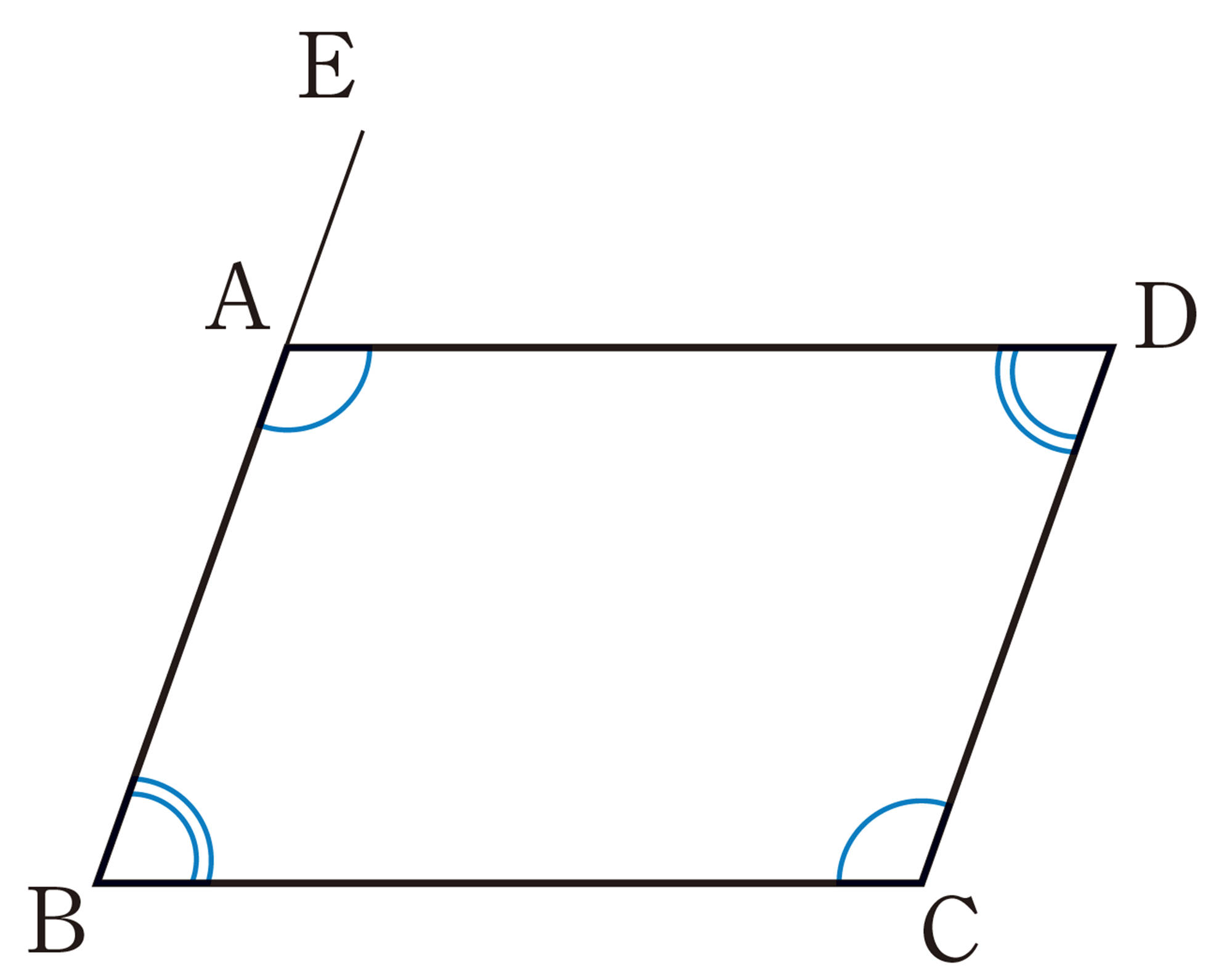
問 2 前ページの例1の▱ABCDで,[mathjax]\(\angle ABC=\angle CDA\)であることを証明しなさい。
これまで調べたことは,次のように,定理としてまとめることができる。
<2年p.165>
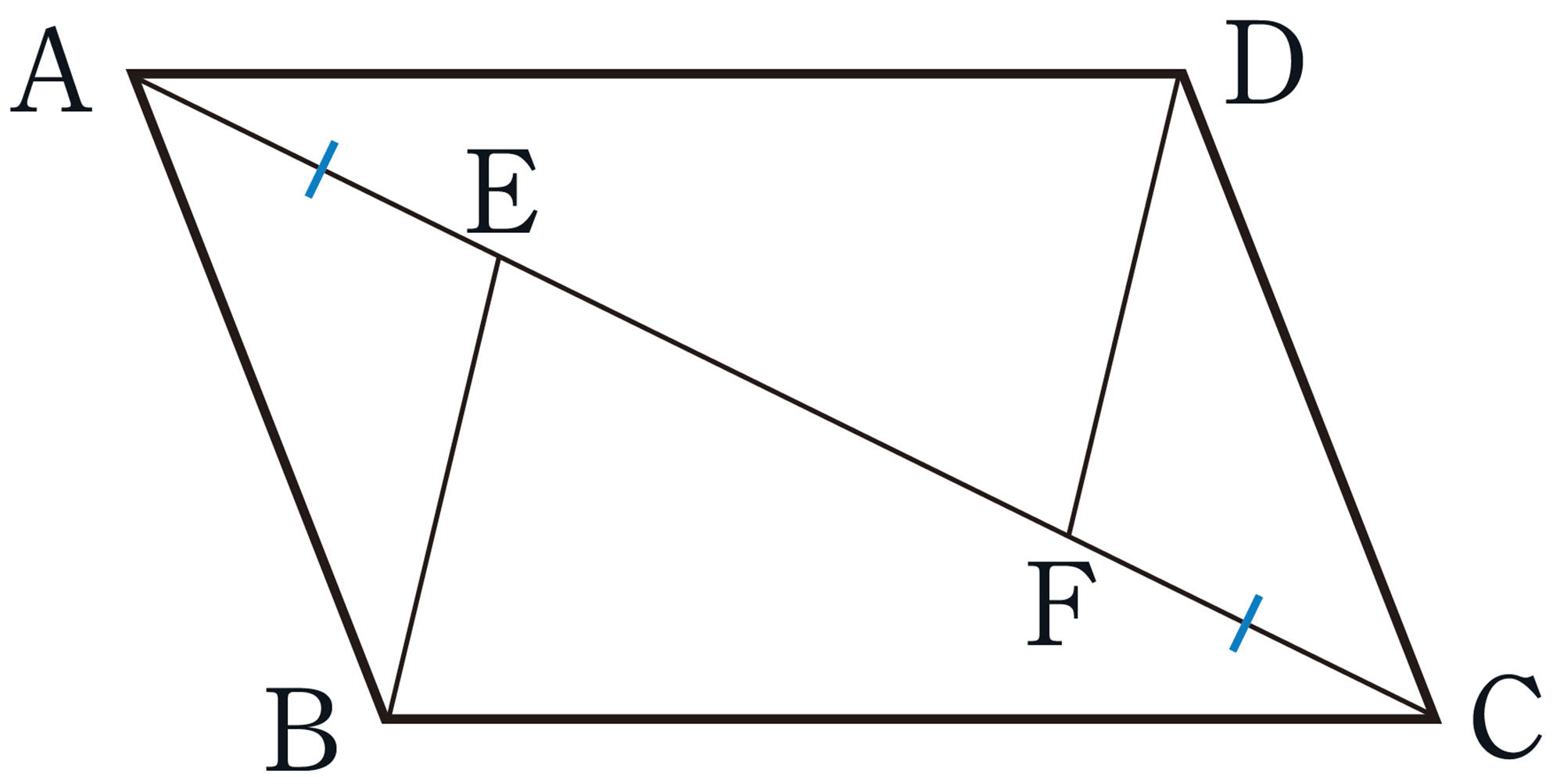
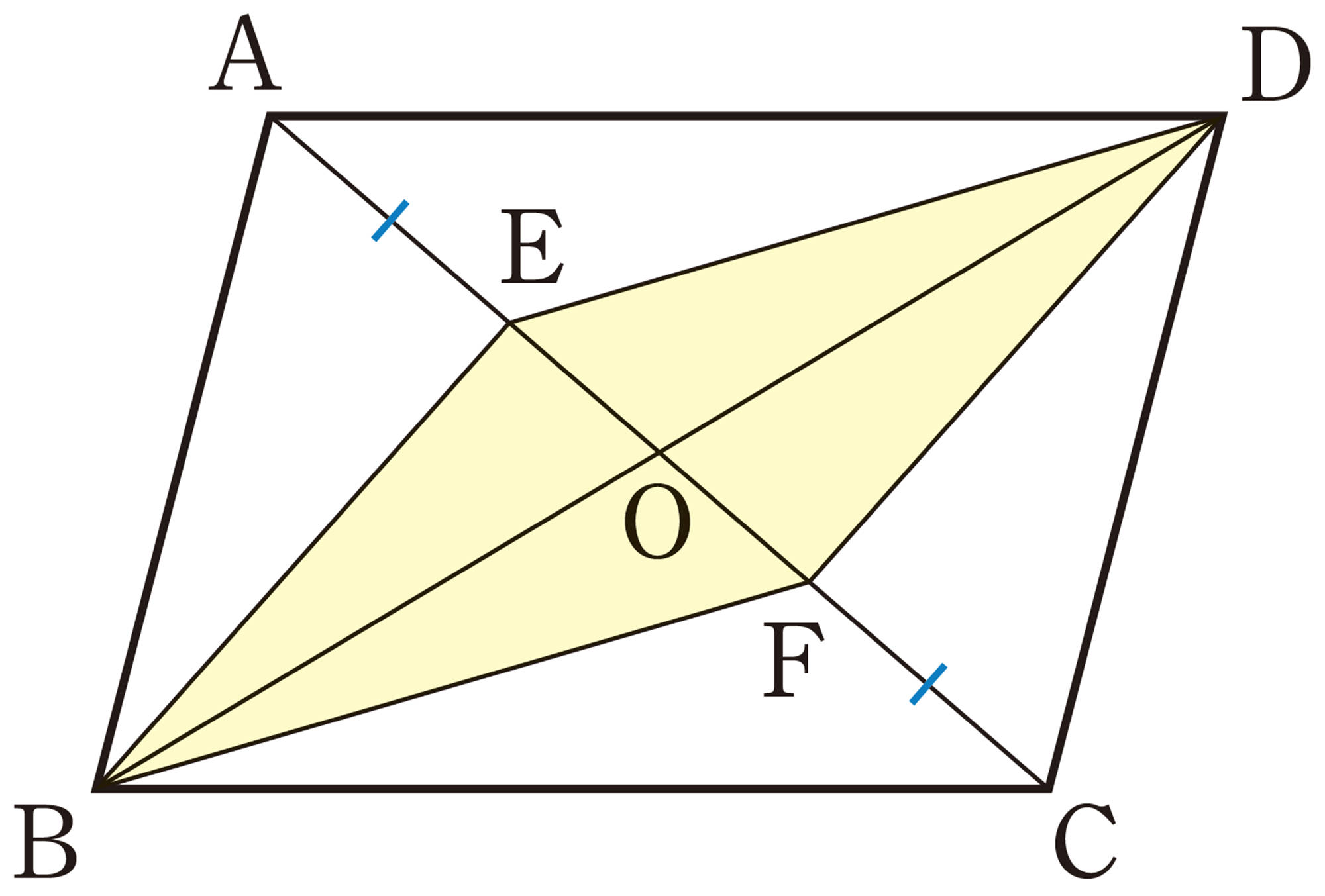
平行四辺形の性質を使って,図形の性質を証明してみよう。
証明
[mathjax]\(\triangle ABE\) と[mathjax]\(\triangle CDF\) において,
仮定から, [mathjax]\(\hspace{40pt}AE=CF\hspace{18pt}\cdots\cdots\text{①}\)
平行線の錯角は等しいから,
[mathjax]\(AB/\!/DC\) より, [mathjax]\(\angle BAE=\angle DCF \ \cdots\cdots\text{②}\)
平行四辺形の対辺は等しいから,
[mathjax]\(\hspace{82pt}AB = CD\hspace{18pt}\cdots\cdots\text{③}\)
①, ②, ③より, 2組の辺とその間の角がそれぞれ等しいから,
[mathjax] \(\hspace{66pt}\triangle ABE\equiv \triangle CDF\)
したがって, [mathjax]\(\hspace{30pt}BE=DF\)
問 5 例2で証明した[mathjax]\(\triangle ABE\equiv\triangle CDF\)から,[mathjax]\(BE=DF\)のほかにどんなことがわかりますか。また,その理由を説明しなさい。
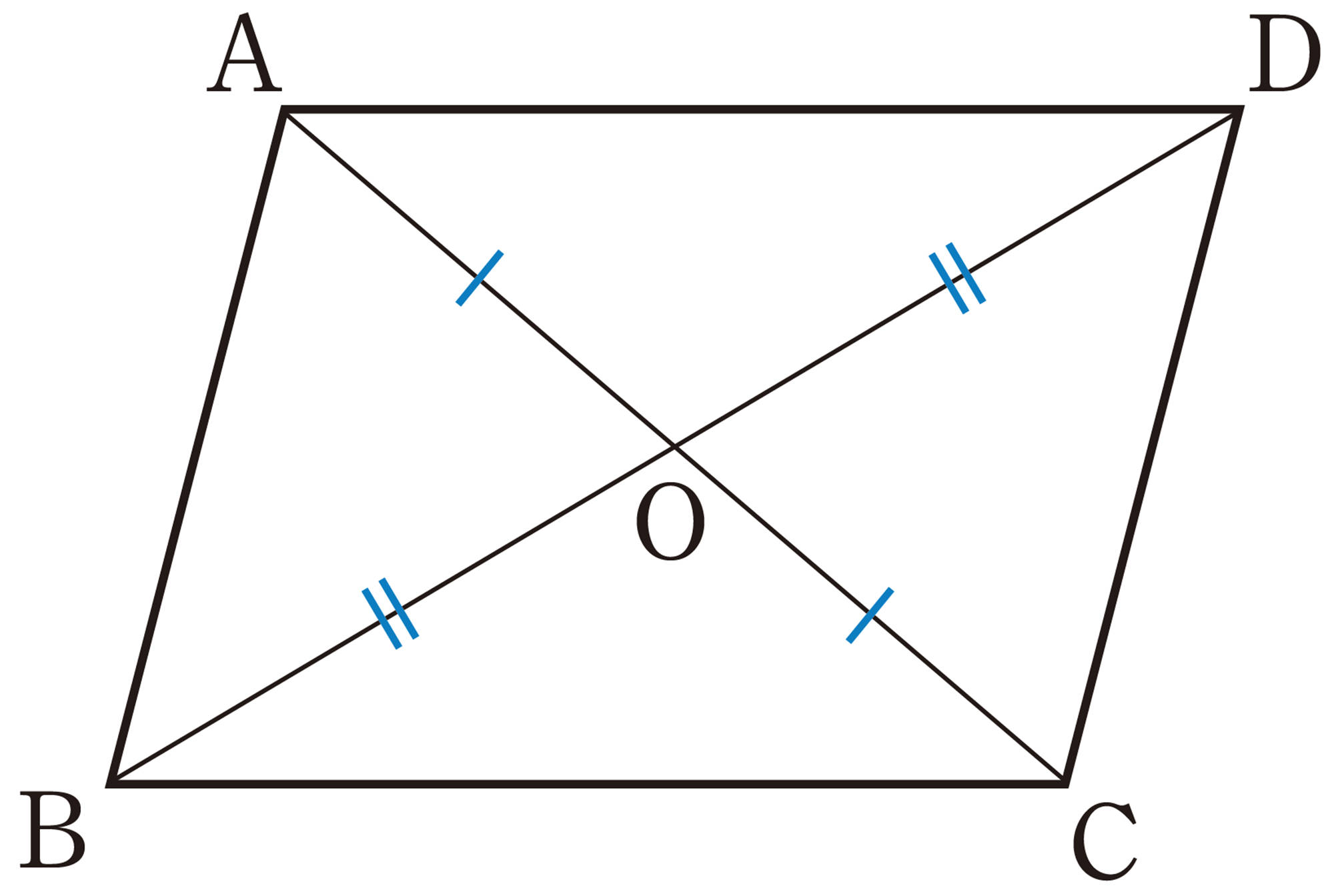
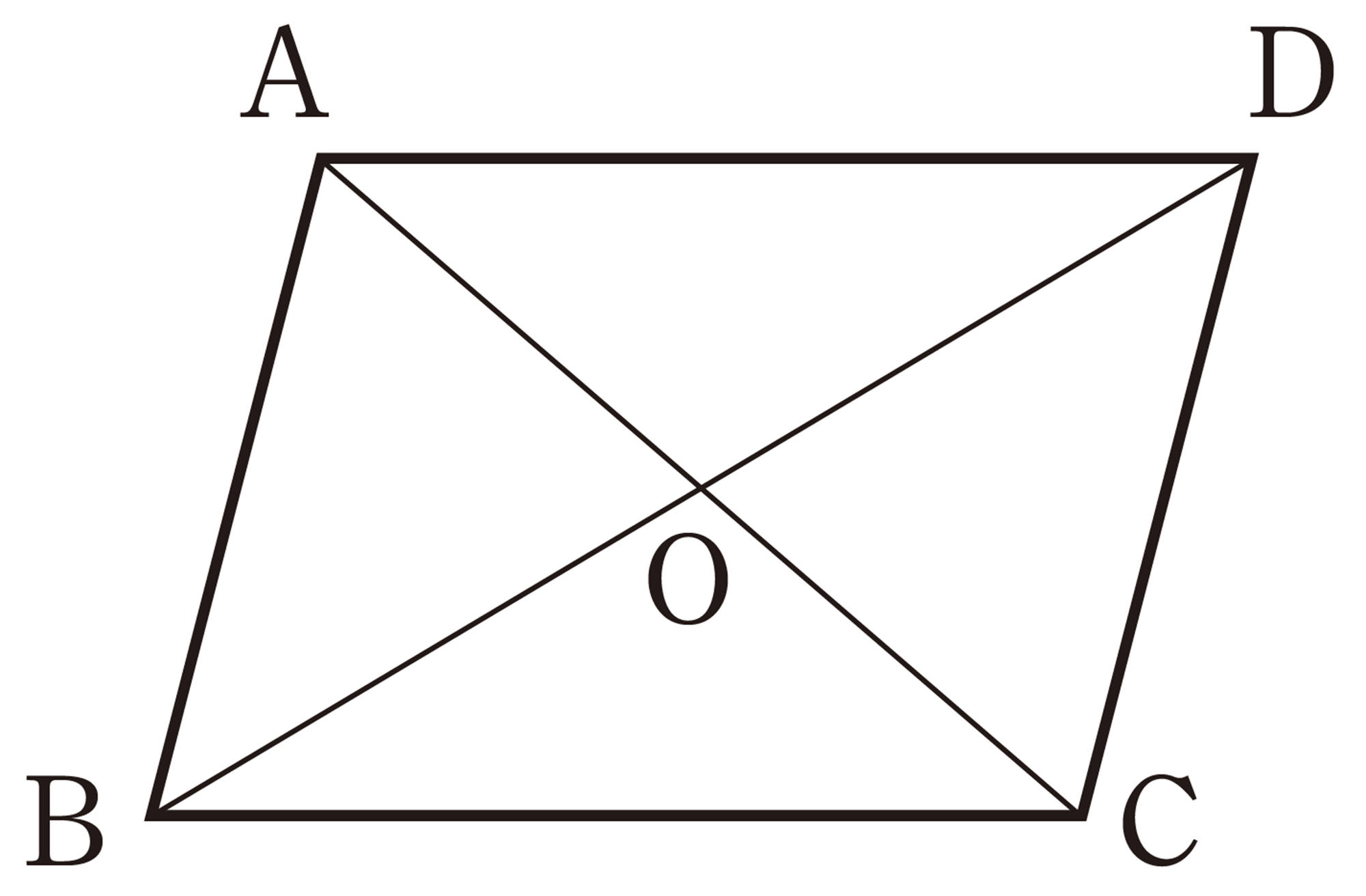
問 6 ▱ABCDの2つの対角線の交点Oを通る直線を引き,AD,BCとの交点をそれぞれP,Qとします。次の問いに答えなさい。
⑴ 図をかきなさい。
⑵ 線分POと長さの等しい線分はどれですか。
⑶ ⑵で調べたことがらを証明しなさい。
どんなことがわかったかな
三角形の合同条件を利用すると,平行四辺形の定義から,平行四辺形の性質を導くことができます。
次の課題へ!
どんな条件のときに平行四辺形になるといえるのかな?
P.166

<2年p.166>
2 平行四辺形になるための条件
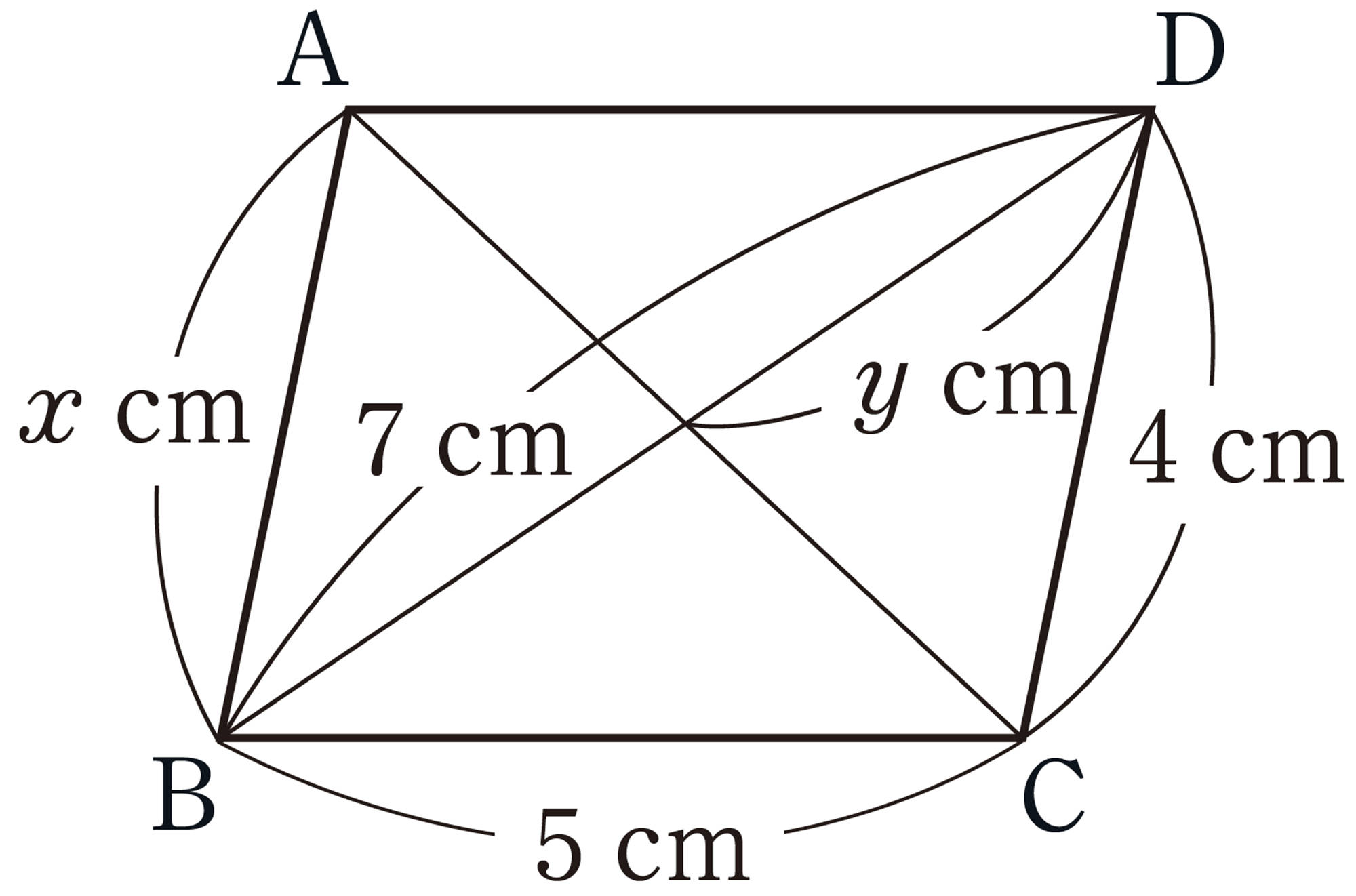
Q Question

ほんとうに,いつも平行なのかな。
対辺の長さは,それぞれ等しいね。

見方・考え方
根拠を明らかにして,説明できるかな。
目標 ▷ 四角形が,どんなときに平行四辺形になるといえるか考えよう。
<2年p.167>
考え方 錯角が等しければ,2直線は平行であることを利用する。錯角が等しいことをいうために,補助線として対角線BDを引き,[mathjax]\(\triangle ABD\)と[mathjax]\(\triangle CDB\)が合同であることを証明する。
証明
対角線BD を引く。
[mathjax]\(\triangle ABD\)と[mathjax]\(\triangle CDB\)において,
仮定から,[mathjax]\(\hspace{40pt}AB=CD\quad\cdots\cdots\text{①}\)
[mathjax]\(\hspace{81pt}AD=CB\quad\cdots\cdots\text{②}\)
また,[mathjax]\(\hspace{54pt}BD\)は共通[mathjax]\(\hspace{17pt}\cdots\cdots\text{③}\)
①, ②, ③より, 3 組の辺がそれぞれ等しいから,
[mathjax]\(\hspace{60pt}\triangle ABD\equiv \triangle CDB\)
したがって,[mathjax]\(\hspace{10pt}\angle ABD=\angle CDB\)
錯角が等しいから,[mathjax]\(AB/\!/DC\)
同様にして,[mathjax]\(\hspace{24pt}AD/\!/BC\)
注意 例1の証明で,「同様にして」というのは,前に述べたことと同じ手順で証明できるという意味である。
例1の証明は,平行四辺形の性質❶の逆になっているね。ほかの性質の逆も正しいのかな。

<2年p.168>
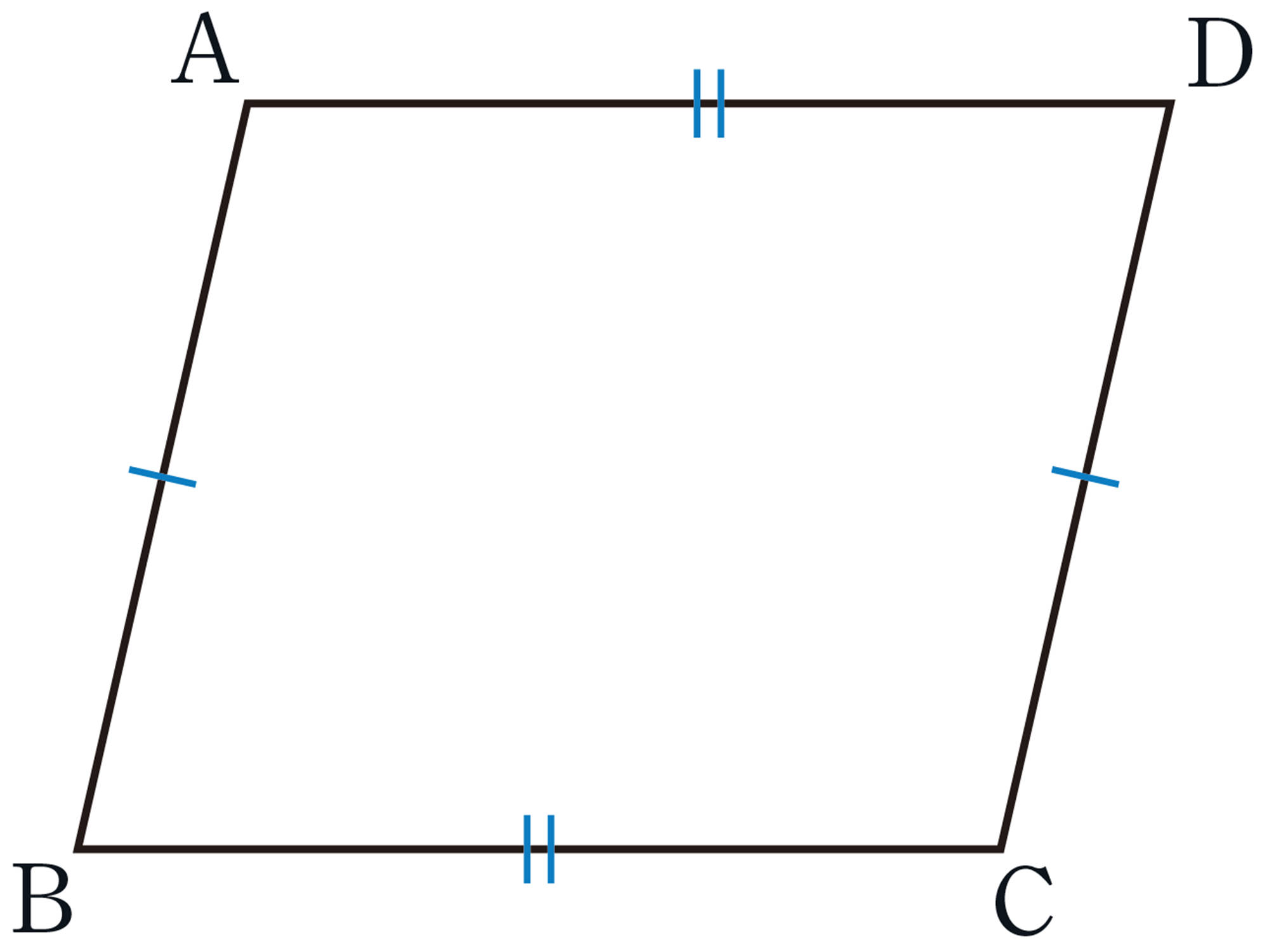
これまで調べたことは,次のようにまとめることができる。
平行四辺形になるための条件
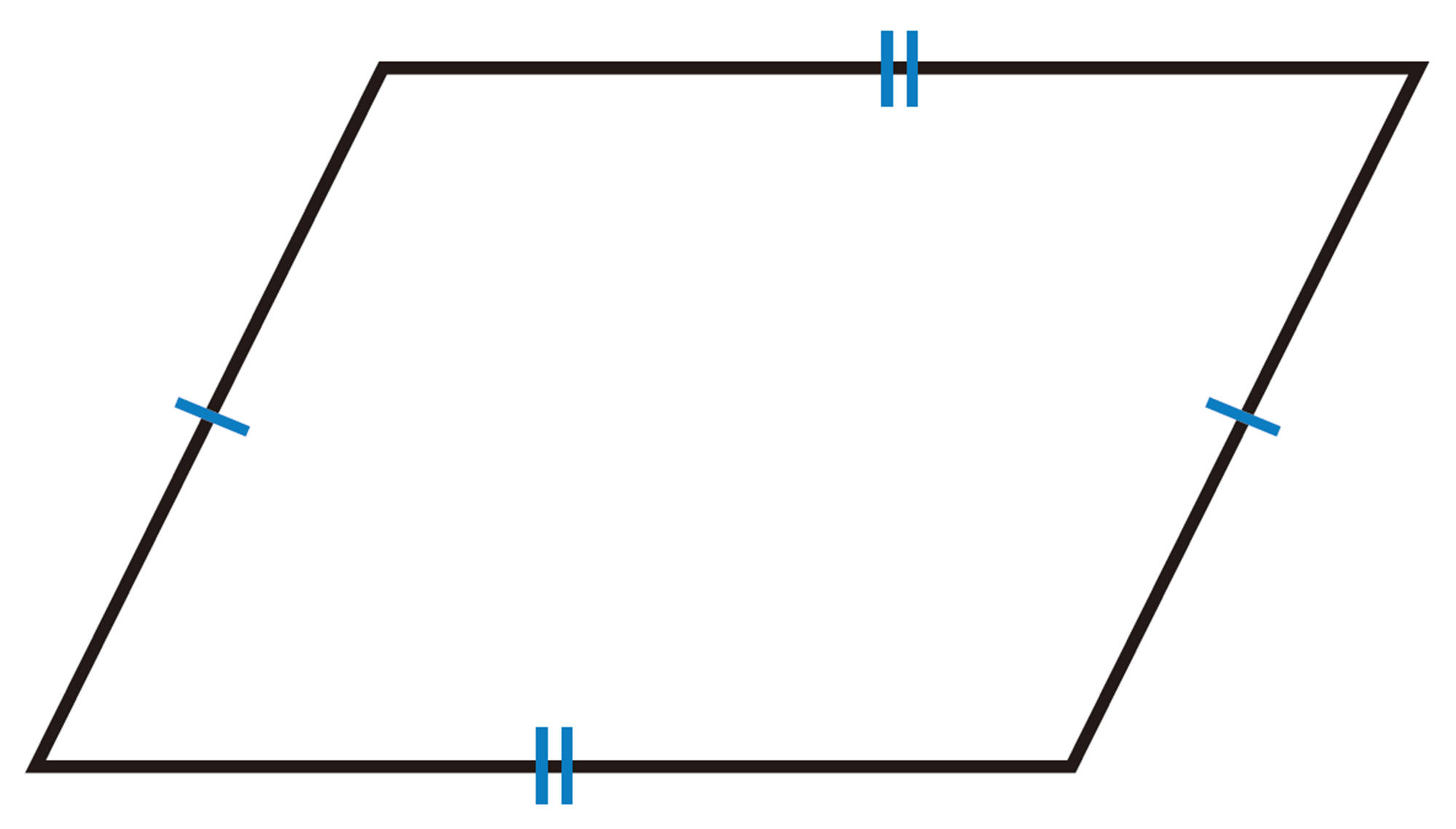
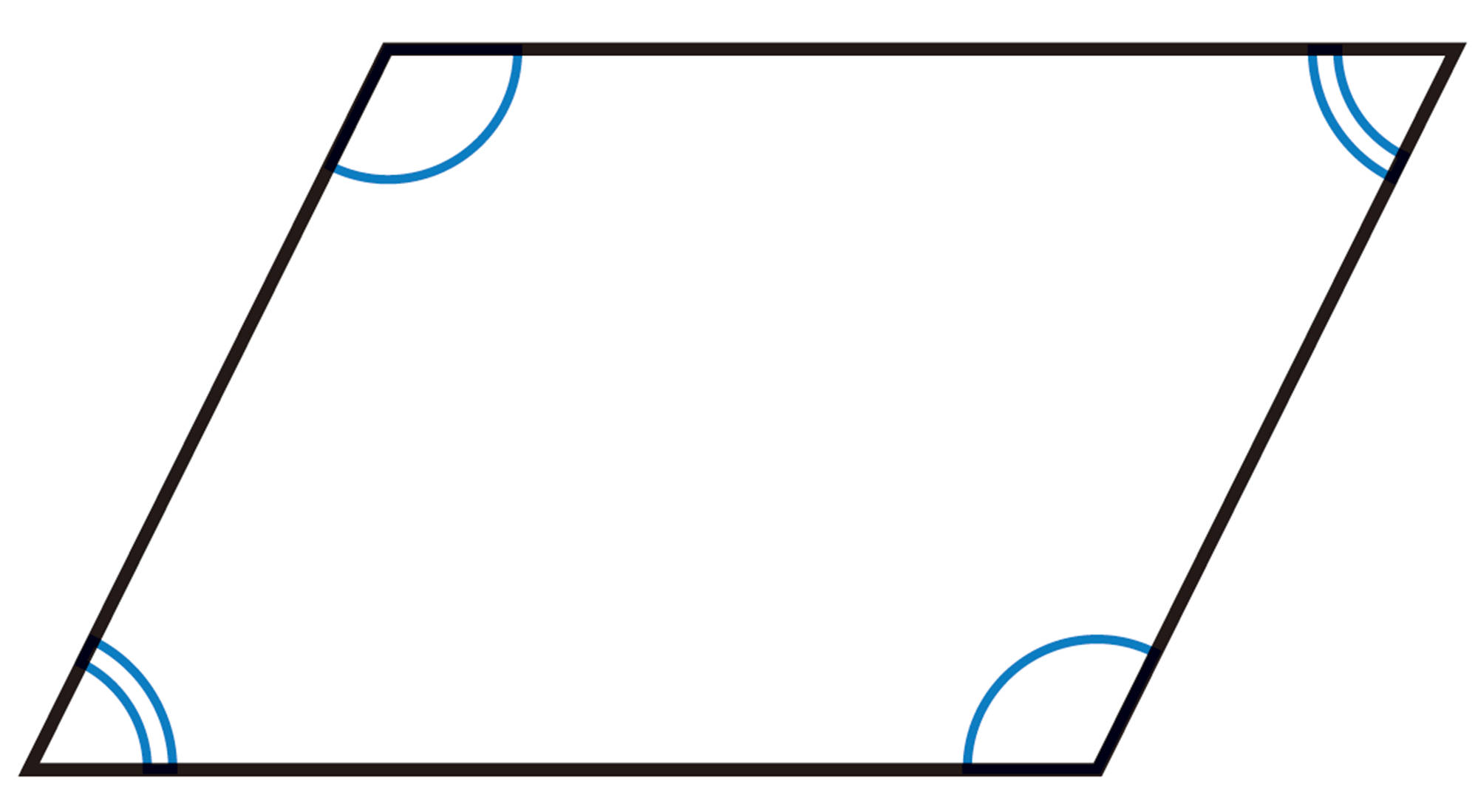
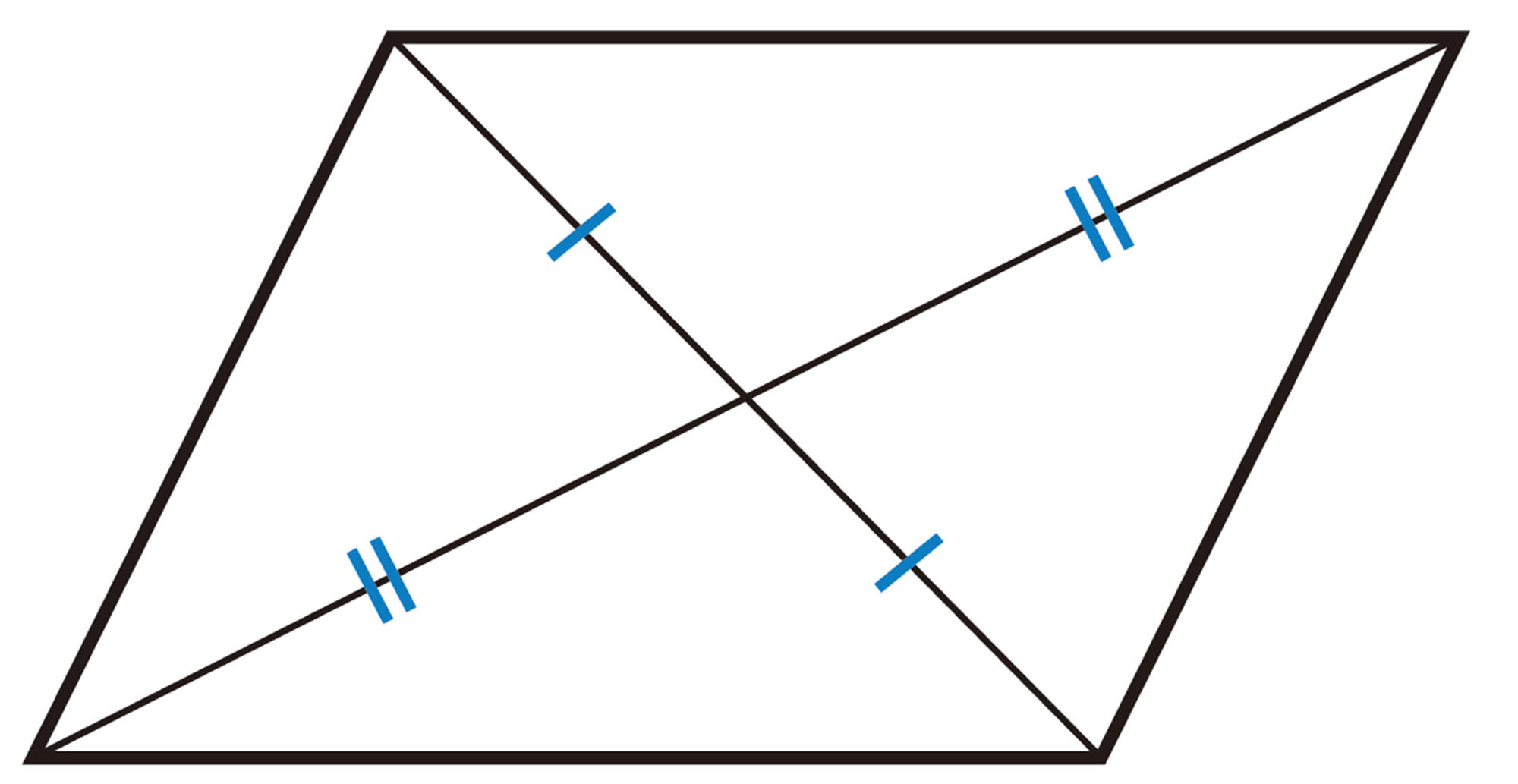
四角形は,次のどれか1つが成り立てば,平行四辺形である。
<2年p.169>
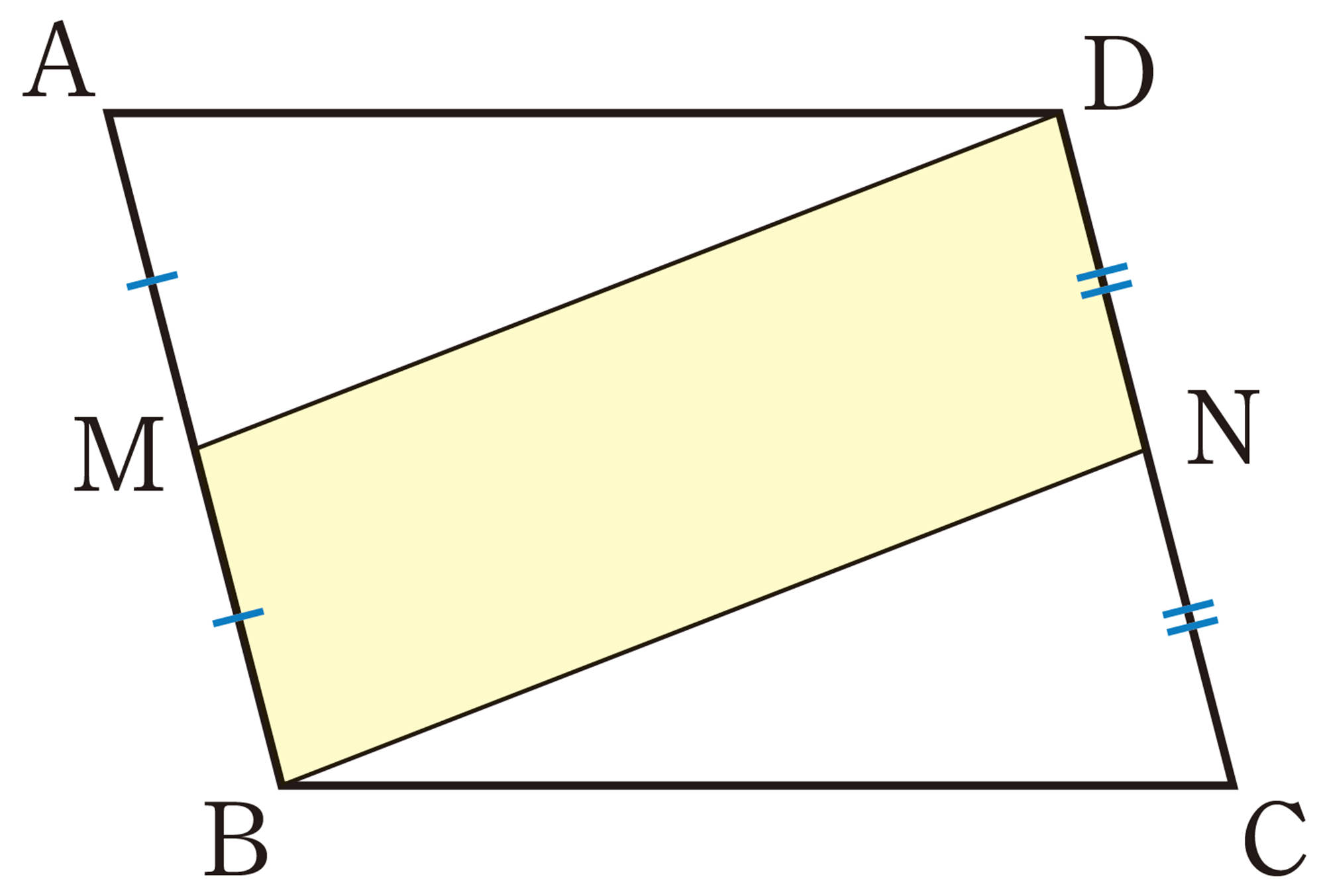
平行四辺形になるための条件を使って,いろいろな問題を考えてみよう。
証明
2つの対角線の交点をOとする。
平行四辺形の2つの対角線はそれぞれの中点で交わるから,
[mathjax]\(\hspace{78pt}BO=DO\quad\cdots\cdots\text{①}\)
[mathjax]\(\hspace{78pt}AO=CO\quad\cdots\cdots\text{②}\)
仮定から, [mathjax]\(\hspace{34pt}AE=CF\quad\cdots\cdots\text{③}\)
②, ③から,[mathjax]\(AO-AE=CO-CF\)
[mathjax]\(EO=AO-AE\), [mathjax]\(FO=CO-CF\) であるから,
[mathjax]\(\hspace{76pt}EO=FO\quad\cdots\cdots\text{④}\)
①, ④より, 2つの対角線がそれぞれの中点で交わるから,
四角形EBFDは平行四辺形である。