<2年p.147>
５章 Chapter ５ 三角形・四角形
1節 三角形
2節 四角形
小学校のとき，いろいろな図形の性質を学んだね。
二等辺三角形の2つの角は等しかったね。
平行四辺形では，向かい合う辺の長さが等しいと学んだよ。
今まで学んだ図形の性質も証明できるのかな。
？ いろいろな図形の性質を証明できるかな？
<2年p.148>
1節 三角形
どんな図形ができるかな？
ふせんを折ったとき，重なった部分は，どんな図形になるでしょうか。
【１】 1枚のふせんを，下の写真のように折って重ねます。重なった部分は，どんな図形になるでしょうか。
重なった部分が三角形になる場合について調べてみよう。
ほかには，どんな三角形ができるかな。
二等辺三角形以外の三角形には，ならないのかな。
どれも二等辺三角形に見えるね。
次の課題へ！
重なった部分の形は，いつでも二等辺三角形になるのかな？
P.149
<2年p.149>
１ 二等辺三角形
二等辺三角形の性質
Q Question
二等辺三角形とは，どんな三角形といえばよいでしょうか。
また，二等辺三角形について，どんなことを知っていますか。
2つの角が等しいことは，小学校で確かめたよ。
どんな二等辺三角形でも成り立つかどうかは，証明する必要があるんじゃないかな。
見方・考え方
根拠を明らかにして，説明できるかな。
目標 ▷ 二等辺三角形や正三角形の性質について調べよう。
用語の意味をはっきり述べたものを，その用語の定義という。定義も証明の根拠として用いることができる。
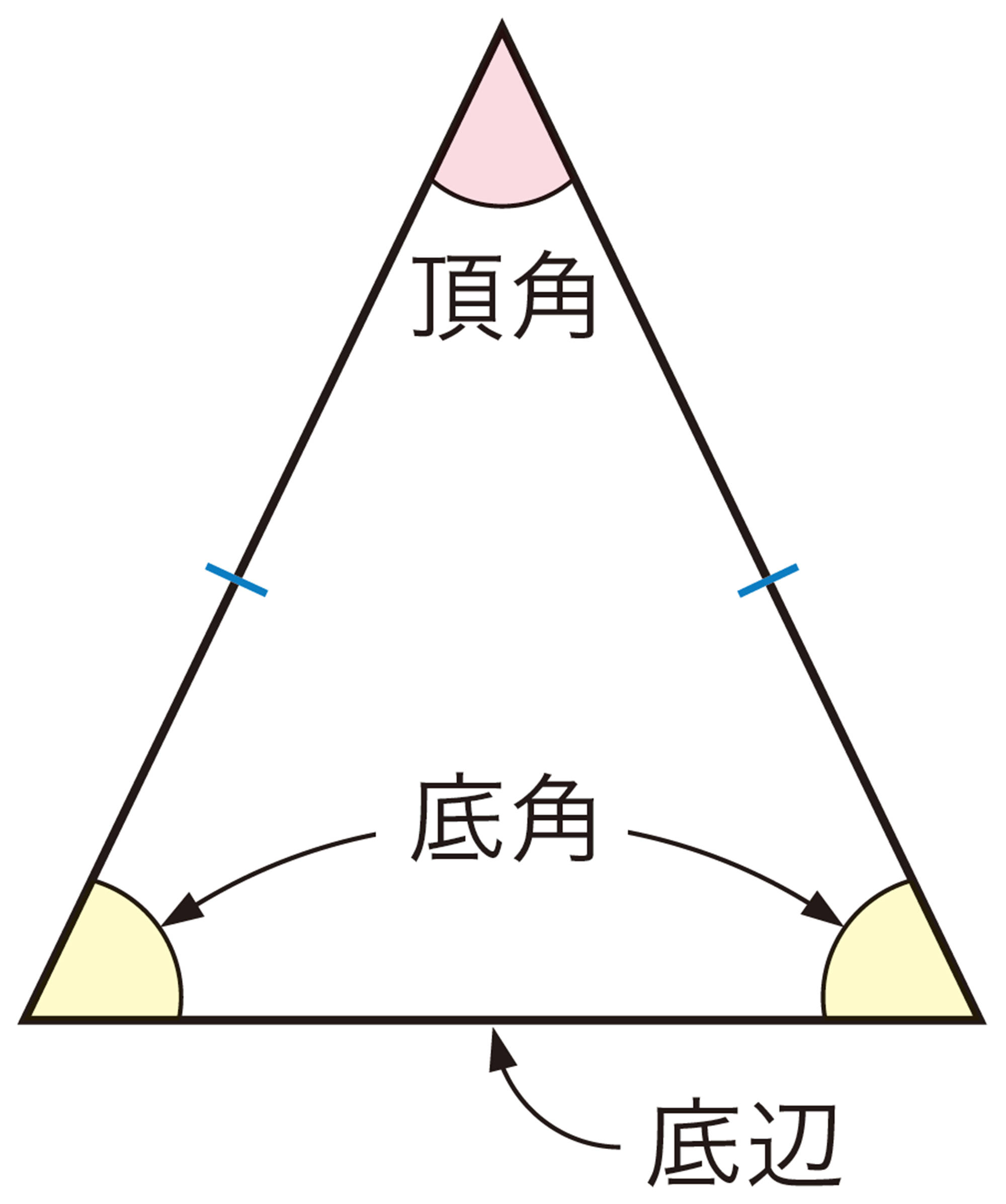
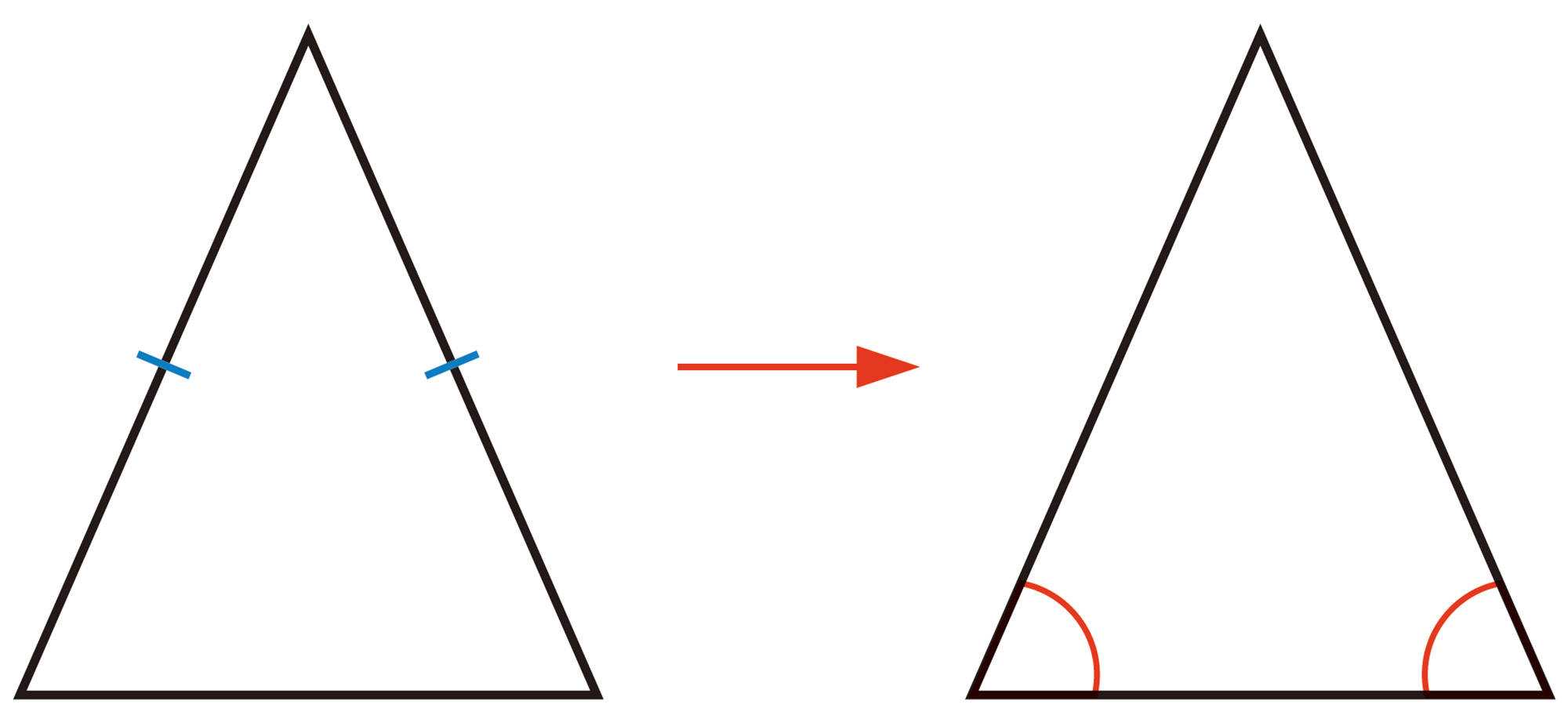
二等辺三角形は，次のように定義される。
定義 2つの辺が等しい三角形を二等辺三角形という。
図形の名前がそのまま定義になっているね。
二等辺三角形で，長さの等しい2つの辺がつくる角を頂角，頂角に対する辺を底辺，底辺の両端の角を底角という。
<2年p.150>
小学校では，二等辺三角形の紙を2つに折って重ねたり，角度を測ったりすることで，二等辺三角形の2つの底角が等しいことを調べた。
しかし，この方法では，すべての二等辺三角形について，2つの底角が等しいことを確かめることはできない。
どんな二等辺三角形でもつねに2つの底角が等しいことを証明してみよう。
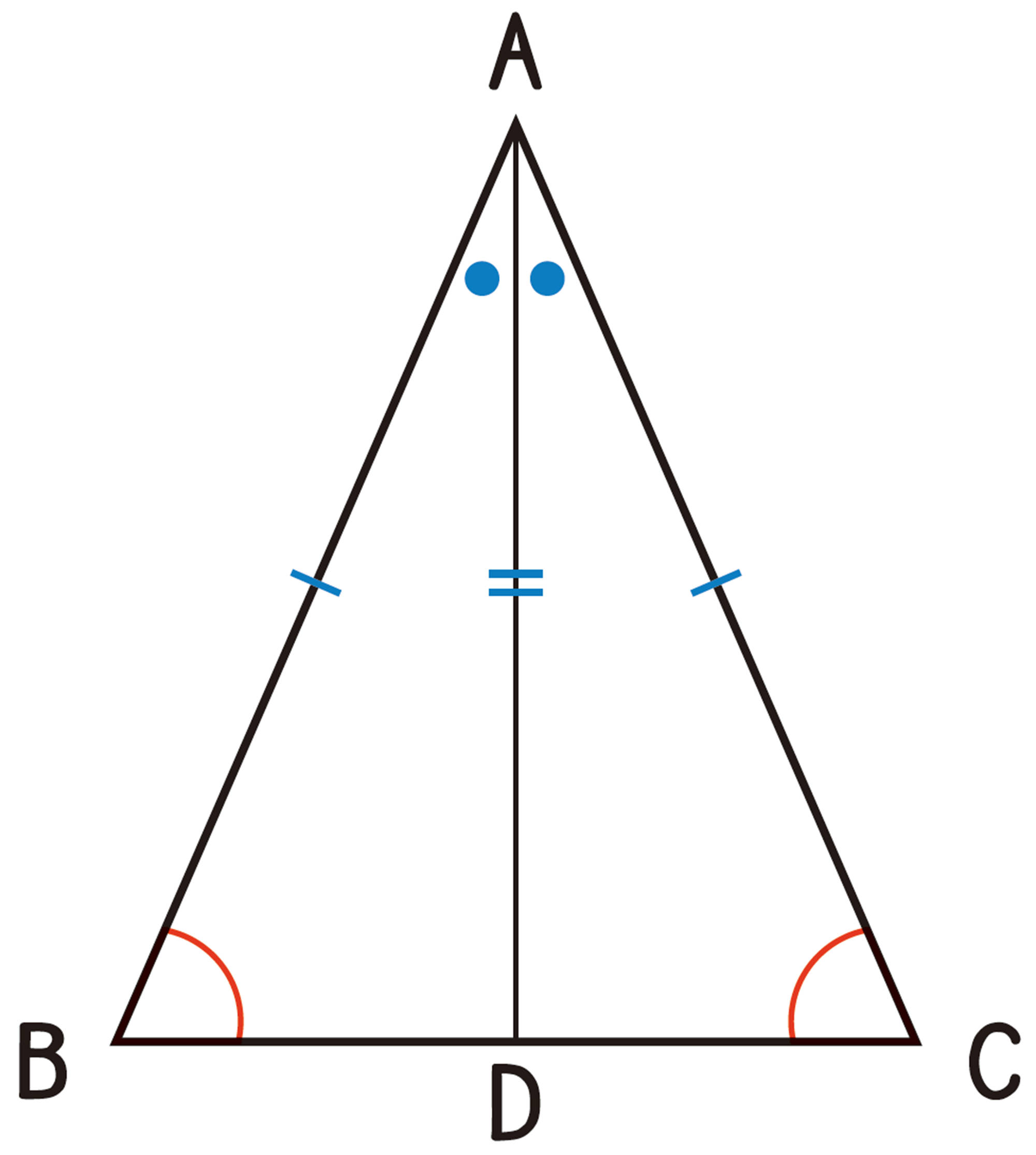
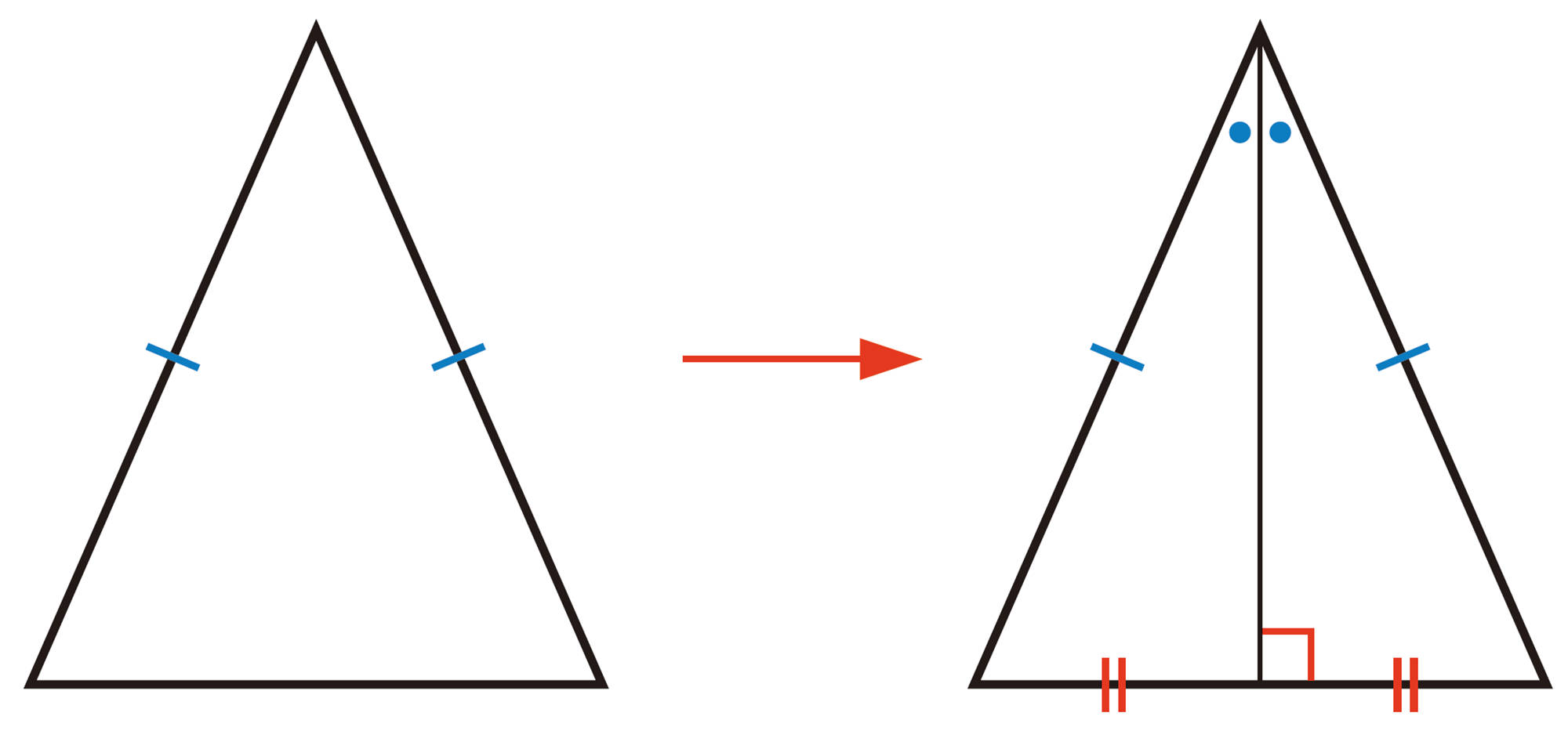
例 １ [mathjax]\(\triangle ABC\) において，[mathjax]\(AB=AC\) ならば，[mathjax]\(\angle B=\angle C\) であることを証明しなさい。
考え方 [mathjax]\(\angle B=\angle C\) を導くために，2つの角が対応する角となるような合同な三角形を見つければよい。そのために，[mathjax]\(\angle A\) の二等分線を引いて，2つの三角形に分けて考える。
証明
[mathjax]\(\angle A\) の二等分線を引き， 辺BCとの交点をDとする。
[mathjax]\(\triangle ABD\) と[mathjax]\(\triangle ACD\)において，
①，②，③より， 2組の辺とその間の角がそれぞれ等しいから [mathjax] \(\triangle ABD \equiv \triangle ACD\)
したがって， [mathjax]\(\angle B=\angle C\)
[mathjax]\(\angle A\) が鈍角でも同じように証明できるかな。
注意 上の証明の③は，「ADは共通」と表してもよい。
例1の証明によって，どんな二等辺三角形でもつねに2つの底角が等しいことが゙示された。このように，正しいことが証明されたことがらのうち，証明の根拠として，特によく利用されるものを【定理】という。
<2年p.151>
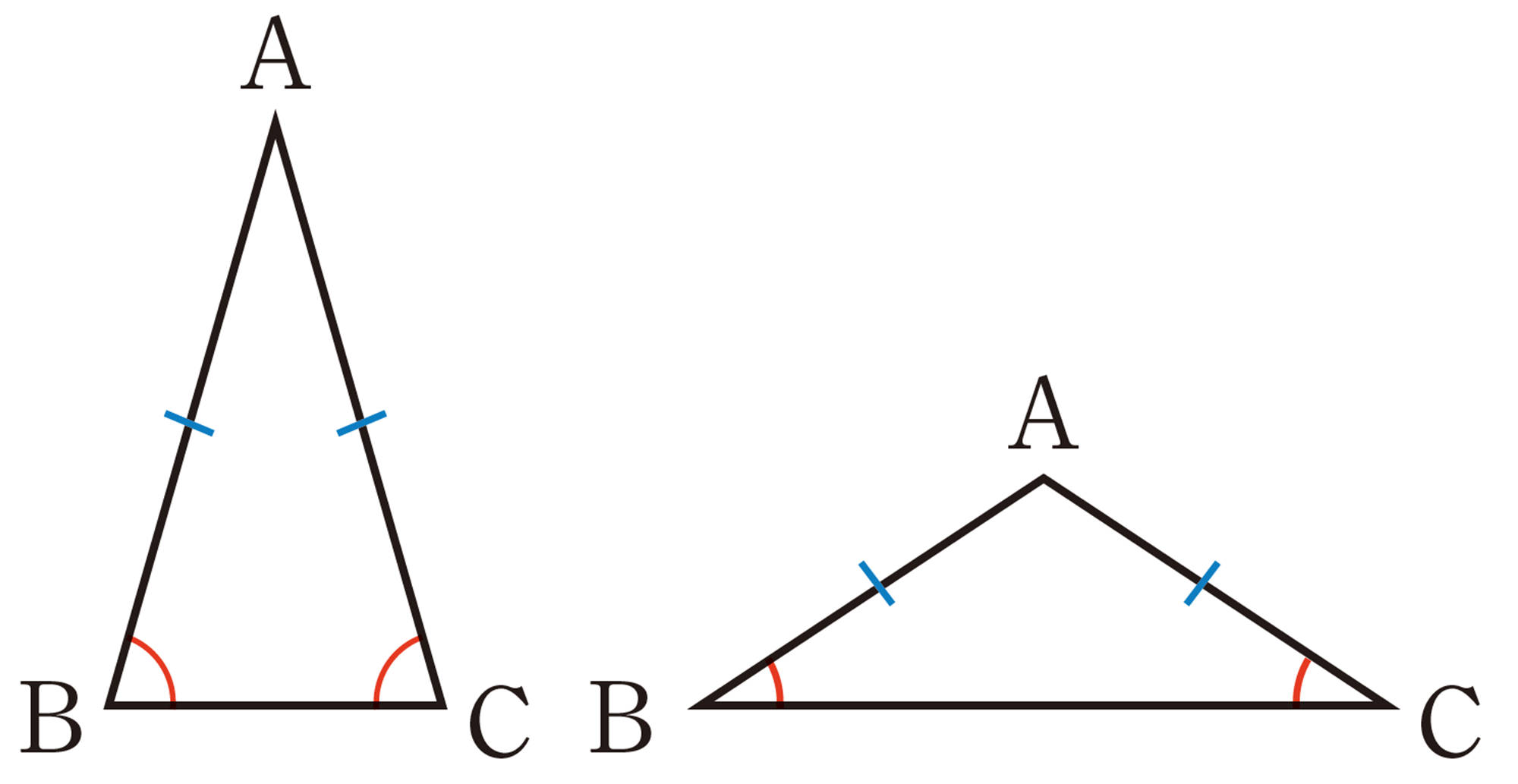
前ページの例1で証明したことは，次のように，定理としてまとめることができる。
定理
二等辺三角形の底角
二等辺三角形の2つの底角は等しい。
111ページの「対頂角の性質」や117ページの「三角形の角の性質」なども，定理として利用することができる。
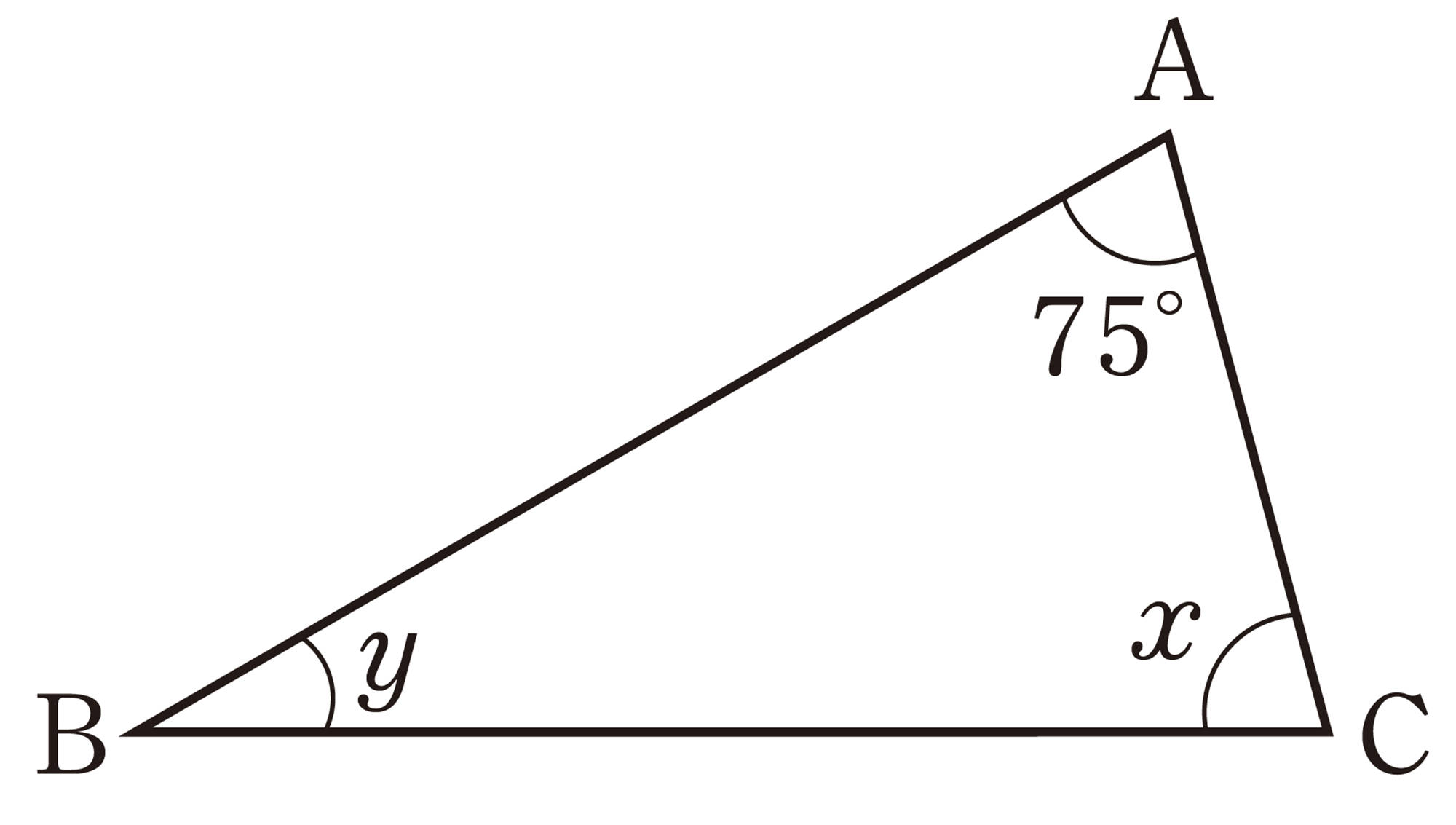
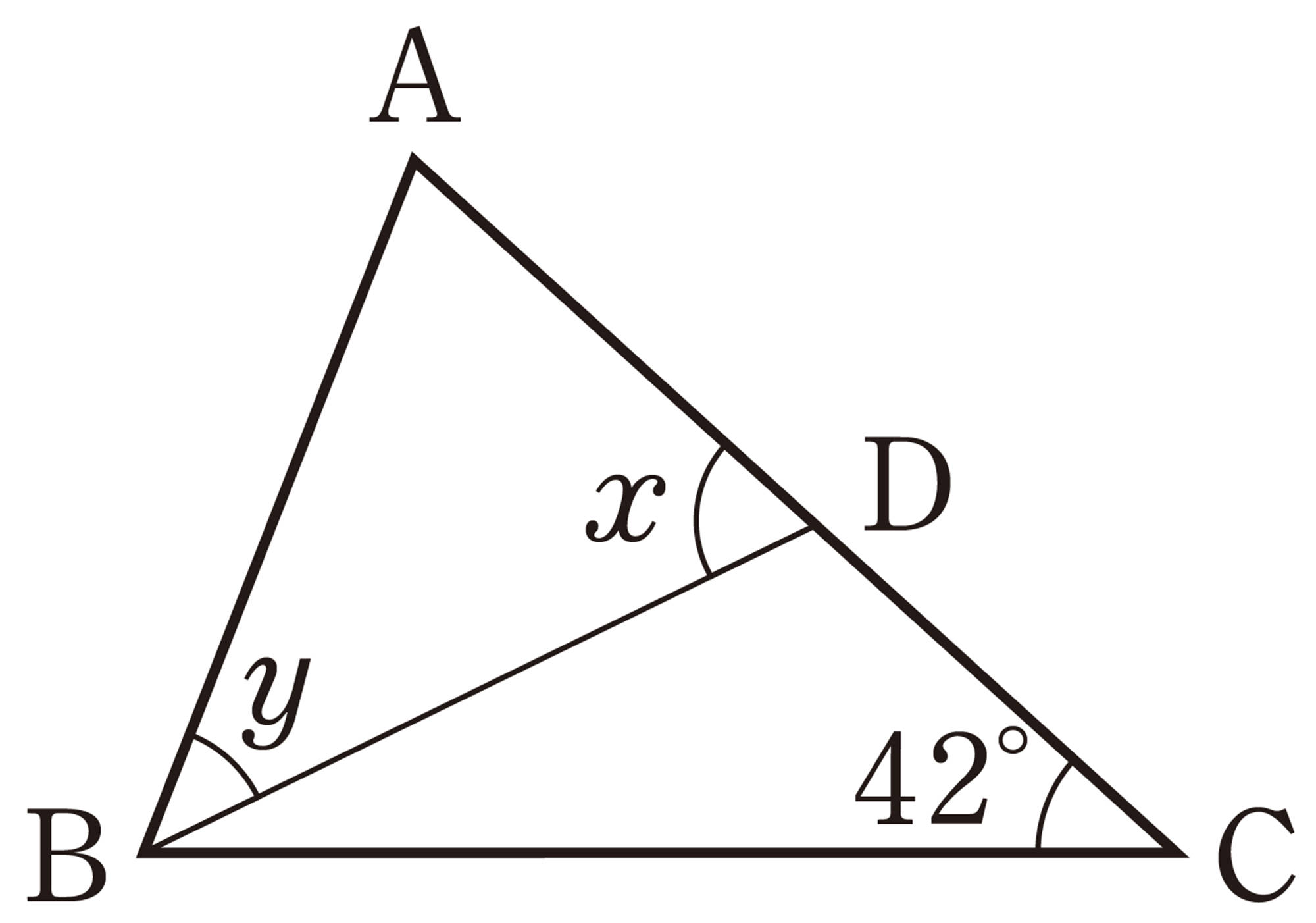
問 １ 次の図で，[mathjax]\(\angle x\)，[mathjax]\(\angle y\)の大きさを求めなさい。
⑴ [mathjax]\(BA=BC\)
⑵ [mathjax]\(CB=CA\)，[mathjax]\(BA=BD\)
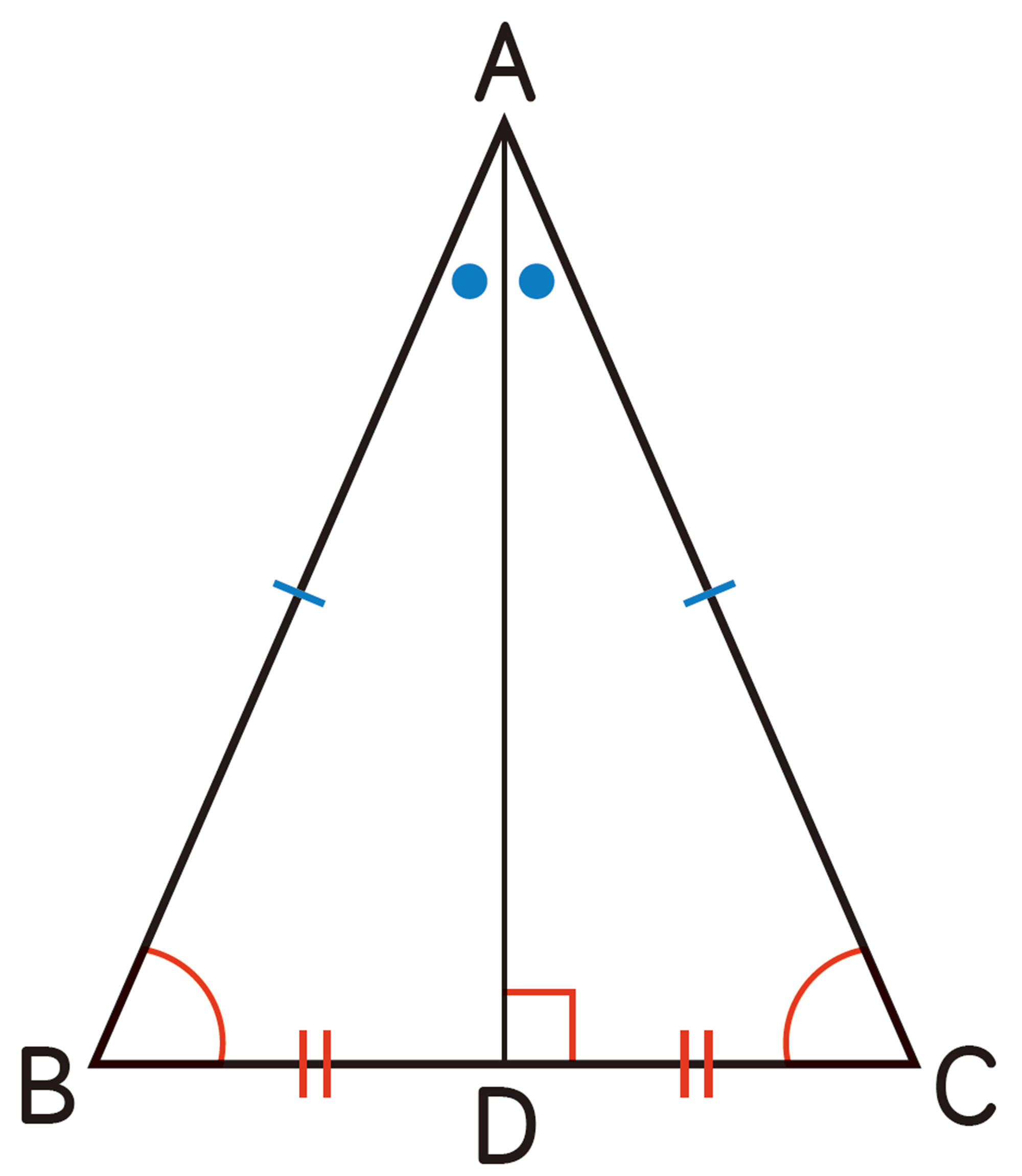
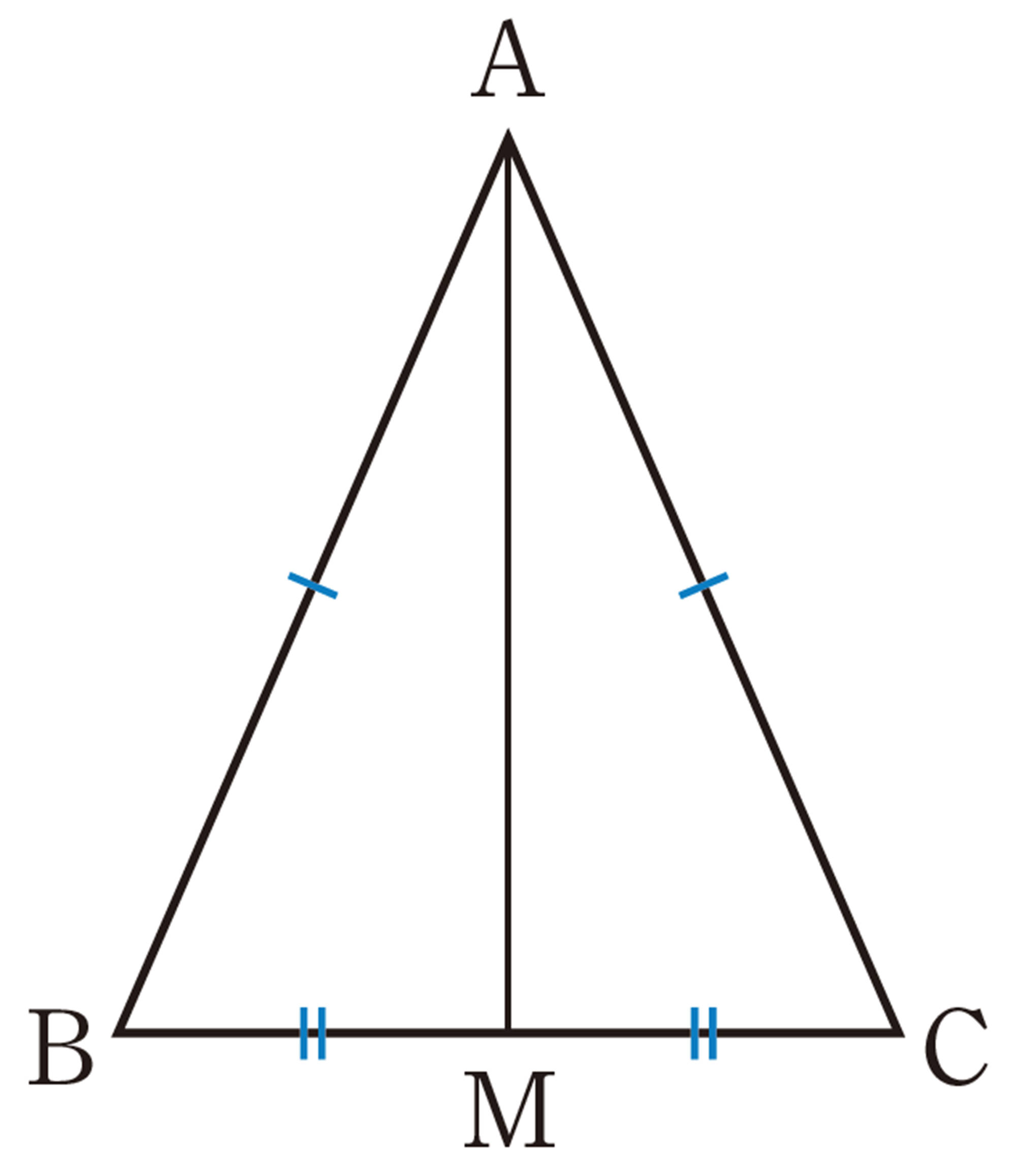
問 ２ 前ページの例1の証明の中で示された [mathjax]\(\triangle ABD \equiv \triangle ACD\) を使うと，
[mathjax]\(BD=CD\) ，[mathjax]\(AD \perp BC\)
も証明することができます。次の [mathjax]\( \boxed{\phantom{00}}\) をうめて，証明を完成させなさい。
［証明］
[mathjax]\(\triangle ABD \equiv \triangle ACD\)から，
<2年p.152>
前ページの問2で証明したことは，次のように，定理としてまとめることができる。
定理
二等辺三角形の底角
二等辺三角形の頂角の二等分線は，底辺を垂直に2等分する。
問 ３ [mathjax]\(AB=AD\) ，[mathjax]\(BC=DC\) である四角形ABCDで，対角線AC，BDの交点をOとするとき，次の⑴，⑵を，順に証明しなさい。
⑴ [mathjax]\(\angle BAC=\angle DAC\)
⑵ ACは線分BDの垂直二等分線である。
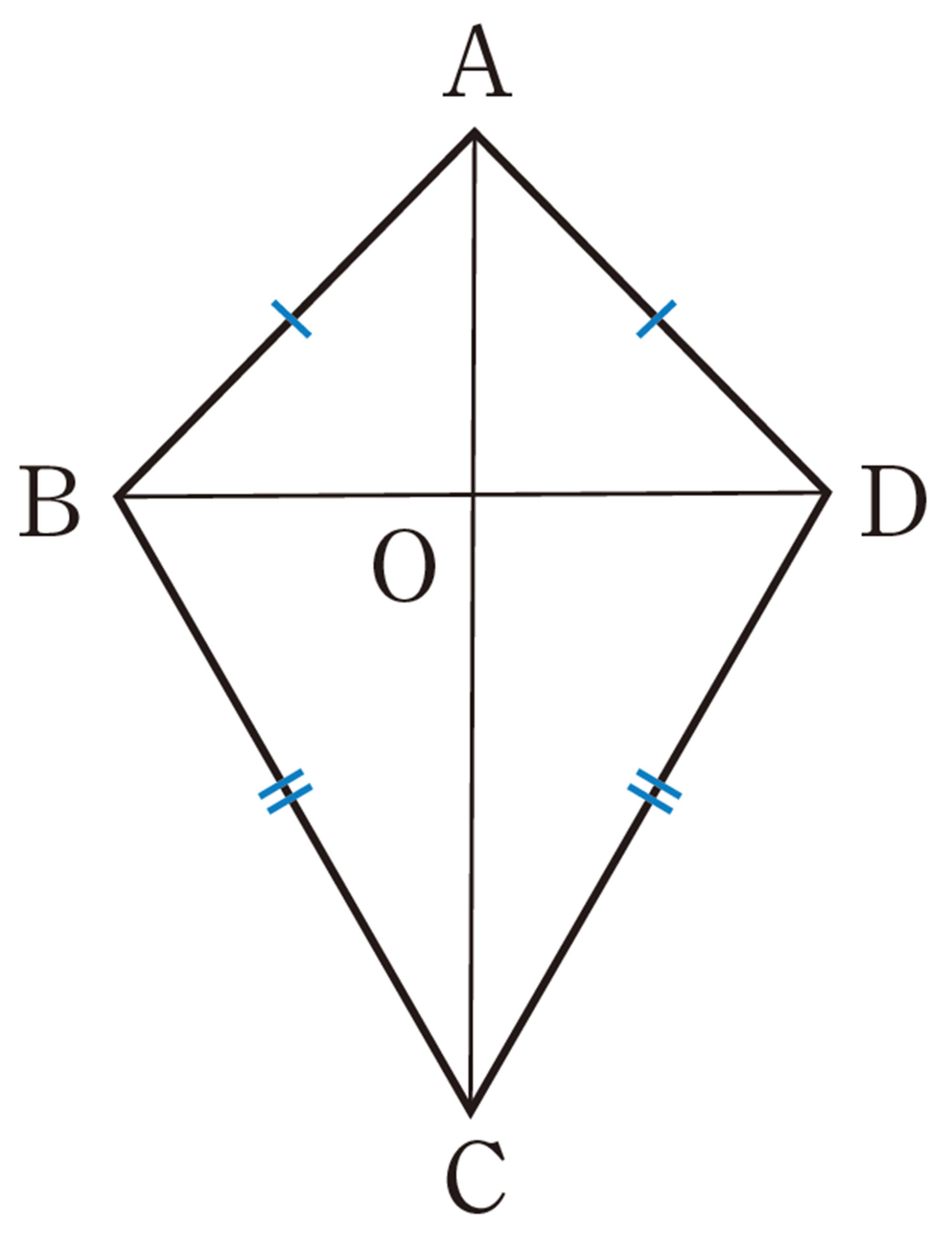
右の四角形ABCDはたこ形といいます。
三角形の合同条件が使えるかな。
問 ４ 二等辺三角形の2つの底角が゙等しいことを， 右の図のように，二等辺三角形ABCの頂点Aと底辺BCの中点Mを結ぶ線分AMを引いて証明しなさい。
どんなことがわかったかな
三角形の合同を利用すると，二等辺三角形の定義から，その性質を導くことができます。
次の課題へ！
「二等辺三角形の2つの底角は等しい」という性質の逆は正しいといえるのかな？
P.153
