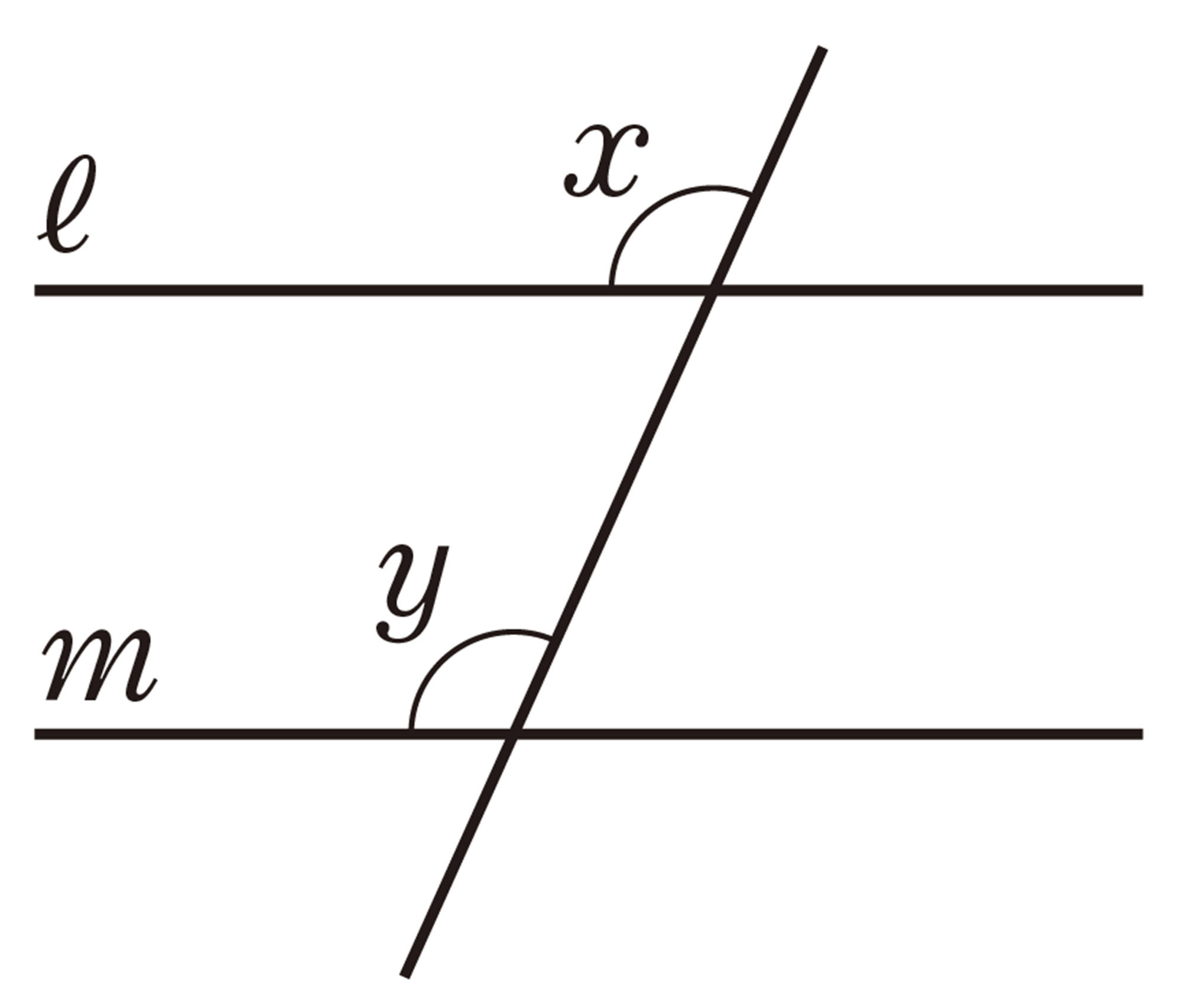<2年p.130>
３ 図形の性質の確かめ方
仮定と結論
Q Question
前ページの問2⑴の問題について，どうして2つの三角形が合同になるか，説明してみましょう。
三角形の合同条件を使えば説明できるね。
うまく人に伝えるには，どうやって整理すればいいのかな。
見方・考え方
根拠を明らかにして，説明できるかな。
目標 ▷ あることがらが成り立つことを説明しよう。
あることがらが成り立つことを説明するには，「わかっていること」と「説明しようとすること」を，はっきりと区別することが必要である。
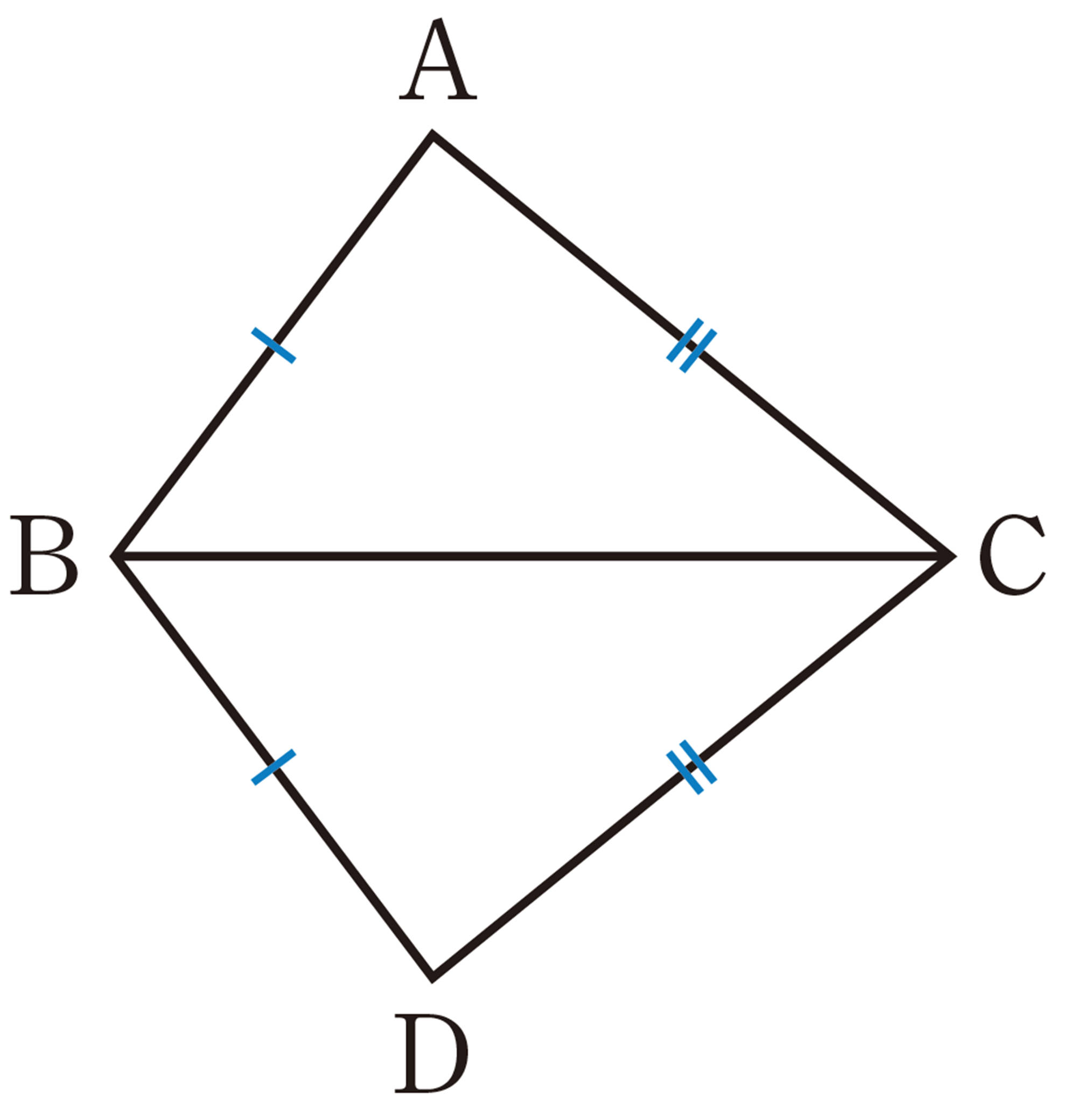
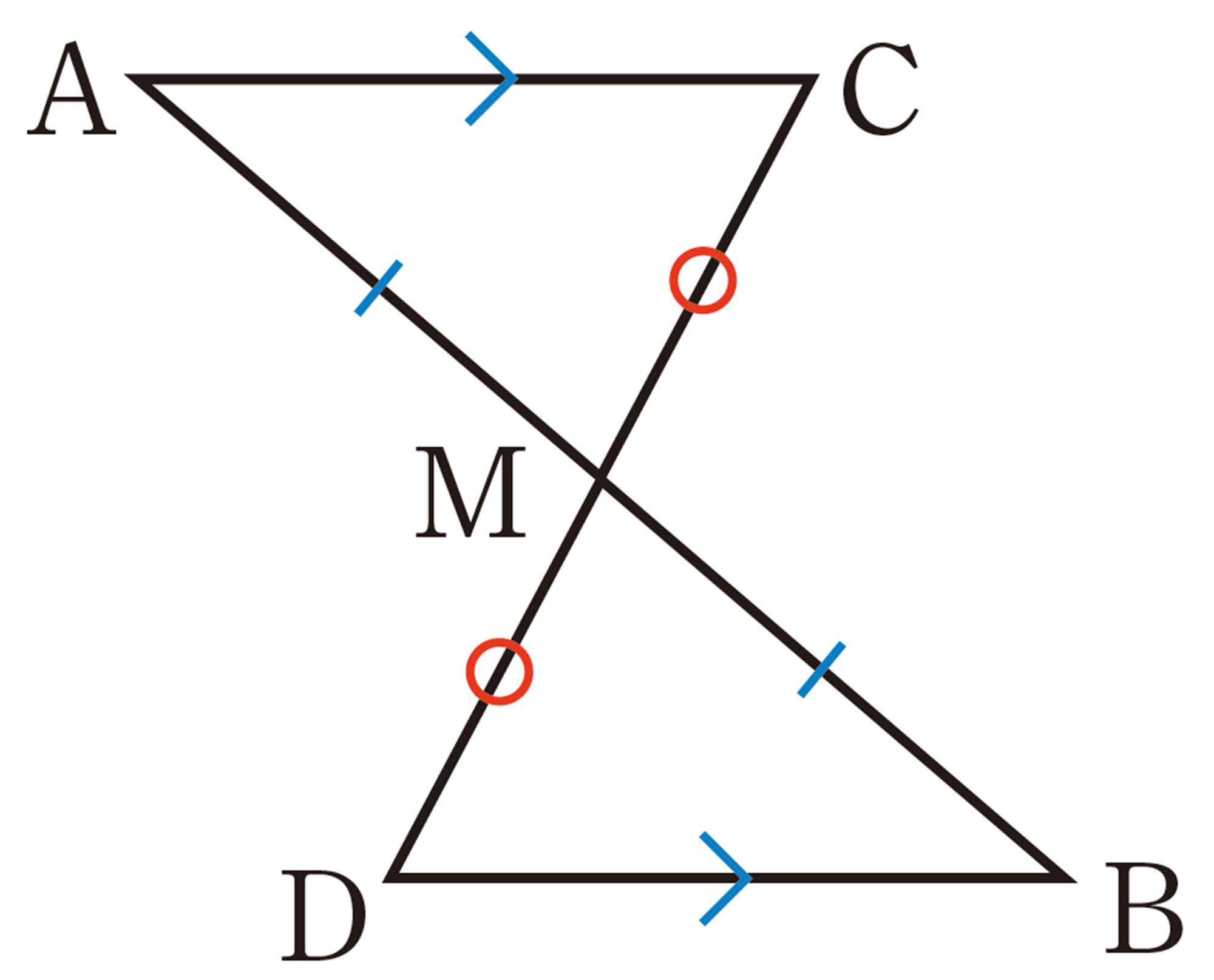
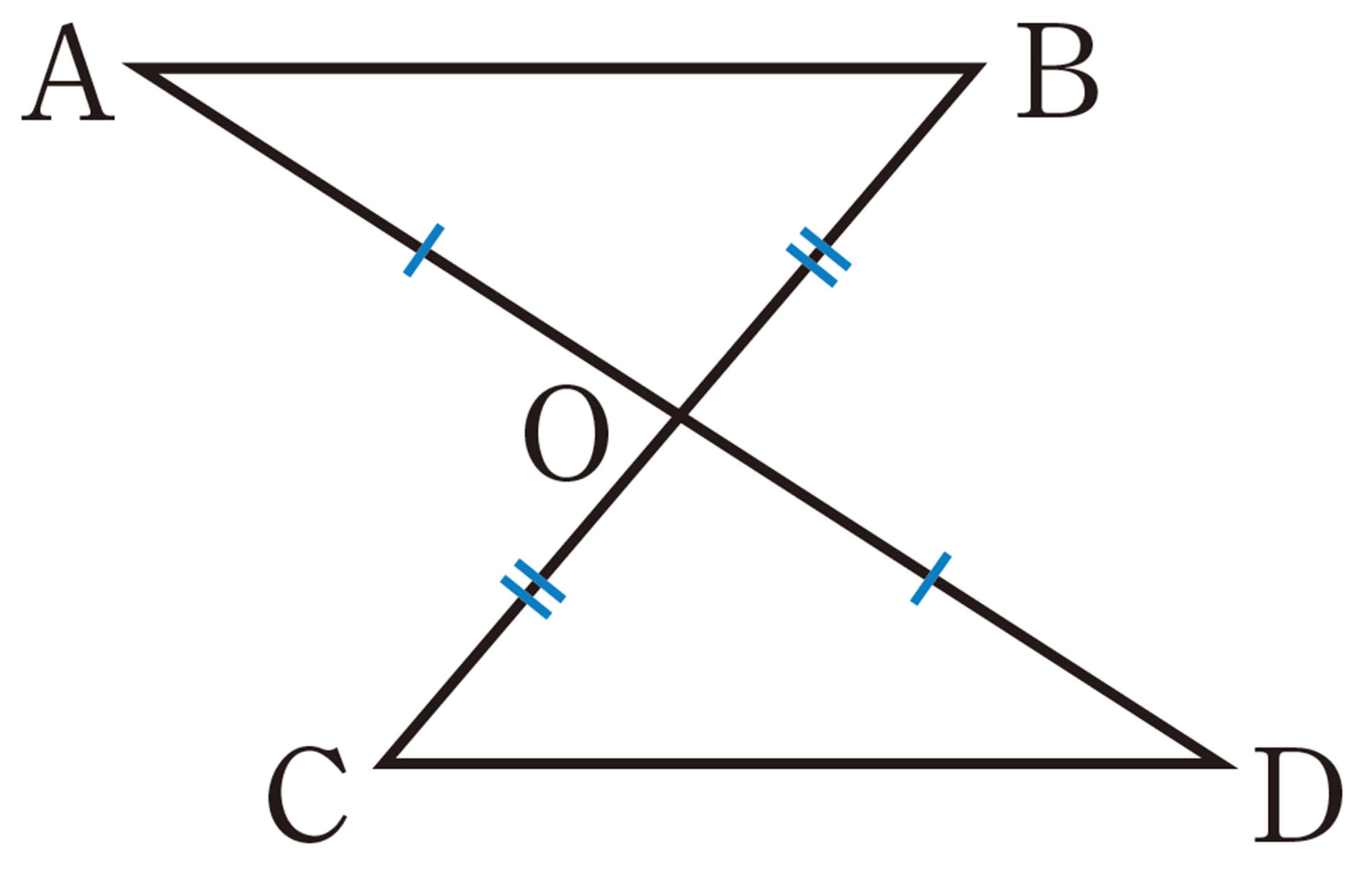
たとえば，Qでは，
（Ⅰ） わかっていることは， [mathjax]\(\underline{AB=DB，AC=DC}\)
（Ⅱ） 説明しようとすることは，[mathjax]\(\underline{\underline{\triangle ABC \equiv \triangle DBC}}\)
したがって，Qで説明しようとすることがらは，次のように書くことができる。
[mathjax]\(\triangle ABC\) と[mathjax]\(\triangle DBC\) において，
「[mathjax]\(\underline{AB=DB，AC=DC}\)ならば，[mathjax]\(\underline{\underline{\triangle ABC \equiv \triangle DBC}}\)」
このとき，[mathjax]\(\underline{\quad\quad}\)の部分を 仮定，[mathjax]\(\underline{\underline{\quad\quad}}\)の部分を 結論 という。
数学では，説明しようとすることがらを，「ならば」を用いた文章で表すことが多い。
問 １ 前ページの問2⑵，⑶について，仮定と結論をいいなさい。
<2年p.131>
問 ２ 次のことがらの仮定と結論をいいなさい。
⑴ [mathjax]\(\triangle ABC \equiv \triangle DEF\) ならば， [mathjax]\(AB=DE\)である。
⑵ [mathjax]\(\triangle ABC\) で，[mathjax]\(\angle A=90^{ \circ }\) ならば，[mathjax]\(\angle B+\angle C=90^{ \circ }\) である。
⑶ 2つの整数 [mathjax]\( a \) ， [mathjax]\( b \) が奇数ならば， [mathjax]\( a+b \) は偶数である。
証明
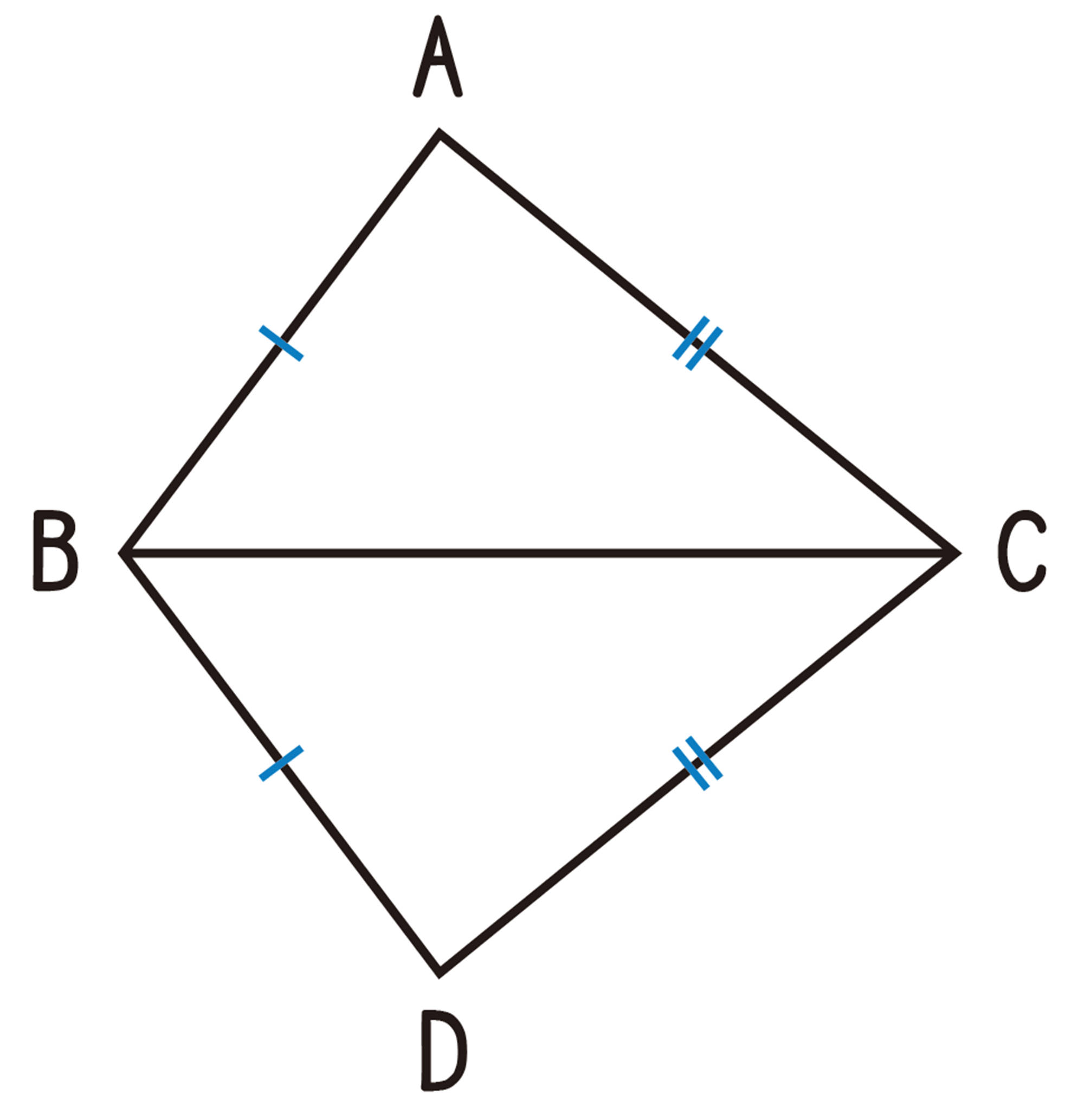
例 １ 前ページの【Q】のことがらについて，[mathjax]\(\triangle ABC \equiv \triangle DBC\) であることを説明しなさい。
仮定 [mathjax]\(AB=DB\)，[mathjax]\(AC=DC\)
結論 [mathjax]\(\triangle ABC \equiv \triangle DBC\)
説明
[mathjax] \(\triangle ABC\) と[mathjax]\(\triangle DBC\) において，
①， ②， ③より，3組の辺がそれぞれ等しいから，
[mathjax] \(\triangle ABC \equiv \triangle DBC\)
上の説明をする際，三角形の辺の長さや角の大きさについて，具体的な値は使っていない。したがって，三角形の辺の長さや角の大きさがどんな三角形でも，2つの三角形は合同であることがいえる。
このように，あることがらが正しいことを，すでに正しいと認められたことがらを根拠にして，筋道を立てて説明することを 証明という。
問 ３ 上で証明したことから，角の大きさについて，どんなことがわかりますか。
合同な図形の性質を考えると，いろいろなことがわかるね。
<2年p.132>
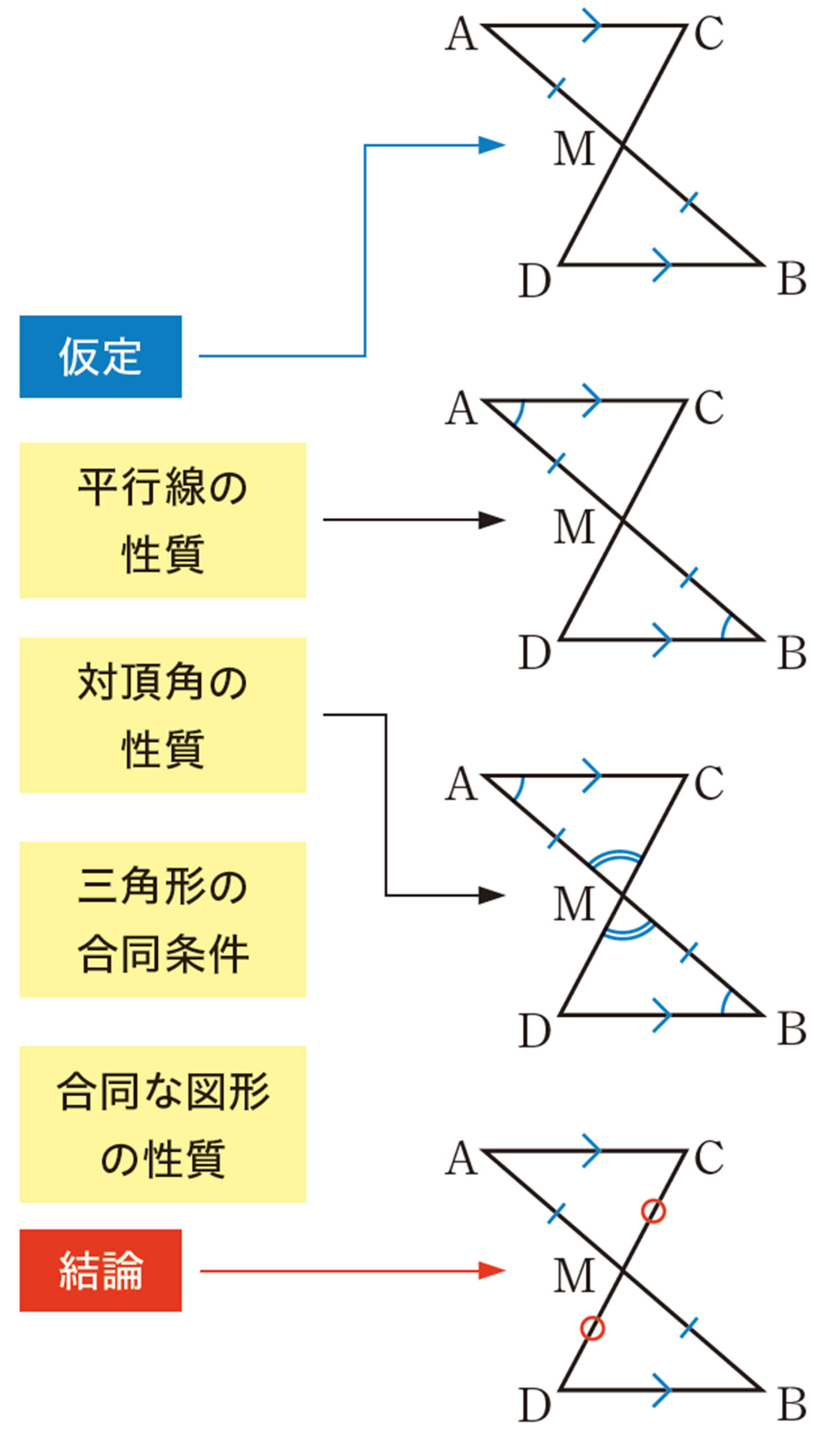
証明のすすめ方
Q Question
線分ABと線分CDが点Mで交わるとき，
[mathjax]\(AC/\!/DB\)，[mathjax]\(AM=BM\) ならば，[mathjax]\(CM=DM\)
です。このことをどのように証明すればよいか考えてみましょう。
2つの三角形が合同であることが示せれば，対応する辺や角が等しいといえるね。
どの合同条件が使えるのかな。
見方・考え方
根拠を明らかにして，説明できるかな。
証明をするときに，どんな手順で考えればよいか整理してみよう。
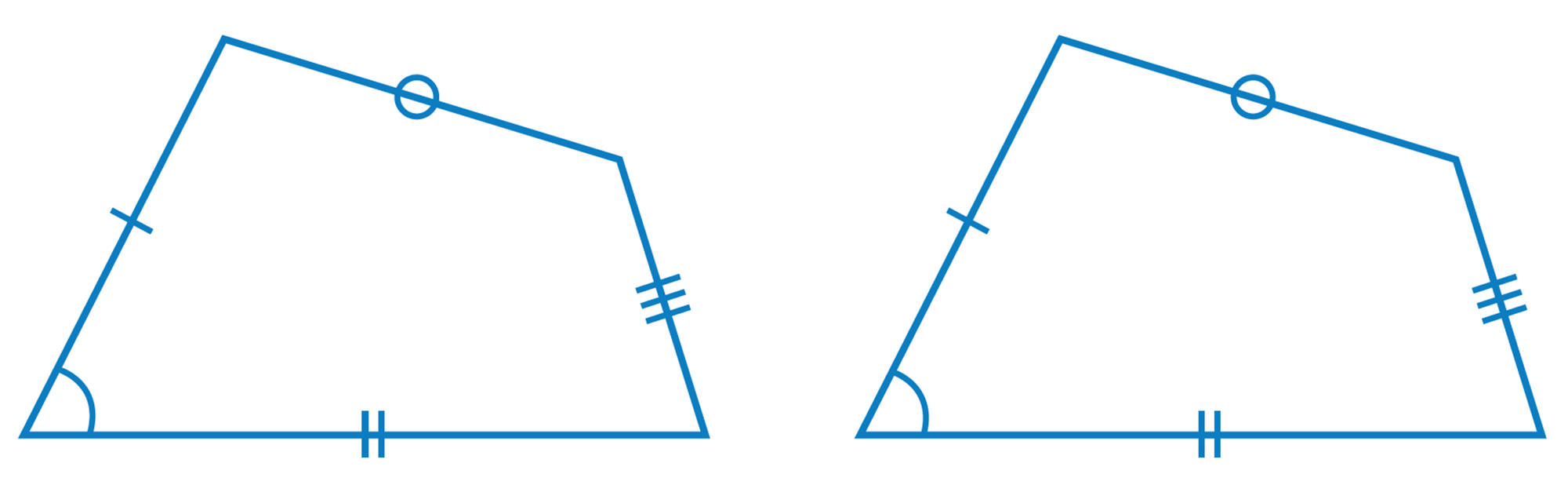
① 仮定と結論を区別して，図に必要な印を記入する。
Qの問題で，仮定は [mathjax]\(AC/\!/DB\)，[mathjax]\(AM=BM\)，結論は[mathjax]\(CM=DM\)である。このとき，たとえば仮定は青い印，結論は赤い印で示すなど，区別がつくようにしておくとわかりやすくなる。
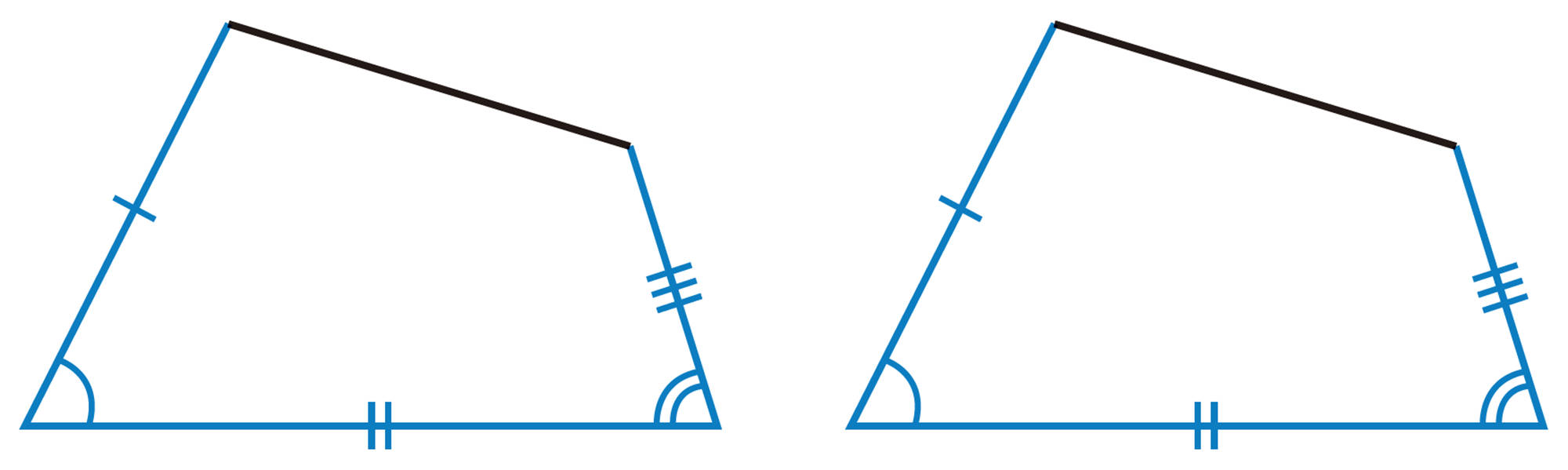
② 結論をいうために何がいえればよいか考える。
[mathjax]\(CM=DM\)であることをいうためには，CMとDMが対応する辺になるような合同な図形を見つければよい。
したがって，[mathjax]\(\triangle AMC\) と [mathjax]\(\triangle BMD\) が合同であるかどうかを確かめればよい。
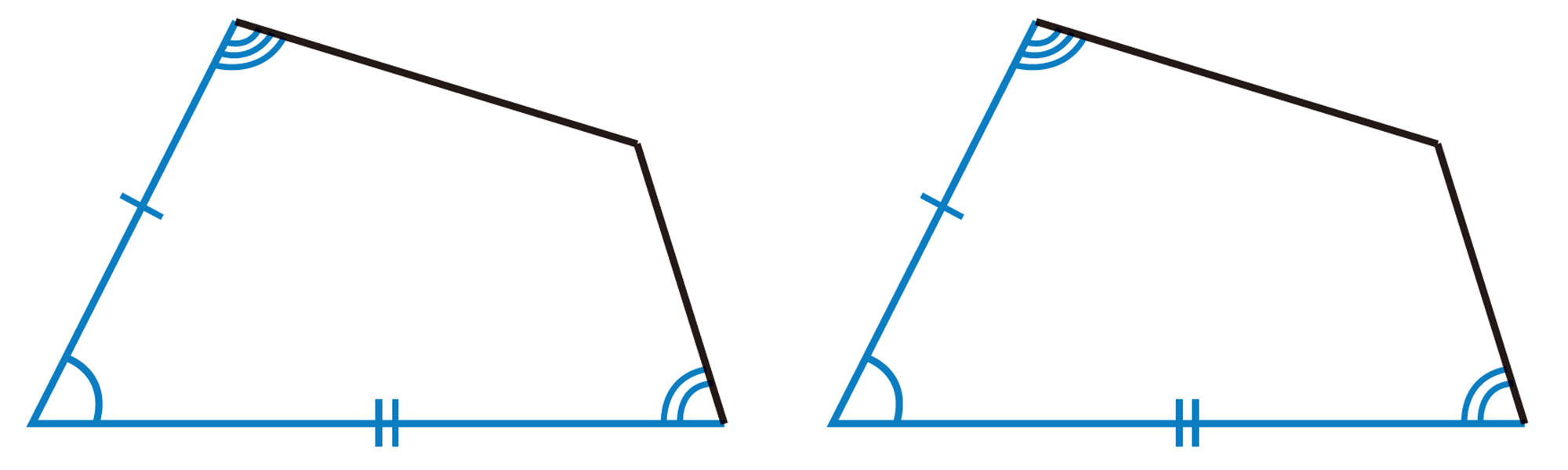
③ 根拠を明らかにしながら，証明を書く。
<2年p.133>
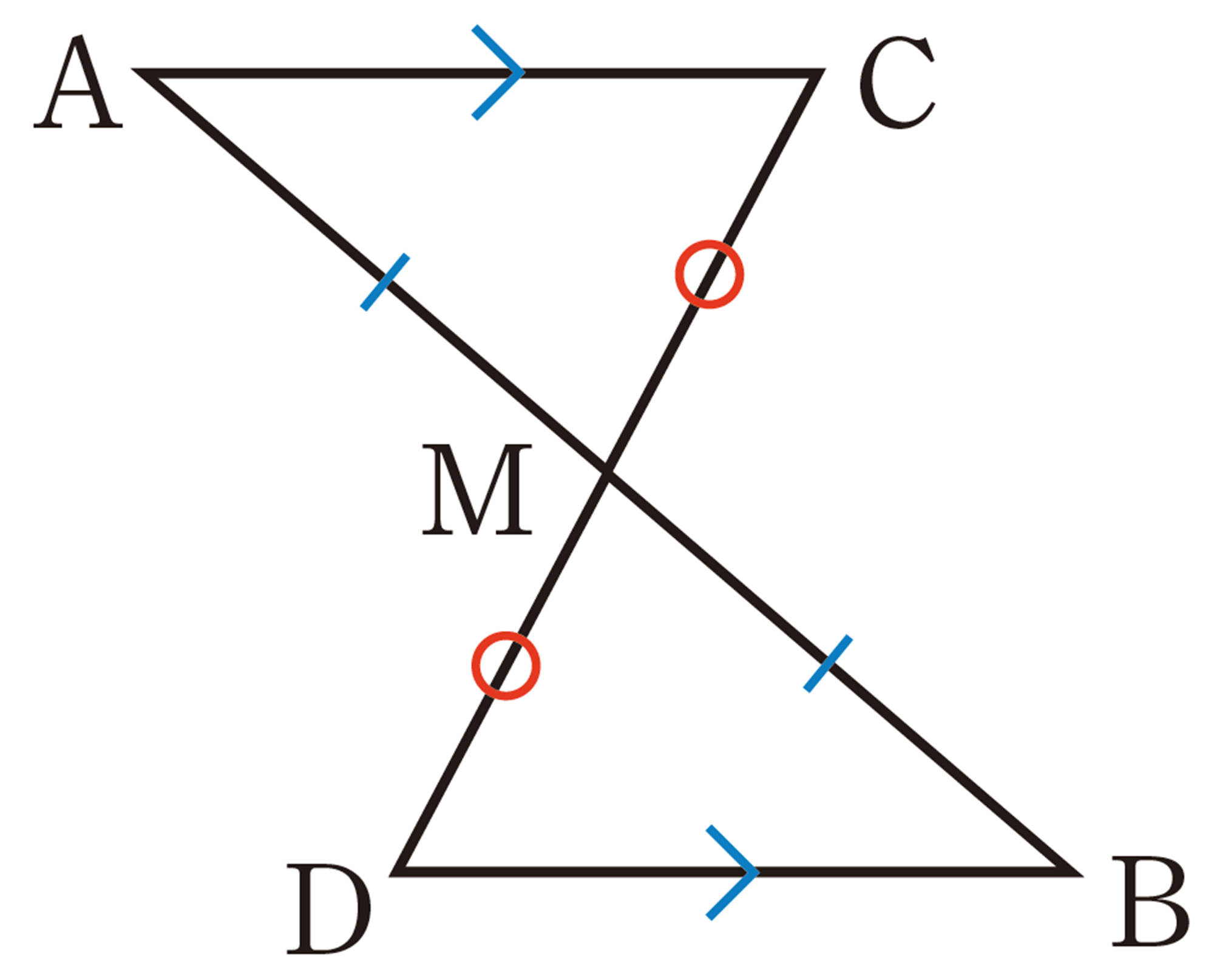
前ページの手順で考えて，証明として書くと，次のようになる。
［仮定］[mathjax]\(AC/\!/DB\)，[mathjax]\(AM=BM\)
［結論］[mathjax]\(CM=DM\)
［証明］
[mathjax]\(\triangle AMC\) と[mathjax]\(\triangle BMD\) において，
仮定から，[mathjax]\(AM=BM\) ･･････①
平行線の錯角は等しいから，
[mathjax]\(AC/\!/DB\)より，
[mathjax]\(\angle CAM=\angle DBM\) ･･････②
対頂角は等しいから，
[mathjax]\(\angle AMC=\angle BMD\) ･･････③
①，②，③より，1組の辺とその両端の角がそれぞれ等しいから，
[mathjax]\(\triangle AMC \equiv \triangle BMD\)
合同な図形の対応する辺は等しいから，
[mathjax]\(CM=DM\)
問 ４ 右の図で，[mathjax]\(AB=DC\)，[mathjax]\(\angle ABC=\angle DCB\) ならば，[mathjax]\(\angle BAC=\angle CDB\) です。このとき，次の問いに答えなさい。
⑴ 仮定と結論をいい，図に必要な印を記入しなさい。
⑵ 結論をいうためには何がいえればよいですか。
⑶ このことを証明しなさい。
⑷ ⑶で証明したことから，[mathjax]\(\angle BAC=\angle CDB\) のほかにどんなことがわかりますか。
<2年p.134>
問 ５ [mathjax]\(\angle XOY\) の二等分線 OCを右の図のように作図しました。次の[mathjax]\(\boxed{\phantom{0000}}\)をうめて，作図した半直線OCが[mathjax]\(\angle XOY\) の二等分線であることを証明しなさい。
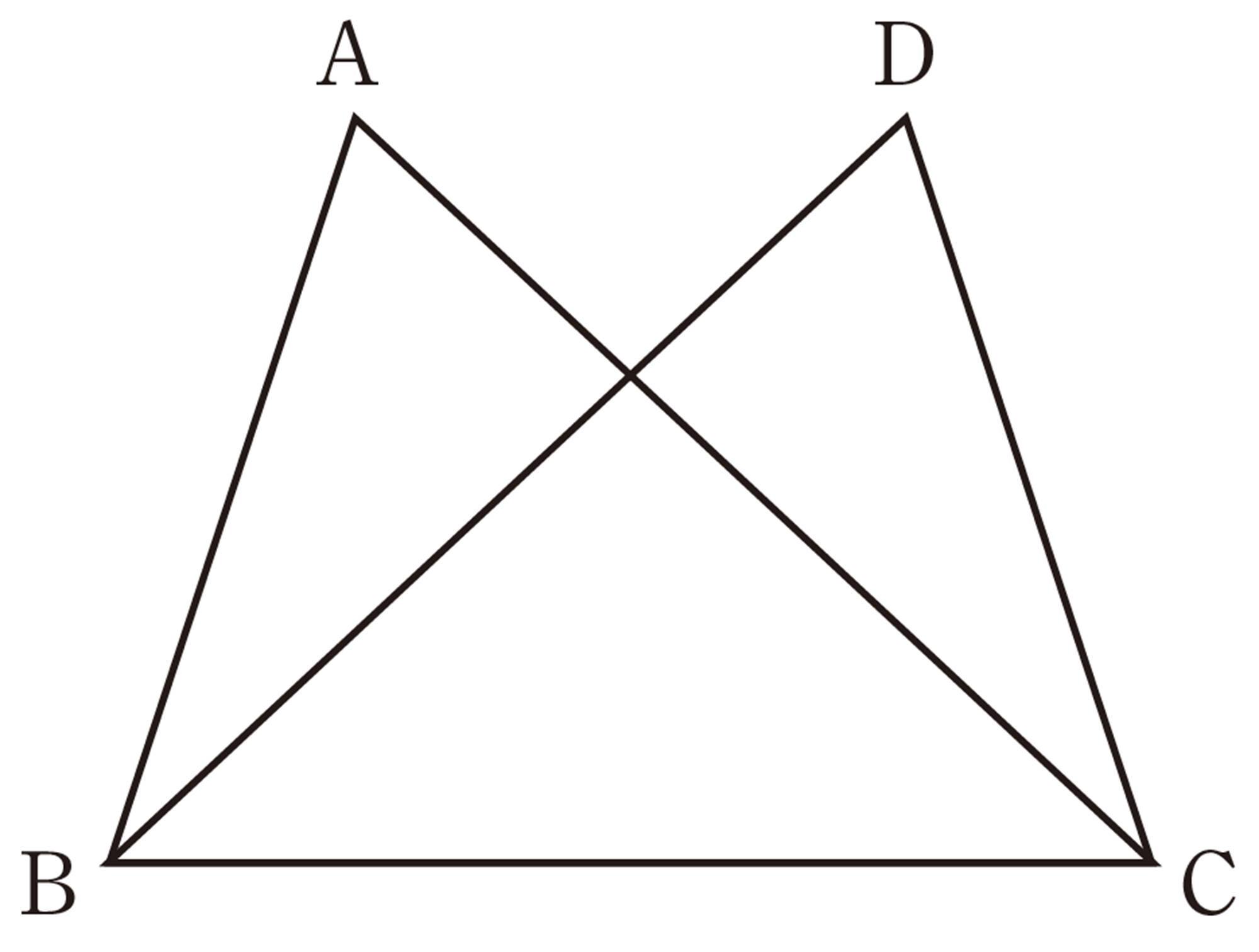
［仮定］[mathjax]\( OA=OB，AC=BC \)
［結論］[mathjax]\( \angle AOC=\angle BOC\)
［証明］
点Aと点C，点Bと点Cをそれぞれ結ぶ。
[mathjax]\(\triangle AOC\) と [mathjax]\(\triangle BOC\)において，
①，②，③より，[mathjax]\(\boxed{\phantom{00000000}}\)がそれぞれ等しいから，
[mathjax]\( \triangle AOC \equiv \triangle BOC\)
合同な図形の対応する角は等しいから，
[mathjax]\(\angle AOC=\boxed{\phantom{000000}}\)
問 ６ 大和さんは，右の問題を次のように証明しました。この証明は正しいですか。誤りがあれば，正しく直しなさい。
次の図で，[mathjax]\(AO=DO\)，[mathjax]\(BO=CO\)ならば，[mathjax]\(AB/\!/CD\)です。このことを証明しなさい。
正しいかな？
[mathjax]\(\triangle AOB\)と[mathjax]\(\triangle DOC\)において，
錯角が等しいから，[mathjax]\(AB/\!/CD\)
<2年p.135>
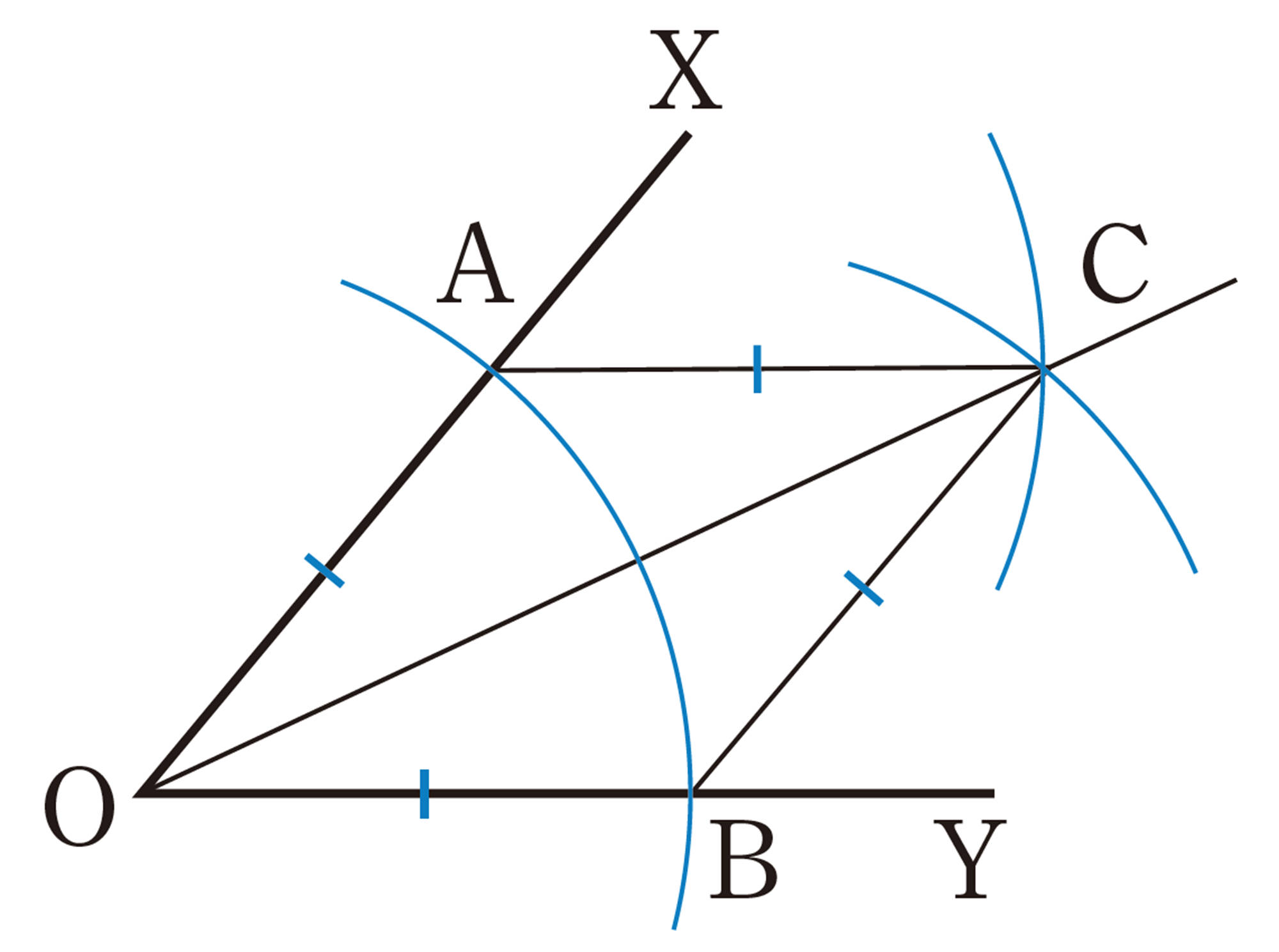
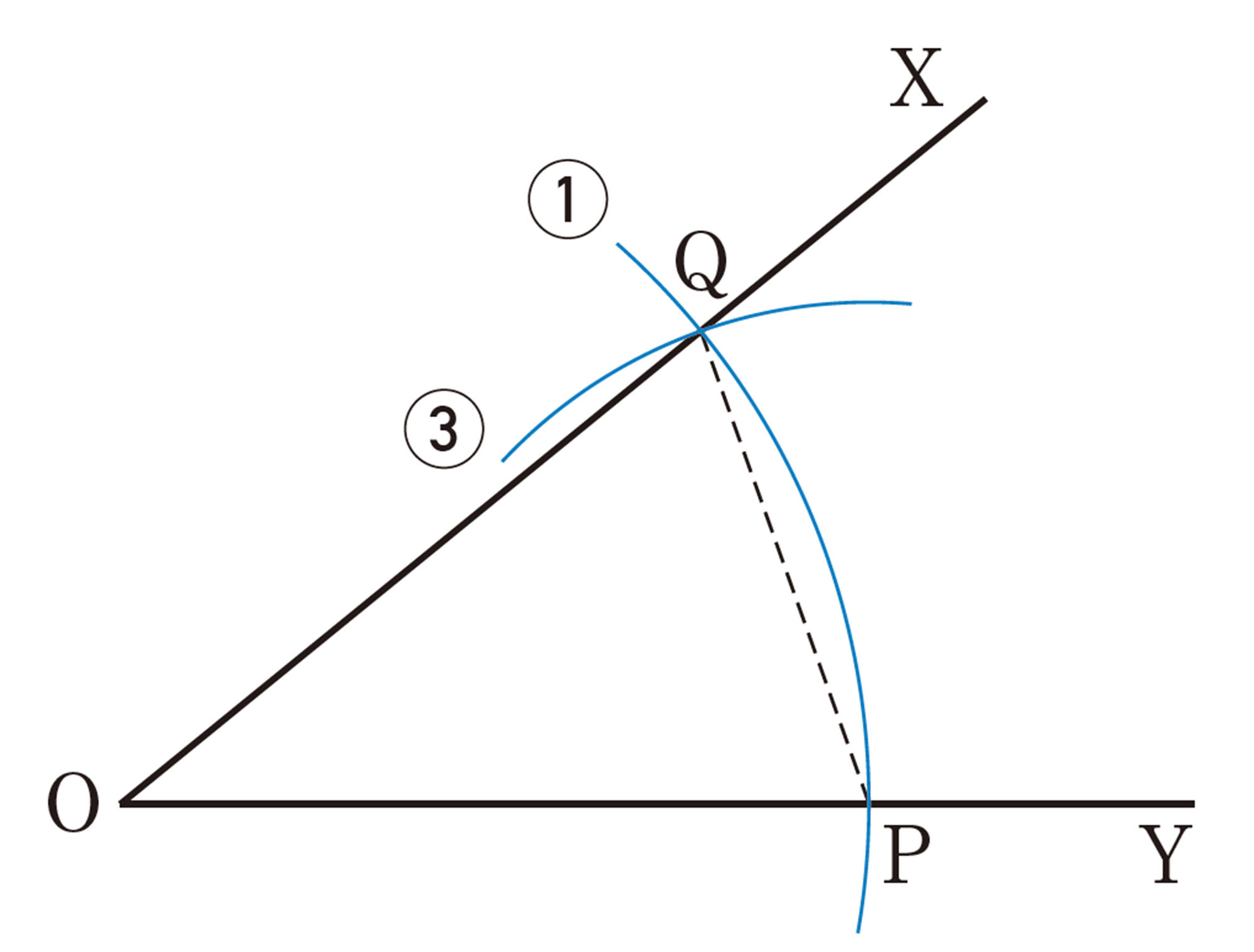
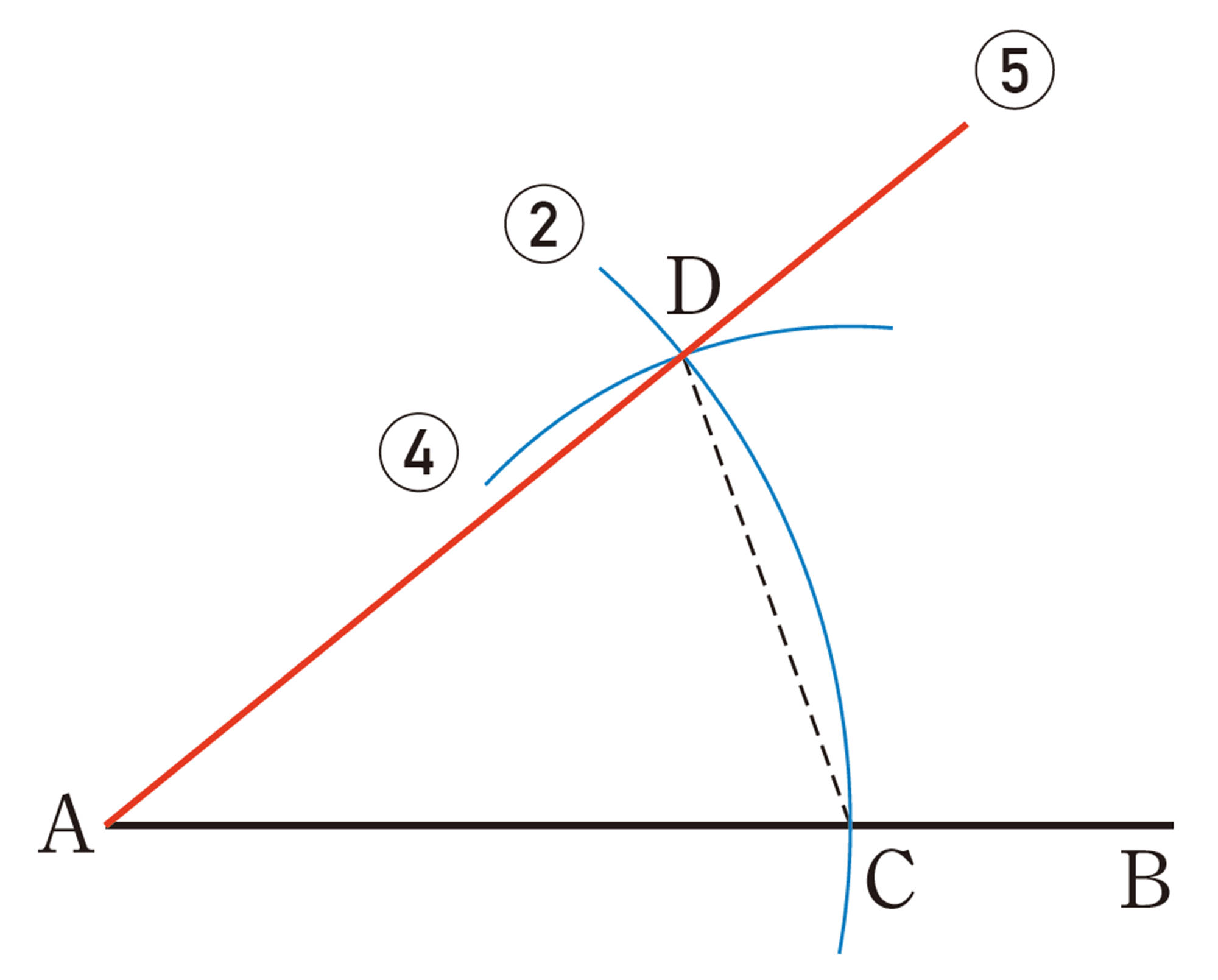
問 ７ 次の図は，[mathjax]\(\angle XOY\) と大きさの等しい角[mathjax]\(\angle DAB\) の作図の方法を示しています。はじめに半直線ABを引き，①〜⑤の手順で作図することができます。
下の問いに答えなさい。
⑴ 適当な大きさの角[mathjax]\(\angle XOY\) をかき，それと大きさの等しい角[mathjax]\(\angle DAB\) を上の手順で作図しなさい。
⑵ この作図の方法が正しいことを証明しようと思います。次の問いに答えなさい。
（Ⅰ） 仮定と結論をいい，図に必要な印を記入しなさい。
（Ⅱ） 仮定から結論をいうためには，何がいえればよいですか。
（Ⅲ） このことを証明しなさい。
▲トライ 次の図は， 「直線[mathjax]\( ℓ \)上にない点Pを通る[mathjax]\( ℓ \)の平行線」の作図の方法を示しています。作図の手順①〜③を説明してみよう。
また，三角形の合同を使って，この作図の方法が正しいことを証明してみよう。
1年のときに学んだ作図のしかたについて，根拠を明らかにして説明できるね。
<2年p.136>
逆
Q Question
次の⑴，⑵のことがらについて，仮定と結論をそれぞれいいましょう。また，⑴，⑵のことがらは正しいといえるでしょうか。
⑴ 2つの三角形が合同ならば，3組の角はそれぞれ等しい。
⑵ 2つの三角形の3組の角がそれぞれ等しいならば，合同である。
仮定と結論が入れかわっているね。
入れかわっているだけだから，どちらも正しいといえるんじゃないかな。
見方・考え方
仮定と結論を入れかえたとき，いつでも正しいといえるか確かめられるかな。
Q⑴，⑵の2つの仮定と結論の関係を整理すると，次のようになる。
Qの図で，
このように，仮定と結論が入れかわっている2つのことがらがあるとき，一方を他方の逆という。たとえば，上の⑵は⑴の逆で，⑴は⑵の逆である。
Qで調べたように，あることがらが正しくても，そのことがらの逆がいつでも正しいとは限らない。したがって，あることがらの逆が正しいことをいうためには，あらためてそのことがらを証明する必要がある。
また，あることがらが正しくないことを示すには，それが成り立たない例を1つあげればよい。このような成り立たない例を反例という。
【Q】では，3組の角の大きさが等しくて，辺の長さがちがう2つの三角形を示せば反例になるね。
<2年p.137>
問 ８ 次のことがらの逆をいいなさい。また，それが正しいかどうかを調べなさい。正しくない場合は，反例をあげて示しなさい。
⑴ 2直線 [mathjax]\( ℓ \) ，[mathjax]\( m \) が平行ならば，同位角[mathjax]\( \angle x \) と [mathjax]\( \angle y \) は等しい。
⑵ [mathjax]\(\triangle ABC \equiv \triangle DEF\) ならば，[mathjax]\(\triangle ABC\) と[mathjax]\(\triangle DEF\) の面積は等しい。
⑶ [mathjax]\(\triangle ABC\) で，[mathjax]\(\angle A=90^{ \circ }\) ならば，[mathjax]\(\angle B+\angle C=90^{ \circ }\) である。
⑷ [mathjax]\(a \gt 0 \) ，[mathjax]\(b \gt 0\) ならば，[mathjax]\(ab \gt 0 \) である。
四角形の合同条件はあるの？ Tea Break
四角形の合同条件は，次の3つがあります。
① 4組の辺と1つの角がそれぞれ等しい。
② 3組の辺とその間の角がそれぞれ等しい。
③ となり合う2組の辺と，その間の角と両端の角がそれぞれ等しい。
4組の辺が等しい四角形では，1つに決まらないのかな。
実際に，四角形が1つに決まることを確かめてみましょう。
