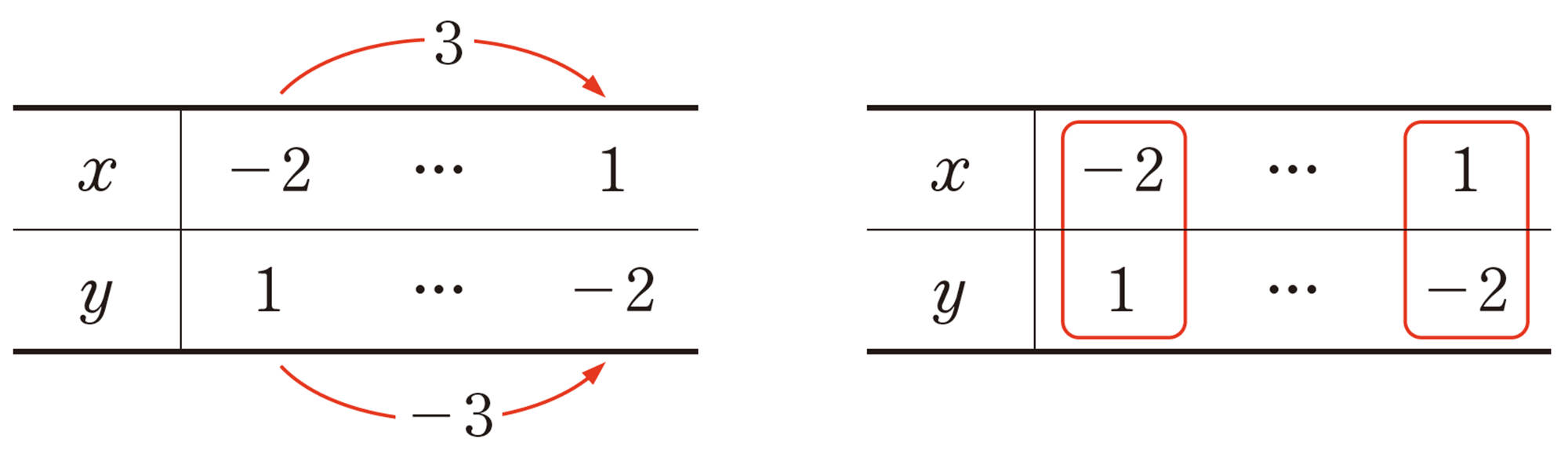<2年p.76>
2 1次関数のグラフ
Q Question
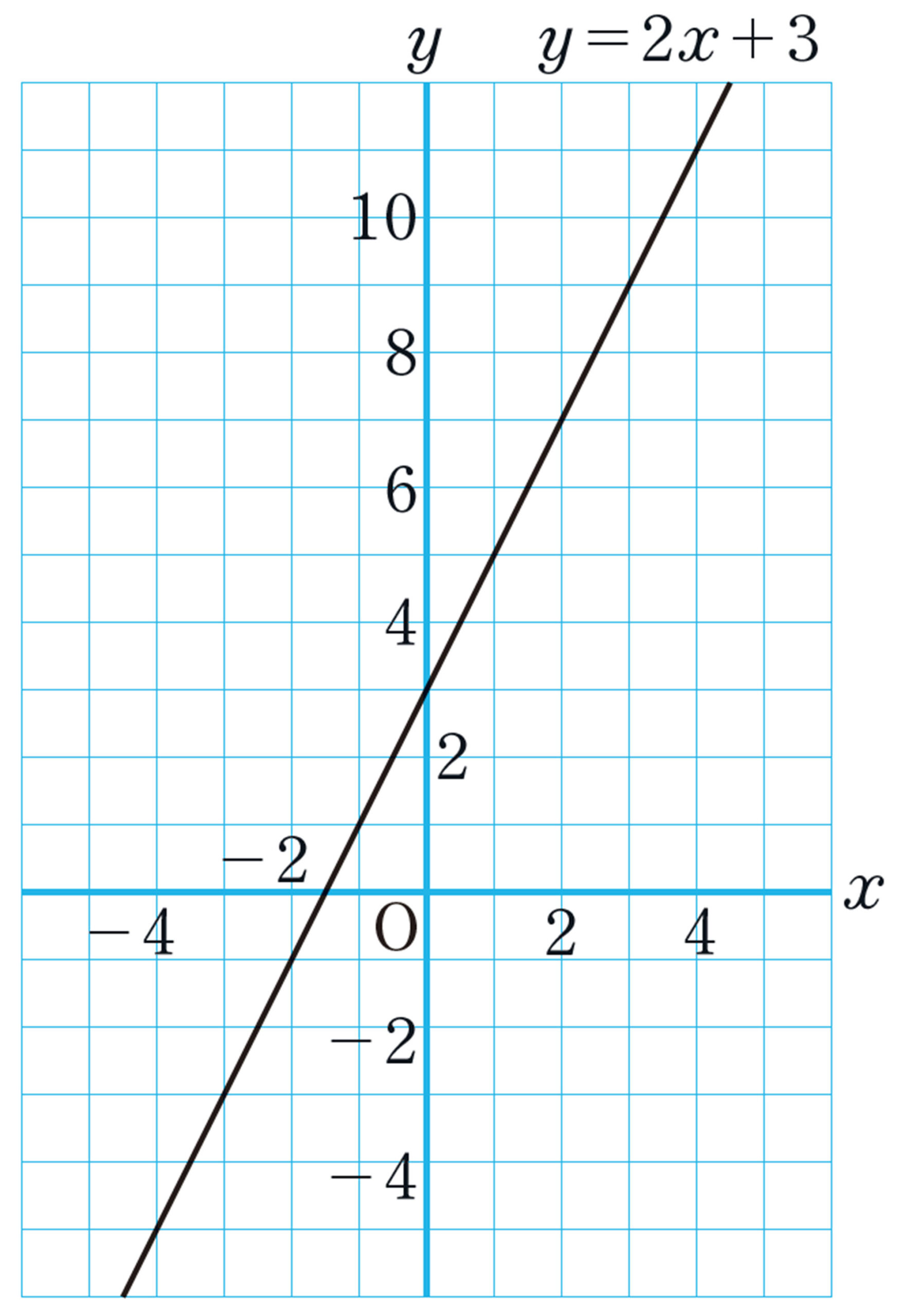
1次関数 [mathjax]\( y=2x+3 \) のグラフについて,次のことを調べてみましょう。
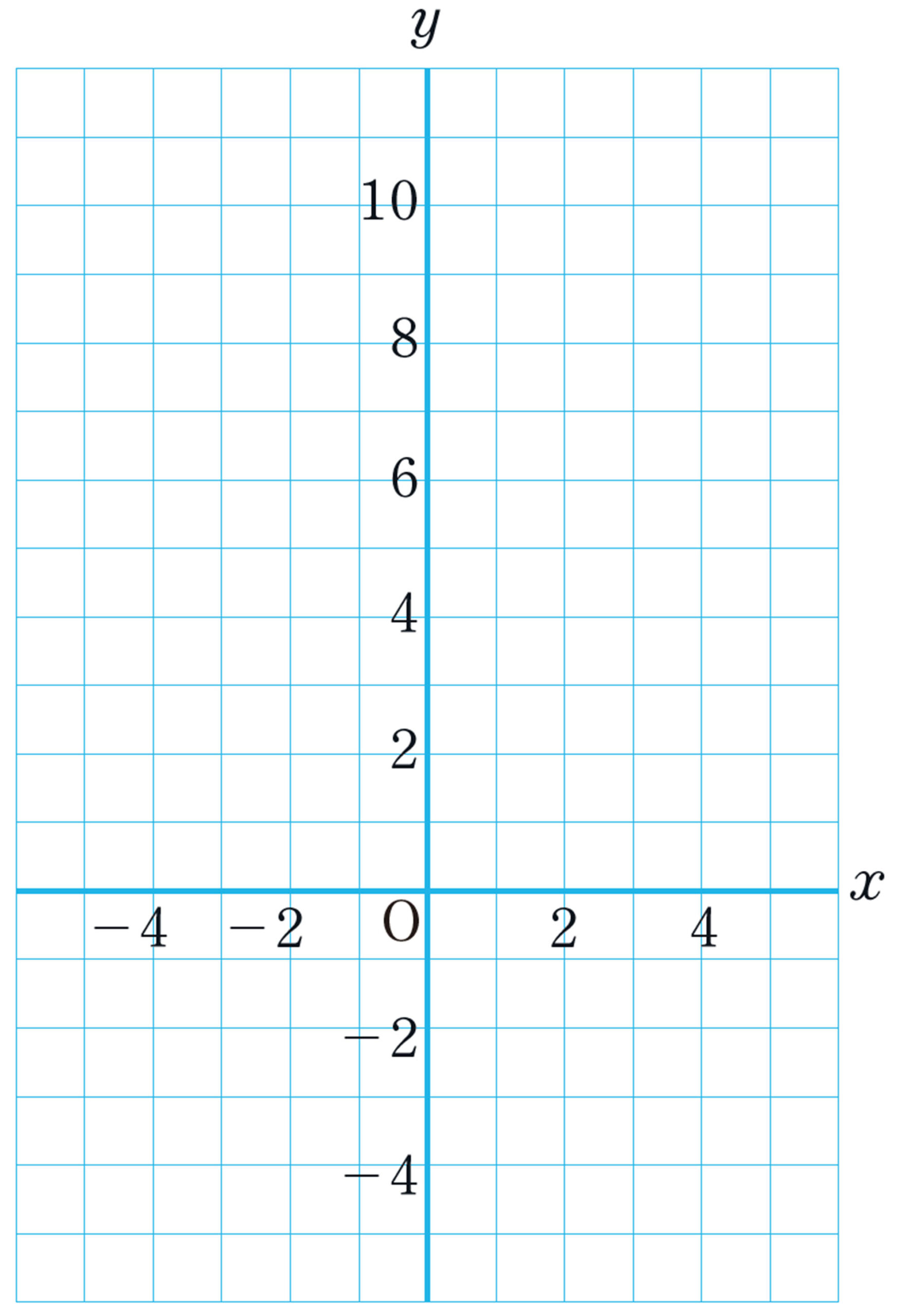
⑴ 次の表は,1次関数[mathjax]\( y=2x+3 \) について,対応する[mathjax]\( x \) ,[mathjax]\( y \) の値を示したものです。これらの[mathjax]\( x \) ,[mathjax]\( y \) の値の組を座標とする点を,下の図にかき入れてみましょう。

比例のグラフは原点を通る直線だったね。
比例も1次関数だから,1次関数のグラフは直線になるのかな。

見方・考え方
比例と同じように,細かく点をとって考えられるかな。
目標 ▷ 1次関数のグラフや,その特徴について調べよう。
<2年p.77>
Q Question
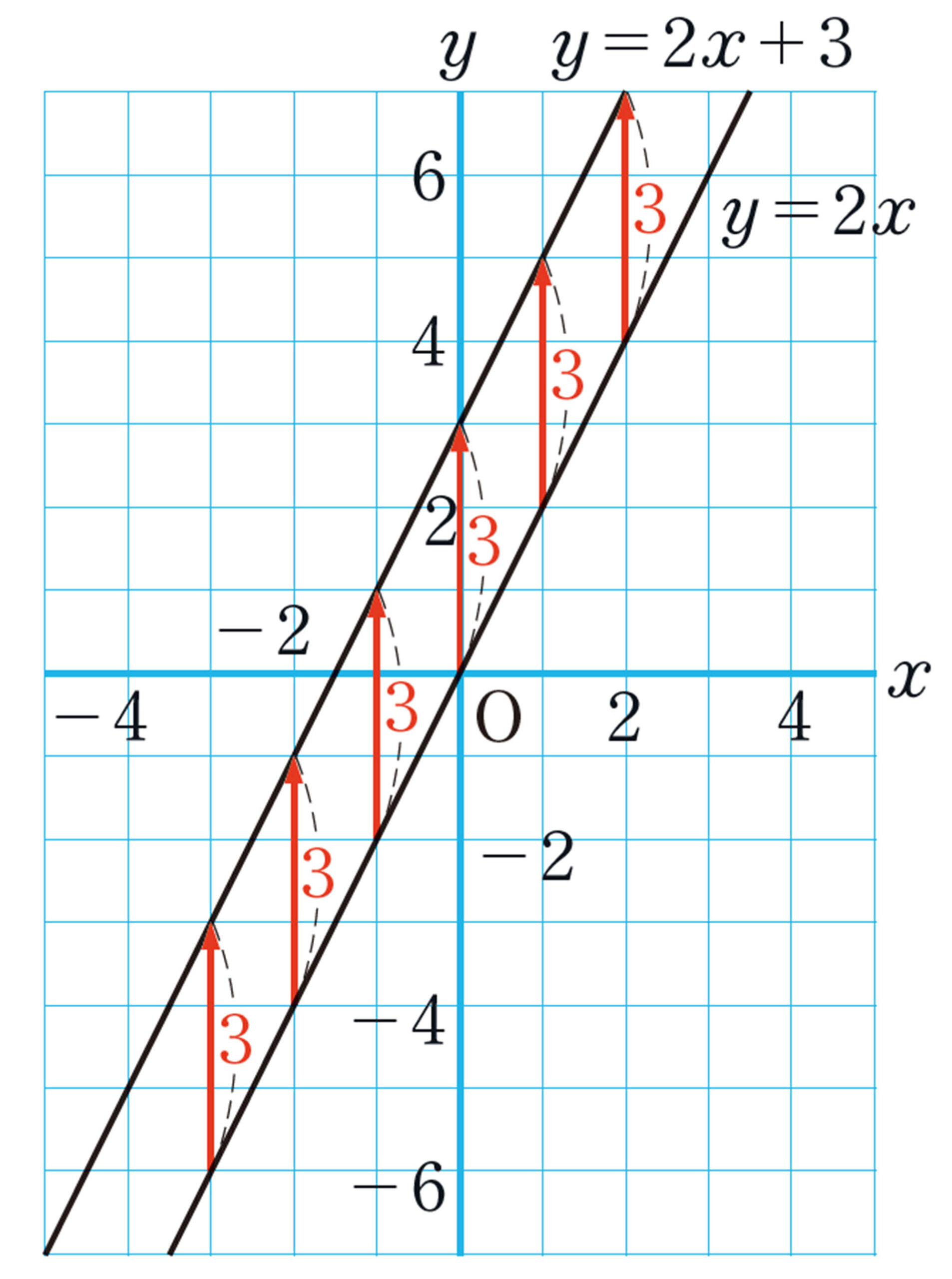
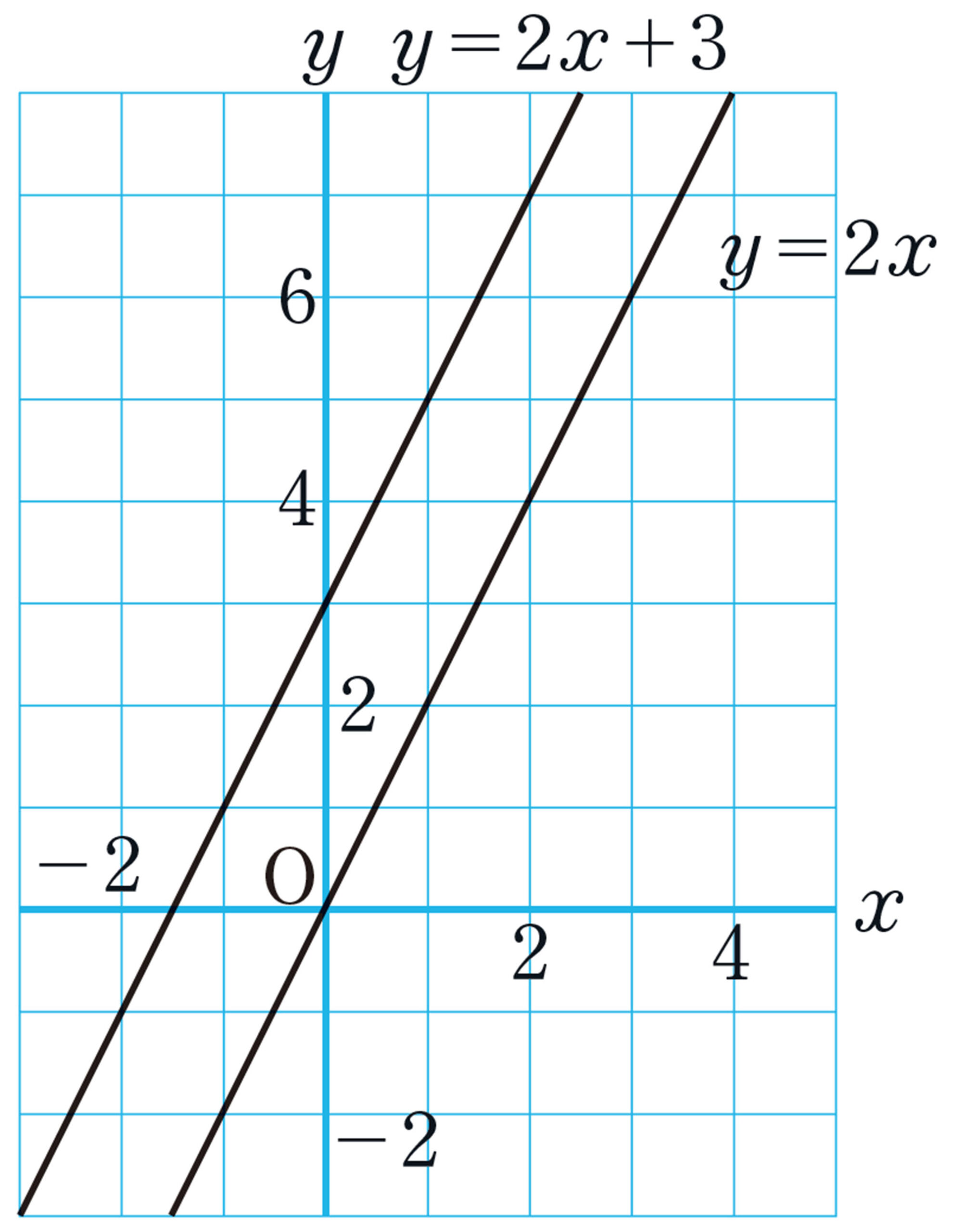
次の表を完成させ,1次関数 [mathjax]\( y=2x \) のグラフを上の図にかき入れ, [mathjax]\( y=2x+3 \) のグラフと比べてみましょう。表やグラフから,どんなことがわかるでしょうか。

[mathjax]\( y=2x+3 \) の [mathjax]\( y \) の値は, [mathjax]\( y=2x \) の [mathjax]\( y \) の値よりいつも3大きいね。
見方・考え方
[mathjax]\( x \) の係数が同じ比例のグラフとのちがいはどこかな。
<2年p.78>
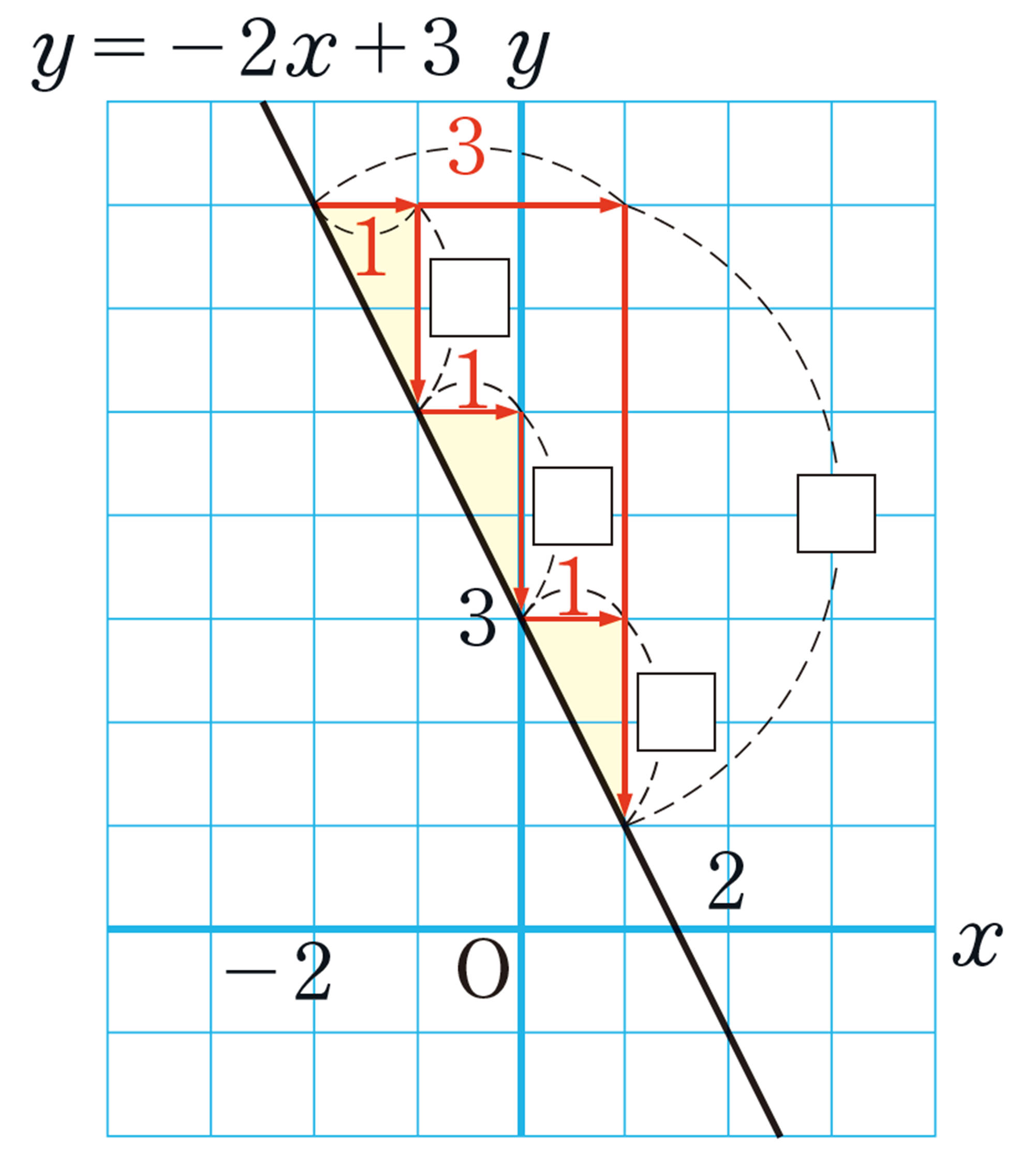
問 2 1次関数 [mathjax]\( y=2x-3 \) のグラフは, [mathjax]\( y=2x \) のグラフをどのように移動した直線といえますか。対応する [mathjax]\( x \) , [mathjax]\( y \) の値を求め,調べなさい。
注意 正の方向に[mathjax] \(-3\)だけ平行移動させることは,負の方向に3だけ平行移動させることである。
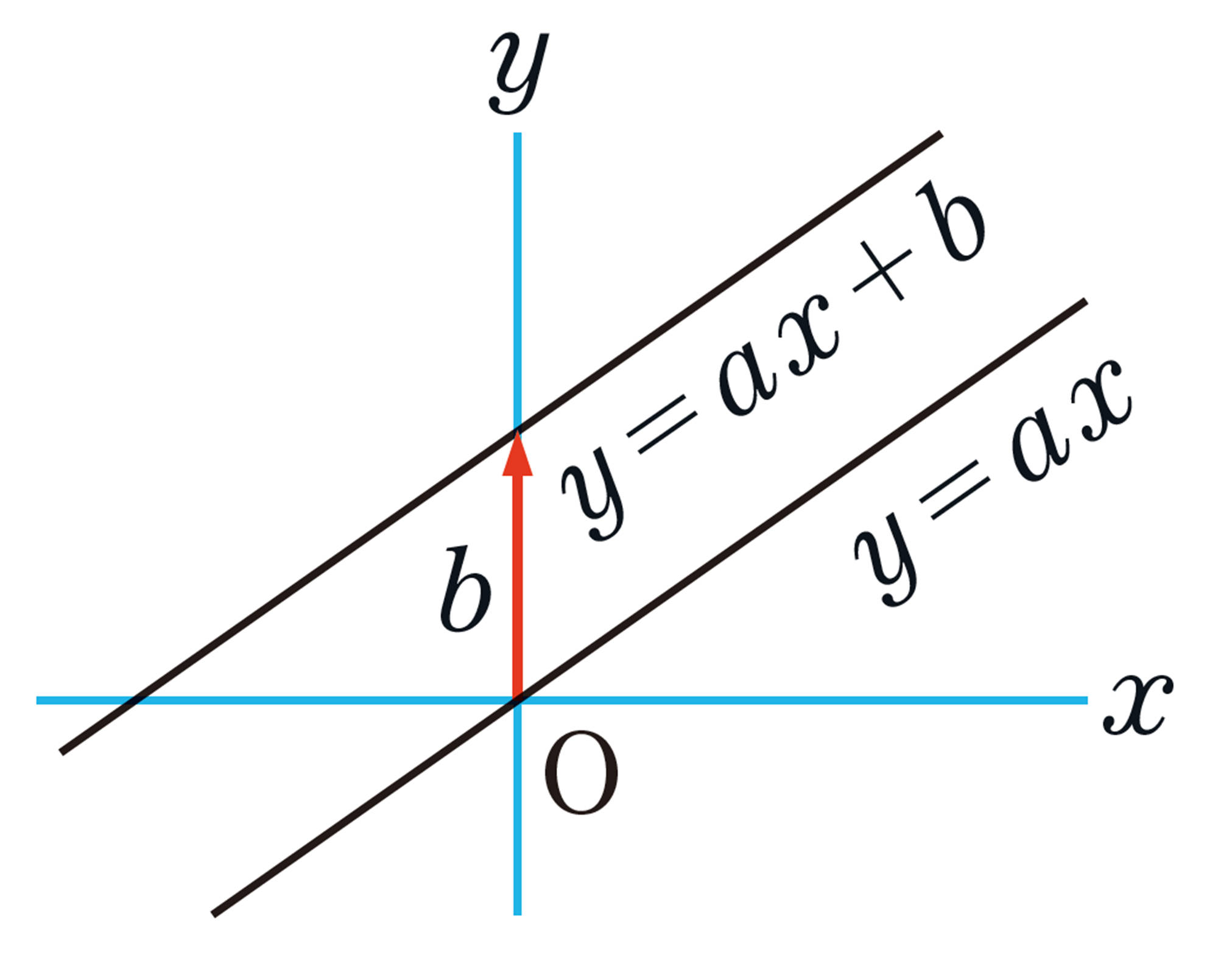
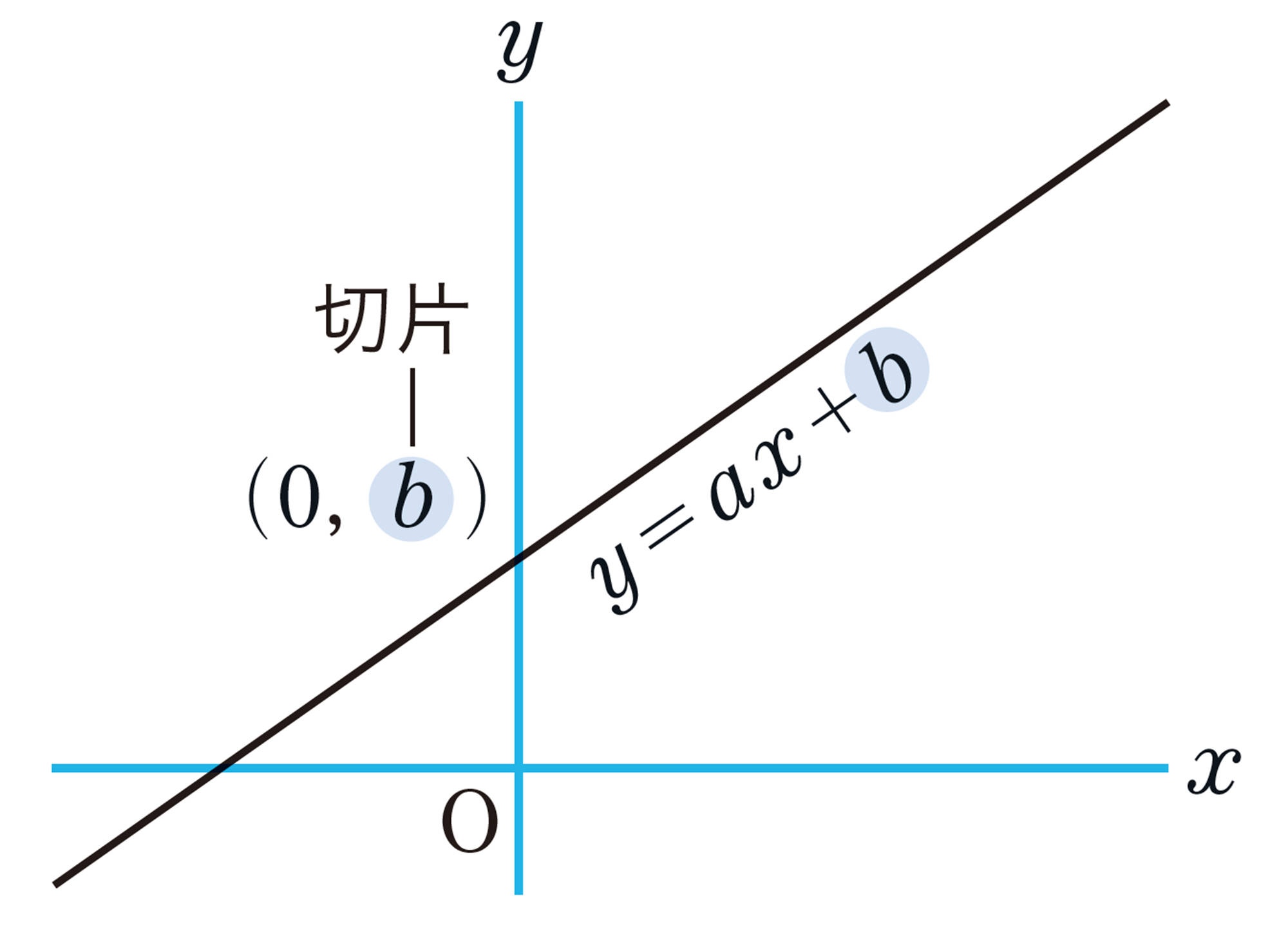
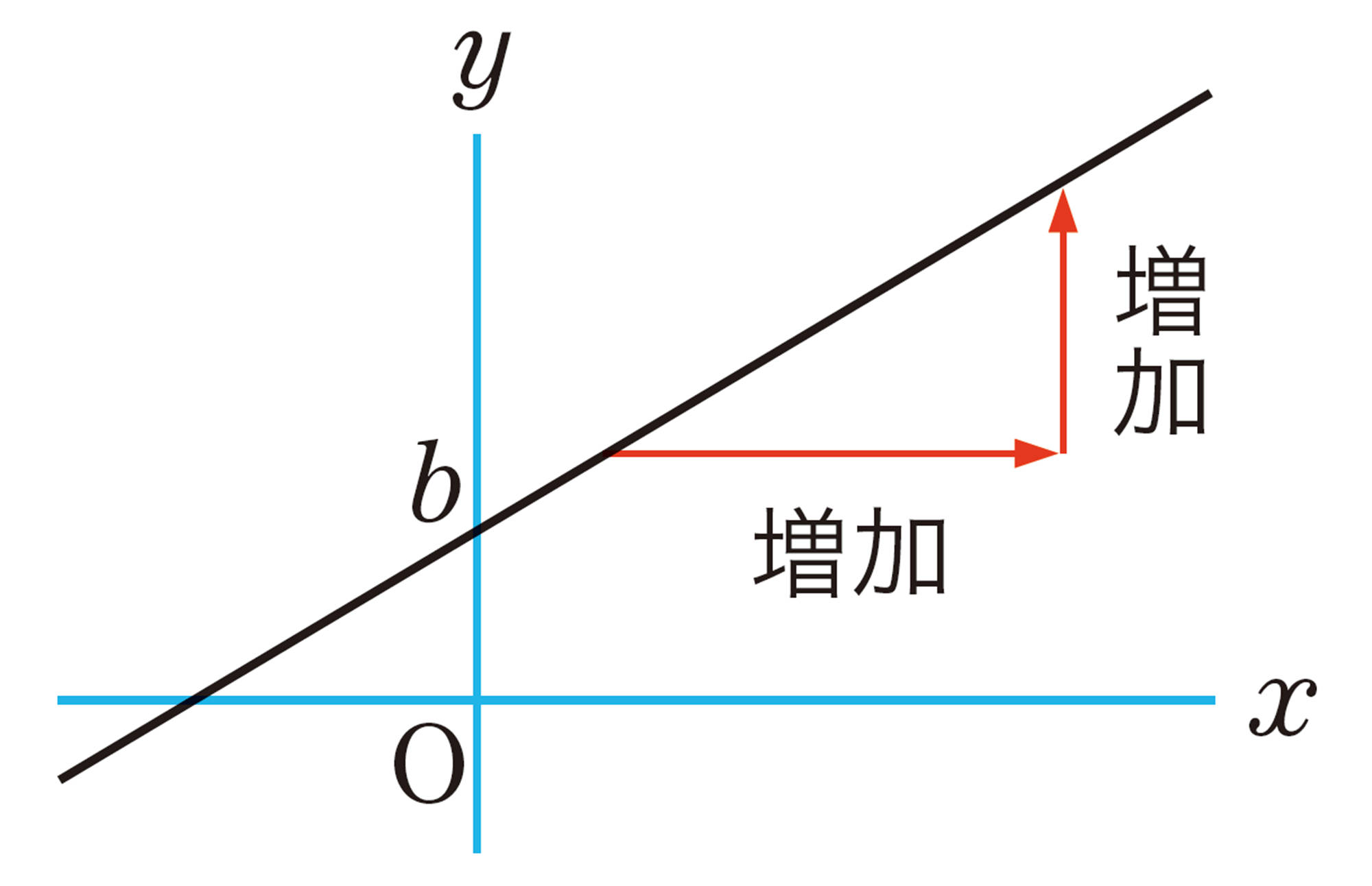
1次関数 [mathjax]\( y=ax+b \) の定数 [mathjax]\( b \) は, [mathjax]\( x=0 \) のときの [mathjax]\( y \) の値である。すなわち, [mathjax]\( b \) は, [mathjax]\( y=ax+b \) のグラフと [mathjax]\( y \) 軸との交点 [mathjax]\( (0,b) \) の [mathjax]\( y \) 座標である。
この [mathjax]\( b \) を,1次関数 [mathjax]\( y=ax+b \) のグラフの切片という。
たとえば, [mathjax]\( y=2x+3 \) のグラフの切片は3である。
<2年p.79>
グラフの傾き
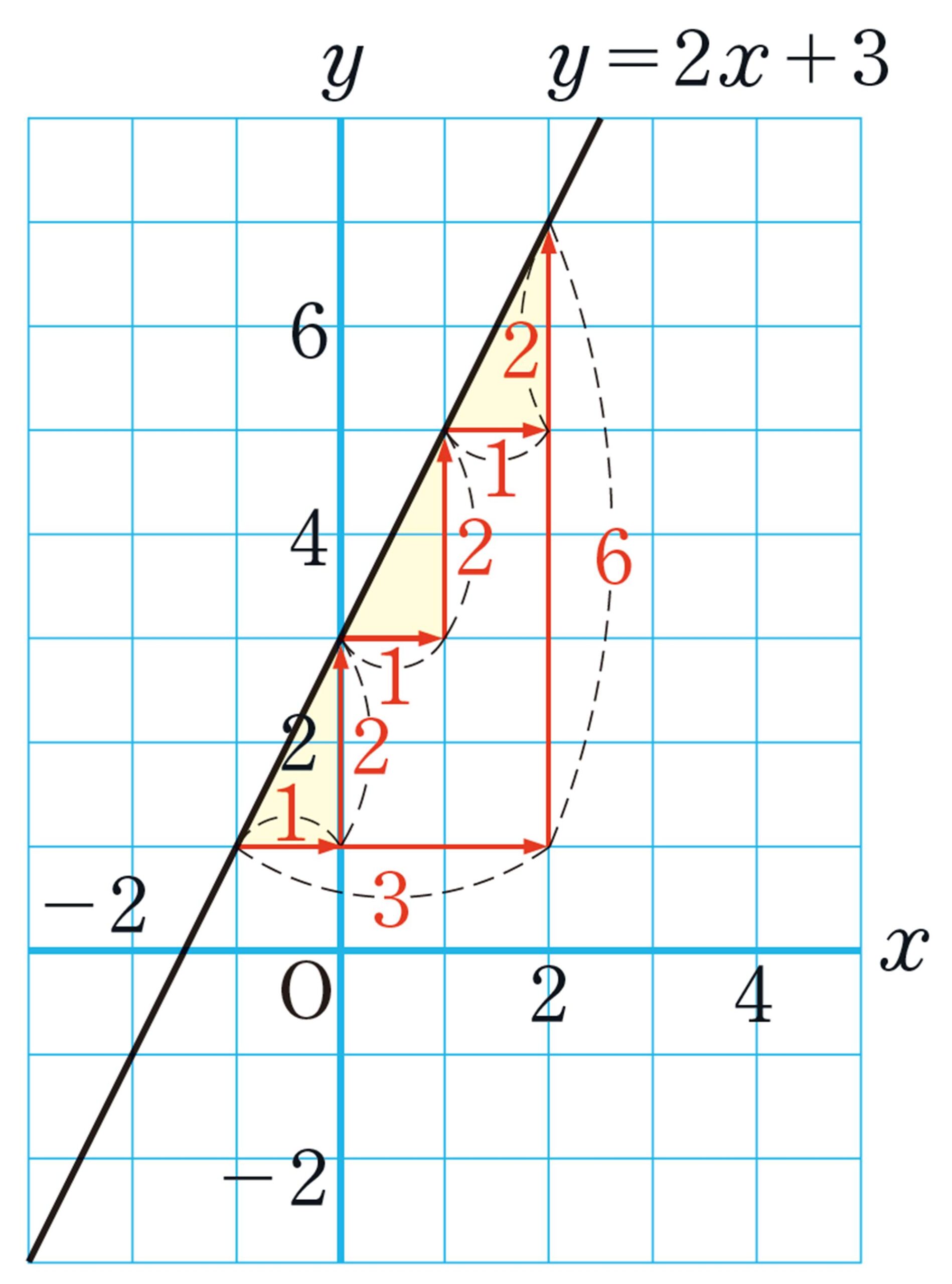
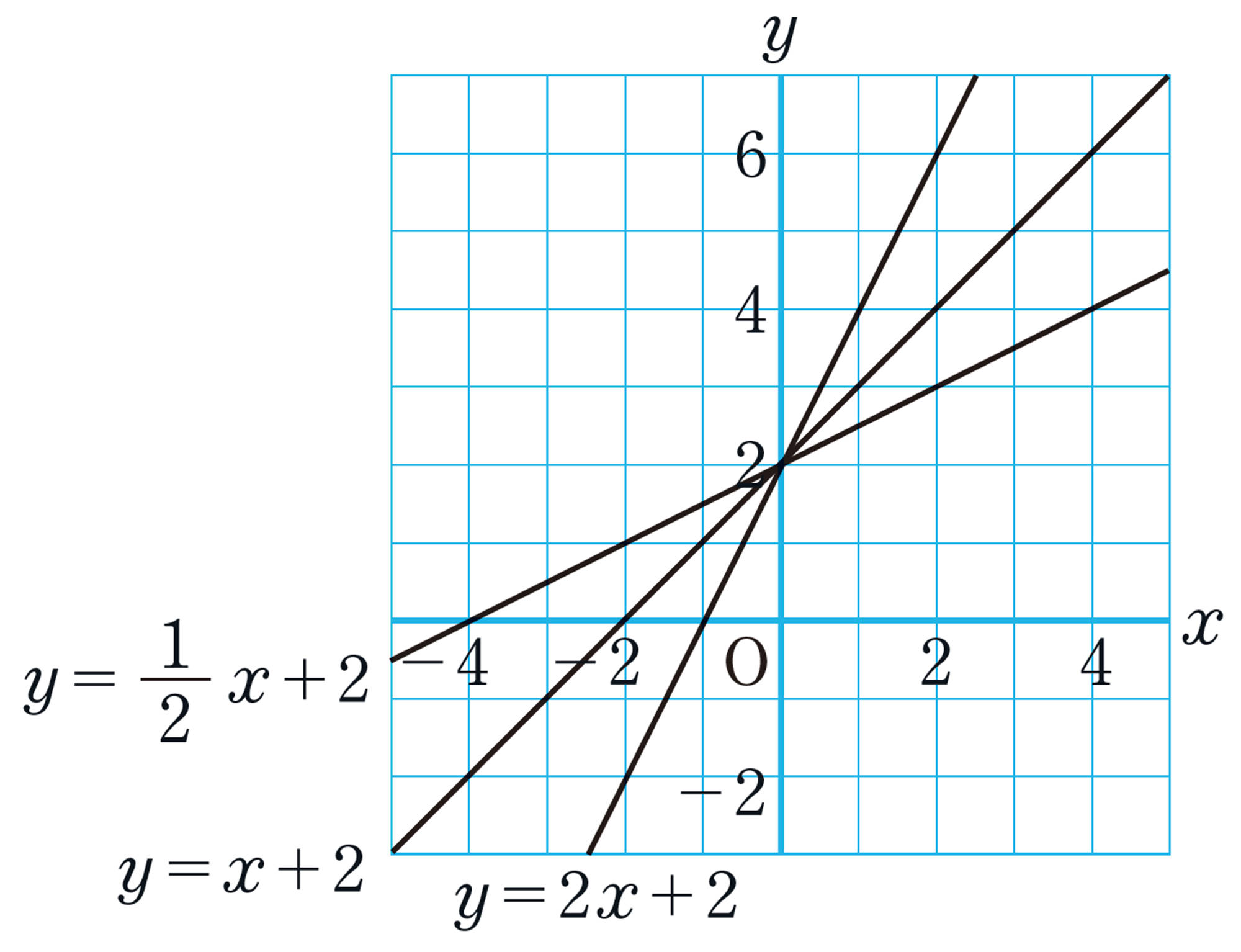
1次関数 [mathjax]\( y=ax+b \) の [mathjax]\( x \) の係数 [mathjax]\( a \) は,グラフではどのようなことを表しているか調べよう。
Q Question
見方・考え方
2つのグラフで似ているところはどこかな。
<2年p.80>
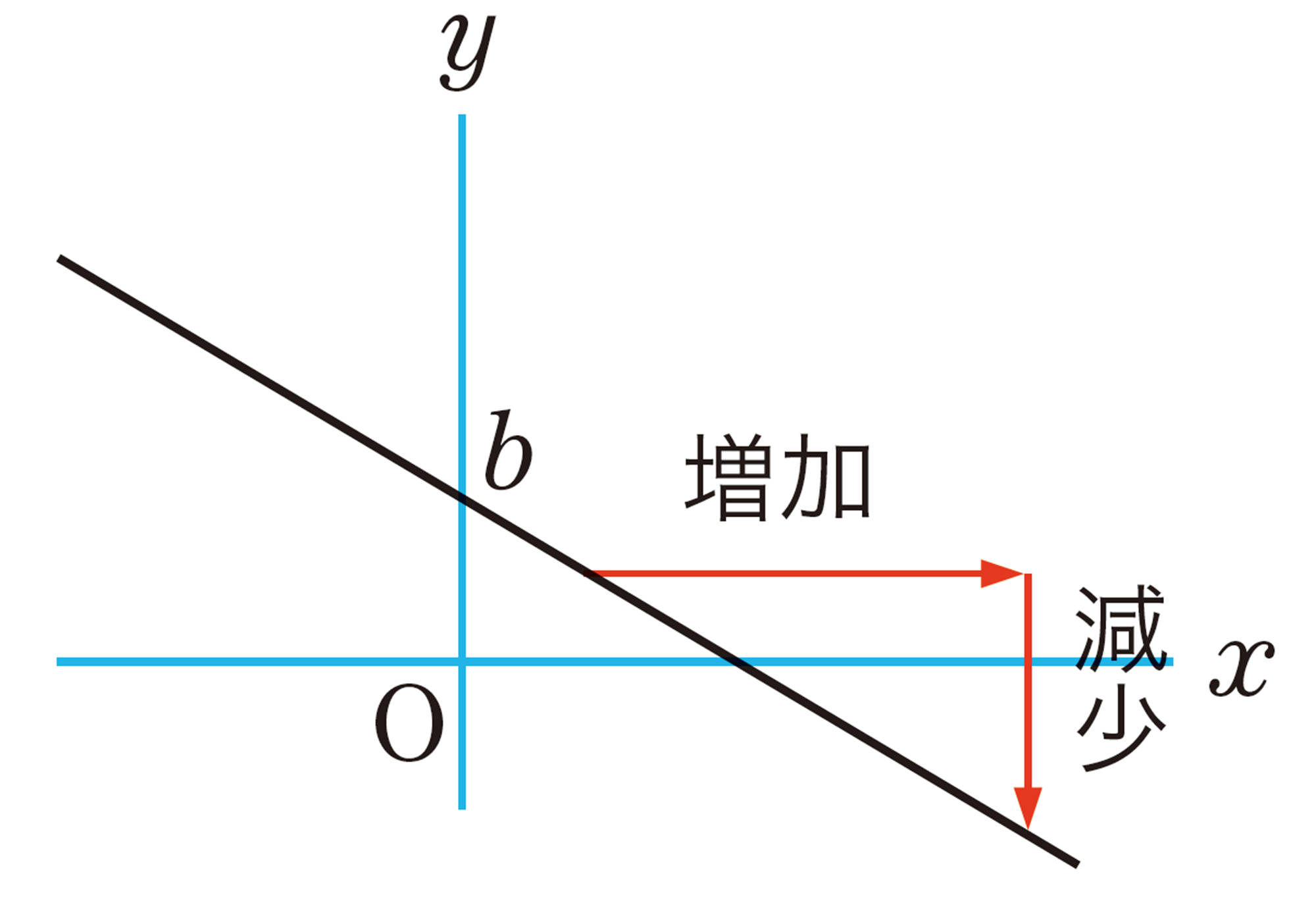
1次関数 [mathjax]\( y=ax+b \) のグラフの傾きぐあいは, [mathjax]\( x \) の係数 [mathjax]\( a \) によって決まる。このことから, [mathjax]\( a \) をその1次関数のグラフの傾きという。
たとえば,1次関数 [mathjax]\( y=2x+3 \) のグラフの傾きは2である。
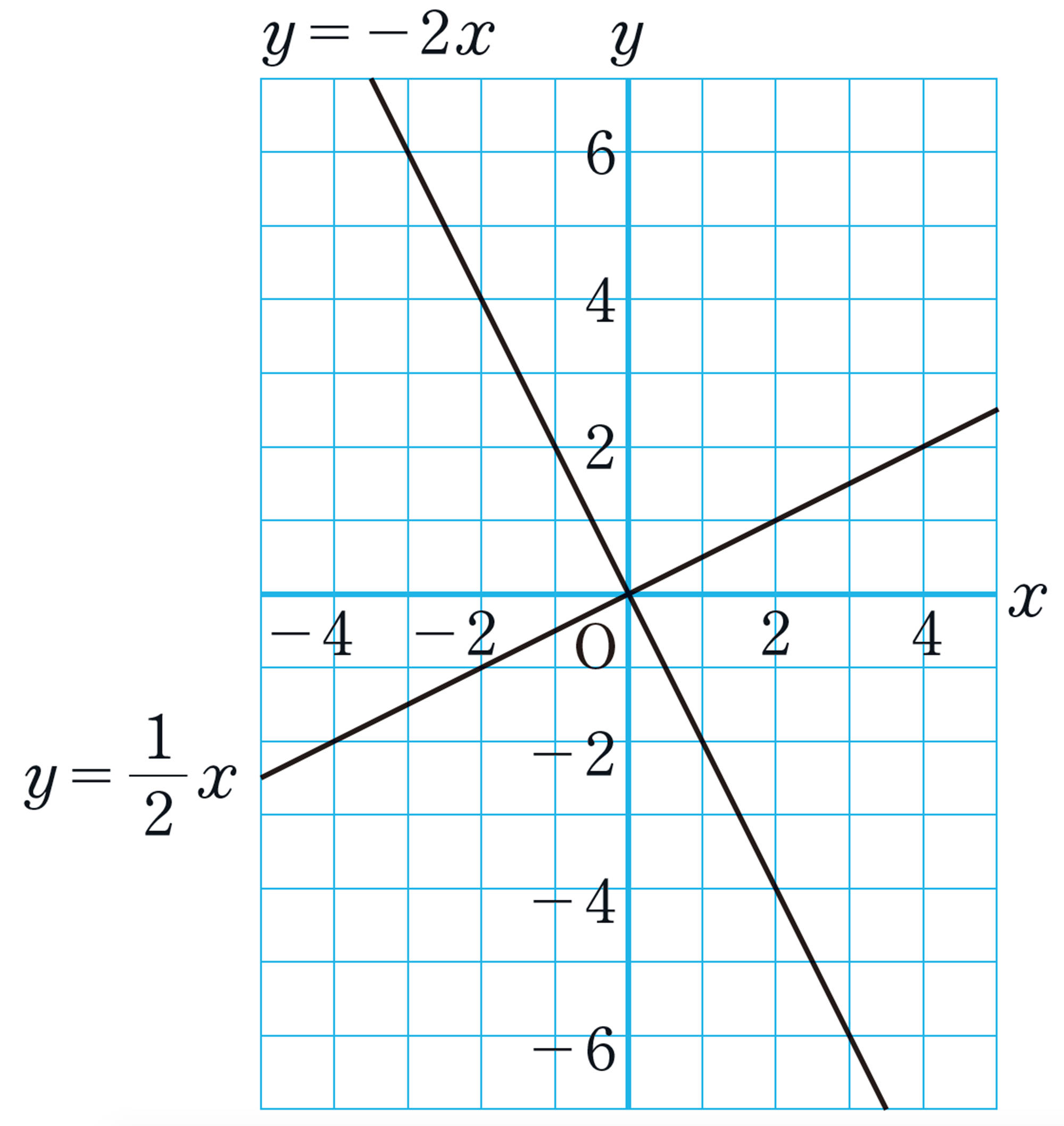
問 7 次の1次関数のグラフの傾きをいいなさい。
⑴ [mathjax]\( y= \dfrac{1}{2}x \)
⑵ [mathjax]\( y=-2x+4 \)
どんな関数なのかな? Tea Break
次の条件に合う関数の式を考えてみましょう。
[mathjax]\( y \) は [mathjax]\( x \) の関数で, [mathjax]\( x=-2 \) のとき [mathjax]\( y=1 \) , [mathjax]\( x=1 \) のとき [mathjax]\( y=-2 \) である。

比例定数が[mathjax]\(-1\),切片が[mathjax]\(-1\)の1次関数 [mathjax]\( y=-x-1 \) だね。
[mathjax]\( x \times y=-2 \) になるから,反比例 [mathjax]\( y=- \dfrac{2}{x} \) だね。

問題の条件に合う関数は,1次関数 [mathjax]\( y=-x-1 \) や反比例 [mathjax]\( y=- \dfrac{2}{x} \) が考えられます。
このように,関数の種類やグラフの形が示されていないと,関数の式を1つに特定できないことがあります。
<2年p.81>
これまで調べたことから,1次関数のグラフについて,次のようにまとめることができる。