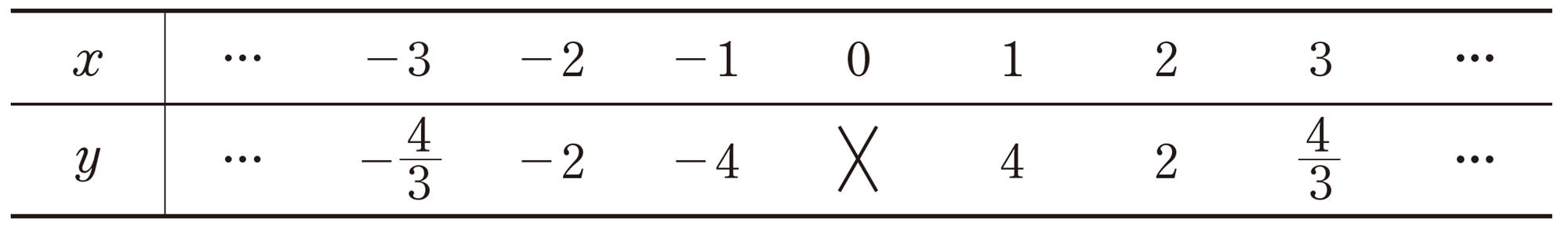<2年p.68>
ふりかえり
【関数】
ともなって変わる2 つの変数 [mathjax]\( x \) , [mathjax]\( y \) があって, [mathjax]\( x \) の値を決めると,それに対応する [mathjax]\( y \) の値がただ1つ決まるとき, [mathjax]\( y \) は [mathjax]\( x \) の関数である。
関数を考えるときは,2つの数量の対応の関係を調べたね。

数直線で負の数を表すときと同じように,座標も負の数が表せるように広げて考えたね。

比例や反比例は,式の形に表して考えるようにしたね。

<2年p.72>
1 1次関数
Q Question
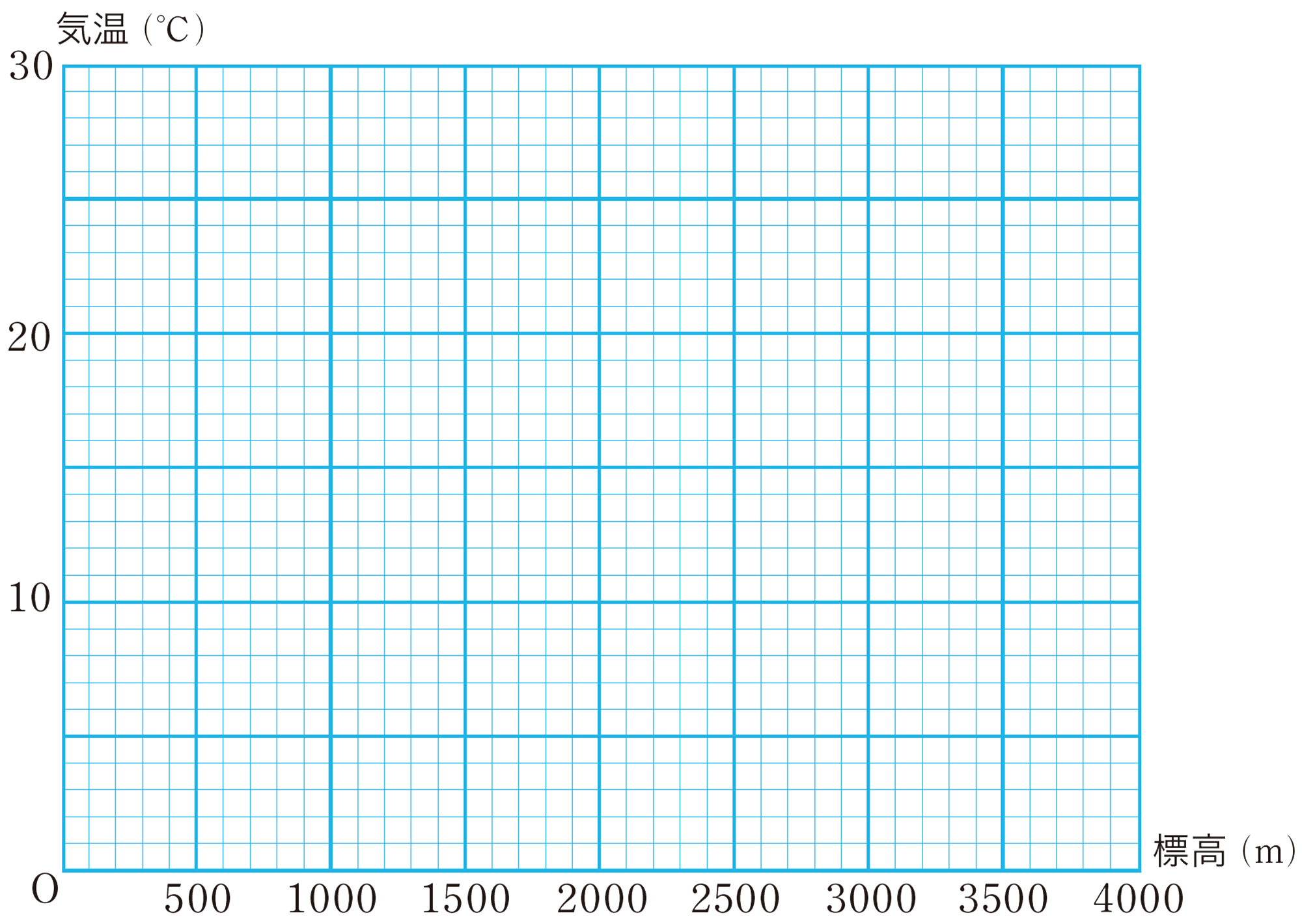
前ページの【1】で,標高を [mathjax]\( x \) m,気温を [mathjax]\( y \) ℃として,その関係をもとに,頂上の気温を予測することができるでしょうか。

標高が決まると,気温も1つに決まるから,気温は標高の関数といえるね。
でも,今までに学習した比例や反比例とはちがうみたいだよ。

見方・考え方
これまでと同じように,2つの数量を関数として考えられるかな。
目標 ▷ ともなって変わる2つの数量の関係を使って予測しよう。
Qでは, [mathjax]\( x \) の値を決めると,それに対応する [mathjax]\( y \) の値がただ1つ決まるから, [mathjax]\( y \) は [mathjax]\( x \) の関数である。
また,地上0mの気温が25℃で,1km上昇するごとに6℃ずつ気温が下がっているとみなすことができる。このとき,地上 [mathjax]\( x \) kmの気温を [mathjax]\( y \) ℃とすると, [mathjax]\( x \) と [mathjax]\( y \) の関係は,次の式で表すことができる。
[mathjax]\( y=-6x+25 \)
気温は,地上11kmまでは,1km上昇するごとに,約6℃ずつ下がるよ。

問 1 Qで,標高3776mの気温は約何℃と考えられますか。上で求めた式や,前ページの表やグラフを用いて,小数第一位まで求めなさい。
<2年p.73>
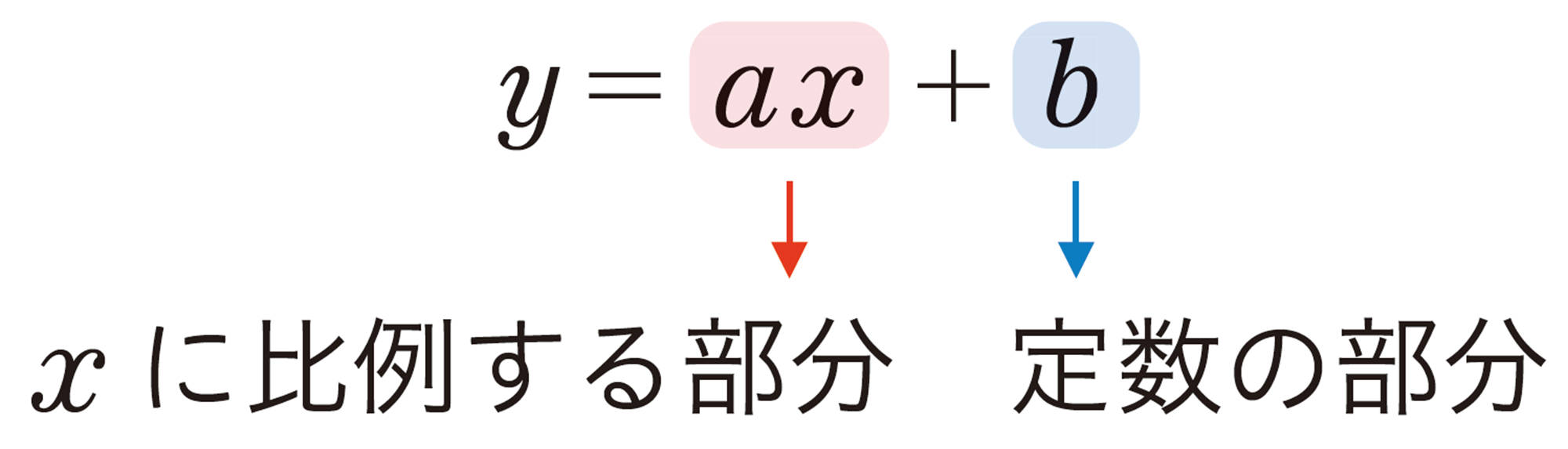
比例 [mathjax]\( y=ax \) は,1次関数 [mathjax]\( y=ax+b \) において, [mathjax]\( b=0 \) の場合と考えることができる。したがって,比例も1次関数である。
問 3 次の⑴〜⑷で, [mathjax]\( y \) を [mathjax]\( x \) の式で表しなさい。また, [mathjax]\( y \) は [mathjax]\( x \) の1次関数であるといえますか。
⑴ 縦6cm,横 [mathjax]\( x \) cmの長方形のまわりの長さが [mathjax]\( y \) cmである。
⑵ 28kmの道のりを [mathjax]\( x \) 時間で走ったときの速さが時速 [mathjax]\( y \) kmである。
⑶ [mathjax]\( x \) 円の品物を2割引きで買ったときの代金が [mathjax]\( y \) 円である。
⑷ 半径 [mathjax]\( x \) cmの円の面積が [mathjax]\( y \) cm²である。
どんなことがわかったかな
身のまわりのことがらの中には,1次関数とみなして考えられるものがあります。
次の課題へ!
1次関数はどんな変化のしかたをするのかな?
P.74

<2年p.74>
変化の割合
Q Question
次の①〜③の関数について,対応する [mathjax]\( x \) , [mathjax]\( y \) の値を,次の表のようにまとめました。
① 比例 [mathjax]\( y=4x \)
② 反比例 [mathjax]\( y= \dfrac{4}{x} \)
③ 1次関数 [mathjax]\( y=4x+3 \)
これらの関数について, [mathjax]\( x \) の値が増えると [mathjax]\( y \) の値はどのように変化しているか気づいたことを話し合ってみましょう。

1年で学んだ比例や反比例と1次関数はどこがちがうのかな。
見方・考え方
どこに着目すると,ちがいがわかりやすいかな。
目標 ▷ 1次関数の変化のしかたについて調べよう。
問 4 Qの①〜③の関数について, [mathjax]\( x \) の値が増えたときの [mathjax]\( y \) の値の変化のしかたがつねに同じものはどれとどれですか。
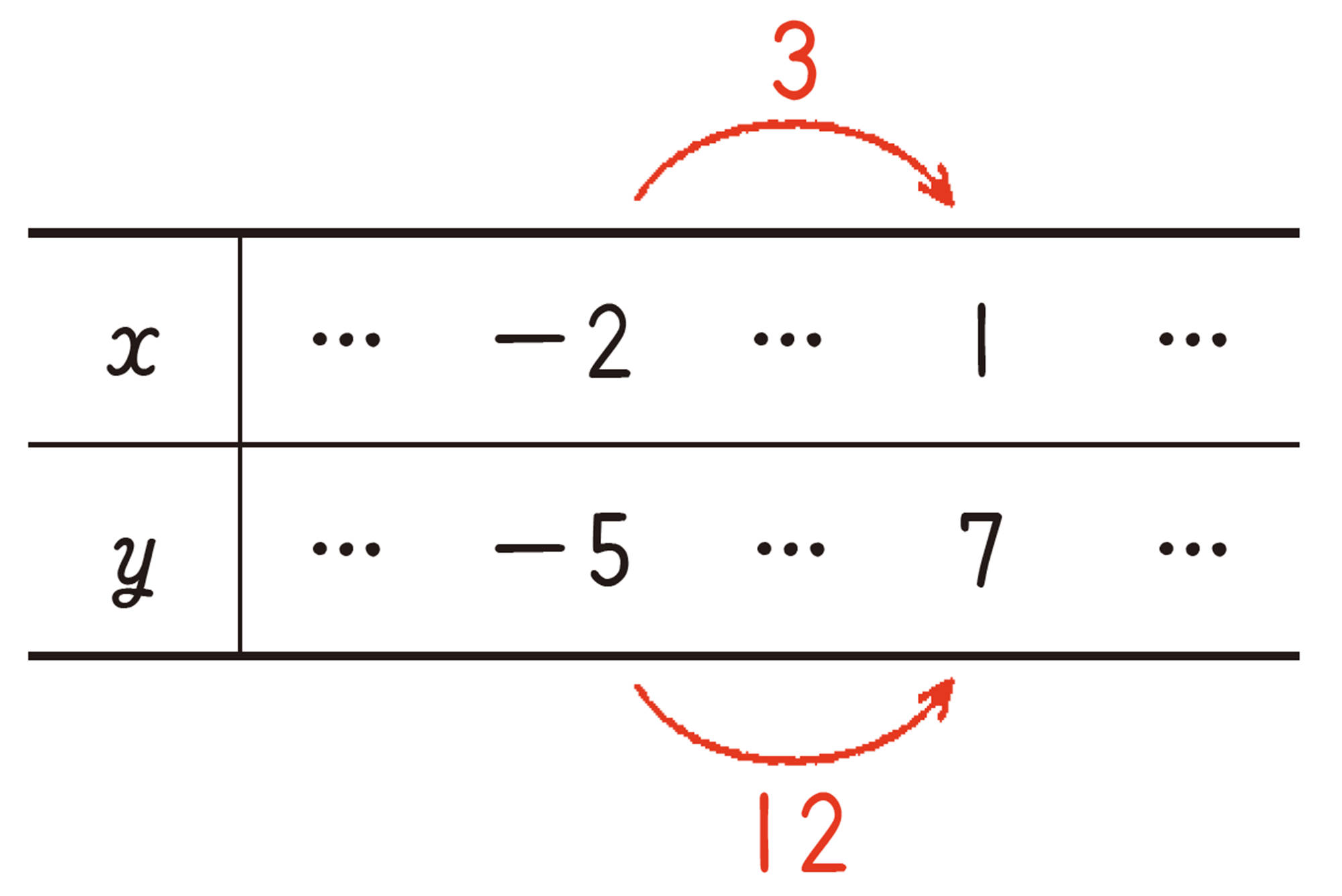
例 2 1次関数 [mathjax]\( y=4x+3 \) で, [mathjax]\( x \) の値が[mathjax] \(-2\)から1まで増加したときの [mathjax]\( x \) の増加量と [mathjax]\( y \) の増加量を比べなさい。
解答
<2年p.75>
[mathjax] \( x \) の増加量に対する [mathjax] \( y \) の増加量の割合を,変化の割合という。
例2では,変化の割合は次のようにして求めることができる。
[mathjax] \( \dfrac{(y \mathsf{の増加量})}{(x \mathsf{の増加量})}= \dfrac{7-(-5)}{1-(-2)}= \dfrac{12}{3}=4 \)
[mathjax] \( ( \mathsf{変化の割合})= \dfrac{(y \mathsf{の増加量})}{(x \mathsf{の増加量})} \)
問 5 1次関数 [mathjax] \( y=4x+3 \) で, [mathjax] \( x \) の値が次のように増加したときの変化の割合を求めなさい。また,⑴,⑵を比べ,気づいたことをいいなさい。
⑴ 0から3まで
⑵ [mathjax] \(-3\)から1まで
問 6 1次関数 [mathjax] \( y=-3x+1 \) で, [mathjax] \( x \) の値が次のように増加したときの変化の割合を求めなさい。また,⑴,⑵を比べ,気づいたことをいいなさい。
⑴ [mathjax] \(-3\)から0まで
⑵ 2から4まで
1次関数の変化の割合
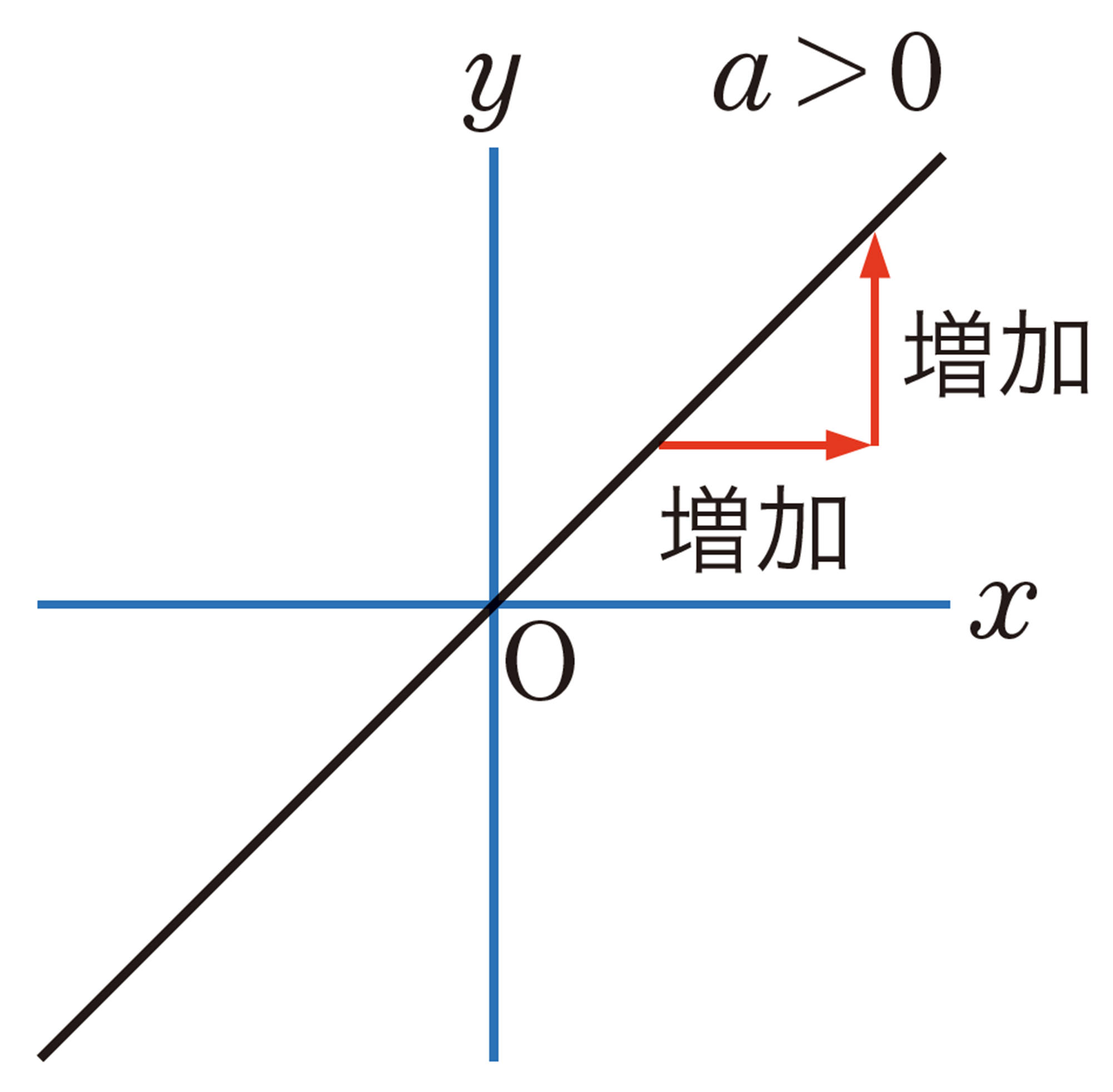
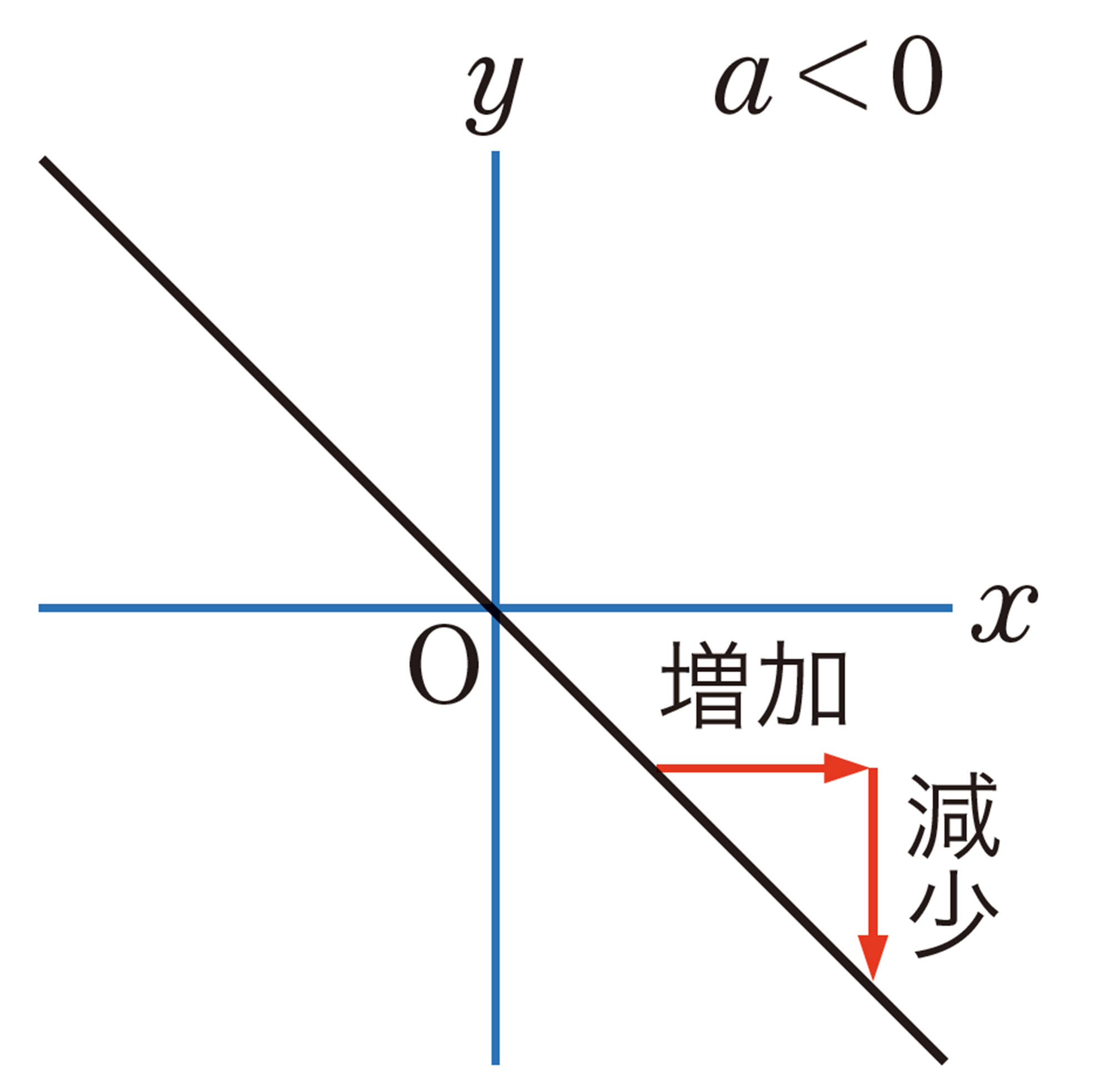
1次関数 [mathjax] \( y=ax+b \) の変化の割合は一定で, [mathjax] \( x \) の係数 [mathjax] \( a \) に等しい。
変化の割合
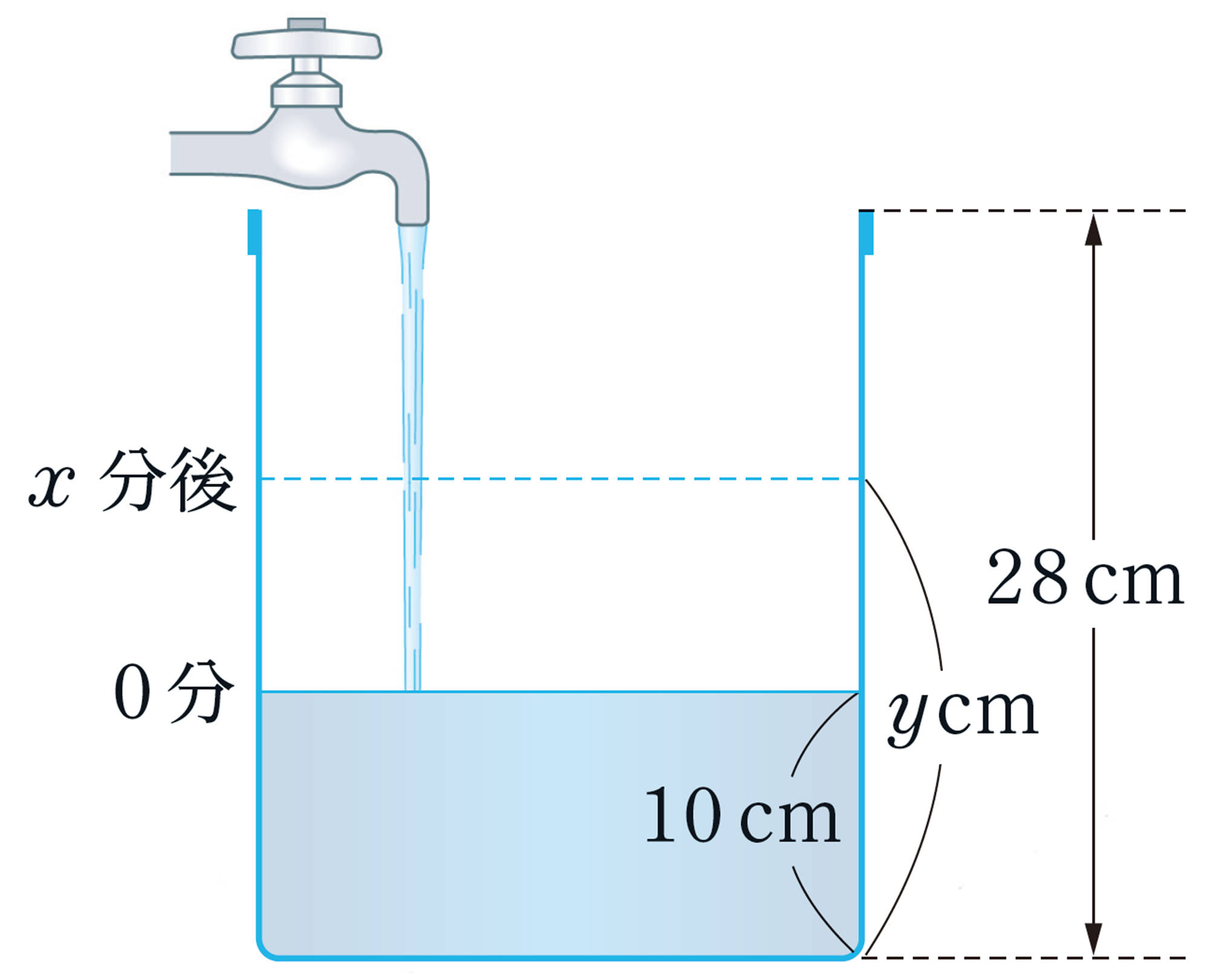
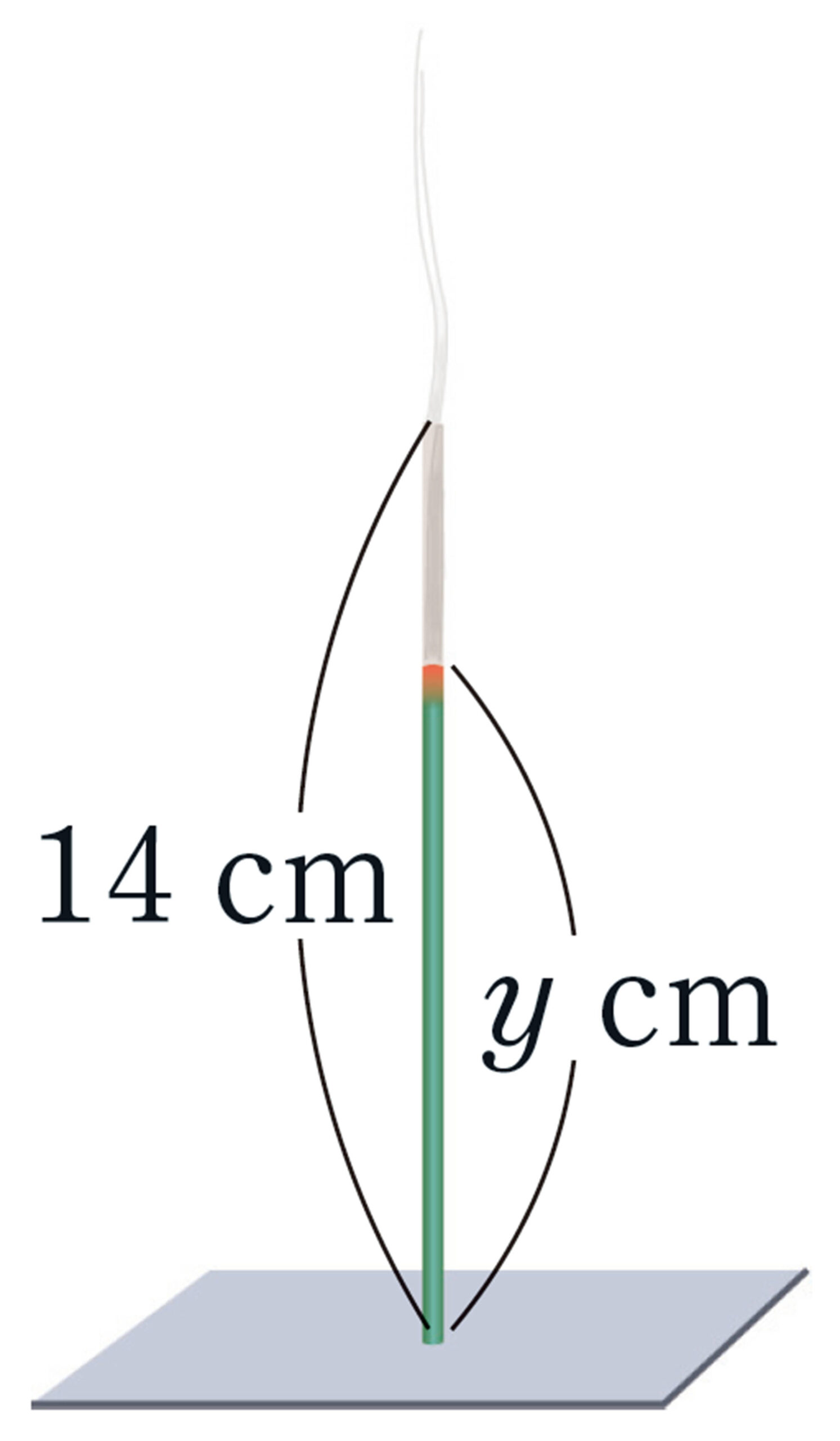
問 7 73ページの例1の1次関数 [mathjax] \( y=3x+10 \) や,問2の1次関数 [mathjax] \( y=-\dfrac{1}{2}x+14 \) の変化の割合をいいなさい。また,それは何を表していますか。
問 8 1次関数 [mathjax] \( y=4x+3 \) と [mathjax] \( y=-3x+1 \) で, [mathjax] \( x \) の増加量が3のときの [mathjax] \( y \) の増加量を,それぞれ求めなさい。
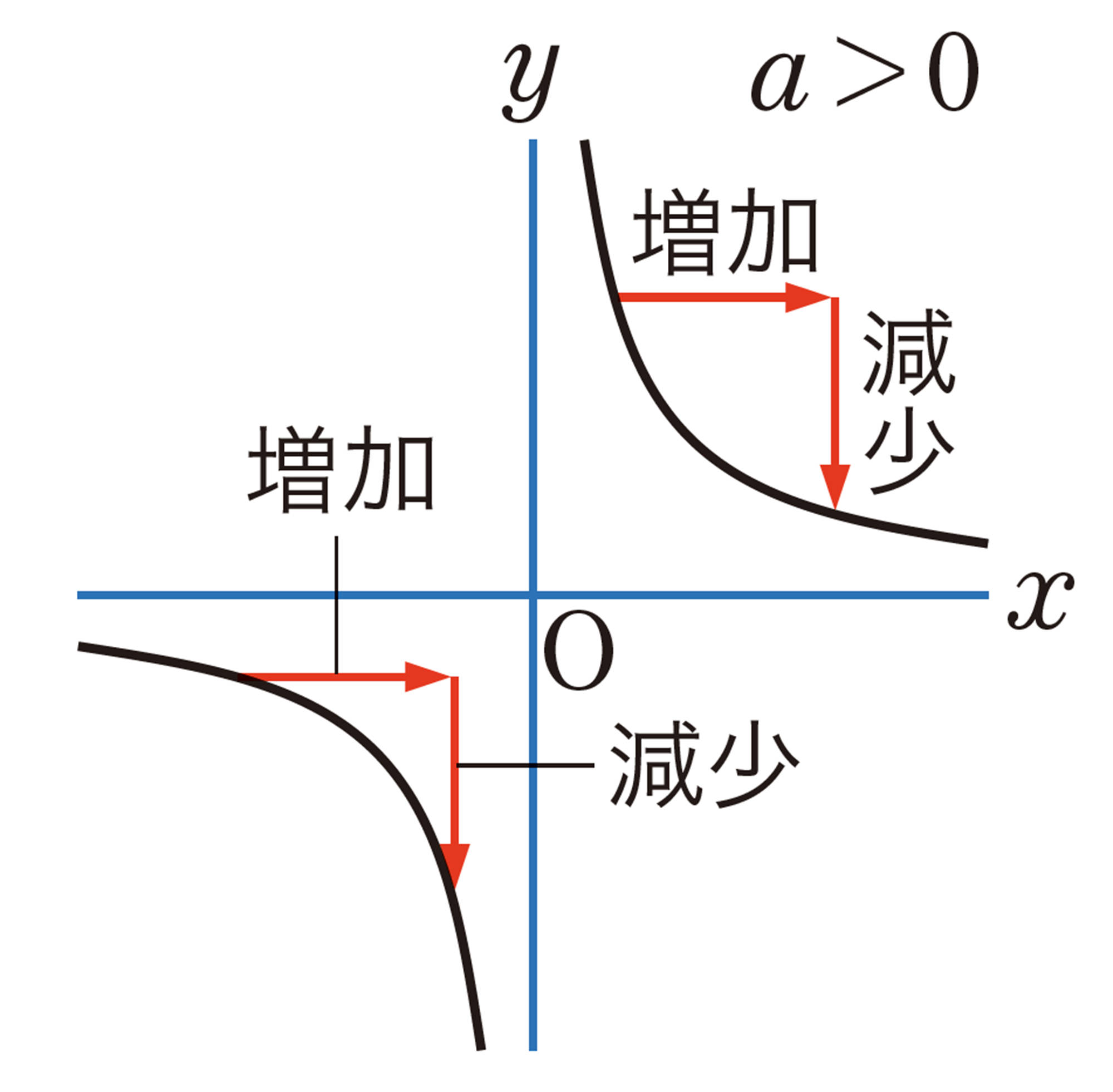
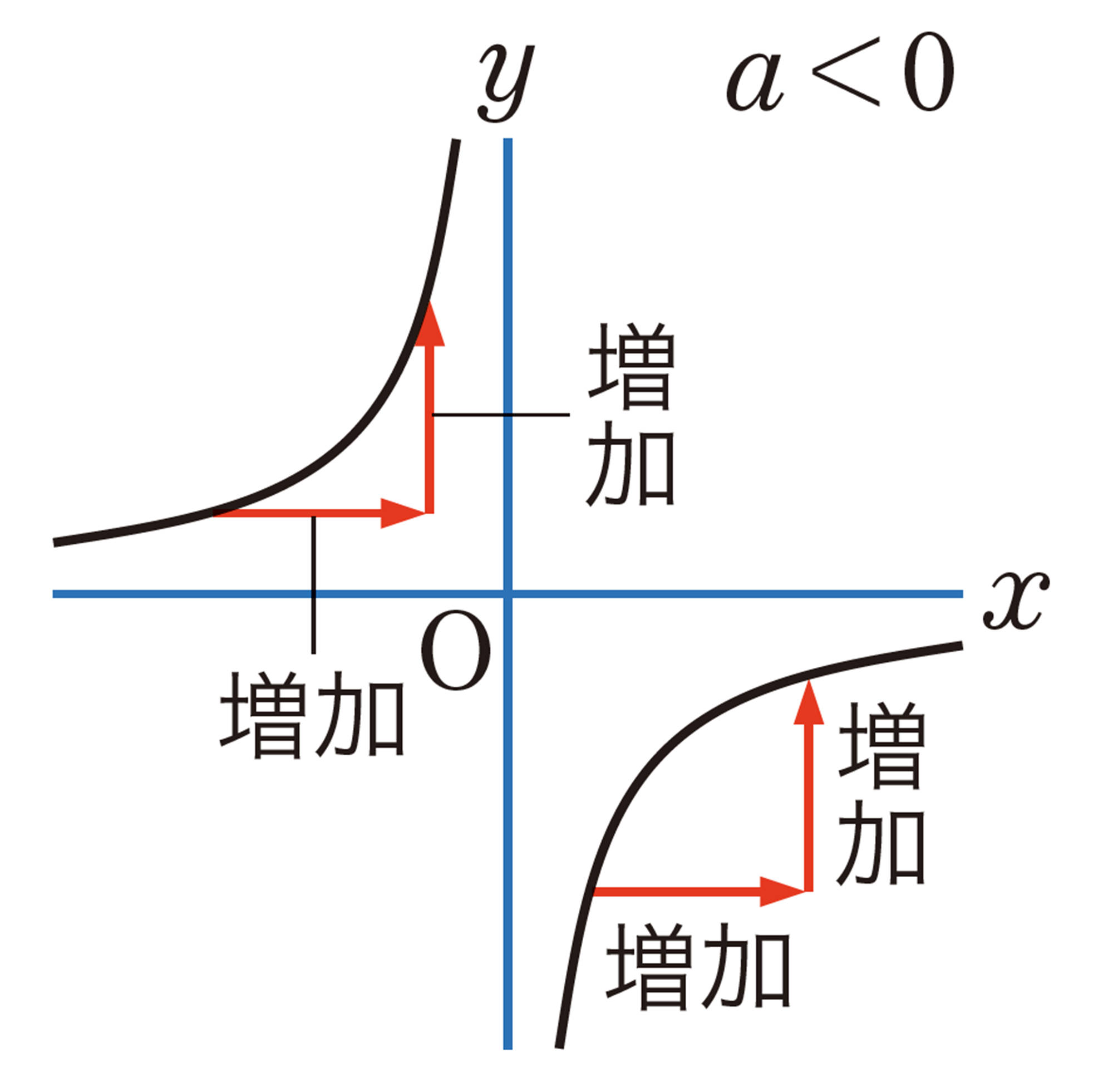
問 9 反比例 [mathjax] \( y= \dfrac{18}{x} \) で, [mathjax] \( x \) の値が次のように増加したときの変化の割合を求めなさい。
また,反比例では,変化の割合は一定といえますか。
⑴ 1 から3 まで
⑵ [mathjax] \(-9\) から[mathjax] \(-2\) まで
どんなことがわかったかな
変化の割合は [mathjax] \( x \) の増加量に対する [mathjax] \( y \) の増加量の割合を表しており, 1次関数では一定の値になります。
次の課題へ!
1次関数のグラフは,どんな形になるのかな?
P.76