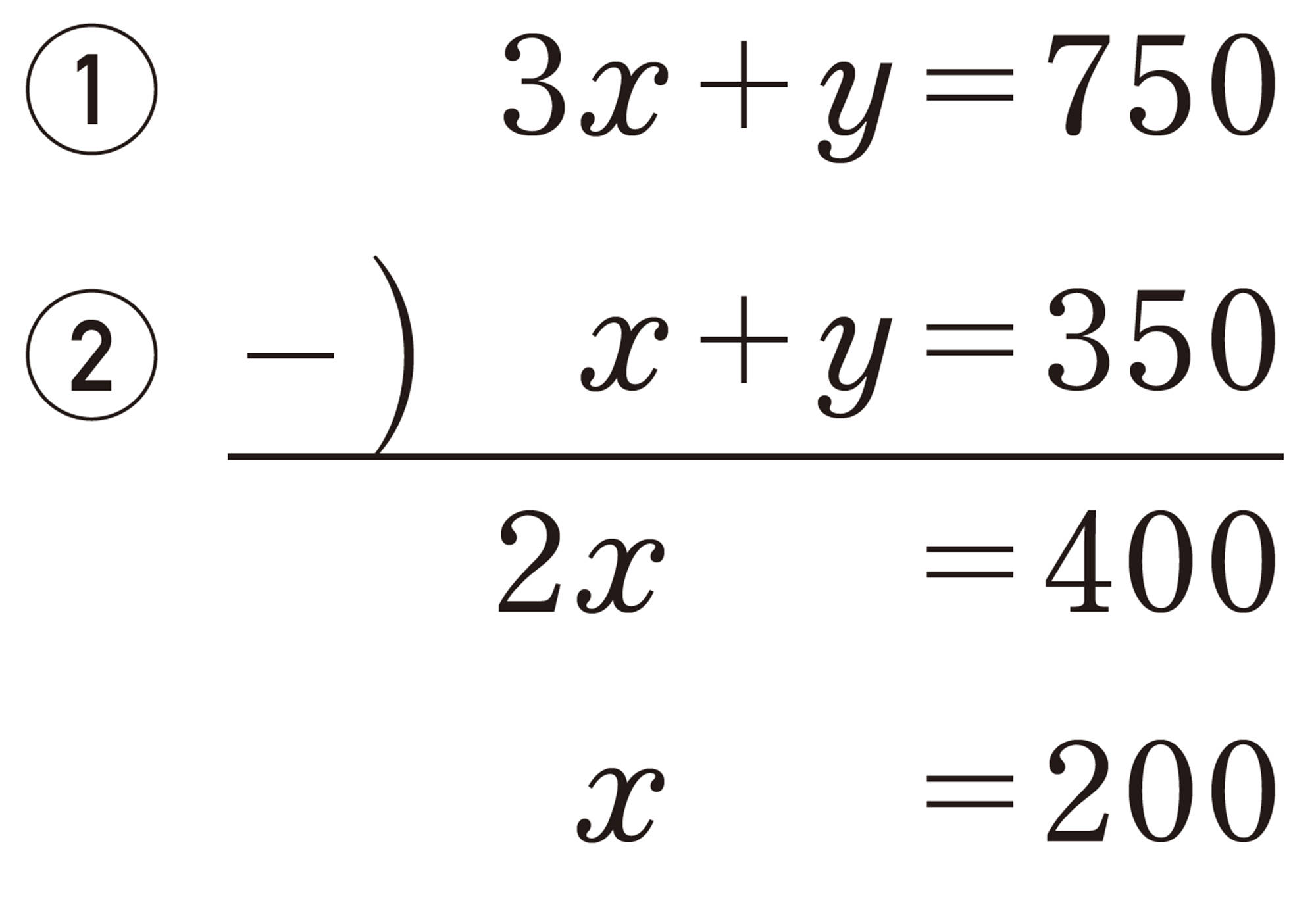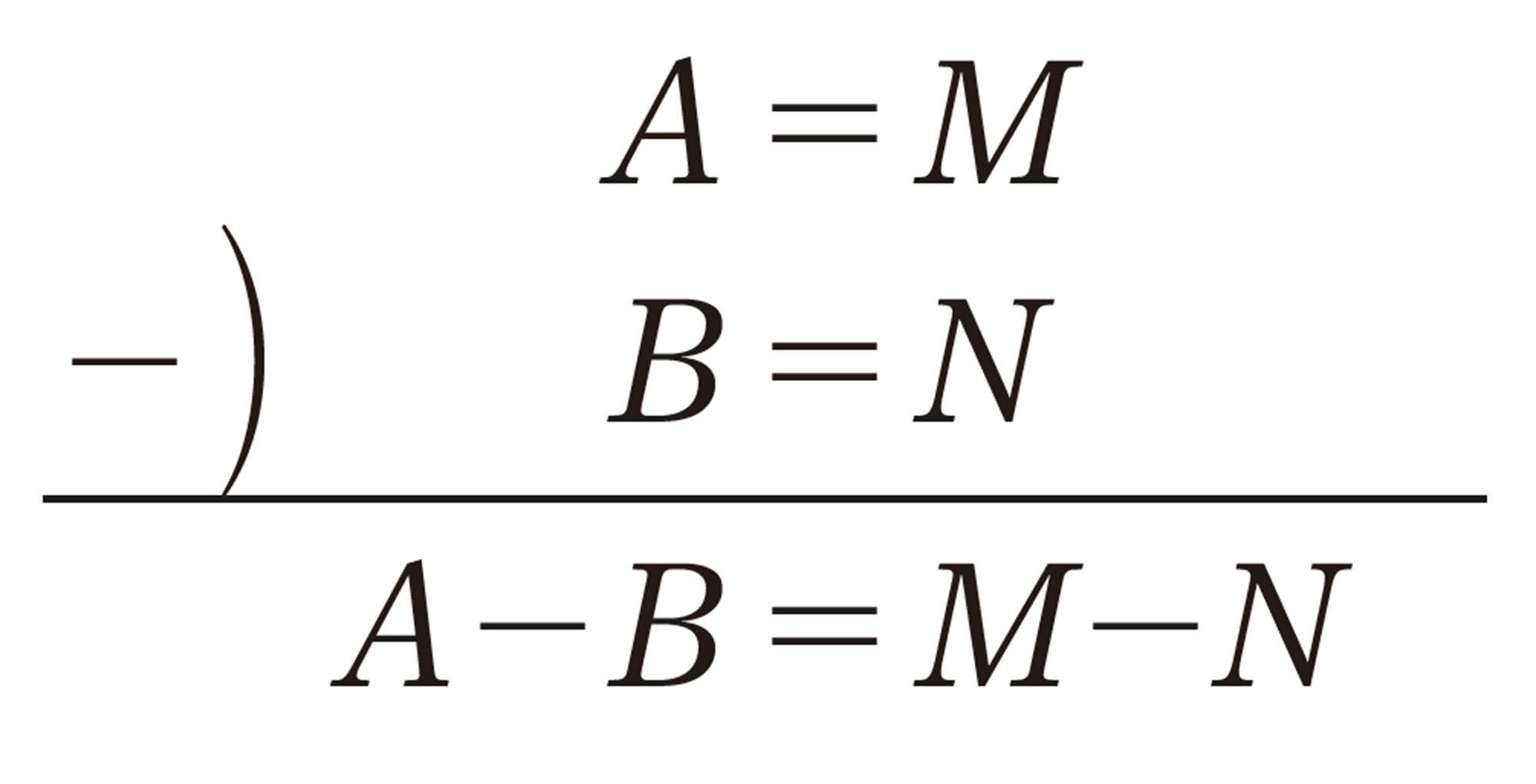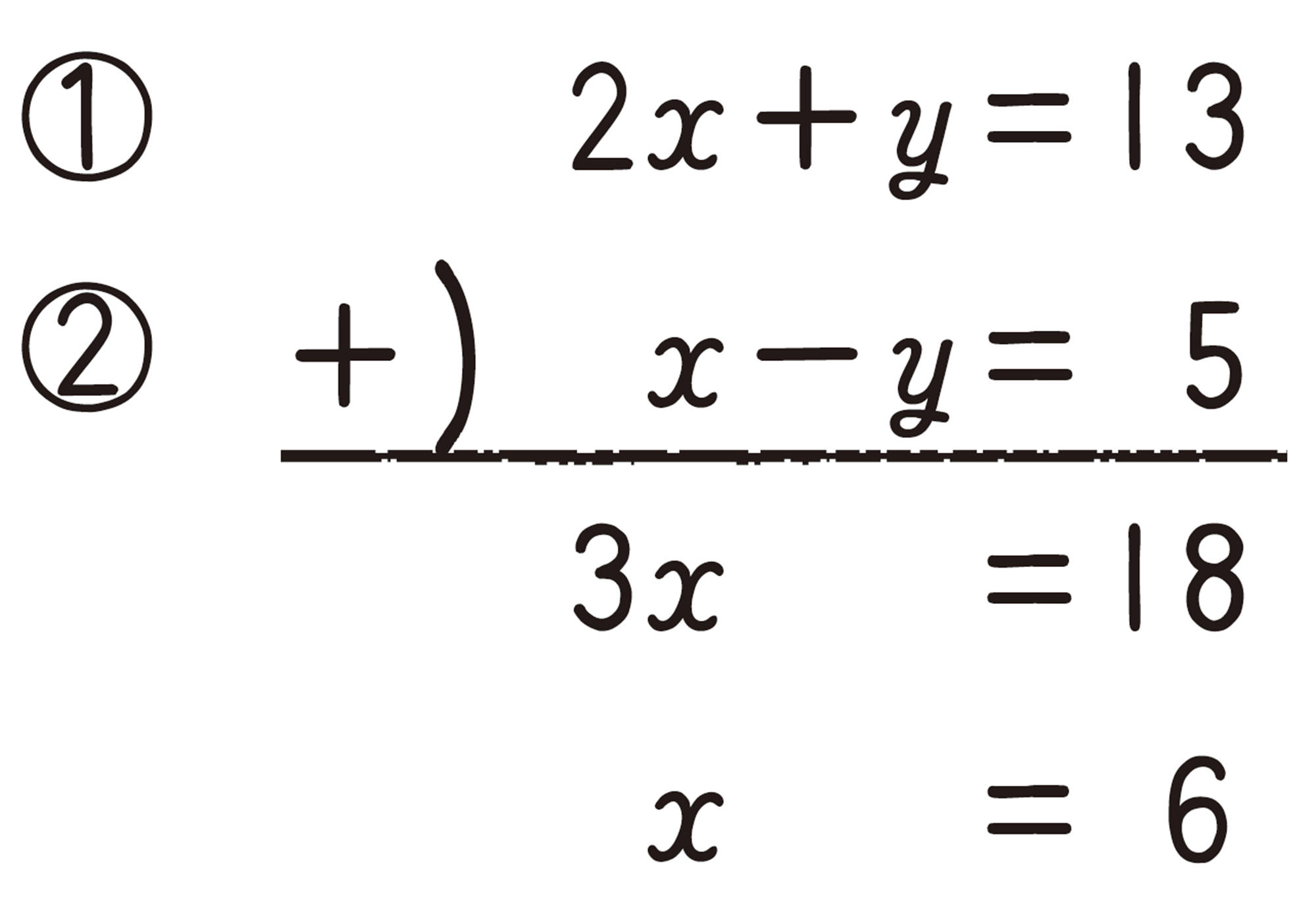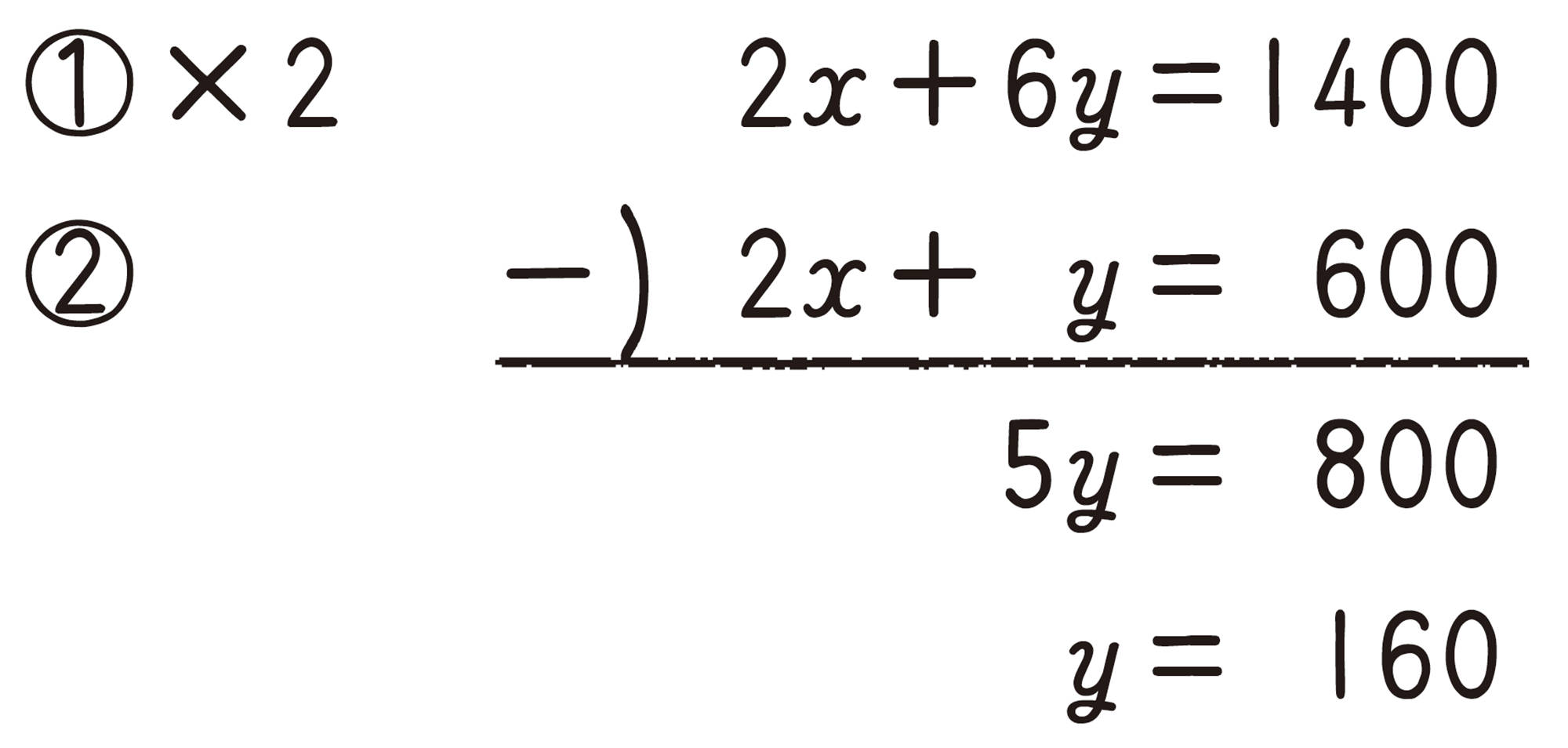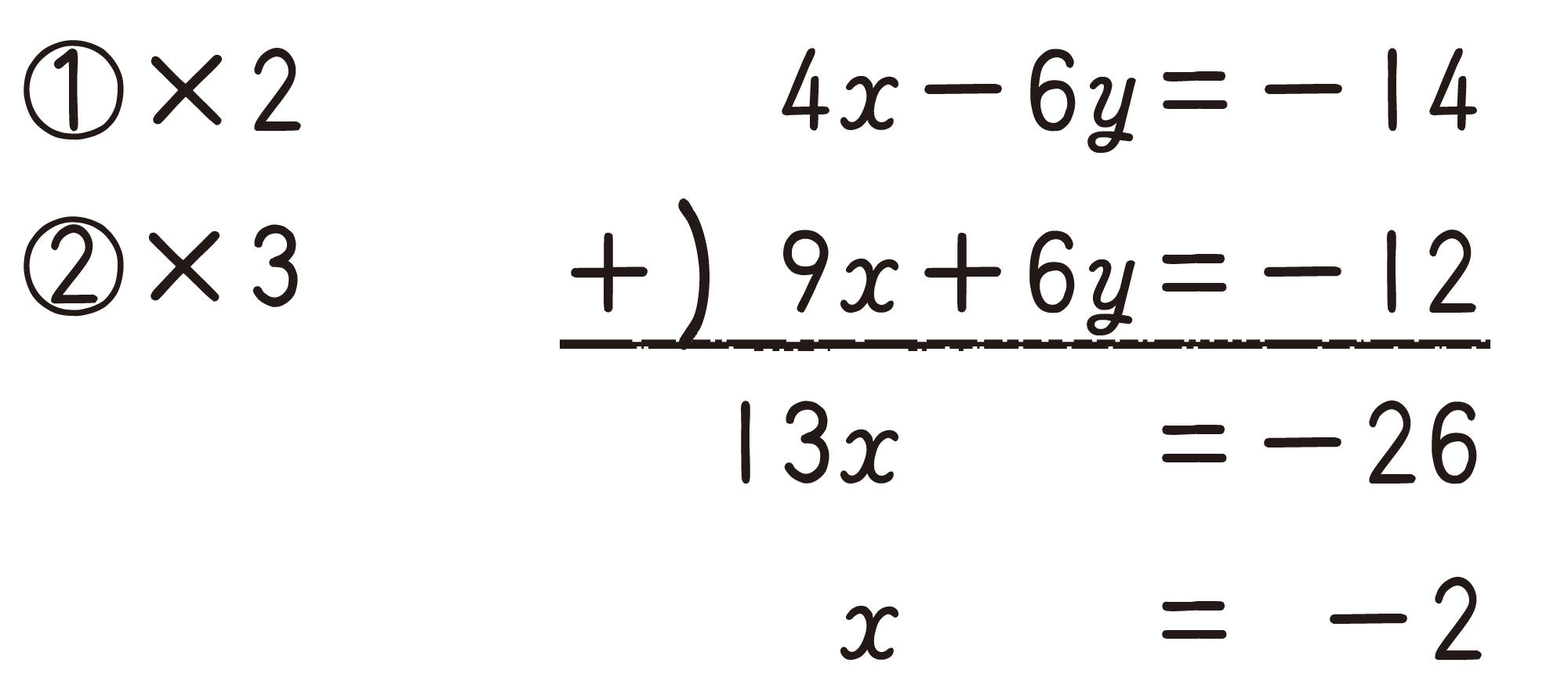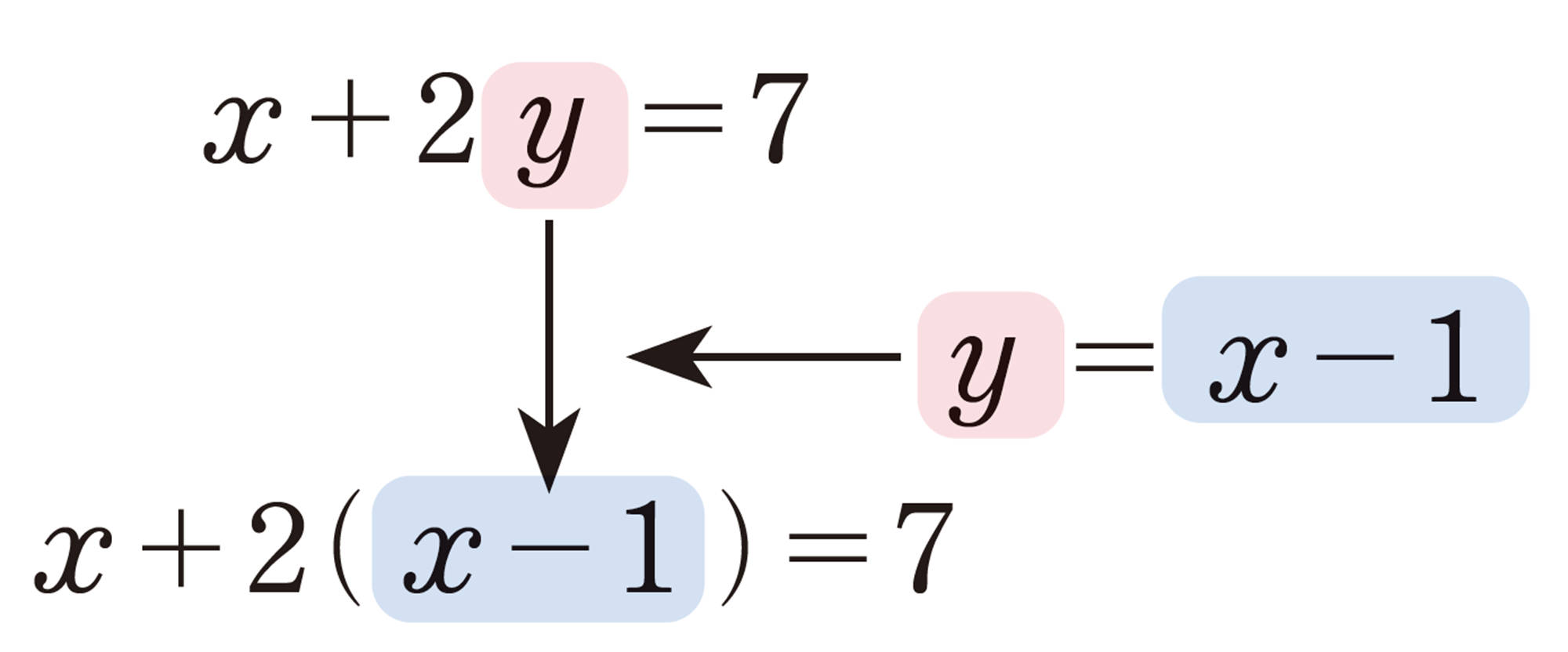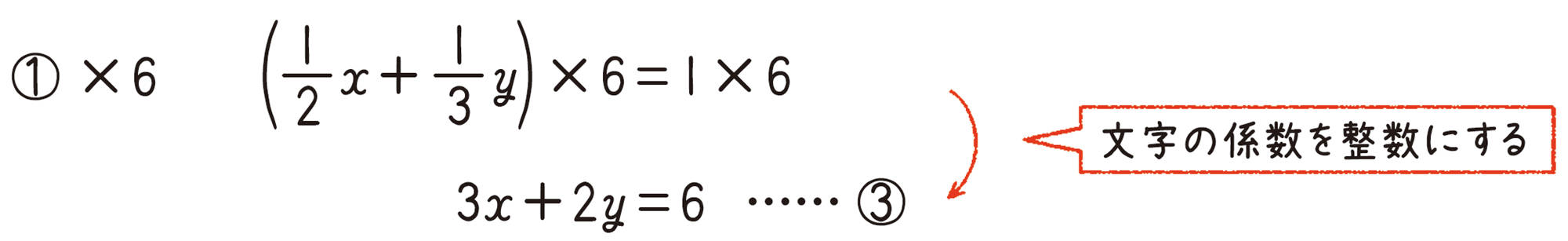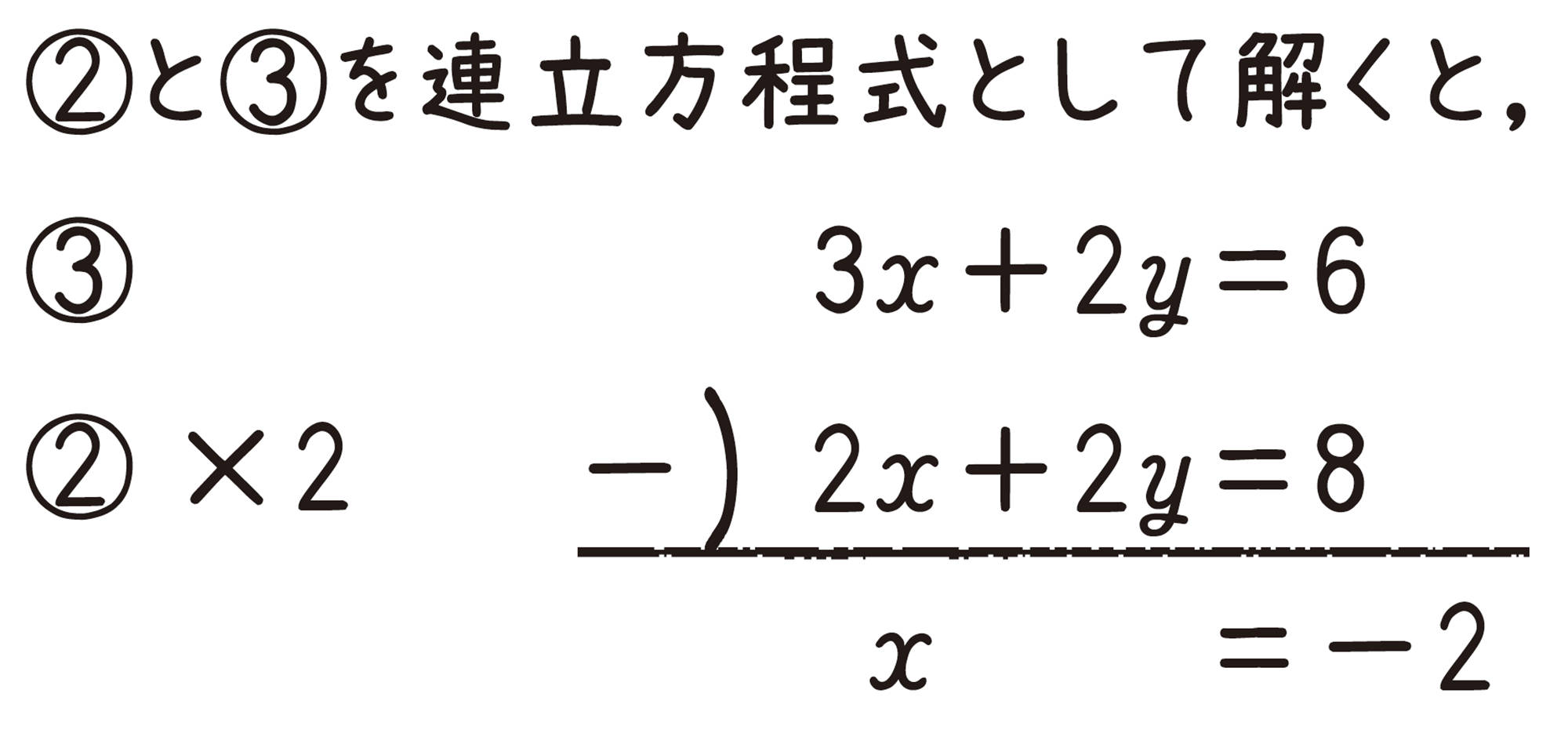教科書アドバイザー「マスマス！」

gkt-horizontal-line

<2年p.44>

２　連立方程式の解き方

文字に数を代入せずに解くには，どうすればいいのかな。

avatar

1元1次方程式なら解けるね。

Q Question

ある店でハンバーガー3個とジュース 1個を買うと750円，ハンバーガー1個とジュース1個を買うと350円です。ハンバーガー1個の値段とジュース1個の値段は，それぞれいくらでしょうか。

avatar

①，②から同じものをとると…。

見方・考え方　

具体的な場面で考えられるかな。

　目標　▷　文字に数を代入せずに，連立方程式を解く方法を考えよう。

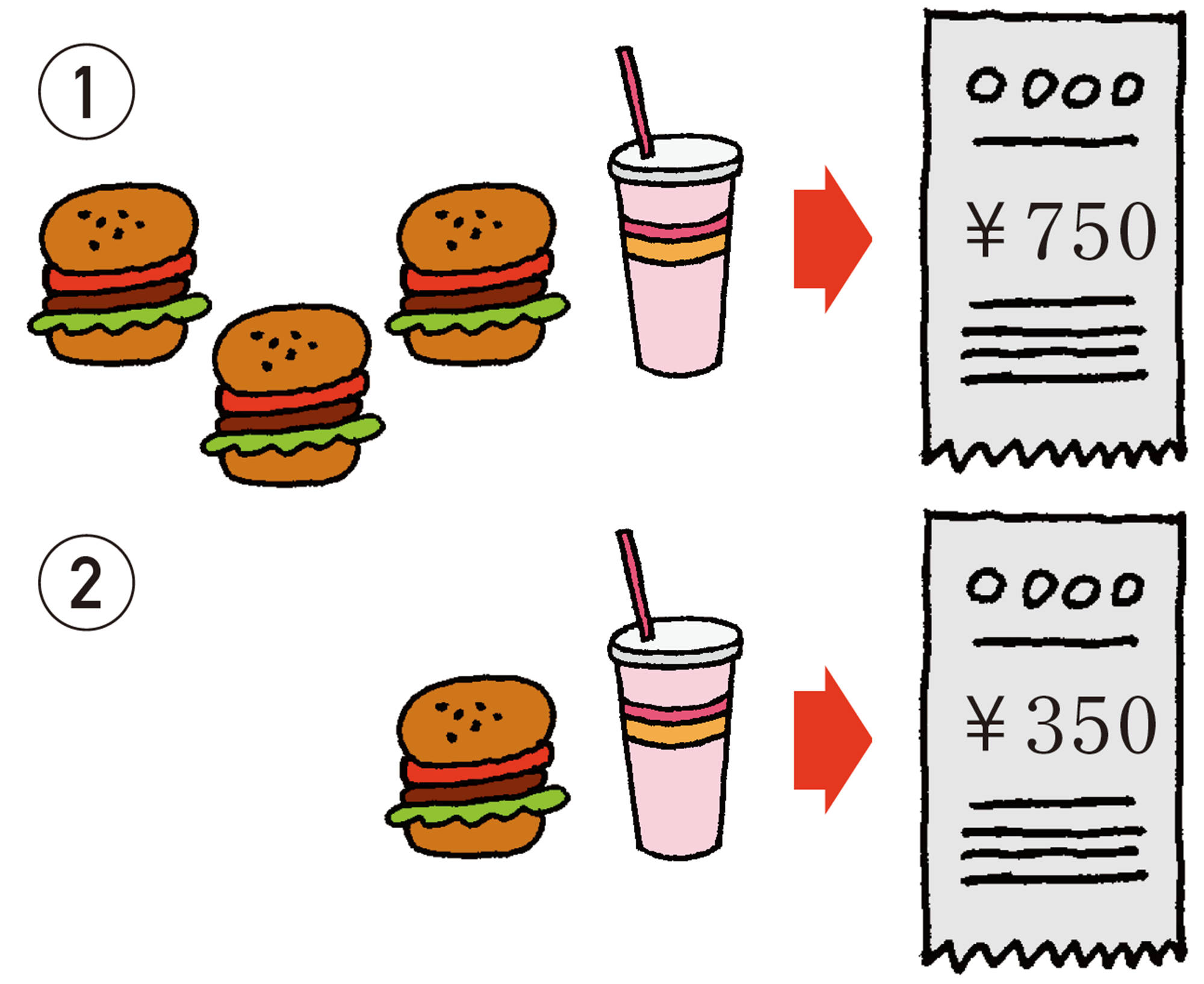
【１】　【Q】について，拓真さんは次のような図をかいて，ハンバーガー1個の値段を求めました。拓真さんの考え方を説明してみましょう。

拓真さんの考え

ハンバーガーを●，ジュースを■で表すと，
　　　　　①…　●●●■　→　750円
　　　　　 ②…　　●■　→　350円　
①と②を比べると，●● 　　→　400円　…③
したがって，　　　 ● 　→　200円

【２】　ハンバーガー1個の値段をx円，ジュース1個の値段をy円とすると，拓真さんの考えの①，②は，それぞれどんな式で表すことができるでしょうか。また，③は，その2つの式をどのように操作すれば導くことができるでしょうか。

gkt-horizontal-line

<2年p.45>

前ページの【Q】は，次の連立方程式を解くことによって，答えを求めることができる。

[mathjax]\(　\begin{eqnarray} \left\{\begin{array}{l} 3x+y=750 \phantom{0} \cdots \cdots ①\\ x+y=350 \phantom{00} \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

【２】で調べたように，この連立方程式は，①，②の左辺どうし，右辺どうしをそれぞれひくと[mathjax]\( y \) の項が消え，1つの文字 [mathjax]\( x \) だけをふくむ1元1次方程式を導くことができる。

[mathjax]\(\begin{array}{r} \textsf{①}\phantom{000.} 3x+y=750\\ \textsf{②}\phantom{0} \underline{-\big{)}\phantom{0}x+y=350}\\ 2x\phantom{000.}=400\\ x\phantom{000.}=200\\ \end{array}\)

[mathjax]\(\begin{array}{r} A=M\phantom{0000} \\ \underline{-\big{)}\phantom{0000}B=N\phantom{0000.}} \\ \ A-B=M-N \\ \end{array}\)

【３】　[mathjax]\( x=200 \) を①に代入して[mathjax]\( y \) の値を求めてみましょう。また，[mathjax]\( x=200 \) を②に代入して [mathjax]\( y \) の値を求め，2つの結果を比べてみましょう。

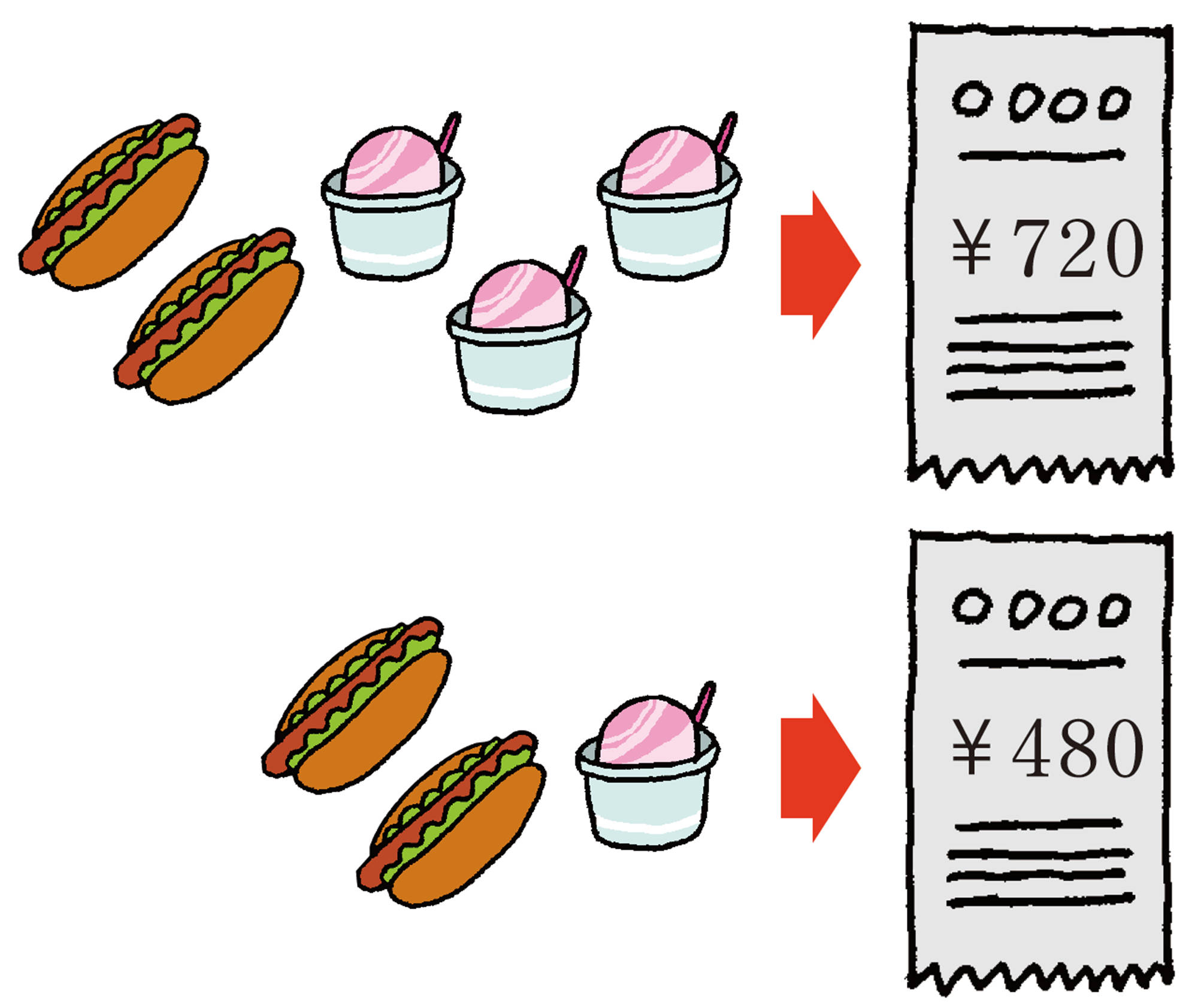
【４】　同じ店で，ホットドッグ2個とアイスクリーム3個を買うと720円，ホットドッグ2個とアイスクリーム1個を買うと480円でした。ホットドッグ1個とアイスクリーム1個の値段は，それぞれいくらでしょうか。連立方程式をつくってそれを解き，答えを求めてみましょう。

【５】　次の連立方程式で2つの式から1元1次方程式を導くにはどうすればよいでしょうか。

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{lr} 2x+y=13 & \cdots \cdots ①\\ x-y=5 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

左辺どうし，右辺どうしをそれぞれひいても文字が消えない場合はどうすればいいのかな。

avatar

どんなことがわかったかな

片方の文字の項を消して1元1次方程式を導けば，連立方程式を解くことができます。

次の課題へ！
1元1次方程式を導くには，ほかにどんな方法があるのかな？
P.46，49

gkt-horizontal-line

<2年p.46>

　加減法

Q Question

前ページの【５】の連立方程式の解き方を考えてみましょう。

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} 2x+y=13 & \cdots \cdots ①\\ x-y=5 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

avatar

[mathjax]\( y \) が消せそうだよ。

どうしたら，[mathjax]\( y \) を消せるのかな。

avatar

見方・考え方　

左辺どうし，右辺どうしをそれぞれひいたときと同じように考えられるかな。

　目標　▷　2つの式から1元1次方程式を導いて，連立方程式を解く方法を考えよう。

　例１　　次の連立方程式を解きなさい。

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} 2x+y=13 & \cdots \cdots ①\\ x-y=5 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

　考え方　　文字を1つにするために，左辺どうし，右辺どうしをそれぞれ加える。

解答

①，②の左辺どうし，右辺どうしをそれぞれ加えると，

[mathjax]\(\begin{array}{r} \mathsf{①}\phantom{000.} 2x+y=13\\ \mathsf{②}\phantom{0} \underline{+\big{)}\phantom{0}x-y=\phantom{0}5}\\ 3x\phantom{000.}=18\\ x\phantom{000.}=\phantom{0}6\\ \end{array}\)

[mathjax]\( x=6 \) を①に代入すると，

[mathjax] \(\begin{eqnarray} 2 \times 6+y &=& 13 \\ y &=& 1 \end{eqnarray}\)

答

[mathjax] \(\underline{\begin{eqnarray} \left\{\begin{array}{l} x=6 \\ y=1 \end{array} \right. \end{eqnarray}}\)

見直したときわかりやすいように，文字や「[mathjax]\( = \)」をそろえて書いておこう。

[mathjax]\( \begin{array}{r} \\ \phantom{0000}A=M \phantom{0000} \\ \underline{+\big{)} \phantom{0000} B=N \phantom{0000}} \\ A+B=M+N \end{array} \)

検算

求めた [mathjax]\( x \) ，[mathjax]\( y \) の値を，もとの連立方程式に代入すると，

[mathjax]\( \begin{array}{ll} \mathsf{①では，左辺}=2 \times 6+1=13 \mathsf{，} \quad &\mathsf{右辺}=13 \\ \mathsf{②では，左辺}=6-1=5 \mathsf{，} &\mathsf{右辺}=5 \end{array} \)

したがって，[mathjax]\( x=6 \) ，[mathjax]\( y=1 \) のとき，①と②はともに成り立つ。

gkt-horizontal-line

<2年p.47>

これまで学んだように，文字 [mathjax] \( y \) をふくむ連立方程式から， [mathjax] \( y \) をふくまない1つの方程式をつくることを， [mathjax] \( y \) を消去するという。

　問１　　次の連立方程式を解きなさい。

⑴

[mathjax]\(\begin{eqnarray}\left\{\begin{array}{l} 3x-y=2 \\ x+y=6 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x+4y=9 \\ x+y=3 \end{array} \right. \end{eqnarray} \)

⑶

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} 3x-2y=-13 \\ -3x+4y=23 \end{array} \right. \end{eqnarray} \)

⑷

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} 2x-y=-4 \\ x-y=-1 \end{array} \right. \end{eqnarray} \)

2種類の文字の係数の絶対値がともに異なる連立方程式を解いてみよう。

　例２　　次の連立方程式を解きなさい。

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} x+3y=700 & \cdots \cdots ①\\ 2x+y=600 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

　考え方　　どちらかの文字を消去するために，一方の式の両辺を何倍かして，消去する文字の係数の絶対値をそろえる。

解答

[mathjax]\(\begin{array}{r} \textsf{①}\times 2\phantom{00000} 2x+6y=1400 \\ \textsf{②}\phantom{00000} \underline{-\big{)}\phantom{0}2x+\phantom{0}y=\phantom{0}600}\\ 5y=\phantom{0}800\\ y=\phantom{0}160\\ \end{array}\)

[mathjax]\( y=160 \) を②に代入すると，

[mathjax] \( \begin{eqnarray} 2x+160 &=& 600 \\ x &=& 220 \end{eqnarray}\)

答

[mathjax]\(\underline{ \begin{eqnarray} \left\{\begin{array}{l} x=220 \\ y=160 \end{array} \right.\end{eqnarray}}\)

ここでは，①の両辺を2倍して [mathjax] \( x \) を消去しているね。

avatar

　問２　　例2の連立方程式を， [mathjax] \( y \) を消去して解きなさい。

　問３　　次の連立方程式を解きなさい。

⑴

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} 2x-3y=12 \\ 3x+y=7 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} 3x-4y=10 \\ 5x-8y=22 \end{array} \right. \end{eqnarray} \)

⑶

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} -2x+3y=-9 \\ 4x-5y=15 \end{array} \right. \end{eqnarray} \)

gkt-horizontal-line

<2年p.48>

　例３　　次の連立方程式を解きなさい。

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} 2x-3y=-7 & \cdots \cdots ①\\ 3x+2y=-4 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

　考え方　　どちらかの文字を消去するために，それぞれの式の両辺を何倍かして，消去する文字の係数の絶対値をそろえる。

解答

[mathjax]\(\begin{array}{r} \mathsf{①}\times 2\phantom{0000000} 4x-6y=-14 \\ \mathsf{②}\times 3\phantom{000.} \underline{+\big{)}\phantom{0}9x+6y=-12}\\ 13x\phantom{0000.}=-26\\ \phantom{0}x\phantom{0000.}=\phantom{}-2\\ \end{array}\)

[mathjax]\( x=-2 \) を②に代入すると，

[mathjax]\( \begin{eqnarray} 3 \times (-2)+2y &=& -4 \\ y &=& 1 \end{eqnarray} \)

答

[mathjax]\( \underline{\begin{eqnarray} \left\{\begin{array}{l} x=-2 \\ y=1 \end{array} \right. \end{eqnarray}} \)

①を2倍，②を3倍して，両辺をそれぞれ加えているね。

avatar

　問４　　例3の連立方程式を，[mathjax]\( x \) を消去して解きなさい。

　問５　　次の連立方程式を解きなさい。

⑴

[mathjax]\(　\begin{eqnarray} \left\{\begin{array}{l} 2x+3y=8 \\ 3x-4y=-5 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\(　\begin{eqnarray} \left\{\begin{array}{l} 3x-2y=13 \\ 4x+5y=2 \end{array} \right. \end{eqnarray} \)

⑶

[mathjax]\(　\begin{eqnarray} \left\{\begin{array}{l} 7x-3y=-5 \\ 6x-5y=3 \end{array} \right. \end{eqnarray} \)

⑷

[mathjax]\(　\begin{eqnarray} \left\{\begin{array}{l} 4x+8y=7 \\ 6x+5y=7 \end{array} \right. \end{eqnarray} \)

やってみよう
計算力を高めよう2-1
▷P.53

これまで学んできたような，どちらかの文字の係数の絶対値をそろえ，2つの式の左辺どうし，右辺どうしを加えたりひいたりすることによって，その文字を消去する連立方程式の解き方を加減法という。

どんなことがわかったかな

加減法を使って1元1次方程式を導けば，連立方程式を解くことができます。

次の課題へ！
連立方程式は，どんなところで使えるのかな？
P.56

gkt-horizontal-line

<2年p.49>

　代入法

Q Question

45ページの 5 で，美月さんは右のように考えました。
美月さんの考えを説明しましょう。
また，美月さんの考えで，この問題を解いてみましょう。

avatar

等式の変形を使っているね。

[mathjax]\( 5+y \) を1つの数として考えれば，[mathjax]\( x \) に代入してもいいのかな。

avatar

美月さんの考え

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} 2x+y=13 & \cdots \cdots ①\\ x-y=5 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

このとき，②の式を [mathjax]\( x \) について解くと，
[mathjax]\(x=5+y \)
この [mathjax]\( 5+y \) を①の式の [mathjax]\( x \) に代入すると，[mathjax]\( y \) だけの方程式になる。

見方・考え方　

どんなことを根拠にして考えているか説明できるかな。

　目標　▷　2つの式から1元1次方程式を導いて，連立方程式を解く方法を考えよう。

　例４　　次の連立方程式を解きなさい。

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} y=x-1 & \cdots \cdots ①\\ x+2y=7 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

　考え方　　①で，[mathjax]\( y \) は [mathjax]\( x-1 \) と等しいから，②の [mathjax]\( y \) を [mathjax]\( x-1 \) におきかえる。すなわち，[mathjax]\( y \) に [mathjax]\( x-1 \) を代入して，[mathjax]\( y \) を消去する。

解答

①を②に代入すると，

[mathjax] \( \begin{eqnarray} x+2(x-1) &=& 7 \\ x+2x-2 &=& 7 \\ 3x &=& 9 \\ x &=& 3 \end{eqnarray} \)

[mathjax] \( x=3 \) を①に代入すると，

[mathjax] \( \begin{eqnarray} y &=& 3-1 \\ &=& 2 \end{eqnarray} \)

答

[mathjax]\(\underline{\begin{eqnarray} \left\{\begin{array}{l} x=3 \\ y=2 \end{array} \right. \end{eqnarray}}\)

多項式を代入するときは，必ずかっこをつける

例4のように，一方の式を他方の式に代入することによって，1つの文字を消去する連立方程式の解き方を代入法という。

gkt-horizontal-line

<2年p.50>

　問６　　次の連立方程式を，代入法で解きなさい。

⑴

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=3y+1 \\ x+2y=11 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x-2y=9 \\ y=x-3 \end{array} \right. \end{eqnarray} \)

⑶

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} y=7x-2 \\ y=4x+1 \end{array} \right. \end{eqnarray} \)

⑷

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x-3y=5 \\ 2x+y=3 \end{array} \right. \end{eqnarray} \)

やってみよう
計算力を高めよう2-2
▷P.53

Q Question

次の連立方程式は，加減法と代入法のどちらで解くのがよいか話し合ってみましょう。また，2つの方法で解き，その解を比べてみましょう。

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} 2x+3y=4 & \cdots \cdots ①\\ x-y=2 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

avatar

[mathjax]\( x \) ，[mathjax]\( y \) の係数のどちらでそろえても解けそうだから，加減法がいいんじゃないかな。

②の式は，[mathjax]\( x \) についても [mathjax]\( y \) についても解けるから，代入法が解きやすそうだよ。

avatar

見方・考え方　

加減法と代入法で，似ているところやちがいはどこかな。

【Q】で考えたように，連立方程式は，加減法で解いても，代入法で解いても同じ結果が得られるため，解きやすい方法で解けばよい。

　問７　　次の連立方程式を，適当な方法で解きなさい。また，なぜその方法を選んだか説明しなさい。

⑴

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} 3x+y=7 \\ x+2y=9 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x+3y=3 \\ x=-y+2 \end{array} \right. \end{eqnarray} \)

おしえて！
P.54
わからない数が3つの連立方程式もあるのかな？

gkt-horizontal-line

　いろいろな連立方程式

　例５　　

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} 5x+3y=0 & \cdots \cdots ①\\ 3x-2(x-y)=7 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

②のかっこをはずして整理すると，

[mathjax]\( x+2y=7 \phantom{0000000} \quad \cdots \cdots ③ \)

①と③を連立方程式として解くと，

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-3 \\ y=5 \end{array} \right. \end{eqnarray} \)

gkt-horizontal-line

<2年p.51>

　問８　　次の連立方程式を解きなさい。

⑴

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} 2(x-y)-x=8 \\ 5x-(3x-y)=1 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} 3(x+2y)=2(x-3) \\ y=4-x \end{array} \right. \end{eqnarray} \)

　例６　　次の連立方程式を解きなさい。

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} \dfrac{1}{2}x+\dfrac{1}{3}y=1 & \cdots \cdots ①\\ x+y=4 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

　考え方　　①の両辺に6をかけて，係数を整数に直してから解くとわかりやすい。

解答

[mathjax]\( \begin{eqnarray} ① \times 6 \quad \require{physics} \left(\dfrac{1}{2}x+ \dfrac{1}{3}y\right) \times 6 &=& 1 \times 6 \\ 3x+2y &=& 6 \quad \cdots \cdots ③ \end{eqnarray} \)

②と③を連立方程式として解くと，

[mathjax]\( \begin{array}{r} \\ \mathsf{③}\hspace{45pt} 3x+2y=6\phantom{-} \\ \mathsf{②}\times 2 \hspace{10pt}\underline{-\big{)}\phantom{0}2x+2y=8\phantom{-}} \\ \ x\phantom{000-}=-2 \\ \end{array}\)

[mathjax]\( x=-2 \) を②に代入すると，

[mathjax]\( \begin{eqnarray} -2+y &=& 4 \\ y &=& 6 \end{eqnarray} \)

答

[mathjax]\(\underline{\begin{eqnarray} \left\{\begin{array}{l} x=-2 \\ y=6 \end{array} \right. \end{eqnarray}}\)

文字の係数を整数にする

式の説明なども書いておこう。

　問９　　次の連立方程式を解くには，どんなくふうをすればよいか考えなさい。

また，その方法で解を求めなさい。

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x+y=6 \\ 0.5x+0.2y=1.5 \end{array} \right. \end{eqnarray} \)

　問 10　　次の連立方程式を，係数を整数に直してから解きなさい。

⑴

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 0.2x+0.3y=0.5 \\ x+5y=-1 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 8x-3y=9 \\ - \dfrac{1}{6}x+ \dfrac{y}{2}=2 \end{array} \right. \end{eqnarray} \)

gkt-horizontal-line

<2年p.52>

　例７　　連立方程式[mathjax]\( 2x+3y=x+y=2 \) のような，[mathjax]\( A=B=C \) の形の連立方程式は，次の㋐，㋑，㋒のうちのどれかの組み合わせをつくって解く。

㋐

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} A=B \\ A=C \end{array} \right. \end{eqnarray} \)

㋑

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} A=B \\ B=C \end{array} \right. \end{eqnarray} \)

㋒

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} A=C \\ B=C \end{array} \right. \end{eqnarray} \)

たとえば，㋒の形に直すと，

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 2x+3y=2 \\ x+y=2 \end{array} \right. \end{eqnarray} \)

これを解くと，

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x=4 \\ y=-2 \end{array} \right. \end{eqnarray} \)

　問 11　　例7の連立方程式を，㋐，㋑の形に直して解きなさい。

　問 12　　次の連立方程式を解きなさい。

⑴　[mathjax]\( 2x-y=-3x+y=1 \)
⑵　[mathjax]\( 3x+2y=5+3y=2x+11 \)

やってみよう

計算力を高めよう2-3

P.53

どんなことがわかったかな

いろいろな連立方程式も，計算しやすい形に変えることで加減法や代入法を使って解くことができます。

次の課題へ！

連立方程式は，どんなところで使えるのかな？
P.56

gkt-horizontal-line

確かめよう　1節　連立方程式

□　連立方程式の解について理解している。　連立方程式とその解　・P.43　問2，問3

１　2元1次方程式[mathjax]\( x+y=11 \cdots ① \) ，[mathjax]\( x-y=5 \cdots ② \) について，下の⑴，⑵にあてはまるものを，次の㋐～㋓の中から選びなさい。

㋐

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x=7 \\ y=2 \end{array} \right. \end{eqnarray} \)

㋑

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x=2 \\ y=7 \end{array} \right. \end{eqnarray} \)

㋒

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x=6\\ y=5 \end{array} \right. \end{eqnarray} \)

㋓

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x=8 \\ y=3 \end{array} \right. \end{eqnarray} \)

⑴　①，②の解はそれぞれどれですか。
⑵　①，②を連立方程式と考えたとき，その解はどれですか。

□　連立方程式を解くことができる。　連立方程式の解き方　・P.46　例1　・P.47　例2　・P.48　例3　・P.49　例4

２　次の連立方程式を解きなさい。

⑴

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 2x+5y=-8 \\ 4x+3y=12 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 3x-2y=8 \\ 2x+3y=1 \end{array} \right. \end{eqnarray} \)

⑶

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 2x+y=-9 \\ x=3y-1 \end{array} \right. \end{eqnarray} \)

２　連立方程式の解き方

Q Question

加減法

Q Question

代入法

Q Question

Q Question

いろいろな連立方程式

＜ミライ教科書３学年分もくじ＞

＜スグラパ＞

＜ドリルまとめ＞

２ 連立方程式の解き方

Q Question

加減法

Q Question

代入法

Q Question

Q Question

いろいろな連立方程式

＜ミライ教科書３学年分もくじ＞

＜スグラパ＞

＜ドリルまとめ＞

２　連立方程式の解き方

　加減法

　代入法

　いろいろな連立方程式