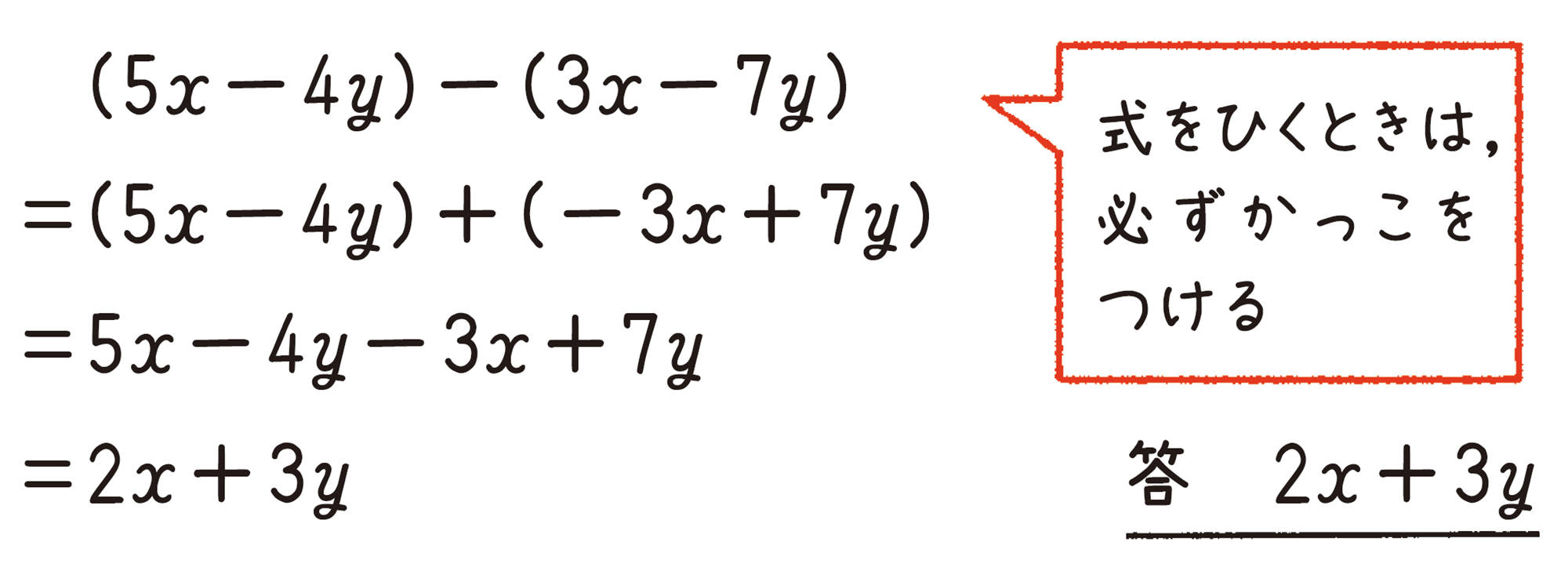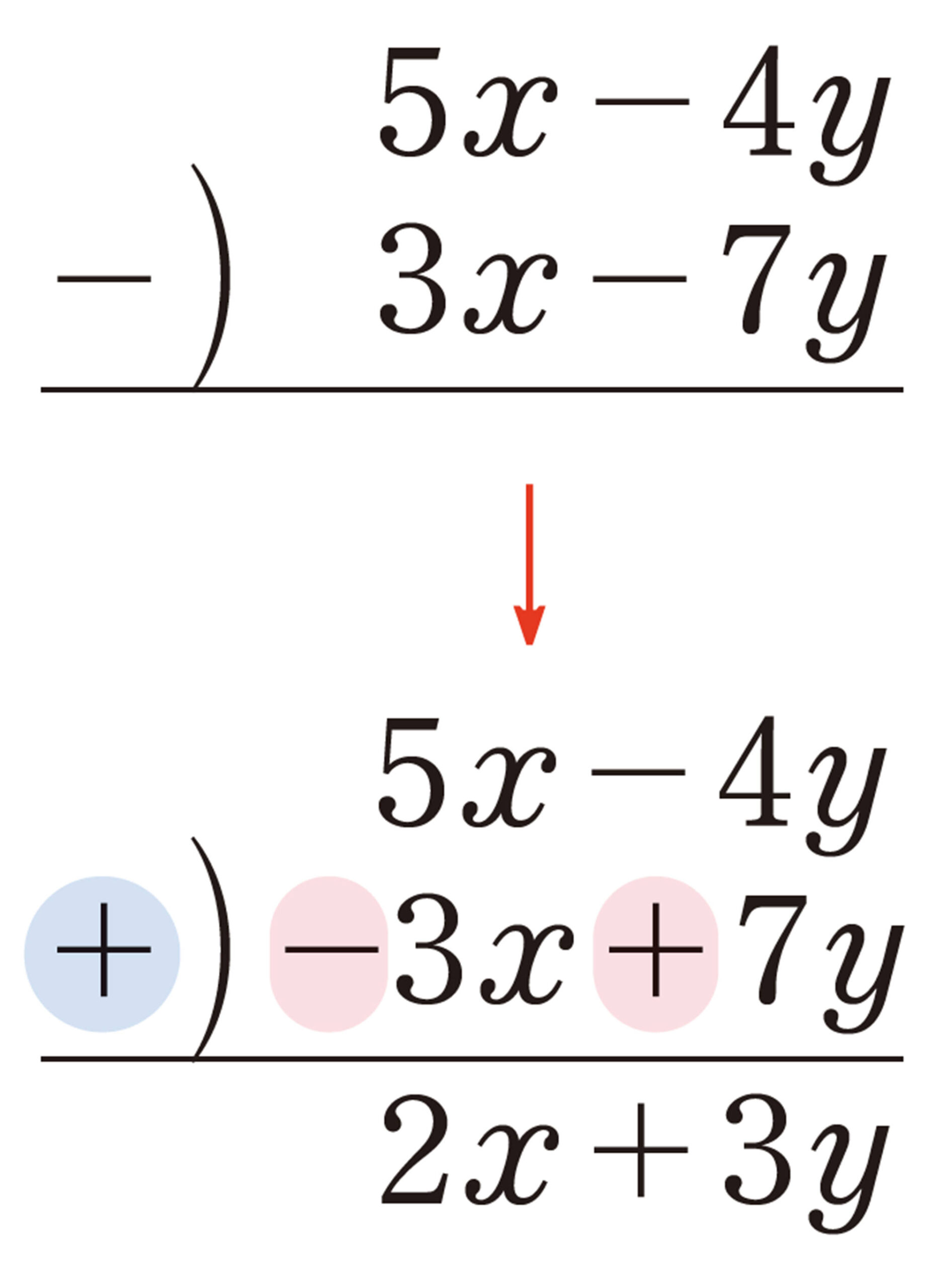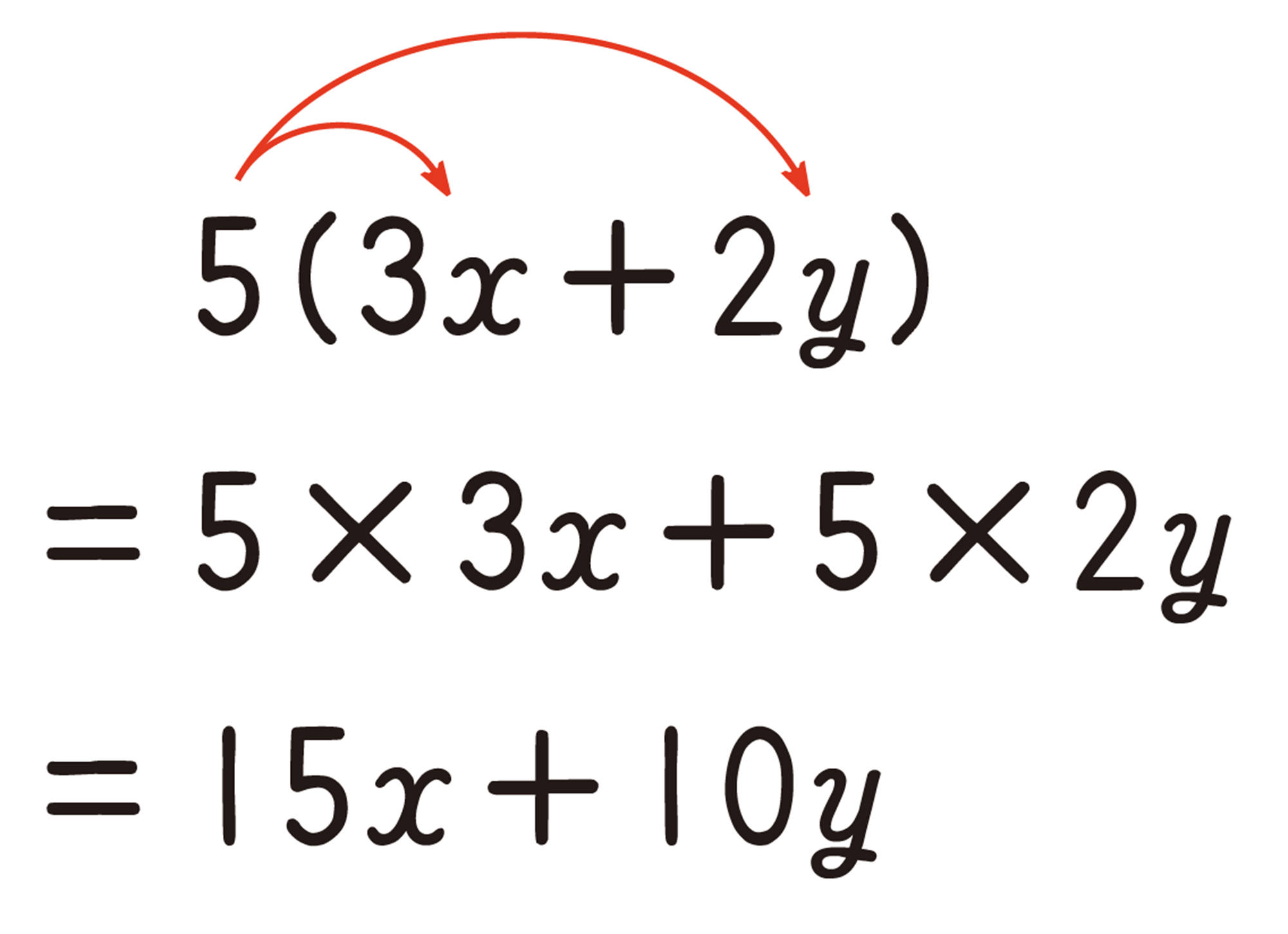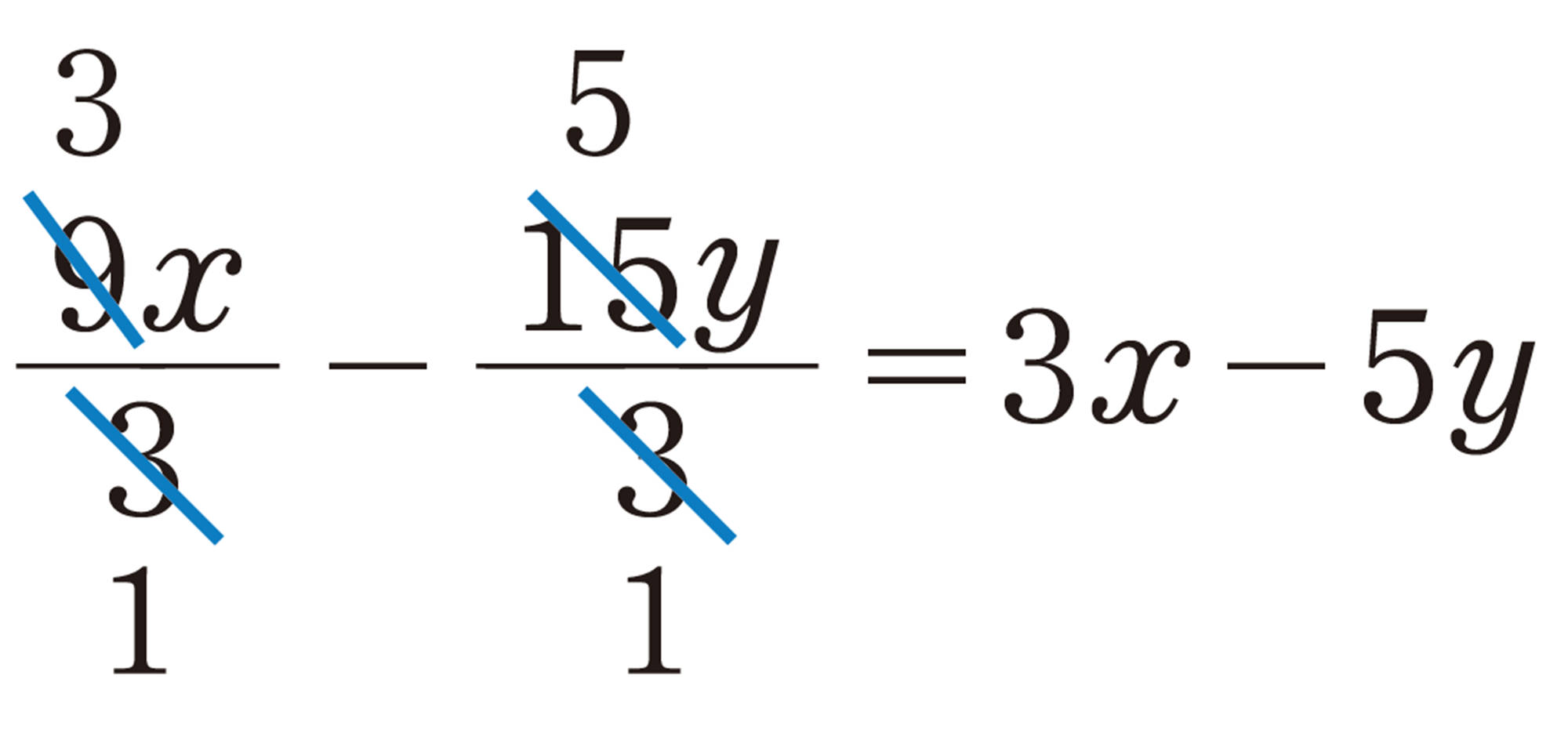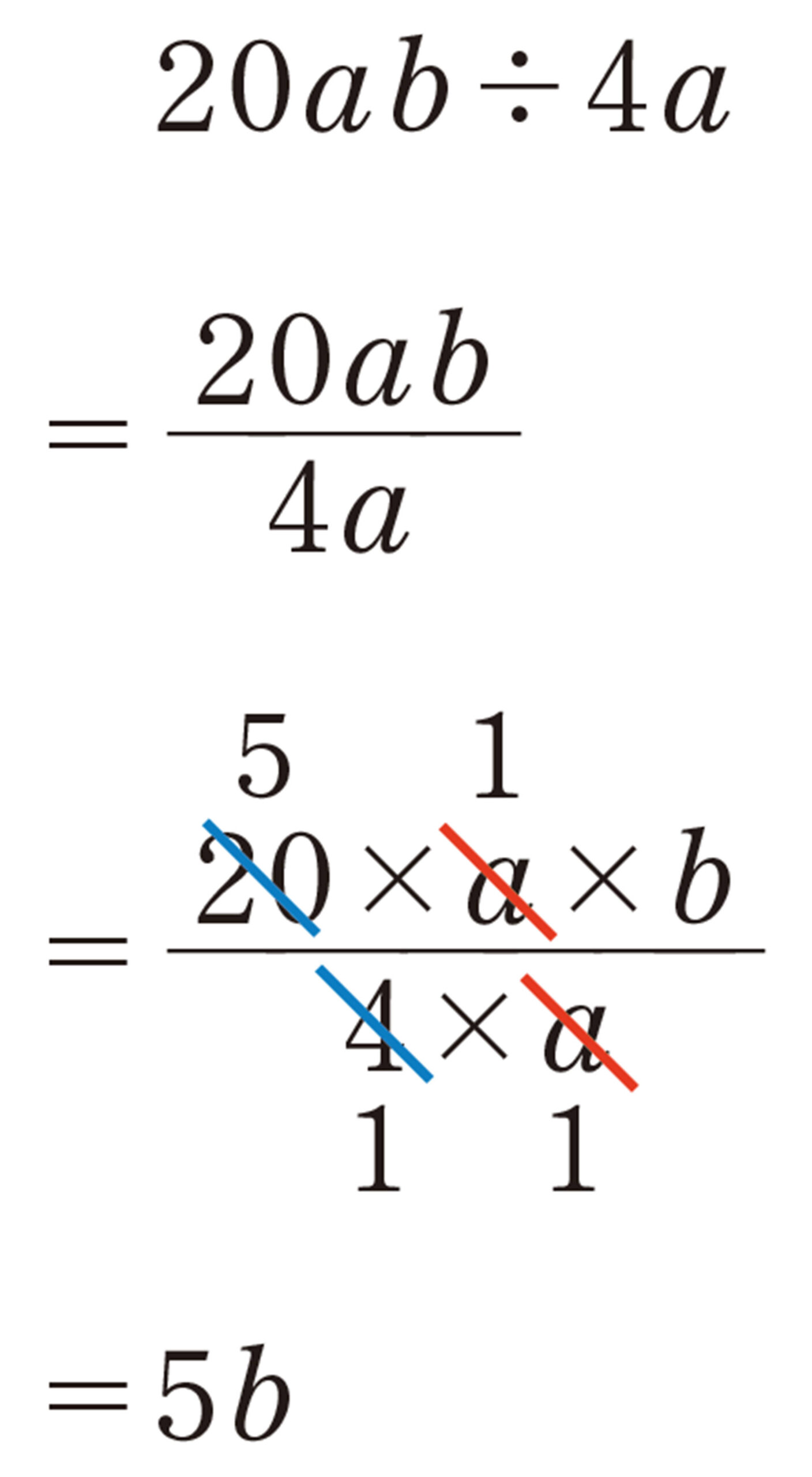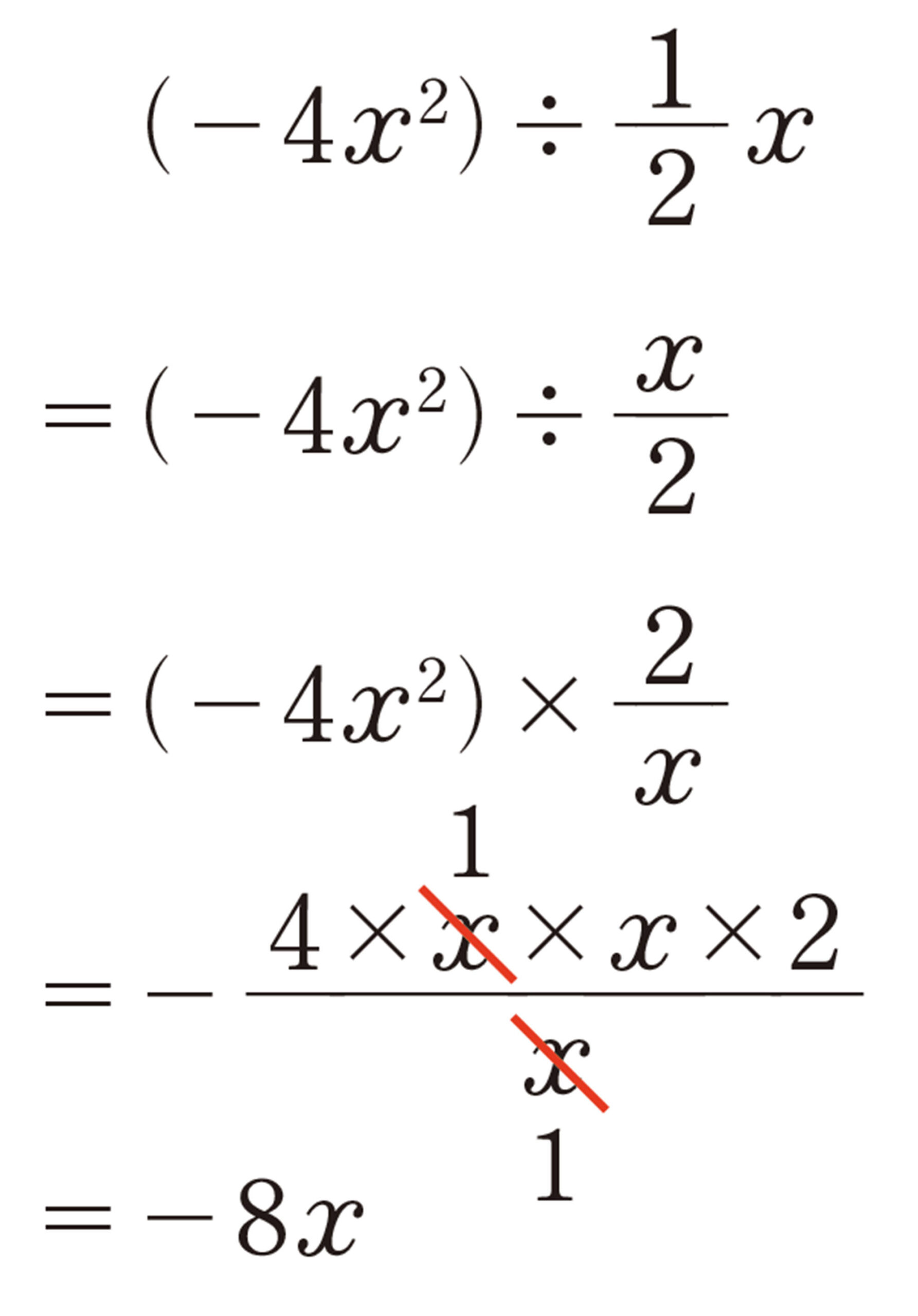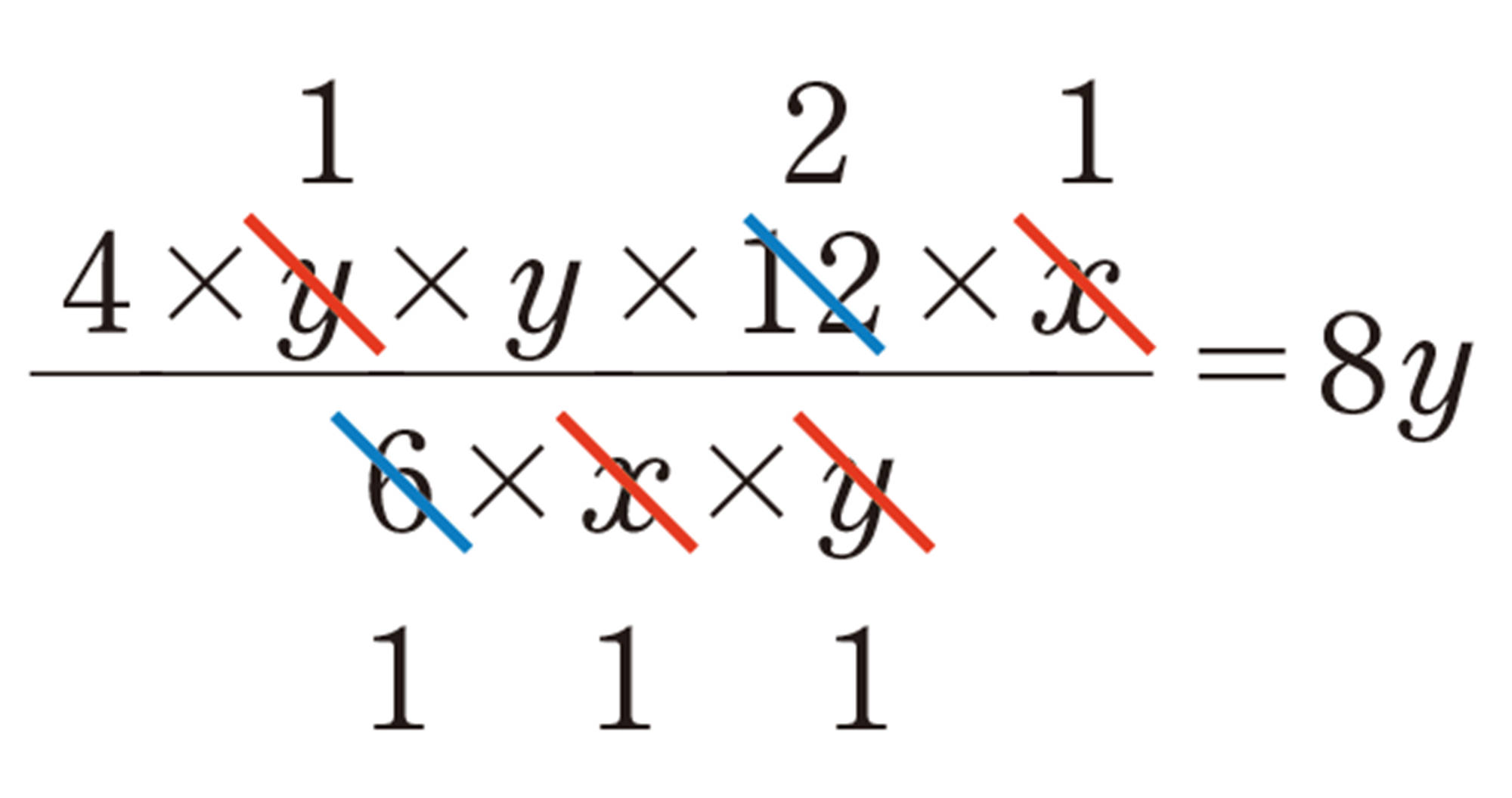<2年p.14>
2 多項式の計算
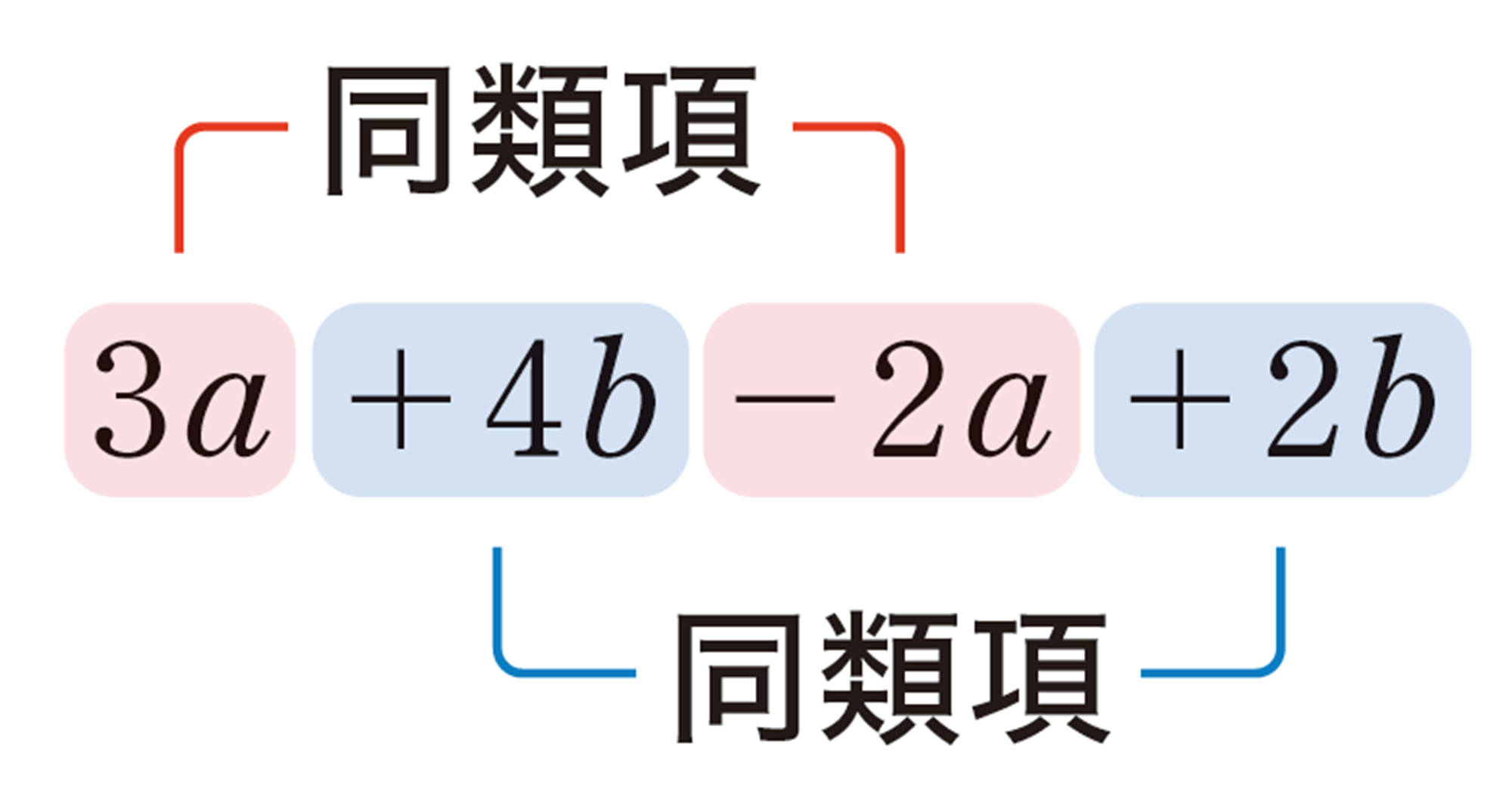
同類項の計算
Q Question

問題のとおりに式に表していけばいいね。
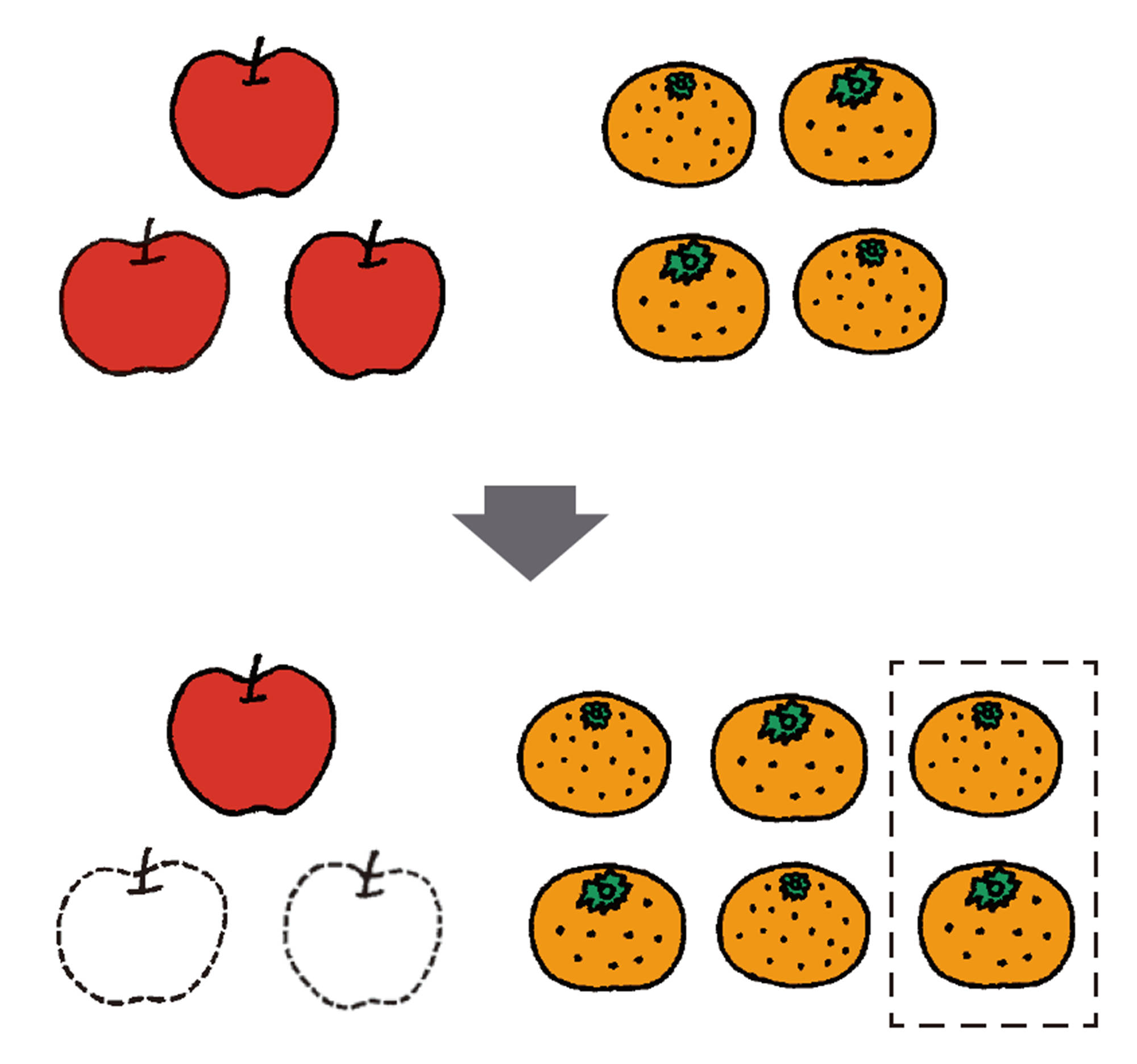
図を使って考えられるかな。

見方・考え方
具体的な場面で考えられるかな。
目標 ▷ 文字が 2 種類の多項式の計算を考えよう。
例 1
項を入れかえる
同類項をまとめる
例 1 の a と [mathjax] \( 6b \) のように,同類項でないものは,1 つの項にまとめることはできない。
a はりんごの代金で, [mathjax] \( 6b \) はみかんの代金だから,[mathjax] \( a+6b \) は[mathjax] \( 6ab \) にならないね。

問 1 次の多項式の同類項をいいなさい。また,同類項をまとめなさい。
⑴ [mathjax] \( 3x-4y-7x+2y \)
⑵ [mathjax] \( a-6b-9b+3a \)
<2年p.15>
問 2 拓真さんは,多項式 [mathjax] \( 4a²-7a+6a+3a² \) の計算を右のように行いました。この計算は正しいですか。また,その理由を説明しなさい。
[mathjax] \( 7a² \) と [mathjax] \( -a \) は,次数が異なるから同類項ではないため,1つの項にまとめることはできない。
問 3 次の式の同類項をまとめなさい。
⑴ [mathjax] \( 5x+2y-3x+y \)
⑵ [mathjax] \( -7a+2b+6b-2a \)
⑶ [mathjax] \( a-4b+7-3a+8b \)
⑷ [mathjax] \( 4x²+3x² \)
⑸ [mathjax] \( x²+9x-8x²-x \)
⑹ [mathjax] \( -3x²-7x+3x²+2x \)
⑺ [mathjax] \( 2y²-6y-2-3y \)
⑻ [mathjax] \( x²-8x+4-3x²+8x\)
多項式の加法
例 2 [mathjax] \( x-2y \) に[mathjax] \( -3x+5y \) を加えた和を求めなさい。
解答
答 [mathjax] \(-2x+3y\)
縦書きで計算するときには,同類項を縦にそろえて書こう。

多項式の加法は,式の各項をすべて加え,同類項をまとめればよい。
問 4 次の 2 つの式で,左の式に右の式を加えた和を求めなさい。
⑴ [mathjax] \( 6a+4b \) ,[mathjax] \(3a+b \)
⑵ [mathjax] \( 2x²+6x \),[mathjax] \( x²-9x \)
問 5 次の計算をしなさい。
⑴ [mathjax] \( (a+7b)+(4a-3b) \)
⑵ [mathjax] \((-6x²+5x-7)+(3x²-5x)\)
⑶
⑷
<2年p.16>
多項式の減法
多項式の減法は,ひく式の各項の符号を変えて加えればよい。
問 6 次の 2 つの式で,左の式から右の式をひいた差を求めなさい。
⑴ [mathjax] \( 6a+4b \),[mathjax] \( 3a+b \)
⑵ [mathjax] \( 2x²+6x \),[mathjax] \( x²-9x \)
問 7 次の計算をしなさい。
⑴ [mathjax] \( (4a-2b)-(a+5b) \)
⑵ [mathjax] \( (x²+3x+7)-(-6x²-2x+5) \)
⑶
⑷
やってみよう
計算力を高めよう1-1
P.23
問 8 美月さんは,[mathjax] \( (2x+y)-(3x-y) \) の計算を右のように行いました。最初の式と結果の式に,[mathjax] \( x=2 \),[mathjax] \( y=1 \)を代入して,それぞれの式の値を求め,正しいかどうか確かめなさい。
正しいかな?
どんなことがわかったかな
文字が2種類の多項式でも,1年の文字式と同じように,加法・減法ができます。
次の課題へ!
多項式と数の乗法や除法も, 1 年の文字式の計算と同じようにできるのかな?
P.17

<2年p.17>
多項式と数の乗法・除法
Q Question
[mathjax] \( 5(3x+2y) \) の計算を,右のように考えました。次の問いに答えましょう。
⑴ どのようなきまりを使って計算しているでしょうか。
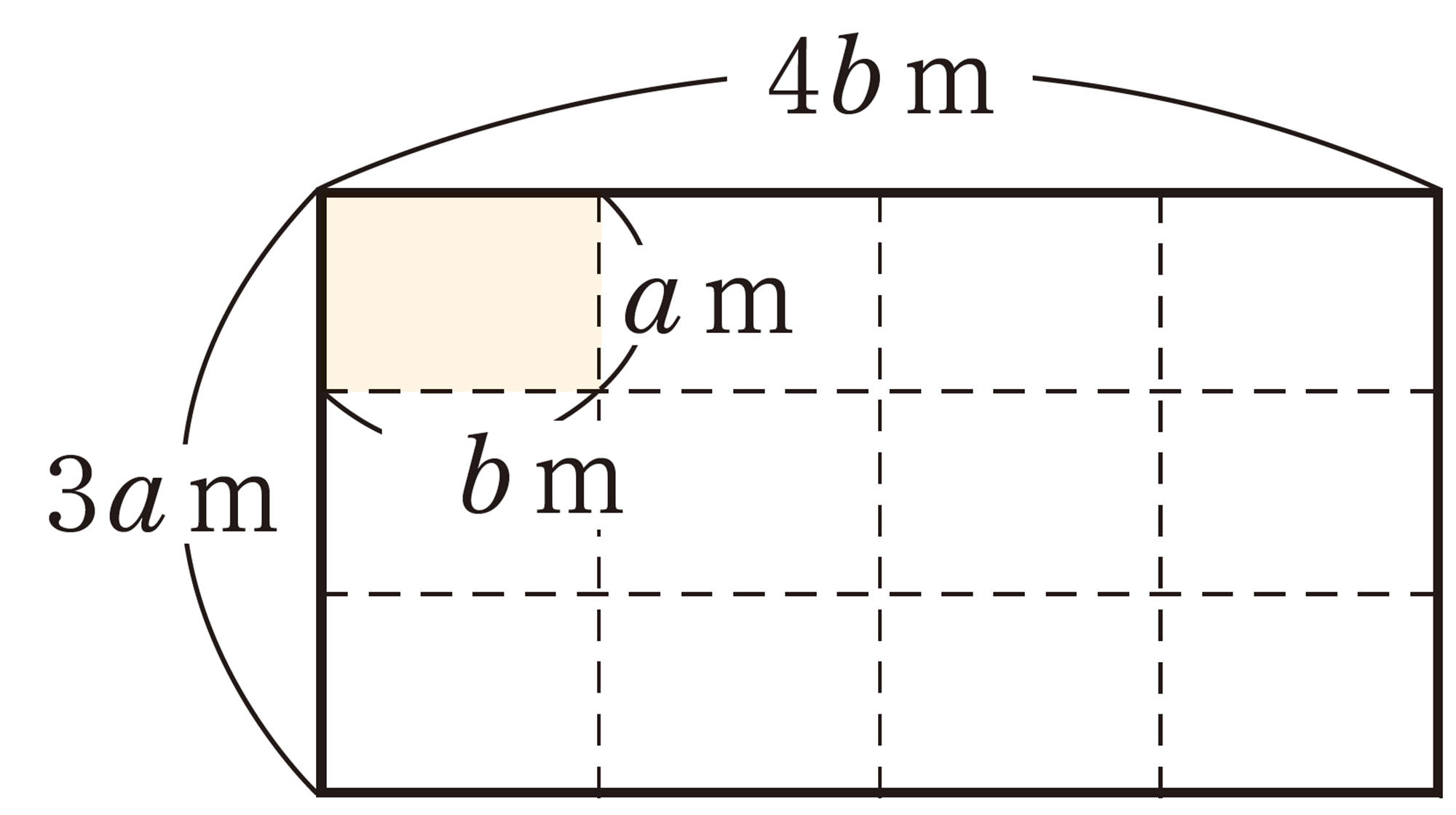
⑵ 計算が正しいかどうか,次の 2 つの方法で調べてみましょう。
① 右のような長方形の面積を考える。
② [mathjax] \( x=1 \) ,[mathjax] \( y=2 \) のときの,最初の式の値と結果の式の値を比べる。
目標 ▷ 多項式と数の乗法・除法を考えよう。
多項式と数の乗法は,分配法則を使ってかっこをはずせばよい。
問 9 次の計算をしなさい。
⑴ [mathjax] \( 3(x+5y) \)
⑵ [mathjax] \( -4(-2a+b) \)
⑶ [mathjax] \( (7a-4b) \times 5 \)
⑷ [mathjax] \( 6(5x-2y+1) \)
⑸ [mathjax] \( (3a+4b-5) \times (-2) \)
⑹ [mathjax] \(\dfrac{1}{4} (-8x-2y)\)
多項式を数でわる除法は,乗法の形に直して計算すればよい。
問 10 次の計算をしなさい。
⑴ [mathjax] \( (10x-25y) \div 5 \)
⑵ [mathjax] \( (-12a+5b) \div (-3) \)
やってみよう
計算力を高めよう1-2
P.23
<2年p.18>
いろいろな計算
例 5
かっこをはずすときは,符号に気をつけよう。

問 11 次の計算をしなさい。
⑴ [mathjax] \( 2(a+2b)+3(2a-b) \)
⑵ [mathjax] \( -3(4x-5y)+6(2x-3y) \)
⑶ [mathjax] \( 3(a-2b)-2(a+5b) \)
⑷ [mathjax] \( 7(x-2y+1)-4(-3y+2) \)
方法②
[mathjax] \(\dfrac{x+2y}{2}- \dfrac{x-y}{3}\)
分数×(多項式)の形にする
[mathjax] \(=\dfrac{1}{2}(x+2y)-\dfrac{1}{3}(x-y)\)
かっこをはずす
[mathjax] \(=\dfrac{1}{2}x+y-\dfrac{1}{3}x+ \dfrac{1}{3}y\)
項を入れかえて,通分する
[mathjax] \(=\dfrac{3}{6}x- \dfrac{2}{6}x+ \dfrac{3}{3}y+ \dfrac{1}{3}y\)
同類項をまとめる
[mathjax] \(=\dfrac{1}{6}x+ \dfrac{4}{3}y\)
問 12 次の計算をしなさい。
⑴ [mathjax] \(\dfrac{x+3y}{4}+ \dfrac{3x-y}{6}\)
⑵ [mathjax] \(\dfrac{x-y}{4}- \dfrac{2x+y}{8}\)
⑶ [mathjax] \(\dfrac{1}{9}(5x+3y)-\dfrac{1}{3}(x-y)\)
⑷ [mathjax] \(x+y- \dfrac{4x-2y}{5}\)
やってみよう
計算力を高めよう1-3
P.23
どんなことがわかったかな
多項式の文字が 2種類になっても,1年の文字式と同じように,分配法則を使って多項式と数の乗法・除法ができます。
次の課題へ!
単項式どうしの乗法や除法もできるのかな?
P.19

<2年p.19>
3 単項式の乗法・除法
単項式と単項式の乗法
Q Question
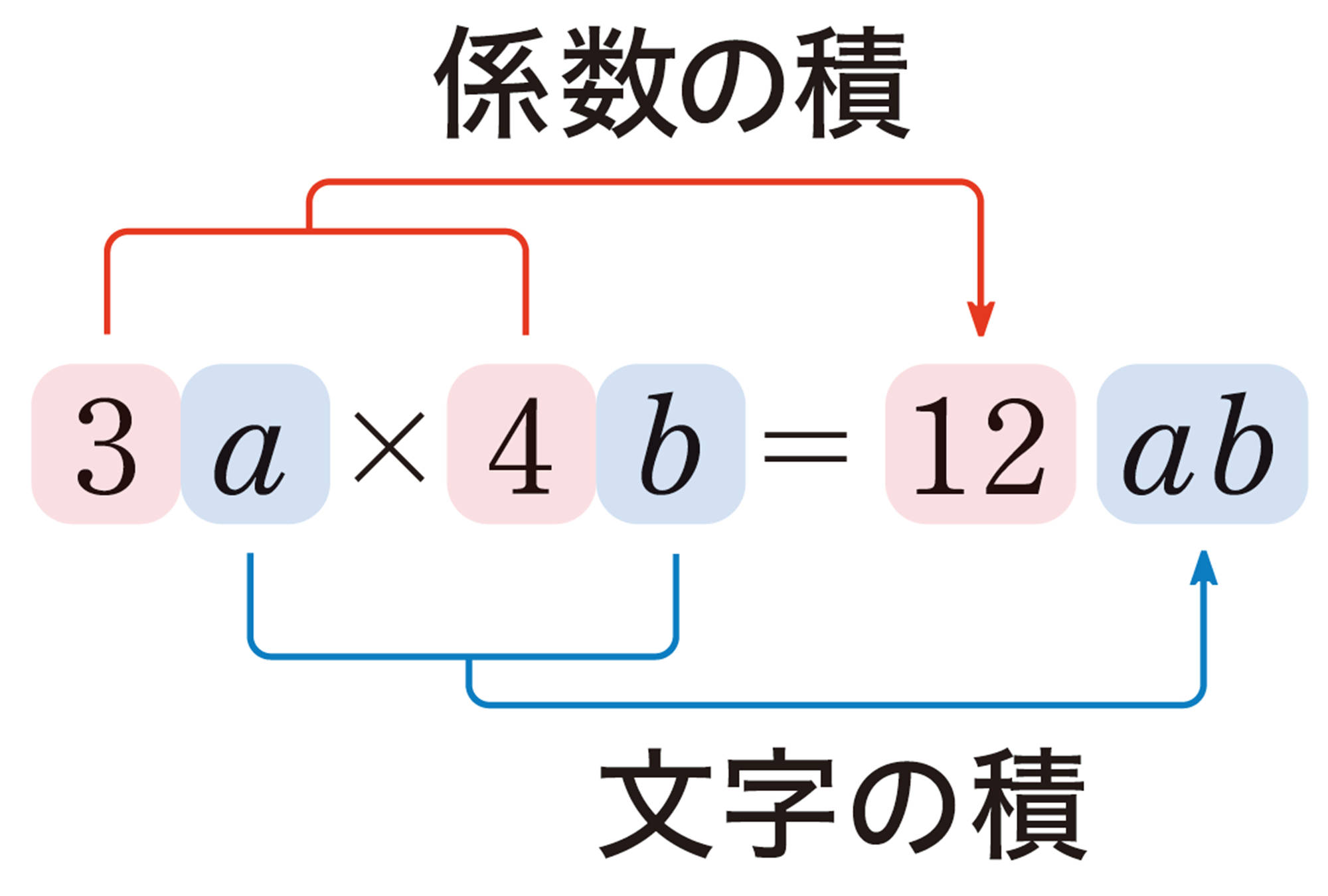
真央さんは,[mathjax] \( 3a \times 4b \) のような単項式どうしの乗法を,計算のきまりが使えると考えて,右のように計算しました。
この計算は正しいといえるでしょうか。

1年では,数と文字を分けて考えたね。
計算した結果が正しいかどうか,確かめられるかな。

見方・考え方
1年の文字式の計算と同じように考えられるかな。
目標 ▷ 文字をふくむ単項式と単項式の乗法・除法を考えよう。
問 2 次の計算をしなさい。
⑴ [mathjax] \( 5a \times 2b \)
⑵ [mathjax] \( (-6x) \times 3y \)
⑶ [mathjax] \( (-x) \times (-7y) \)
⑷ [mathjax] \( 0.4x \times (-5y) \)
⑸ [mathjax] \( 8a \times \dfrac{1}{4}b \)
⑹ [mathjax] \( \require{physics} \left(- \dfrac{2}{3}x \right) \times (-9y) \)
例 1
⑴
⑵
<2年p.20>
問 3 次の計算をしなさい。
⑴ [mathjax] \( a³ \times a² \)
⑵ [mathjax] \( 2a² \times 4a \)
⑶ [mathjax] \( (3x)² \)
⑷ [mathjax] \( (-4a)² \)
⑸ [mathjax] \( (-6xy) \times 2y \)
⑹ [mathjax] \( 8x \times (-x)² \)
⑺ [mathjax] \( 5 \times (-2x)² \)
⑻ [mathjax] \( 5 \times (-2x²) \)
⑼ [mathjax] \(\require{physics} \left(- \dfrac{1}{2}x\right)^{2} \times 4y\)
単項式と単項式の除法
例 2
同じ文字は数と同じように約分できるんだね。

問 4 次の計算をしなさい。
⑴ [mathjax] \( 12xy \div 6y \)
⑵ [mathjax] \( (-9ab) \div 3b \)
⑶ [mathjax] \( a³ \div a² \)
⑷ [mathjax] \( 10x²y \div (-2xy) \)
⑸ [mathjax] \( 9x² \div \dfrac{3}{5}x \)
⑹ [mathjax] \( 4ab \div \require{physics} \left(- \dfrac{2}{3}b\right) \)
乗法と除法の混じった計算
問 5 次の計算をしなさい。
⑴ [mathjax] \( 3x² \times 4y \div 2xy \)
⑵ [mathjax] \( x³ \div 2x² \times 8x \)
⑶ [mathjax] \( 12a²b \times (-3ab) \div 9ab² \)
⑷ [mathjax] \( 27a² \div (-3a)² \)
やってみよう
計算力を高めよう1-4
▷P.23
<2年p.21>
問 6 健太さんは,[mathjax] \( 8x² \div \dfrac{2}{3}x \times 4x \) の計算を右のように行いました。この計算は正しいですか。
正しくない場合はその理由を説明し,正しく計算を行いなさい。
正しいかな?
問 7 次のような問題について,拓真さんと美月さんは,それぞれ下のようにして答えを求めました。 2人の考え方を説明しなさい。
[mathjax] \( x=-5 \) ,[mathjax] \( y=4 \) のとき,[mathjax] \( 7x-(6x-2y) \) の値を求めなさい。
 拓真さんの考え
拓真さんの考え
 美月さんの考え
美月さんの考え
式の値を求めるとき,式を簡単にしてから数を代入すると,計算しやすくなることがある。
問 8 [mathjax] \( x=5 \),[mathjax] \( y=-3 \) のとき,次の式の値を求めなさい。
⑴ [mathjax] \( 4(x-2y)-(2x-9y) \)
⑵ [mathjax] \( -2x+y-3(x+2y) \)
問 9 [mathjax] \( x=-2 \) ,[mathjax] \( y=\dfrac{1}{3} \) のとき,次の式の値を求めなさい。
⑴ [mathjax] \( 2(3x-6y)+3(5y-2x) \)
⑵ [mathjax] \( (-12x²y) \div (-4x) \)
どんなことがわかったかな
文字をふくむ単項式どうしの乗法・除法も,1年の文字式と同じように計算できます。
次の課題へ!
これまでに学んだ文字式を使って,どんなことができるのかな?
P.24,31

<2年p.22>
確かめよう 1節 式の計算
□ 式の項や次数について理解している。 文字式のしくみ ・P.12 例1 ・P.13 例3
1 次の㋐~㋓の式について,下の問いに答えなさい。
㋐[mathjax] \( \dfrac{2}{3}x \)
㋑[mathjax] \( 5x-4y \)
㋒[mathjax] \( -8x² \)
㋓[mathjax] \( x²-5x+2 \)
⑴ ㋓の式の項をすべていいなさい。
⑵ それぞれ何次式かをいいなさい。
□ 多項式の加法・減法の計算をすることができる。 多項式の計算 ・P.14 例1 ・P.15 例2 ・P.16 例3
2 次の計算をしなさい。
⑴ [mathjax] \( 3x-7y+x+4y \)
⑵ [mathjax] \( 2a²-7a+5+6a²-1 \)
⑶ [mathjax] \( (-5x+6y)+(9x-8y) \)
⑷ [mathjax] \( (x-3y)-(-2x+5y) \)
□ 多項式と数の乗法・除法の計算をすることができる。 多項式の計算 ・P.17 問9 例4 ・P.18 例5
3 次の計算をしなさい。
⑴ [mathjax] \( -3(4x-y+7) \)
⑵ [mathjax] \( (18a-10b)\div 2 \)
⑶ [mathjax] \( 5(-2a+4b)+3(4a-7b) \)
⑷ [mathjax] \( 3(4x-2y)-2(3x+y) \)
□ 単項式の乗法・除法の計算をすることができる。 単項式の乗法 ・ 除法 ・P.19 問2 例1 ・P.20 例2 例3
4 次の計算をしなさい。
⑴ [mathjax] \( (-2a) \times 9b \)
⑵ [mathjax] \( 3a \times 5a² \)
⑶ [mathjax] \( (-6x)² \)
⑷ [mathjax] \( 8ab \div 4a \)
⑸ [mathjax] \( 6x² \div \dfrac{2}{5}x \)
⑹ [mathjax] \( 12xy \div (-6x) \times 2y \)
□ 式の値を求めることができる。 単項式の乗法 ・ 除法 ・P.21 問8 問9
5 [mathjax] \( x=-2 \) ,[mathjax] \( y=3 \) のとき,次の式の値を求めなさい。
⑴ [mathjax] \( (x+7y)+(4x-3y) \)
⑵ [mathjax] \( 4x² \times xy \div (-2x) \)
<2年p.23>
計算力を高めよう 1
家庭学習や計算練習で利用しましょう。
式の計算 解答P.246
1 多項式の加法・減法
⑴ [mathjax] \( 2x+3y+7x+5y \)
⑵ [mathjax] \( -4a+8b-2a-5b \)
⑶ [mathjax] \( 5a²+a² \)
⑷ [mathjax] \( 3x²-6x+1-2x²+4x \)
⑸ [mathjax] \( (7a+b)+(-9a+8b) \)
⑹ [mathjax] \( (-3x²-4x)+(5x²-x) \)
⑺ [mathjax] \( (8x-6y)-(2x+4y) \)
⑻ [mathjax] \( (-x²+9x+6)-(7x²-5x+8) \)
⑼
⑽
2 多項式と数の乗法・除法
⑴ [mathjax] \( 2(6a-5b+1) \)
⑵ [mathjax] \( (9x-4y) \times (-3) \)
⑶ [mathjax] \( (20a+16b) \div 4 \)
⑷ [mathjax] \( (8x-12y) \div (-3) \)
3 いろいろな計算
⑴ [mathjax] \( 3(a+2b)+6(a-b) \)
⑵ [mathjax] \( -(5x-y)+4(3x-y) \)
⑶ [mathjax] \( 2(4x+y)-7x \)
⑷ [mathjax] \( 8a-5b-3(a-4b) \)
⑸ [mathjax] \( 4(2x-y)-2(x-y+1) \)
⑹ [mathjax] \( \dfrac{1}{4}(a-3b)- \dfrac{1}{6}(2a-3b) \)
⑺ [mathjax] \( \dfrac{2a-b}{6}+ \dfrac{a+b}{8} \)
⑻ [mathjax] \( \dfrac{4x-y}{3}- \dfrac{x-3y}{2} \)
⑼ [mathjax] \( x- \dfrac{x+5y}{2} \)
4 単項式の乗法・除法
⑴ [mathjax] \( 9a \times (-5b) \)
⑵ [mathjax] \( 12x \times \dfrac{5}{6}y \)
⑶ [mathjax] \( 3x² \times 7x \)
⑷ [mathjax] \( (-7a)² \)
⑸ [mathjax] \( 4a \times (-ab) \)
⑹ [mathjax] \( (3x)² \times \require{physics} \left(-\dfrac{1}{2}y\right) \)
⑺ [mathjax] \( (-18xy) \div (-9x) \)
⑻ [mathjax] \( x³ \div x \)
⑼ [mathjax] \( 6x² \div \dfrac{3}{4}x \)
⑽ [mathjax] \( \dfrac{1}{2}ab \div \require{physics} \left(-\dfrac{2}{3}b\right) \)
⑾ [mathjax] \( x² \times 4x \div 8xy \)
⑿ [mathjax] \( 15a²b \div (-6ab²) \times 2ab \)
⒀ [mathjax] \( 12x²y \div 2xy \div 6x \)