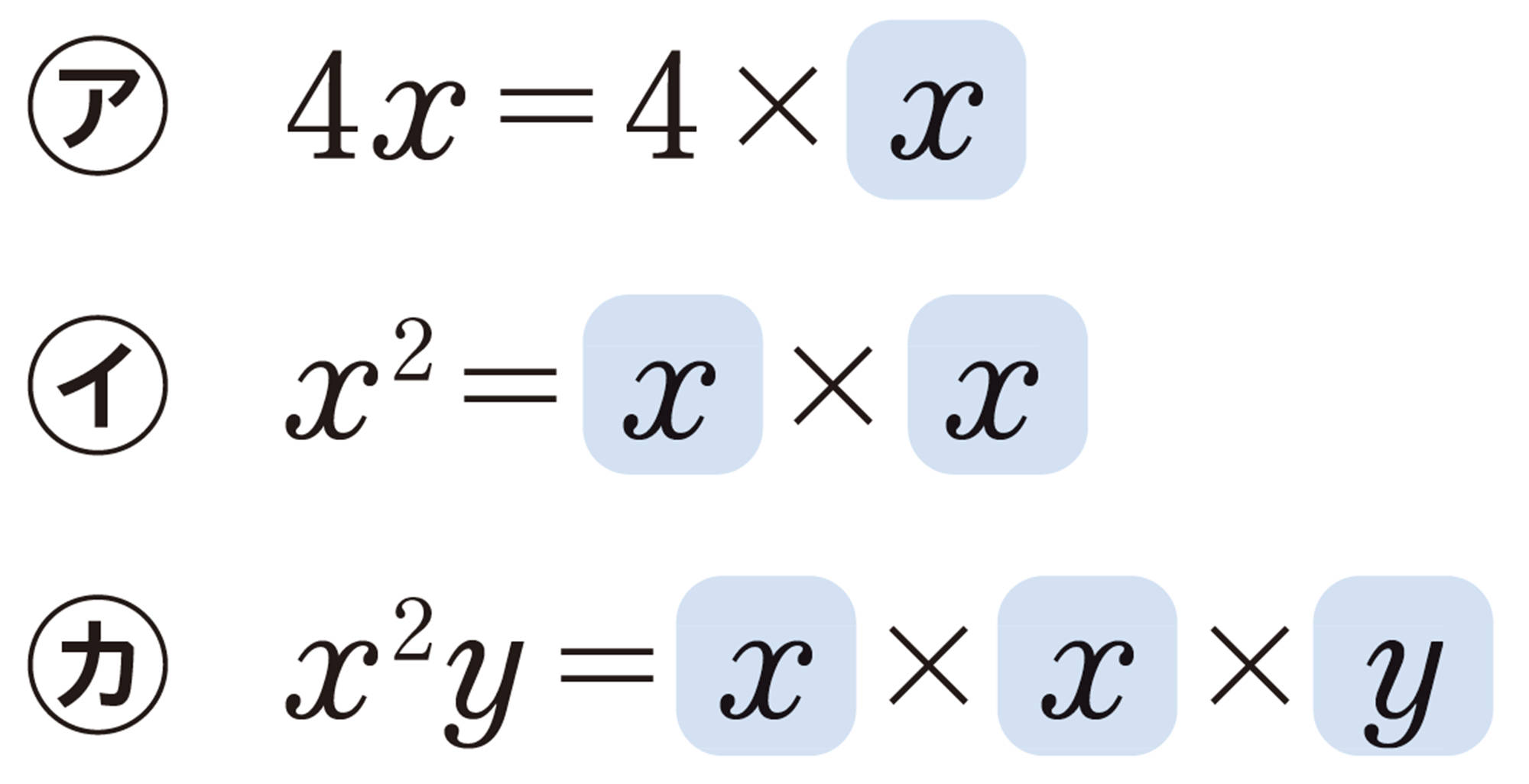<2年p.10>
1節 式の計算
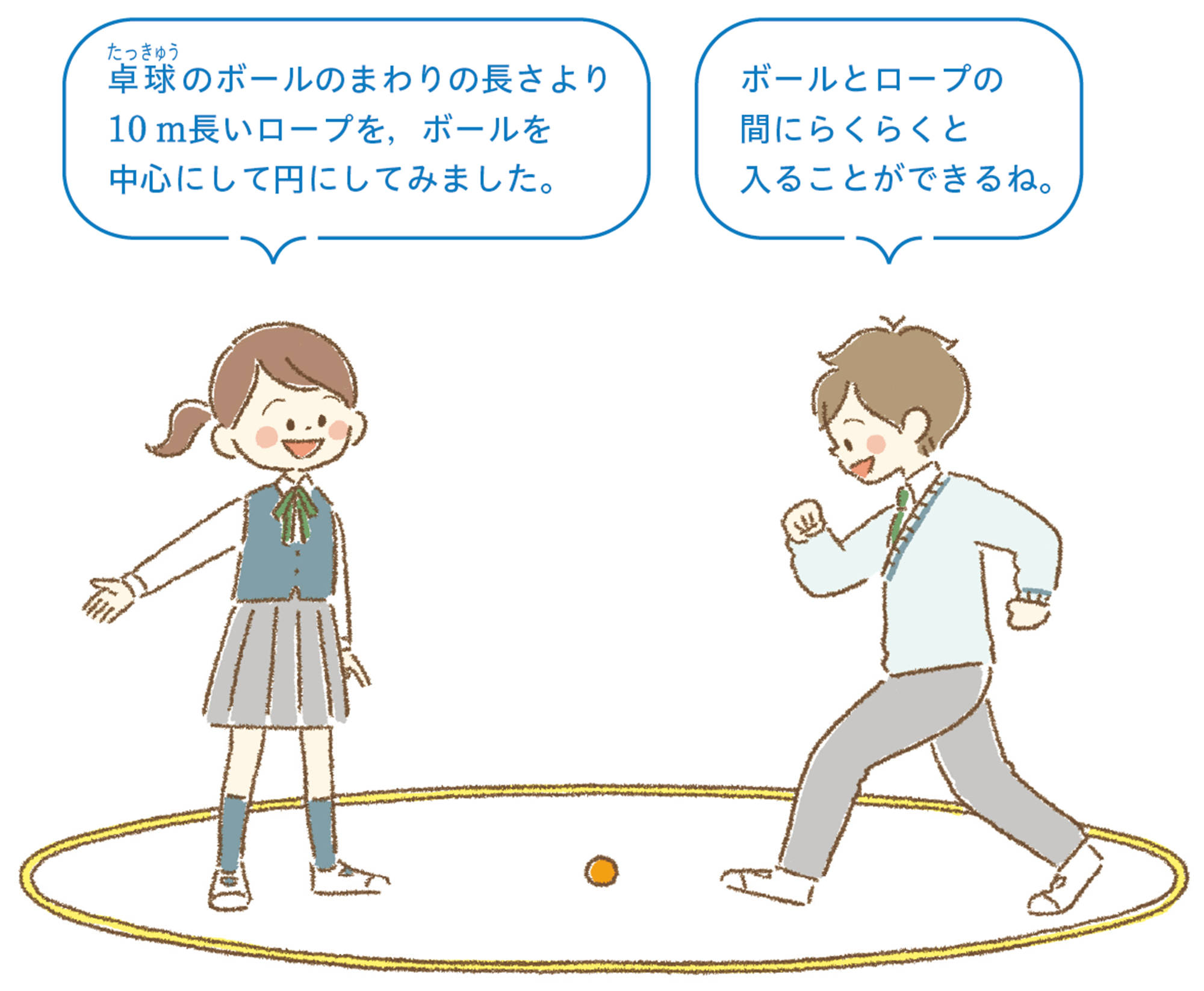
数に何か秘密があるのかな?
【1】 3つの数字を選んで,3桁の数をつくります。同じ数字を選んでもかまいません。その3桁の数を2回続けて6桁の数をつくります。
その6桁の数を7でわります。どんなことがわかるでしょうか。
[mathjax] \( \bigcirc \square \triangle \bigcirc \square \triangle \div 7 \)
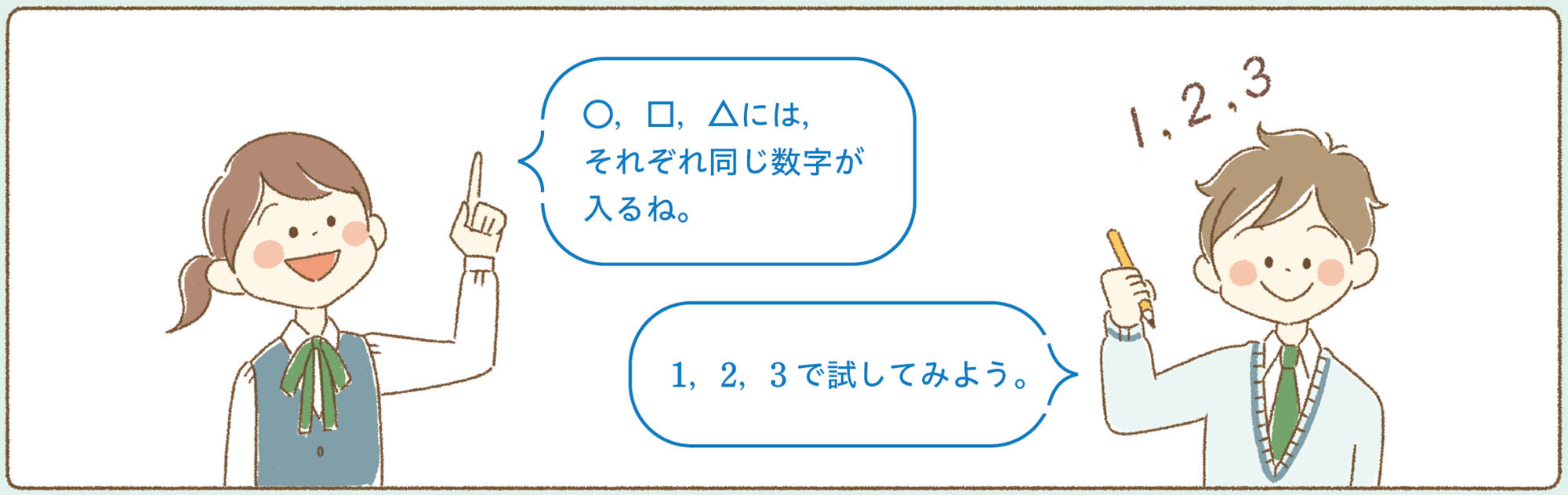
[mathjax] \( \bigcirc \),[mathjax] \( \square \),[mathjax] \( \triangle \)には,それぞれ同じ数字が入るね。
[mathjax] \(1\),[mathjax] \(2\),[mathjax] \(3\)で試してみよう。
[mathjax] \( 123123 \div 7 \)を計算すると,どうなるかな。
わり切れるね。
3つの数字を[mathjax] \(9\),[mathjax] \(8\),[mathjax] \(7\)にしたら,どうなるかな。
電卓を使って,いろいろ試してみよう。


0を選んでもいいのかな。
<2年p.11>
【2】 前ページの1について,気づいたことを話し合ってみましょう。また,それがどんな数字のときでも成り立つか考えてみましょう。
[mathjax] \(987987 \div 7=141141 \)
[mathjax] \(853853 \div 7=121979\)
[mathjax] \(701701 \div 7=100243\)
いろいろ試したけど,いつでも 7でわり切れそうだよ。
いつでも7でわり切れるといっていいかな。
【3】 【1】でつくった6 桁の数は,文字を使うとどのように表せるでしょうか。また,それを使って,どんな数字のときでも 7 でわり切れるかどうか調べられるでしょうか。
6桁の数を,[mathjax] \( abcabc \)と表せばいいのかな。


それだと,[mathjax] \( a \times b \times c \times a \times b \times c \) の意味になってしまうよ。
3桁の数で考えてみよう。小学校では,右のように表したよ。


1年では,文字が1種類のときの式の計算だけだったね。
次の課題へ!
文字が 2 種類以上の文字式も,1年の文字式と同じように考えていいのかな?
P.12

<2年p.12>
1 文字式のしくみ
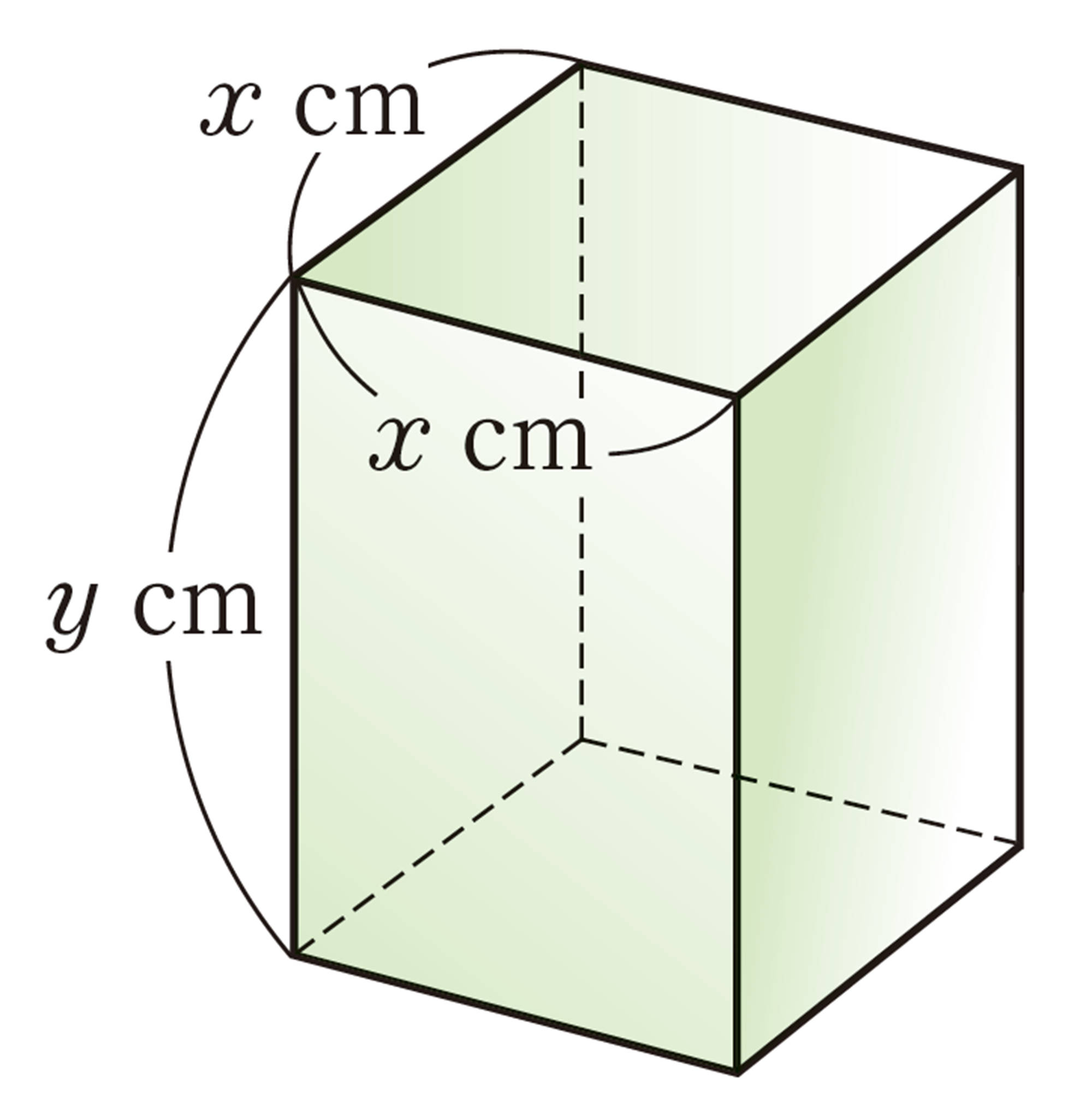
Q Question

2 種類の文字をふくむ式があるね。
1 年で学んだ文字式とは,どんなところがちがうのかな。

見方・考え方
文字式のどこに着目して分類すれば いいかな。
目標 ▷ 文字式を分類・整理しよう。
単項式と多項式
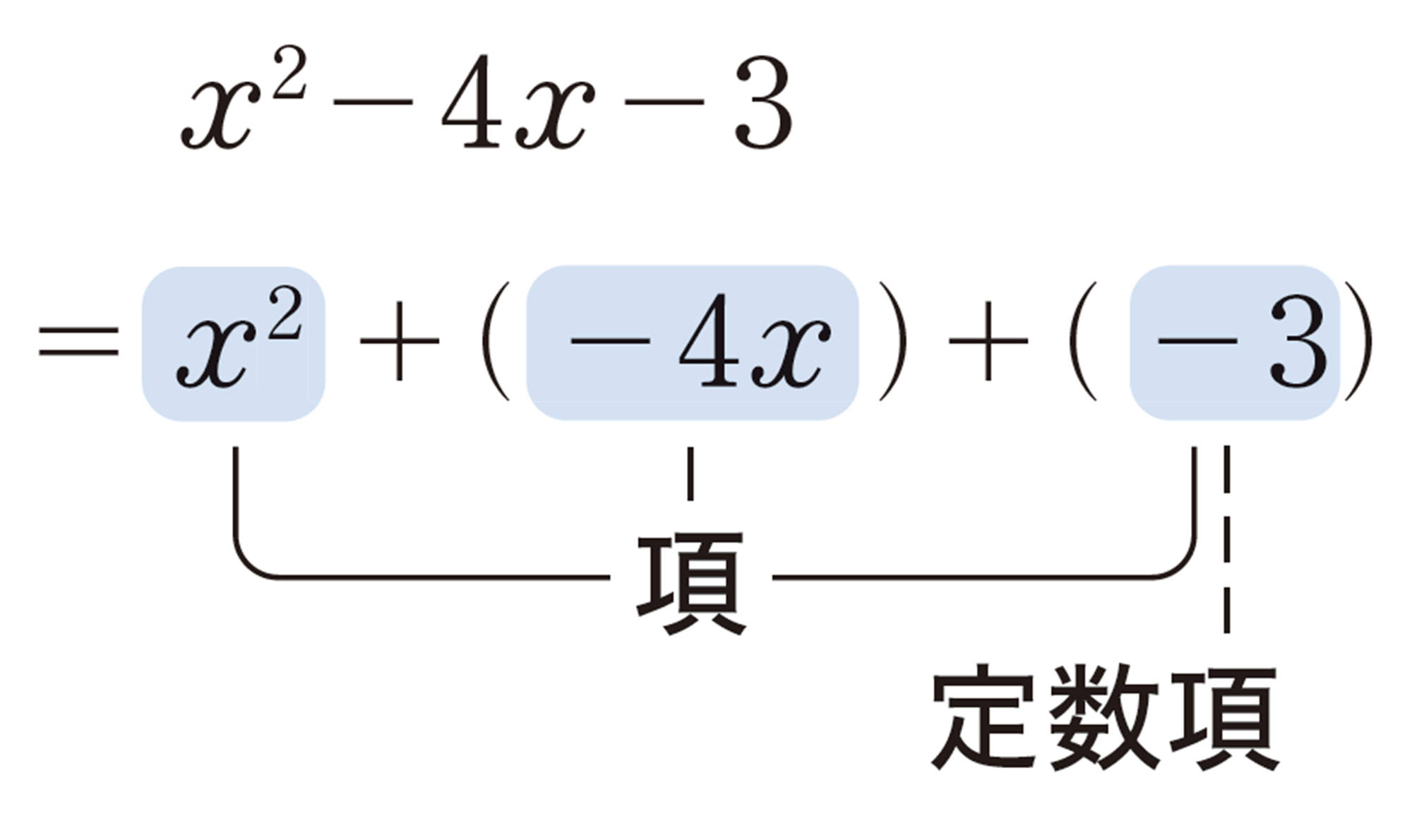
【Q】の [mathjax] \( 4x \)や [mathjax] \( xy \) のように,数や文字をかけ合わせた形の式を 単項式 という。 [mathjax] \( y \) や [mathjax] \( -6 \) のように,1 つの文字や 1 つの数も単項式と考える。また,[mathjax] \( 10x+20 \) や [mathjax] \( 2x+2y \) のように,単項式の和の形で表された式を 多項式 といい,それぞれの単項式を,その多項式の 項 という。
多項式で,文字をふくまない数だけの項を 定数項 という。
問 1 次の多項式の項をすべていいなさい。
⑴ [mathjax] \( 5a+1 \)
⑵ [mathjax] \( 7x-8y \)
⑶ [mathjax] \( 4x²+7x-9 \)
<2年p.13>
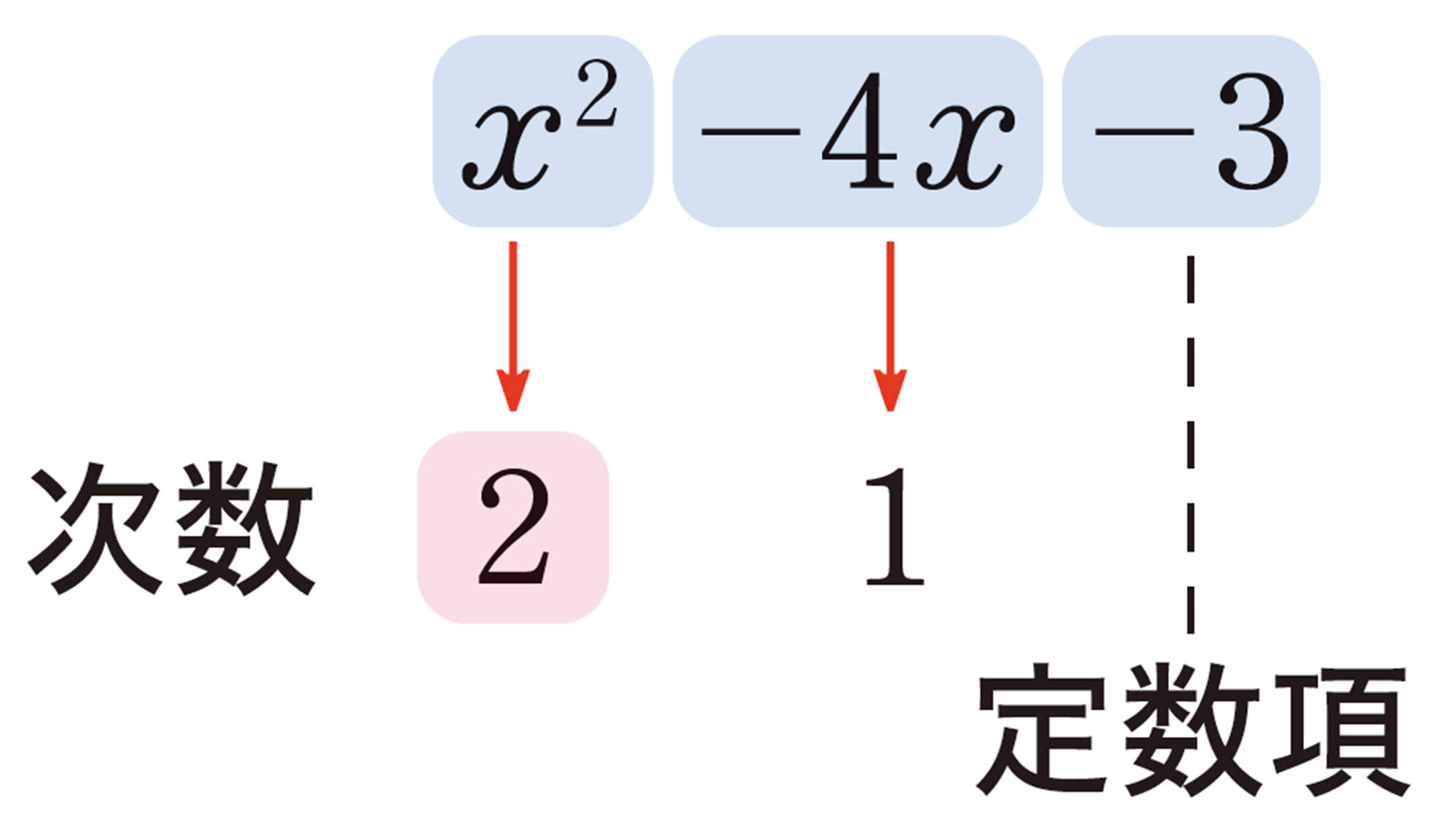
式の次数
単項式で,かけ合わされている文字の個数を,その単項式の 次数 という。
例 2 前ページのQ の ㋐,㋑,㋕の単項式の次数は,それぞれ次のようになる。
問 2 次の単項式の次数をいいなさい。
⑴ [mathjax] \( -6a \)
⑵ [mathjax] \( a² \)
⑶ [mathjax] \( \dfrac{1}{2} ab \)
⑷ [mathjax] \( -xy² \)
多項式では,各項の次数のうちでもっとも大きいものを,その多項式の次数という。
注意 次数の大小は,「次数が高い」,「次数が低い」で表すこともある。
次数が1の式を1次式,次数が2の式を2次式,…という。
問 3 前ページの【Q】の㋒~㋔の式は,それぞれ何次式ですか。
どんなことがわかったかな
文字式は,式の形やかけ合わされている文字の個数に着目することで,分類することができます。
次の課題へ!
文字が 2 種類以上でも,1年の文字式の計算と同じようにできるのかな?
P.14