<1年p.261>
2節 データの活用
都道府県の人口はどれくらい？
日本では，5年ごとに国勢調査が行われています。日本に住んでいるすべての人と世帯を対象にした調査で，国が人口や世帯の実態を把握するために行っています。
身近なこととして，日本の人口について調べてみたいな。
都道府県の人口がどうなっているのか調べてみよう。
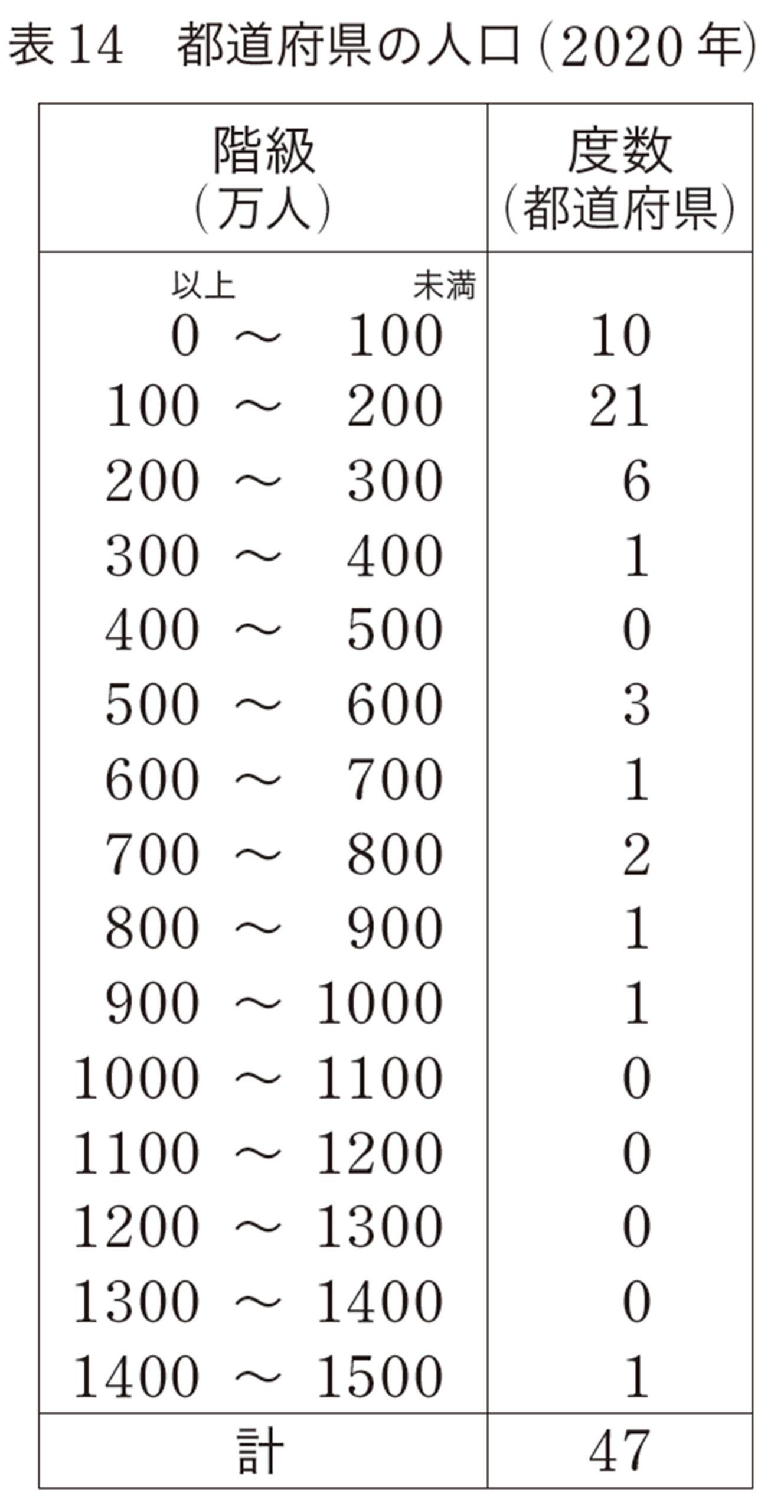
【１】 表14は，2020年の47都道府県の人口を，国勢調査をもとに，100万人を階級の幅として度数分布表に表したものです。また，図12は，それをヒストグラムに表したものです。
47都道府県の人口の傾向について話し合ってみましょう。
ずいぶん少ない方に，かたよっているね。
表14 都道府県の人口(2020年)
自分たちの住んでいる都道府県は，人口が多い方なのかな。
次の課題へ！
身のまわりのデータの傾向を読み取ったり，分析したりできるかな？
P.262
<1年p.262>
１ データの傾向の読み取り方
Q Question
「自分の住んでいる都道府県は，47都道府県の中で人口が多い方か少ない方か」を考える場合には，何を代表値とすればよいでしょうか。
平均値と比べて，多いか少ないかを考えればいいのかな。
何番目から多い方といえるのかな。
見方・考え方
代表値を選んだ根拠を説明できるかな。
目標 ▷ 身のまわりのデータの傾向をくふうして読み取ろう。
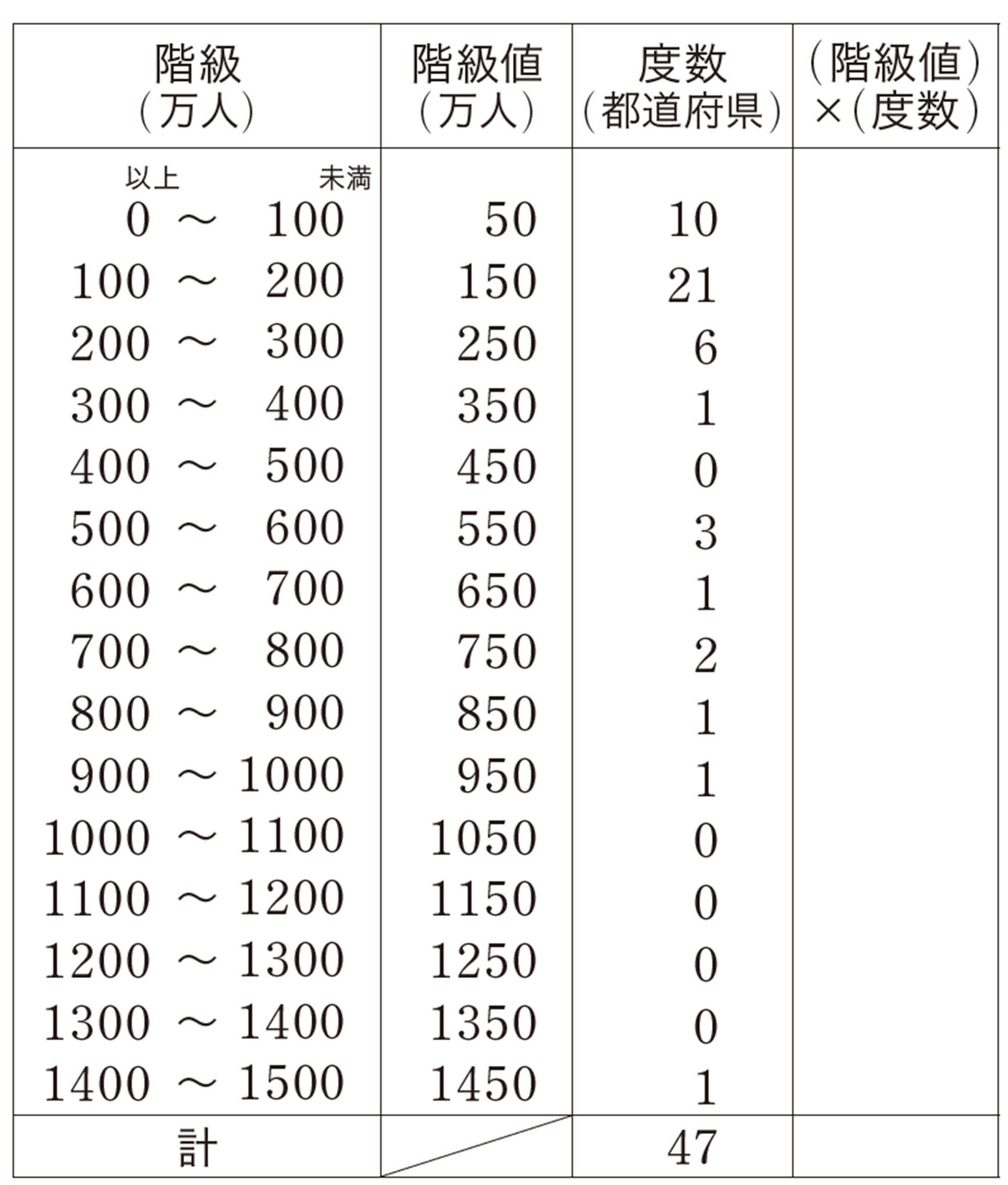
平均値を求めるとき，一つひとつのデータの値を調べなくても，度数分布表からおよその値を求めることができる。
たとえば，表14で，都道府県の人口が0人以上100万人未満の階級には 10個の値がふくまれているが，それらがそれぞれどんな値であるかはわからない。そこで，もとの値の代わりに，ある階級にふくまれる値は，どれもその階級値をとるとみなして計算する。
度数分布表から平均値を求めるには，次の手順で行えばよい。
① 階級値を求める。
② 各階級値と度数の積を求める。
③ ②で求めた値の総和を求める。
④ ③で求めた値を総度数でわって平均値を求める。
<1年p.263>
問 １ 前ページの表15から，47都道府県の人口の平均値を求めて，実際の平均値約268万人と比べなさい。
問1からわかるように，度数分布表から平均値を求めても，データから直接求めた平均値に近い値が得られる。
問 ２ 前ページの表15について，次の問いに答えなさい。
⑴ 中央値は，どの階級に入っていますか。
⑵ 最頻値を求めなさい。
⑶ 300万人未満の都道府県は，約何割ですか。
47都道府県の人口の平均値は約268万人であるが，これより人口が多いのは，実際には12都道府県しかない。
このように，データの中に極端にかけ離れた値があるときには，平均値はそれに影響を受けやすく，代表値として適さない場合がある。一方，中央値や最頻値は極端にかけ離れた値があってもあまり影響を受けないため，このようなときは中央値や最頻値を代表値として用いるとよい。
代表値として何を用いるかは，データの分布を見た上で，データを活用する目的によって判断する必要がある。
問 ３ 261ページの1で，「日本には，人口何万人くらいの都道府県が多いか」を調べるときには，何を代表値とすればよいですか。
問 ４ 表16は，東京と那覇の2022年8月の日ごとの最高気温を度数分布表にまとめたものです。この表から，どちらの方が暑かったといえるか話し合いなさい。
<1年p.264>
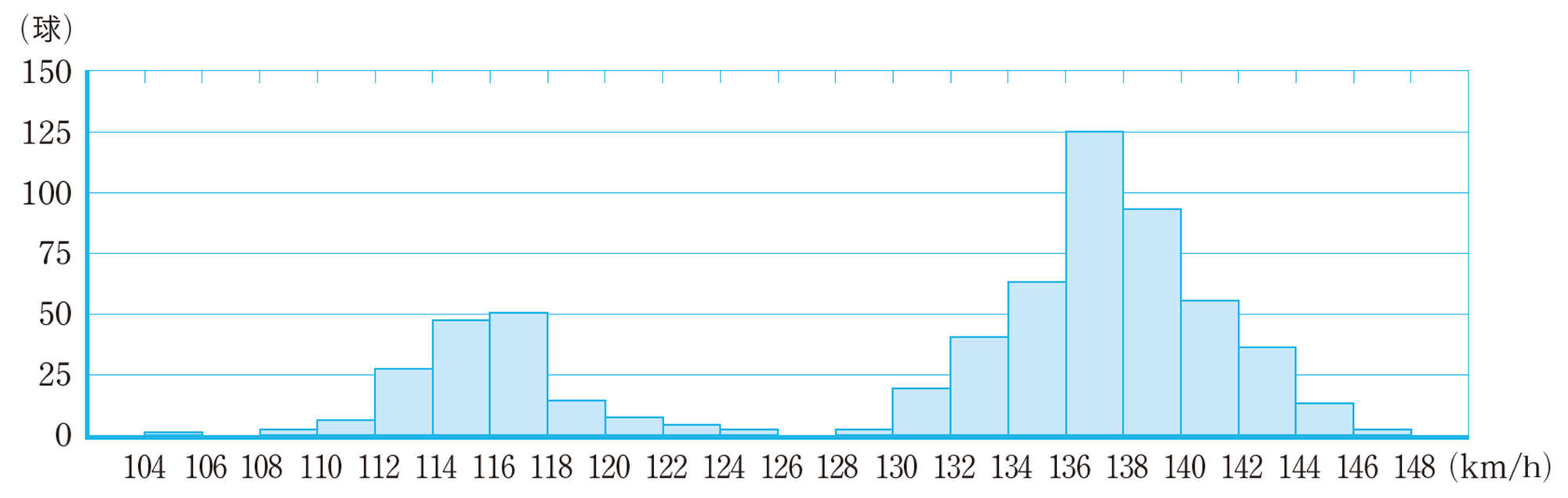
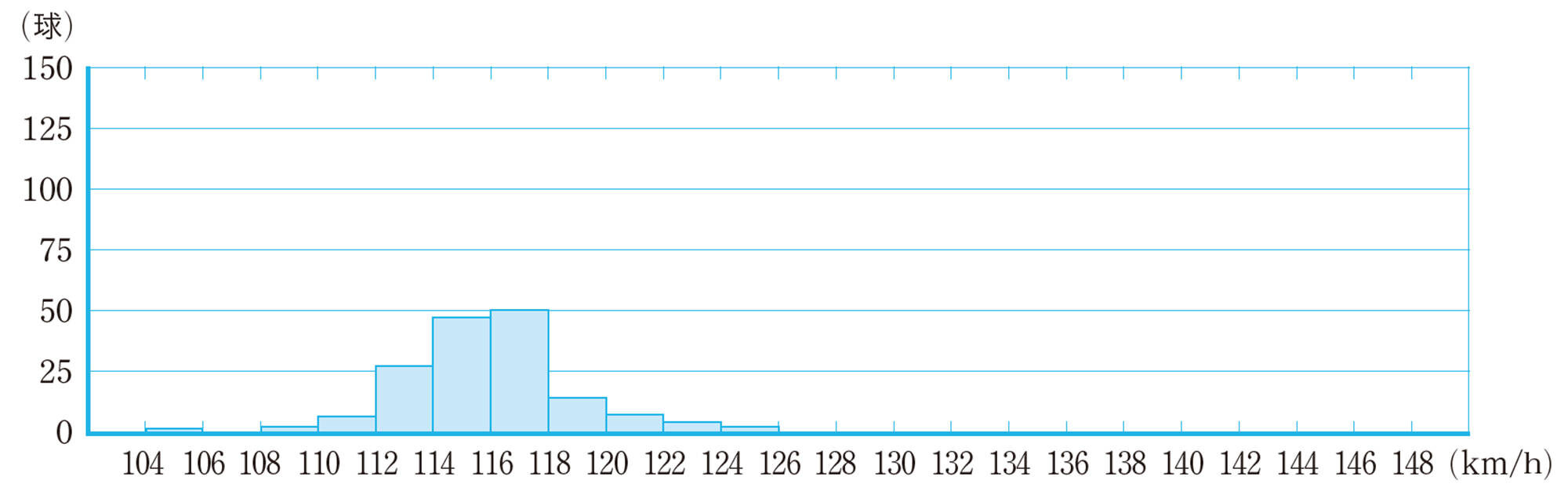
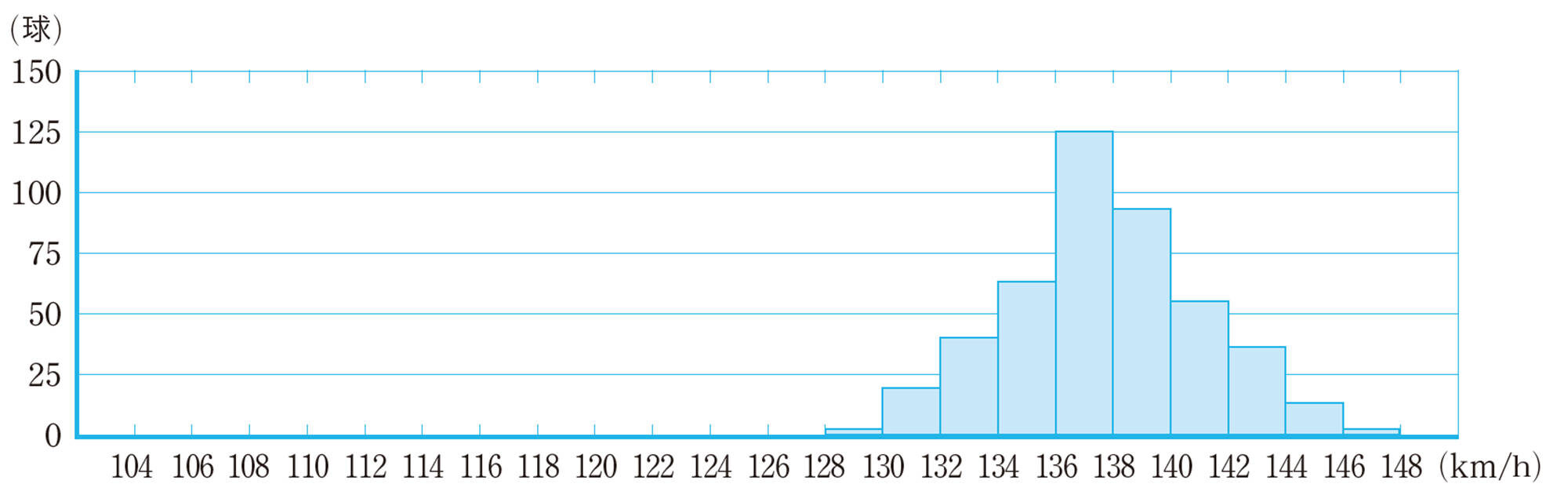
図13のように，ヒストグラムが2つの山の形になる場合，質の異なる集団が混じっている可能性がある。このような場合，目的によってはヒストグラムの山が1つになるようにデータを分けてから，分布の傾向を読み取ることがある。図13の場合，遅い球と速い球があると考えられるから，次のように2つに分けて考えると，分布の傾向が読み取りやすくなる。
どんなことがわかったかな
度数分布表やヒストグラムをもとにして，データの傾向を読み取ることができます。
<1年p.265>
２ データの活用
身のまわりの問題で，解決したい問題があるとき，その問題を解決していく方法の1つに，PPDACサイクルと呼ばれるものがある。このサイクルは，次の5つの手順があり，それぞれの頭文字をとっている。
Problem ［ 問題 ］
調べてみたいことを見つけ，「問題」と「予想」を考える。
生活の中，環境や社会などにかかわる問題の中から，全体的な傾向や特徴を調べたり比べたりしたいことがらを見つける。テーマを決めるには，それに必要なデータを集められるかも考えておく。
ルーラーキャッチの例では
2年生や3年生の反応の速さと比べてみたいね。
Plan ［ 計画 ］
データの調査方法やルールを決めて，調査計画を立てる。
どのようなデータをどのように収集するかを決める。正確なデータを集めるには，しっかりと調査計画を立て，手順にしたがって実施していくことが重要になる。
2年生や3年生にも，自分たちと同じ方法でルーラーキャッチの実験をやってもらおう。
Data ［ データ ］
データを集めて整理する。
調査計画の手順にしたがいデータを収集し，データを集計・加工してまとめる。どんな方法で整理したら全体の傾向が読み取りやすく比べやすいかを考える。
集めたデータをもとにして，データを整理しよう。
Analysis ［ 分析 ］
まとめたデータを分析する。
データをまとめた表やグラフなどから，データについてどんな特徴が読み取れるかを見つける。
それぞれの学年と比べるには，どんな表し方をするとわかりやすいかな。
Conclusion ［ 結論 ］
分析の結果から，結論を出す。
テーマ，調査方法，結果をまとめ，レポートなどで結論を作成し，発表する。
関連 P.282
結果から，どんなことがわかるかな。根拠をもとに説明しよう。
Problem ［ 問題 ］
新たな問題を見つける。
先生たちと比べるとどちらの方が反応が速いか調べてみたいね。
目標 ▷ 身のまわりからデータを集め，分析しよう。
<1年p.266>
みんなはどのくらい家で勉強しているのかな。
みんなの勉強時間のアンケートをとってみたらどうかな。
Q Question
拓真さんは，みんながどのくらい家で勉強しているかを調べるために，自分の中学校の1年生全員に，平日1日に家で勉強する時間を聞きました。その結果は右の表の通りです。この表から，どのようなことを調べればよいでしょうか。
平均値を求めればわかるかな。
見方・考え方
どこに着目して考えればよいかな。
１ 右の表を完成させて，平均値を求めましょう。
短い方にかたよっているけど，平均値で比べていいのかな。
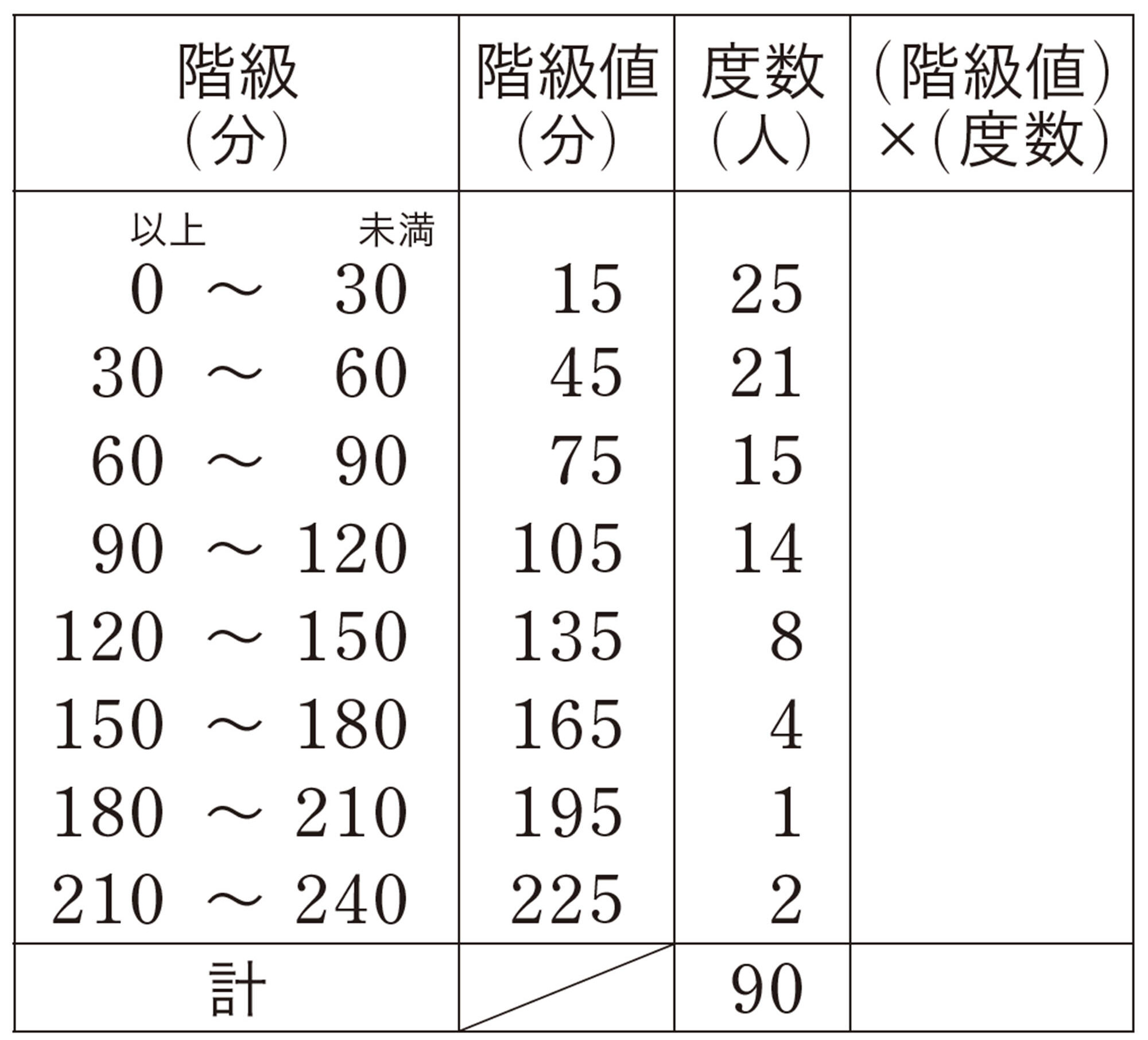
２ 表18について，次の問いに答えなさい。
⑴ 中央値は，どの階級に入っているでしょうか。
⑵ 最頻値を求めましょう。
⑶ 拓真さんが平日1日に家で勉強する時間は65分です。1年生の中で長い方といえるでしょうか。その理由も説明しましょう。
休日の勉強時間はどうなのかな。
平日とはちがった結果になると思うな。
<1年p.267>
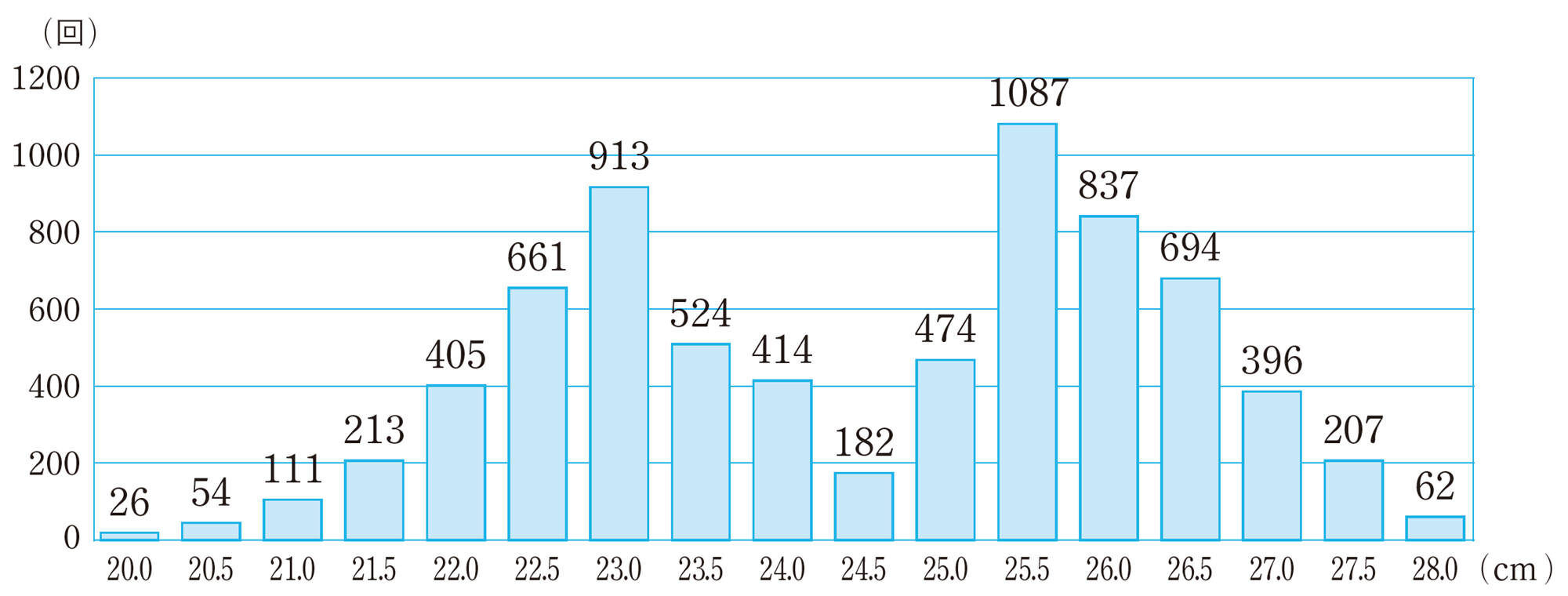
問 １ あるボーリング場で，貸し出し用の靴200足をすべて新しいものに買いかえます。どのサイズを何足買えばよいかを決めるために，過去1か月間にどのサイズが何回貸し出されたかを調べました。貸し出された回数の合計は7260回です。その結果は次の図の通りです。このとき，下の問いに答えなさい。
⑴ 上のデータの平均値は[mathjax]\(24.5\) cmです。「[mathjax]\(24.5\) cmの靴をもっとも多く買う」という考えは適切かどうかを説明しなさい。
⑵ どのサイズの靴をもっとも多く買えばよいと考えられますか。また，そのサイズの靴は，何足買えばよいと考えられますか。
どんなことがわかったかな
これまで学んだことを利用すれば，身のまわりのことがらのデータを集め，分析することができます。
確かめよう 2節 データの活用
１ 次のデータは，美月さんをふくむ15人の生徒が，10点満点の漢字テストをしたときの点数です。下の問いに答えなさい。
[mathjax] \(4\)，[mathjax] \(5\)，[mathjax] \(5\)，[mathjax] \(6\)，[mathjax] \(7\)，[mathjax] \(7\)，[mathjax] \(8\)，[mathjax] \(8\)，[mathjax] \(8\)，[mathjax] \(9\)，[mathjax] \(9\)，[mathjax] \(9\)，[mathjax] \(9\)，[mathjax] \(10\)，[mathjax] \(10\)
⑴ 平均値，中央値，最頻値，範囲を求めなさい。
⑵ 美月さんの点数がほかの14人と比べて高い方か低い方かを知りたいとき，代表値のうち，何を参考にすればよいですか。
