<1年p.253>
２ 相対度数
Q Question
表5は， 1年 A組31人と 1年生126人のルーラーキャッチのデータです。A組は1年生の中で，反応が速い人が多いといえるでしょうか。
見方・考え方
全体の数がちがうときは，どのように比べたらいいかな。
たとえば，｢10 cm以上13 cm未満」の人がそれぞれ何人いるかで比べられるかな。
全体の人数がちがうのに，人数で比べてもいいのかな。
目標 ▷ 全体の数がちがう複数の集団のデータの比べ方を考えよう。
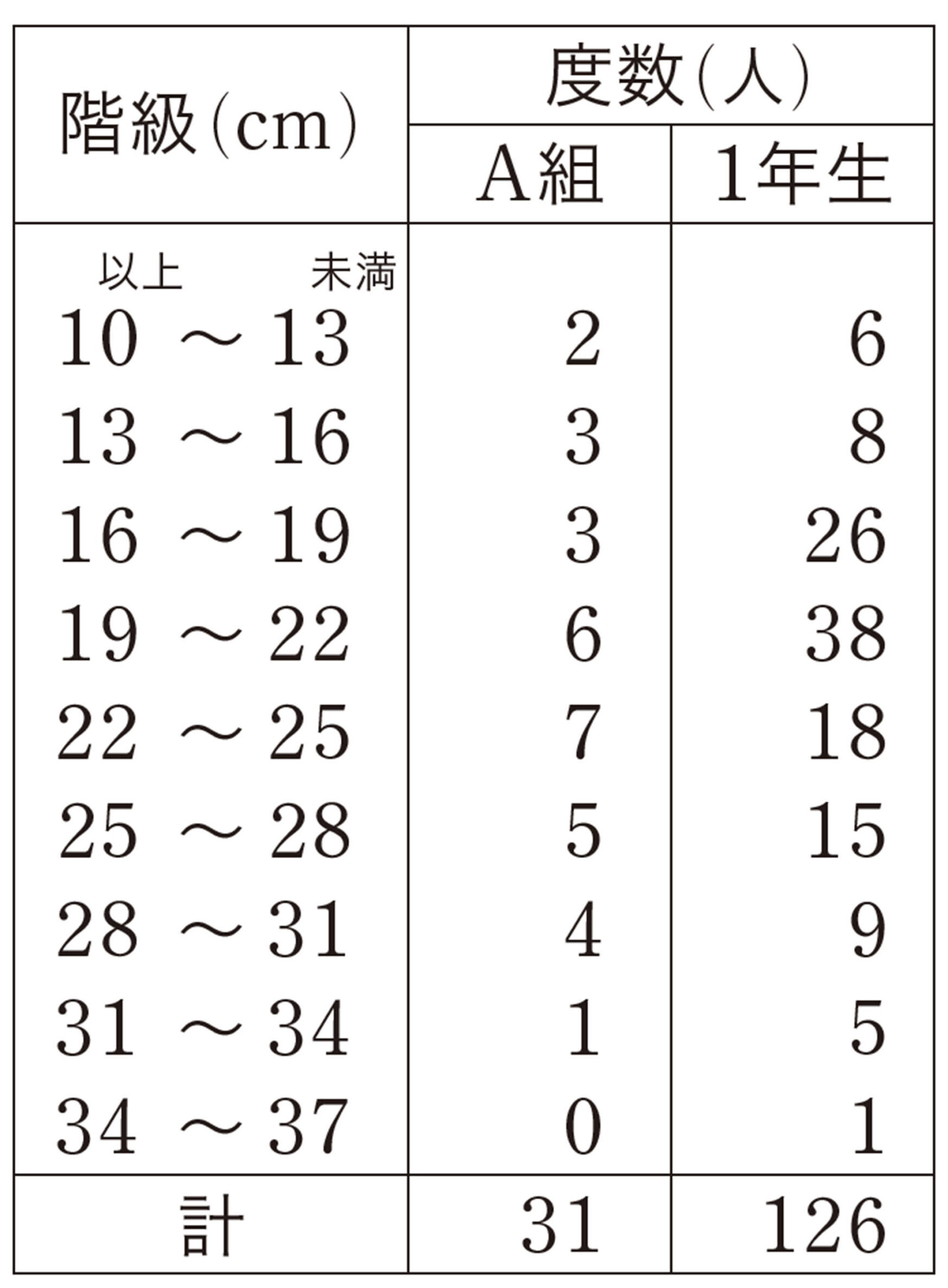
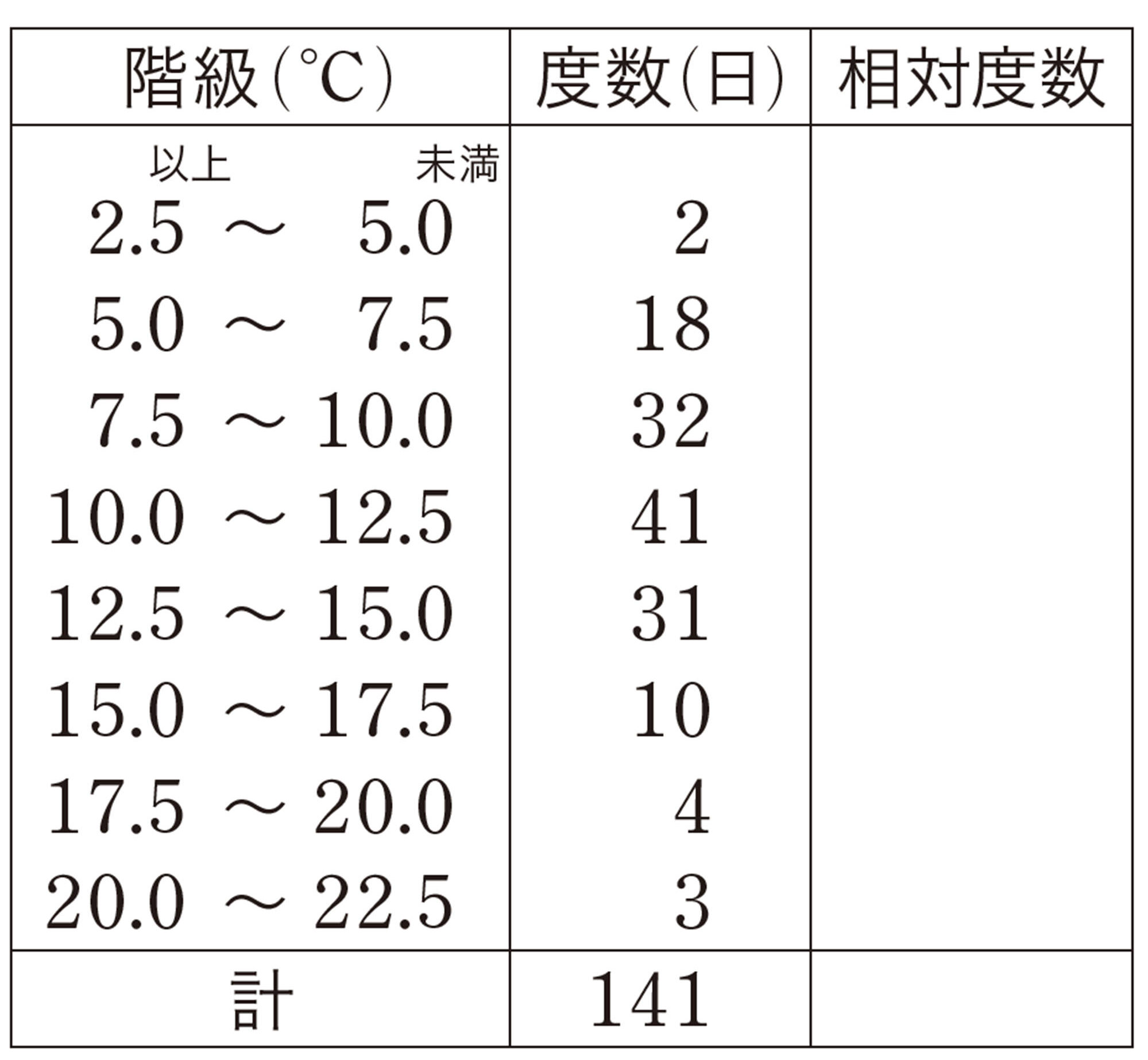
表5で，「10 cm以上13 cm未満」の階級に入る生徒は，1年A組が2人，1年生が6人である。全体の人数は，1年A組が31人，1年生が126人なので，度数で比べても意味がない。
そこで，これを割合で比べると，
1年A組は，[mathjax]\(2 \div 31=0.064 \cdots\)
1年生は，[mathjax]\(6 \div 126=0.047\cdots\)
となる。すなわち，全体に対するこの階級に入る生徒の割合は，A組の方が大きいことがわかる。
このように，各階級の度数を，度数の総和すなわち総度数でわった値を，その階級の 相対度数 という。
[mathjax]\(\textsf{(ある階級の相対度数)}=\dfrac{\textsf{(その階級の度数)}}{\textsf{(総度数)}}\)
<1年p.254>
前ページの表5で， A組の各階級の相対度数を小数第三位を四捨五入して小数第二位まで求めると， 表6のようになる。このような表を， 相対度数分布表という。
注意 相対度数の総和は1となる。また，小数第二位まで求めるとき，小数第二位の数が0でも，そのまま書く。
問 １ 前ページの表5をもとにして，1年生の各階級の相対度数を小数第二位まで求め，表6に書き入れなさい。
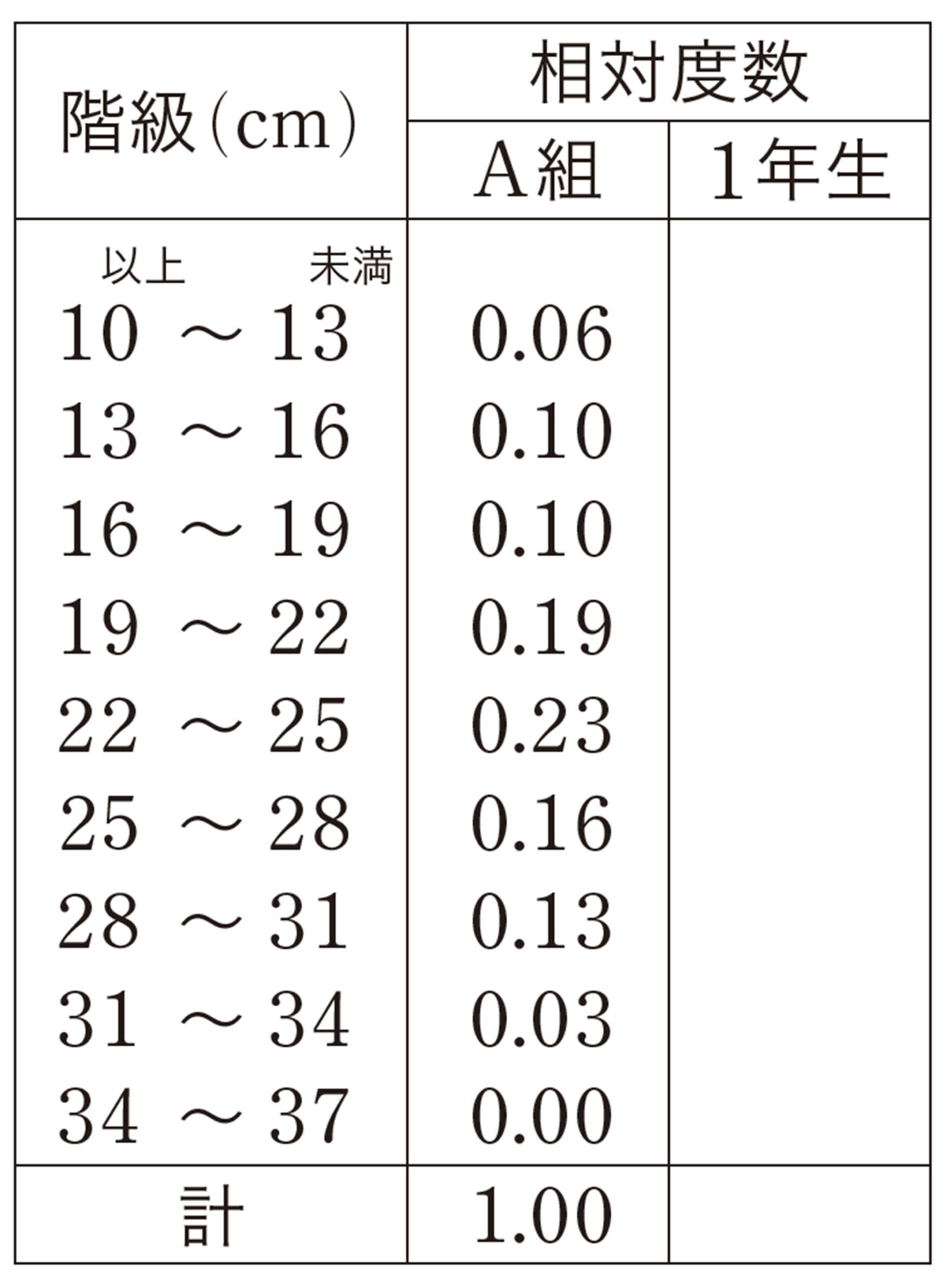
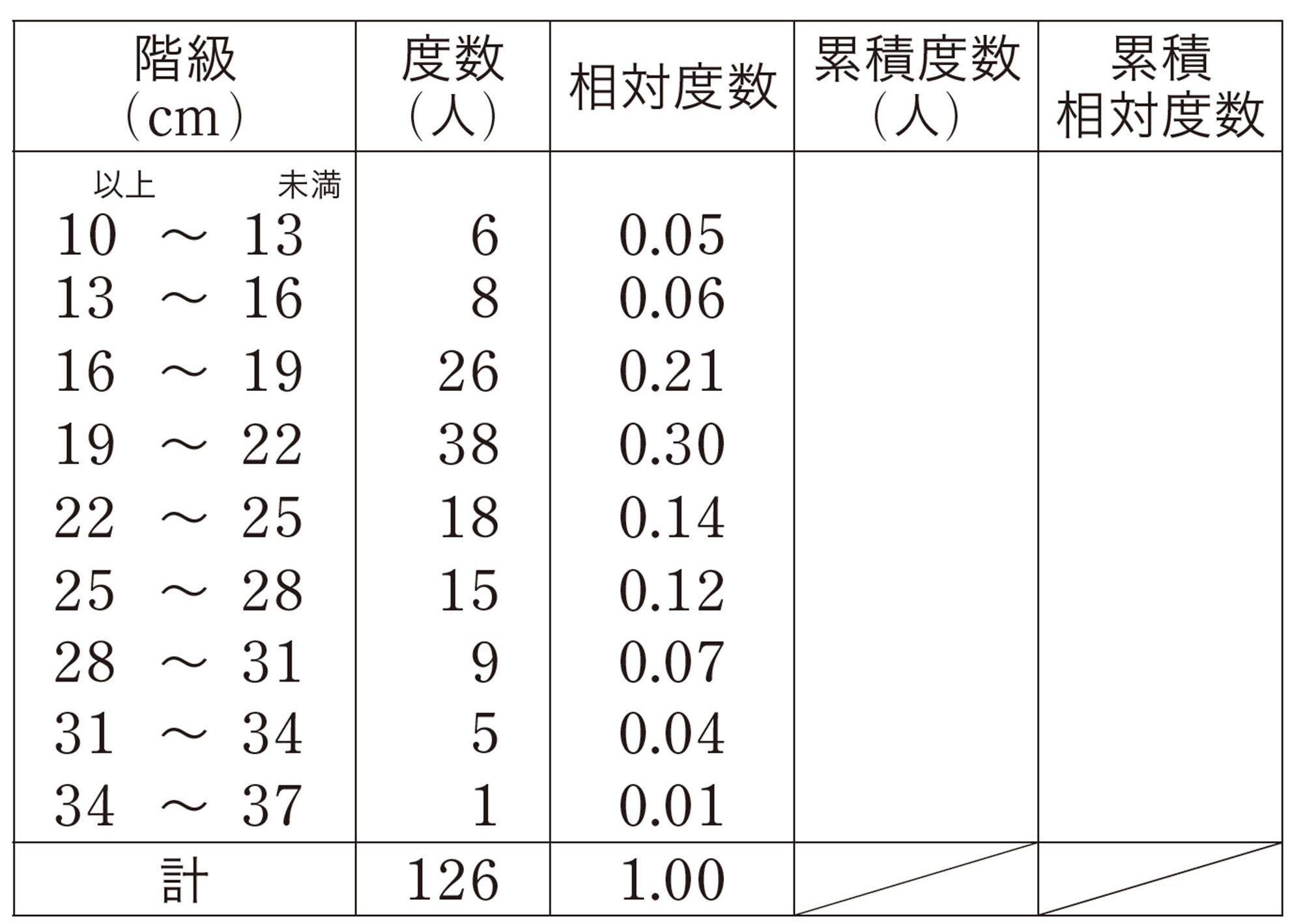
問 ２ 表6をもとに，次の問いに答えなさい。
⑴ ルーラーキャッチの記録が19 cm 以上22 cm 未満の生徒の割合は，A組と1年生ではどちらが大きいですか。
⑵ ルーラーキャッチの記録が19 cm 未満である生徒の割合は，A組と1年生ではどちらが大きいですか。
問 ３ 表6をもとにして，A組の相対度数の分布を度数折れ線で表すと，図9のようになります。1年生の相対度数の分布を度数折れ線で表し，図9にかき入れなさい。
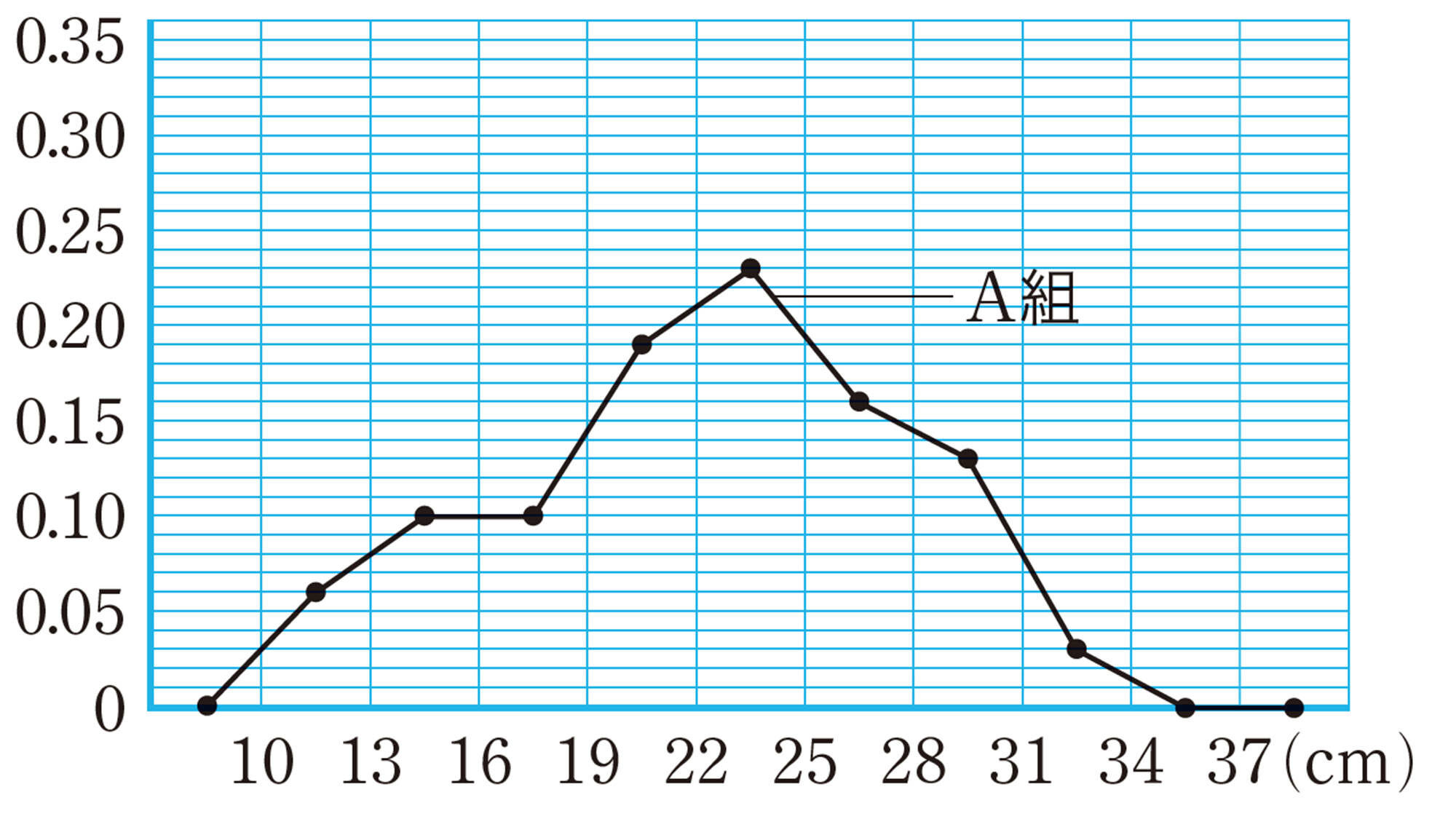
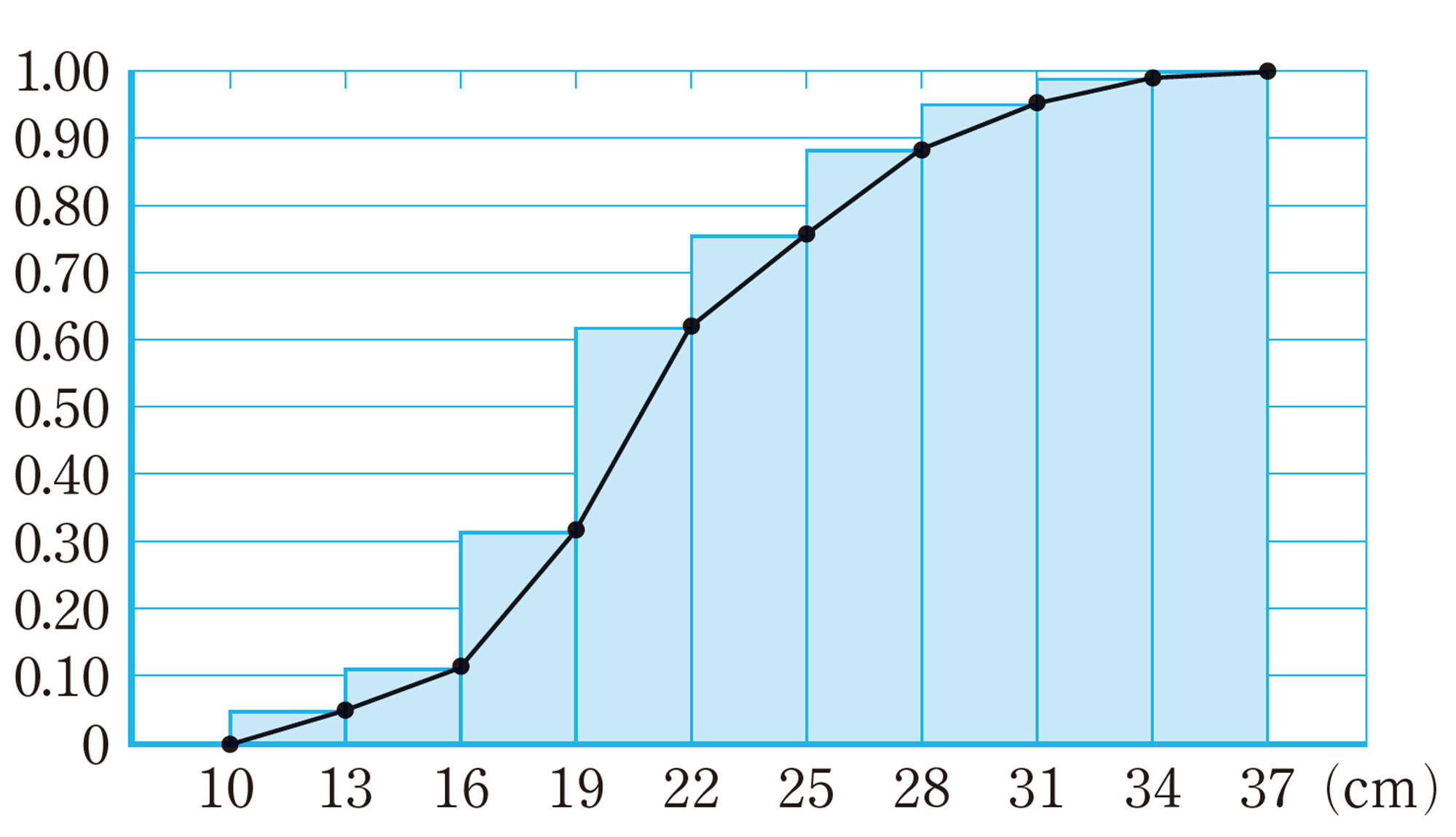
問 ４ 表6や図9をもとにして，A組と1年生の分布を比べ，似ているところや異なるところをいいなさい。
これまで調べたように， 相対度数は，同じことがらについて，総度数の異なる集団のデータを比較するときによく用いられる。
相対度数は，ほかにはどんなところで使われているのかな。
<1年p.255>
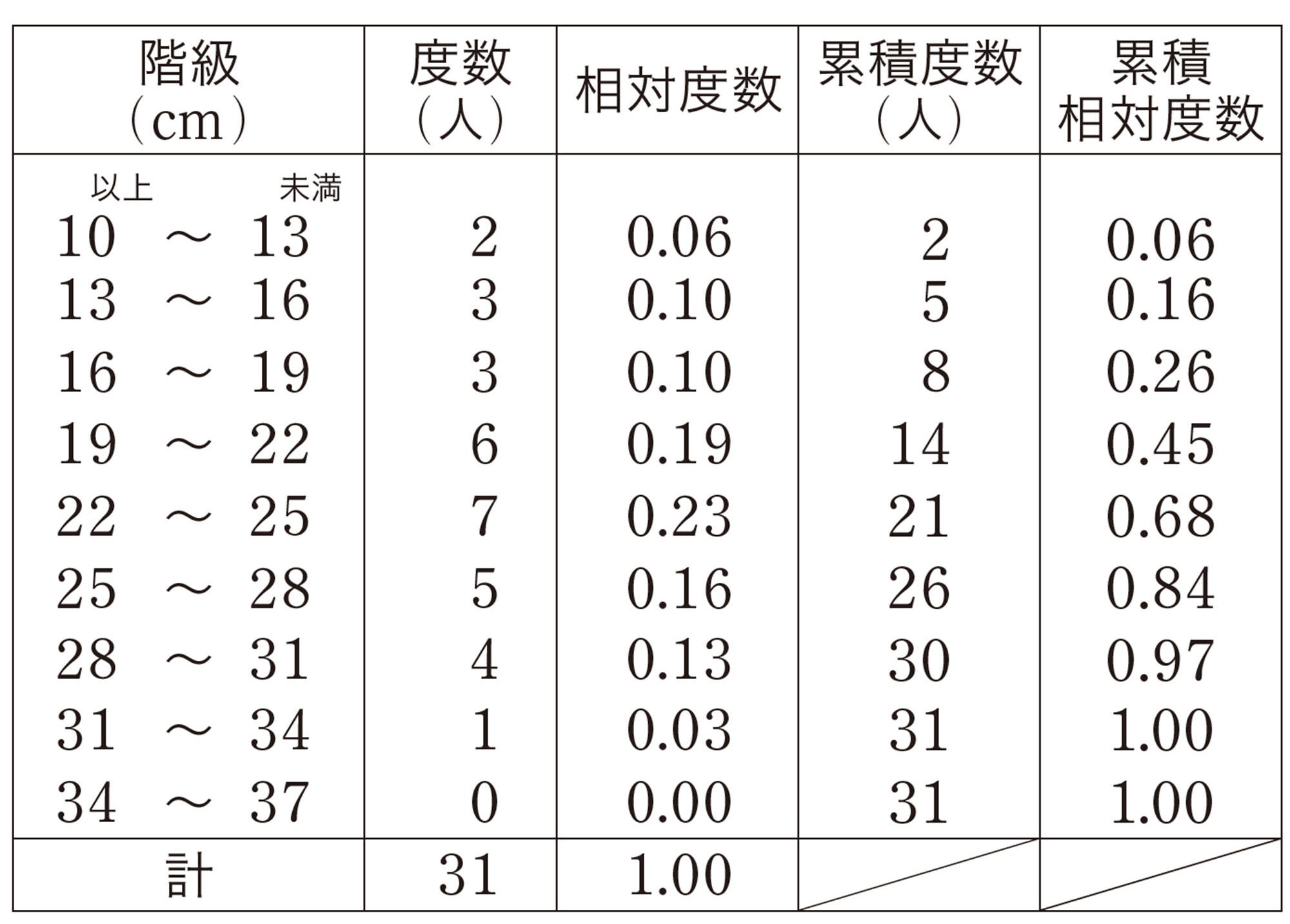
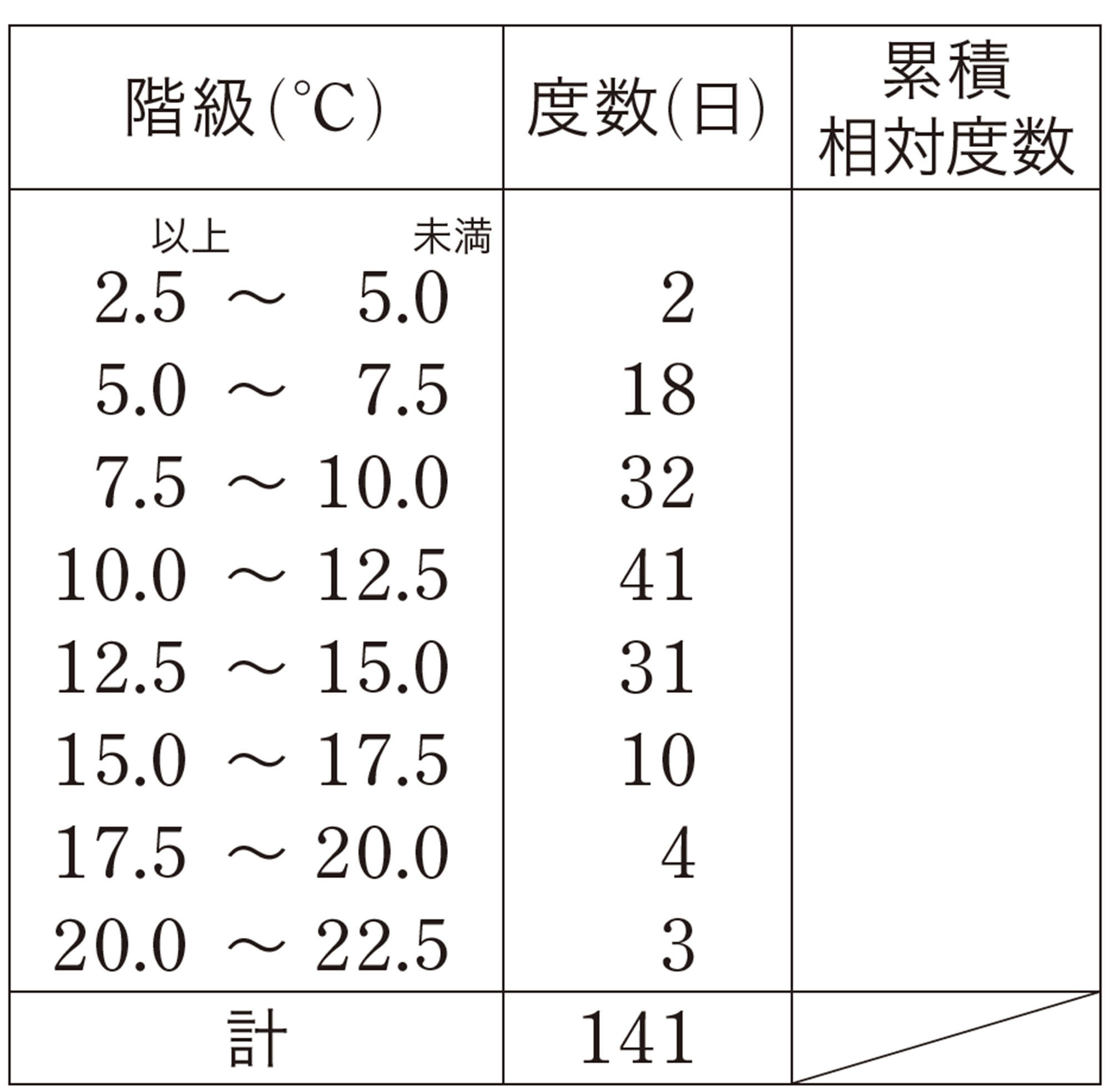
累積度数・累積相対度数
度数分布表において，最小の階級から各階級までの度数を加えたものを累積度数 という。また，最小の階級から各階級までの相対度数を加えたものを 累積相対度数 という。
分布のようすを調べるために，累積度数や累積相対度数を用いることがある。
例 １ 次の表7は，A組のルーラーキャッチのデータの累積度数と累積相対度数を求めたものである。この表から，このデータの中央値が22 cm以上25 cm 未満の階級に入っていることがわかる。また，10 cm 以上22 cm 未満の中に，全体の[mathjax]\(0.45\)，すなわち45％の値がふくまれていることがわかる。
問 ５ 次の表8は，1年生のルーラーキャッチのデータです。表を完成させて，下の問いに答えなさい。累積相対度数は，小数第二位まで求めなさい。
⑴ 中央値は，どの階級に入っていますか。
⑵ 22 cm 未満の人数は，全体の人数の何％ですか。
<1年p.256>
例 ２ 前ページの表8について，累積相対度数を度数折れ線に表すと，右の図のようになります。
注意 累積相対度数を折れ線で表すには，累積相対度数のヒストグラムの各長方形の右上の頂点を結ぶ。
ことがらの起こりやすさ
Q Question
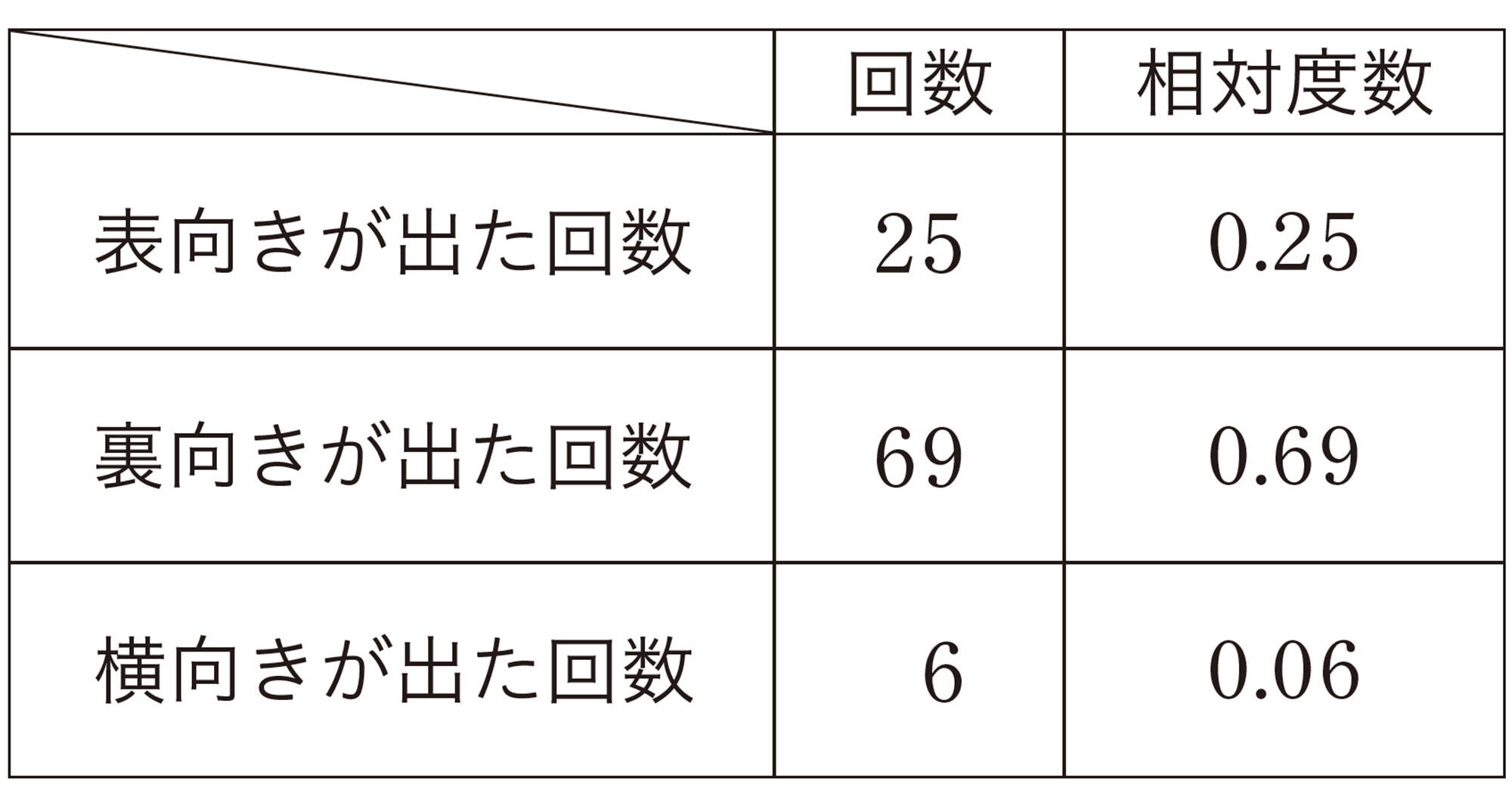
右のようなペットボトルのキャップを投げる実験を100回行ったところ，表9のような結果になりました。このペットボトルのキャップを20回投げると，表向きが何回出ると予想できるでしょうか。
100回投げて25回表向きが出たから， 4回に1回は表向きが出ているといえるね。
20回投げたときも，同じ割合で表向きが出るといえるのかな。
見方・考え方
実際に実験して確かめることができるかな。
問 ６ 実際に，ペットボトルのキャップを50回投げて，表向きが出た相対度数を調べなさい。また，実験回数を100回，150回，200回，…と増やしたとき，表向きが出た相対度数がどのように変わるか調べなさい。相対度数は，小数第二位まで求めなさい。
<1年p.257>
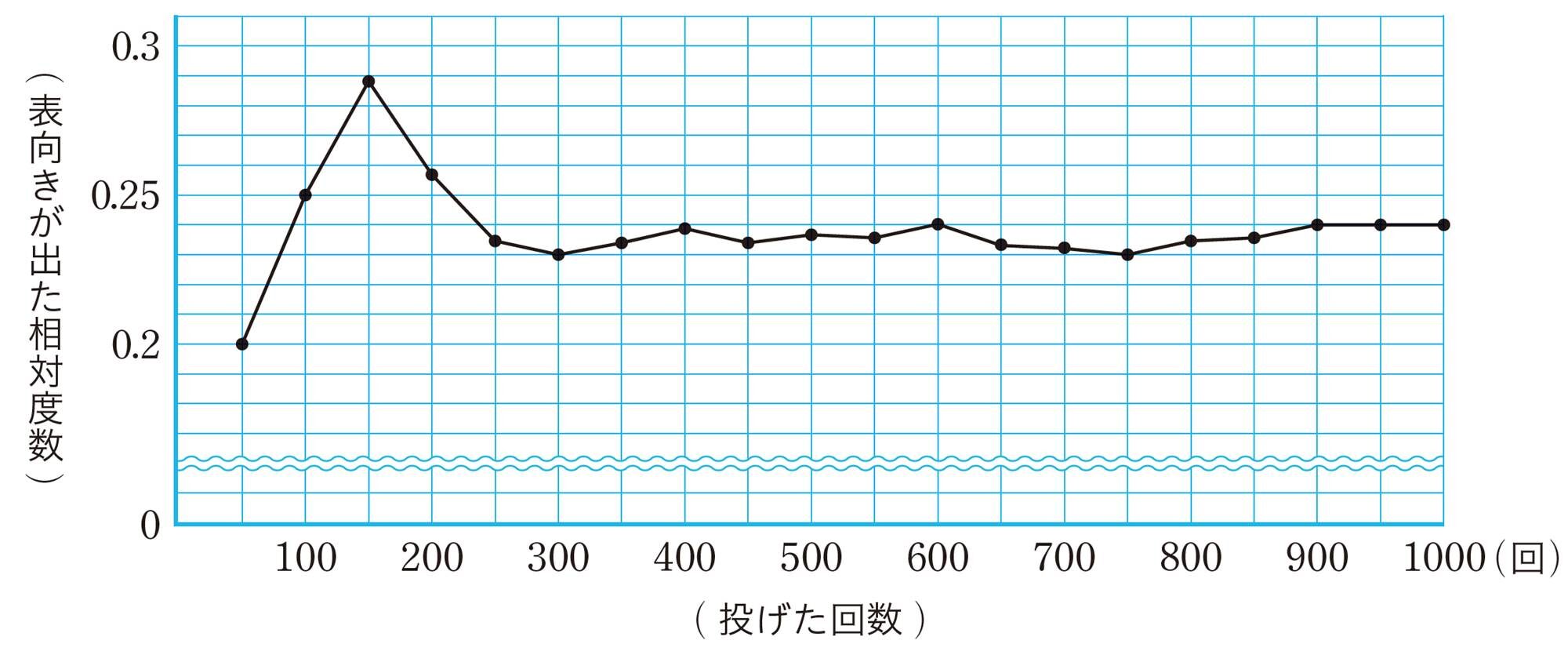
次の図は， 前ページの問6の実験結果をグラフに表した1つの例である。
上のグラフで，はじめ大きく変動していた相対度数は，ペットボトルのキャップを投げる回数が増えるにつれてあまり変動しなくなり，一定の数値[mathjax]\(0.24\)に近づいていく。この数値は，表向きが出ることの起こりやすさを表していると考えられる。
多数回の実験の結果，そのことがらの起こる相対度数が一定の数値に近づくとき，その数値でことがらの起こりやすさを表すことができる。このように，あることがらの起こりやすさの程度を表す数を，そのことがらの起こる 確率 という。
前ページの実験において，ペットボトルのキャップを投げるとき，表向きが出る確率は[mathjax]\(0.24\)と考えられる。
問 ７ 1つの王冠を投げて表向きが出た回数を調べたところ，次の表のような結果になりました。表向きが出た相対度数をそれぞれ求め，表を完成させなさい。また，この王冠を投げるとき，表向きが出る確率はいくらと考えられますか。
<1年p.258>
Q Question
右の表は，堺市の5年間の2月の日ごとの最高気温をまとめたものです。
各階級の相対度数を小数第二位まで求め，表12に書き入れてみましょう。また，堺市では，今年の2月に最高気温が10℃未満になる日は何日ぐらいあるか予想することができるでしょうか。
全体の中で，10℃未満の日の割合はいくらになるのかな。
見方・考え方
相対度数を割合とみなして考えられるかな。
問 ８ 右の表について，次の問いに答えなさい。
⑴ 表12をもとにして，累積相対度数を小数第二位まで求め，表13に書き入れなさい。
⑵ 中央値は，どの階級に入っていますか。
⑶ 最高気温が10℃未満だったのは，何%ですか。
【Q】 では，過去のデータにおける相対度数は厳密には確率とはいえないが，相対度数を確率とみなして考えることにより，過去のデータから未来のことがらの起こりやすさの傾向を予測することができる。
堺市で，2月に最高気温が10℃未満になる日は，その確率を37%と考えることにより，10日ぐらいと予測することができる。
どんなことがわかったかな
相対度数を利用すると，全体の数がちがう複数の集団のデータを比較することができます。また，相対度数を確率とみなすことにより，未来の予測をすることもできます。
次の課題へ！
これまで学んだデータの傾向の調べ方を利用すると，身のまわりのデータの傾向を読み取ったり，分析したりできるのかな？
P.261，265
<1年p.259>
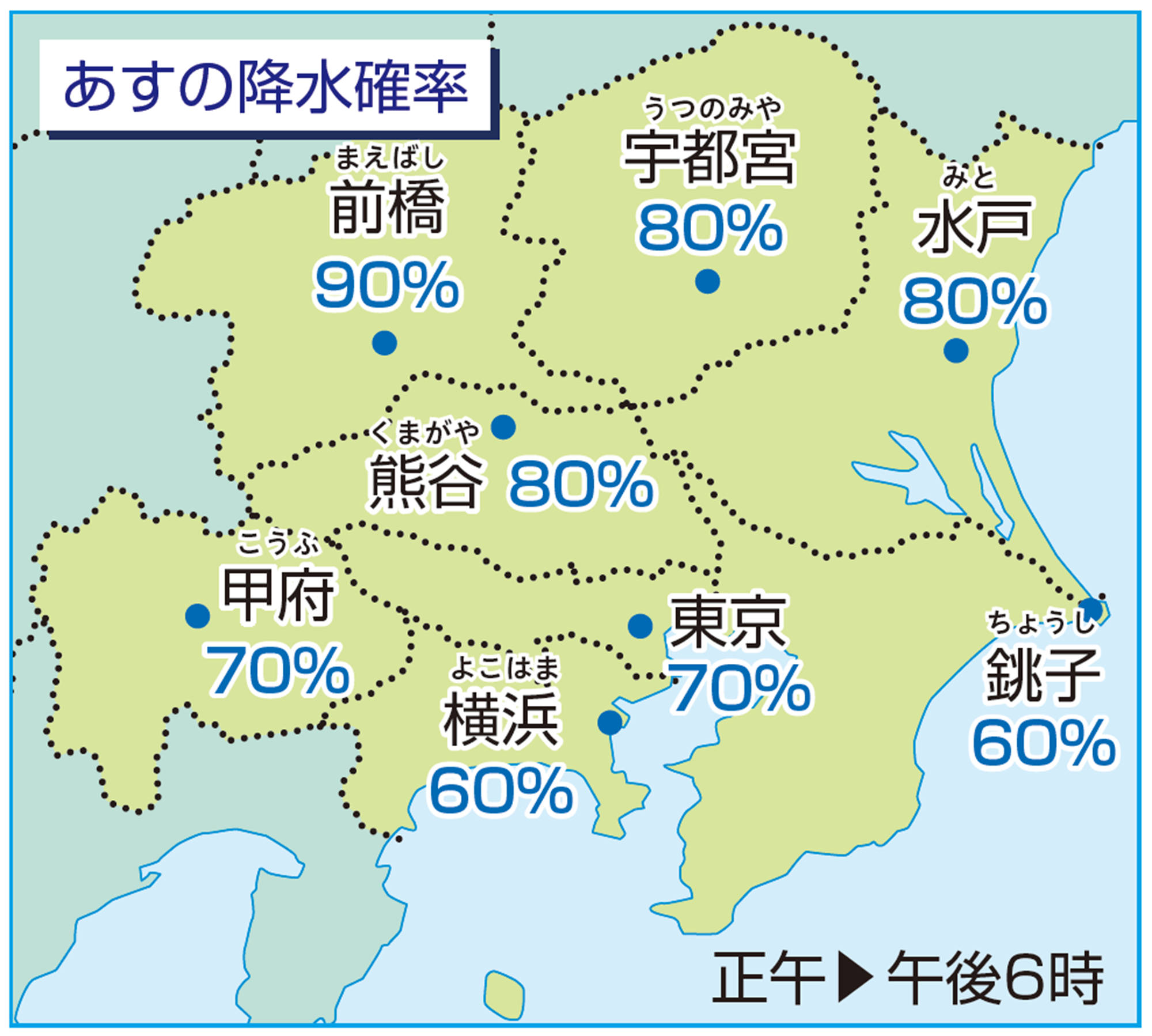
降水確率 Tea Break
天気予報で発表される降水確率は，過去の気象状況のデータをもとに，スーパーコンピュータを使って将来の大気の状態を予測し，雨や雪の降る確率を算出しています。
ところで，「東京地方の正午から午後6時までの降水確率が70 ％」とは，どんなことを意味しているのでしょうか。
降水確率は，予報する地域内で，指定された時間帯に1 mm以上の雨や雪が降る確率を示しています。これは，降り方の強弱や降る時間の長短，降水量の多少などについてはまったく関係がありません。また，予報する地域内のどの地点も同じ確率で示されています。
したがって，「東京地方の正午から午後6時までの降水確率が70 ％」の意味は，「東京地方のどの地点も，正午から午後6時までの降水量の合計が1 mm 以上となる確率が70 ％である」ということになります。
なお，「降水確率70 ％」とは「70 ％の予報が100回出されたとき，そのうち約70回は1 mm 以上の降水がある」ということを意味しています。
また，降水確率は10 ％きざみで発表され，「降水確率 0 ％」は，降水確率が5 ％未満を意味し，「降水確率100 ％」は，降水確率が95 ％以上を意味しています。
降水確率40%のとき，かさを持っていくべきか，置いていくべきか，君ならどうする？
＞＞ 関連する職業・仕事 ［気象予報士］
<1年p.260>
確かめよう 1節 データの傾向の調べ方
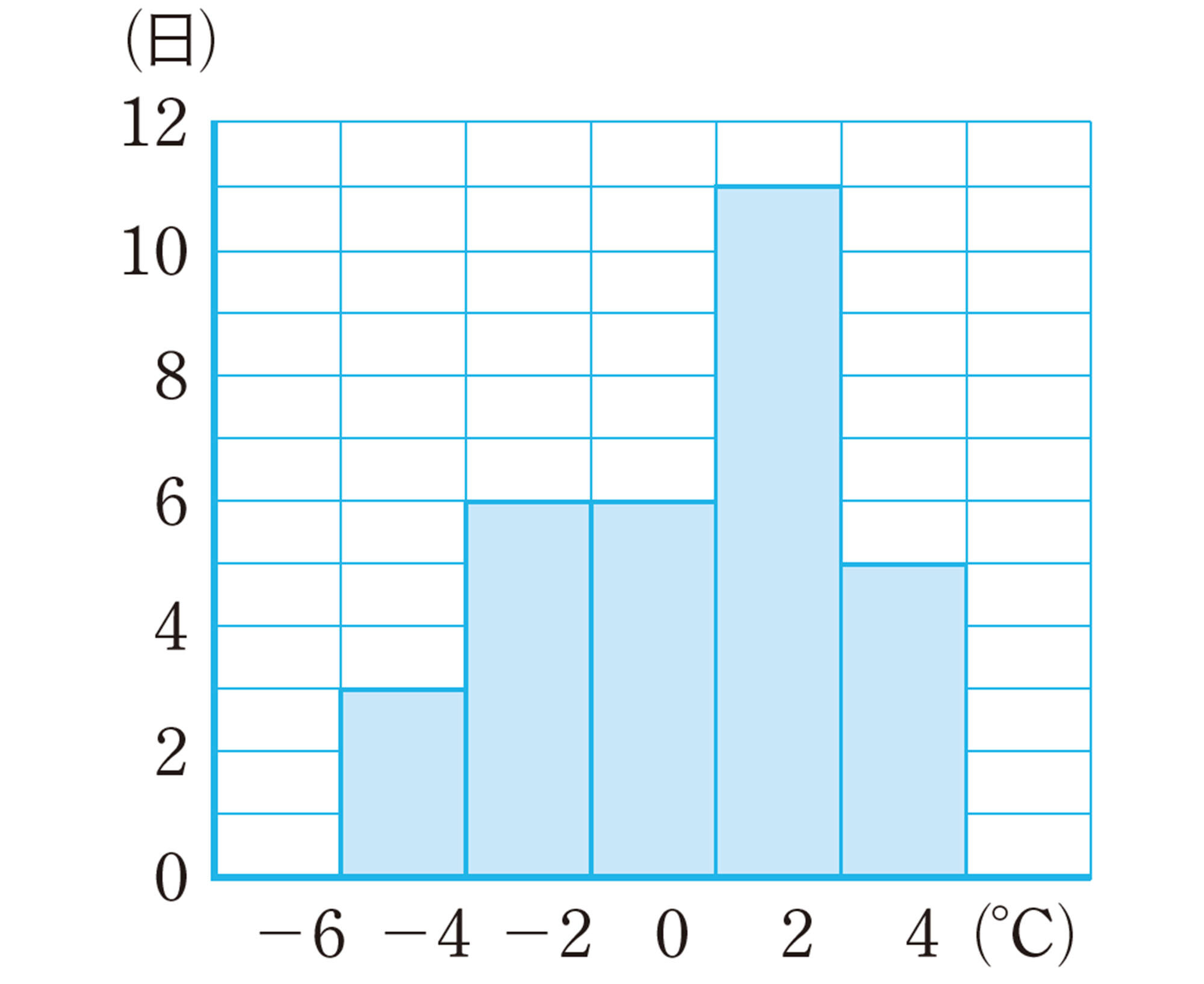
１ 右の図は，札幌の2022年1月の日ごとの最高気温をヒストグラムに表したものです。たとえば，いちばん左の階級は，「[mathjax] \(-6\)℃以上[mathjax] \(-4\)℃未満」を表しています。次の問いに答えなさい。
⑴ このヒストグラムの階級の幅は何℃ですか。
⑵ 度数折れ線を，右上の図にかき入れなさい。
⑶ 「[mathjax] \(-2\)℃以上0℃未満」の階級の度数をいいなさい。また，この階級の相対度数を小数第二位まで求めなさい。
⑷ 最頻値をいいなさい。また，中央値をふくむ階級の階級値をいいなさい。
⑸ 最高気温が0℃未満だった日は，何日ですか。
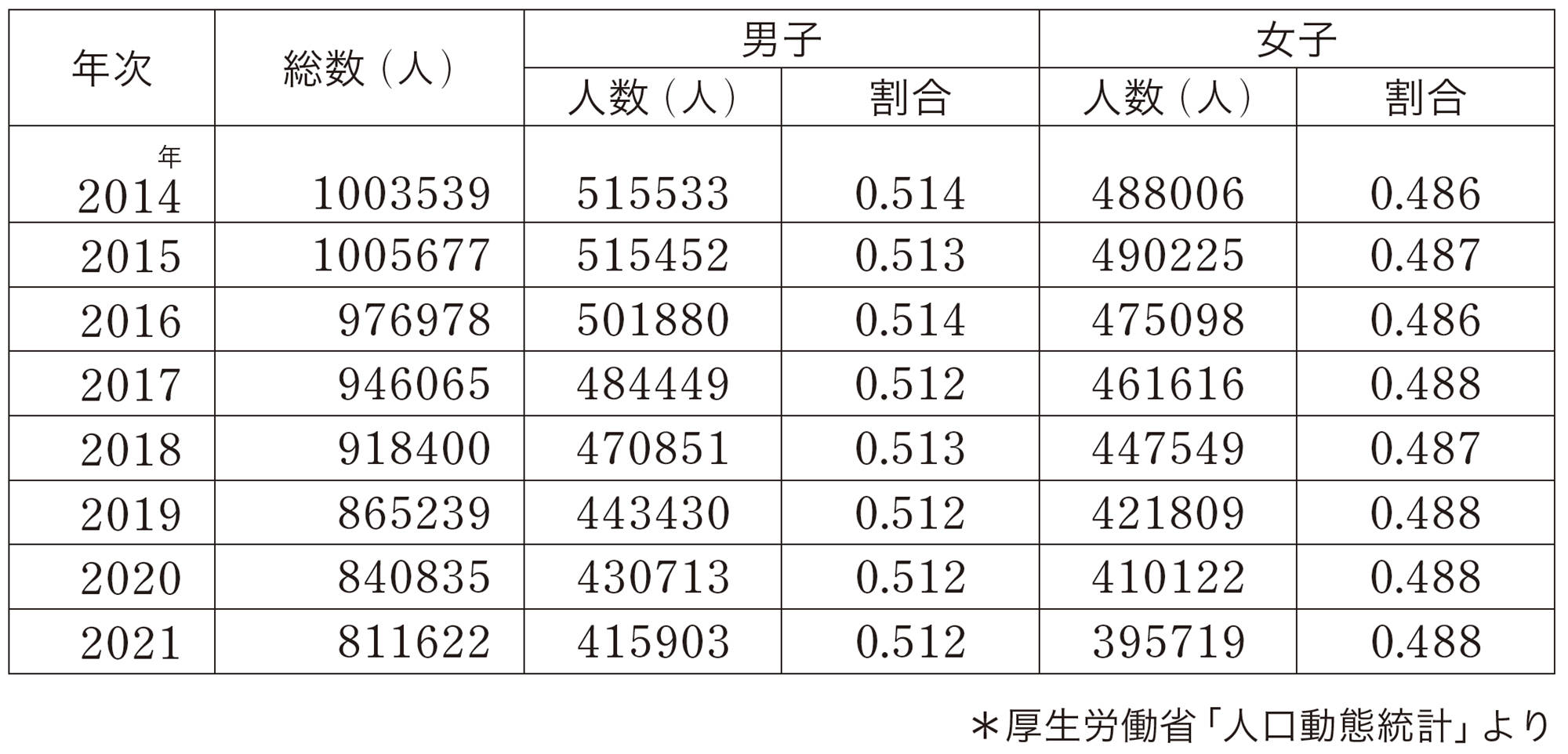
２ 次の表は，日本での男女別の出生児の数とその割合を調べたものです。この表から，日本での男子が生まれる確率と女子が生まれる確率は，それぞれいくらと考えられますか。
