<1年p.242>
ふりかえり 〜算数から数学へ〜
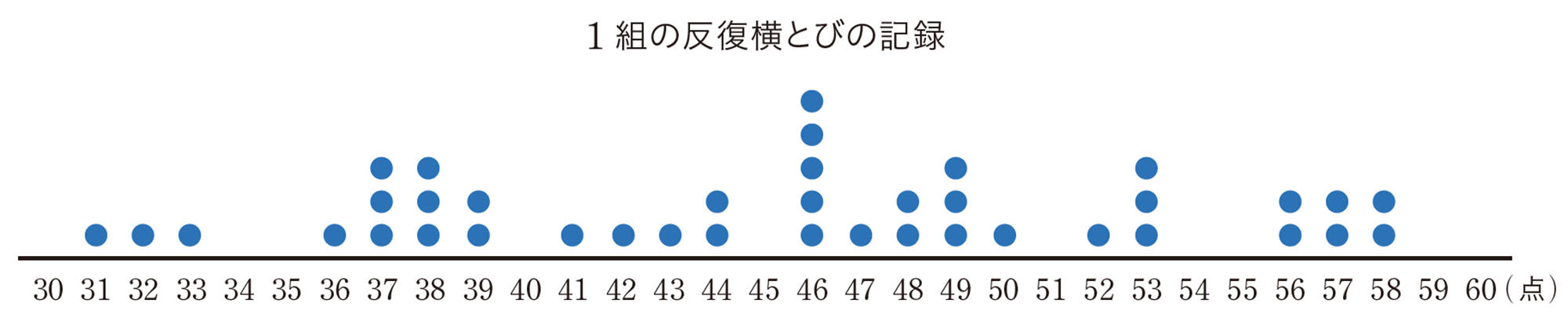
【ドットプロット】
上のようなグラフを,ドットプロットという。
【階級】
「5m以上10m未満」などのように分けた区間を階級という。
【階級の幅】
5mなどのような区間の大きさを,階級の幅という。
【度数】
階級ごとに数えたデータの個数を階級の度数という。
【度数分布表】
階級や度数でデータの散らばりのようすを表している表を,度数分布表という。
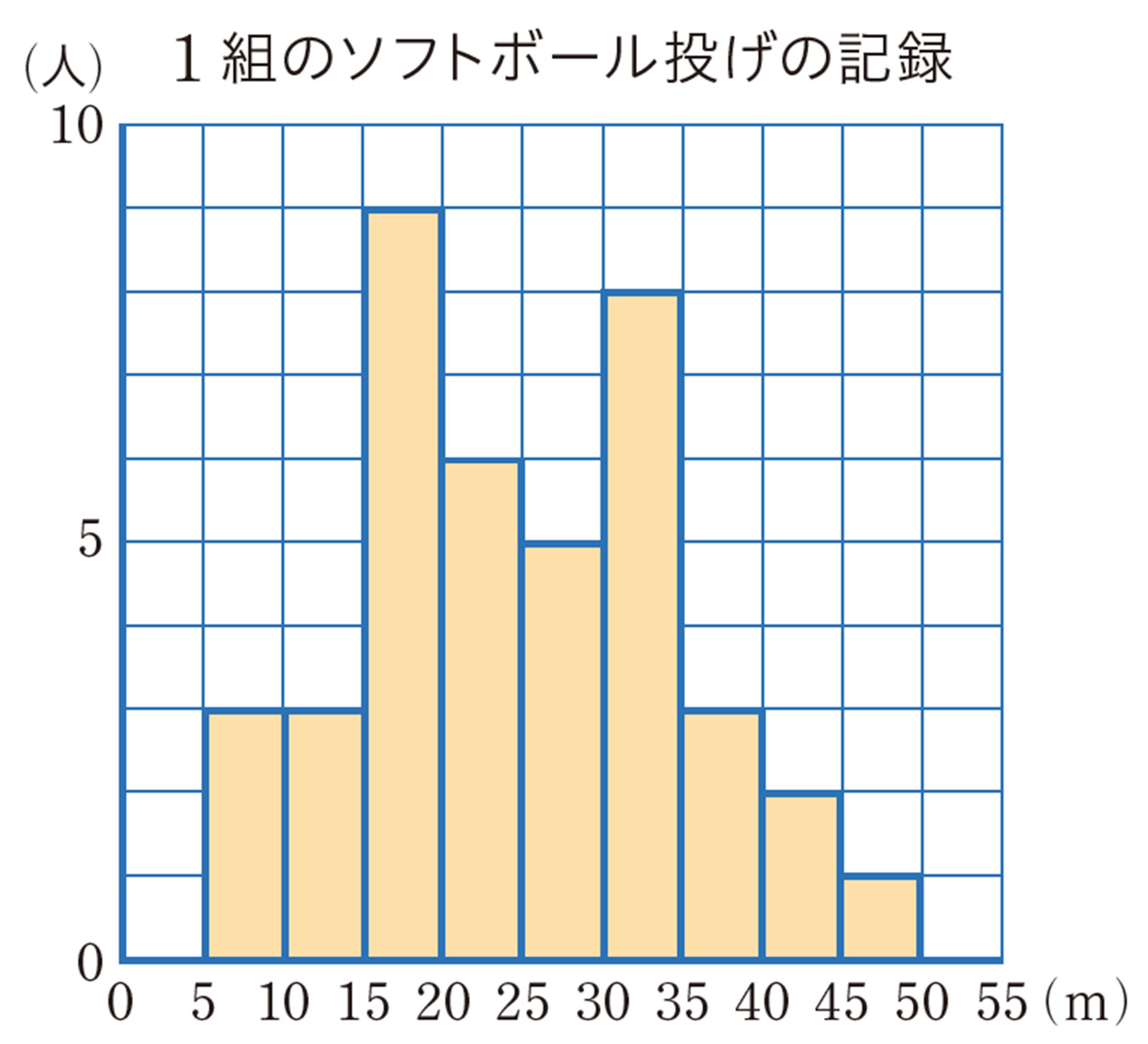
【柱状グラフ】
度数分布表を使って,階級の幅を横,度数を縦とする長方形を順に並べてかいたグラフを柱状グラフという。
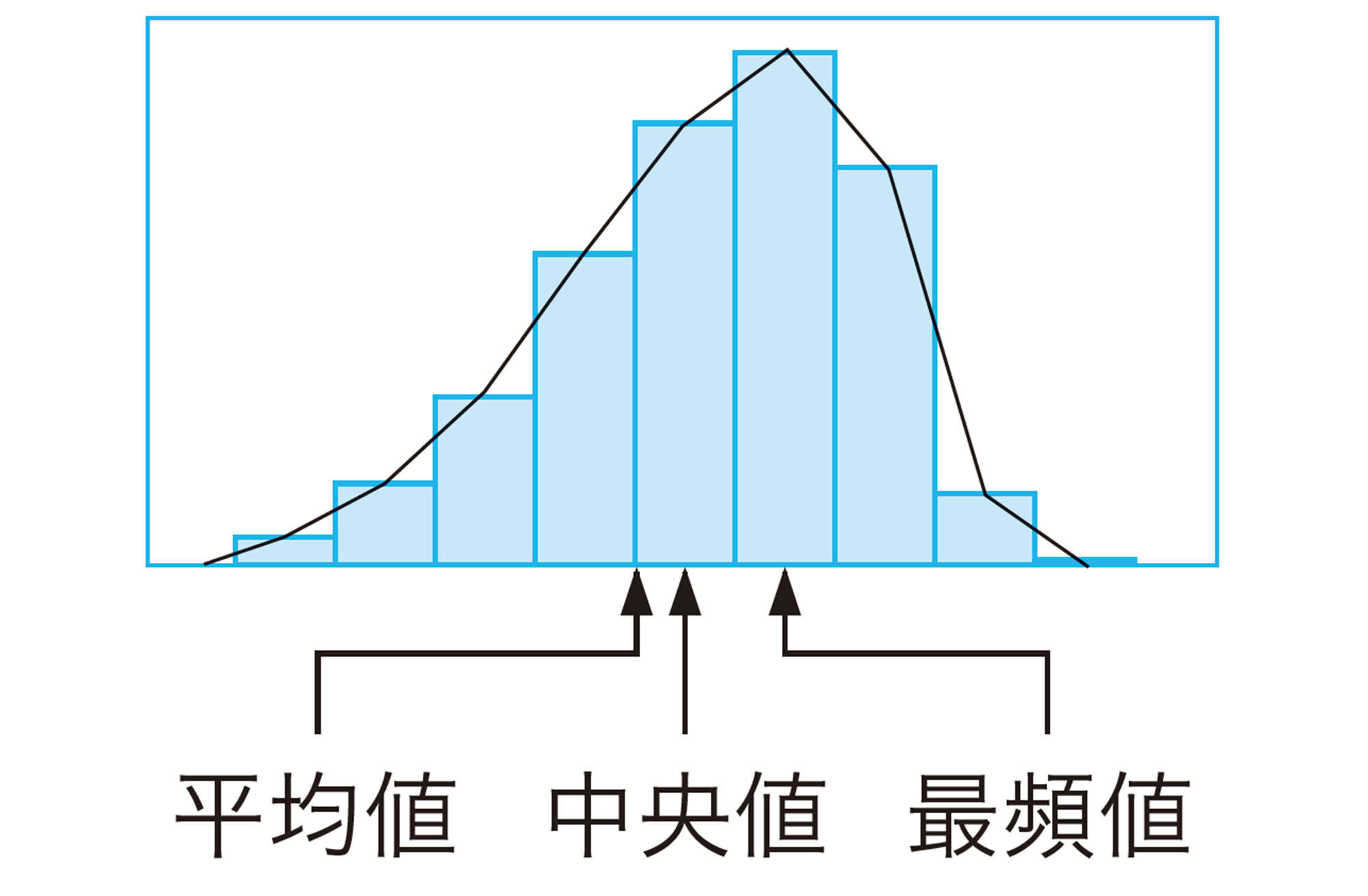
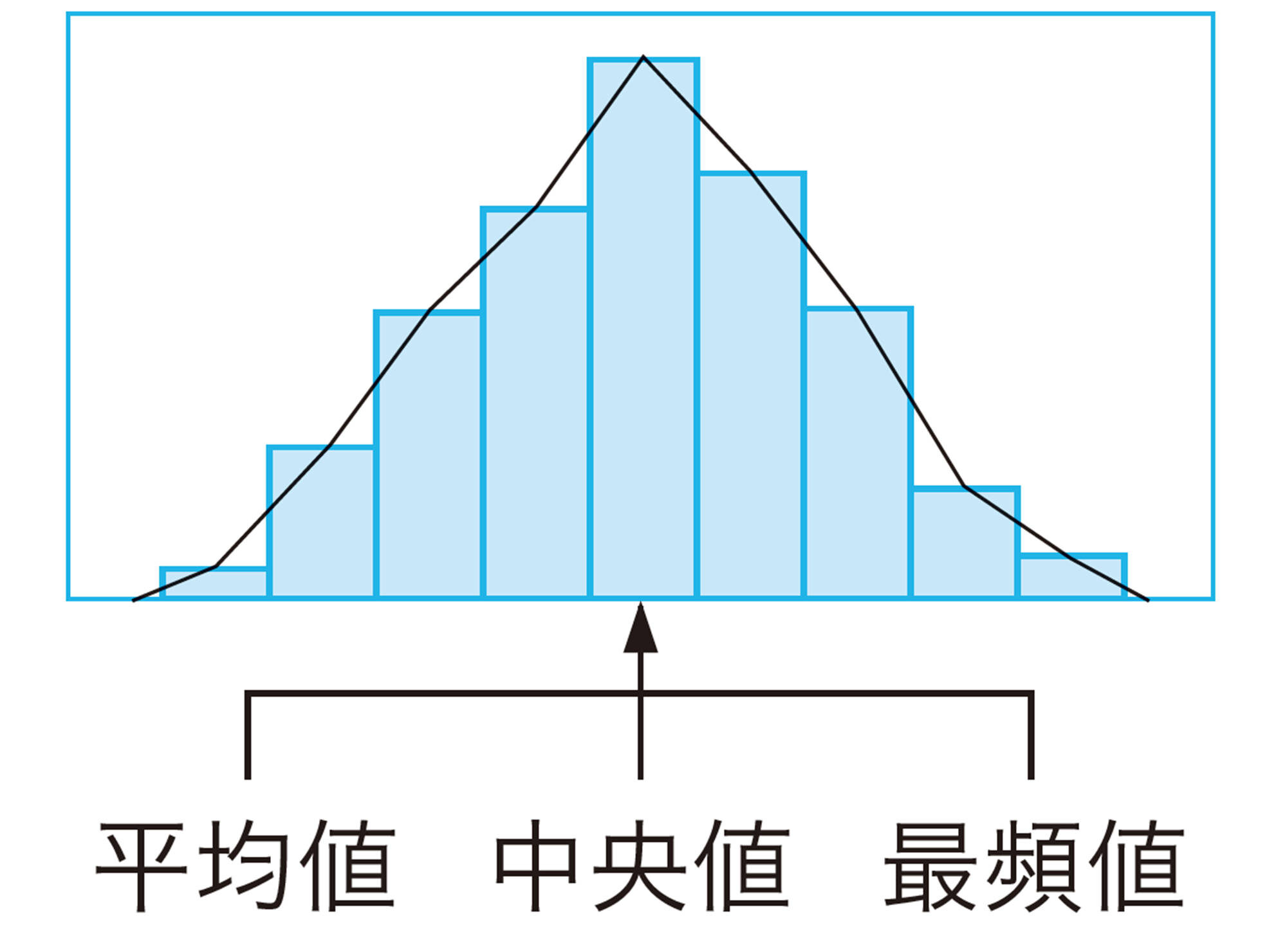
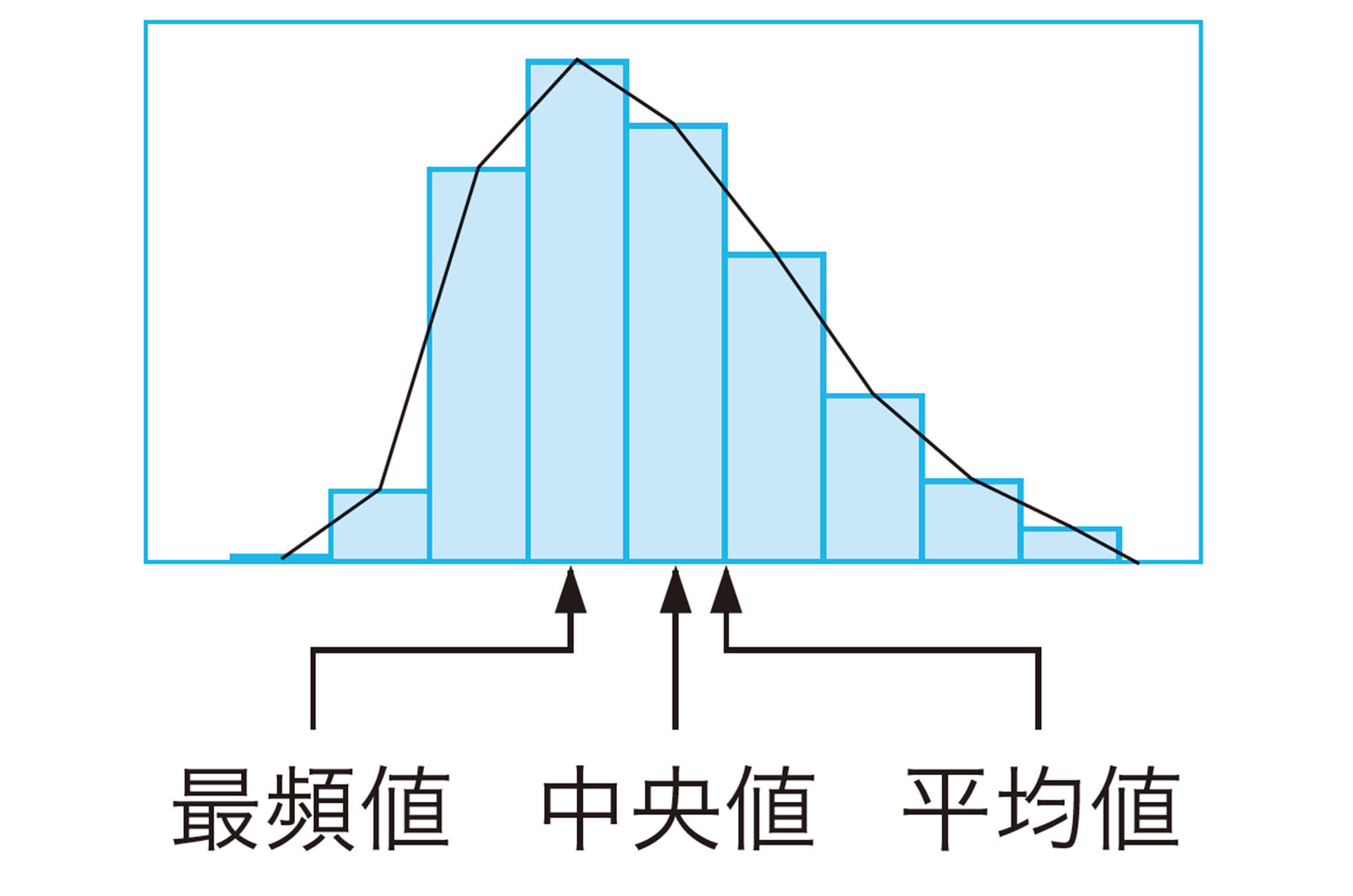
【平均値】
データの値の合計をデータの個数でわった値を,平均値という。
【最頻値】
データの中で,もっとも多く現れた値を最頻値という。
【中央値】
データを大きさの順に並べかえたときに,ちょうど真ん中に位置する値のことを中央値という。
【代表値】
平均値や,最頻値,中央値のように,データを代表する値のことを,代表値という。
1組のソフトボール投げの記録
調べたいことによって,使う表やグラフを変えて考えたね。

いろいろな表やグラフを使うと,データをまとめることができたね。

<1年p.244>
1節 データの傾向の調べ方
反応の速さはどのくらいかな?
美月さんは,拓真さんが机の上から落ちた鉛筆をつかみとるのを見て,どのくらいの速さで反応できるのかを知りたいと考えました。そこで,みんなの反応の速さを知るために,落下する定規を使った「ルーラーキャッチ」という実験で,つかんだ位置を調べることにしました。つかんだ位置が短い方が,反応が速いことになります。
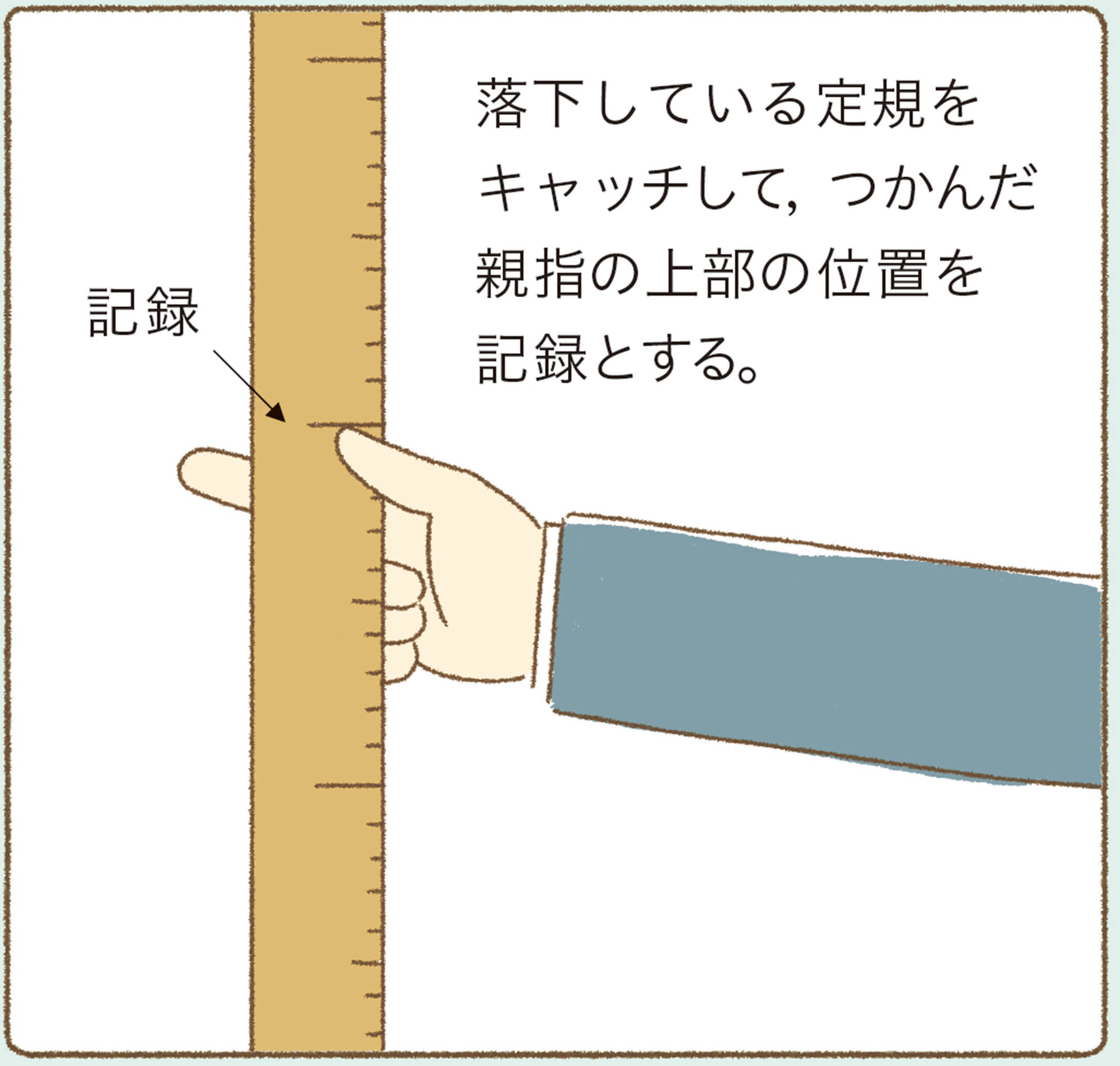
ルーラーキャッチ
2人1組で行う。
1人は指の間に50cm定規を構える。
1人は机の上に腕を置き,人差し指と親指を[mathjax]\(90^{\circ}\)に開く。
親指の上部を,定規の0の目盛りの位置に合わせる。
号令のあと,10秒以内に定規を落とす。
落下している定規をキャッチして,つかんだ親指の上部の位置を記録とする。
<1年p.245>
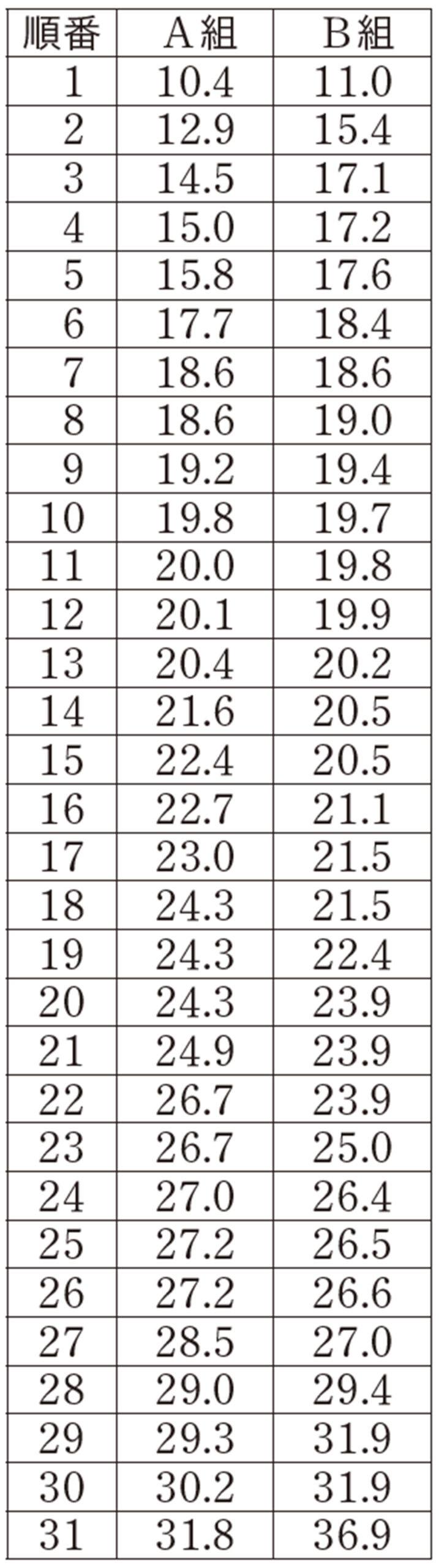
【1】 美月さんの学校のクラスA組,B組でルーラーキャッチを行ったところ,それぞれの組の記録は次のようになりました。
A 組(単位:cm)
B 組(単位:cm)
A組とB組では,どちらの組の方が反応が速いといえるかを調べます。どんなことを調べればよいか話し合いましょう。
クラスの平均値を比べればいいよ。
中央値を比べる方法もあるね。
平均値や中央値のような1つの値だけで比べていいのかな。
どのくらいの記録の人が多いのかな。
次の課題へ!
2つの集団のデータを比べるには,どのようなことを調べればいいのかな?
P.246

<1年p.246>
1 データの整理
Q Question
右の表は,前ページのA組, B組のルーラーキャッチのデータの値を,短い順に示したものです。2つのクラスのデータを比べるには,どのような比べ方があるか話し合ってみましょう。
見方・考え方
小学校のときと同じように比べられるかな。

小学校では,平均値や最頻値,中央値で比べたよ。
散らばりのようすを調べるために,表やグラフで表せないかな。

ふりかえり 小学校6年
[mathjax]\(\textsf{平均値}=\dfrac{\textsf{データの値の合計}}{\textsf{データの総数}}\)
最頻値…データの中でもっとも多く出てくる値
中央値…データを大きさの順に並べたとき,中央にくる値
代表値…平均値や最頻値,中央値のように,データを代表する値
表1 ルーラーキャッチのデータ(cm)
目標 ▷ 2つの集団のデータをどのように比べればよいか考えよう。
問 1 表1から,A組,B組のルーラーキャッチのデータの平均値,中央値を求めなさい。また, A組とB組の平均値や中央値を比べると,どちらの組の方が反応が速いといえますか。
代表値だけで比べていいのかな。

表計算ソフトを使ってみよう
データの並べかえ P.273
代表値などの求め方 P.274
<1年p.247>
次に,全体の散らばりのようすを比べてみよう。
データの範囲
データを比べるには,代表値だけでは見えない「データの散らばり」のようすを見ることが大切である。
前ページの表1から, A組の値の 最大値 は[mathjax]\(31.8\) cm, 最小値は[mathjax]\(10.4\) cm であることがわかる。
データの散らばりの程度を表すのに,データの最大値と最小値の差を用いることがある。この値を,そのデータの 範囲 またはレンジ という。
A組のデータの範囲は,
[mathjax]\(31.8-10.4=21.4\)
より,[mathjax]\(21.4\) cmである。
問 2 前ページの表1で,B組のデータの最大値,最小値,範囲を求めなさい。また,それぞれの値をA組と比べると,どんなことがわかりますか。
このようなデータの散らばりのようすを, 分布 という。
<1年p.248>
分布のようすを表やグラフで表してみよう。
度数分布表
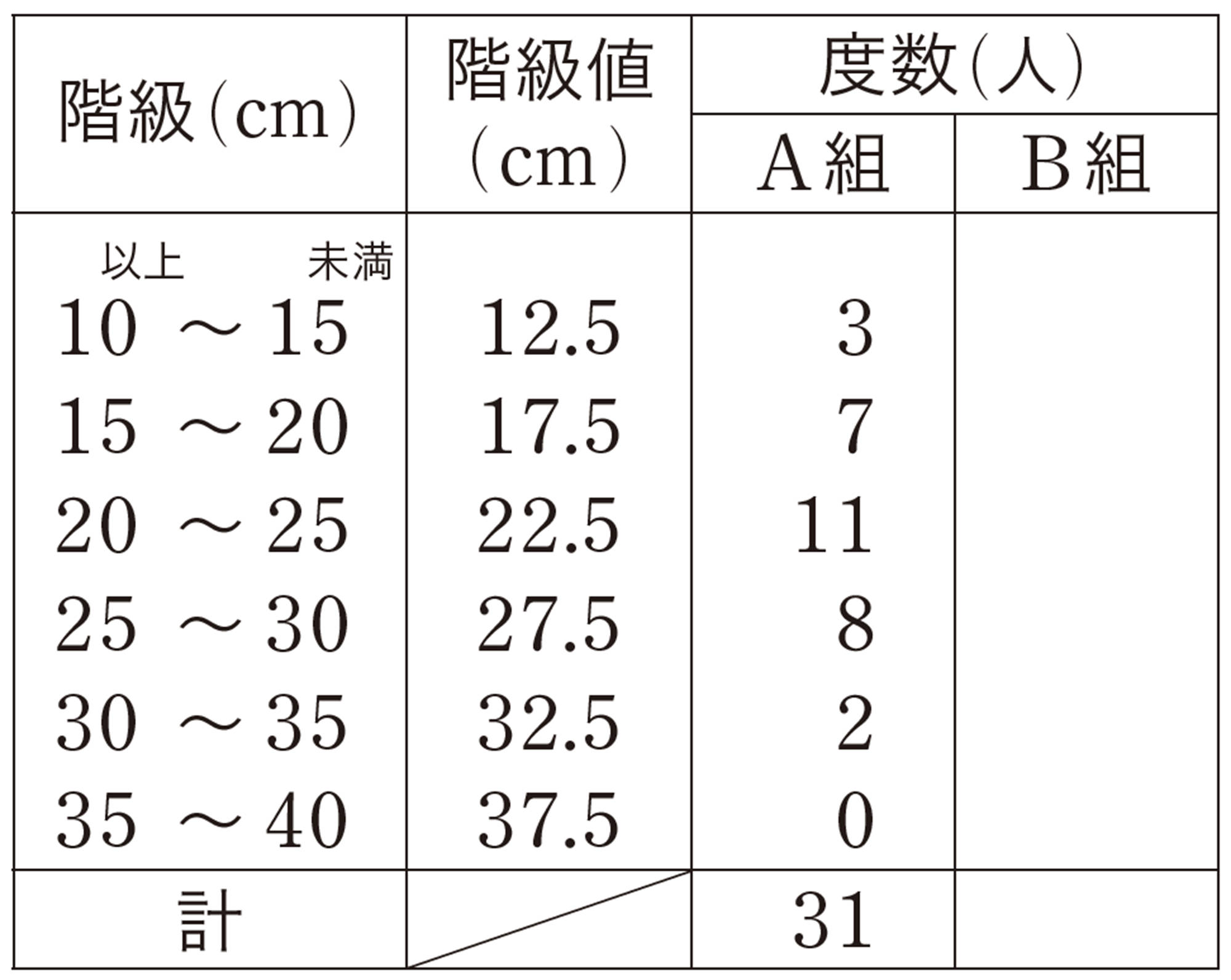
問 3 表2について,次の問いに答えなさい。
⑴ 246ページの表1をもとにして, B組のデータについて各階級の度数を調べ,表2に書き入れなさい。
⑵ それぞれのクラスで,度数がもっとも多い階級と,その階級値をいいなさい。
度数分布表では,度数がもっとも多い階級の階級値を最頻値とする。ふつう,代表値として最頻値を用いる場合は,データの中でもっとも多く出てくる値より,度数がもっとも多い階級の階級値にすることが多い。
たとえば,表2から,A組の記録の最頻値を求めると,度数がもっとも多い階級は「20 cm 以上25 cm未満」であるから,最頻値はその階級値である[mathjax]\(22.5\) cmとなる。
問 4 表2をもとにして,B組の記録の最頻値を求めなさい。
表計算ソフトを使ってみよう
度数分布表P.273
<1年p.249>
ヒストグラム・度数折れ線
度数分布表を用いて,階級の幅を横,度数を縦とする長方形を順に並べてかいたグラフをヒストグラム または柱状グラフという。
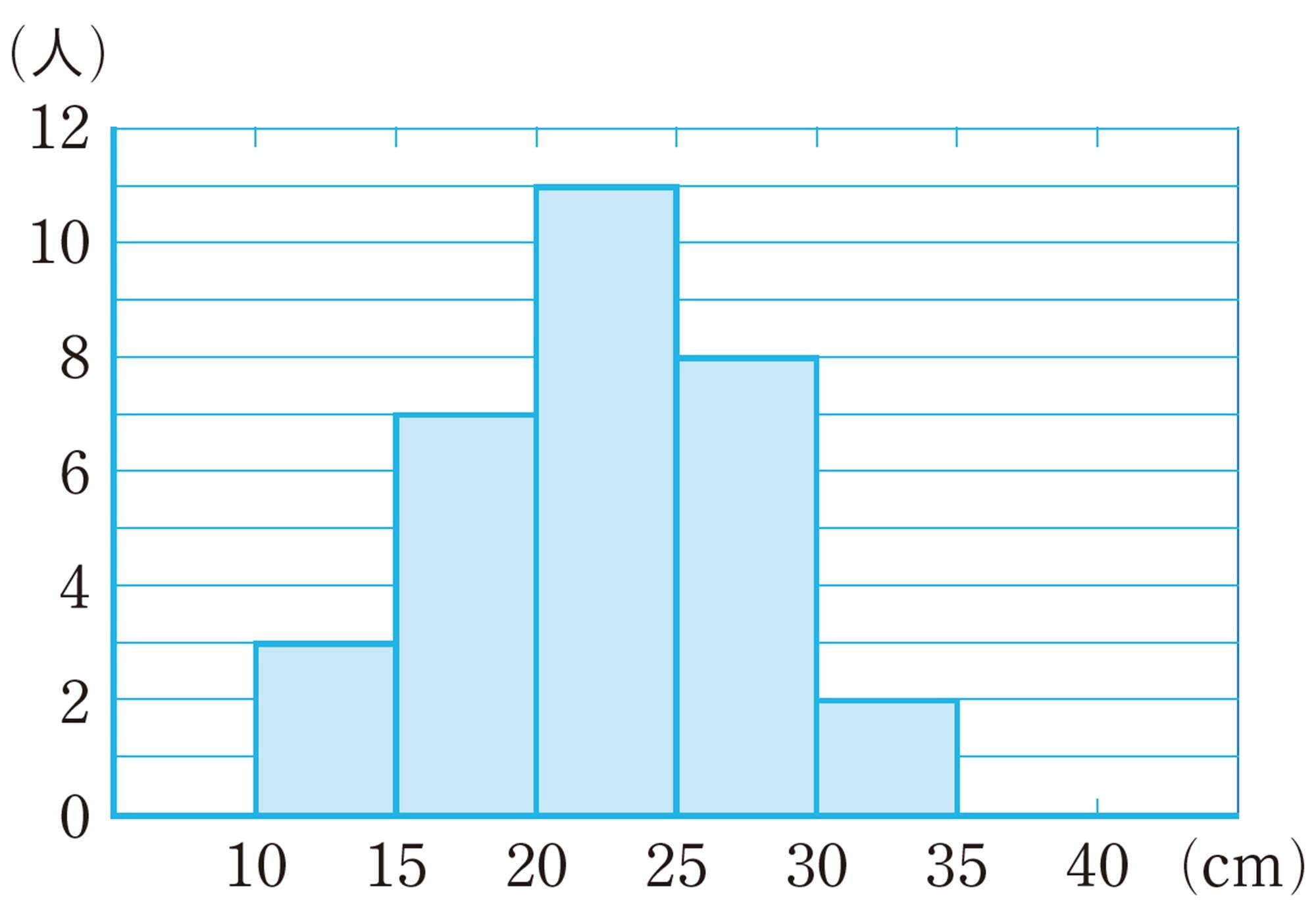
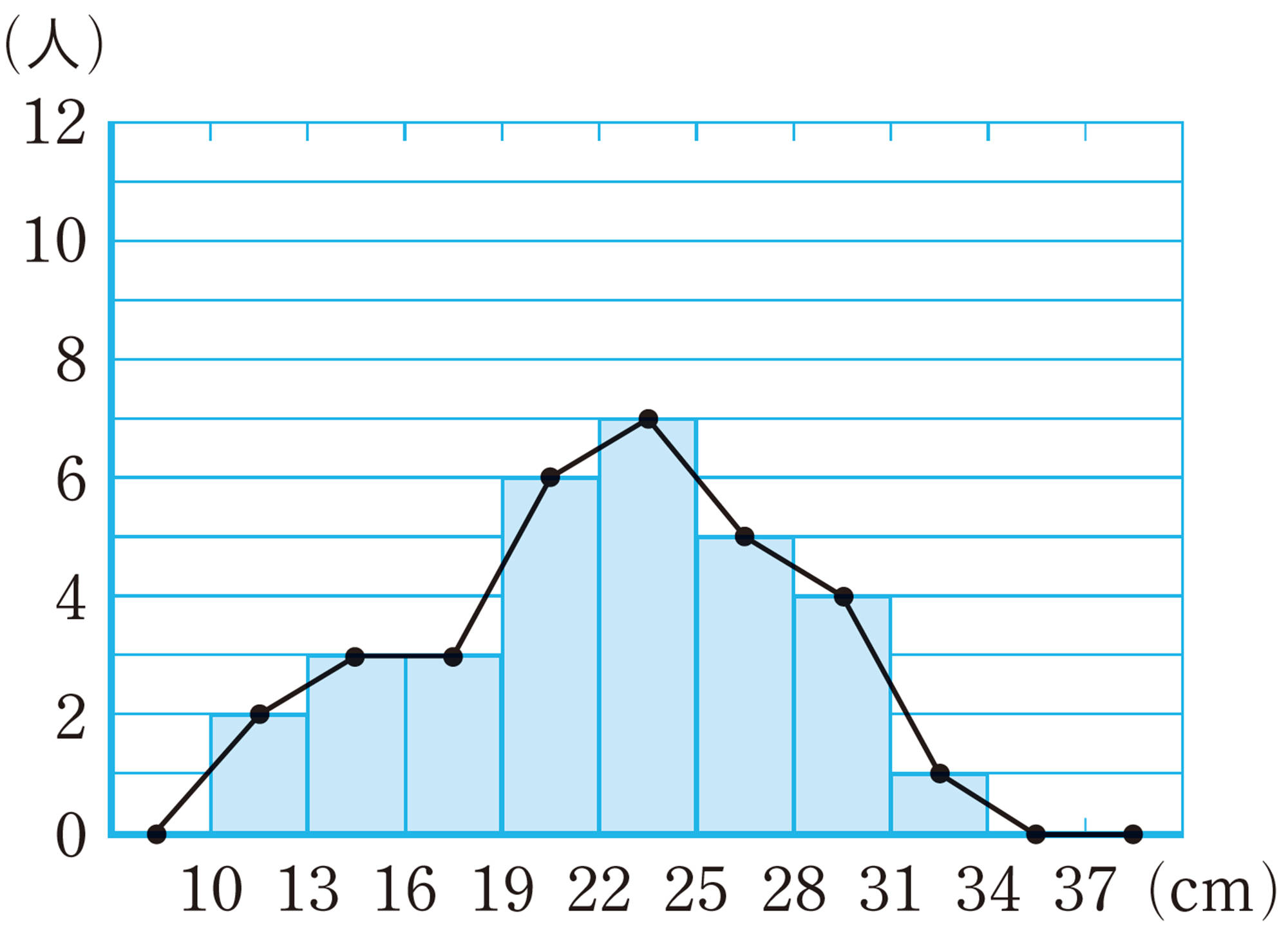
前ページの表2の A組のルーラーキャッチのデータをヒストグラムに表すと,図1のようになる。このように,度数分布表からヒストグラムをつくると,データの分布が一目でわかるようになる。
柱状グラフとヒストグラムは,同じものだね。

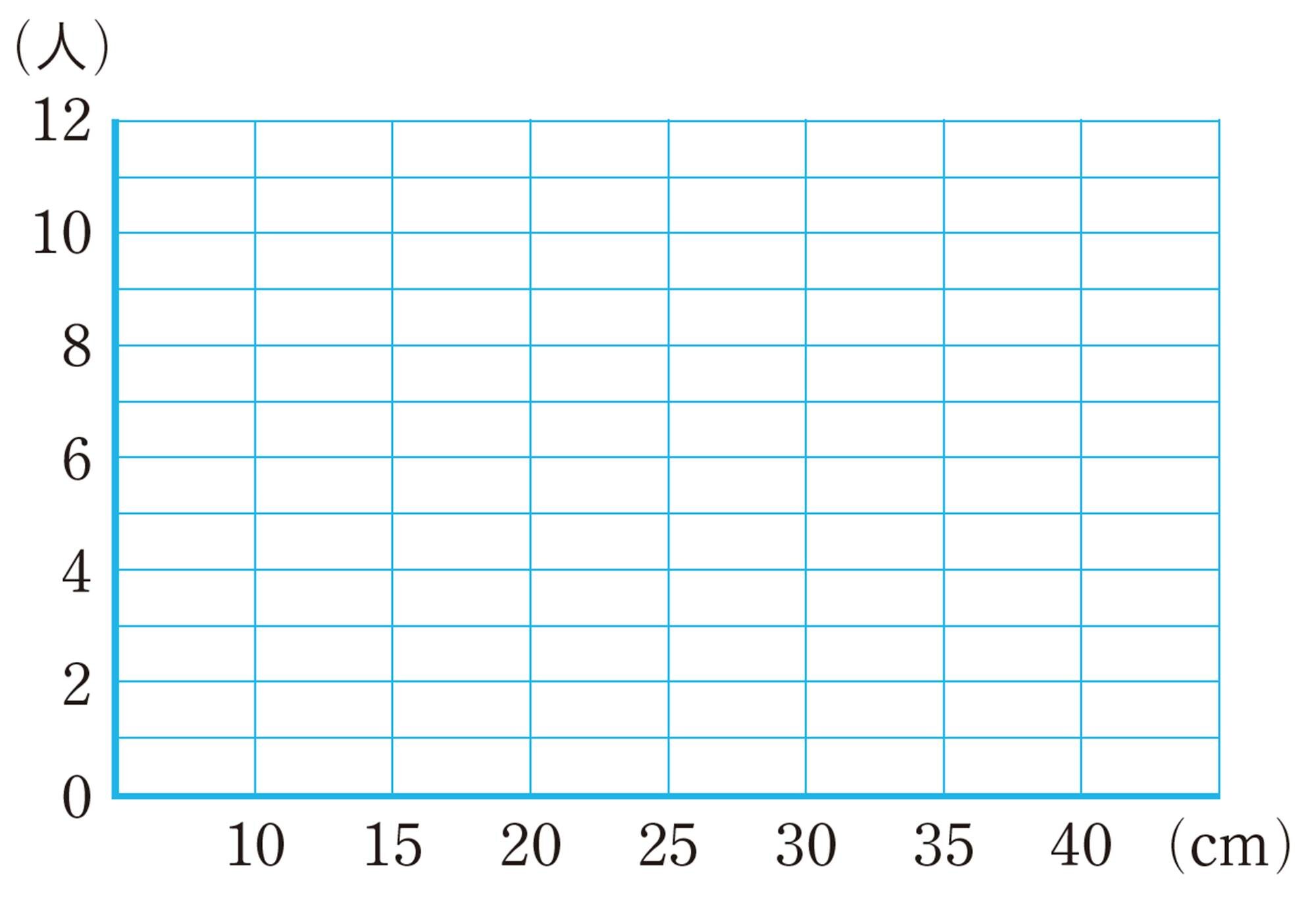
問 5 前ページの表2をもとにして, B組のルーラーキャッチのデータのヒストグラムを,図2にかき入れなさい。また,2つのクラスのデータの分布を比べ,気づいたことをいいなさい。
<1年p.250>
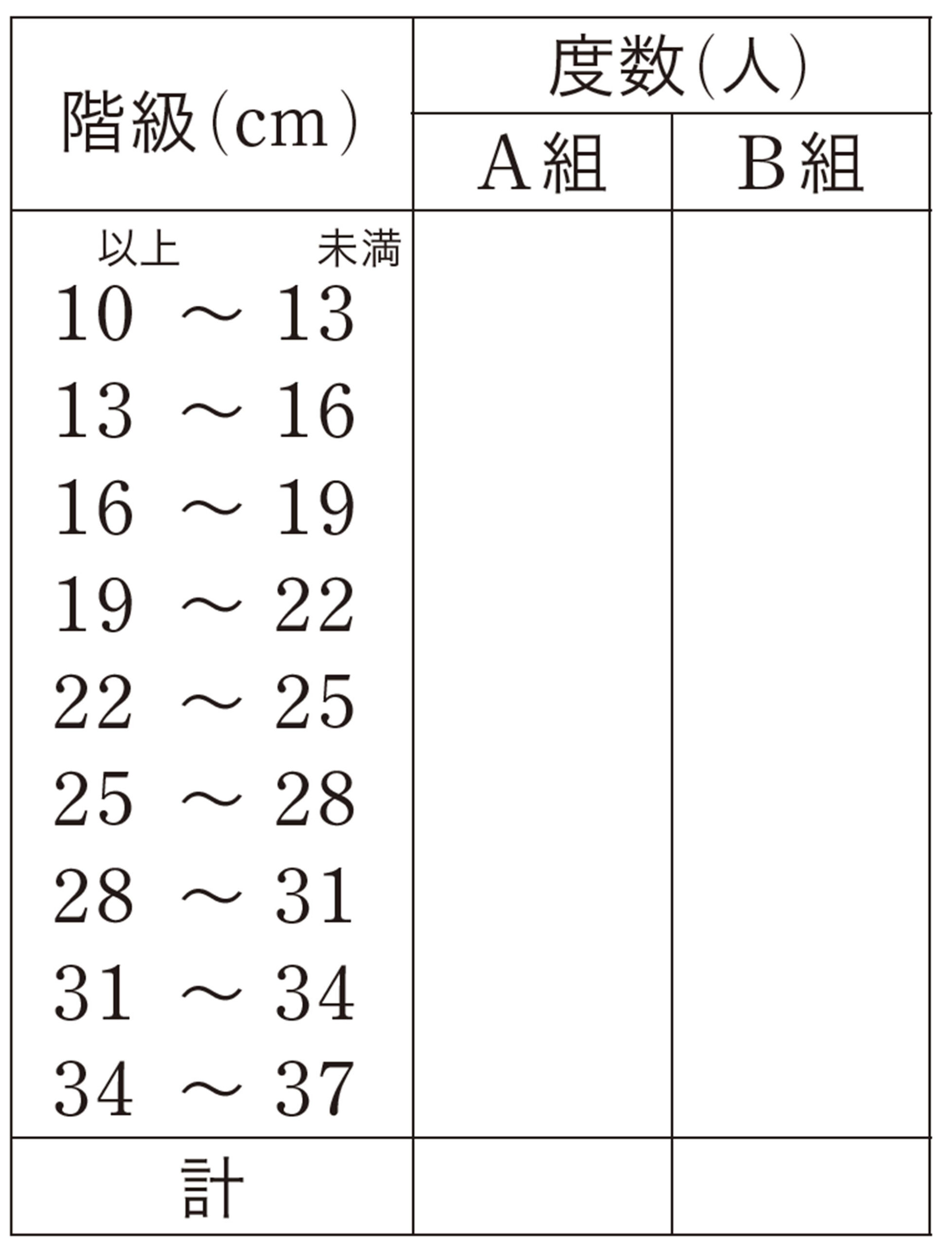
問 7 前ページの表3をもとにして,A組とB組のルーラーキャッチのヒストグラムを,次の図3,4にかき入れなさい。
問 8 前ページの図1と図3のヒストグラムから読み取れることがらにどんなちがいがありますか。また,図2と図4ではどうですか。
同じデータを用いても,階級の幅を変えてヒストグラムをかくと,データの特徴の見え方や読み取れることがらが異なる場合がある。データの分布を調べるときは,階級の幅の異なるヒストグラムを何通りかつくって調べることも大切である。
<1年p.251>
問 9 前ページの問7でつくったヒストグラムをもとにして,前ページの図4に度数折れ線をかき入れなさい。また,前ページの図5と図4の度数折れ線を比べ,気づいたことを話し合いなさい。
問 10 これまで調べたことから,A組とB組のルーラーキャッチのデータを比べると,どちらの組の方が反応が速いといえるか話し合いなさい。
問 11 表4は,1年生のルーラーキャッチのデータを,度数分布表に表したものです。次の図6に,ヒストグラムと度数折れ線をかき入れなさい。
<1年p.252>
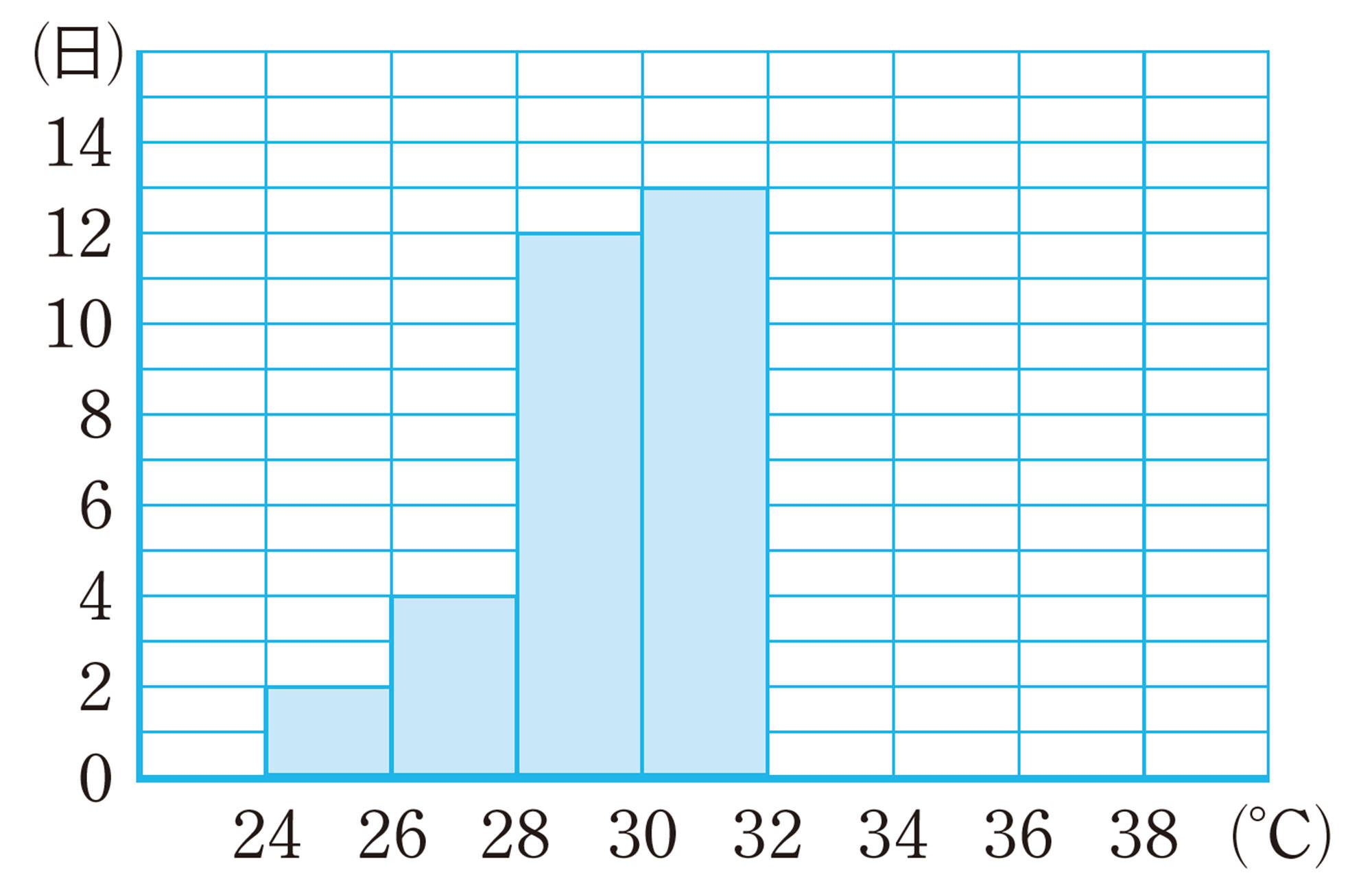
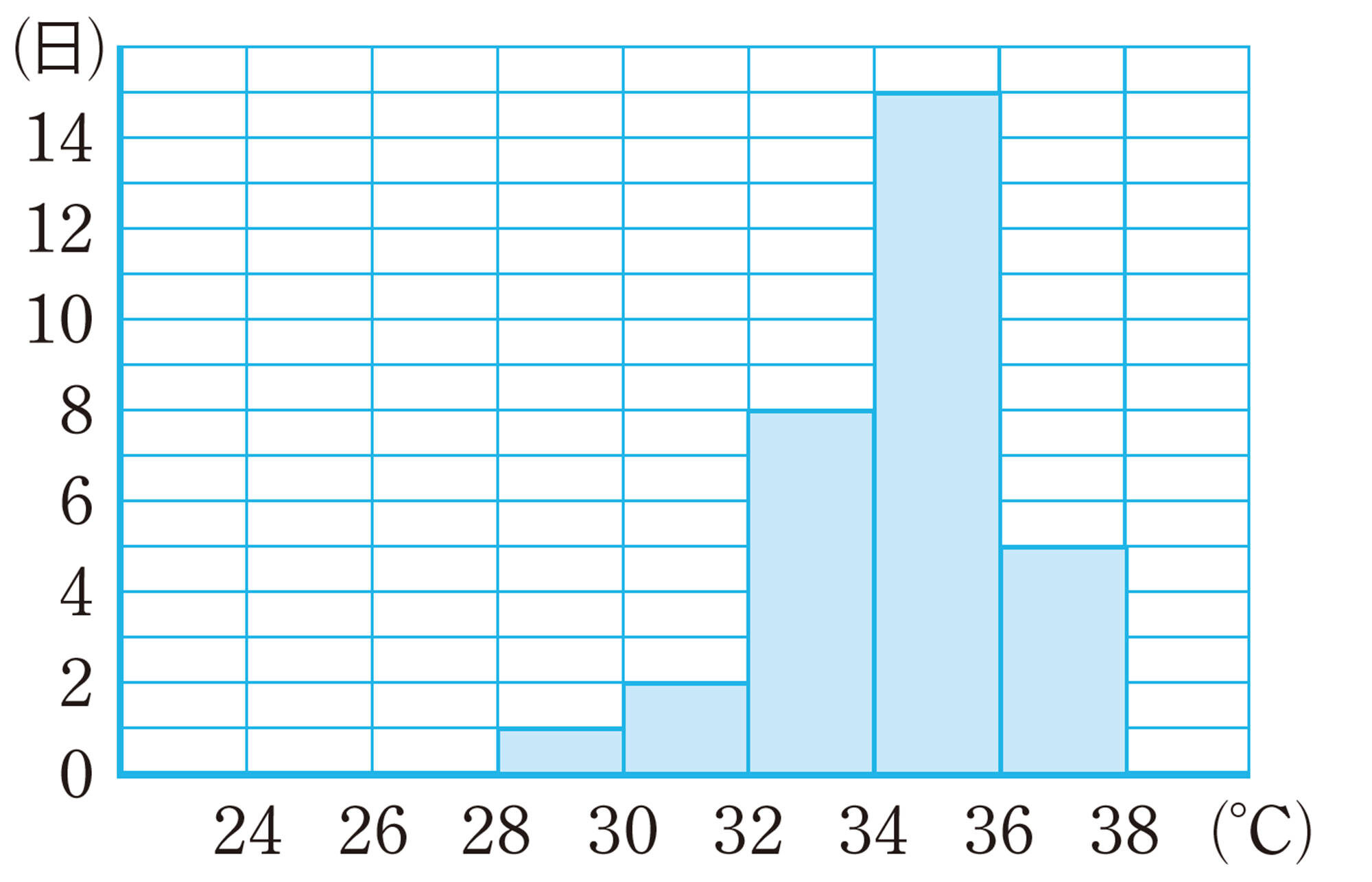
問 12 次の図は,東京の1920年と2020年の8月の日ごとの最高気温をヒストグラムに表したものです。美月さんたちのグループは,このヒストグラムから分析したことをクラスで発表しようと考えています。
美月さんは,2つのヒストグラムから,次のことを読み取りました。
「1920年より2020年の方が,最高気温の高い日が多い傾向がある。」
この読み取ったことを,スライドにまとめて発表しようと思います。
⑴ どのようなグラフや理由をかけばよいか話し合いなさい。

ヒストグラムを横に並べると,ちがいが見えにくいね。グラフを重ねたらどうかな。
重ねるなら,度数折れ線の方が見やすいよ。あと,理由はどう書けばいいかな。

⑵ 次のような発表用のスライドを完成させなさい。
どんなことがわかったかな
2つの集団のデータを度数分布表やヒストグラムに表すと,そのデータの傾向を比べることができます。
次の課題へ!
全体の数が同じ複数の集団のデータは比べやすいけど,全体の数がちがう場合も,同じように比べられるのかな。
P.253