gkt-horizontal-line
<1年p.184>
3 作図の利用
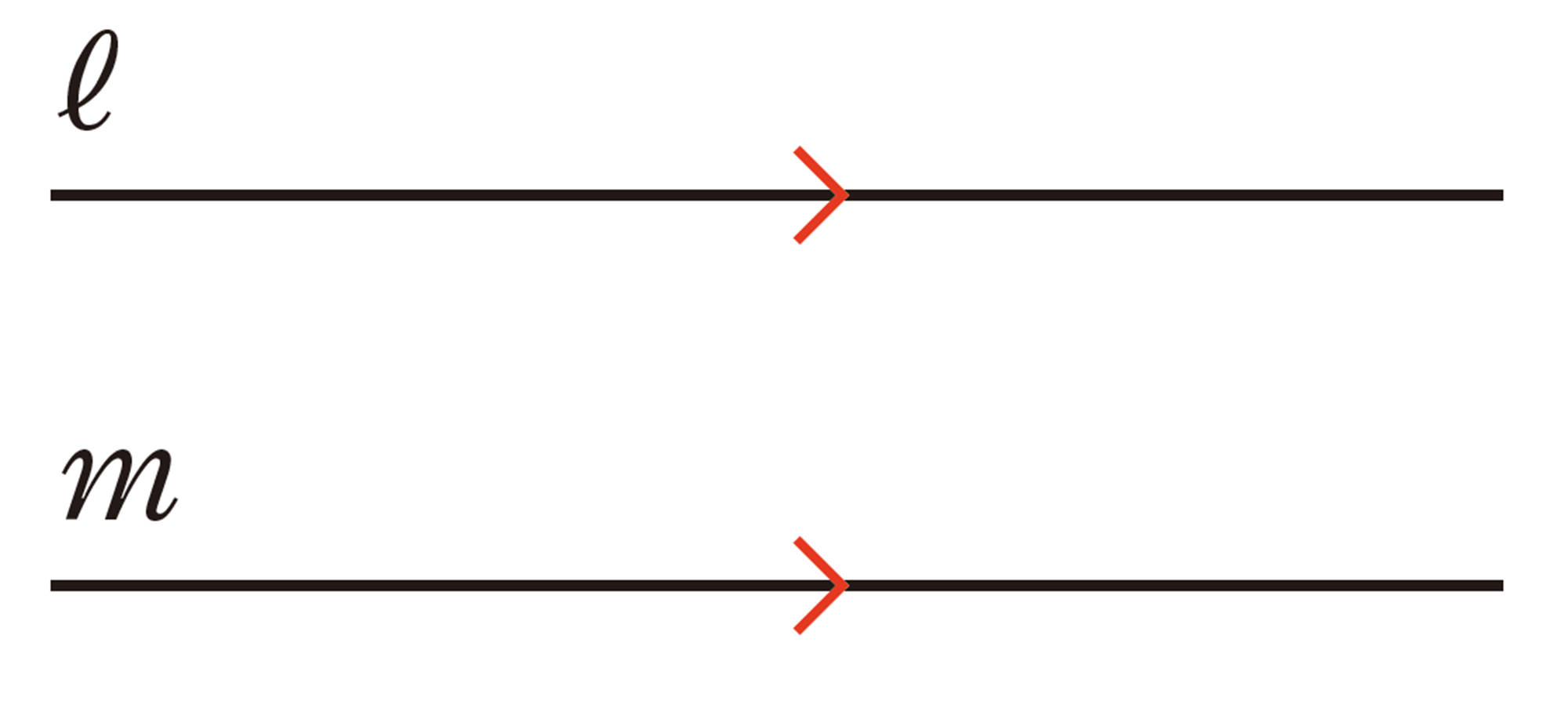
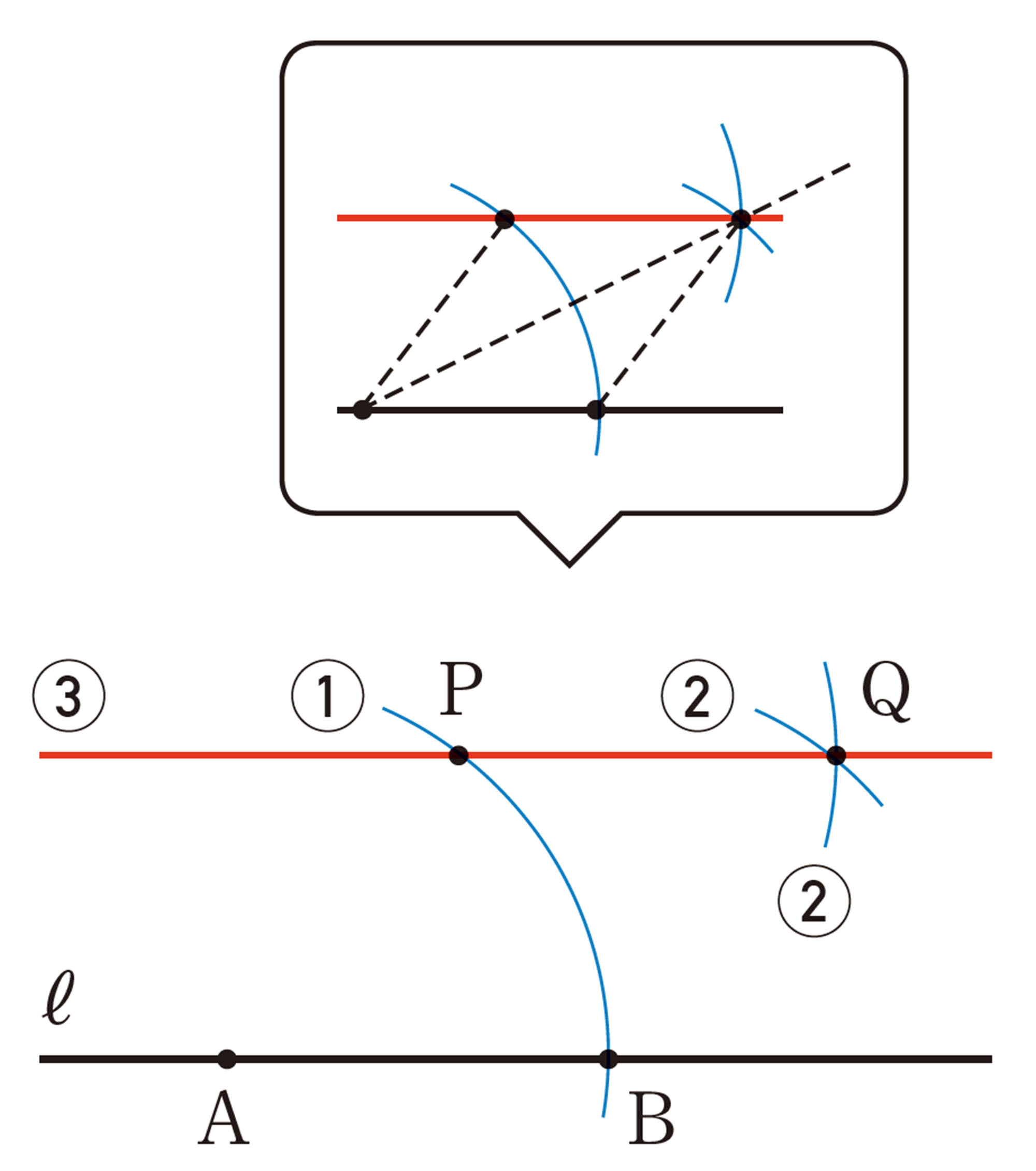
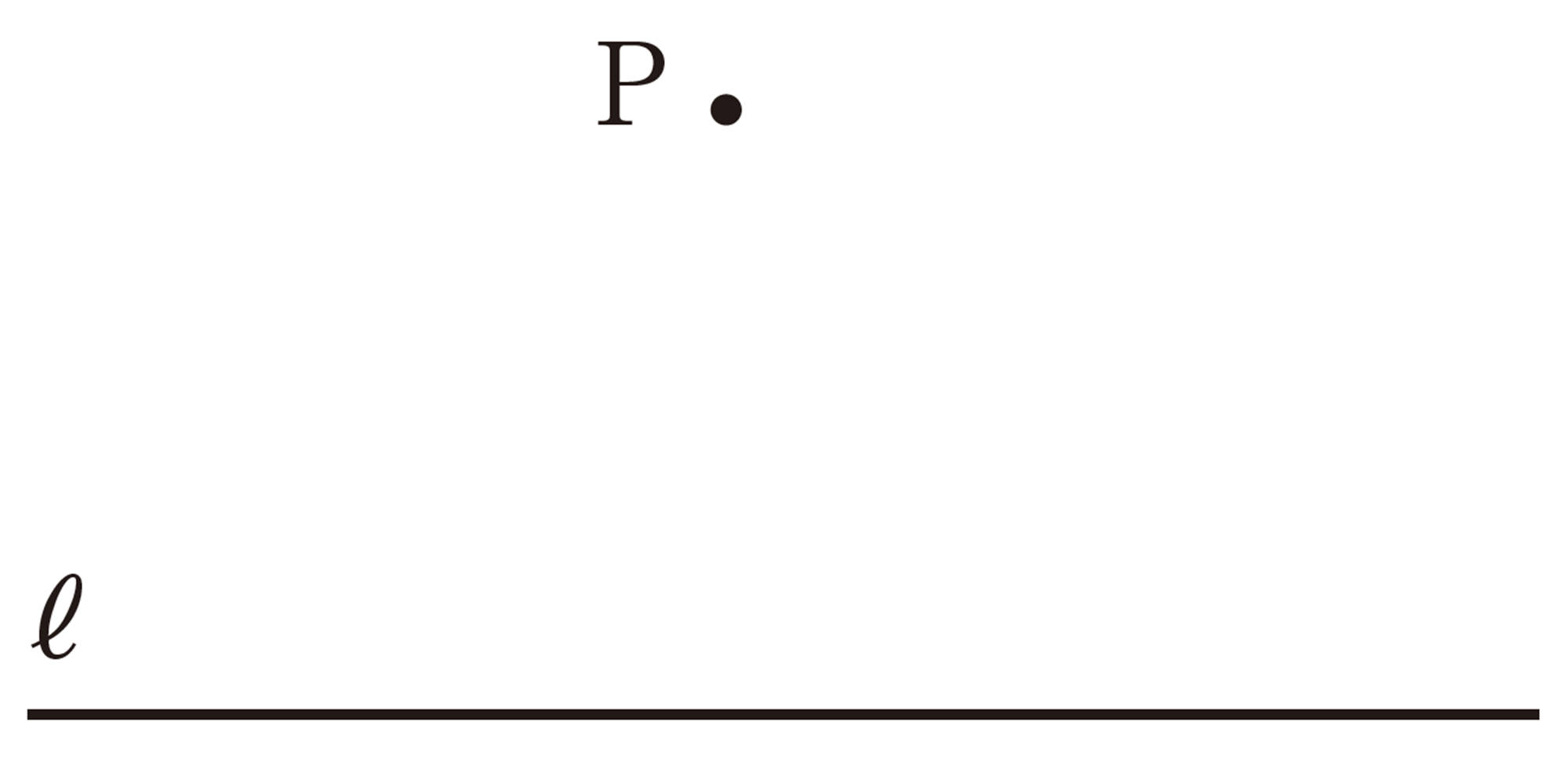
平行な直線の作図
Q Question
gkt-horizontal-line
<1年p.185>
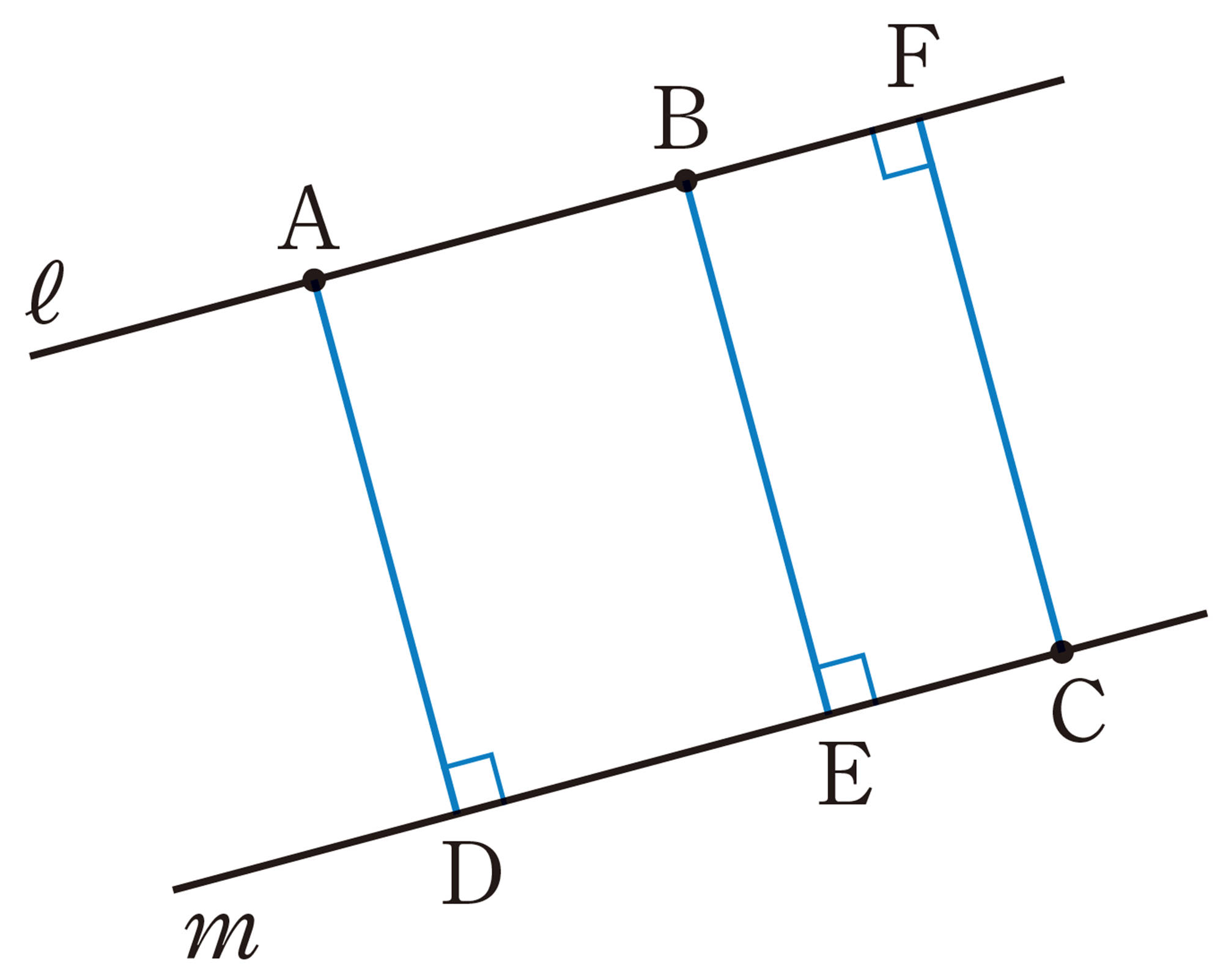
㋐ 直線 ℓ上の点 Aと直線 m
㋑ 直線 ℓ上の点 Bと直線 m
㋒ 直線 m上の点 Cと直線 ℓ
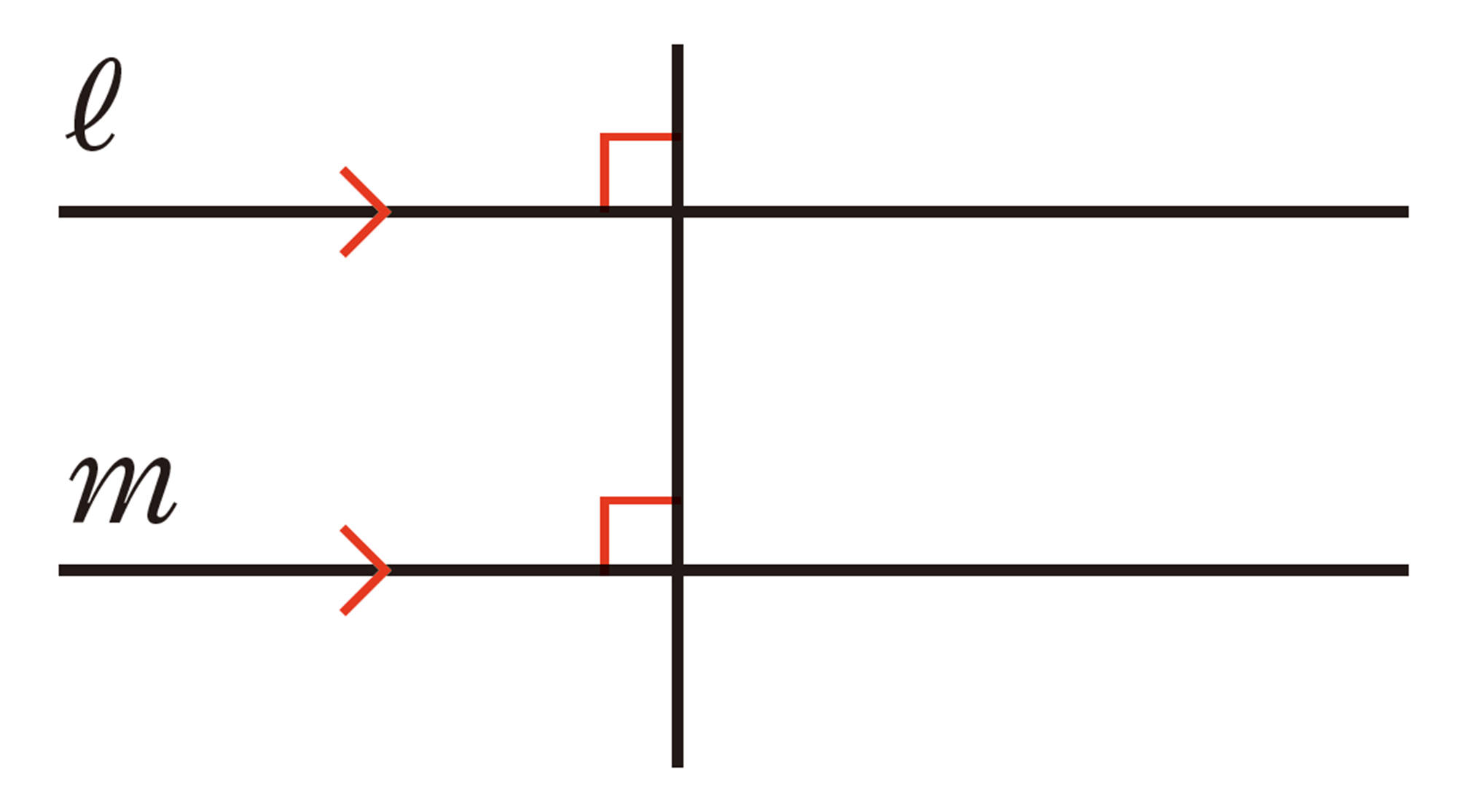
平行な2直線 ℓ,mがあるとき,一方の直線上の点と他方の直線との距離はつねに等しくなる。この距離を,平行な2直線 ℓ,m間の距離という。
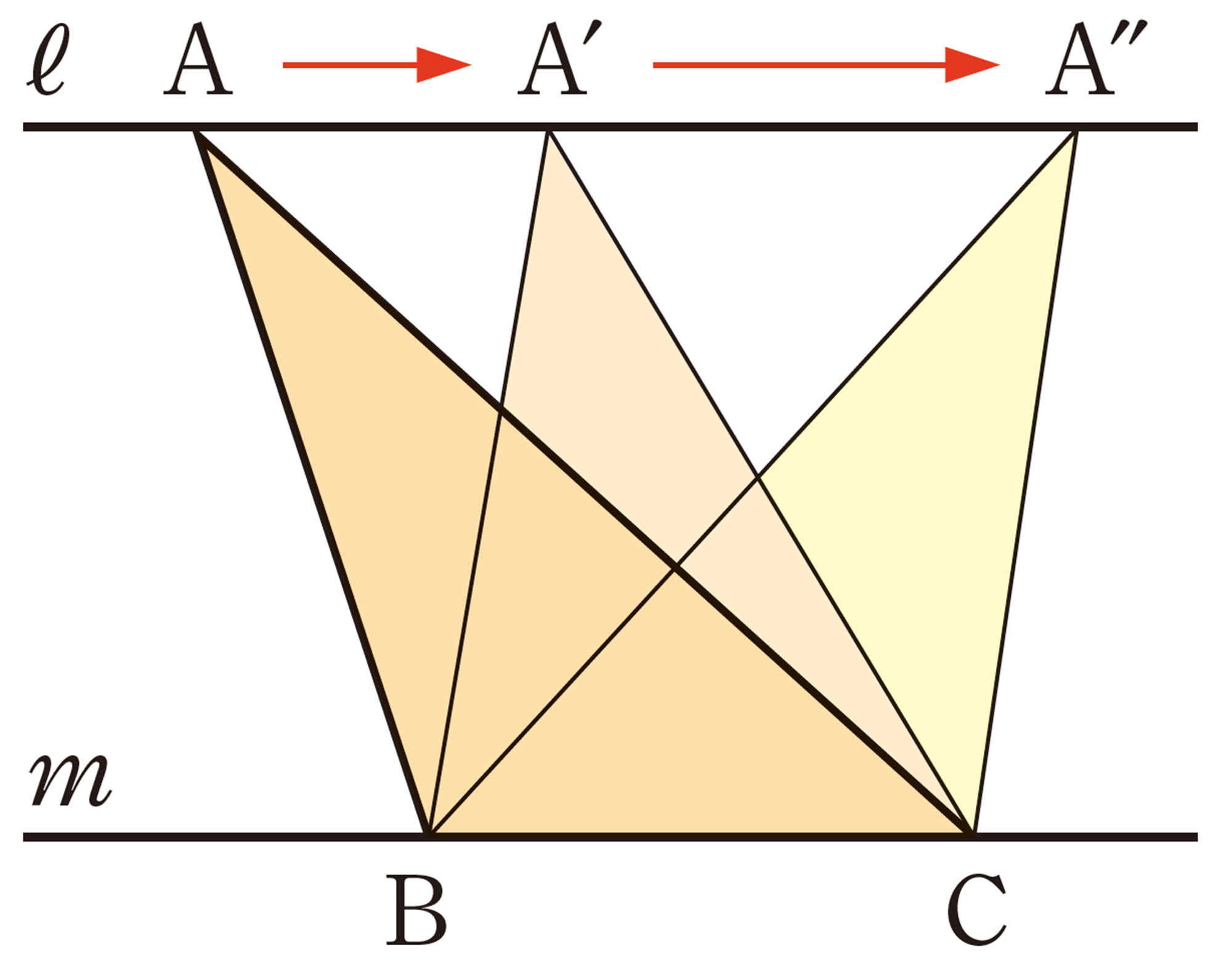
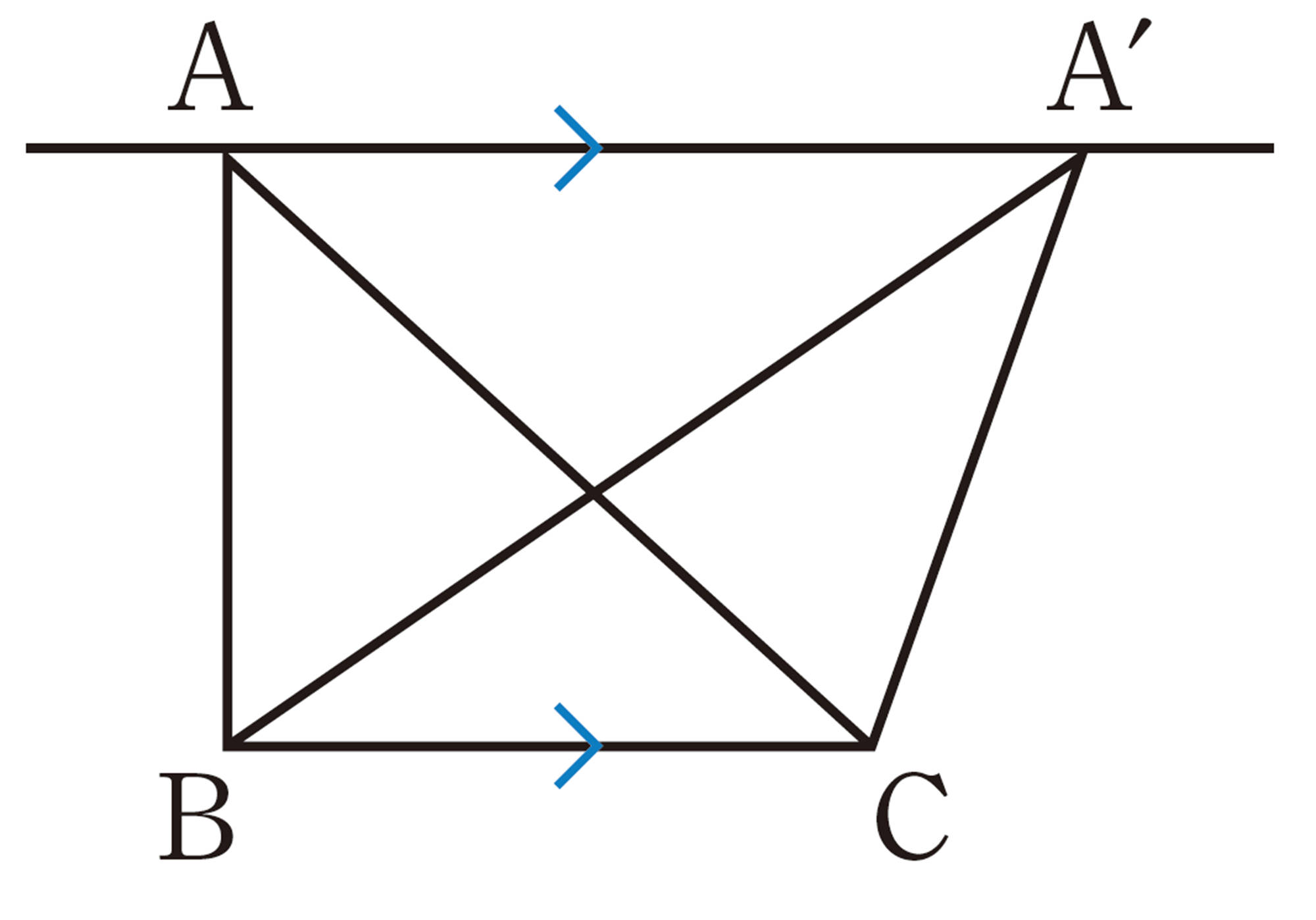
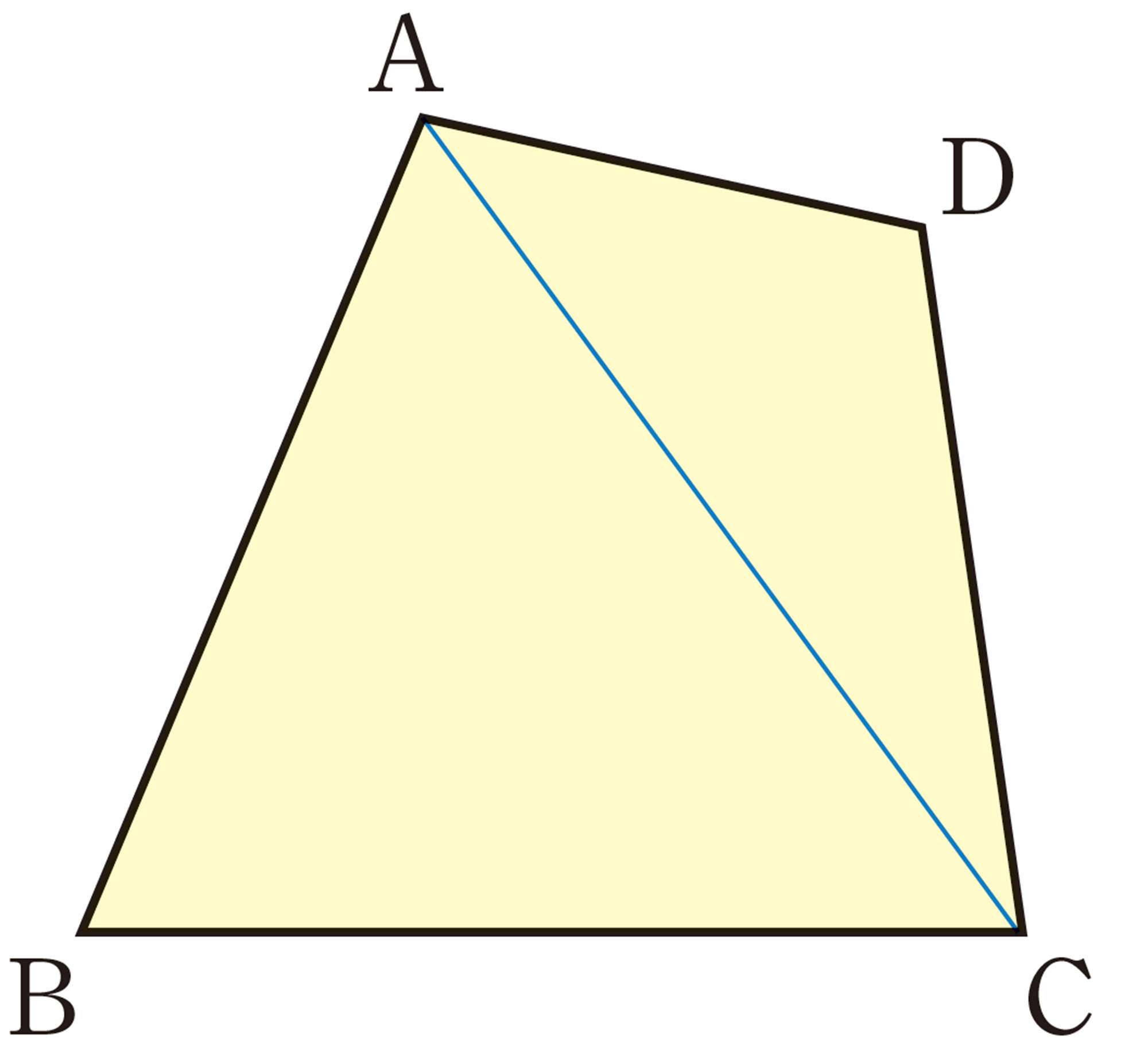
三角形 ABCを記号[mathjax]\(\triangle\)を使って[mathjax]\(\triangle ABC\)と表し,「三角形 ABC」と読む。
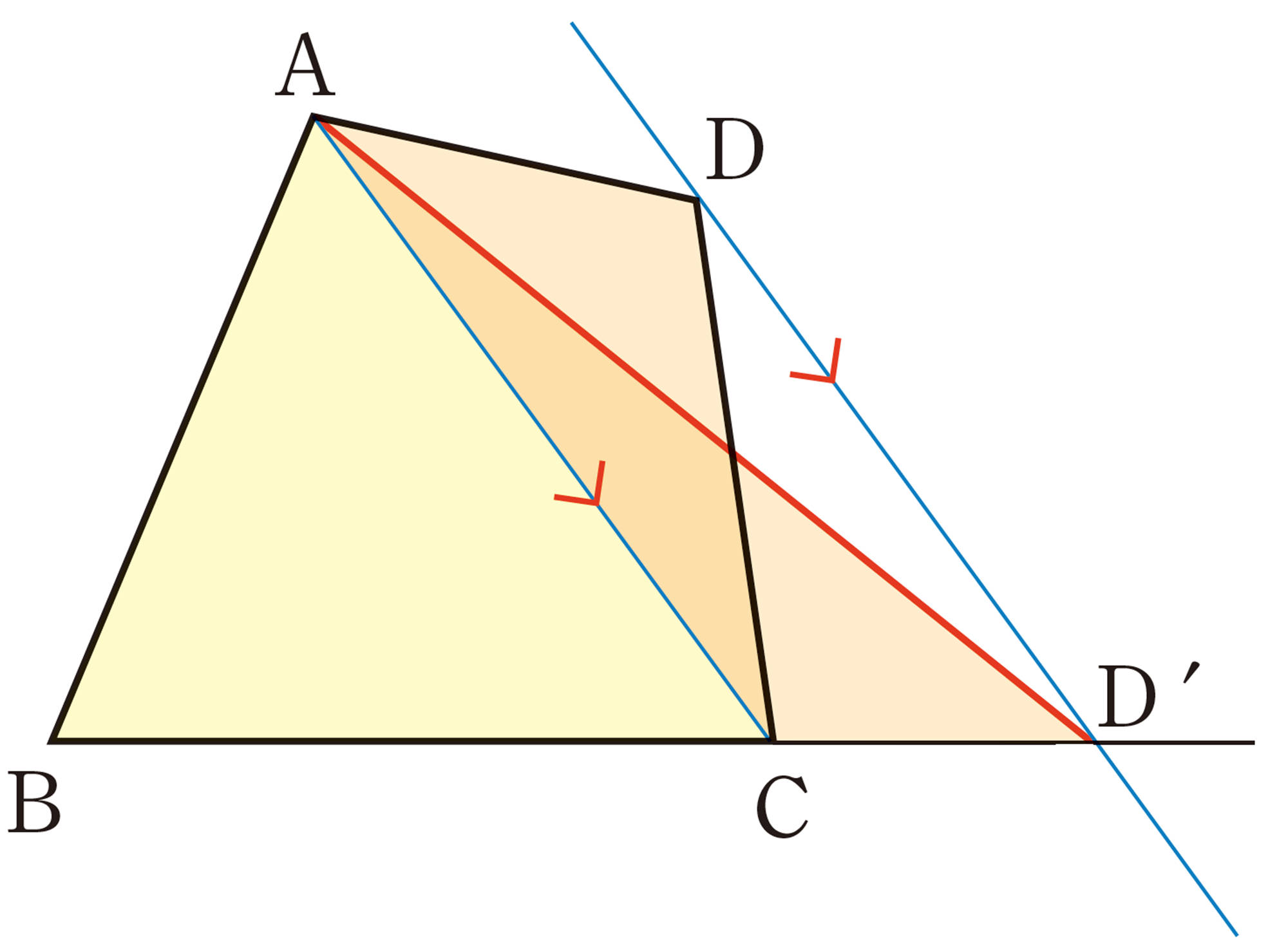
注意 [mathjax]\(\triangle ABC= \triangle A´BC\)は,2つの三角形の面積が等しいことを表している。
平行線と面積の性質を利用してみよう。
⑴ [mathjax]\(\triangle ABC\)
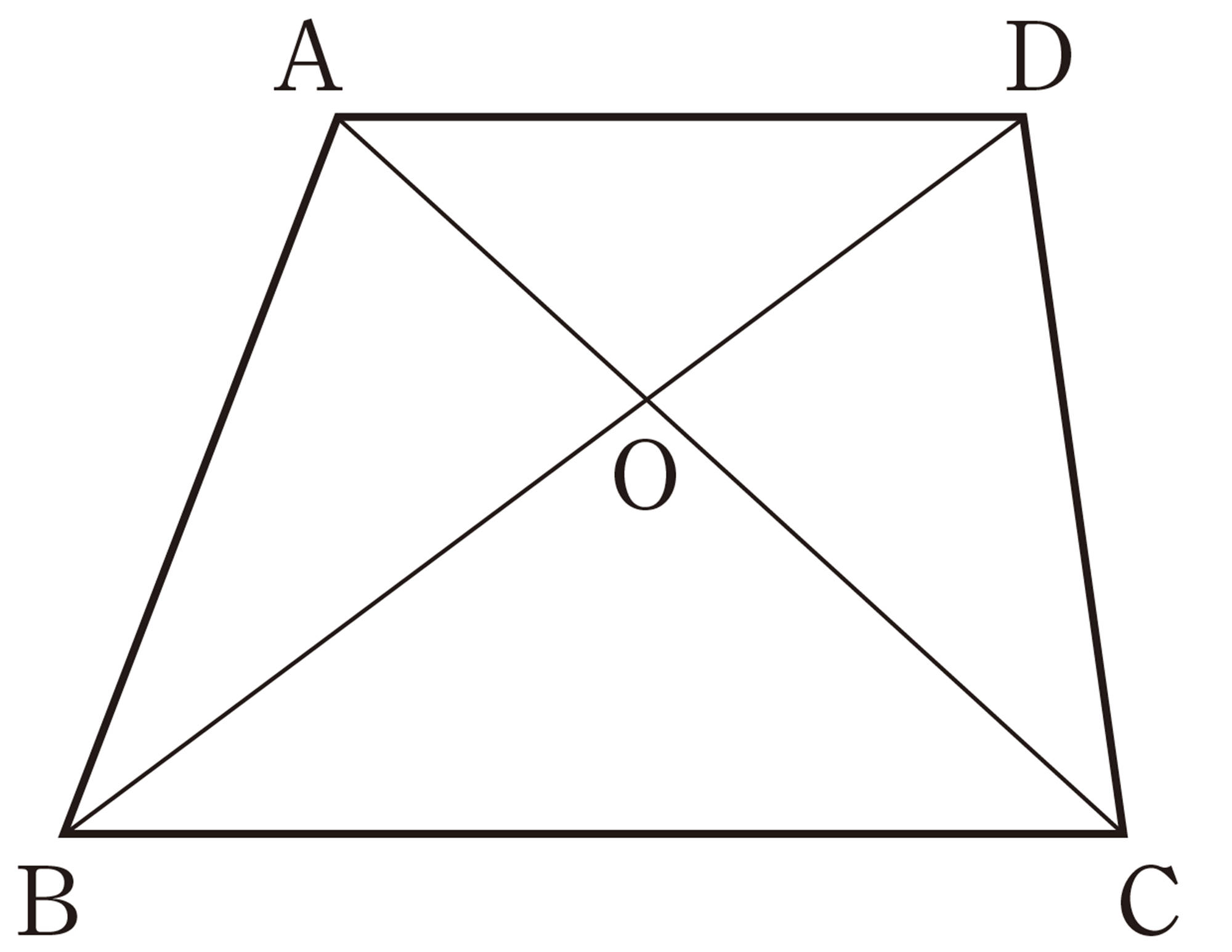
⑵ [mathjax]\(\triangle ADB\)
⑶ [mathjax]\(\triangle ABO\)
gkt-horizontal-line
<1年p.186>
円と直線の作図
Q Question
gkt-horizontal-line
<1年p.187>
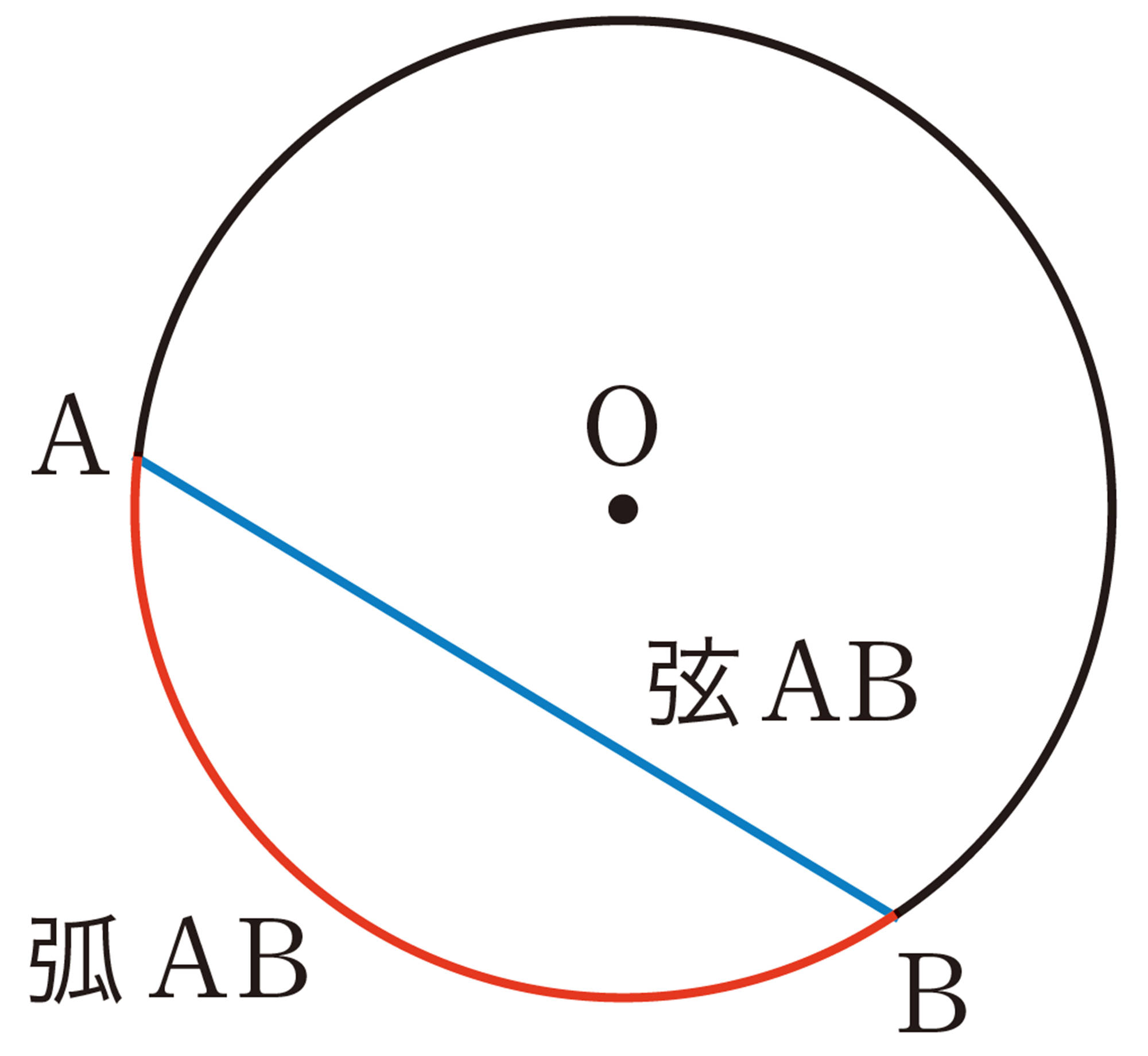
注意 [mathjax]\(\stackrel{\huge\frown}{AB}\)といえば,ふつう,小さい方の弧を指す。
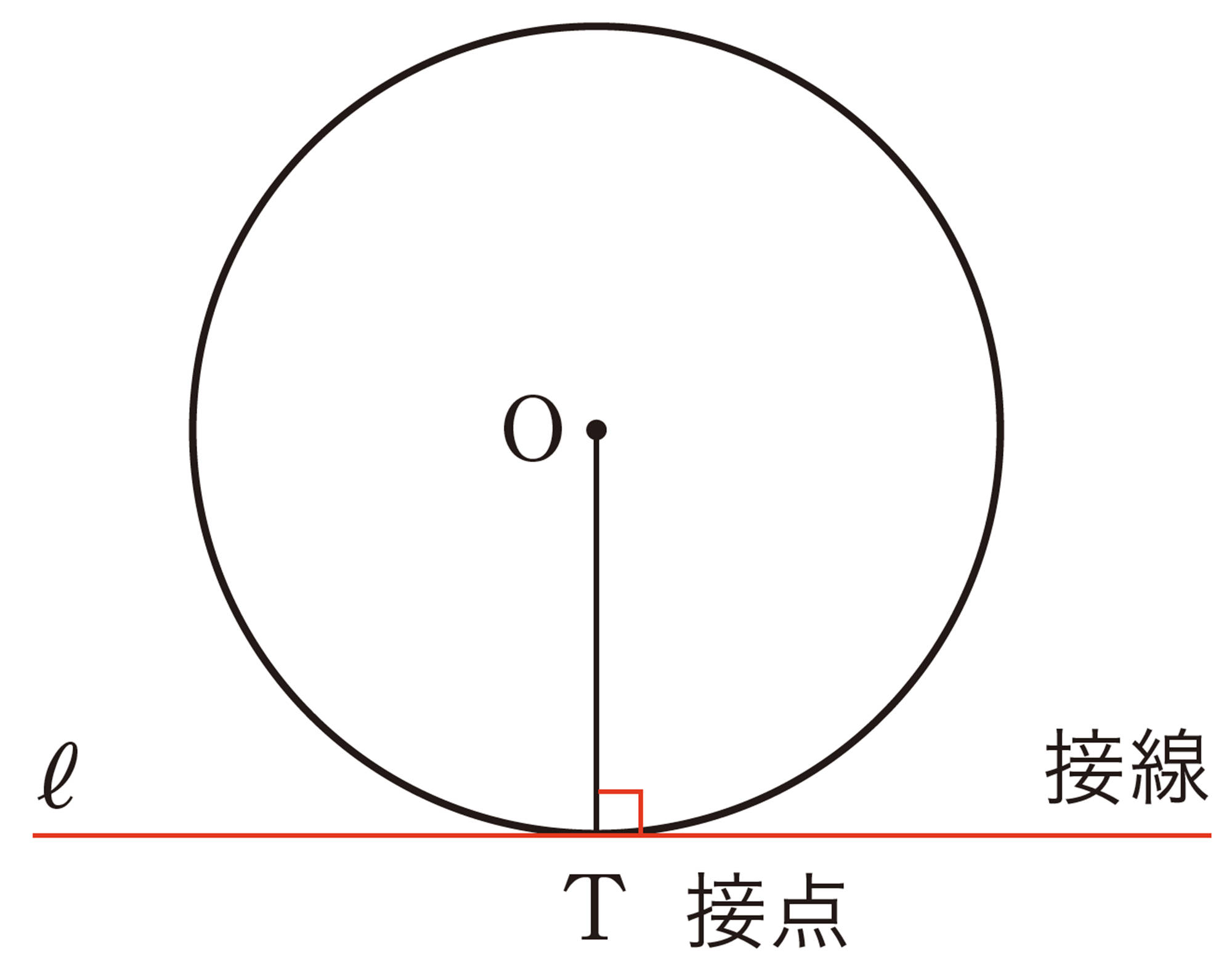
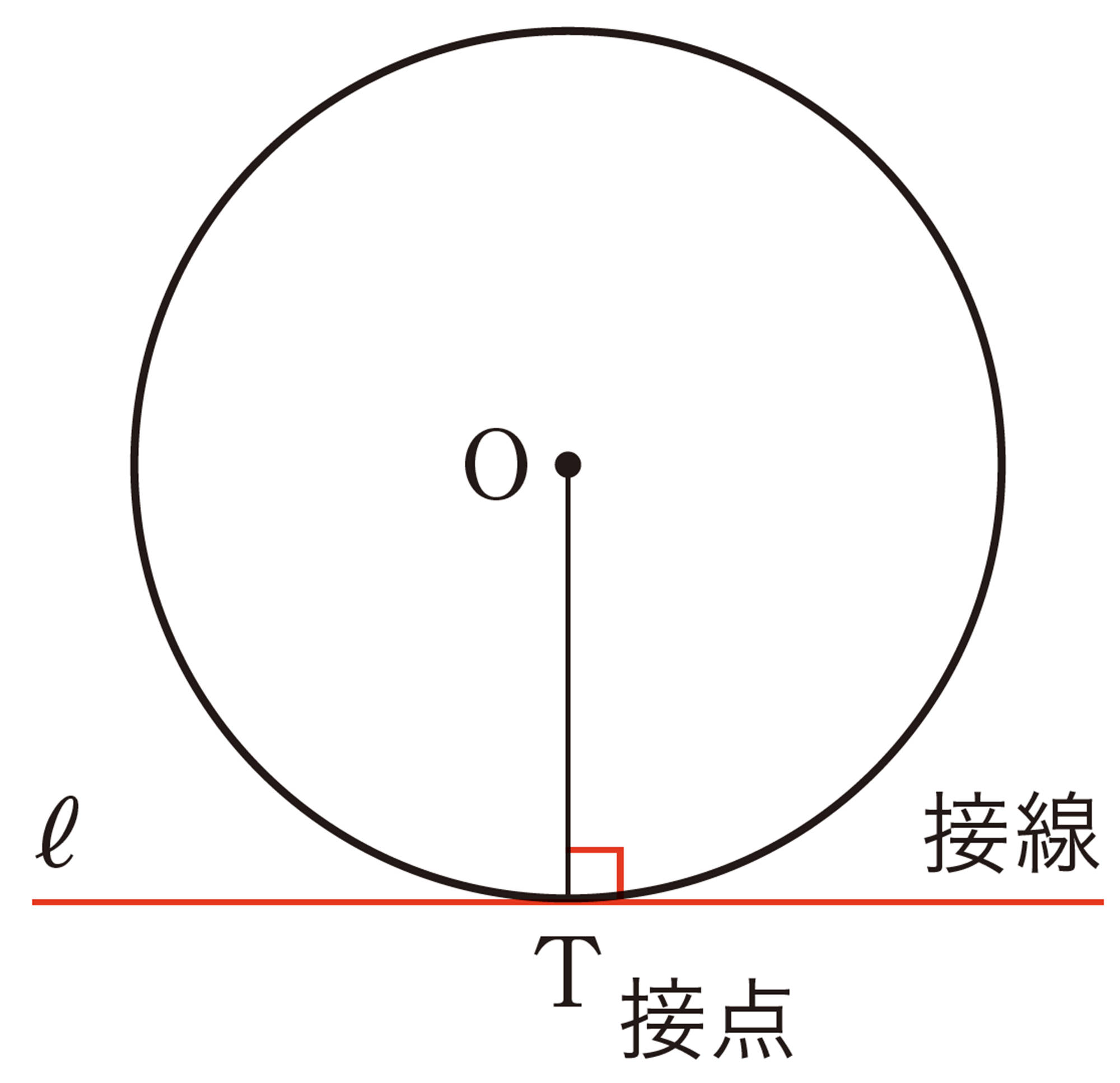
円の接線
円の接線は,接点を通る半径に垂直である。
gkt-horizontal-line
<1年p.188>

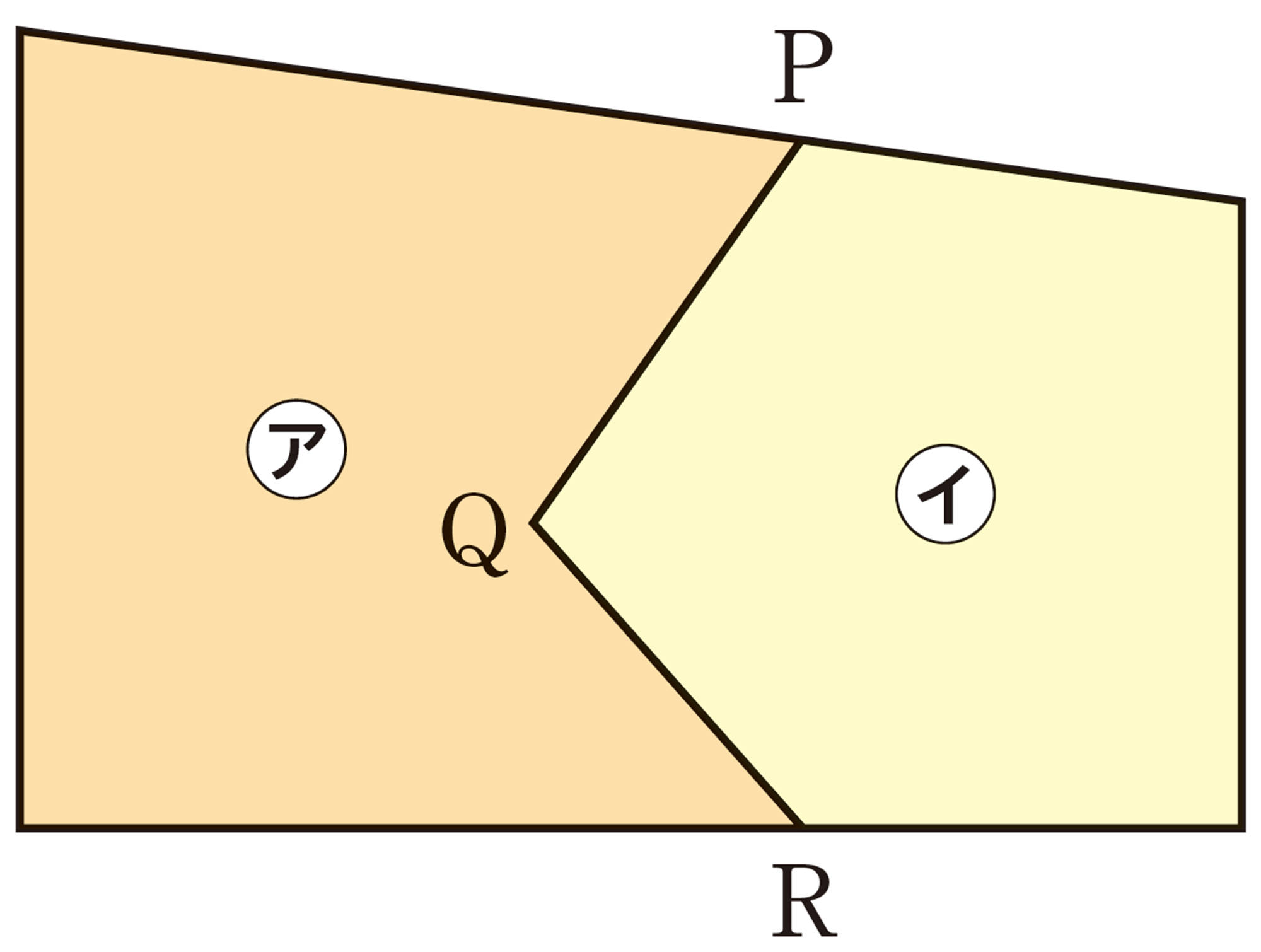
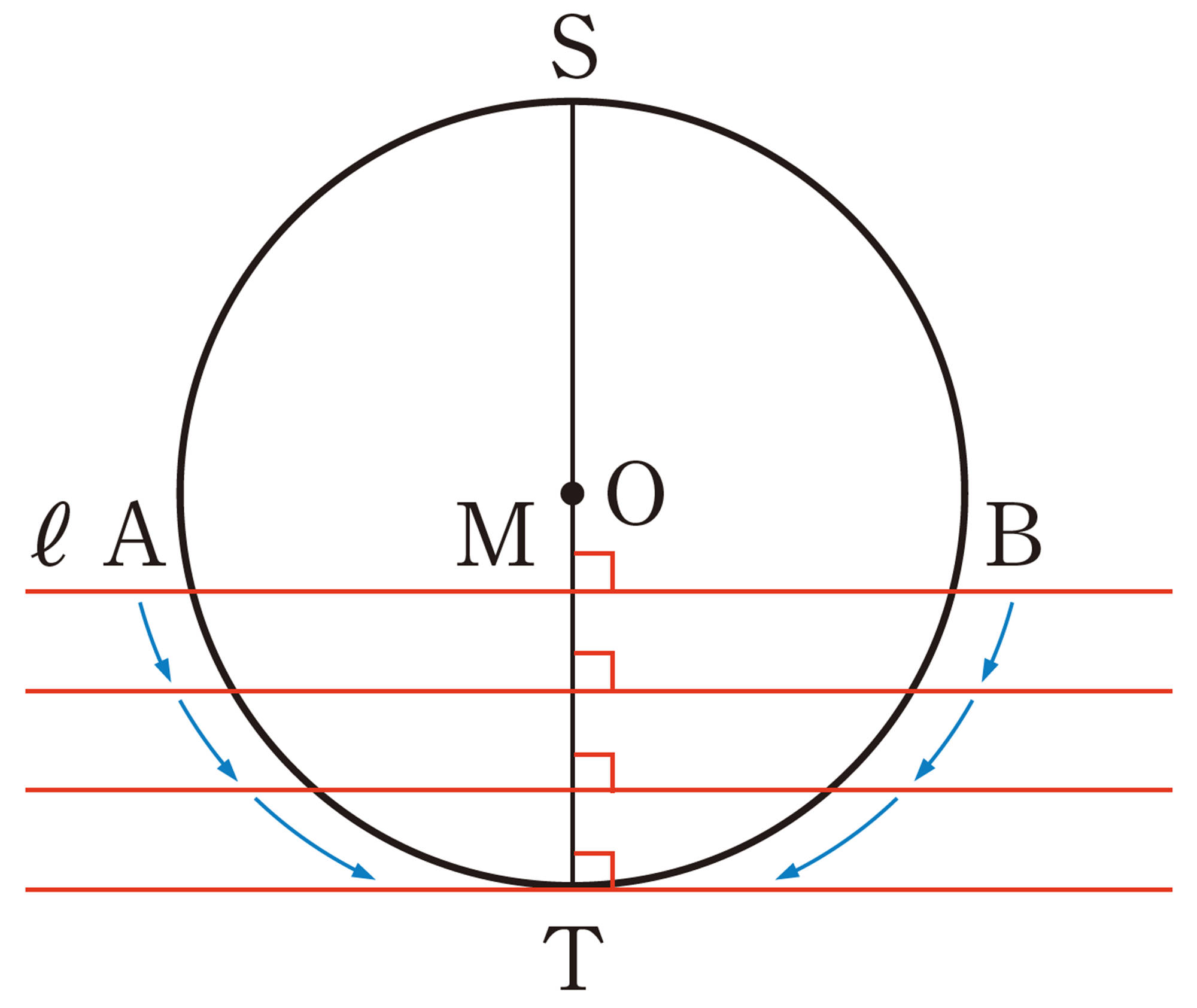
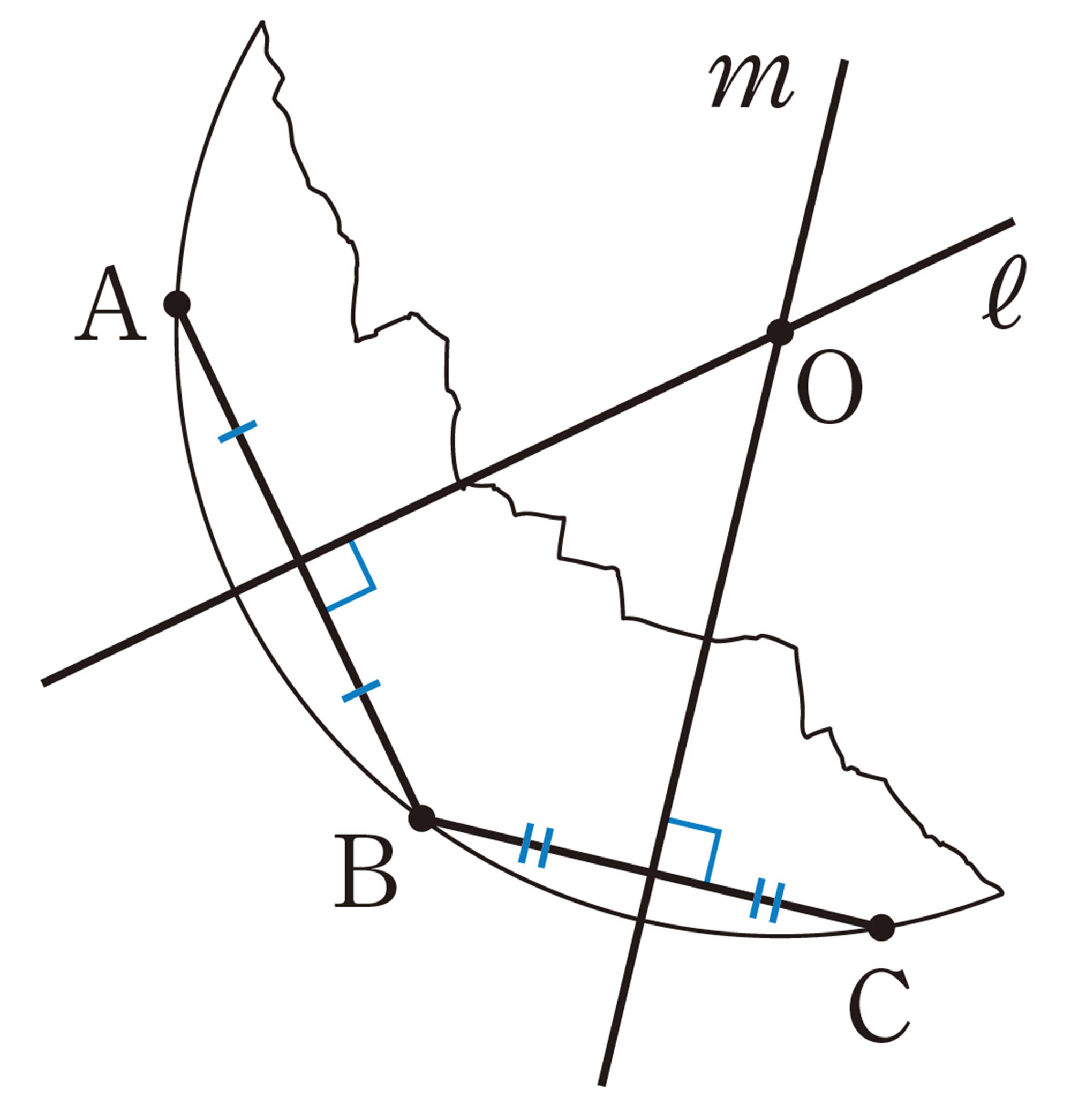
銅鏡の一部が見つかったよ。もとはどんな形だったのかな。
もとの形は,円形をしていたんじゃないかな。

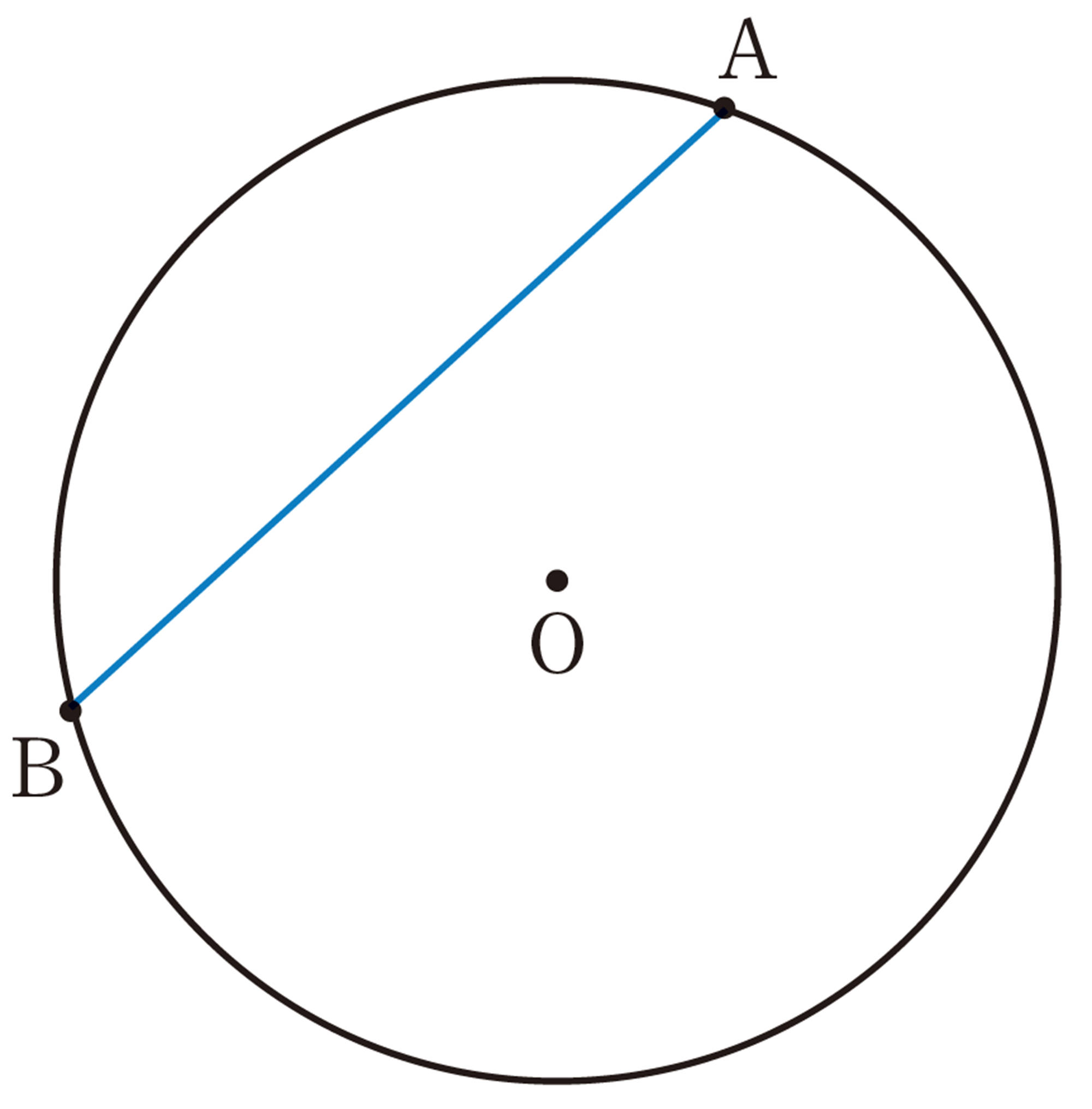
Q Question
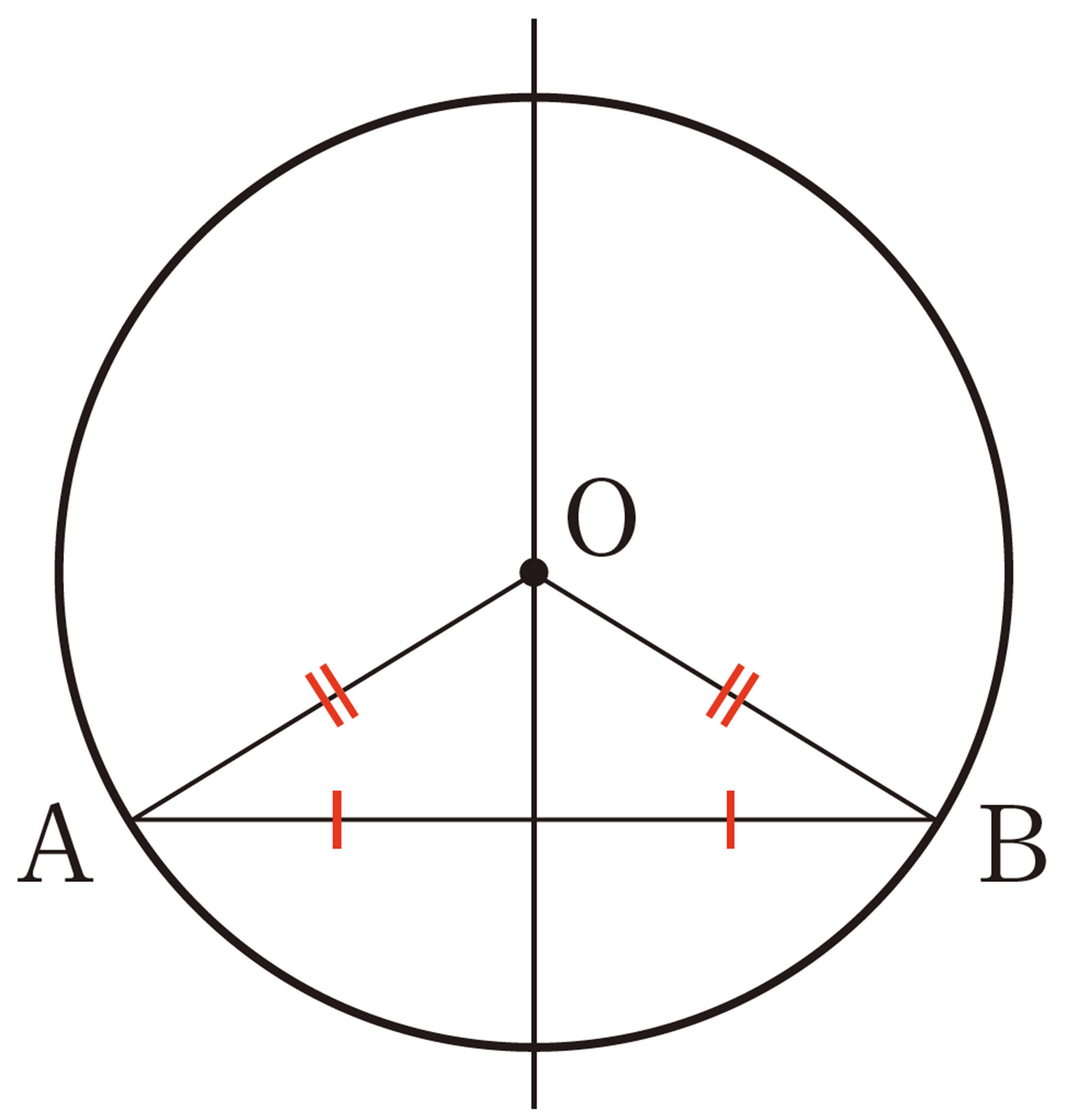
1 弦の垂直二等分線を1つ作図しただけでは,円の中心はわかりませんでした。どうすれば円の中心がわかるでしょうか。
条件をもう1つ加えればいいのかな。

gkt-horizontal-line
<1年p.189>
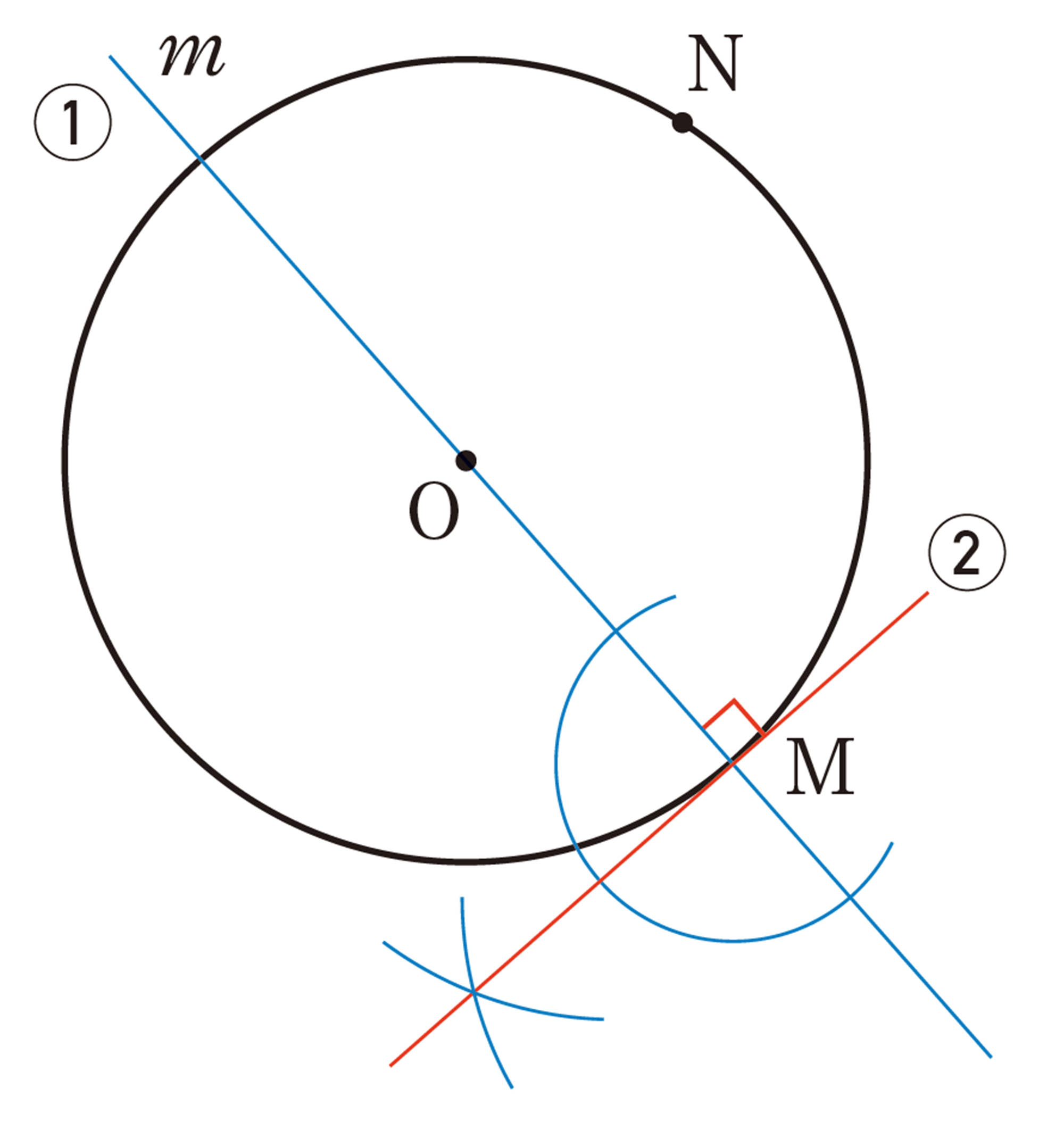
Q Question
問 7 例3の図で,点 Nを通る円 Oの接線を作図しなさい。
gkt-horizontal-line
<1年p.190>
どんなことがわかったかな
垂線や垂直二等分線の作図を利用すると,円の中心,円の接線などを作図することができます。
gkt-horizontal-line