<1年p.170>
ふりかえり 〜算数から数学へ〜
【垂直】
2本の直線が直角に交わるとき，この2本の直線は，垂直であるという。
【平行】
1 つの直線に，垂直に交わっている 2本の直線は，平行であるという。
【円周率】
[mathjax]\(\textsf{円周}\div\textsf{直径}\)で求められる数を円周率という。円周率は，[mathjax]\(3.1415 \cdots \)と限りなく続く数であるが，ふつう[mathjax]\(3.14\) を使う。
図形の問題を考えるときは，辺の長さや角の大きさに着目して分類したね。
【線対称な図形】
1 本の直線を折り目にして2 つに折るとき，折り目の両側の形がきちんと重なり合う図形を，線対称な図形という。また，折り目になる直線を，対称の軸という。
【点対称な図形】
1つの点を中心にして180° 回転すると，もとの図形にきちんと重なり合う図形を，点対称な図形という。
また，中心にした点を，対称の中心という。
変わらないものを見つけて，図形の性質やきまりを見つけたね。
どうしてそうなるのか，理由を考えて説明したね。
<1年p.171>
５章 Chapter 5 平面図形
1節 いろいろな角の作図
2節 図形の移動
銅鏡の一部を見つけたけど，もとはどんな大きさだったのかな。
銅鏡を円と考えて復元するには，何がわかればいいのかな。
円の中心がわかれば，できそうだよ。
どうしたら中心がわかるのかな。円の性質をいろいろ調べてみないといけないね。
？ いろいろな図形には，どんな性質があるのかな？
<1年p.172>
1節 いろいろな角の作図
宝の隠し場所はどこ？
大和さんは，宝の隠し場所を示した文書と地図を見つけました。大和さんたちは，宝を見つけられるでしょうか。
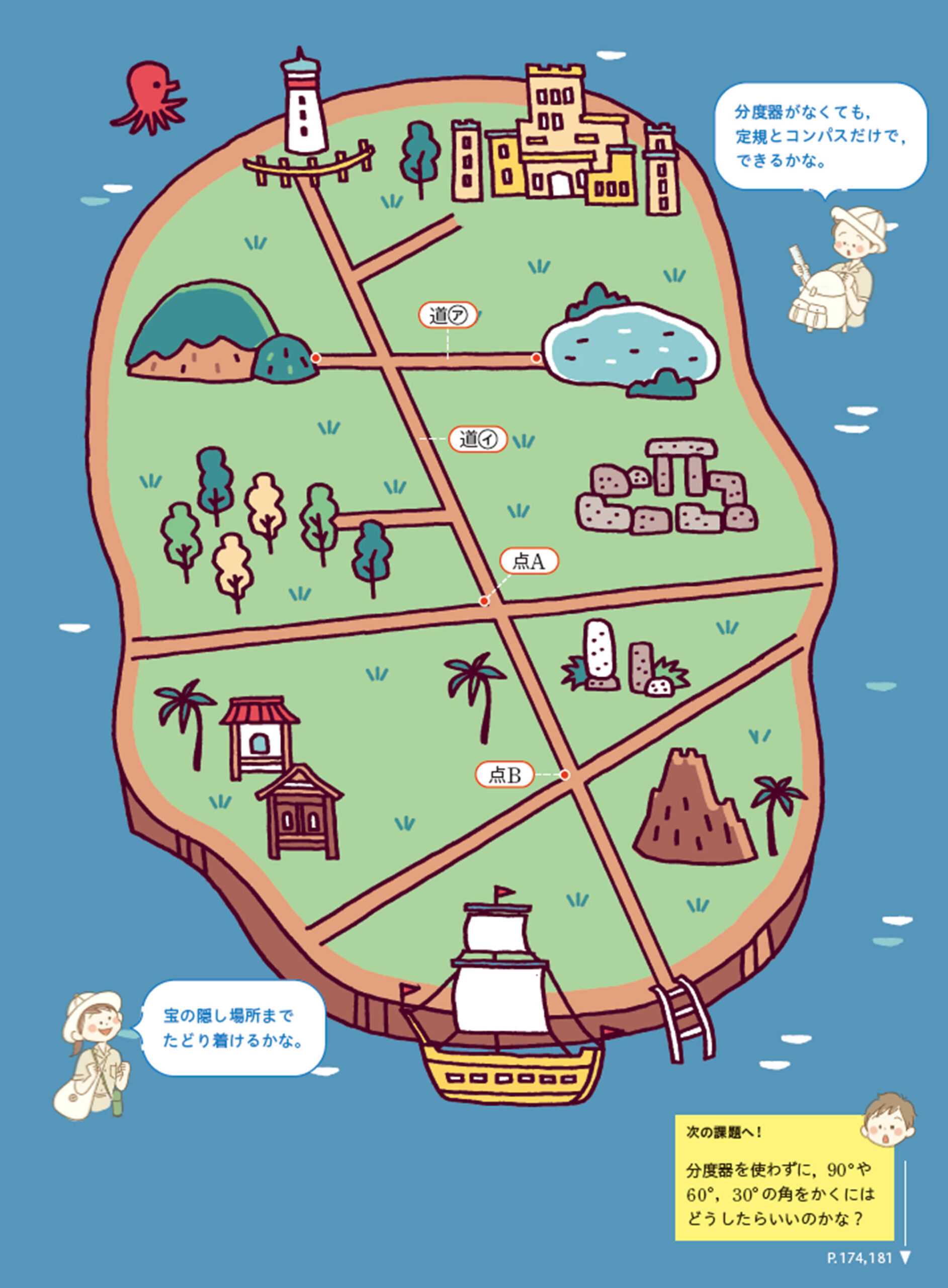
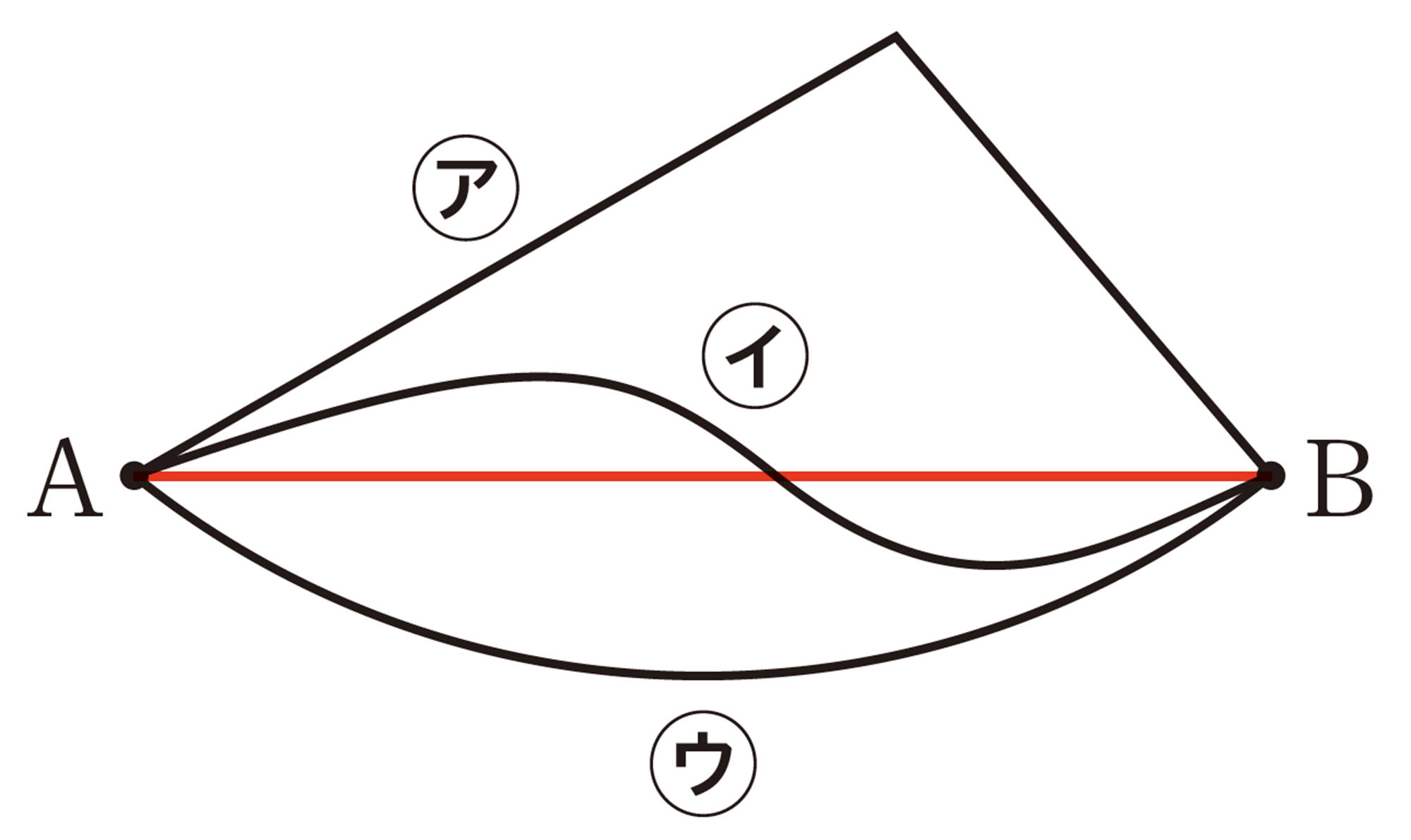
【１】 次の文書と次ページの地図をもとに，定規やコンパスなどを使って，宝の隠し場所を見つけてみましょう。
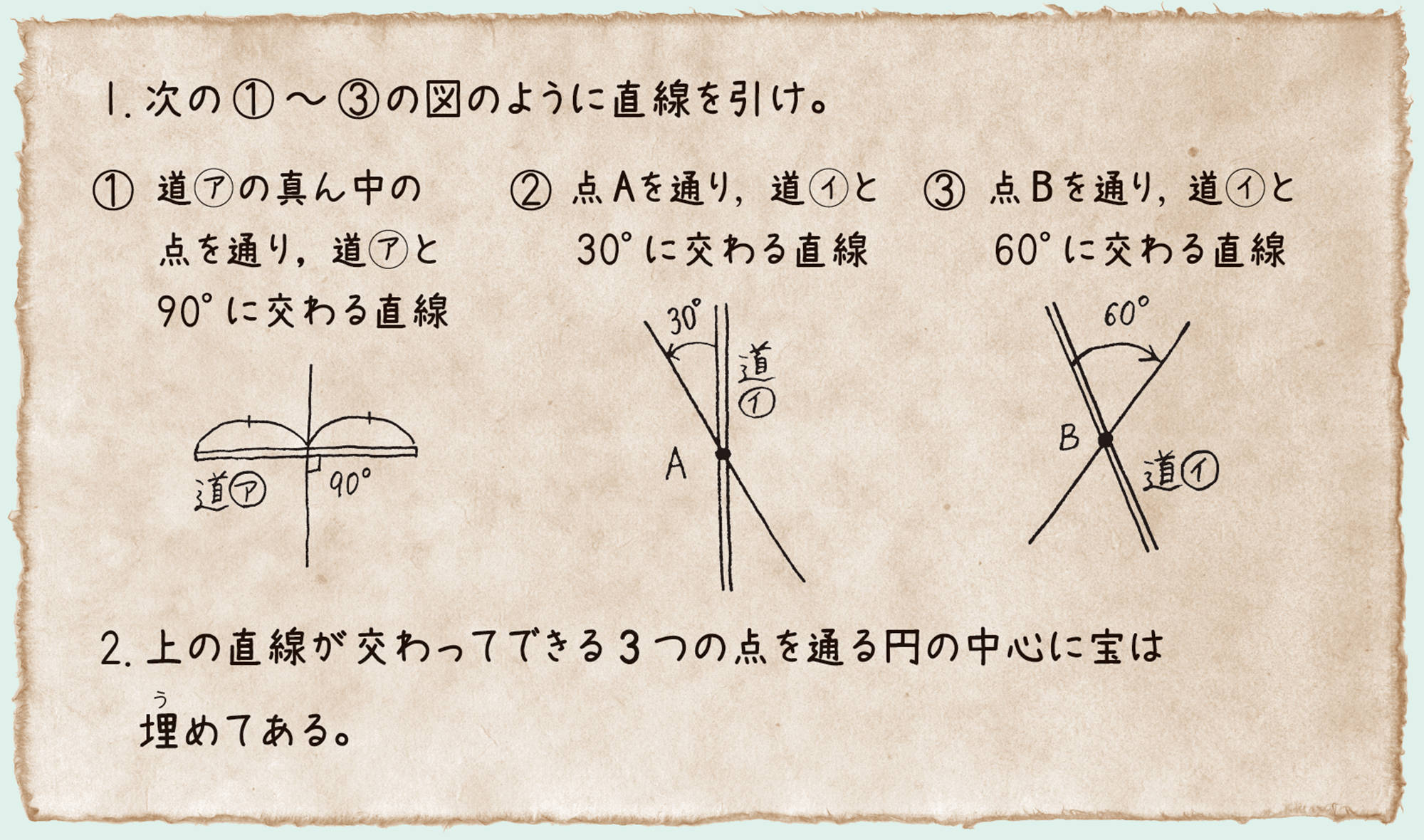
1. 次の①〜 ③の図のように直線を引け。
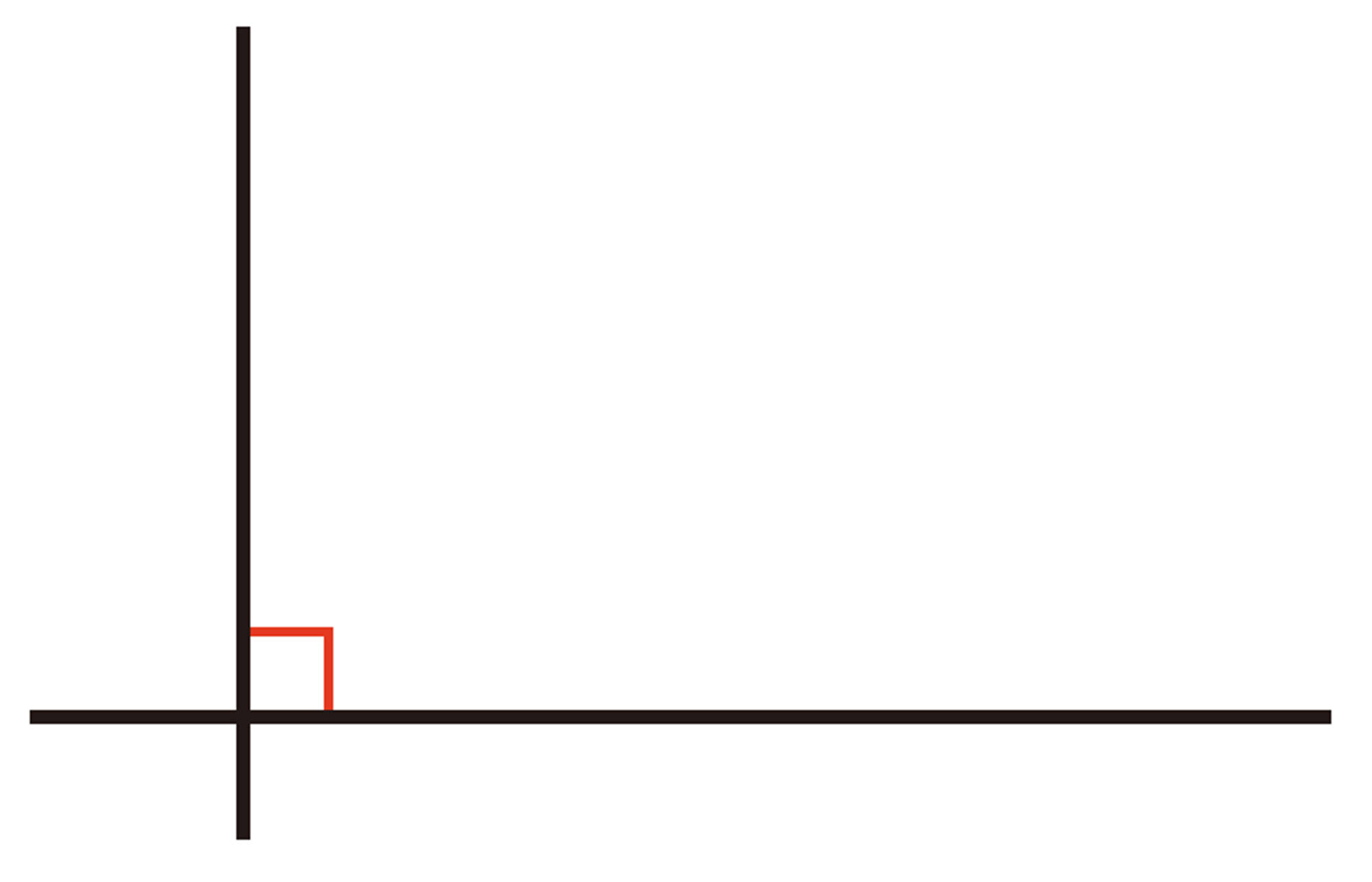
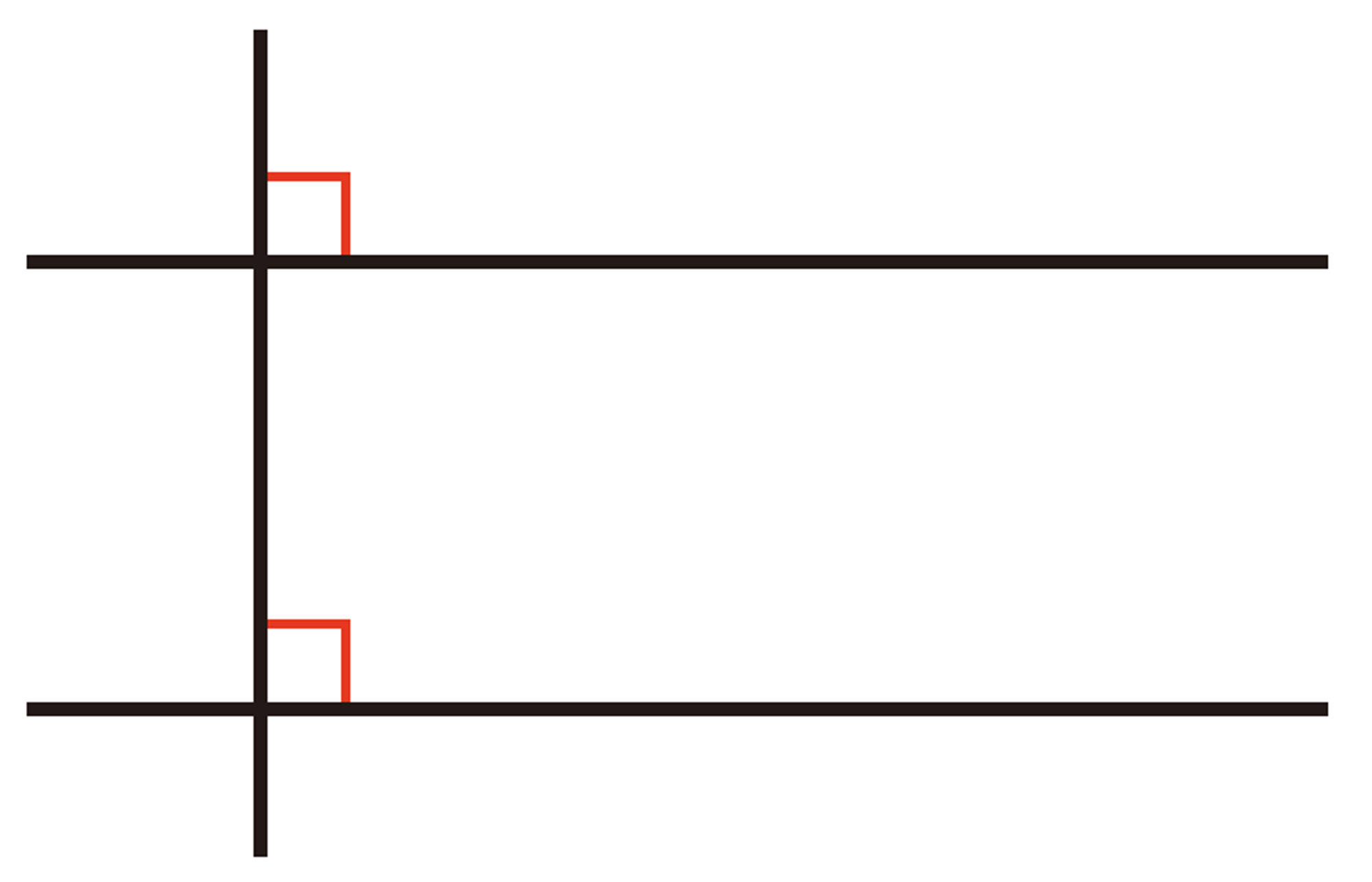
①道㋐の真ん中の点を通り，道㋐と[mathjax]\(90^{\circ}\)に交わる直線
②点Aを通り，道㋑と[mathjax]\(30^{\circ}\)に交わる直線
③点Bを通り，道㋑と[mathjax]\(60^{\circ}\)に交わる直線
2. 上の直線が交わってできる3つの点を通る円の中心に宝は埋めてある。
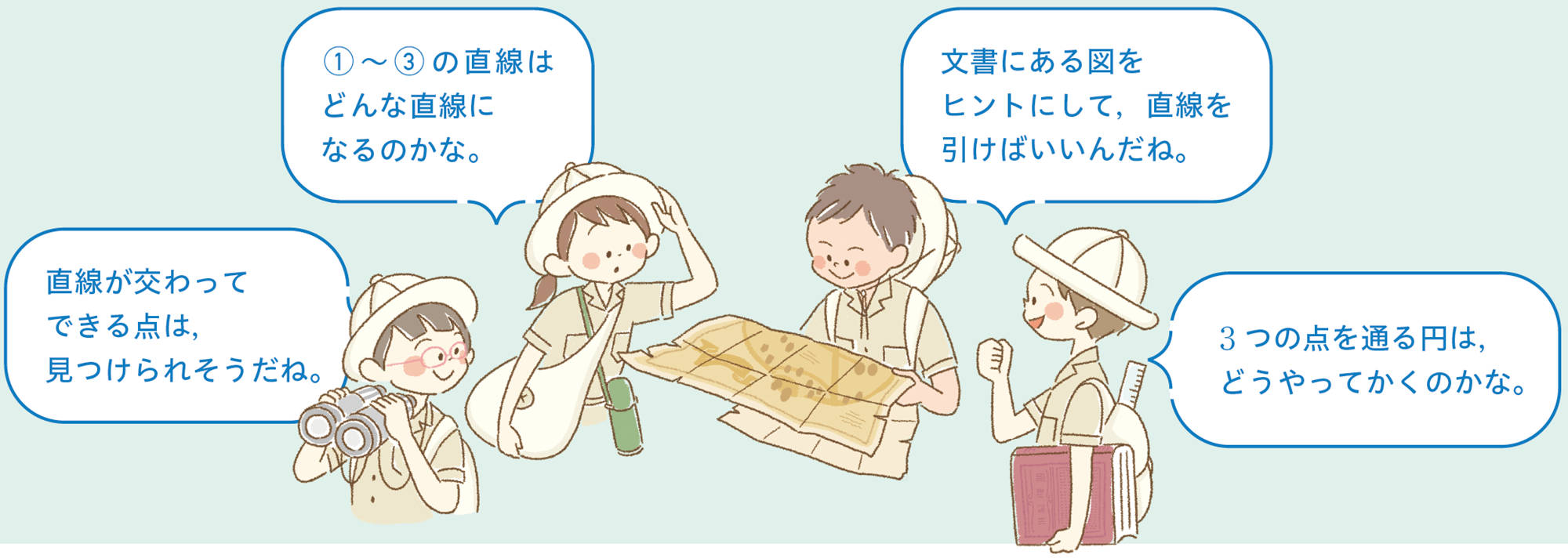
① 〜③ の直線はどんな直線になるのかな。
文書にある図をヒントにして，直線を引けばいいんだね。
直線が交わってできる点は，見つけられそうだね。
3つの点を通る円は，どうやってかくのかな。
<1年p.173>
分度器がなくても，定規とコンパスだけで，できるかな。
宝の隠し場所までたどり着けるかな。
次の課題へ！
分度器を使わずに，[mathjax]\(90^{\circ}\)や[mathjax]\(60^{\circ}\)，[mathjax]\(30^{\circ}\)の角をかくにはどうしたらいいのかな？
P.174，181
<1年p.174>
１ [mathjax]\(90^{\circ}\)の角の作図
まず，[mathjax]\(90^{\circ}\)の角をかく方法を考えてみよう。
小学校で学習した図形の中に，参考にできるものがあるかな。
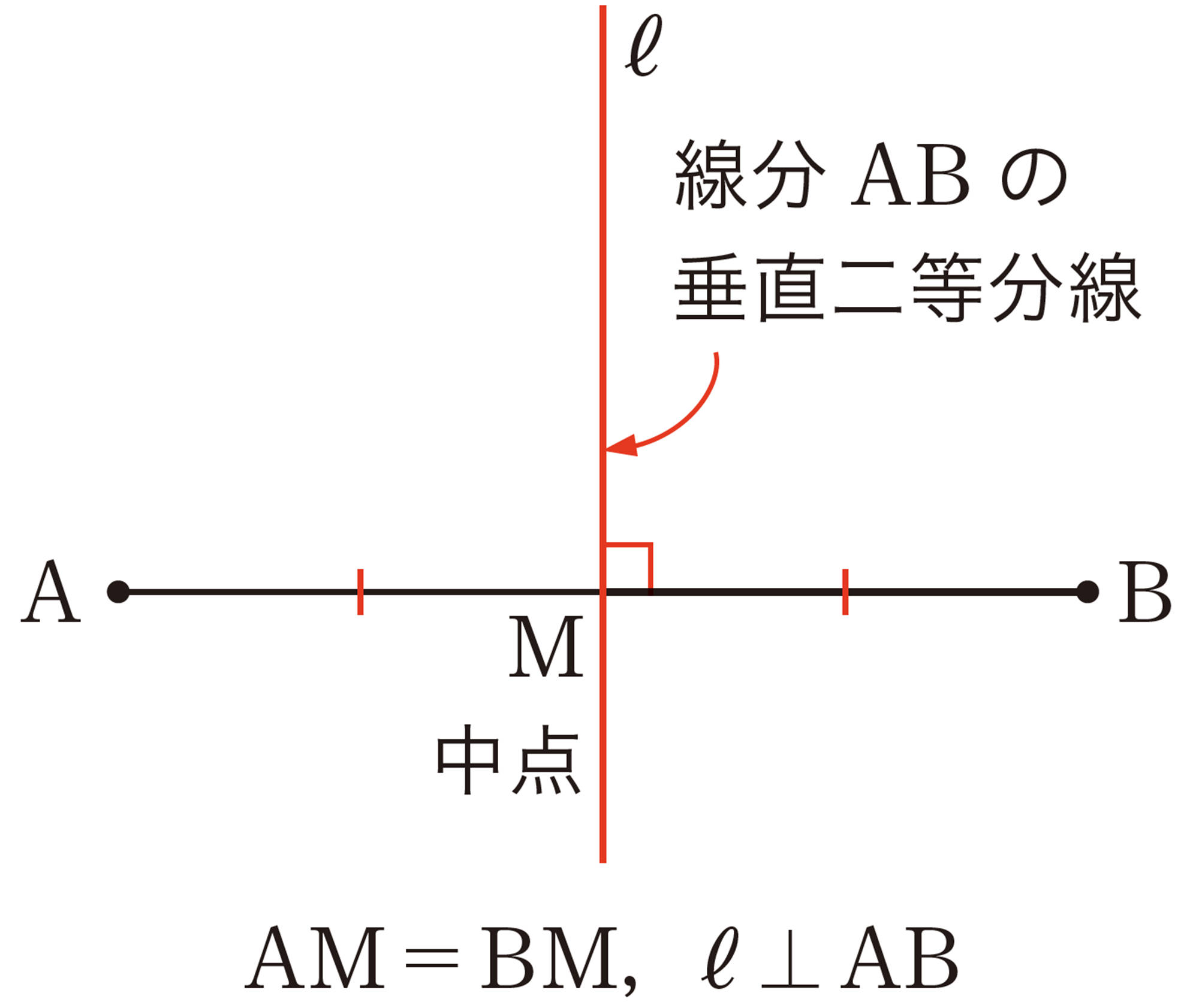
垂直二等分線
Q Question
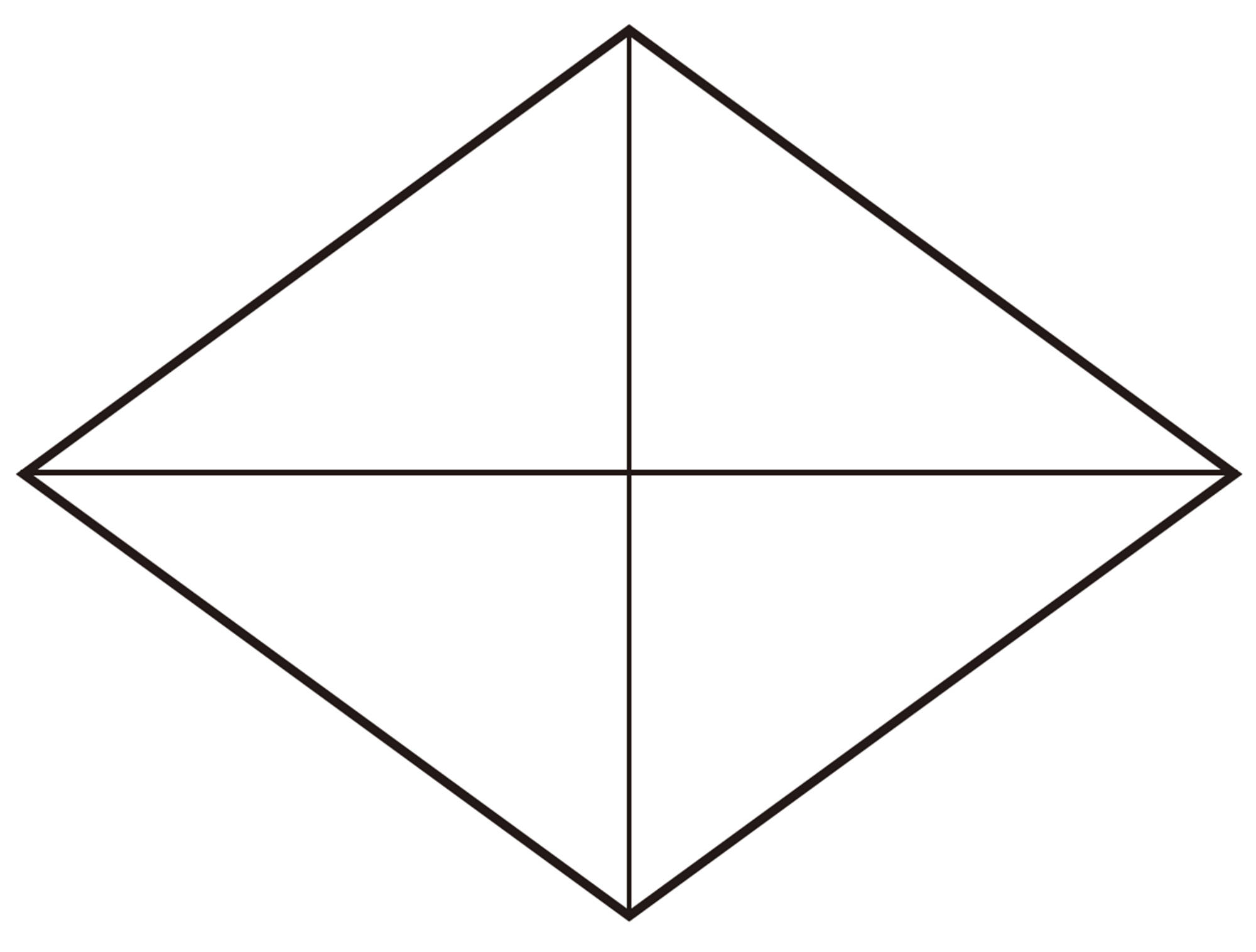
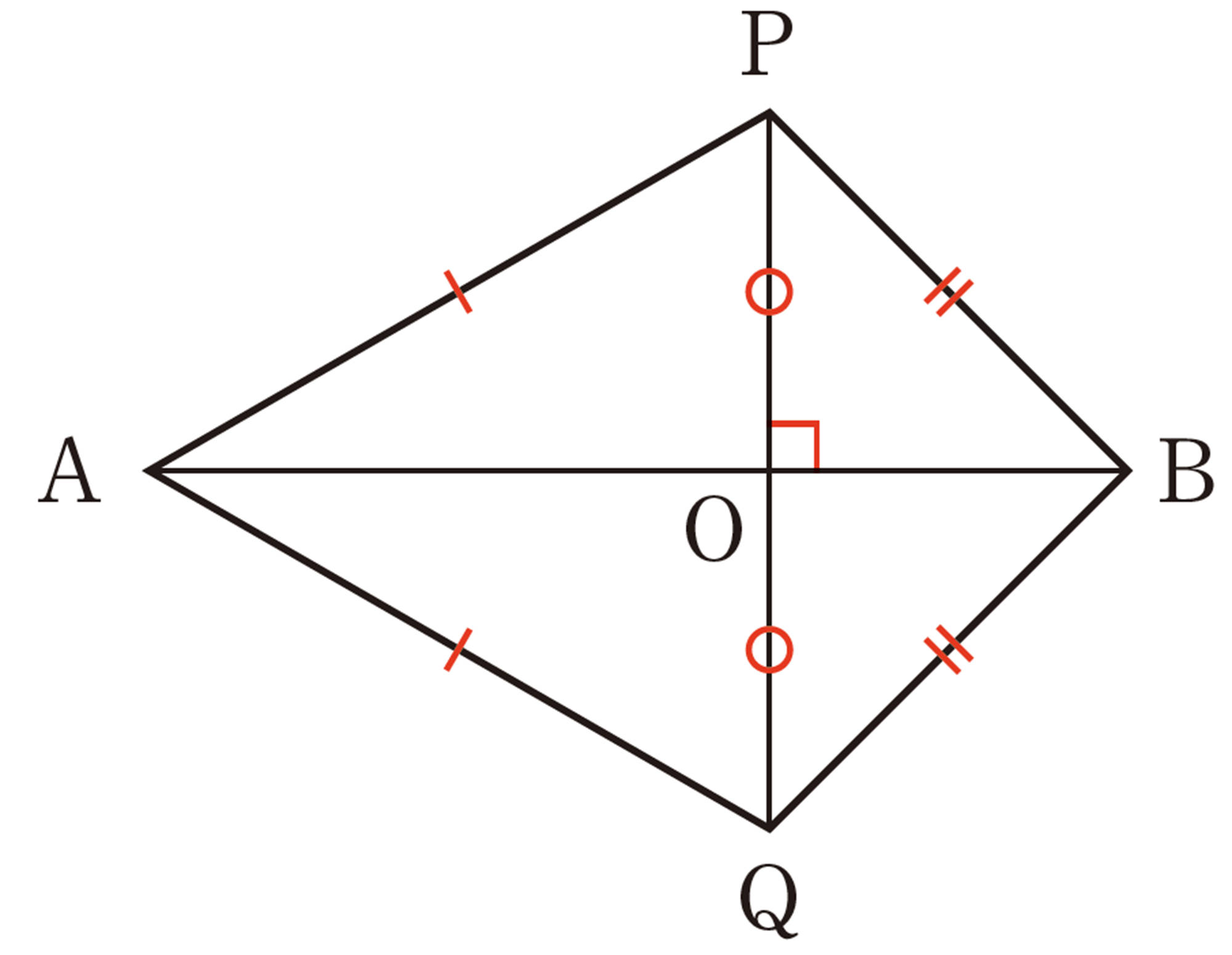
これまでに学習した図形の中で，[mathjax]\(90^{\circ}\)で交わる2本の直線がある図形について調べ，[mathjax]\(90^{\circ}\)の角をかくことに利用できるか話し合ってみましょう。
辺が[mathjax]\(90^{\circ}\)で交わる図形には，どんなものがあったかな。
2本の直線は，対角線でもいいのかな。
見方・考え方
図形の中にある[mathjax]\(90^{\circ}\)で交わる直線に着目して考えられるかな。
目標 ▷ [mathjax]\(90^{\circ}\)で交わる2本の直線がある図形の性質について調べよう。
2点 A，Bを通る直線を 直線 ABという。これからは，直線といえば，両方向に限りなくのびているまっすぐな線と考える。
直線 ABのうち，点 Aから点 Bまでの部分を線分ABという。
また，点 Aを端として点 Bの方向に限りなくのびているまっすぐな線を 半直線 AB という。
問 １ 点 Aを通る直線を引くとき，直線がただ1本に決まるには，ほかにどんな条件が必要ですか。
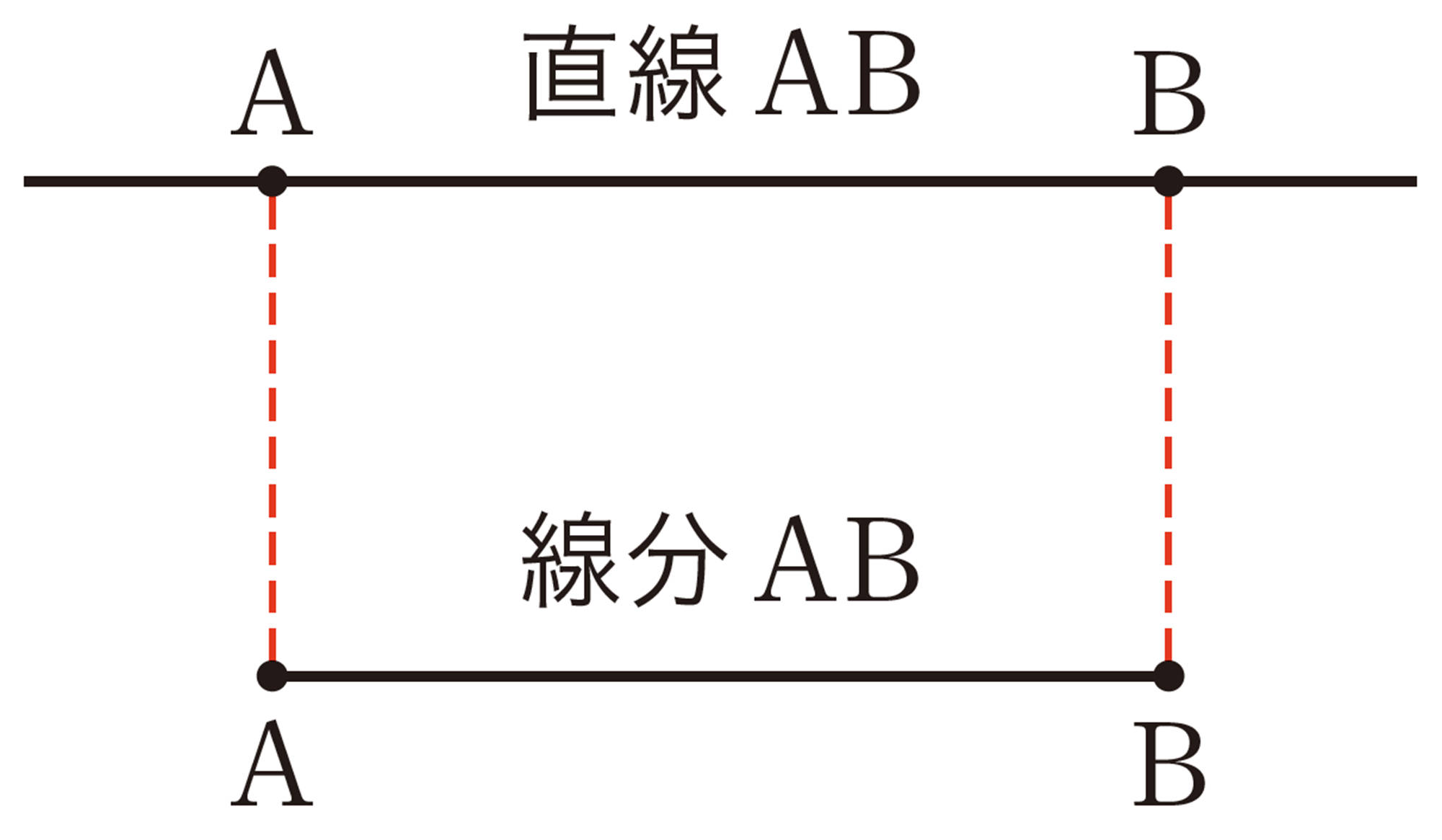
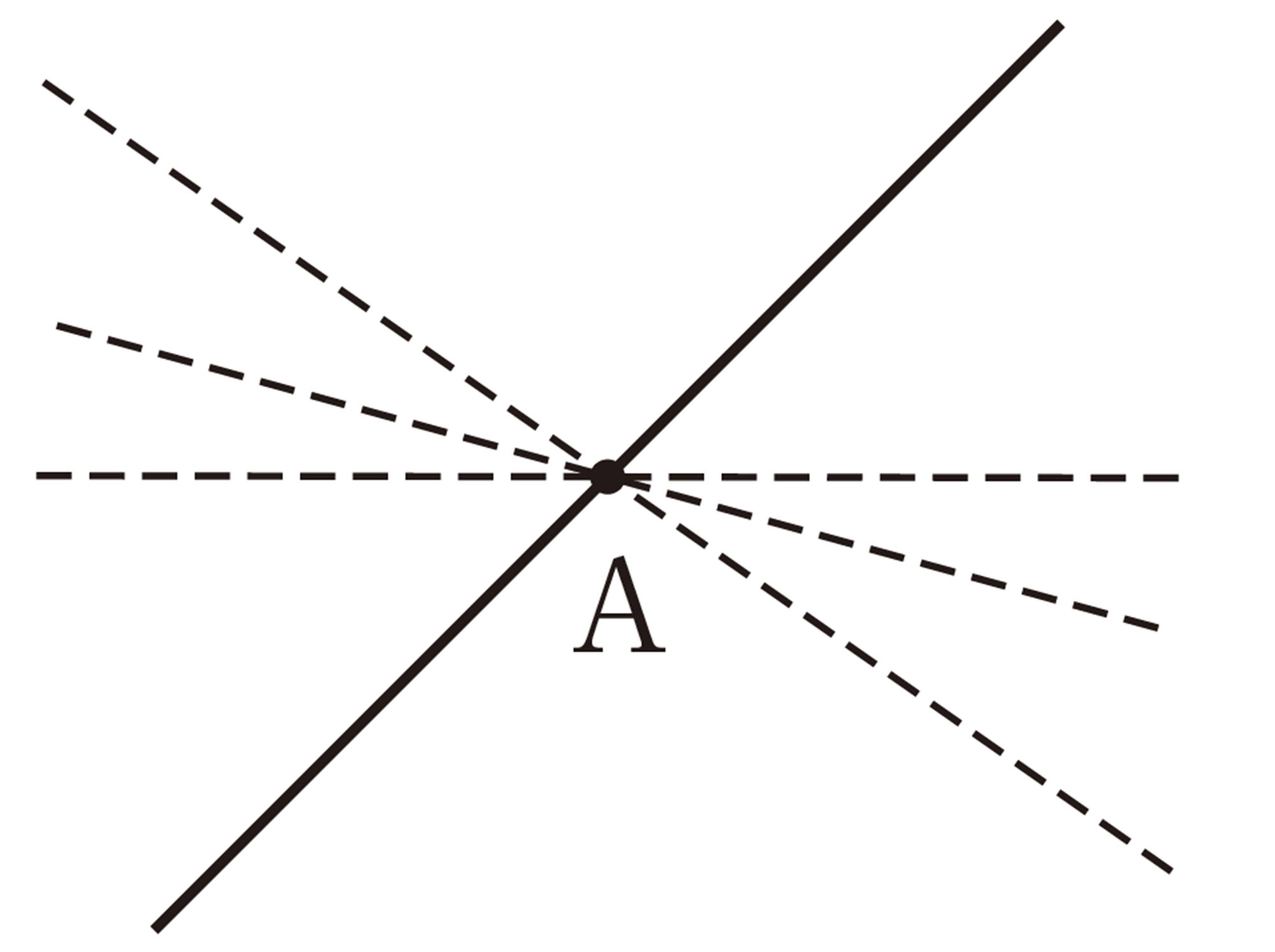
1つの点 Aを通る直線は無数にあるが，2点を通る直線は，ただ1本しかない。つまり，2点を通る直線は1本に決まる。
<1年p.175>
点 Aと点 Bを結ぶ線のうち， ㋐のような折れ線や㋑ ，㋒のような曲線に比べて，線分 ABの長さがもっとも短くなる。このとき，線分ABの長さを2点 A，B間の 距離 という。
この距離を[mathjax]\(AB=4\)cm などと書いて，線分ABの長さを表すことがある。
問 ２ ひし形の対角線に，どんな性質があるか調べなさい。
頂点や交わった点に記号をつけると，説明しやすいね。
2つの線が交わる点を 交点 という。
2直線 ℓ，mが交わってできる角が直角であるとき，2直線 ℓ，mは垂直であるという。
このとき，記号 [mathjax]\(\bot\)を使って [mathjax]\(ℓ \bot m\)と表し，｢ℓ垂直m」と読む。2直線が垂直であるとき，一方を他方の 垂線 という。
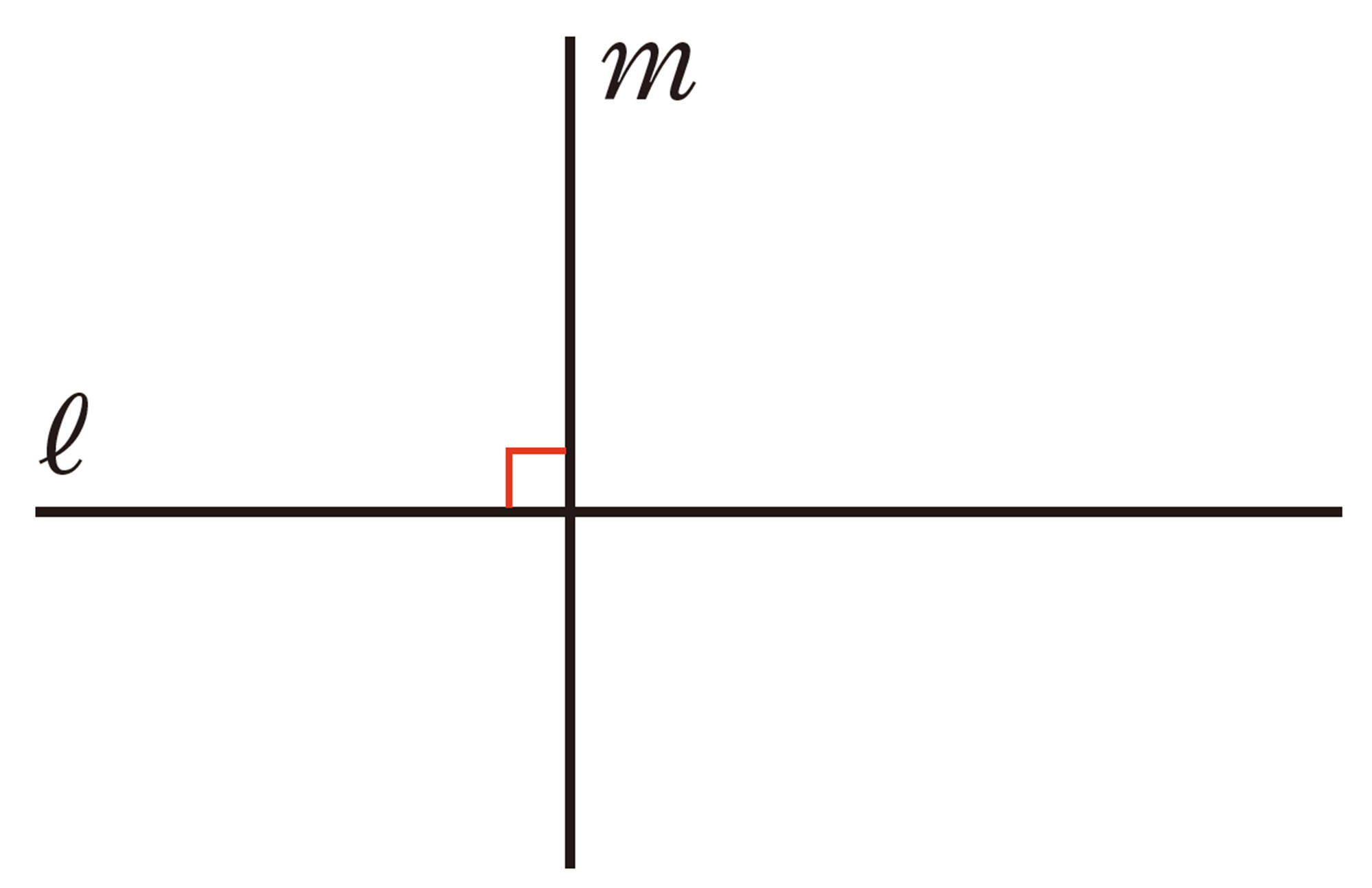
注意 直線を，ℓ やmなどの小文字1つで表すことがある。
ひし形は，対角線を対称の軸とする線対称な図形であるから，対応する辺の長さや対応する角の大きさはそれぞれ等しい。右の図のように，対角線 PQ，ABの交点をOとするとき，次のことが成り立つ。
[mathjax]\(AB \bot PQ\)，[mathjax]\(PO=QO\)，[mathjax]\(AO=BO\)
右の図のように，[mathjax]\(AM=BM\)のとき，点 Mを線分 AB の 中点 という。また，線分 ABの中点 Mを通り，ABに垂直な直線 ℓを線分 ABの 垂直二等分線 という。
<1年p.176>
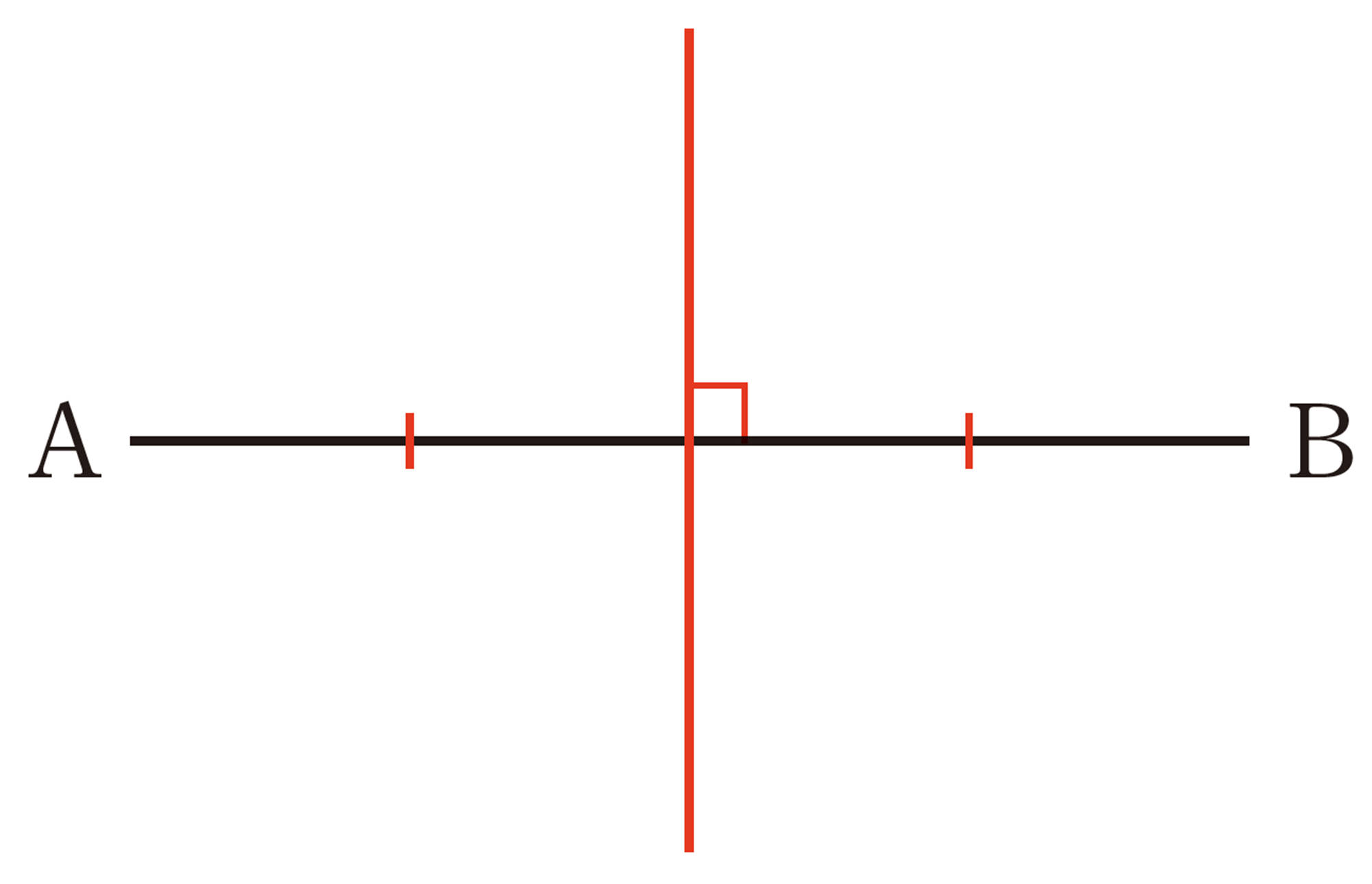
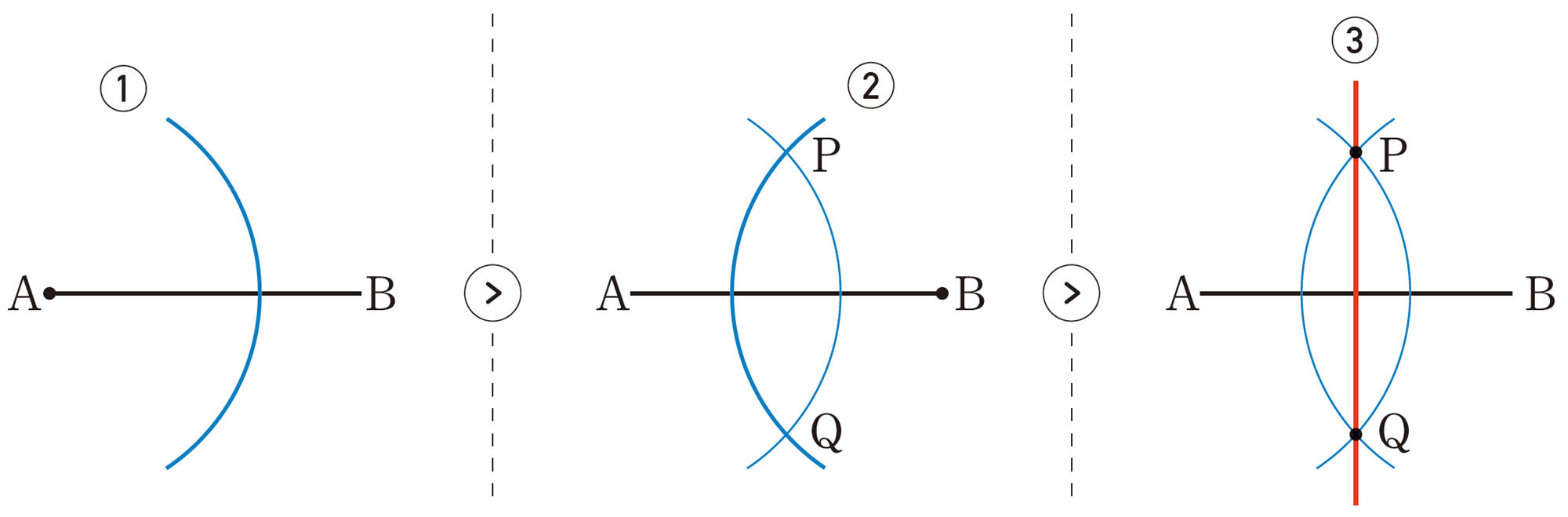
垂直二等分線の作図
Q Question
線分 ABの垂直二等分線を，定規とコンパスだけを使ってかくには，どのようにすればよいでしょうか。
ひし形の対角線が利用できそうだね。
ひし形の対角線には，どんな性質があったかな。
見方・考え方
垂直二等分線がかける根拠を説明できるかな。
定規とコンパスだけを使って図をかくことを，作図 という。
定規は直線を引くためだけに使い，コンパスは円をかいたり，長さをうつしたりするために使う。
例 １ 線分 ABの垂直二等分線を作図しなさい。
考え方 ひし形の一方の対角線は，もう一方の対角線の垂直二等分線になっていることを利用する。
手順
①点 Aを中心として，適当な半径の円をかく。
②点 Bを中心として，① と同じ半径の円をかき，①の円との交点をそれぞれ P，Qとする。
③ P，Qを通る直線を引く。
注意 作図に用いた線は残しておく。また，円は必要な部分だけかけばよい。
問 ３ 適当な線分 ABを引き，線分 ABの垂直二等分線を作図しなさい。また，線分 ABの中点 Mを求めなさい。
<1年p.177>
垂直二等分線の性質
Q Question
右の図で，線分 ABの垂直二等分線 ℓ上に点 Pをとり，Pを中心として半径 PAの円をかいてみましょう。
どんなことがいえるでしょうか。
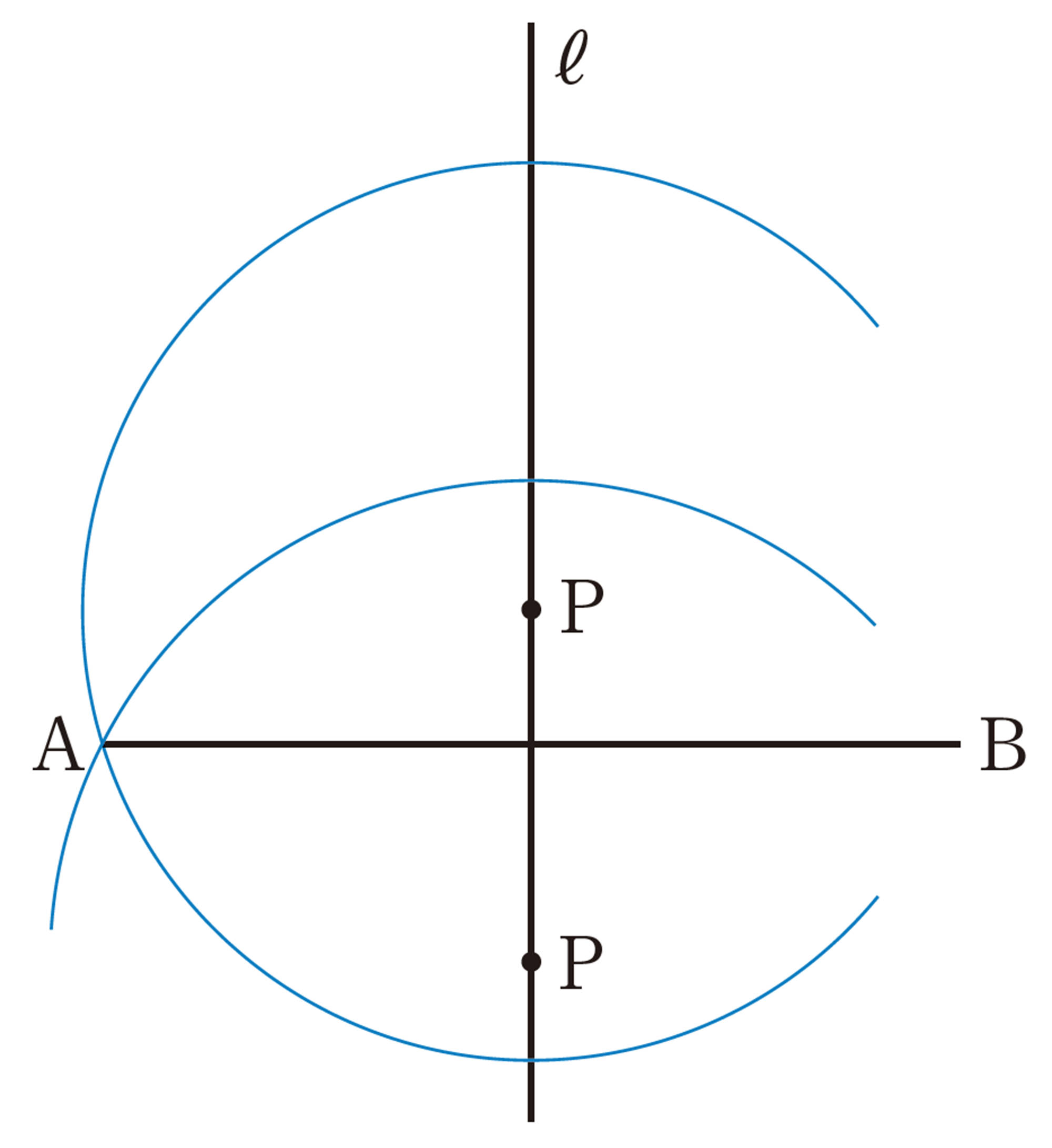
Pをℓ上のどこにとっても，円はすべて点Bを通るね。
PAと PBはいつでも同じ長さになるのかな。
見方・考え方
いろいろな点で調べて，どんな性質があるか見つけられるかな。
右の図のように，線分 ABの垂直二等分線ℓ上の点をPとすると，ℓは線分 ABの対称の軸だから，[mathjax]\(AP=BP\)であることがわかる。
すなわち，線分 ABの垂直二等分線上の点は，線分 ABの両端の点 A，Bから等しい距離にある。
また，2点 A，Bから等しい距離にある点は，線分 ABの垂直二等分線上にある。
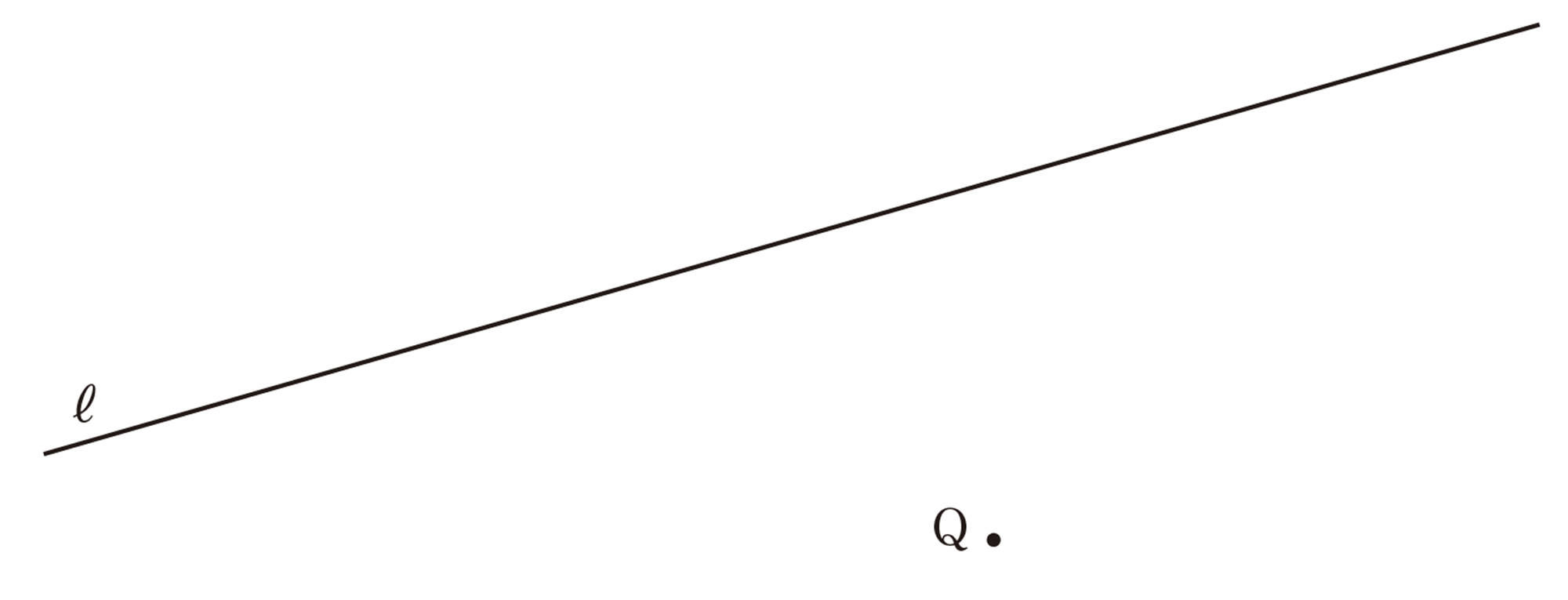
問 ４ 次の図で，2点A，Bから等しい距離にある直線 ℓ上の点 Pを，作図によって求めなさい。
<1年p.178>
垂線の作図
Q Question
直線 ℓ上にない点 Pを通る，ℓの垂線の作図の方法を考えてみましょう。
ひし形の対角線が使えそうだね。
点Pをひし形の頂点と考えればいいのかな。
見方・考え方
垂直二等分線の作図のしかたと同じように考えられるかな。
例 ２ 直線ℓ上にない点 Pを通る，ℓの垂線を作図しなさい。
考え方 直線ℓ上にひし形の頂点をとるには，どうしたらよいかを考える。
手順
① 点Pを中心として，適当な半径の円をかき，ℓとの交点をA，Bとする。
② A，Bを中心として，①と同じ半径の円をかき，その交点を Qとする。
③ P，Qを通る直線を引く。
問 ５ 次の図で，点 Pを通る直線 ℓの垂線を作図しなさい。
<1年p.179>
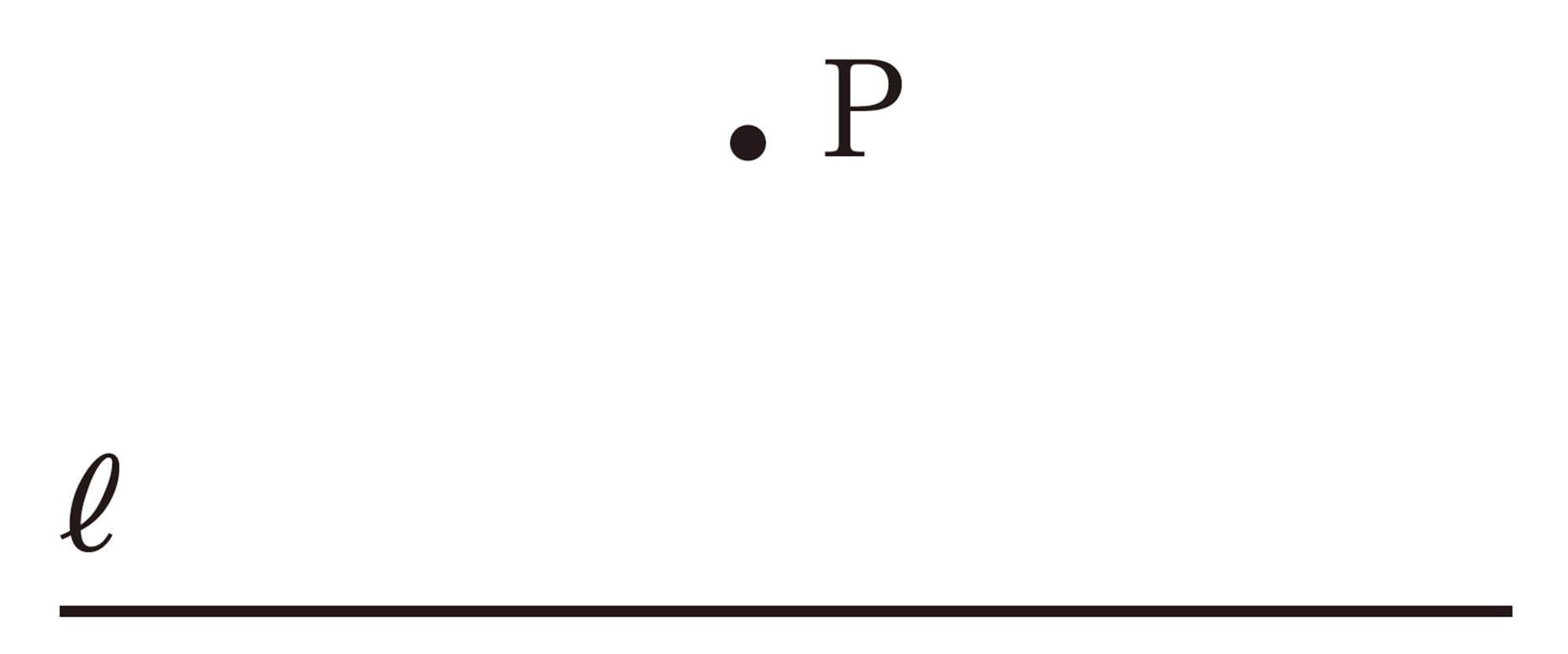
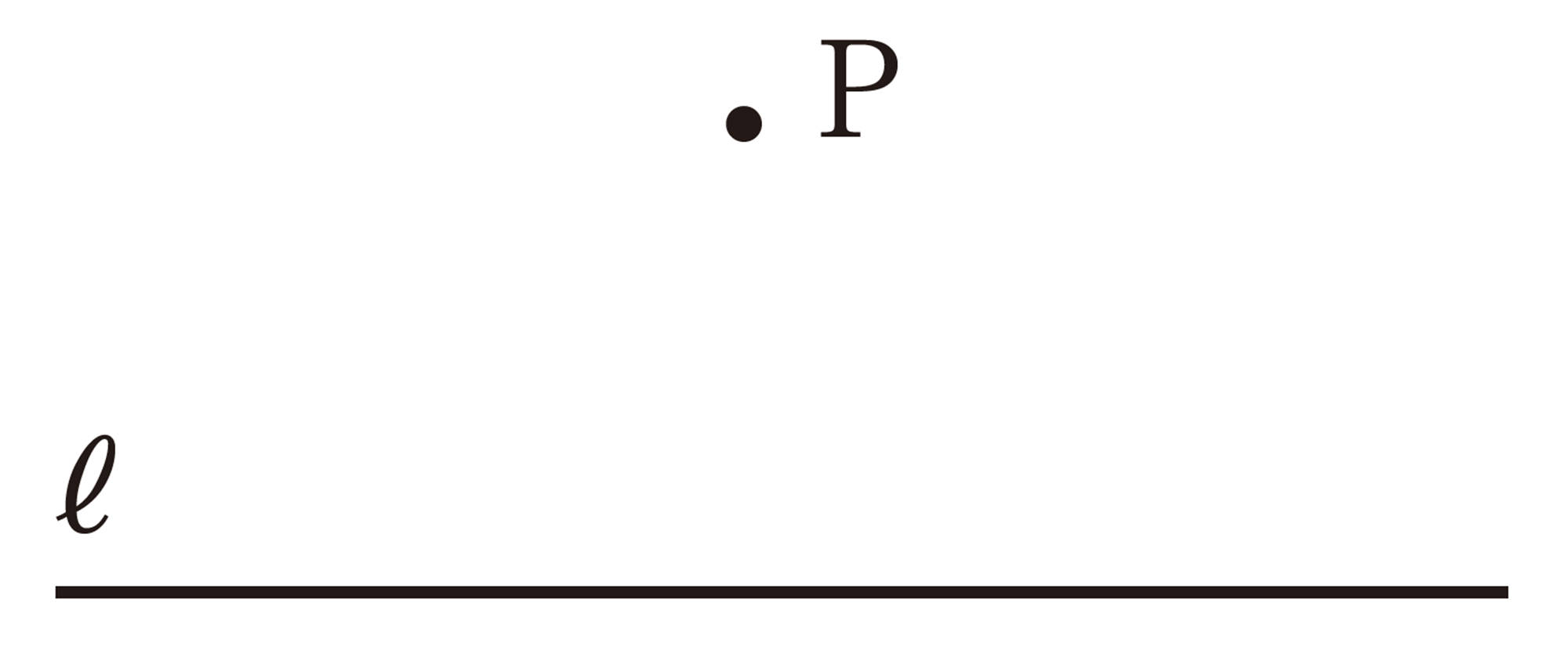
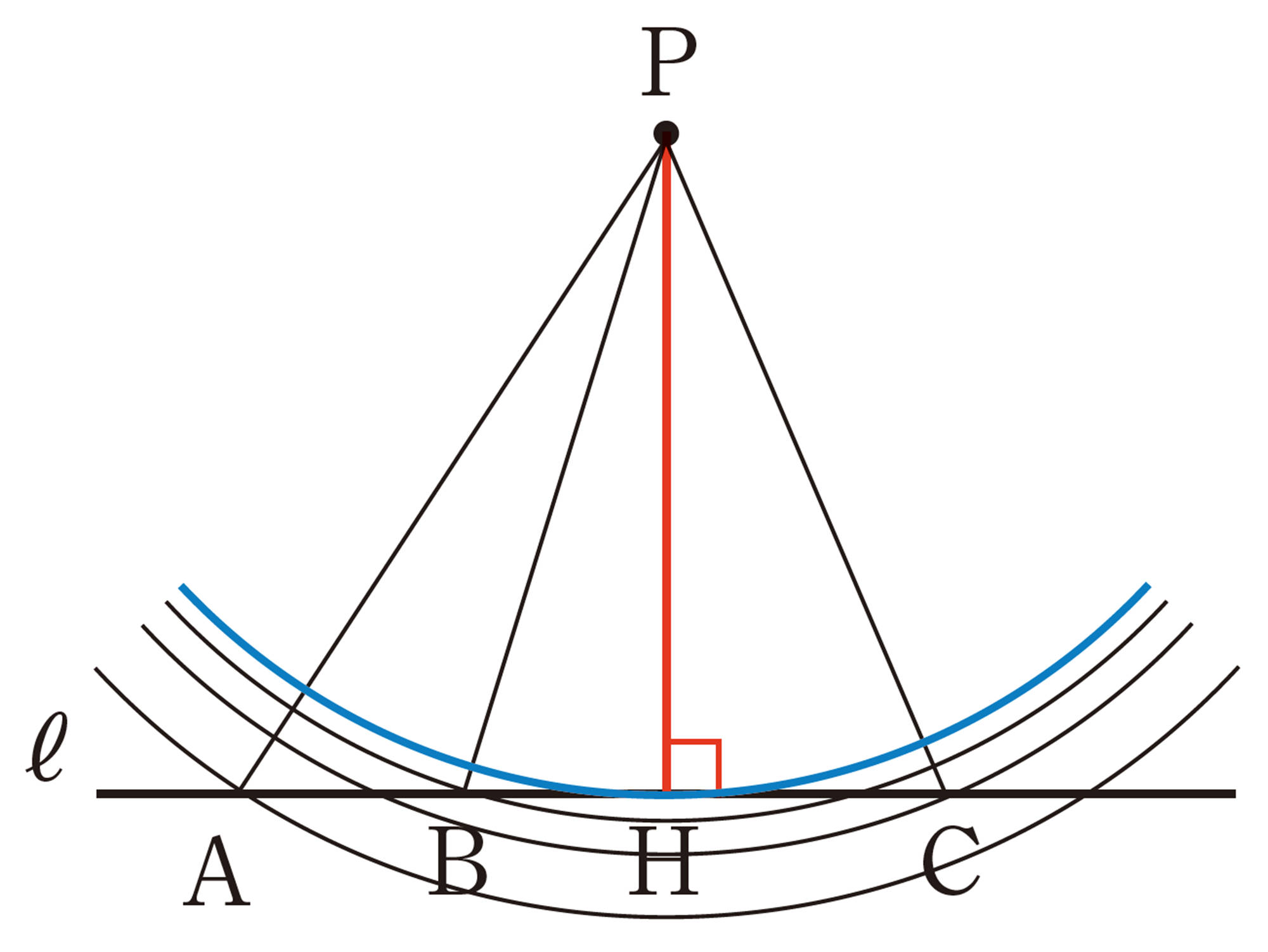
問 ６ 砂浜の P 地点で卵からかえったウミガメの赤ちゃんが，海に向かって歩いていきます。もっとも短い距離で海に着くには，どのようなコースを進めばよいですか。ただし，海岸線は直線とします。
右の図のように，直線 ℓ上にない点 Pからℓに垂線を引き，ℓとの交点を Hとするとき，線分 PHの長さを，点 Pと直線 ℓとの距離という。
問 ７ 右の図で，点 Aと直線ℓとの距離は何mmですか。
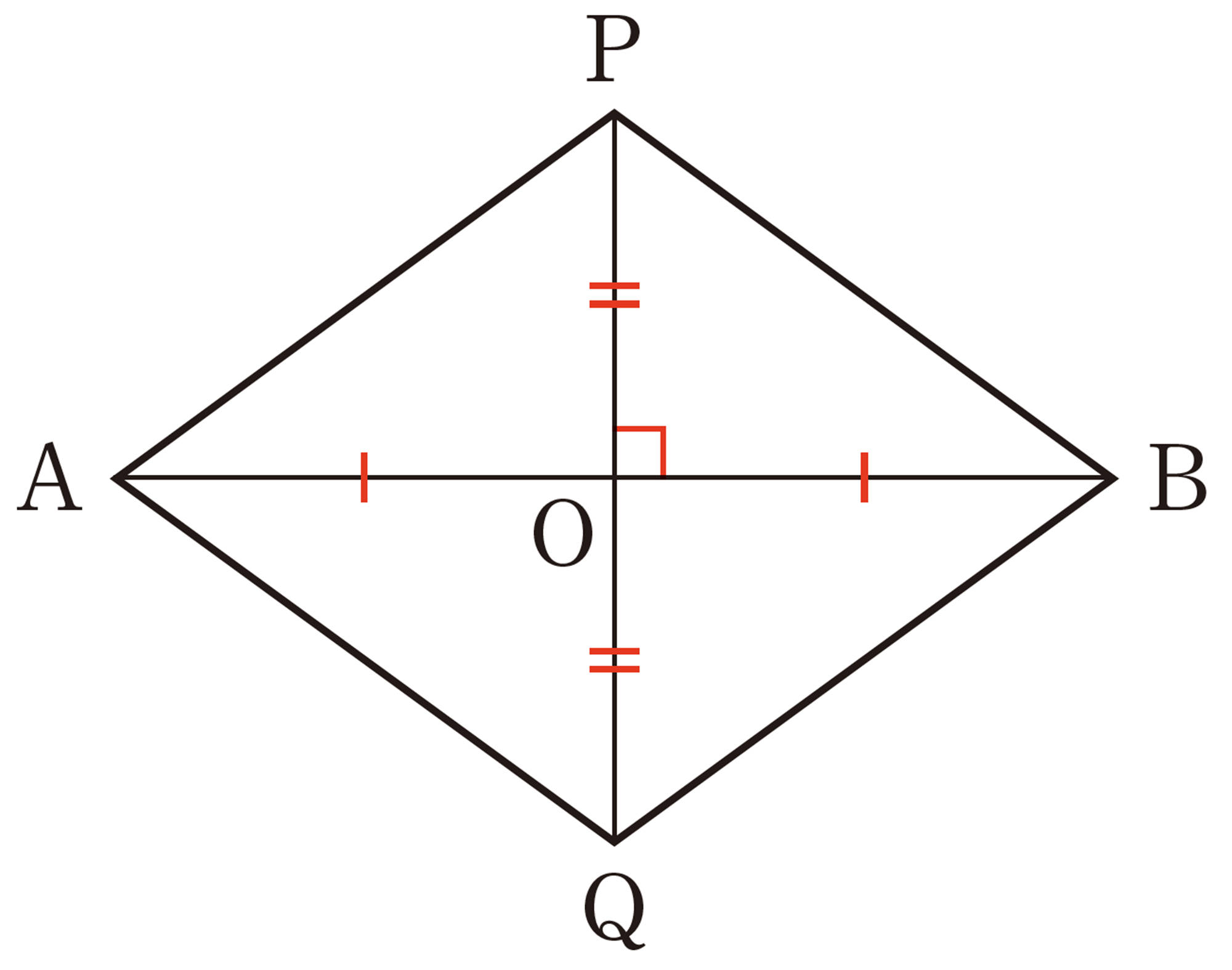
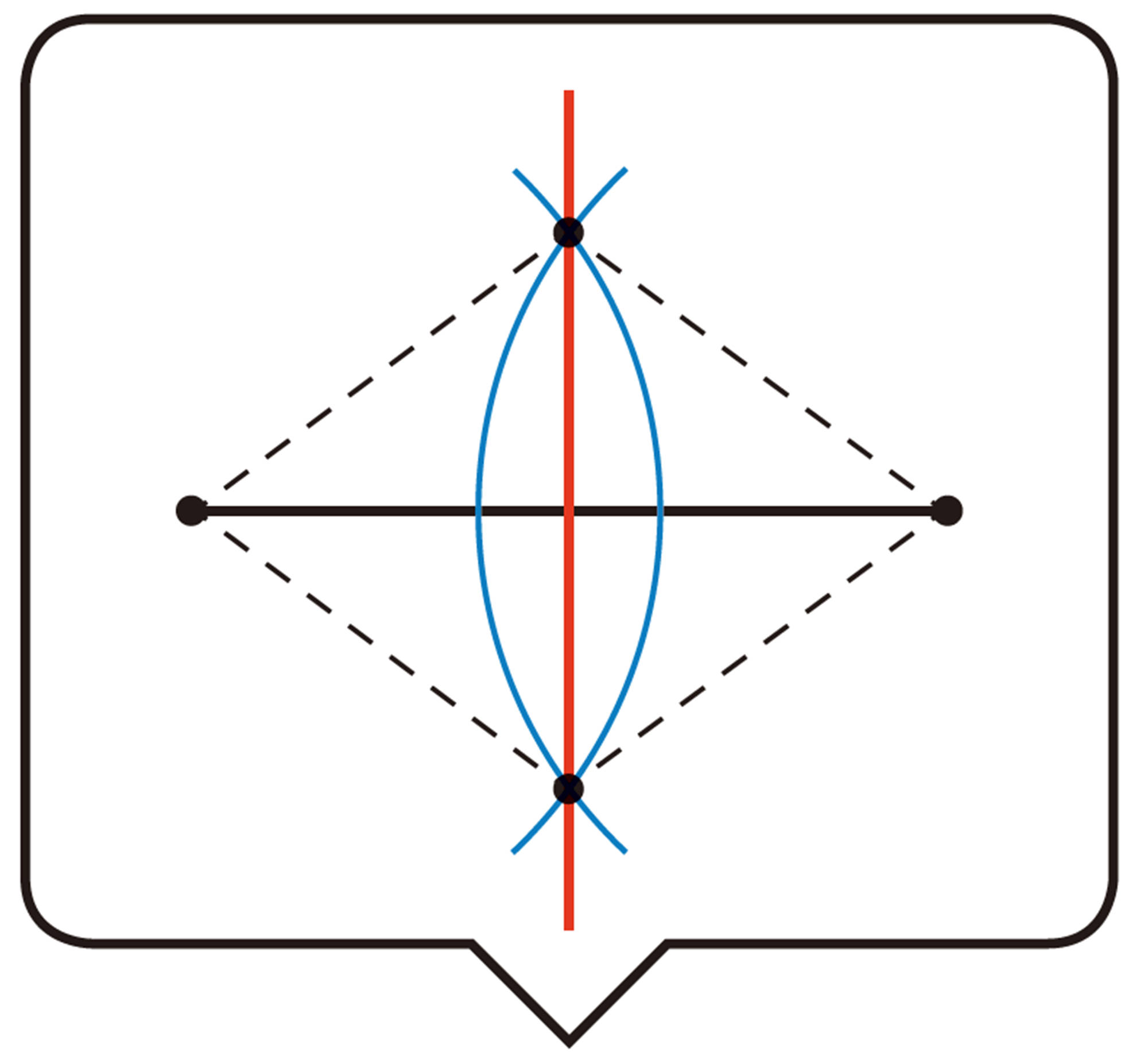
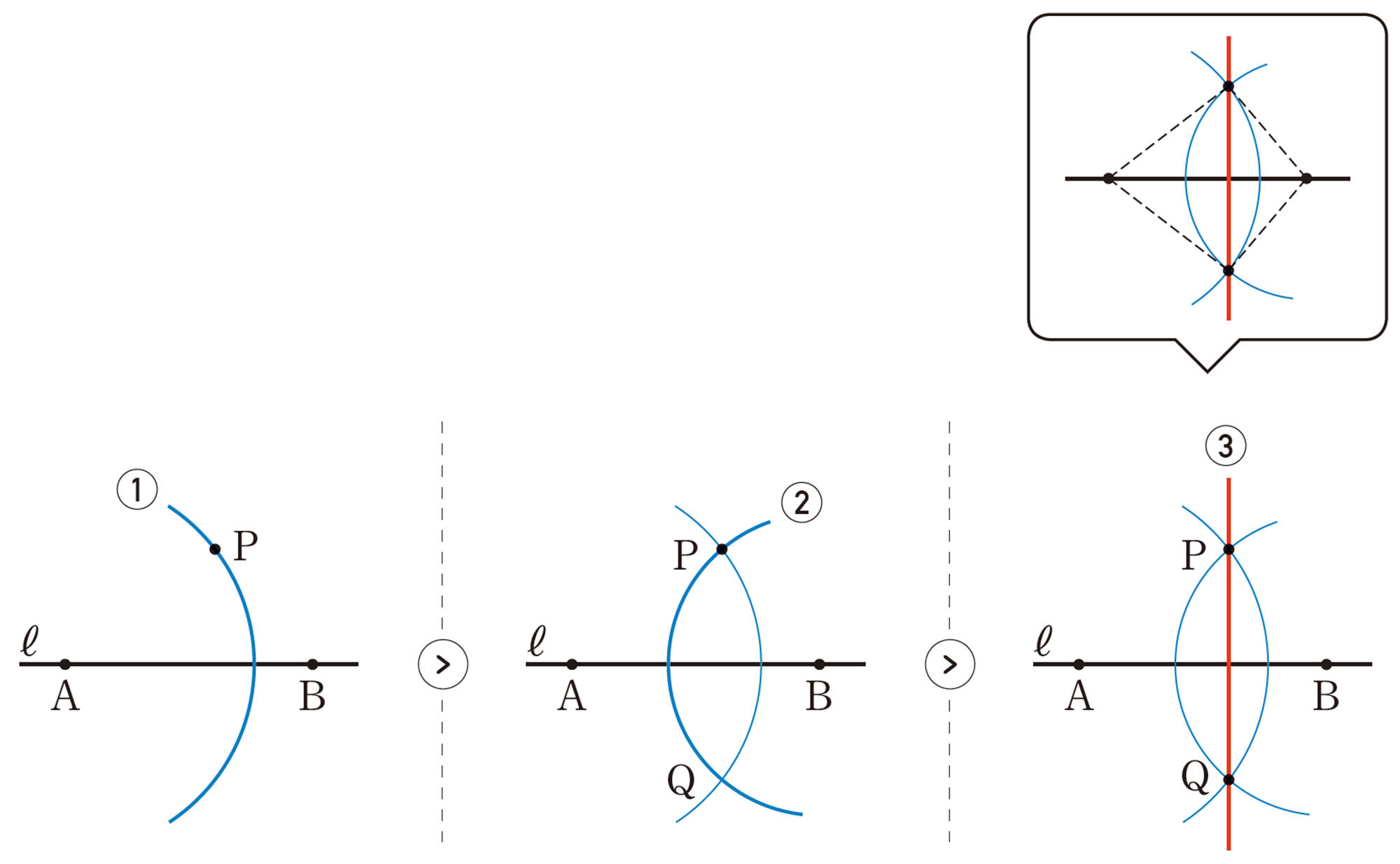
たこ形を利用した垂線の作図
右の図のように，となり合う2組の辺がそれぞれ等しい四角形を，たこ形という。
たこ形は，一方の対角線を対称の軸とする線対称な図形であり，対応する辺の長さや対応する角の大きさはそれぞれ等しい。
右のたこ形では，対角線 AB が対称の軸になる。右のたこ形 PAQBでは，2本の対角線の交点をOとするとき，対応する点P，Qを結ぶ線分PQは，ABと垂直に交わり，点 Oで2等分される。
[mathjax]\(AB \bot PQ\)，[mathjax]\(PO=QO\)
<1年p.180>
例 ３ 178ページの例2のような垂線を，たこ形を利用して作図しなさい。
手順
①ℓ上に適当な2点 A，Bをとり，Aを中心として，半径 APの円をかく。
②Bを中心として，半径 BPの円をかき，①の円との交点のうち，Pでない方をQとする。
③P，Qを通る直線を引く。
問 ８ 次の図で，点 Qを通る直線 ℓ の垂線を，例3のように，たこ形を利用して作図しなさい。
どんなことがわかったかな
対角線が[mathjax]\(90^{\circ}\)で交わるひし形やたこ形を利用して，垂直二等分線や垂線を作図すると，[mathjax]\(90^{\circ}\)の角をかくことができます。
