<1年p.162>
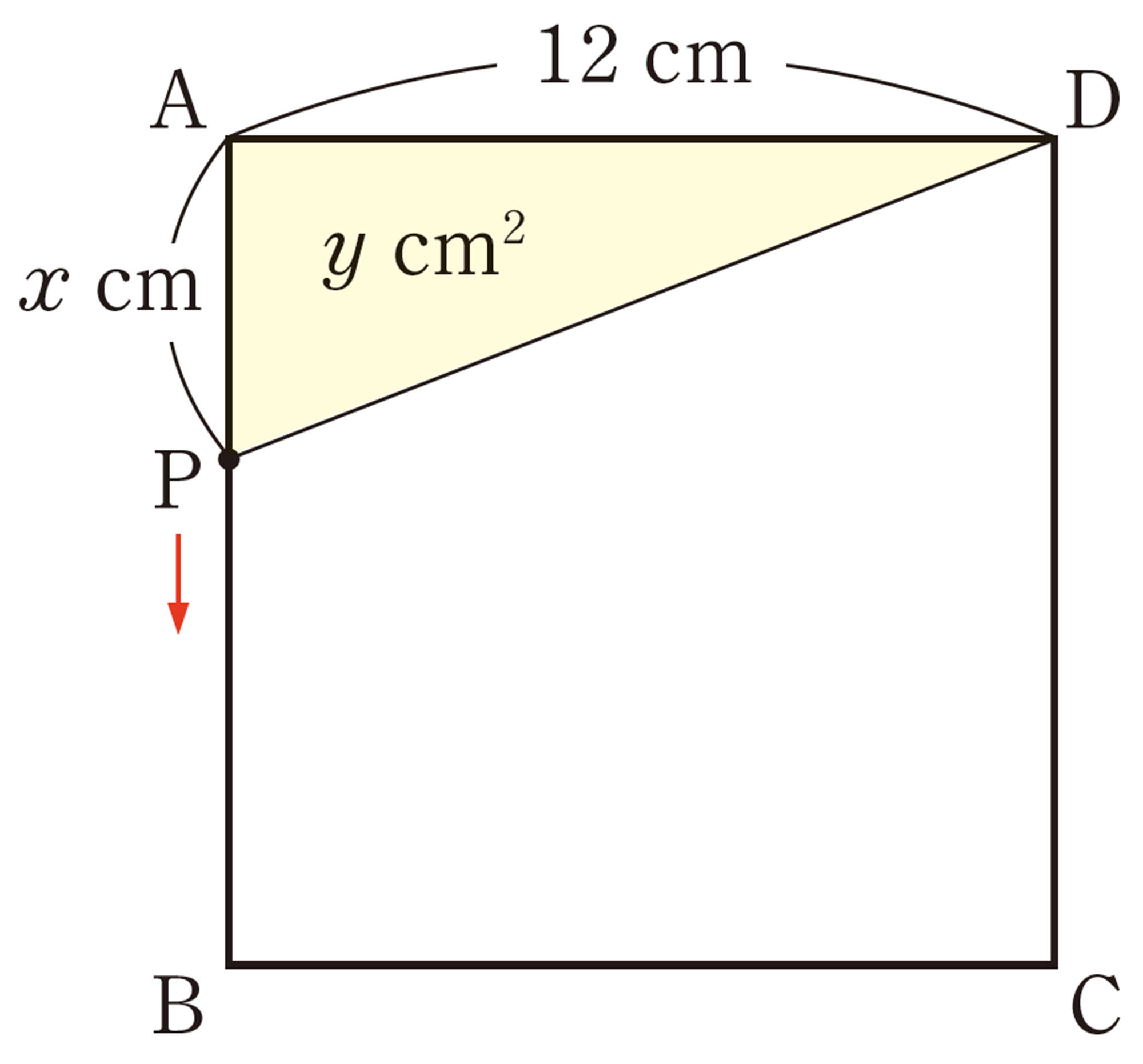
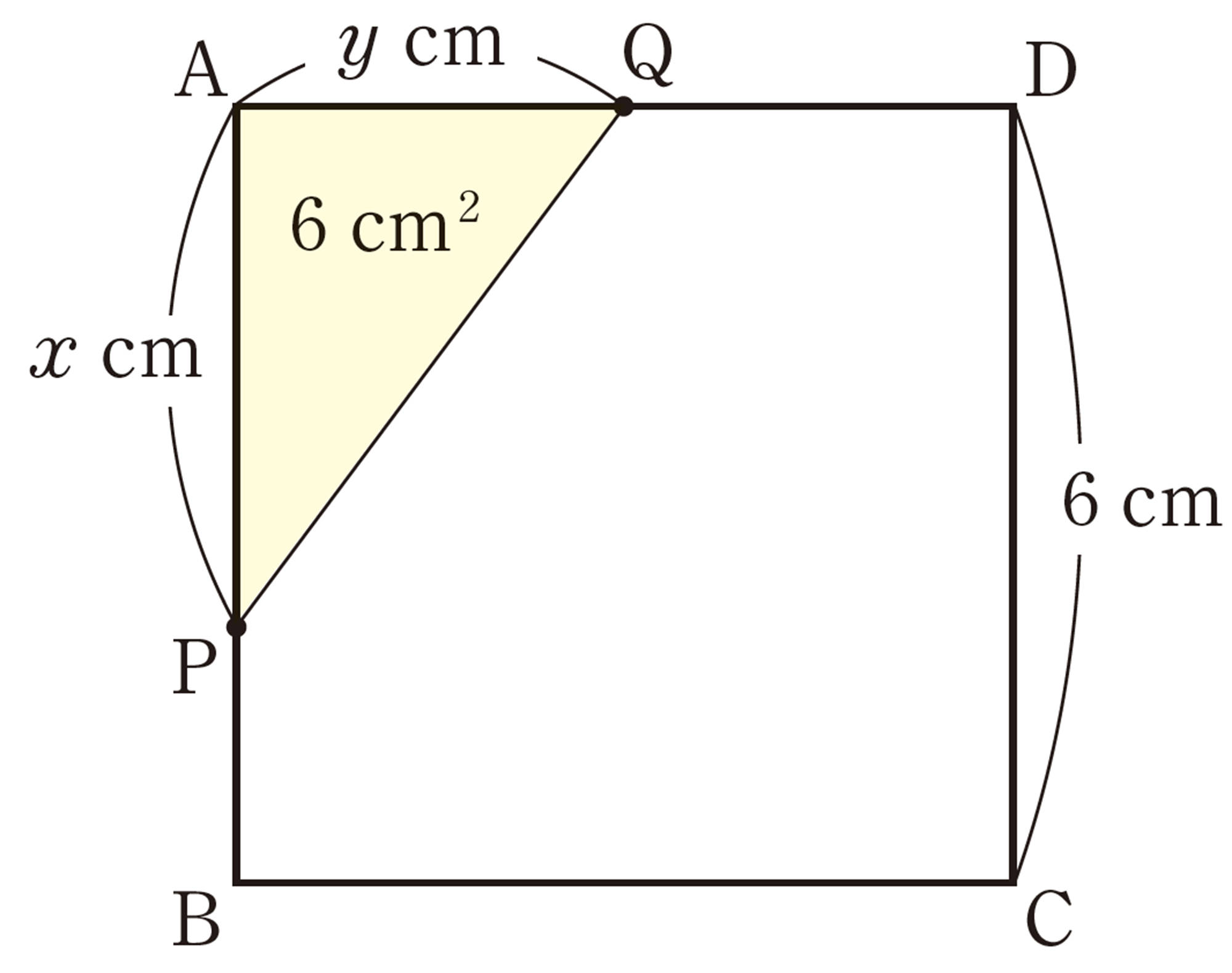
図形における利用
例 ３ 右の図のような正方形 ABCD があります。点 P は，辺 AB 上を A から B まで動きます。 AP の長さをx cm，三角形 APD の面積をy cm² とすると，yはxに比例しますか。それとも反比例しますか。
解答
三角形APDの面積は，
[mathjax] \(\hspace{27pt}y= \dfrac{1}{2}\times x\times 12 \)
より， [mathjax] \(y=6x\)
これは比例の式であるから， [mathjax] \(y \) は [mathjax] \(x \) に比例する。
答 比例する
問 ３ 例3について，次の問いに答えなさい。
⑴ 点 P が A から5 cm 動いたときの三角形 APDの面積を求めなさい。
⑵ xとyの変域をそれぞれ求めなさい。
問 ４ 右の図のような正方形ABCDがあります。点Pは辺AB上を，点Qは辺AD上を，三角形APQの面積がつねに6 cm² であるように動きます。APの長さがx cmのときのAQの長さをy cmとして，次の問いに答えなさい。
⑴ yをxの式で表しなさい。
⑵ yはxに比例しますか。それとも反比例しますか。
⑶ xとyの変域をそれぞれ求めなさい。
<1年p.163>
グラフの利用
例 ４ 陸さんと妹が同時に家を出発して，駅までの1200m の道のりを歩きます。2人が，家を出てからx分間に歩いた道のりをymとします。次の図は，陸さんについて，xとyの関係をグラフに表したものです。このグラフから，陸さんの歩く速さを求めなさい。
解答
グラフより， 10 分で800m 歩いていることがわかるから，
[mathjax]\(\mathsf{(道のり)}\div \mathsf{(時間)}=\mathsf{(速さ)}\)
より，
[mathjax]\(800\div 10= 80\)
したがって， 陸さんの歩く速さは， 分速80 m である。
答 分速80 m
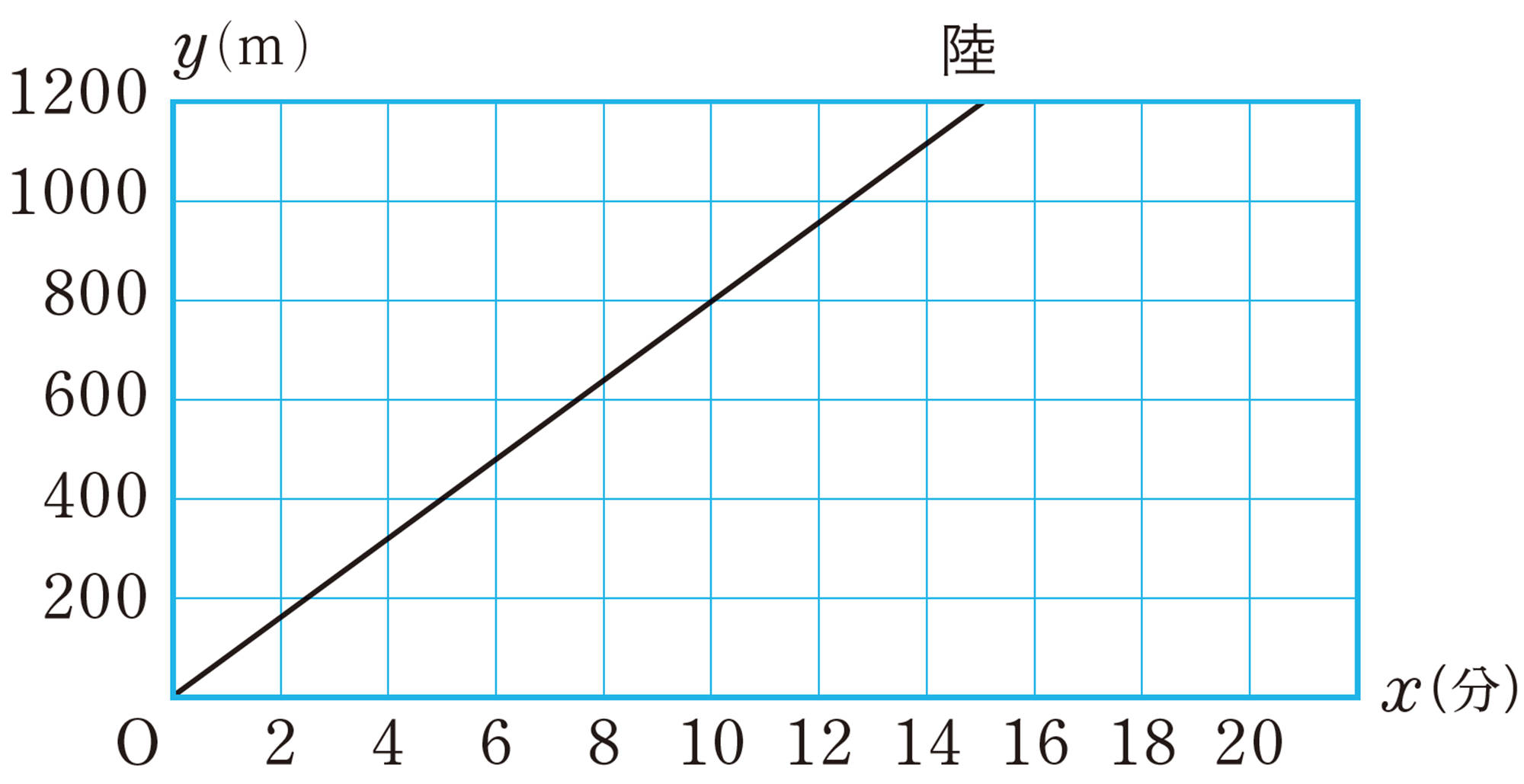
問 ５ 例4について，次の問いに答えなさい。
⑴ 陸さんについて，yをxの式で表しなさい。
⑵ 妹が分速60 mで歩くとするときのグラフを上の図にかき入れ，yをxの式で表しなさい。また，妹は陸さんが駅に着いてから何分後に駅に着きますか。
⑶ 陸さんが駅に着いたとき，妹は駅の手前何m の地点にいますか。
⑷ 陸さんは，10時の電車に乗るために，その10分前に駅に着こうと思います。家を何時何分に出発すればよいですか。
▲トライ 例4で，妹が分速100 m で歩くとしたときのグラフをかいてみよう。また，そのグラフと陸さんのグラフを利用して，問題をつくってみよう。
どんなことがわかったかな
身のまわりには，比例や反比例の関係になっていることがらがあります。また，比例や反比例の関係とみなすことで，問題を解決できることがあります。
<1年p.164>
確かめよう 4節 比例と反比例の利用
１ 同じくぎ20本の重さを調べたところ，50 g でした。くぎx 本の重さをy g として，次の問いに答えなさい。
⑴ yをxの式で表しなさい。
⑵ このくぎ300本を用意するためには，何 g を量り取ればよいですか。
樹木の成長に見られる比例 Tea Break
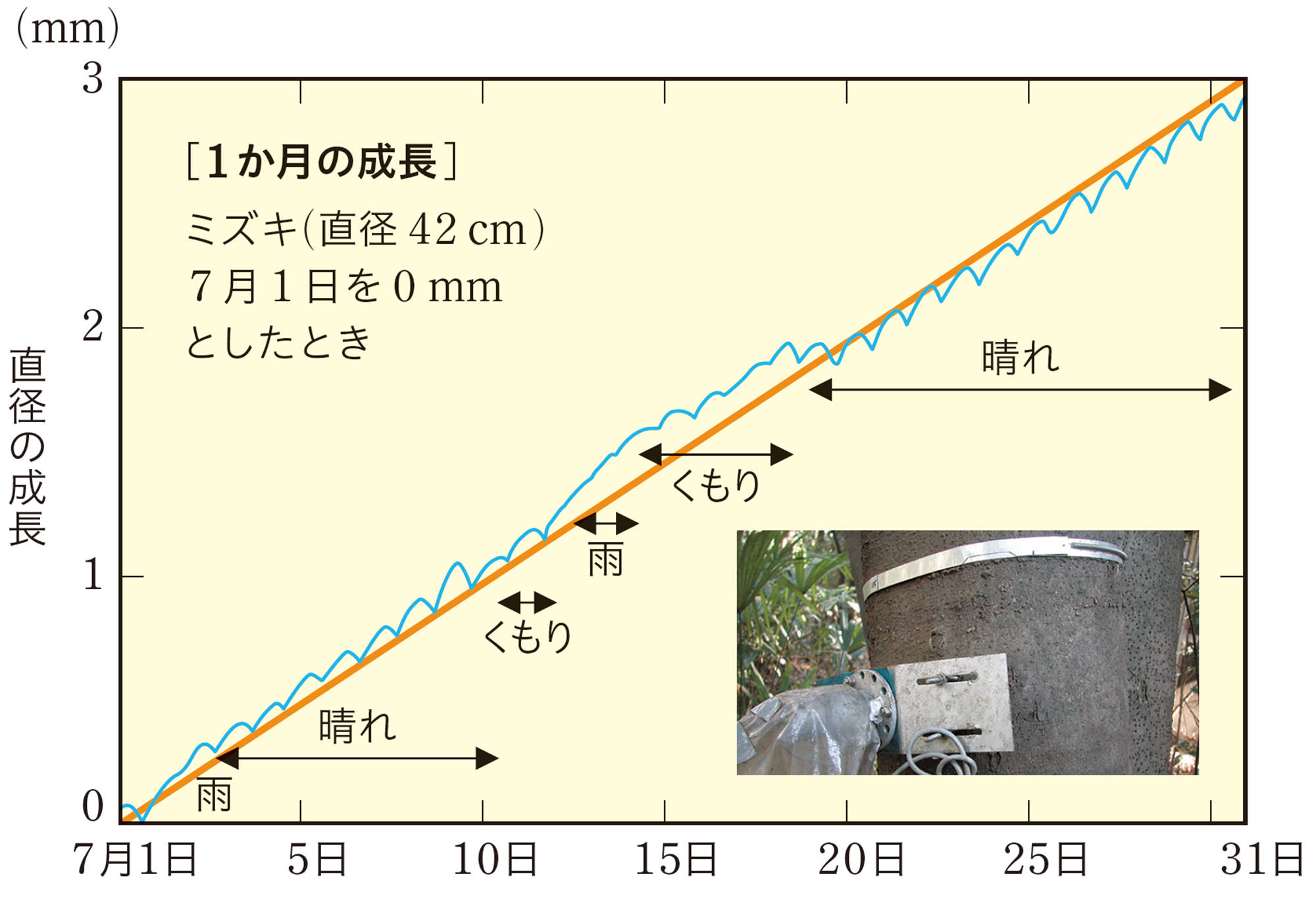
樹木の幹の太さの成長はとてもゆっくりしているため，私たちの目には成長しているかどうか，すぐにはわかりません。幹の太さの成長を測るためには，右下の写真のように，両端をスプリングでとめたアルミ製のバンドを幹に巻きつけ，バンドの重なりがずれる位置によって成長を測定します。
右下のグラフは，7 月の1 か月間に，1 本のミズキの幹の太さがどれだけ成長したかを記録したものです。これを見ると，天候によって成長の差はあるものの，グラフはほぼ直線で，幹の太さは1 日に約[mathjax]\(0.1\)mm 成長していることが読み取れます。
樹木の成長は，季節や樹齢(樹木の年齢)によって変化しますが，このように，ある一定の期間の中では，幹の太さの成長は，日数にほぼ比例するとみなすことができます。
<1年p.165>
4章 「比例と反比例」を学んで
できるようになったこと 身のまわりの課題へ P.168，169，288
ともなって変わる2つの数量x，yがあって，xの値を決めるとyの値がただ1つ決まるとき，yはxの関数であると判断できる。
2つの数量xとyの関係が比例や反比例であるかどうか判断できる。
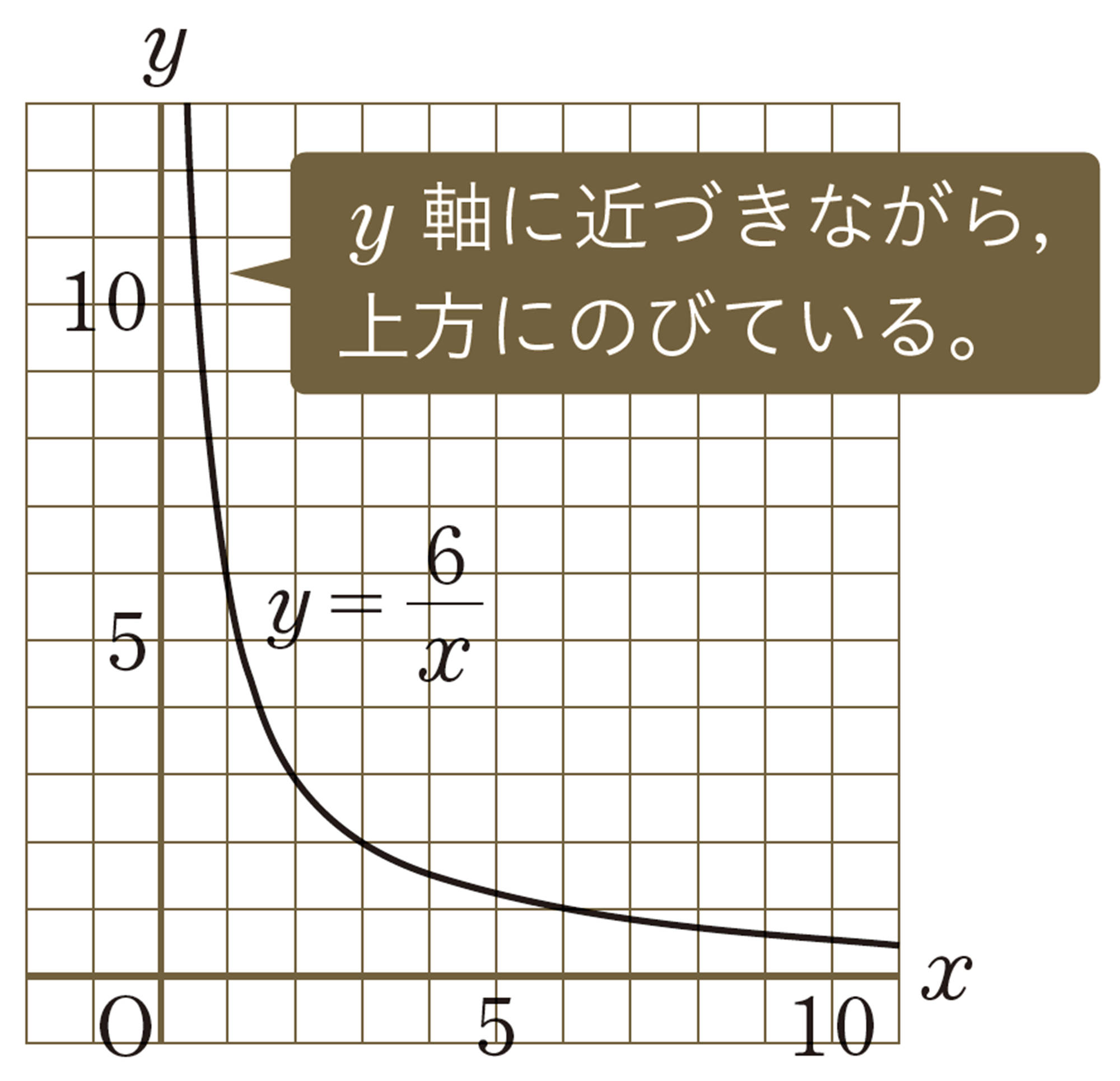
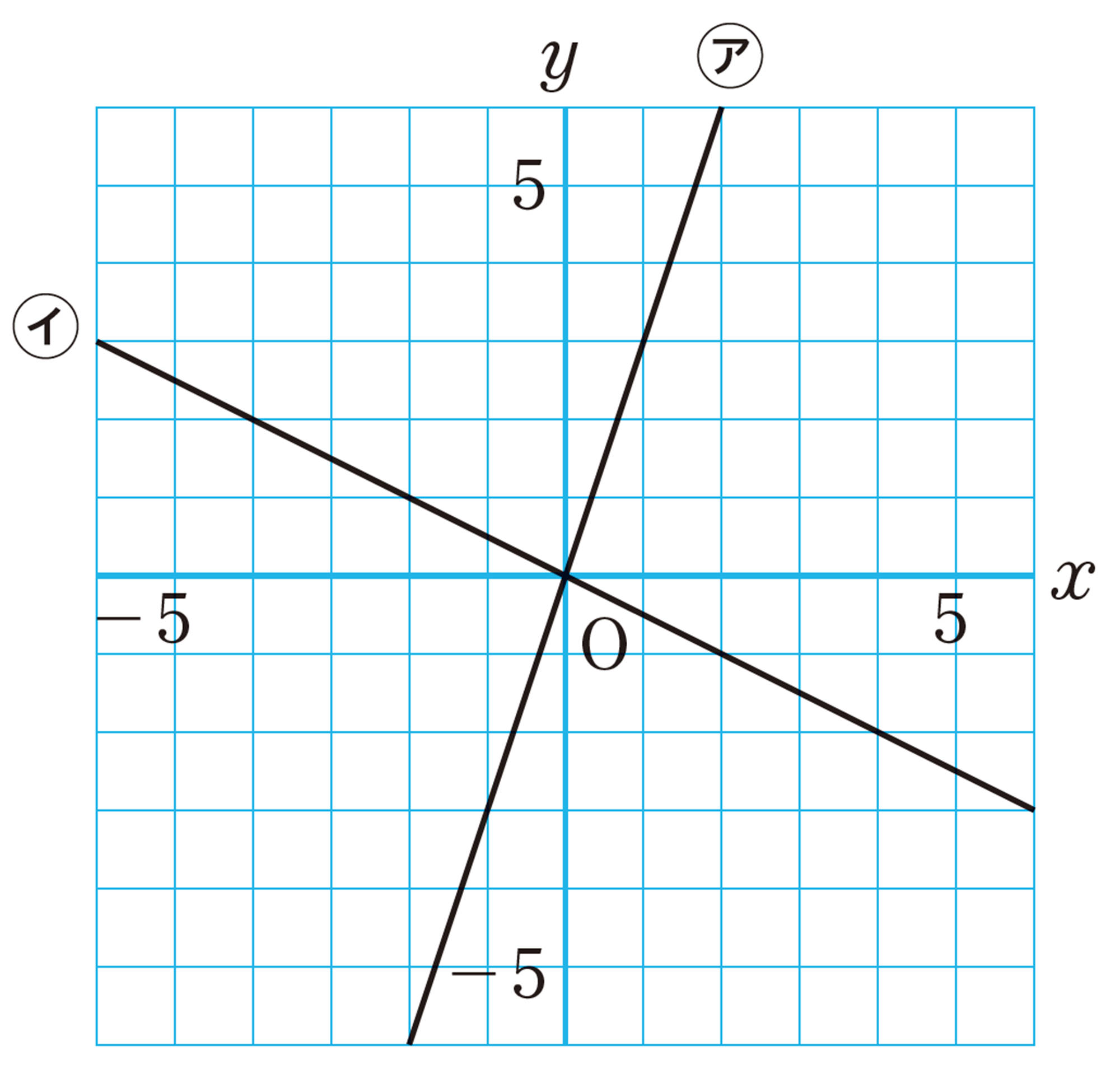
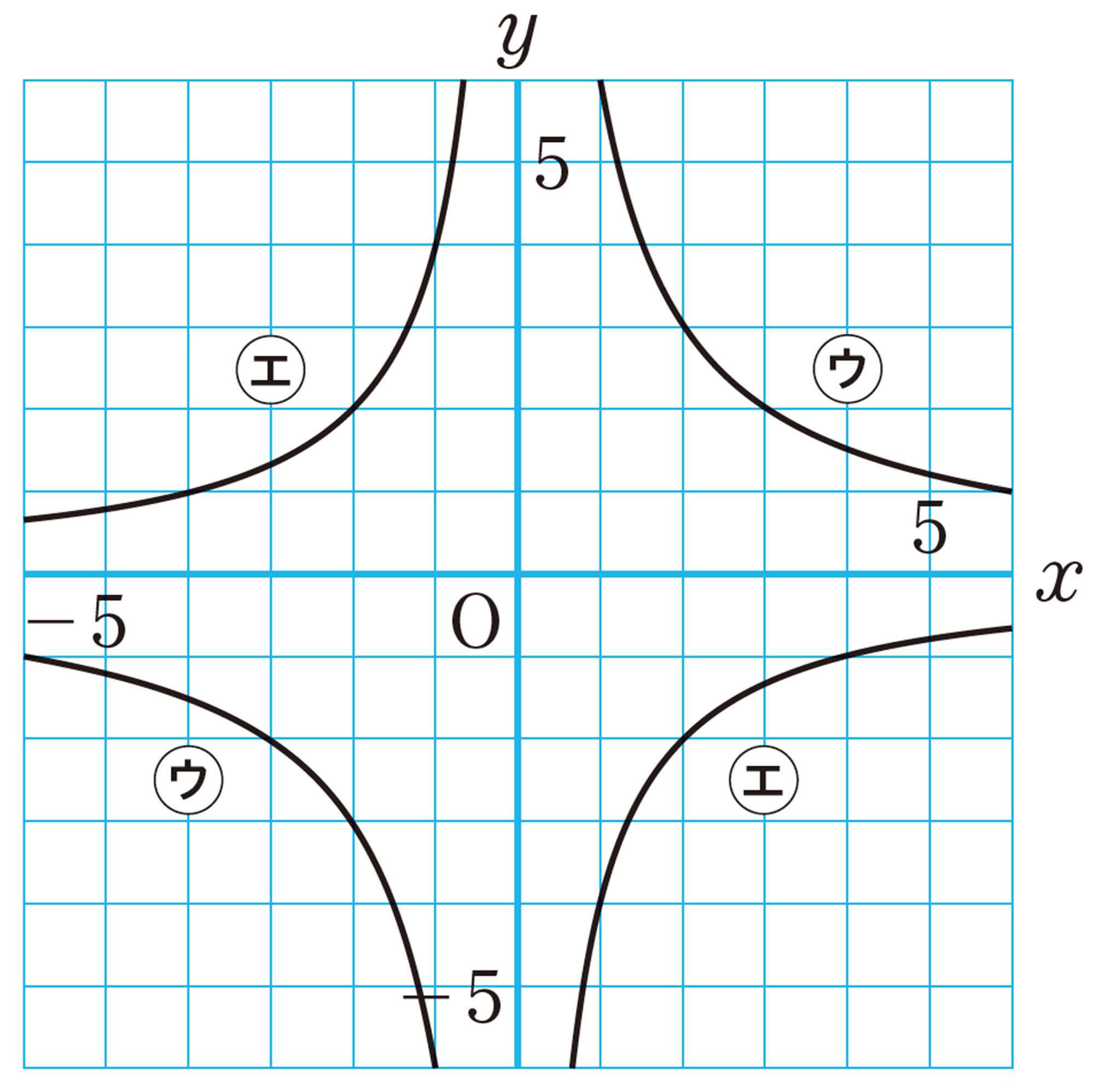
比例のグラフが原点を通る直線になること，反比例のグラフが双曲線になることがわかり，それを座標軸上に表したり，そこから式を読み取ったりすることができる。
身のまわりや数学の中から見つけた問題を，比例や反比例とみなして，その特徴を見つけて解決に利用することができる。
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない 双曲線の先端は？
関数[mathjax]\(y=\dfrac{6}{x}\)では，
[mathjax]\(x=0.1\)のとき[mathjax]\(\hspace{10pt}y=60\)
[mathjax]\(x=0.01\)のとき[mathjax]\(\hspace{5pt}y=600\)
[mathjax]\(x=0.001\)のとき[mathjax]\(y=6000\)
︙
のように，[mathjax]\(x \gt 0\)のとき，xの値を0に近づけていくと，yの値は限りなく大きくなっていきます。
したがって，右の図で，グラフの左側の先端は， y軸に近づきながら限りなく上方にのびていることがわかります。
[mathjax]\(x=10\text{，}100\text{，}1000\text{，}10000\text{，}\cdots\)と，xの値を大きくしていくとき，反比例のグラフについてどんなことがわかるでしょうか。
<1年p.166>
４章のまとめの問題 解答 P.305 基本
１ 次の[mathjax]\(\boxed{\phantom{000}}\)にあてはまることばをいいなさい。
⑴ ともなって変わる2つの変数x，yがあって，xの値を決めると，それに対応するy の値がただ1つ決まるとき，yはxの[mathjax]\(\boxed{\phantom{000}}\)であるという。
⑵ 比例を表す関数[mathjax]\(y=-3x\)では，xの値が1ずつ増加すると，それに対応するyの値は[mathjax]\(\boxed{\phantom{000}}\)ずつ[mathjax]\(\boxed{\phantom{000}}\)する。
⑶ 反比例を表す関数[mathjax]\(y=\dfrac{12}{x}\) で，定数12のことを[mathjax]\(\boxed{\phantom{00000}}\)という。
２ 次の関数について，yをxの式で表しなさい。また，[mathjax]\(x=4\)のときのyの値を求めなさい。
⑴ yはxに比例し，[mathjax]\(x=6\)のとき[mathjax]\(y=9\)
⑵ yはxに反比例し，[mathjax]\(x=-2\)のとき[mathjax]\(y=2\)
３ ハイキングコースを時速3 km で歩きます。出発してからx時間歩いたときの道のりをy km とするとき，次の問いに答えなさい。
⑴ yをxの式で表しなさい。
⑵ xの変域を[mathjax]\(0 \leqq x \leqq 4\)とするとき，yの変域を求めなさい。
４ 細い管を水の中に立てると，水は管の中を上がります。次の表は，管の直径がx mm のときの水の上がる高さをy mmとして，xとyの関係をまとめたものです。
下の問いに答えなさい。
⑴ yをxの式で表しなさい。
⑵ 直径[mathjax]\(0.5\) mm の管では，水は何 mm 上がると考えられますか。
<1年p.167>
５ 真央さんは，「反比例とは，一方が増加すると，もう一方が減少する関係だよ」と言っています。このことは正しいですか。正しくない場合には，その理由を例をあげて説明しなさい。
応用
１ 次の図の㋐～㋓は，比例や反比例のグラフです。それぞれ比例定数を求め，y をx の式で表しなさい。
２ 右の図のような長方形 ABCD があります。点 P は，Bを出発して，秒速2 cm で辺 BC 上をCまで動きます。 点 P が B を出発してからx 秒後の三角形 ABP の面積をy cm² として，次の問いに答えなさい。
⑴ 点 P が B を出発してから3秒後の三角形ABPの面積を求めなさい。
⑵ yをxの式で表しなさい。
⑶ xとyの変域をそれぞれ求めなさい。
<1年p.168>
4章のまとめの問題 活用
１ リサイクル活動の1つに，エコキャップ運動があります。これは，ペットボトルのキャップをゴミとして焼却せずに，リサイクルするものです。この運動は，環境によいだけでなく，ペットボトルのキャップ約430個で10円のワクチン代として寄付できるため，途上国の子どもたちの力になることもできる活動です。
芽衣さんの学校では，生徒や先生からペットボトルのキャップを集め，それを寄付することにしました。
⑴ 芽衣さんの学校では，大量のペットボトルのキャップが集まりました。一つひとつ数えることなく，およその個数を知るにはどのようにすればよいか，その方法と理由を説明しなさい。
⑵ 1人分のワクチンは，20円です。ペットボトルのキャップの個数をx個，寄付できるワクチンをy 人分としたとき，yをxの式で表しなさい。
⑶ 100人分のワクチンを寄付するには，約何個のペットボトルのキャップが必要ですか。
＞＞ 関連する職業・仕事 ［ボランティア団体，医師］
<1年p.169>
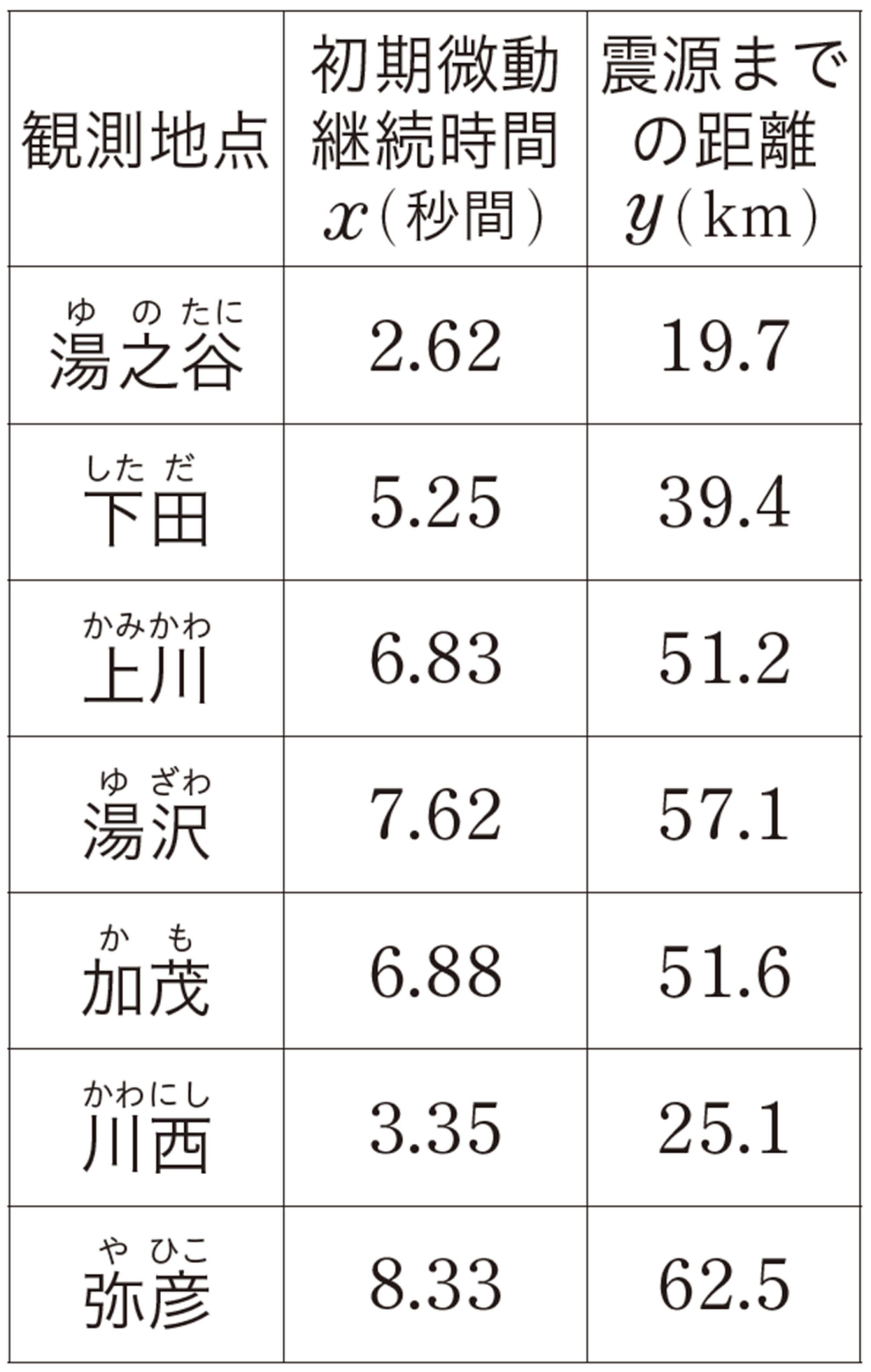
深めよう 震源までの距離は？
地震が起きると，ふつう，はじめにカタカタ…という小さなゆれがしばらく続き，次にユサユサ…という大きなゆれがやってきます。はじめの小さなゆれの続く時間を初期微動継続時間といい，震源までの距離と深い関係があることが知られています。
② 県内の長岡では，初期微動継続時間が[mathjax]\(2.15\)秒間でした。震源までの距離は約何 kmと考えられるでしょうか。
地震を目の前で観測することはほぼ不可能です。「震源の位置を特定するためには何を調べればよいのか」という大きな課題の解決に力を注いだ研究者の1人が，大森房吉(1868〜1923)です。
彼は1899年(明治32年)に，初期微動継続時間から震源までの距離を求める「大森公式」を発表しました。現在，彼の研究は，緊急地震速報や電車の早期地震警報システムなどにも活用されています。
