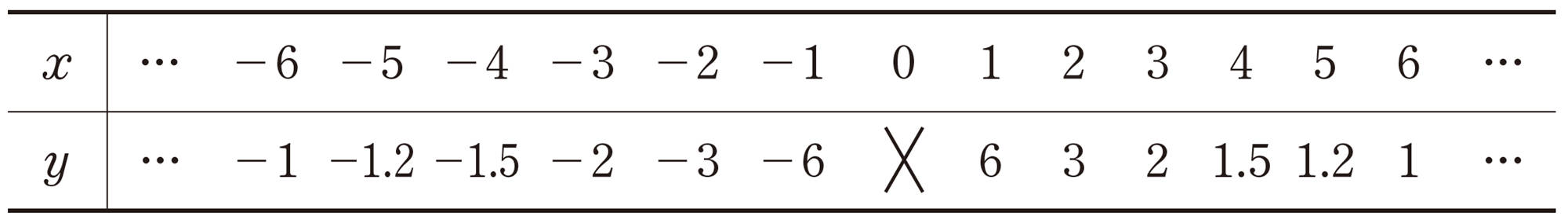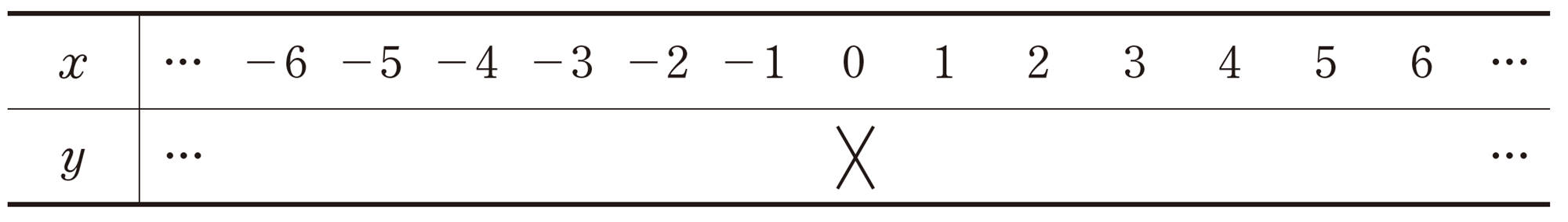<1年p.151>
２ 反比例のグラフ
Q Question
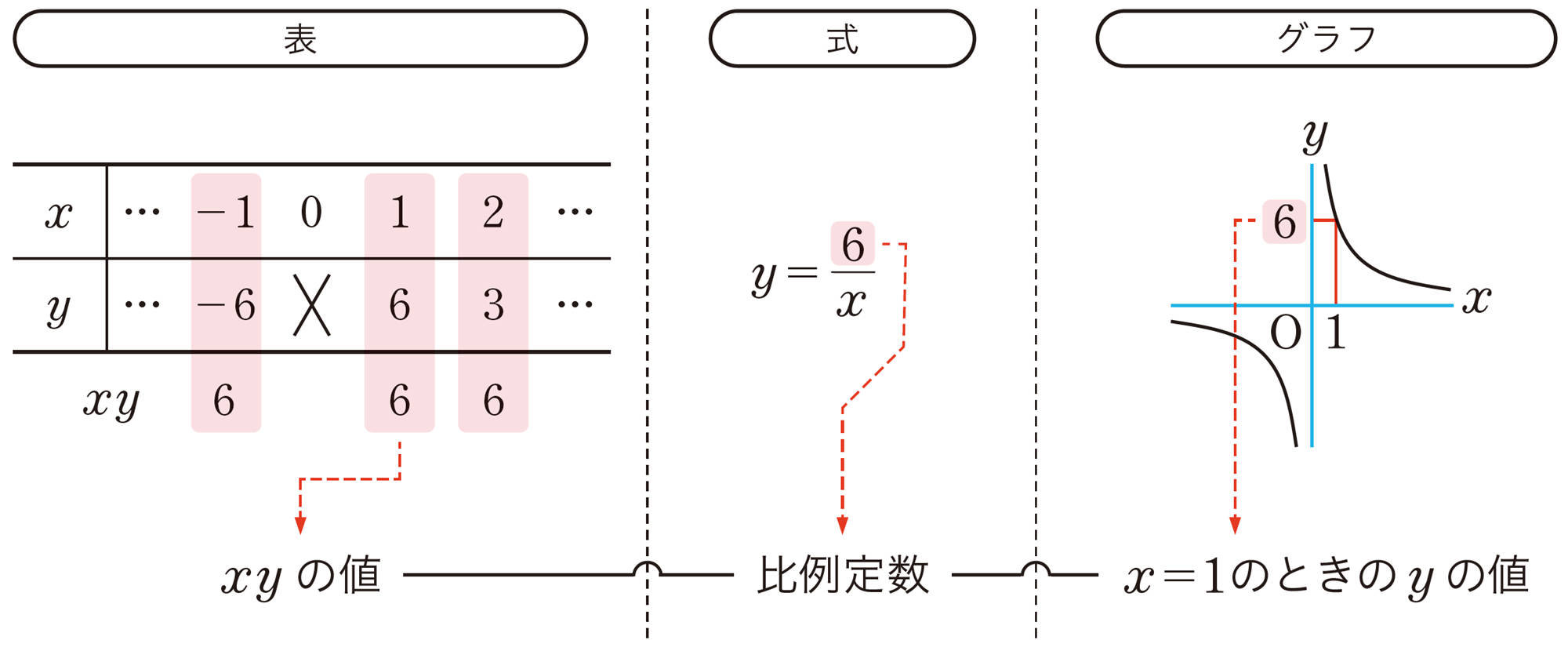
関数[mathjax]\(y=\dfrac{6}{x}\)について，次のような表をつくることができます。関数[mathjax]\(y=\dfrac{6}{x}\)のグラフがどんな形になるか予想してみましょう。
比例のように，直線になるのかな。
[mathjax]\( x=0\) のとき y の値がないけど，グラフはどうなるのかな。
見方・考え方
比例と同じように，細かく点をとって考えられるかな。
目標 ▷ 反比例のグラフについて調べよう。
問 １ 【Q】の表の対応するx，yの値の組を座標とする点を，次の図にかき入れなさい。
<1年p.152>
問 ２ 前ページの【Q】で，xの値を[mathjax] \(-6\)から6まで[mathjax]\(0.5\)おきにとり，それらに対応する点を，前ページの図にかき入れなさい。
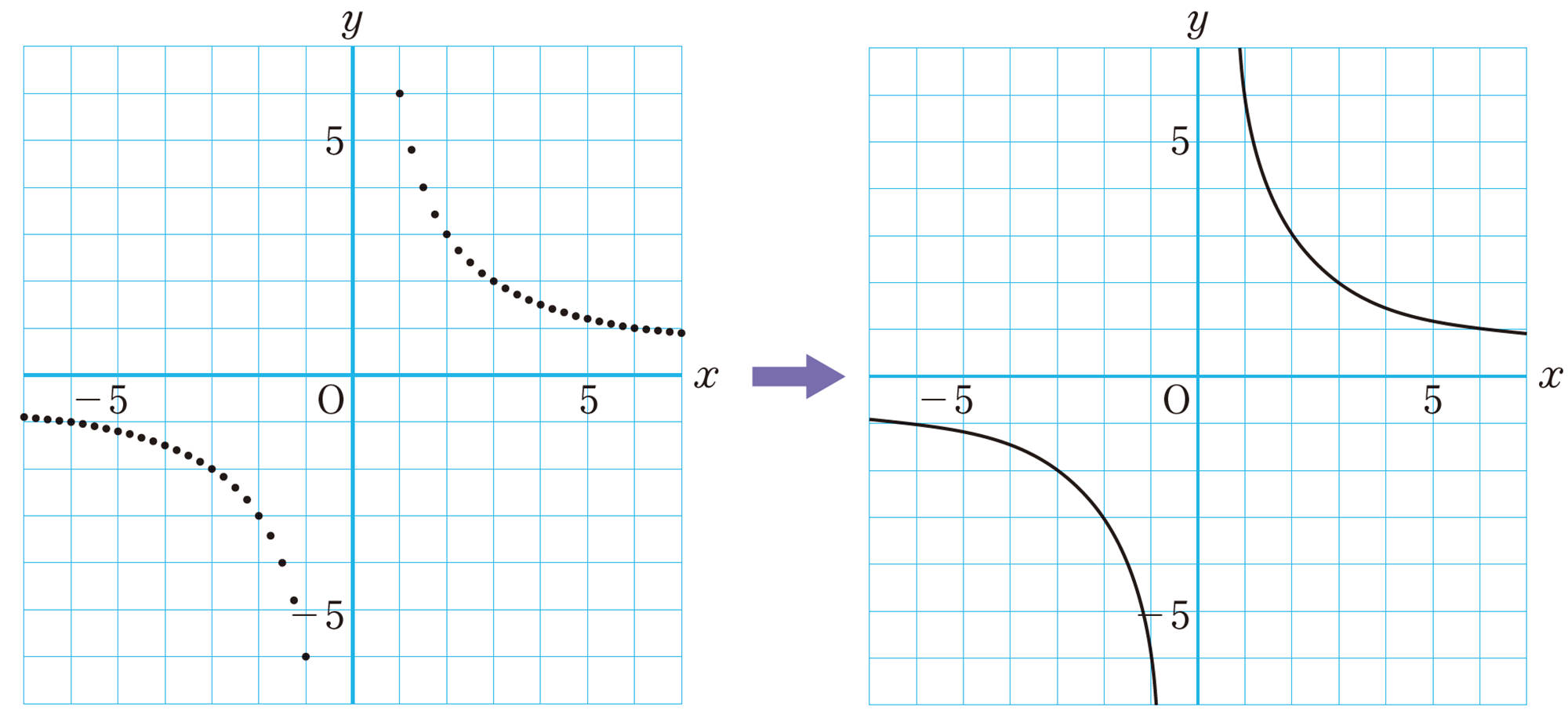
左下の図のように，[mathjax]\(y=\dfrac{6}{x}\)が成り立つx，yの値の組を座標とする点をさらに多くとっていくと，点の集合は右下の図のような2つのなめらかな曲線になる。
この曲線が，関数[mathjax]\(y=\dfrac{6}{x}\)のグラフである。
このような1組の曲線を 双曲線 という。
問 ３ 関数[mathjax]\(y=-\dfrac{6}{x}\)のグラフを，x，yの対応の表をつくり，右上の図にかき入れなさい。
問 ４ 関数[mathjax]\(y=\dfrac{6}{x}\)と関数[mathjax]\(y=-\dfrac{6}{x}\)のそれぞれについて，次の問いに答えなさい。
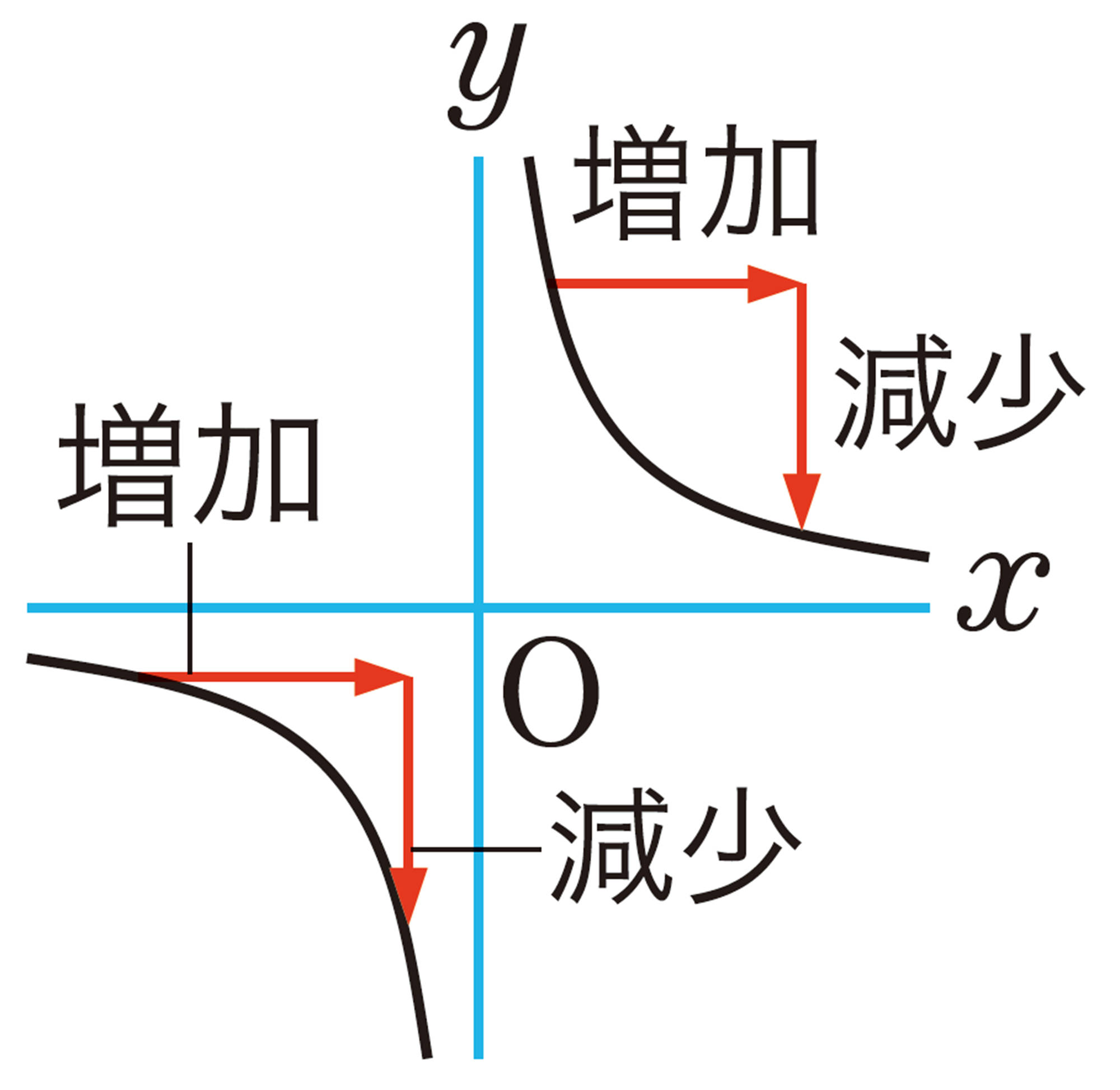
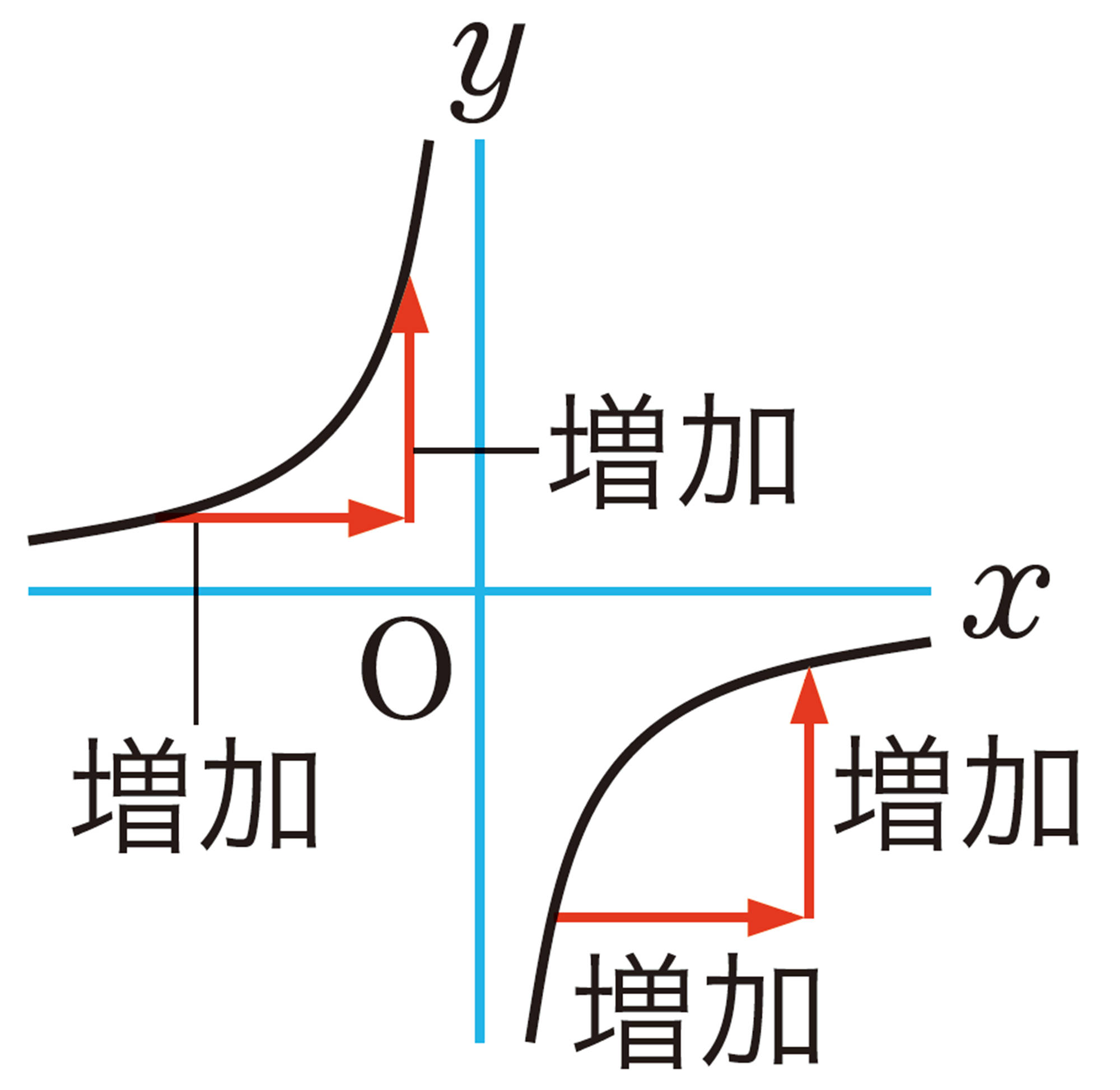
⑴ [mathjax]\(x \gt 0\)のとき，xの値が増加すると，yの値は増加しますか。それとも減少しますか。
⑵ [mathjax]\(x \lt 0\)のとき，⑴と同じことを調べなさい。
<1年p.153>
これまで調べたことから，反比例のグラフについて，次のようにまとめることができる。
反比例のグラフ
反比例を表す関数[mathjax]\(y=\dfrac{a}{x}\) のグラフは，双曲線である。
❶ [mathjax]\(a \gt 0\)のとき
[mathjax]\(x \lt 0\)，[mathjax]\(x \gt 0\)のそれぞれの変域で，xの値が増加すると，y の値は減少する。
❷ [mathjax]\(a \lt 0\)のとき
[mathjax]\(x \lt 0\)，[mathjax]\(x \gt 0\)のそれぞれの変域で，xの値が増加すると， y の値も増加する。
関数[mathjax]\(y＝\dfrac{6}{x}\)を例として ，反比例の表，式，グラフの関係を示すと，次のようになる。
どんなことがわかったかな
反比例のグラフは，変域を負の数まで広げると双曲線になります。
次の課題へ！
身のまわりで，比例や反比例の関係にあることがらは，ほかにもあるのかな？
P.155
<1年p.154>
確かめよう 3節 反比例
１ 面積24 cm² ，底辺x cmの平行四辺形の高さをy cmとするとき，次の問いに答えなさい。
⑴ xとyの関係を，次の表にまとめなさい。
⑵ yをxの式で表しなさい。
⑶ yはxに反比例するといえますか。
２ yはxに反比例し，[mathjax]\(x=-2\)のとき[mathjax]\(y=9\)です。yをxの式で表しなさい。また，[mathjax]\(x=6\)のときのyの値を求めなさい。
３ 関数[mathjax]\(y=\dfrac{12}{x}\)のグラフを，次の図にかき入れなさい。
