<1年p.135>
2節 比例
変域を負の数まで広げたらどうなる？
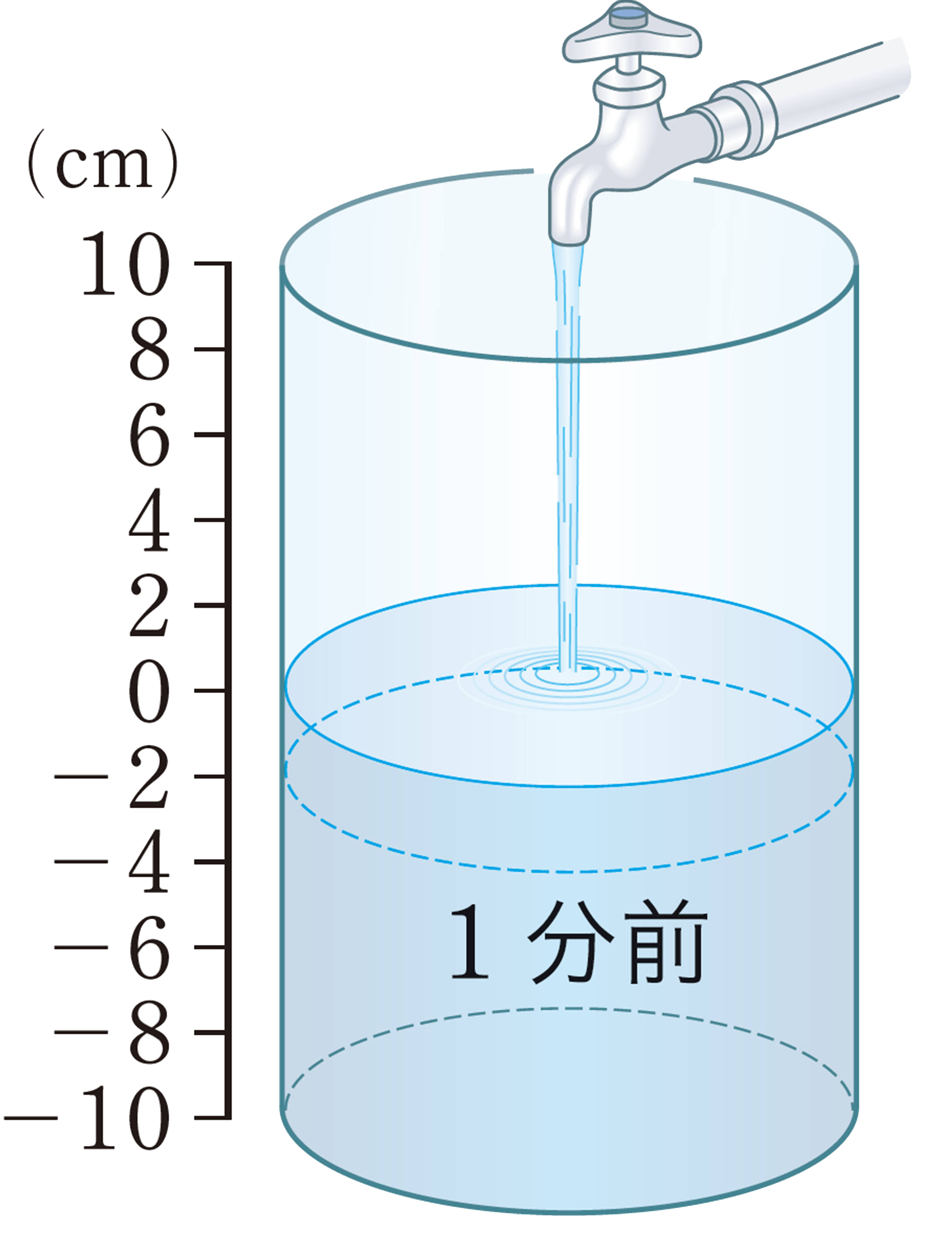
変域を負の数まで広げて，水そうに水を入れるときの時間と水位の関係を調べてみよう。
小学校でも比例の学習をしたけど，0と正の数だけだったね。
数の範囲を負の数まで広げて考えられるかな。
【１】 右の図のように，深さ20cm の空の水そうに1分間に2cm ずつ水位が増加するように，水を入れています。現在の水位を基準の0cm とし，x分後の水位をycm とします。
xとyの関係を，次の表にまとめ，気づいたことを話し合いましょう。
[mathjax] \(-1\)分は，現在より1分前を表しているね。
xが負の数のときでも，表はつくれそうだね。
変域を負の数まで広げても，比例しているように見えるけど…。
次の課題へ！
変域を負の数まで広げても，比例といえるのかな？
P.136
<1年p.136>
１ 比例と式
Q Question
前ページの1について，次のことを考えてみましょう。
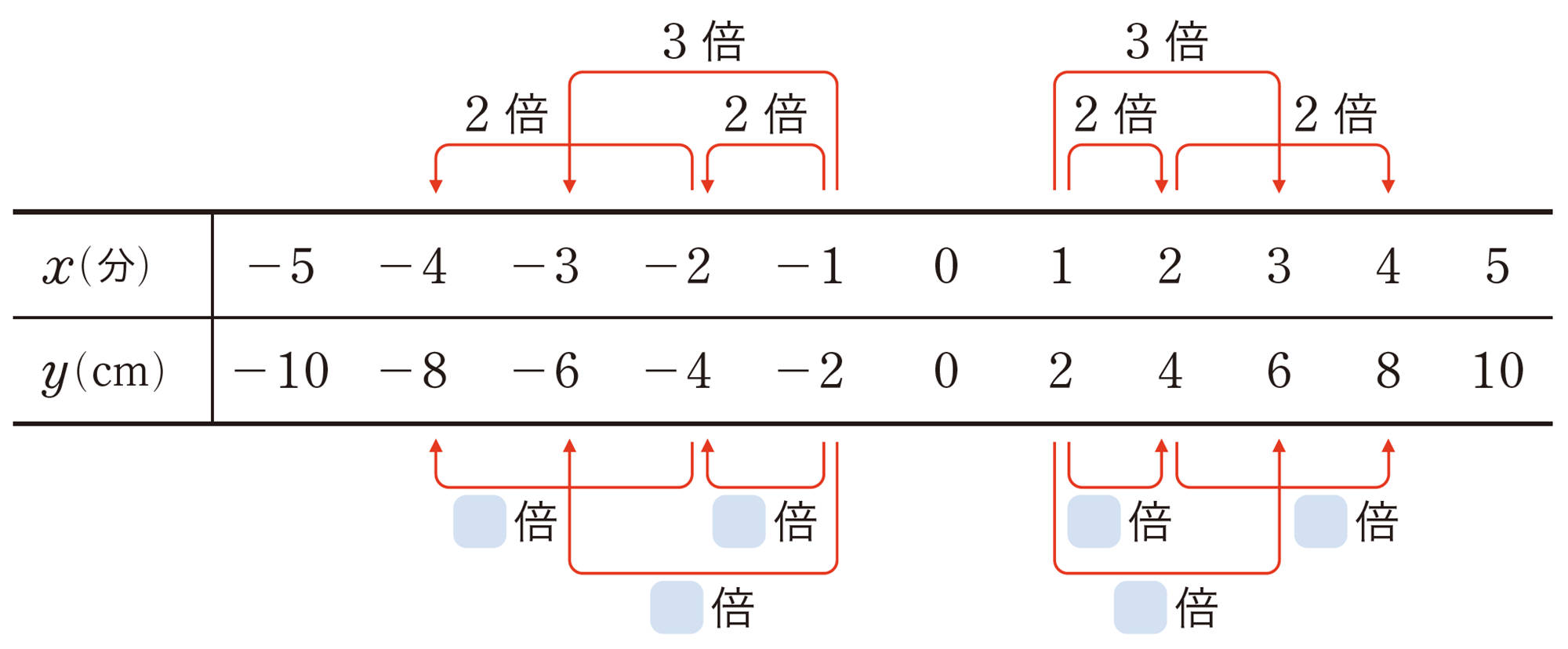
⑴ xの値が2倍，3倍，…になると，yの値はどうなるでしょうか。[mathjax]\(x \gt 0\)，[mathjax]\(x \lt 0\)のそれぞれの変域で調べてみましょう。
⑵ [mathjax]\(x \neq 0\)のとき，対応するxとyの値について，[mathjax]\(\dfrac{y}{x}\)の値をそれぞれ求めてみましょう。
⑶ [mathjax]\(\dfrac{y}{x}\)の値は何を表しているでしょうか。
変域を負の数まで広げても比例といえるのかな。
見方・考え方
どんな関係なら，比例しているといえるかな。
目標 ▷ 変域を負の数まで広げたときの比例について考えよう。
水そうに一定の割合で水を入れるとき，次のような関係がある。
[mathjax]\(\mathsf{(水位)}=\mathsf{(1分間当たりの水位の増加量)}\times\mathsf{(時間)}\)
したがって，【Q】 では，xとyの関係は，次の式で表すことができる。
[mathjax]\(y=2x\)
[mathjax]\(y=2x\)の式で，xとyは変数であるが，xの係数2は1分間当たりの水位の増加量を表し，xやyの値が変化しても変わらない一定の数である。このような数を 定数 という。
<1年p.137>
比例
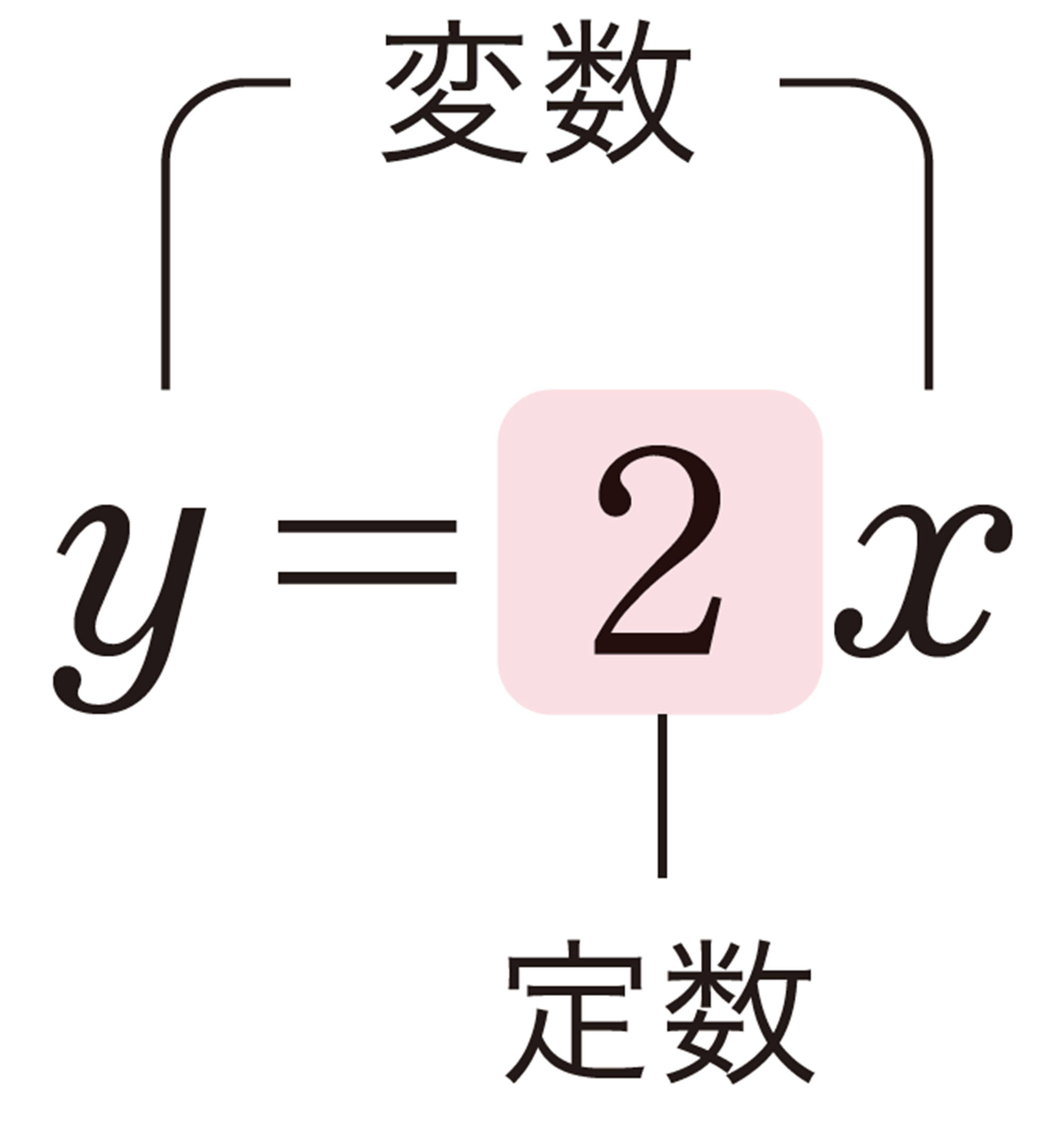
yがxの関数であり，次のような式で表されるとき，yはxに比例する という。
[mathjax]\(y=ax\)
ただし，aは0でない定数で，このaを 比例定数 という。
y がxに比例するとき，[mathjax]\(x \neq 0\)のときの商 は一定で，この値が比例定数aである。
注意 比例[mathjax]\(y=ax\)は関数であるから，関数[mathjax]\(y=ax\)ということもある。
これからは，式の形に着目して，どんな関数なのかを考えていこう。
例 １ 1 m 当たりの重さが20 g の針金x m の重さがy g であるとき，yをxの式で表すと，
[mathjax]\(y=20x\)
となる。したがって，yはxに比例し，比例定数は20である。
問 １ 132ページの【Q】の縦90 cmの長方形の窓をx cm 開けたとき，開けた部分の面積をy cm²とします。このとき，次の問いに答えなさい。
⑴ xとyの関係を，次の表にまとめなさい。
⑵ y をx の式で表しなさい。
⑶ y はx に比例するといえますか。
問 ２ 次の⑴ ～⑷について，yをxの式で表しなさい。また，yがxに比例するものはどれですか。比例しているものについては，比例定数をいいなさい。
⑴ 時速40 kmで走る自動車が，x時間に進む道のりはy kmである。
⑵ 1辺の長さがx cmのひし形のまわりの長さはy cmである。
⑶ 4 Lのジュースをx人で等分すると，1人当たりy Lである。
⑷ x人の5％はy人である。
<1年p.138>
Q Question
右の図のように，水がいっぱいに入った深さ20 cm の水そうから，1分間に2 cmずつ水位が減少するように水を抜いています。現在の水位を基準の0 cmとし，x分後の水位をy cm とします。
このとき，136ページの【Q】と比べながら，xとyがどのような関係にあるか調べてみましょう。
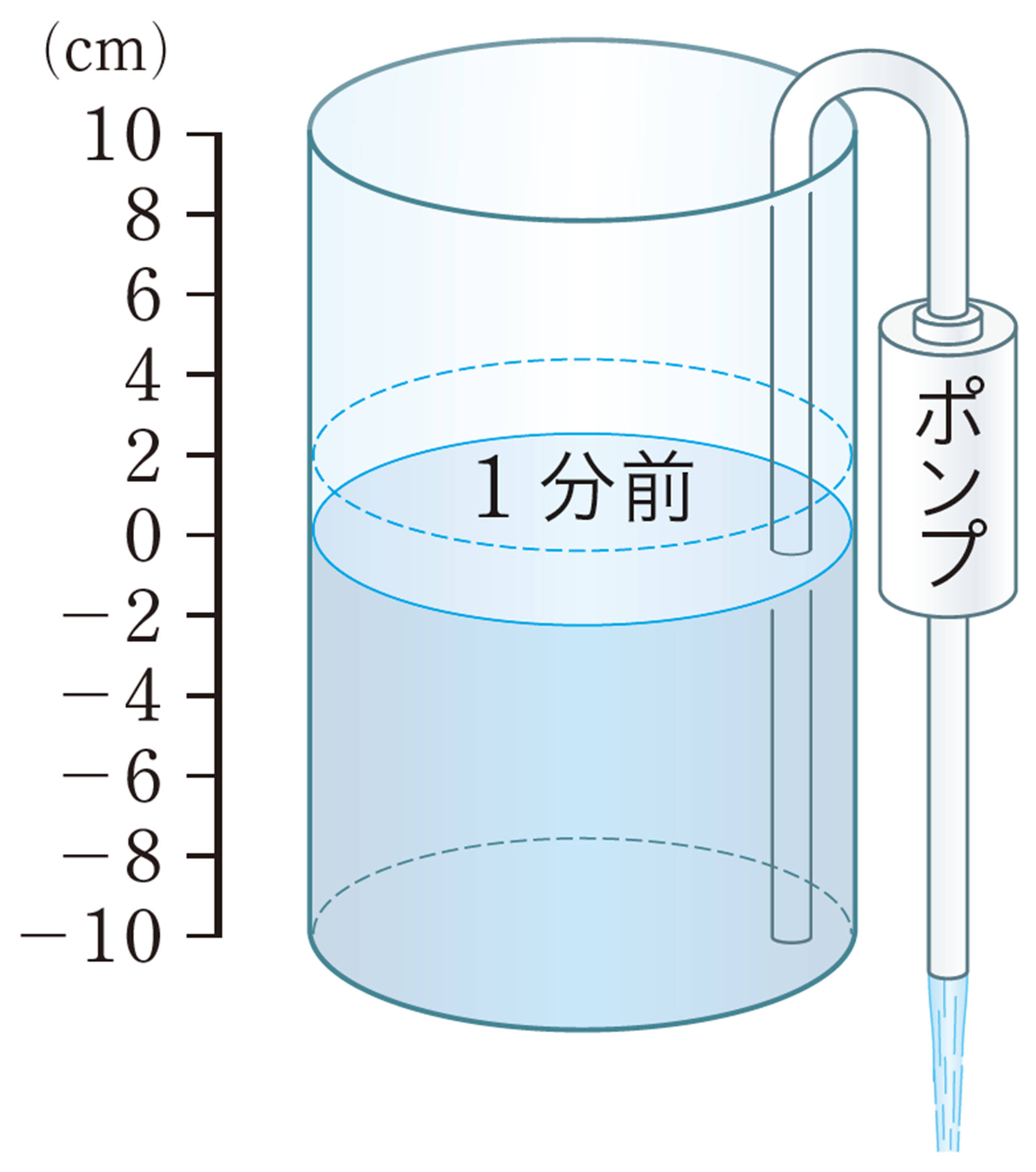
減っていくものも比例といっていいのかな。
減っていくときも，式に表せるのかな。
見方・考え方
水位が増えていくときと同じように考えられるかな。
問 ３ 【Q】について，次の問いに答えなさい。
⑴ xとyの関係を，次の表にまとめなさい。
⑵ yはxに比例するといえますか。その理由も説明しなさい。
⑶ xの値が増加すると，yの値はどうなりますか。
【Q】では，xとyの関係は，次の式で表すことができるので，yはxに比例するといえる。
[mathjax]\(y=-2x\)
このように，比例には，比例定数が負の数になる場合がある。比例定数が負の数のときは，xの値が増加すると，それに対応するyの値は減少する。
問 ４ 【Q】で，1分間に3 cm ずつ水位が減少するように水を抜くとき，yをxの式で表しなさい。
問 ５ 次の式で表すことができる関数のうち， yがxに比例するものはどれですか。また，そのときの比例定数をいいなさい。
㋐ [mathjax]\(y=8x\)
㋑ [mathjax]\(y=x+4\)
㋒ [mathjax]\(y=-10x\)
㋓ [mathjax]\(y=\dfrac{x}{4}\)
<1年p.139>
比例式の求め方
例 ２ yはxに比例し，[mathjax]\(x=2\)のとき[mathjax]\(y=-8\)です。yをxの式で表しなさい。また，[mathjax]\(x=-5\)のときのyの値を求めなさい。
解答
[mathjax]\(y\) は[mathjax]\(x\) に比例するから， 比例定数を[mathjax]\(a\) とすると，
[mathjax]\(\hspace{ 59pt }y=ax\)
[mathjax]\(x =2\) のとき[mathjax]\(y =-8\) であるから， これらを代入すると，
[mathjax] \(\hspace{ 51pt }-8=a\times 2\)
これを解くと，[mathjax]\( a=-4\)
したがって，[mathjax]\(\hspace{ 10pt } y=-4x\)
この式に [mathjax]\(x=-5\)を代入すると，
[mathjax]\(\hspace{ 59pt } y=-4\times (-5)\)
[mathjax]\(\hspace{ 67pt }=20\)
答 [mathjax] \(y=-4x\)，[mathjax] \( y=20\)
問 ６ yがxに比例するとき，次の ⑴，⑵のそれぞれの場合について，yをxの式で表しなさい。また，[mathjax] \(x=-4\)のときのyの値を求めなさい。
⑴ [mathjax] \(x=3\)のとき[mathjax] \(y=-15\)
⑵ [mathjax] \(x=-2\)のとき[mathjax] \(y=-5\)
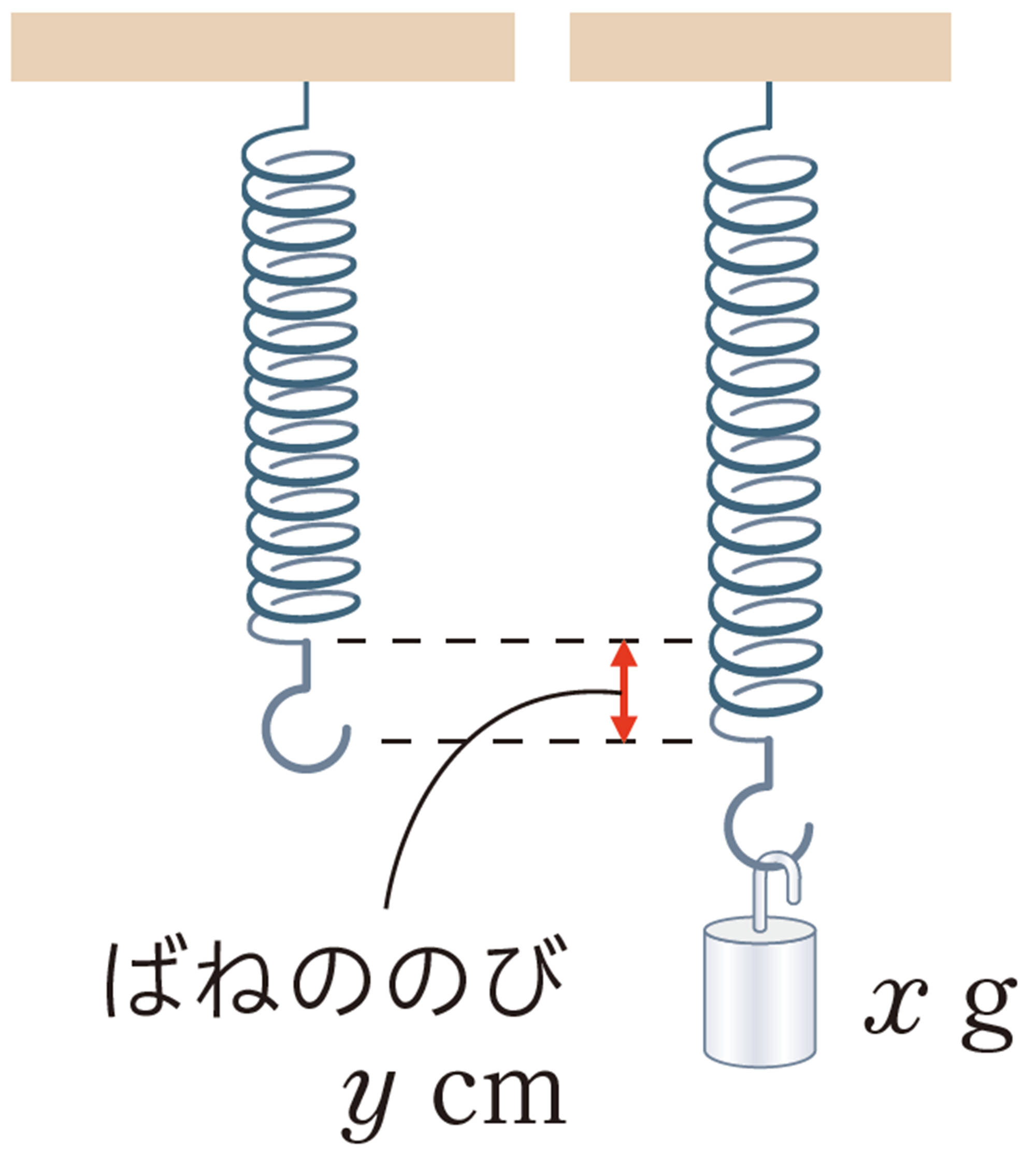
問 ７ 50 g のおもりをつるすと，4 cm のびるばねがあります。ばねののびはおもりの重さに比例します。このとき，次の問いに答えなさい。
⑴ このばねにx g のおもりをつるすとy cmのびるとして，yをxの式で表しなさい。
⑵ このばねに80 g のおもりをつるすと何cm のびますか。
⑶ xの変域が[mathjax] \(0 \leqq x \leqq 100\)のとき，yの変域を求めなさい。
どんなことがわかったかな
比例では，変域や比例定数を負の数まで広げて考えることができます。
次の課題へ！
変域や比例定数を負の数まで広げたとき，比例のグラフはどうなるのかな？
P.140
